Stepped Confocal Microlens Array Fabricated by Femtosecond Laser
Abstract
1. Introduction
2. Experimental
2.1. Materials and Methods
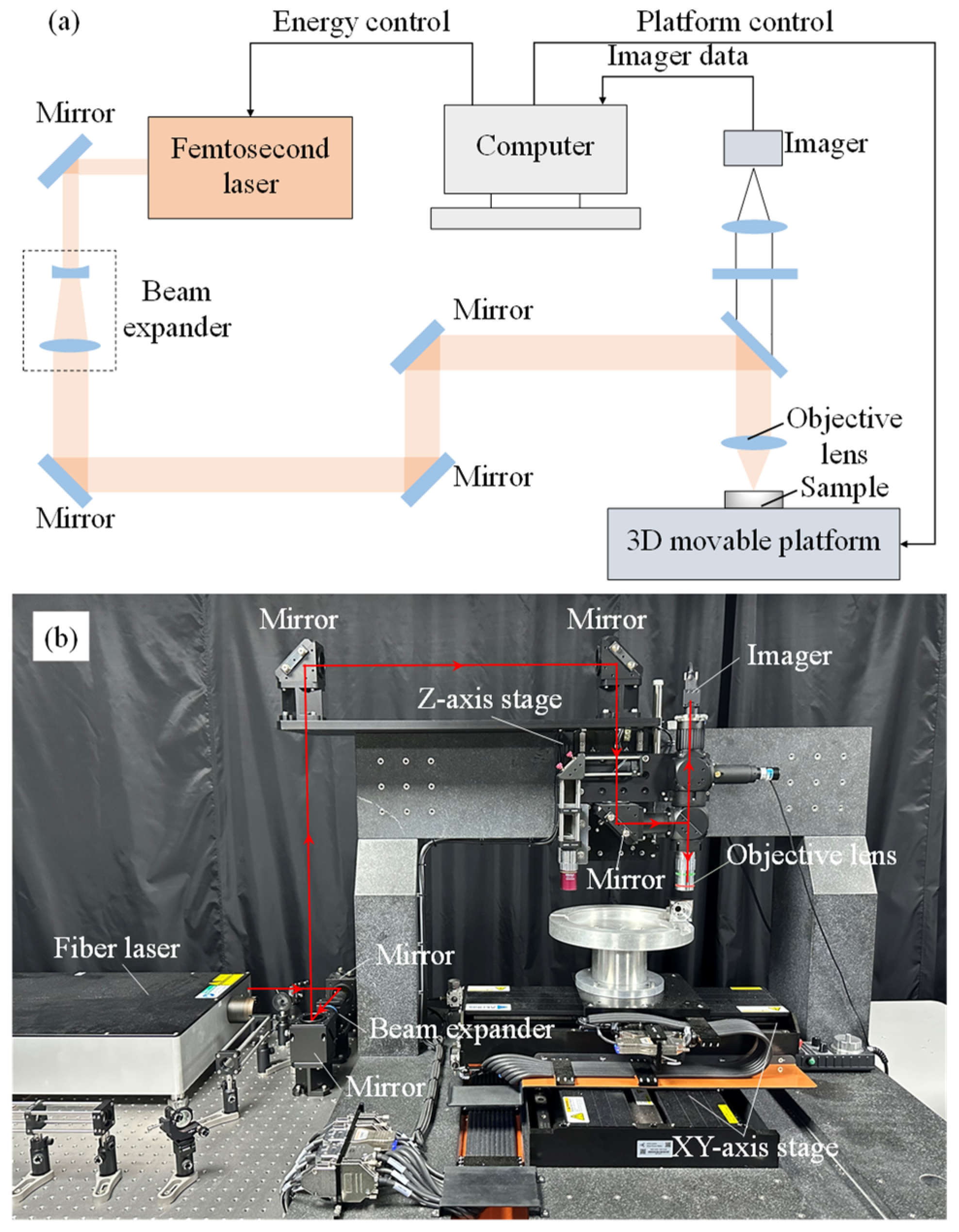
2.2. Experimental Setup
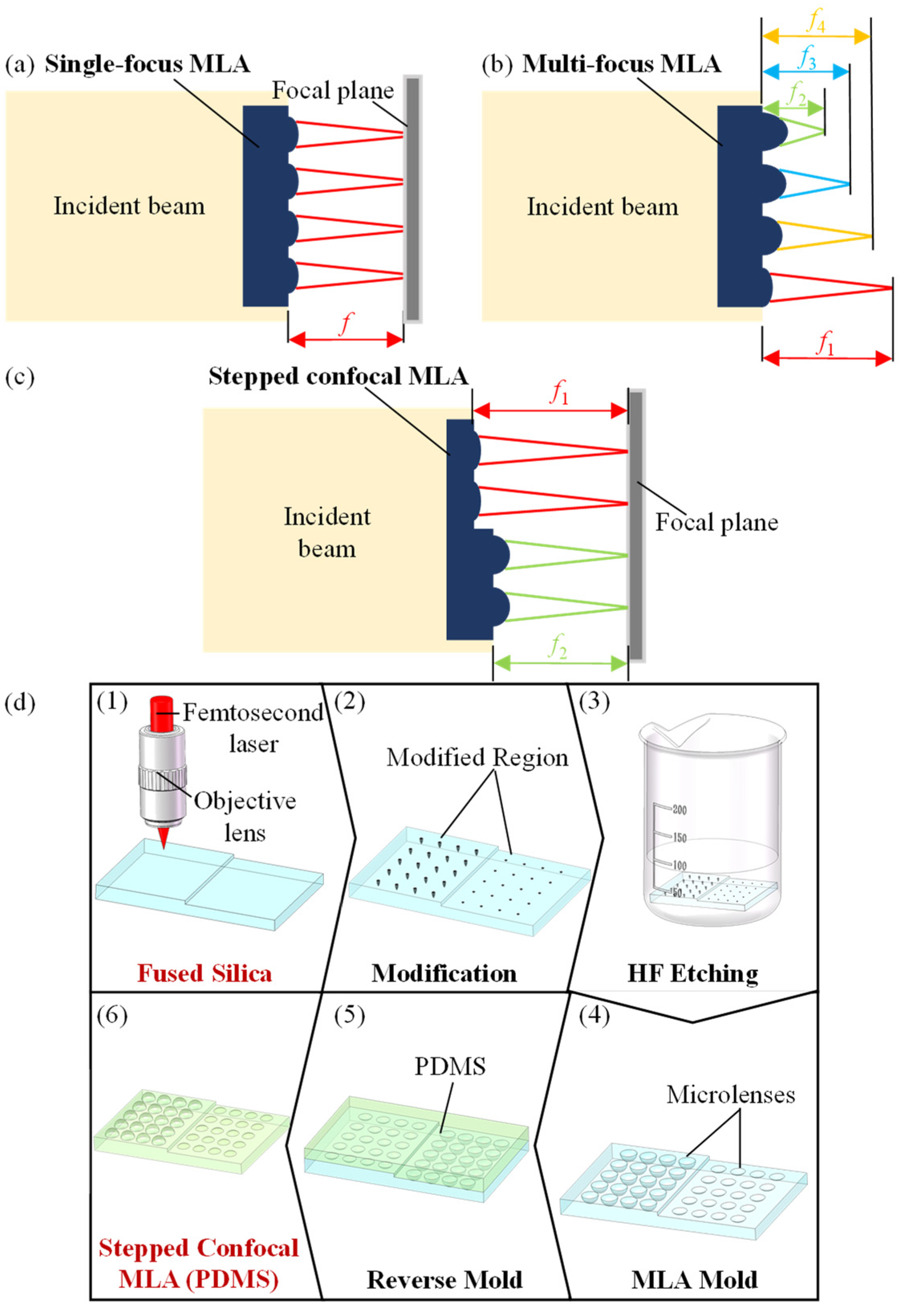
2.3. Fabrication of the SCMLA
2.4. Morphology Characterization
3. Results and Discussion
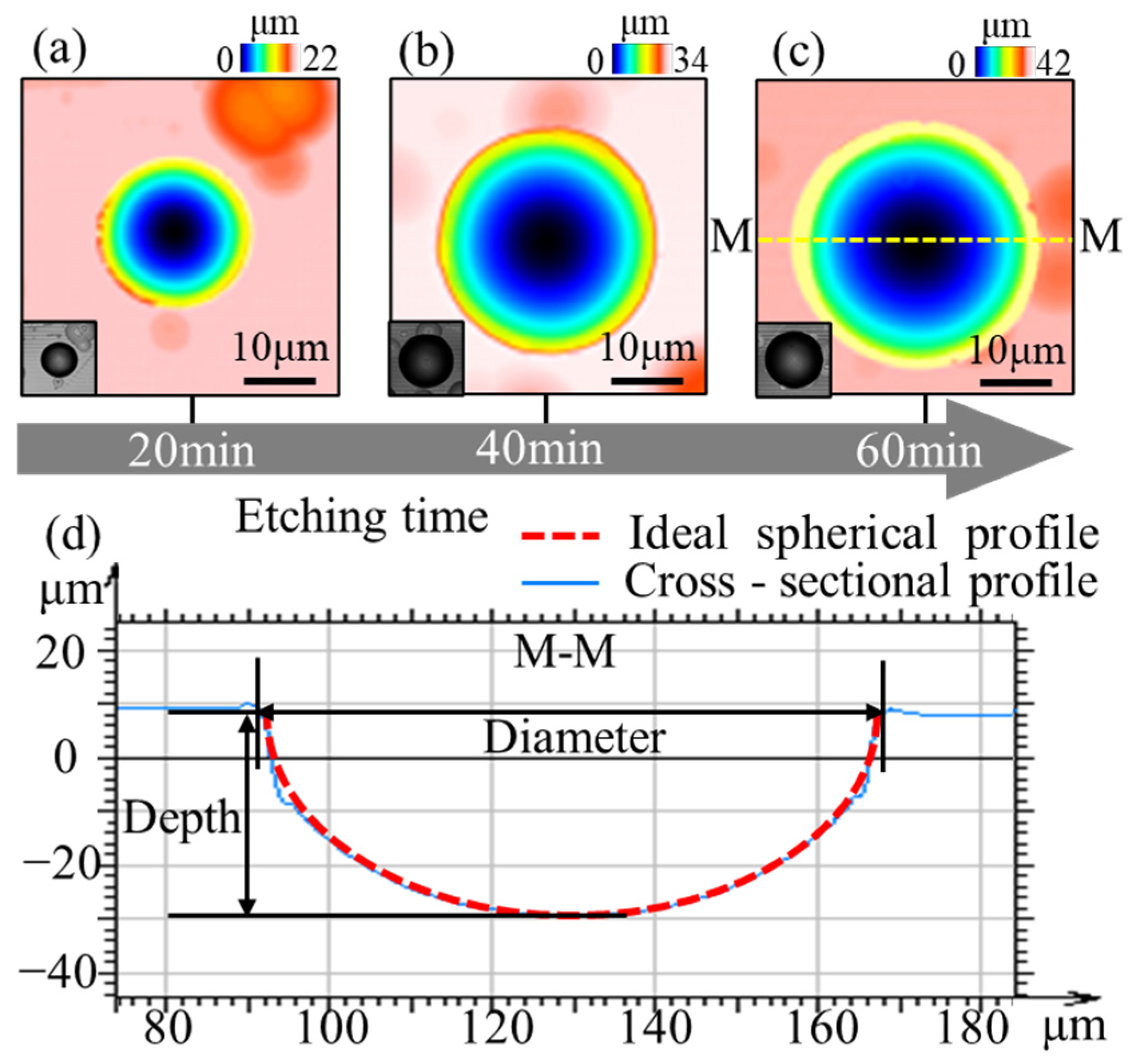
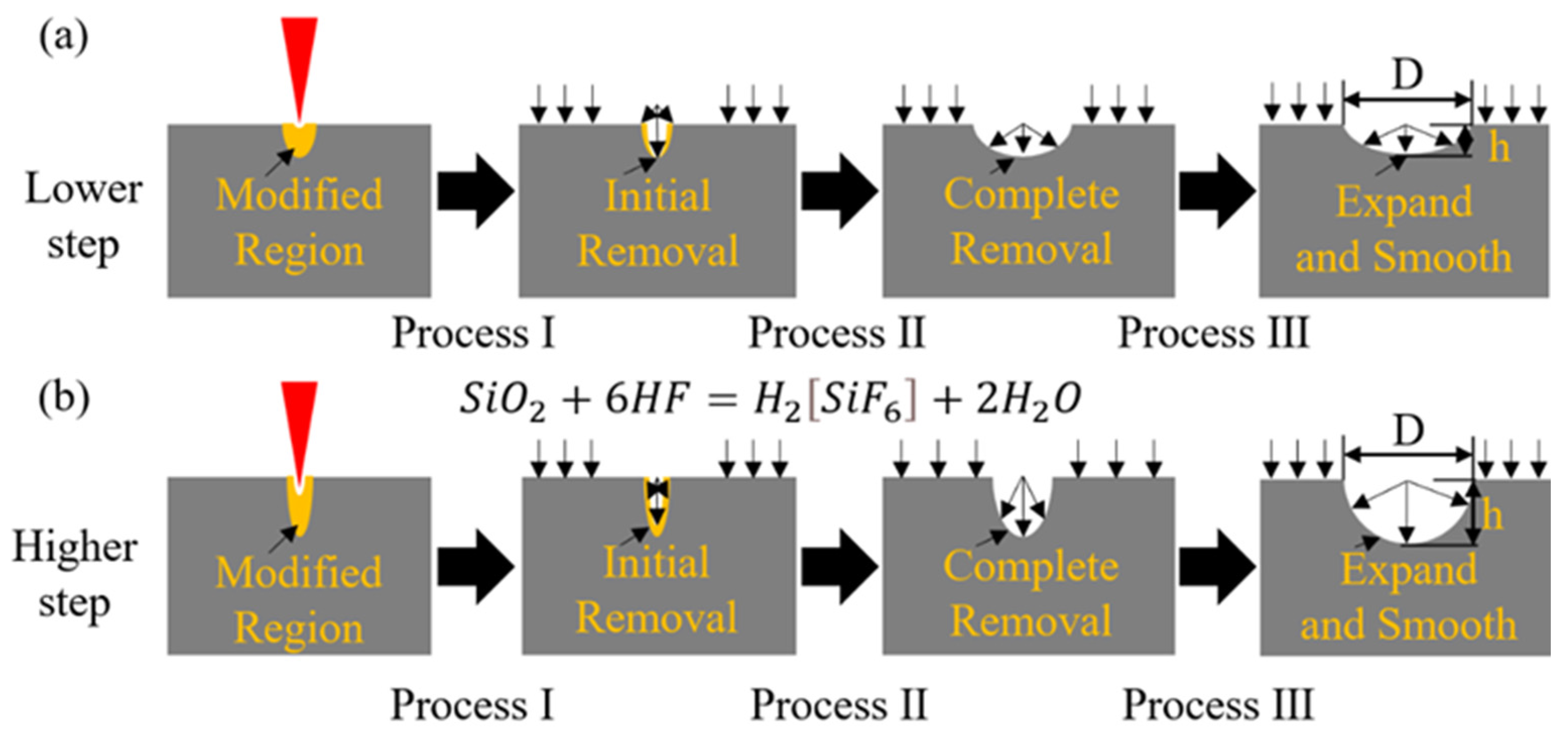
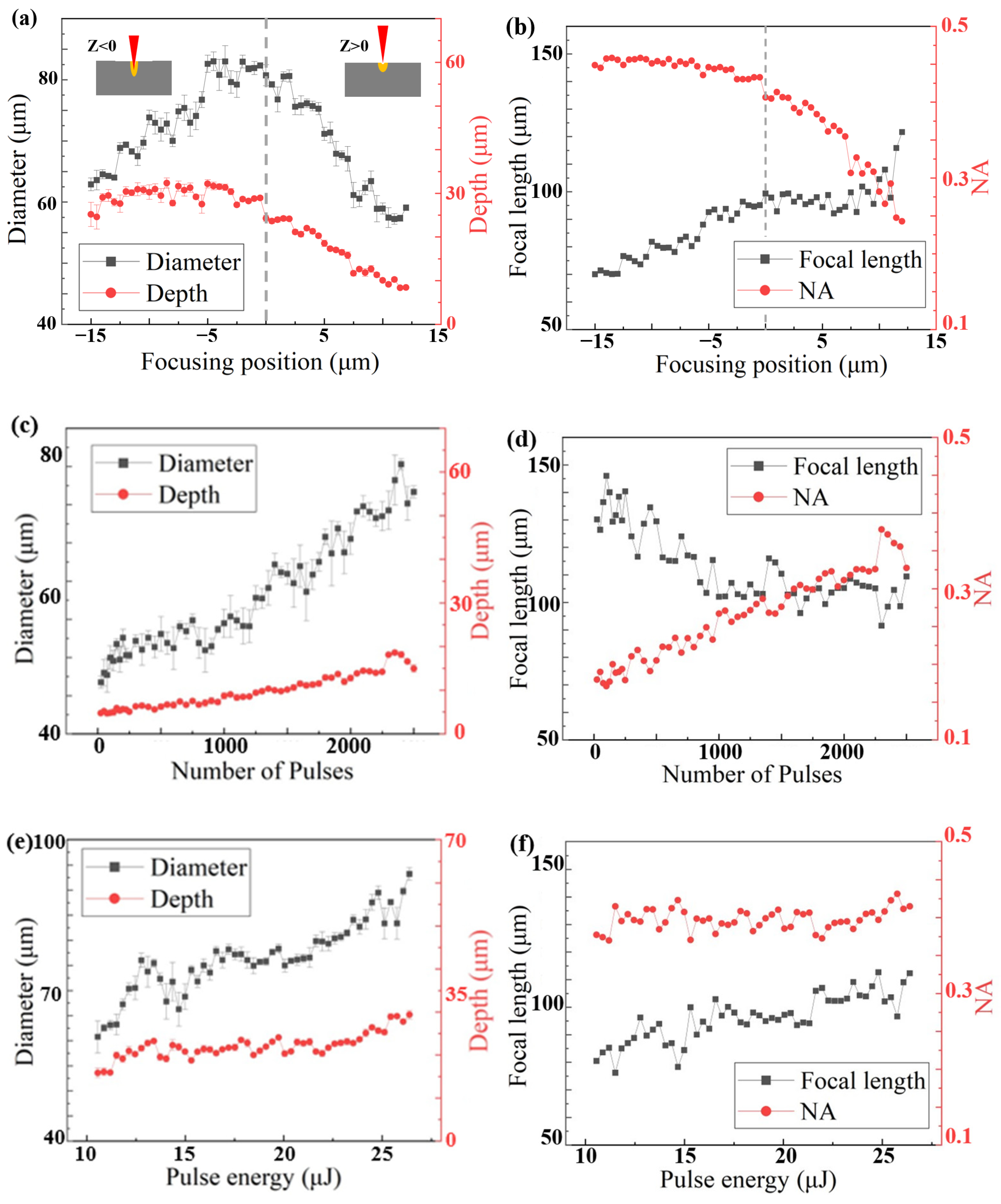
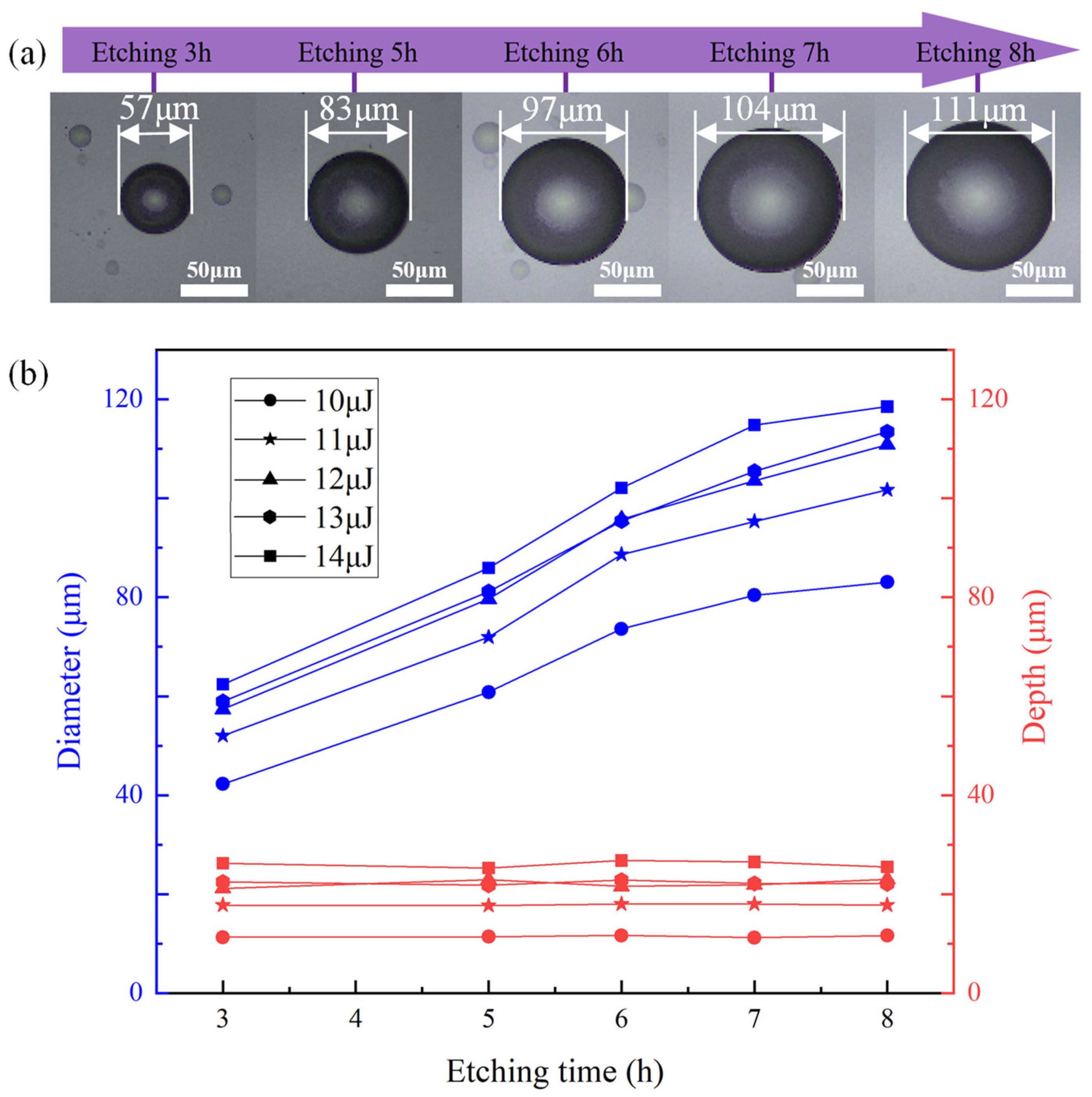
3.1. Morphology Control of Microlenses
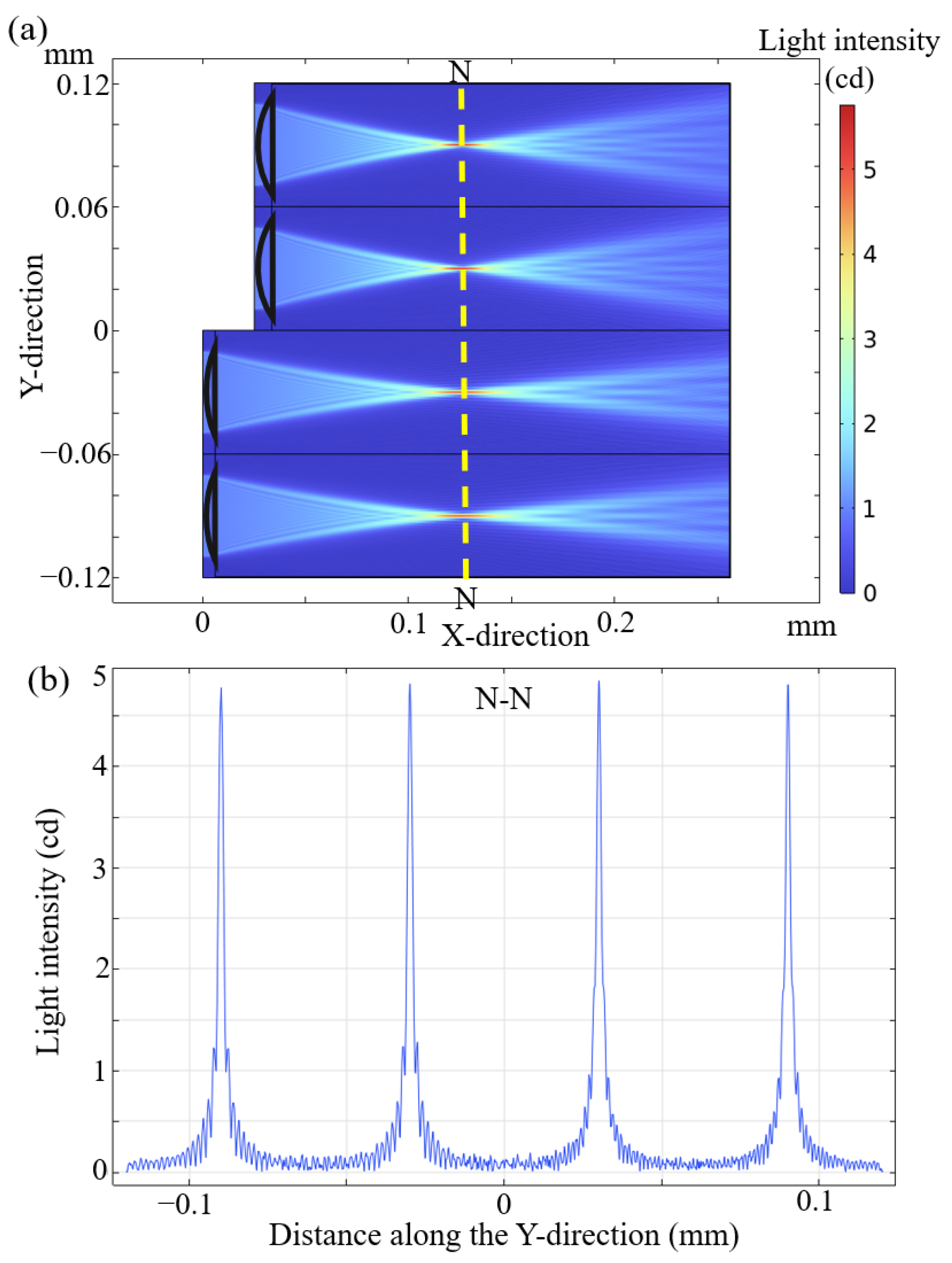
3.2. Simulation
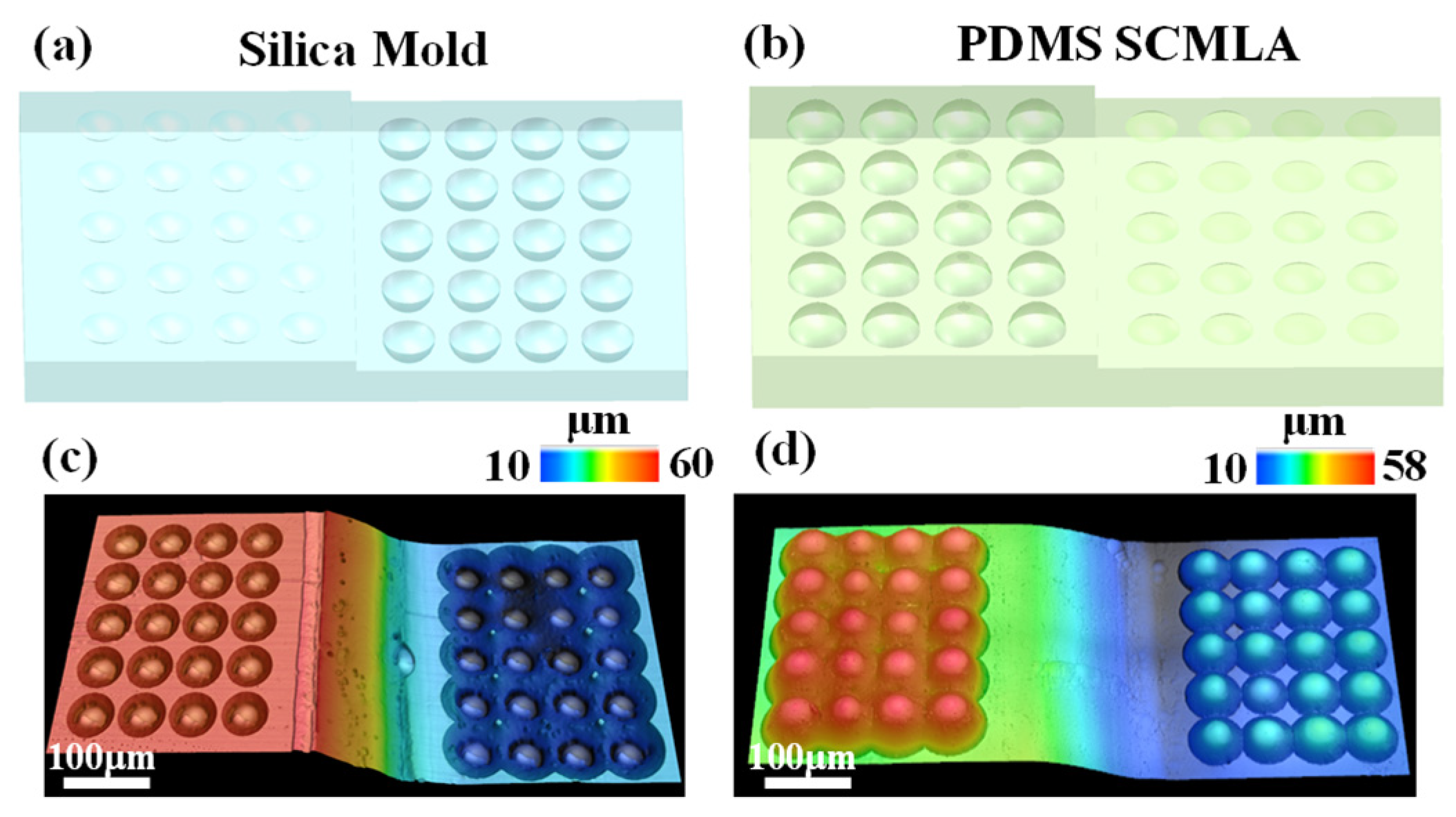
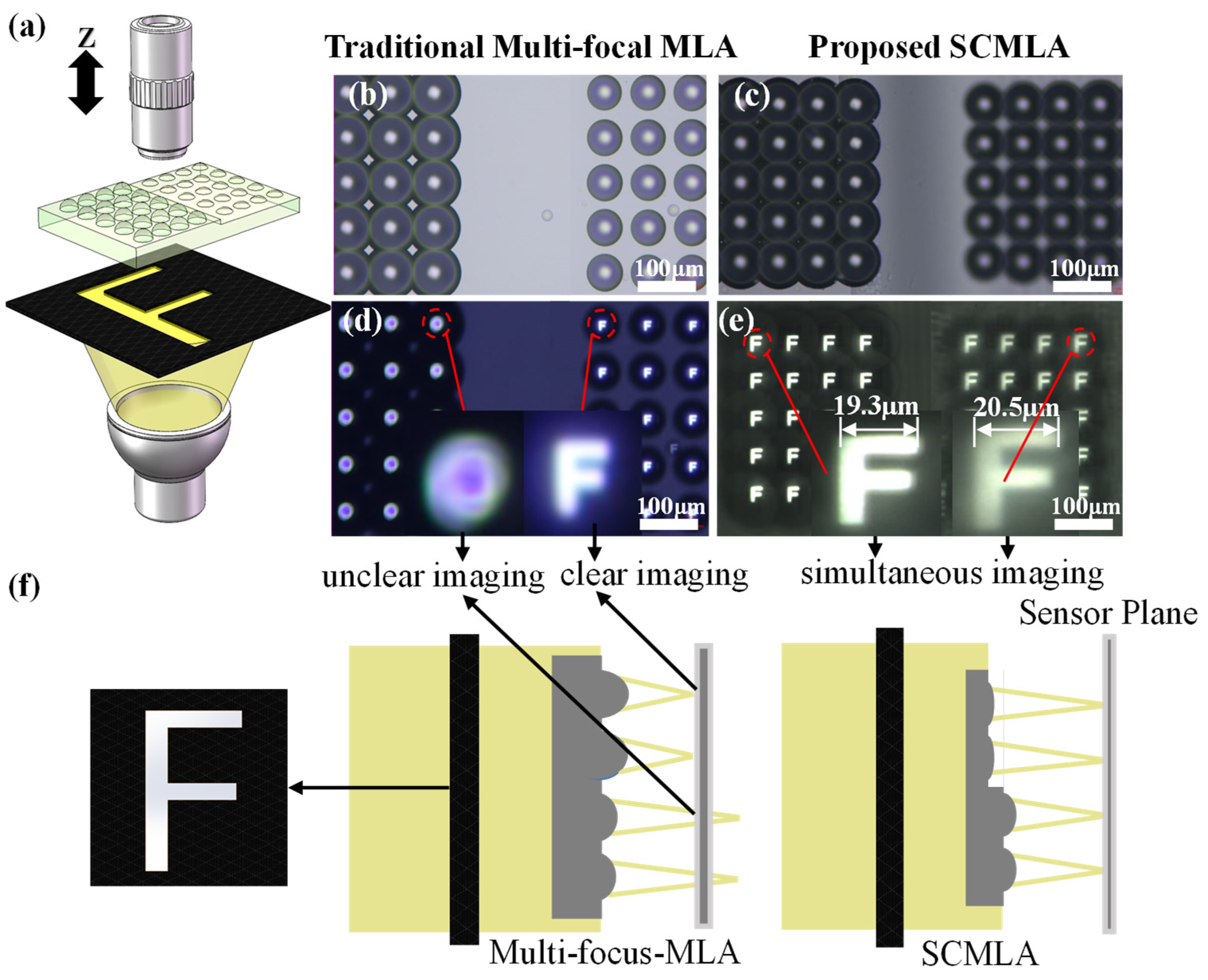
3.3. Fabrication and Imaging Characterization of SCMLA
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Suleski, T.; Kolste, R. Fabrication trends for free-space microoptics. J. Light. Technol. 2005, 23, 633–646. [Google Scholar] [CrossRef]
- Hsu, C.J.; Antony, M.; Huang, C.Y. Laser beam homogenization based on a multifocal liquid crystal microlens array. Opt. Lett. 2024, 49, 670–673. [Google Scholar] [CrossRef]
- Cao, J.-J.; Hou, Z.-S.; Tian, Z.-N.; Hua, J.-G.; Zhang, Y.-L.; Chen, Q.-D. Bioinspired Zoom Compound Eyes Enable Variable-Focus Imaging. ACS Appl. Mater. Interfaces 2020, 12, 10107–10117. [Google Scholar] [CrossRef]
- Liu, X.; Yang, S.; Yu, L.; Chen, Q.; Zhang, Y.; Sun, H. Rapid Engraving of Artificial Compound Eyes from Curved Sapphire Substrate. Adv. Funct. Mater. 2019, 29, 1900037. [Google Scholar] [CrossRef]
- Wu, D.; Wang, J.N.; Niu, L.G.; Zhang, X.L.; Wu, S.Z.; Chen, Q.D.; Lee, L.P.; Sun, H.B. Bioinspired Fabrication of High-Quality 3D Artificial Compound Eyes by Voxel—Modulation Femtosecond Laser Writing for Distortion-Free Wide-Field-of-View Imaging. Adv. Opt. Mater. 2014, 2, 751–758. [Google Scholar] [CrossRef]
- Yuan, C.; Kowsari, K.; Panjwani, S.; Chen, Z.; Wang, D.; Zhang, B.; Ng, C.J.-X.; Alvarado, P.V.Y.; Ge, Q. Ultrafast Three-Dimensional Printing of Optically Smooth Microlens Arrays by Oscillation-Assisted Digital Light Processing. ACS Appl. Mater. Interfaces 2019, 11, 40662–40668. [Google Scholar] [CrossRef]
- Ko, C.H.; Lin, C.H.; Tsai, B.C.; Shih, H.H.; Wu, C.T.; Chao, Y.L.; Chou, Y.K.; Chu, C.H.; Chiou, Y.T.; Chen, R. Development of microlens arrays for high-speed optical communi-cation. Proc. SPIE 2004, 5454, 121–128. [Google Scholar]
- Li, K.; Huang, X.; Chen, Q.; Xu, G.; Xie, Z.; Wan, Y.; Gong, F. Flexible fabrication of optical glass micro-lens array by using contactless hot embossing process. J. Manuf. Process. 2020, 57, 469–476. [Google Scholar] [CrossRef]
- Lim, J.; Gruner, P.; Konrad, M.; Baret, J.-C. Micro-optical lens array for fluorescence detection in droplet-based microfluidics. Lab A Chip 2013, 13, 1472–1475. [Google Scholar] [CrossRef]
- Nakamura, M.; Mano, I.; Taniguchi, J. Fabrication of micro-lens array with antireflection structure. Microelectron. Eng. 2019, 211, 29–36. [Google Scholar] [CrossRef]
- Ratcliff, J.; Supikov, A.; Alfaro, S.; Azuma, R. ThinVR: Heterogeneous microlens arrays for compact, 180 degree FOV VR near-eye displays. IEEE Trans. Vis. Comput. Graph. 2020, 26, 1981–1990. [Google Scholar] [CrossRef]
- Joo, K.-I.; Park, M.-K.; Park, H.; Lee, T.-H.; Kwon, K.-C.; Lim, Y.-T.; Erdenebat, M.-U.; Lee, H.; Lee, G.; Kim, N.; et al. Light-Field Camera for Fast Switching of Time-Sequential Two-Dimensional and Three-Dimensional Image Capturing at Video Rate. IEEE Trans. Ind. Electron. 2019, 67, 6975–6985. [Google Scholar] [CrossRef]
- Zhang, Y. Exploring the autoinhibition mechanism of the C-terminal guanine nucleotide exchange factor module of Trio through molecular dynamics simulations. Chem. Phys. Lett. 2019, 730, 100–104. [Google Scholar] [CrossRef]
- Wang, W.; Chen, G.; Weng, Y.; Weng, X.; Zhou, X.; Wu, C.; Guo, T.; Yan, Q.; Lin, Z.; Zhang, Y. Large-scale microlens arrays on flexible substrate with improved numerical aperture for curved integral imaging 3D display. Sci. Rep. 2020, 10, 11741. [Google Scholar] [CrossRef]
- Cha, Y.-G.; Na, J.-W.; Kim, H.-K.; Kwon, J.-M.; Huh, S.-H.; Jo, S.-U.; Kim, C.-H.; Kim, M.H.; Jeong, K.-H. Microlens array camera with variable apertures for single-shot high dynamic range (HDR) imaging. Opt. Express 2023, 31, 29589–29595. [Google Scholar] [CrossRef]
- Chang, S.; Rioux, M.; Grover, C. Range face recognition based on the phase Fourier transform. Opt. Commun. 2003, 222, 143–153. [Google Scholar] [CrossRef]
- Derrode, S.; Ghorbel, F. Robust and Efficient Fourier–Mellin Transform Approximations for Gray-Level Image Reconstruction and Complete Invariant Description. Comput. Vis. Image Underst. 2001, 83, 57–78. [Google Scholar] [CrossRef]
- Li, Y.; Mund, M.; Hoess, P.; Deschamps, J.; Matti, U.; Nijmeijer, B.; Sabinina, V.J.; Ellenberg, J.; Schoen, I.; Ries, J. Real-time 3D single-molecule localization using experimental point spread functions. Nat. Methods 2018, 15, 367–369. [Google Scholar] [CrossRef]
- Stallinga, S.; Rieger, B. Accuracy of the Gaussian Point Spread Function model in 2D localization microscopy. Opt. Express 2010, 18, 24461–24476. [Google Scholar] [CrossRef]
- Chao, G.L.L.X.A. Synthetic Aperture Imaging Lidar Tran-receiver Optical System Based on Microlens Array. Acta Photonica Sin. 2023, 52, 1111002. [Google Scholar]
- Huang, K.-Y.; Wang, C.-F.; Shih, D.-L.; Chang, K.-P.; Chang, Y.-P.; Liu, C.-N.; Cheng, W.-H. Scheme of flash LiDAR employing glass aspherical microlens array with large field of illumination for autonomous vehicles. Opt. Express 2024, 32, 35854–35870. [Google Scholar] [CrossRef]
- Arai, J.; Kawai, H.; Okano, F. Microlens arrays for integral imaging system. Appl. Opt. 2006, 45, 9066–9078. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Cheng, M.; Kong, D.; Ma, Z.; Liu, Y.J. Switchable liquid crystal lenticular microlens arrays based on photopolymerization-induced phase separation for 2D/3D autostereoscopic displays. Opt. Express 2023, 32, 625–638. [Google Scholar] [CrossRef] [PubMed]
- Ko, D.; Gu, B.; Ma, Y.; Jo, S.; Hyun, D.C.; Kim, C.S.; Oh, H.-J.; Kim, J. Characterization of optical manipulation using microlens arrays depending on the materials and sizes in organic photovoltaics. RSC Adv. 2021, 11, 9766–9774. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Liu, X.; Cheng, Q.; Liang, Z. Long-term photovoltaic performance of thin-film solar cells with diffractive microlens arrays on glass substrates. Results Phys. 2021, 21, 103841. [Google Scholar] [CrossRef]
- Luo, Y.; Wang, L.; Ding, Y.; Wei, H.; Hao, X.; Wang, D.; Dai, Y.; Shi, J. Direct fabrication of microlens arrays with high numerical aperture by ink-jetting on nanotextured surface. Appl. Surf. Sci. 2013, 279, 36–40. [Google Scholar] [CrossRef]
- Zang, Z.; Tang, X.; Liu, X.; Lei, X.; Chen, W. Fabrication of high quality and low cost microlenses on a glass substrate by direct printing technique. Appl. Opt. 2014, 53, 7868–7871. [Google Scholar] [CrossRef]
- Zhang, Q.; Schambach, M.; Jin, Q.; Heizmann, M.; Lemmer, U. Compact multispectral light field camera based on an inkjet-printed microlens array and color filter array. Opt. Express 2024, 32, 23510–23523. [Google Scholar] [CrossRef]
- Zhou, X.; Peng, Y.; Peng, R.; Zeng, X.; Zhang, Y.-A.; Guo, T. Fabrication of Large-Scale Microlens Arrays Based on Screen Printing for Integral Imaging 3D Display. ACS Appl. Mater. Interfaces 2016, 8, 24248–24255. [Google Scholar] [CrossRef]
- Yabu, H.; Shimomura, M. Simple Fabrication of Micro Lens Arrays. Langmuir 2005, 21, 1709–1711. [Google Scholar] [CrossRef]
- Xiao, G.; Zhang, X.; Lou, F.; Lei, L.; Cheng, X. Wide-angle vertical coupling gratings enabled by nano-imprinted microlens array. In Proceedings of the 2024 Optical Fiber Communications Conference and Exhibition (OFC), San Diego, CA, USA, 24–28 March 2024; p. W2B.9. [Google Scholar]
- Wang, M.; Yu, W.; Wang, T.; Han, X.; Gu, E.; Li, X. A novel thermal reflow method for the fabrication of microlenses with an ultrahigh focal number. RSC Adv. 2015, 5, 35311–35316. [Google Scholar] [CrossRef]
- Huang, S.; Li, M.; Shen, L.; Qiu, J.; Zhou, Y. Flexible fabrication of biomimetic compound eye array via two-step thermal reflow of simply pre-modeled hierarchic microstructures. Opt. Commun. 2017, 393, 213–218. [Google Scholar] [CrossRef]
- Liu, Y.; Li, X.; Wang, Z.; Qin, B.; Zhou, S.; Huang, J.; Yao, Z. Morphology adjustable microlens array fabricated by single spatially modulated femtosecond pulse. Nanophotonics 2021, 11, 571–581. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.Y.; Chiang, T.H.; Lai, N.D.; Do, D.B.; Hsu, C.C. Fabrication of microlens arrays based on the mass transport effect of SU-8 photoresist using a multiexposure two-beam interference technique. Appl. Opt. 2009, 48, 2473–2479. [Google Scholar] [CrossRef]
- He, Z.; Lee, Y.-H.; Chanda, D.; Wu, S.-T. Adaptive liquid crystal microlens array enabled by two-photon polymerization. Opt. Express 2018, 26, 21184–21193. [Google Scholar] [CrossRef]
- Wang, B.-X.; Zheng, J.-X.; Qi, J.-Y.; Guo, M.-R.; Gao, B.-R.; Liu, X.-Q. Integration of Multifocal Microlens Array on Silicon Microcantilever via Femtosecond-Laser-Assisted Etching Technology. Micromachines 2022, 13, 218. [Google Scholar] [CrossRef]
- Liu, Y.; Qiao, Z.; Qu, D.; Wu, Y.; Xue, J.; Li, D.; Wang, B. Experimental Investigation on Form Error for Slow Tool Servo Diamond Turning of Micro Lens Arrays on the Roller Mold. Materials 2018, 11, 1816. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Z.; Chen, J.; Wang, Z.; Zhu, L. Fabrication of a microlens array featuring a high aspect ratio with a swinging diamond tool. J. Manuf. Process. 2022, 75, 485–496. [Google Scholar] [CrossRef]
- Yang, T.; Li, M.; Yang, Q.; Lu, Y.; Cheng, Y.; Zhang, C.; Du, B.; Hou, X.; Chen, F. Femtosecond Laser Fabrication of Submillimeter Microlens Arrays with Tunable Numerical Apertures. Micromachines 2022, 13, 1297. [Google Scholar] [CrossRef]
- Li, M.; Yang, Q.; Bian, H.; Yang, T.; Hou, X.; Chen, F. Microlens arrays enable variable-focus imaging. Opt. Laser Technol. 2022, 153, 108260. [Google Scholar] [CrossRef]
- Deng, C.; Kim, H.; Ki, H. Fabrication of a compound infrared microlens array with ultrashort focal length using femtosecond laser-assisted wet etching and dual-beam pulsed laser deposition. Opt. Express 2019, 27, 28679–28691. [Google Scholar] [CrossRef] [PubMed]
- Pan, A.; Chen, T.; Li, C.; Hou, X. Parallel fabrication of silicon concave microlens array by femtosecond laser irradiation and mixed acid etching. Chin. Opt. Lett. 2016, 14, 052201. [Google Scholar] [CrossRef]
- Zhang, F.; Yang, Q.; Bian, H.; Li, M.; Hou, X.; Chen, F. Fabrication of Chalcogenide Glass Based Hexagonal Gapless Microlens Arrays via Combining Femtosecond Laser Assist Chemical Etching and Precision Glass Molding Processes. Materials 2020, 13, 3490. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Yang, Q.; Bian, H.; Wang, S.; Li, M.; Hou, X.; Chen, F. Fabrication of a Chalcogenide Glass Microlens Array for Infrared Laser Beam Homoge-nization. Materials 2021, 14, 5952. [Google Scholar] [CrossRef]
- Bian, H.; Wei, Y.; Yang, Q.; Chen, F.; Zhang, F.; Du, G.; Yong, J.; Hou, X. Direct fabrication of compound-eye microlens array on curved surfaces by a facile femtosecond laser enhanced wet etching process. Appl. Phys. Lett. 2016, 109, 221109. [Google Scholar] [CrossRef]
- Zhou, W.; Li, R.; Li, M.; Tao, P.; Wang, X.; Dai, S.; Song, B.; Zhang, W.; Lin, C.; Shen, X.; et al. Fabrication of microlens array on chalcogenide glass by wet etching-assisted femtosecond laser direct writing. Ceram. Int. 2022, 48, 18983–18988. [Google Scholar] [CrossRef]
- Tian, Z.-N.; Yao, W.-G.; Xu, J.-J.; Yu, Y.-H.; Chen, Q.-D.; Sun, H.-B. Focal varying microlens array. Opt. Lett. 2015, 40, 4222–4225. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wu, H.; Lin, Z.; Zhang, H. Stepped Confocal Microlens Array Fabricated by Femtosecond Laser. Photonics 2025, 12, 494. https://doi.org/10.3390/photonics12050494
Wu J, Wu H, Lin Z, Zhang H. Stepped Confocal Microlens Array Fabricated by Femtosecond Laser. Photonics. 2025; 12(5):494. https://doi.org/10.3390/photonics12050494
Chicago/Turabian StyleWu, Jinchi, Hao Wu, Zheli Lin, and Honghao Zhang. 2025. "Stepped Confocal Microlens Array Fabricated by Femtosecond Laser" Photonics 12, no. 5: 494. https://doi.org/10.3390/photonics12050494
APA StyleWu, J., Wu, H., Lin, Z., & Zhang, H. (2025). Stepped Confocal Microlens Array Fabricated by Femtosecond Laser. Photonics, 12(5), 494. https://doi.org/10.3390/photonics12050494




