Combining Kronecker-Basis-Representation Tensor Decomposition and Total Variational Constraint for Spectral Computed Tomography Reconstruction
Abstract
1. Introduction
2. Fundamental Theory Methods
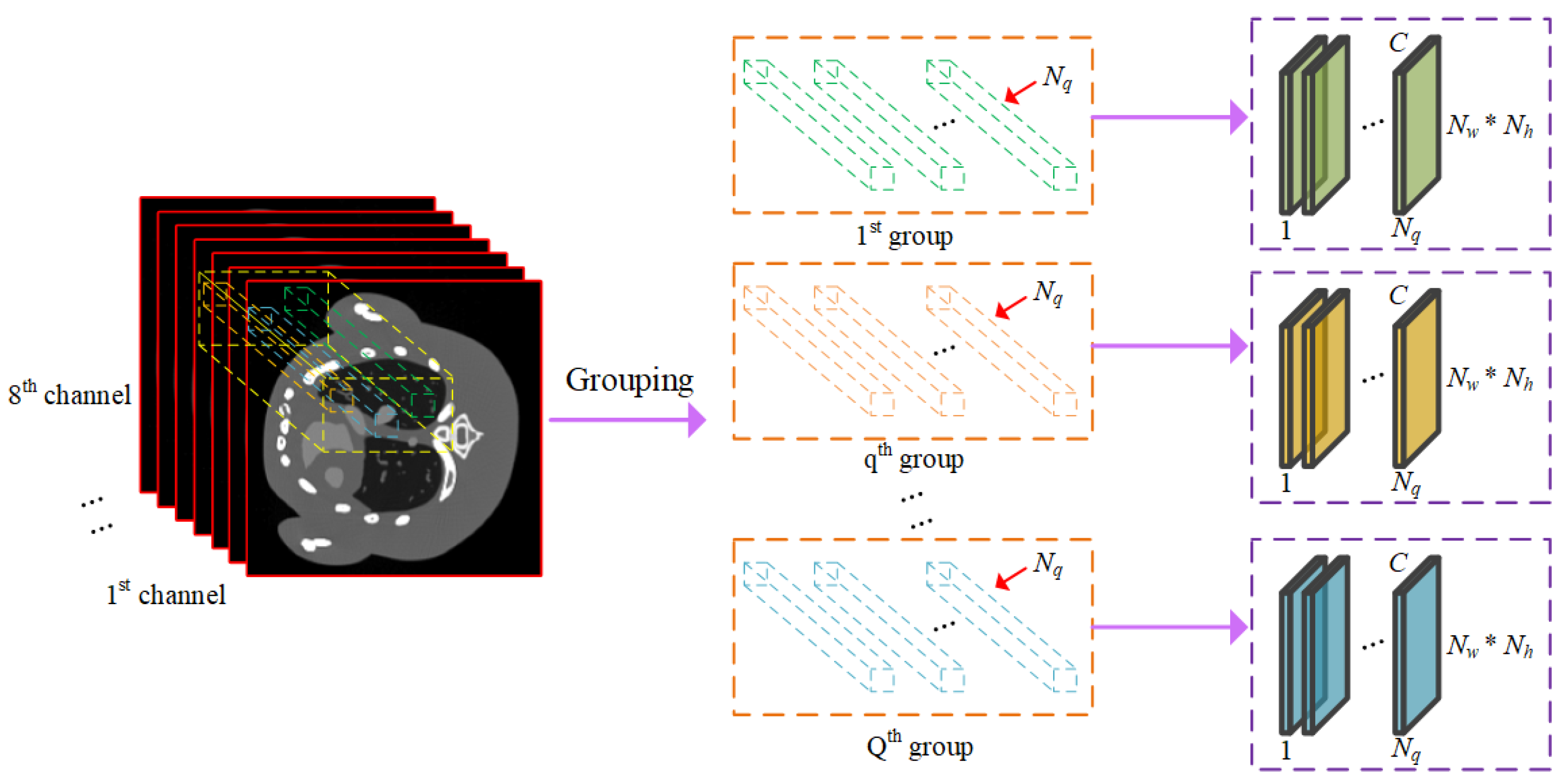
2.1. KBR Tensor Decomposition
2.2. TV Regularization Term
3. Methods
3.1. Mathematical Model
3.2. Solution
| Algorithm 1: KBR-TV Algorithm |
| Input:, parameters α, α1, α2, λ, λ1, δ, θ. Initialization:←0; ←0; ←0; ←HOSVD of ; n = 0 while not satisfy the convergence criteria do Perform the projection data normalization; Update the tensor image through Equation (16); Construct the tensor cube from (q = 1,…, Q); Update using Equation (26); Update using Equation (30); Update using Equation (34); Update using Equation (36); Update using Equation (37); Update , using Equations (17) and (18); Update by minimizing Equation (39); Non-negativity constraints are applied to the tensor image ; end while Output: The final reconstructed spectral CT image |
4. Results
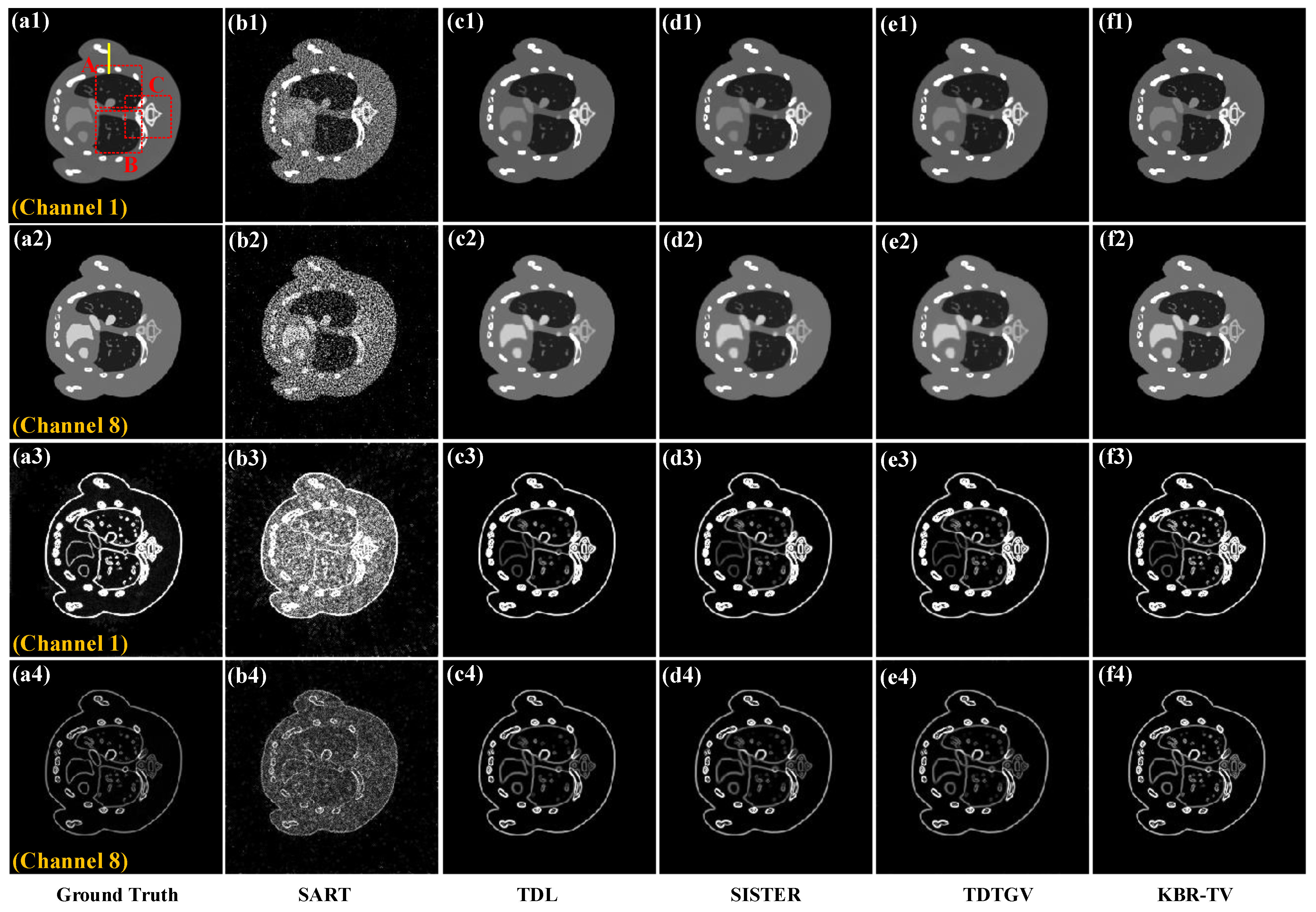
4.1. Numerical Simulation Study
4.2. Actual Clinical Mouse Study
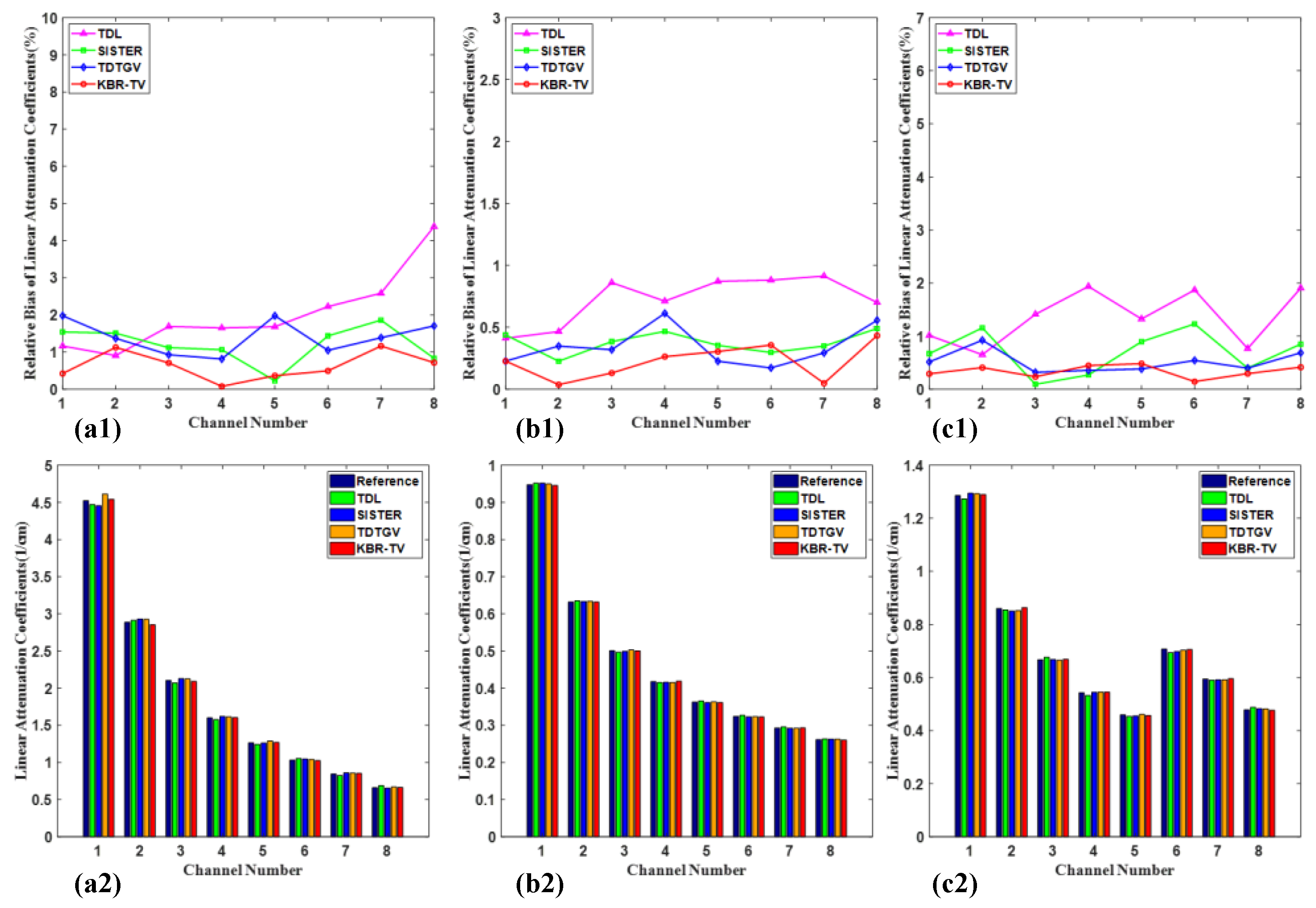
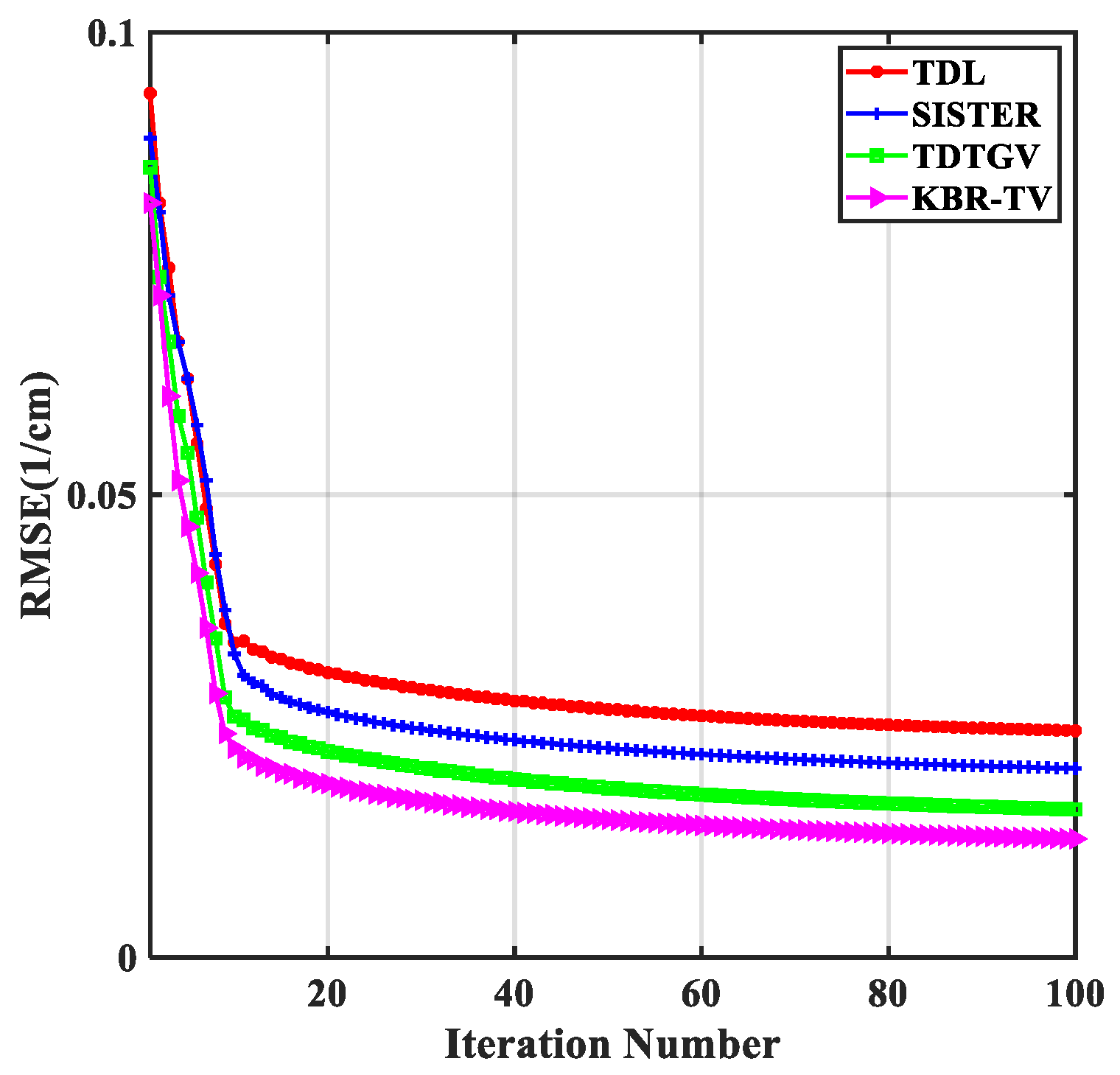
4.3. Parameter Analysis
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, G.; Yu, H.; De Man, B. An outlook on X-ray CT research and development. Med. Phys. 2008, 35, 1051–1064. [Google Scholar] [CrossRef]
- Nakano, M.; Haga, A.; Kotoku, J.; Magome, T.; Masutani, Y.; Hanaoka, S.; Kida, S.; Nakagawa, K. Cone-beam CT reconstruction for non-periodic organ motion using time-ordered chain graph model. Radiat. Oncol. 2017, 12, 145. [Google Scholar] [CrossRef]
- Brooks, R.A.; Di Chiro, G. Beam hardening in X-ray reconstructive tomography. Phys. Med. Biol. 1976, 21, 390–398. [Google Scholar] [CrossRef]
- Zhao, W.; Li, D.; Niu, K.; Qin, W.; Peng, H.; Niu, T. Robust Beam Hardening Artifacts Reduction for Computed Tomography Using Spectrum Modeling. IEEE Trans. Comput. Imaging 2018, 5, 333–342. [Google Scholar] [CrossRef]
- Kim, Y.; Kudo, H. Nonlocal Total Variation Using the First and Second Order Derivatives and Its Application to CT image Reconstruction. Sensors 2020, 20, 3494–3511. [Google Scholar] [CrossRef]
- Nikzad, S.; Pourkaveh, M.; Vesal, N.J.; Gharekhanloo, F. Cumulative radiation dose and cancer risk estimation in common diagnostic radiology procedures. Iran. J. Radiol. 2018, 15, e60955. [Google Scholar] [CrossRef]
- Greffier, J.; Frandon, J. Spectral photon-counting CT system: Toward improved image quality performance in conventional and spectral CT imaging. Diagn. Interv. Imaging 2021, 102, 271–272. [Google Scholar] [CrossRef]
- Xi, Y.; Chen, Y.; Tang, R.; Sun, J.; Zhao, J. United Iterative Reconstruction for Spectral Computed Tomography. IEEE Trans. Med. Imaging 2015, 34, 769–778. [Google Scholar] [CrossRef]
- Xu, Q.; Yu, H.; Bennett, J.; He, P.; Zainon, R.; Doesburg, R.; Opie, A.; Walsh, M.; Shen, H.; Butler, A.; et al. Image Reconstruction for Hybrid True-Color Micro-CT. IEEE Trans. Biomed. Eng. 2012, 59, 1711–1719. [Google Scholar] [CrossRef]
- Xu, Q.; Yu, H.Y.; Mou, X.Q.; Zhang, L.; Hsieh, J.; Wang, G. Low-dose X-ray CT reconstruction via dictionary learning. IEEE Trans. Med. Imaging 2012, 31, 1682–1697. [Google Scholar] [CrossRef]
- Xu, Q.; Liu, H.; Yu, H.; Wang, G.; Xing, L. Dictionary Learning Based Reconstruction with Low-Rank Constraint for Low-Dose Spectral CT. Med. Phys. 2016, 43, 3701. [Google Scholar] [CrossRef]
- Zhao, B.; Ding, H.; Lu, Y.; Wang, G.; Zhao, J.; Molloi, S. Dual-dictionary learning-based iterative image reconstruction for spectral computed tomography application. Phys. Med. Biol. 2012, 57, 8217. [Google Scholar] [CrossRef]
- Zhao, B.; Gao, H.; Ding, H.; Molloi, S. Tight-frame based iterative image reconstruction for spectral breast CT. Med. Phys. 2013, 40, 031905. [Google Scholar] [CrossRef]
- Zeng, D.; Gao, Y.; Huang, L.; Bian, Z.; Zhang, H.; Lu, L.; Ma, J. Penalized weighted least-squares approach for multienergy computed tomography image reconstruction via structure tensor total variation regularization. Comput. Med. Imaging Graph. 2016, 53, 19–29. [Google Scholar] [CrossRef]
- Wang, Q.; Salehjahromi, M.; Yu, H. Refined Locally Linear Transform-Based Spectral-Domain Gradient Sparsity and Its Applications in Spectral CT Reconstruction. IEEE Access 2021, 9, 58537–58548. [Google Scholar] [CrossRef]
- Gao, H.; Yu, H.; Osher, S.; Wang, G. Multi-energy CT based on a prior rank, intensity and sparsity model (PRISM). INVERSE Probl. 2011, 27, 115012. [Google Scholar] [CrossRef]
- Li, L.; Chen, Z.; Wang, G.; Chu, J.; Gao, H. A tensor PRISM algorithm for multi-energy CT reconstruction and comparative studies. J. Xray Sci. Technol. 2014, 22, 147–163. [Google Scholar] [CrossRef]
- Rigie, D.S.; La Riviere, P.J. Joint reconstruction of multi-channel, spectral CT data via constrained total nuclear variation minimization. Phys. Med. Biol. 2015, 60, 1741–1762. [Google Scholar] [CrossRef]
- He, Y.; Zeng, L.; Xu, Q.; Wang, Z.; Yu, H.; Shen, Z.; Yang, Z.; Zhou, R. Spectral CT reconstruction via low-rank representation and structure preserving regularization. Phys. Med. Biol. 2023, 68, 2996–3007. [Google Scholar] [CrossRef]
- Zhang, Y.; Mou, X.; Wang, G.; Yu, H. Tensor-Based Dictionary Learning for Spectral CT Reconstruction. IEEE Trans. Med. Imaging 2017, 36, 142–154. [Google Scholar] [CrossRef]
- Wu, W.; Zhang, Y.; Wang, Q.; Liu, F.; Chen, P.; Yu, H. Low-dose spectral CT reconstruction using image gradient ℓ0–norm and tensor dictionary. Appl. Math. Model. 2018, 63, 538–557. [Google Scholar] [CrossRef]
- Li, X.; Sun, X.; Zhang, Y.; Pan, J.; Chen, P. Tensor Dictionary Learning with an Enhanced Sparsity Constraint for Sparse-View Spectral CT Reconstruction. Photonics 2022, 9, 35. [Google Scholar] [CrossRef]
- Wang, M.; Hong, D.; Han, Z.; Li, J.; Yao, J.; Gao, L.; Zhang, B.; Chanussot, J. Tensor Decompositions for Hyperspectral Data Processing in Remote Sensing: A comprehensive review. IEEE Geosci. Remote Sens. Mag. 2023, 11, 26–72. [Google Scholar] [CrossRef]
- Lin, J.; Huang, T.-Z.; Zhao, X.-L.; Ji, T.-Y.; Zhao, Q. Tensor Robust Kernel PCA for Multidimensional Data. IEEE Trans. Neural Netw. Learn. Syst. 2024, 36, 2662–2674. [Google Scholar] [CrossRef]
- Osipov, D.; Chow, J.H. PMU Missing Data Recovery Using Tensor Decomposition. IEEE Trans. Power Syst. 2020, 35, 4554–4563. [Google Scholar] [CrossRef]
- Zhang, S.; Guo, X.; Xu, X.; Li, L.; Chang, C.-C. A video watermark algorithm based on tensor decomposition. Math. Biosci. Eng. 2019, 16, 3435–3449. [Google Scholar] [CrossRef]
- Peng, Y.; Meng, D.; Xu, Z.; Gao, C.; Yang, Y.; Zhang, B. Decomposable Nonlocal Tensor Dictionary Learning for Multispectral Image Denoising. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 2949–2956. [Google Scholar]
- Zhang, Y.; Salehjahromi, M.; Yu, H. Tensor decomposition and non-local means based spectral CT image denoising. J. Xray Sci. Technol. 2019, 27, 397–416. [Google Scholar] [CrossRef]
- Hu, D.; Wu, W.; Xu, M.; Zhang, Y.; Liu, J.; Ge, R.J.; Chen, Y.; Luo, L.; Coatrieux, G. SISTER: Spectral-Image Similarity-Based Tensor with Enhanced-Sparsity Reconstruction for Sparse-View Multi-Energy CT. IEEE Trans. Comput. Imaging 2020, 6, 477–490. [Google Scholar] [CrossRef]
- Wu, W.; Yu, H.; Liu, F.; Zhang, J.; Vardhanabhuti, V. Spectral CT reconstruction via Spectral-Image Tensor and Bidirectional Image-gradient minimization. Comput. Biol. Med. 2022, 151, 106080. [Google Scholar] [CrossRef]
- Wang, S.; Wu, W.; Cai, A.; Xu, Y.; Vardhanabhuti, V.; Liu, F.; Yu, H. Image-spectral decomposition extended-learning assisted by sparsity for multi-energy computed tomography reconstruction. Quant. Imaging Med. Surg. 2023, 13, 610–630. [Google Scholar] [CrossRef]
- Chen, X.; Xia, W.J.; Liu, Y.; Chen, H.; Zhou, J.L.; Zha, Z.Y.; Wen, B.H.; Zhang, Y. FONT-SIR: Fourth-Order Nonlocal Tensor Decomposition Model for Spectral CT Image Reconstruction. IEEE Trans. Med. Imaging 2022, 41, 2144–2156. [Google Scholar] [CrossRef]
- Li, X.; Wang, K.; Xue, X.; Li, F. Sparse-View Spectral CT Reconstruction Based on Tensor Decomposition and Total Generalized Variation. Electronics 2024, 13, 1868. [Google Scholar] [CrossRef]
- Wu, W.; Hu, D.; An, K.; Wang, S.; Luo, F. A High-Quality Photon-Counting CT Technique Based on Weight Adaptive Total-Variation and Image-Spectral Tensor Factorization for Small Animals Imaging. IEEE Trans. Instrum. Meas. 2021, 70, 2502114. [Google Scholar] [CrossRef]
- Xie, Q.; Zhao, Q.; Meng, D.; Xu, Z. Kronecker-Basis-Representation Based Tensor Sparsity and Its Applications to Tensor Recovery. IEEE Trans. Pattern Anal. Mach. Intell. 2018, 40, 1888–1902. [Google Scholar] [CrossRef]
- Xie, Q.; Zhao, Q.; Meng, D.; Xu, Z.; Gu, S.; Zuo, W.; Zhang, L. Multispectral Images Denoising by Intrinsic Tensor Sparsity Regularization. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 1692–1700. [Google Scholar]
- Zeng, D.; Xie, Q.; Cao, W.; Lin, J.; Zhang, H.; Zhang, S.; Huang, J.; Bian, Z.; Meng, D.; Xu, Z.; et al. Low-Dose Dynamic Cerebral Perfusion Computed Tomography Reconstruction via Kronecker-Basis-Representation Tensor Sparsity Regularization. IEEE Trans. Med. Imaging 2017, 36, 2546–2556. [Google Scholar] [CrossRef]
- Rudin, L.I.; Osher, S.; Fatemi, E. Nonlinear total variation based noise removal algorithms. Phys. D Nonlinear Phenom. 1992, 60, 259–268. [Google Scholar] [CrossRef]
- Sidky, E.Y.; Pan, X. Image reconstruction in circular cone-beam computed tomography by constrained, total-variation minimization. Phys. Med. Biol. 2008, 53, 4777–4807. [Google Scholar] [CrossRef]
- Gong, C.C.; Zeng, L. Self-Guided Limited-Angle Computed Tomography Reconstruction Based on Anisotropic Relative Total Variation. IEEE Access 2020, 8, 70465–70476. [Google Scholar] [CrossRef]
- Du, X.S.; Kong, H.H.; Pan, J.X.; Qi, Z.W.; Li, J.X. Laplacian and bilateral weighted relative total variation sparse angle CT reconstruction. Phys. Scr. 2024, 99, 105212. [Google Scholar] [CrossRef]
- Wu, J.F.; Wang, X.F.; Mou, X.Q.; Chen, Y.; Liu, S.G. Low Dose CT Image Reconstruction Based on Structure Tensor Total Variation Using Accelerated Fast Iterative Shrinkage Thresholding Algorithm. Sensors 2020, 20, 1647. [Google Scholar] [CrossRef]
- Zhu, H.; Liu, X.X.; Huang, L.; Lu, Z.S.; Lu, J.; Ng, M.K. Augmented Lagrangian method for tensor low-rank and sparsity models in multi-dimensional image recovery. Adv. Comput. Math. 2024, 50, 75. [Google Scholar] [CrossRef]





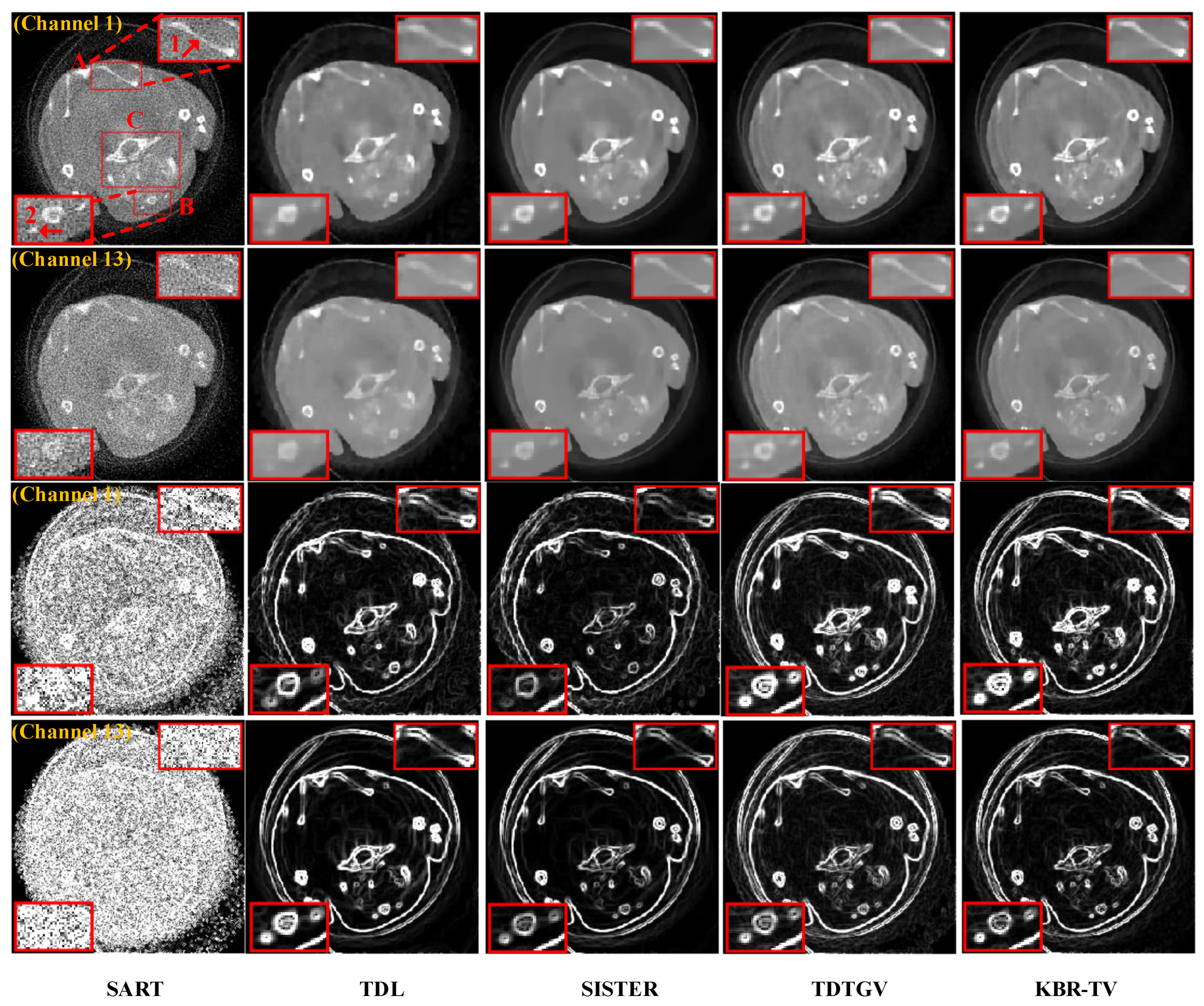
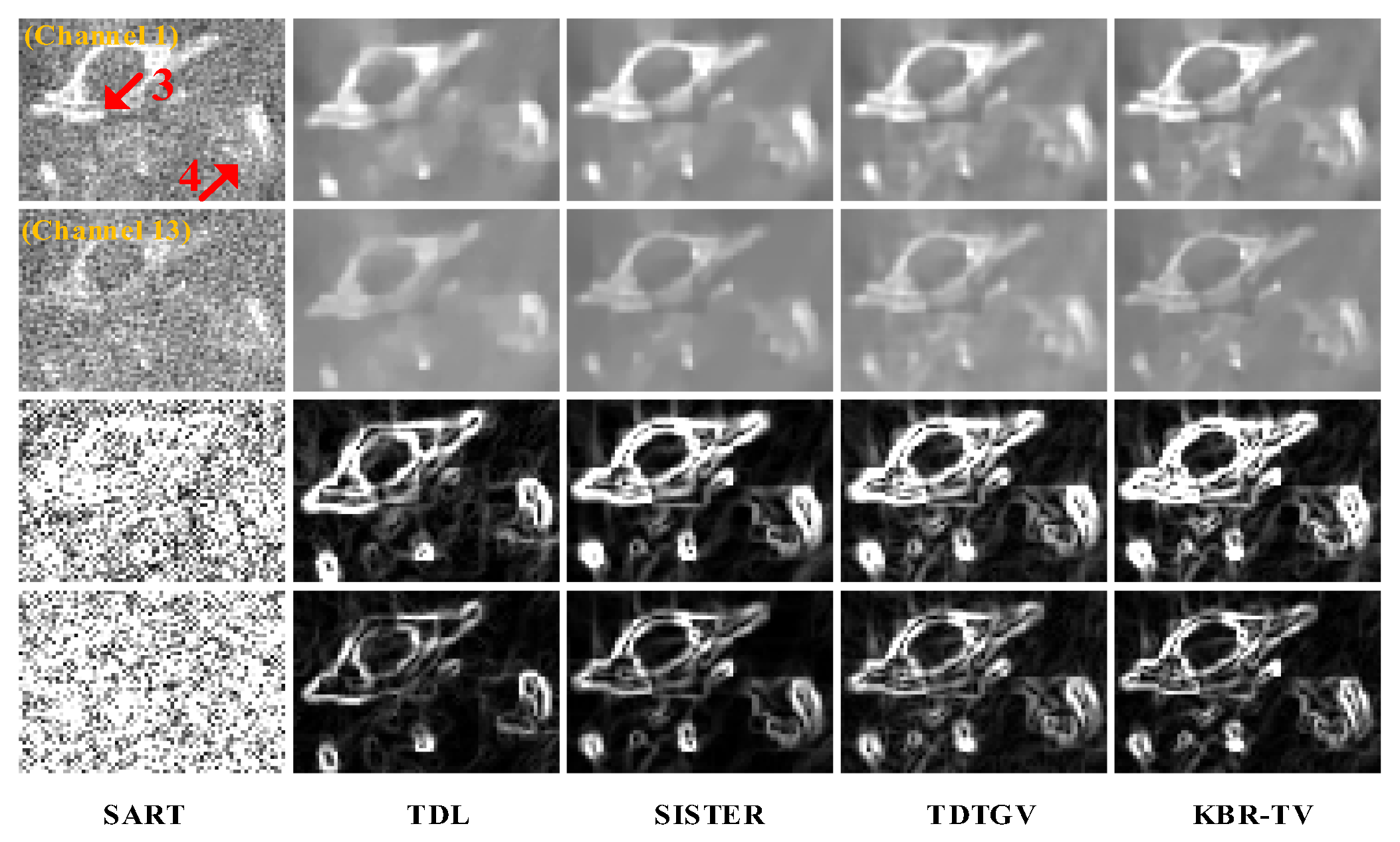
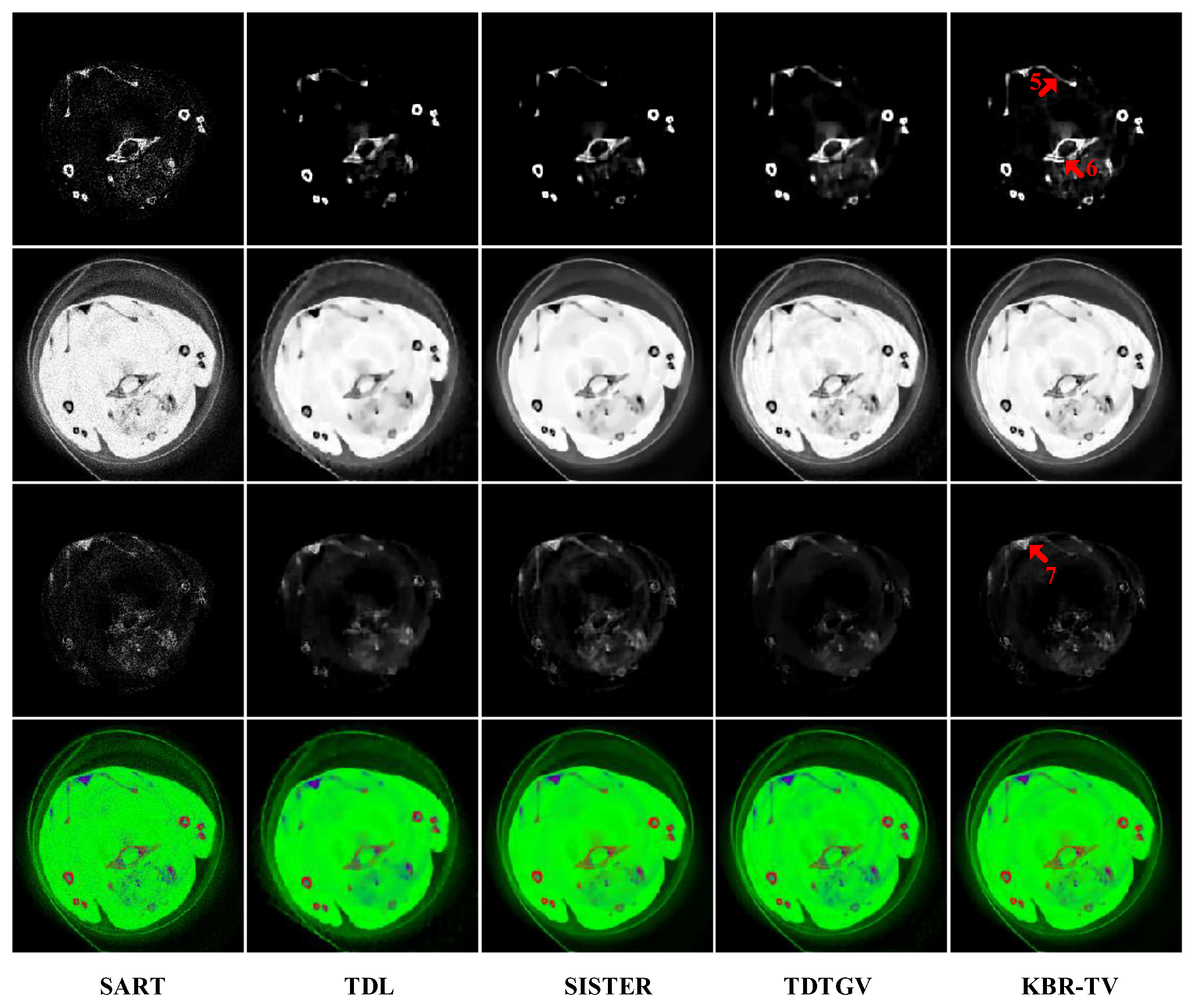
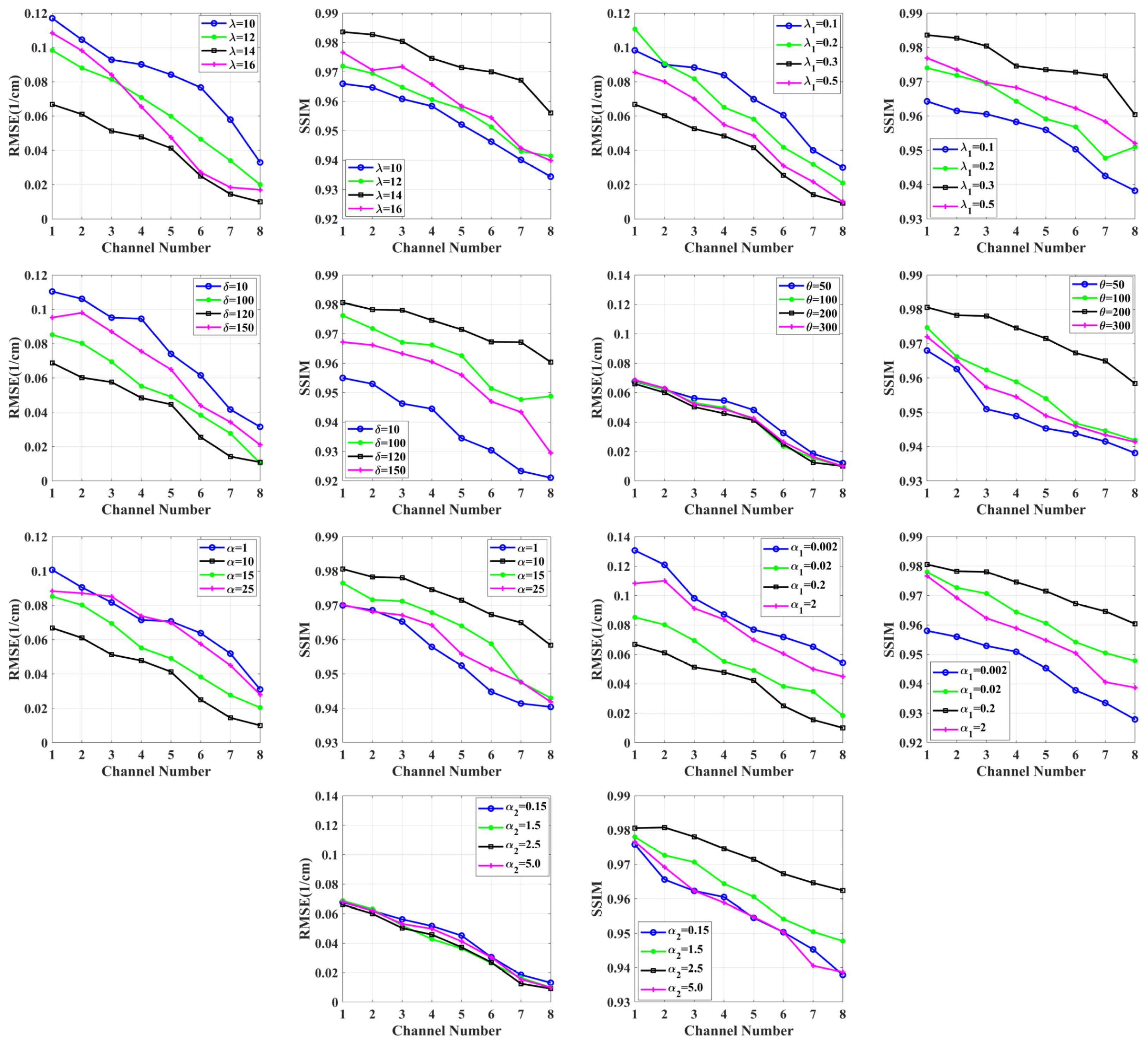
| Photon Numbers | Number of Projections | α | α1 | α2 | λ | λ1 | δ | θ | |
|---|---|---|---|---|---|---|---|---|---|
| Simulation experiment | 5 × 103 | 160 | 10 | 0.2 | 2.5 | 14 | 0.3 | 120 | 200 |
| Real experiment | — | 120 | 12 | 0.6 | 3.0 | 18 | 0.5 | 130 | 200 |
| Number | Parameter | Value |
|---|---|---|
| 1 | The distance between X-ray source and PCD | 180 mm |
| 2 | The distance between X-ray source and rotation center | 132 mm |
| 3 | The number of detectors | 512 |
| 4 | The size of detector element | 0.1 mm |
| 5 | The size of image | 256 × 256 × 8 |
| 6 | The size of image pixel | 0.15 mm |
| Index | Method | 1st | 2nd | 3rd | 4th | 5th | 6th | 7th | 8th |
|---|---|---|---|---|---|---|---|---|---|
| RMSE (10−2) | SART | 21.98 | 19.29 | 17.51 | 16.02 | 15.76 | 15.42 | 15.31 | 15.11 |
| TDL | 12.51 | 10.79 | 8.97 | 8.65 | 7.76 | 6.34 | 4.14 | 2.39 | |
| SISTER | 10.34 | 9.11 | 7.58 | 7.12 | 6.28 | 5.57 | 3.14 | 1.87 | |
| TDTGV | 8.52 | 8.02 | 6.94 | 5.49 | 4.85 | 3.82 | 2.74 | 1.04 | |
| KBR-TV | 6.68 | 6.02 | 5.26 | 4.84 | 4.16 | 2.55 | 1.42 | 0.92 | |
| SSIM | SART | 0.7867 | 0.7644 | 0.7210 | 0.6993 | 0.6873 | 0.6780 | 0.6518 | 0.6249 |
| TDL | 0.9528 | 0.9548 | 0.9514 | 0.9508 | 0.9423 | 0.9311 | 0.9282 | 0.9235 | |
| SISTER | 0.9631 | 0.9600 | 0.9590 | 0.9577 | 0.9564 | 0.9526 | 0.9477 | 0.9406 | |
| TDTGV | 0.9740 | 0.9701 | 0.9686 | 0.9644 | 0.9576 | 0.9502 | 0.9496 | 0.9487 | |
| KBR-TV | 0.9836 | 0.9807 | 0.9814 | 0.9746 | 0.9735 | 0.9728 | 0.9717 | 0.9604 | |
| PSNR | SART | 16.57 | 20.09 | 22.54 | 24.17 | 25.02 | 26.12 | 25.91 | 26.78 |
| TDL | 25.38 | 28.03 | 30.57 | 33.72 | 32.43 | 34.75 | 37.67 | 40.02 | |
| SISTER | 30.72 | 34.21 | 37.82 | 39.01 | 40.07 | 41.43 | 41.96 | 43.12 | |
| TDTGV | 32.36 | 34.99 | 38.84 | 41.73 | 42.23 | 42.89 | 43.87 | 44.25 | |
| KBR-TV | 34.48 | 36.63 | 40.85 | 42.68 | 42.35 | 43.69 | 44.64 | 45.37 |
| Algorithm | Bone | Soft Tissue | Iodine Contrast | |
|---|---|---|---|---|
| RMSE | SART | 0.0894 | 0.1690 | 0.1029 |
| TDL | 0.0282 | 0.0520 | 0.0311 | |
| SISTER | 0.0130 | 0.0423 | 0.0265 | |
| TDTGV | 0.0113 | 0.0408 | 0.0233 | |
| KBR-TV | 0.0092 | 0.0315 | 0.0207 |
| Number | Parameter | Value |
|---|---|---|
| 1 | The distance between X-ray source and PCD | 255 mm |
| 2 | The distance between X-ray source and rotation center | 158 mm |
| 3 | The number of detectors | 512 |
| 4 | The size of detector element | 55 µm |
| 5 | The size of image | 256 × 256 × 13 |
| Methods | TDL | SISTER | TDTGV | KBR-TV |
|---|---|---|---|---|
| Running time | 20.7 ± 1.1 | 40.5 ± 1.2 | 58.7 ± 1.6 | 120.6 ± 2.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Wang, K.; Chang, Y.; Wu, Y.; Liu, J. Combining Kronecker-Basis-Representation Tensor Decomposition and Total Variational Constraint for Spectral Computed Tomography Reconstruction. Photonics 2025, 12, 492. https://doi.org/10.3390/photonics12050492
Li X, Wang K, Chang Y, Wu Y, Liu J. Combining Kronecker-Basis-Representation Tensor Decomposition and Total Variational Constraint for Spectral Computed Tomography Reconstruction. Photonics. 2025; 12(5):492. https://doi.org/10.3390/photonics12050492
Chicago/Turabian StyleLi, Xuru, Kun Wang, Yan Chang, Yaqin Wu, and Jing Liu. 2025. "Combining Kronecker-Basis-Representation Tensor Decomposition and Total Variational Constraint for Spectral Computed Tomography Reconstruction" Photonics 12, no. 5: 492. https://doi.org/10.3390/photonics12050492
APA StyleLi, X., Wang, K., Chang, Y., Wu, Y., & Liu, J. (2025). Combining Kronecker-Basis-Representation Tensor Decomposition and Total Variational Constraint for Spectral Computed Tomography Reconstruction. Photonics, 12(5), 492. https://doi.org/10.3390/photonics12050492





