Directional Excitation of Multi-Dimensional Coupled Topological Photonic States Based on Higher-Order Chiral Source
Abstract
1. Introduction
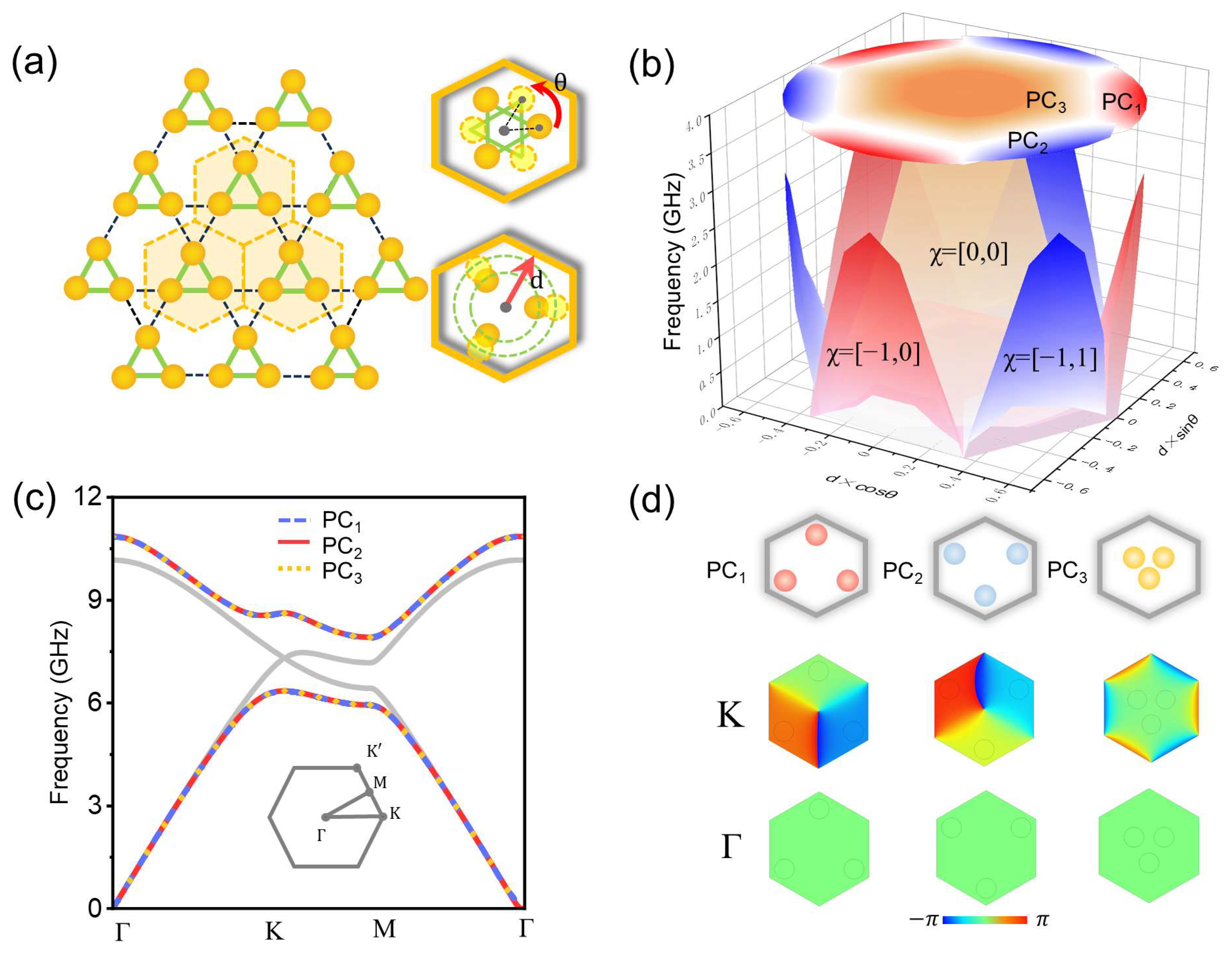
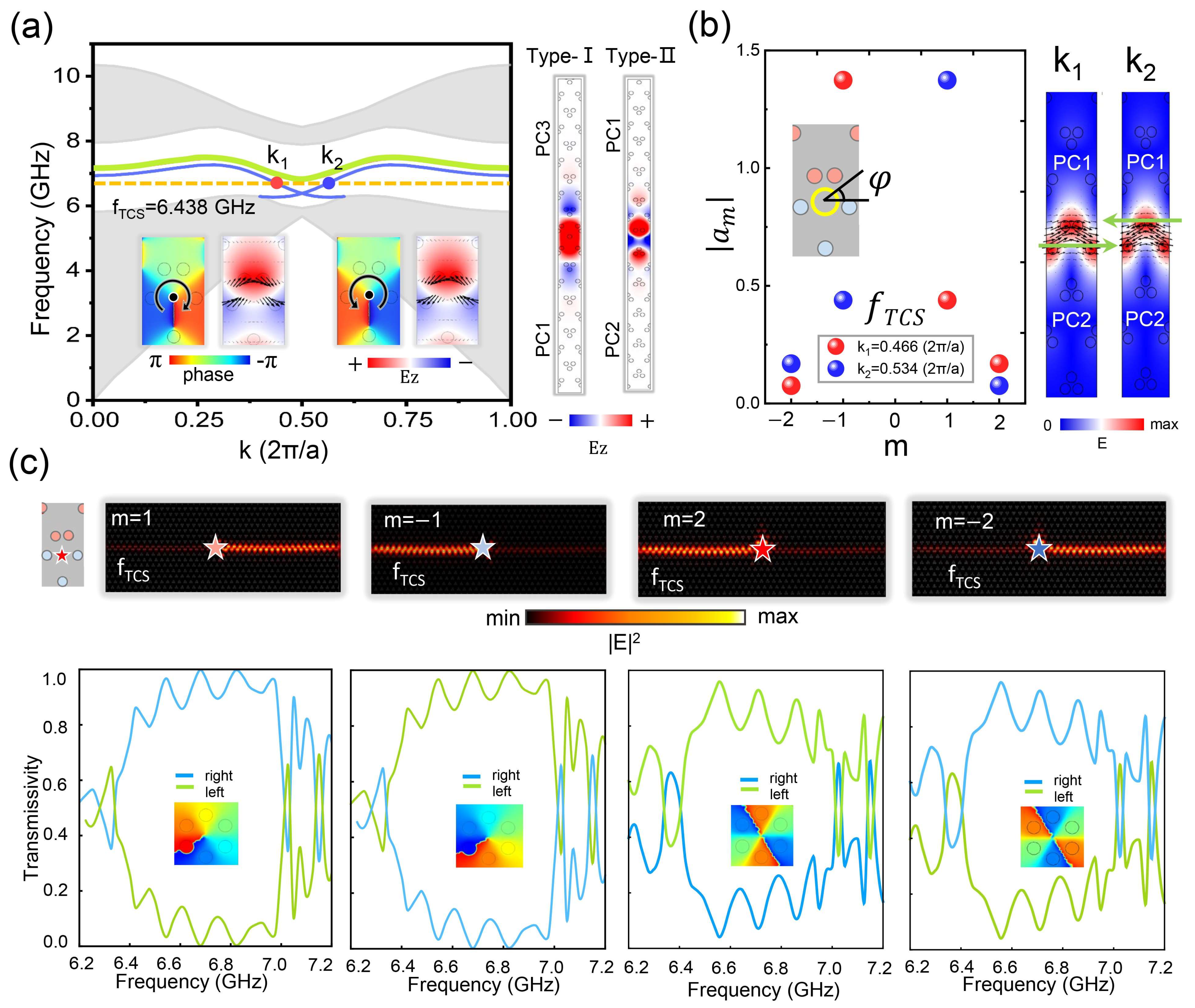
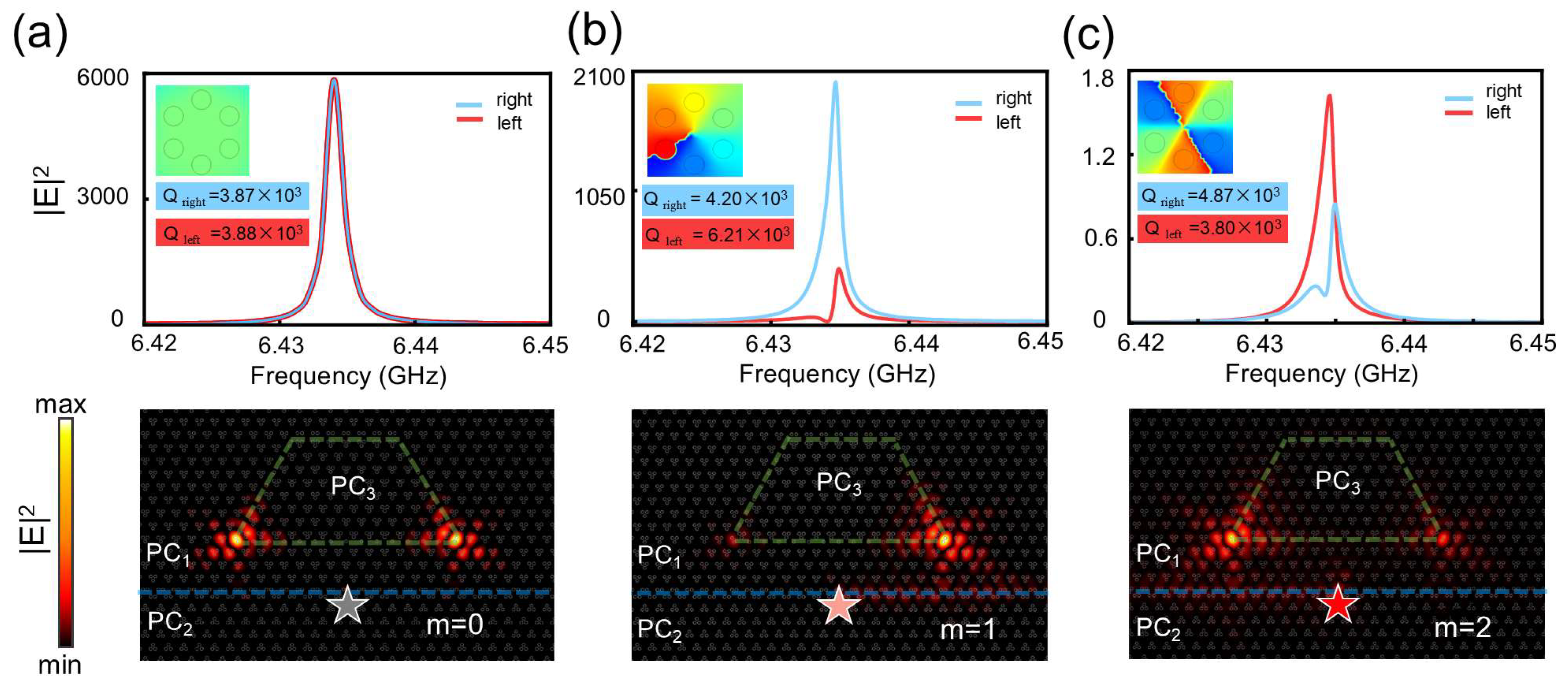
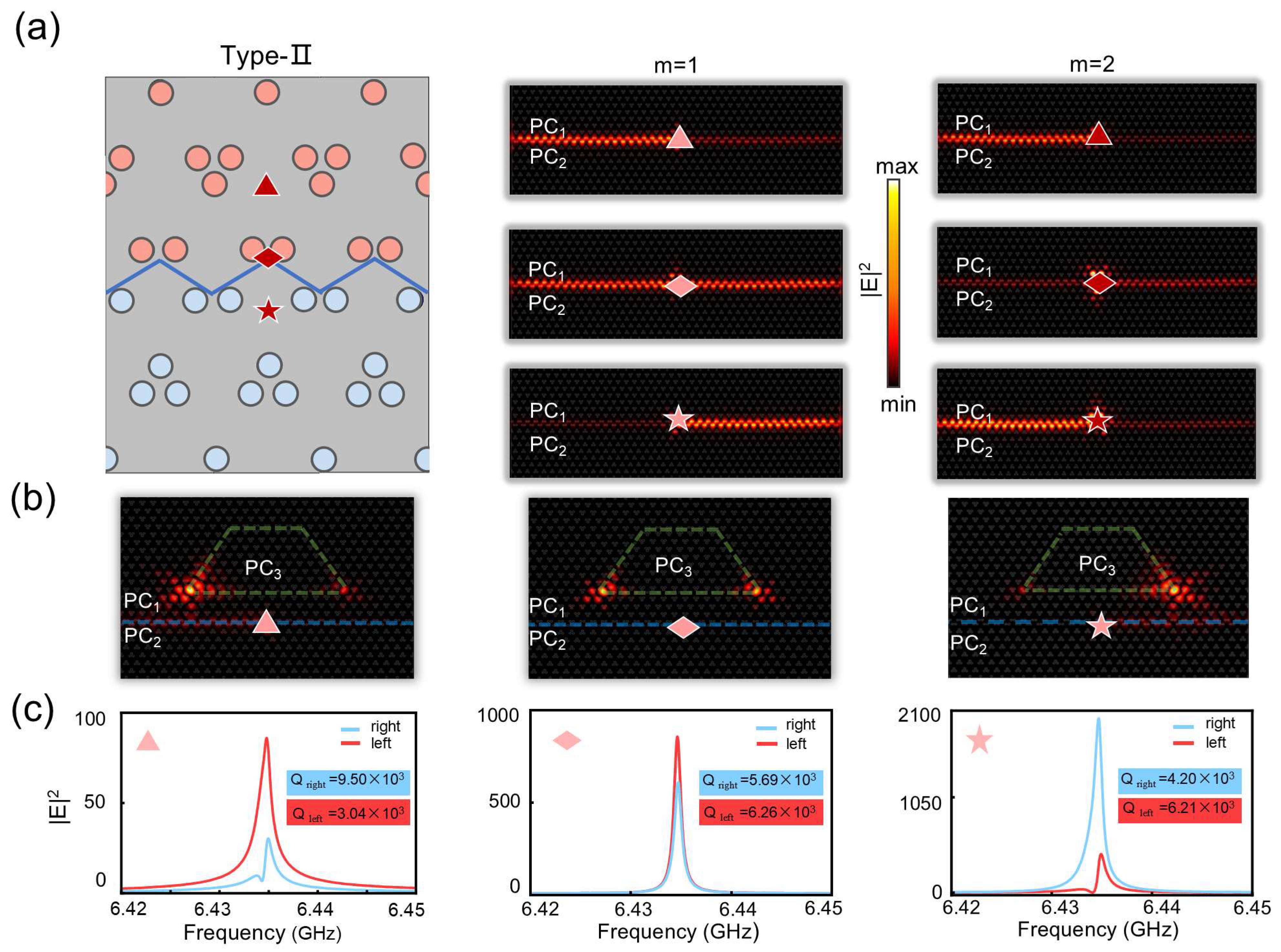
2. Results and Disscussion
3. Summary
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, Z.; Chong, Y.; Joannopoulos, J.D.; Soljačić, M. Reflection-free one-way edge modes in a gyromagnetic photonic crystal. Phys. Rev. Lett. 2008, 100, 013905. [Google Scholar] [CrossRef] [PubMed]
- Lu, L.; Joannopoulos, J.D.; Soljačić, M. Topological photonics. Nat. Photonics 2014, 8, 821. [Google Scholar] [CrossRef]
- Weimann, S.; Kremer, M.; Plotnik, Y.; Lumer, Y.; Nolte, S.; Makris, K.G.; Segev, M.; Rechtsman, M.C.; Szameit, A. Topologically protected bound states in photonic parity–time-symmetric crystals. Nat. Mater. 2017, 16, 433. [Google Scholar] [CrossRef]
- Harari, G.; Bandres, M.A.; Lumer, Y.; Rechtsman, M.C.; Chong, Y.D.; Khajavikhan, M.; Christodoulides, D.N.; Segev, M. Topological insulator laser: Theory. Science 2018, 359, 6381. [Google Scholar] [CrossRef]
- Bandres, M.A.; Wittek, S.; Harari, G.; Parto, M.; Ren, J.; Segev, M.; Christodoulides, D.N.; Khajavikhan, M. Topological insulator laser: Experiments. Science 2018, 359, eaar4005. [Google Scholar] [CrossRef]
- Ozawa, T.; Price, H.M.; Amo, A.; Goldman, N.; Hafezi, M.; Lu, L.; Rechtsman, M.C.; Schuster, D.; Simon, J.; Zilberberg, O.; et al. Topological photonics. Rev. Mod. Phys. 2019, 91, 015006. [Google Scholar] [CrossRef]
- Khanikaev, A.B.; Alù, A. Topological photonics: Robustness and beyond. Nat. Commun. 2024, 15, 931. [Google Scholar] [CrossRef]
- Shi, A.; Bao, L.; Peng, P.; Ning, J.; Wang, Z.; Liu, J. Non-Hermitian Floquet higher-order topological states in two-dimensional quasicrystals. Phys. Rev. B 2025, 111, 094109. [Google Scholar] [CrossRef]
- Ni, X.; Yin, S.; Li, H.; Alù, A. Topological wave phenomena in photonic time quasicrystals. Phys. Rev. B 2025, 111, 125421. [Google Scholar] [CrossRef]
- Zhang, Z.; Lan, Z.; Xu, P.; Wu, L.; Chen, M.; Sha, W.; Xu, Y.; Qin, Y. Observation of spatiotemporal dynamics for topological surface states with on-demand dispersion. Photon. Res. 2024, 12, 2919–2930. [Google Scholar] [CrossRef]
- Tang, G.; He, X.; Shi, F.L.; Liu, J.; Chen, X.; Dong, J. Topological photonic crystals: Physics, designs, and applications. Laser Photonics Rev. 2022, 16, 2100300. [Google Scholar] [CrossRef]
- Lan, Z.; Chen, M.; Gao, F.; Zhang, S.; Sha, W.E. A brief review of topological photonics in one, two, and three dimensions. Rev. Phys. 2022, 9, 100076. [Google Scholar] [CrossRef]
- Zeng, Y.; Chattopadhyay, U.; Zhu, B.; Qiang, B.; Li, J.; Jin, Y.; Li, L.; Davies, A.G.; Linfield, E.H.; Zhang, B.; et al. Electrically pumped topological laser with valley edge modes. Nature 2020, 578, 246. [Google Scholar] [CrossRef]
- Barik, S.; Karasahin, A.; Flower, C.; Cai, T.; Miyake, H.; DeGottardi, W.; Hafezi, M.; Waks, E. A topological quantum optics interface. Science 2018, 359, 666. [Google Scholar] [CrossRef]
- Blanco-Redondo, A.; Bell, B.; Oren, D.; Eggleton, B.J.; Segev, M. Topological protection of biphoton states. Science 2018, 362, 568. [Google Scholar] [CrossRef]
- Smirnova, D.; Kruk, S.; Leykam, D.; Melik-Gaykazyan, E.; Choi, D.Y.; Kivshar, Y. Third-harmonic generation in photonic topological metasurfaces. Phys. Rev. Lett. 2019, 123, 103901. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Willner, A.E.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488. [Google Scholar] [CrossRef]
- Nicolas, A.; Veissier, L.; Giner, L.; Giacobino, E.; Maxein, D.; Laurat, J. A quantum memory for orbital angular momentum photonic qubits. Nat. Photonics 2014, 8, 234. [Google Scholar] [CrossRef]
- Baresch, D.; Thomas, J.L.; Marchiano, R. Orbital angular momentum transfer to stably trapped elastic particles in acoustical vortex beams. Phys. Rev. Lett. 2018, 121, 074301. [Google Scholar] [CrossRef]
- Wu, L.; Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 2015, 114, 223901. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Smirnova, D.; Nori, F. Quantum spin Hall effect of light. Science 2015, 348, 1448. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yun, F.; Tao, X.; Wang, H.; Jiang, J.; Hu, X.; Hang, Z. Visualization of a unidirectional electromagnetic waveguide using topological photonic crystals made of dielectric materials. Phys. Rev. Lett. 2018, 120, 217401. [Google Scholar] [CrossRef]
- Peng, Y.; Shi, A.; Peng, P.; Liu, J. Pseudospin-induced asymmetric field in non-Hermitian photonic crystals with multiple topological transitions. Phys. Rev. B 2025, 111, 085148. [Google Scholar] [CrossRef]
- Wu, X.; Meng, Y.; Tian, J.; Huang, Y.; Xiang, H.; Han, D.; Wen, W. Direct observation of valley-polarized topological edge states in designer surface plasmon crystals. Nat. Commun. 2017, 8, 1304. [Google Scholar] [CrossRef]
- Dong, J.; Chen, X.; Zhu, H.; Wang, Y.; Zhang, X. Valley Photonic Crystals for Control of Spin and Topology. Nat. Mater. 2017, 16, 298–302. [Google Scholar] [CrossRef]
- Yang, Y.; Yamagami, Y.; Yu, X.; Pitchappa, P.; Webber, J.; Zhang, B.; Fujita, M.; Nagatsuma, T.; Singh, R. Terahertz Topological Photonics for On-Chip Communication. Nat. Photonics 2020, 14, 446–451. [Google Scholar] [CrossRef]
- Lan, Z.; You, J.W.; Ren, Q.; Sha, W.E.I.; Panoiu, N.C. Second-Harmonic Generation via Double Topological Valley-Hall Kink Modes in All-Dielectric Photonic Crystals. Phys. Rev. A 2021, 103, L041502. [Google Scholar] [CrossRef]
- Wong, S.; Saba, M.; Hess, O.; Oh, S.S. Gapless Unidirectional Photonic Transport Using All-Dielectric Kagome Lattices. Phys. Rev. Res. 2020, 2, 012011. [Google Scholar] [CrossRef]
- Yan, B.; Liao, B.; Shi, F.; Xi, X.; Cao, Y.; Xiang, K.; Meng, Y.; Yang, L.; Zhu, Z.; Chen, J.; et al. Realization of Topology-Controlled Photonic Cavities in a Valley Photonic Crystal. Phys. Rev. Lett. 2025, 134, 033803. [Google Scholar] [CrossRef] [PubMed]
- Noh, J.; Benalcazar, W.A.; Huang, S.; Collins, M.J.; Chen, K.P.; Hughes, T.L.; Rechtsman, M.C. Topological Protection of Photonic Mid-Gap Defect Modes. Nat. Photonics 2018, 12, 408–415. [Google Scholar] [CrossRef]
- Chen, X.; Deng, W.; Shi, F.; Zhao, F.; Chen, M.; Dong, J. Direct Observation of Corner States in Second-Order Topological Photonic Crystal Slabs. Phys. Rev. Lett. 2019, 122, 233902. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Su, G.; Wang, H.; Su, H.; Shen, X.; Zhan, P.; Lu, M.; Wang, Z.; Chen, Y. Visualization of Higher-Order Topological Insulating Phases in Two-Dimensional Dielectric Photonic Crystals. Phys. Rev. Lett. 2019, 122, 233903. [Google Scholar] [CrossRef] [PubMed]
- Ota, Y.; Liu, F.; Katsumi, R.; Watanabe, K.; Wakabayashi, K.; Arakawa, Y.; Iwamoto, S. Photonic Crystal Nanocavity Based on a Topological Corner State. Optica 2019, 6, 786. [Google Scholar] [CrossRef]
- Li, M.; Zhirihin, D.; Gorlach, M.; Ni, X.; Filonov, D.; Slobozhanyuk, A.; Alù, A.; Khanikaev, A.B. Higher-Order Topological States in Photonic Kagome Crystals with Long-Range Interactions. Nat. Photonics 2020, 14, 89–94. [Google Scholar] [CrossRef]
- Kim, M.; Jacob, Z.; Rho, J. Recent Advances in 2D, 3D and Higher-Order Topological Photonics. Light Sci. Appl. 2020, 9, 130. [Google Scholar] [CrossRef]
- Xie, B.; Su, G.; Wang, H.; Liu, F.; Hu, L.; Yu, S.; Zhan, P.; Lu, M.; Wang, Z.; Chen, Y. Higher-Order Quantum Spin Hall Effect in a Photonic Crystal. Nat. Commun. 2020, 11, 3768. [Google Scholar] [CrossRef]
- Guo, K.; Wu, J.; Chen, F.; Zhou, K.; Liu, S.; Guo, Z. Second Harmonic Generation Enhancement and Directional Emission from Topological Corner State Based on the Quantum Spin Hall Effect. Opt. Express 2021, 29, 26841. [Google Scholar] [CrossRef]
- Su, G.; Huang, R.; Jia, S.; He, J.; Song, Z.; Hu, J.; Lu, M.; Liu, F.; Zhan, P. Space- and Frequency-Division Multiplexing in Photonic Second-Order Topological Insulators. Photonics Res. 2024, 12, 2323. [Google Scholar] [CrossRef]
- Hu, Z.; Bongiovanni, D.; Wang, Z.; Wang, X.; Song, D.; Xu, J.; Buljan, H.; Morandotti, R.; Chen, Z. Topological orbital angular momentum extraction and twofold protection of vortex transport. Nat. Photonics 2025, 19, 162–169. [Google Scholar] [CrossRef]
- Deng, W.; Chen, X.; Chen, W.; Zhao, F.; Dong, J. Vortex index identification and unidirectional propagation in Kagome photonic crystals. Nanophotonics 2019, 8, 833–840. [Google Scholar] [CrossRef]
- Shi, A.; Yan, B.; Ge, R.; Xie, J.; Peng, Y.; Li, H.; Sha, W.; Liu, J. Coupled cavity-waveguide based on topological corner state and edge state. Opt. Lett. 2021, 46, 1089. [Google Scholar] [CrossRef] [PubMed]
- Su, G.; He, J.; Ye, X.; Yao, H.; Li, Y.; Hu, J.; Lu, M.; Zhan, P.; Liu, F. Tailored Triggering of High-Quality Multi-Dimensional Coupled Topological States in Valley Photonic Crystals. Nanomaterials 2024, 14, 885. [Google Scholar] [CrossRef]
- Gao, Y.; He, Y.; Si, J.; Subinuer, R.; Jin, M.; He, Y.; Yang, M. Waveguide–cavity coupling system based on topological edge states and corner states in kagome photonic crystals. Adv. Quantum Technol. 2024, 7, 2300265. [Google Scholar] [CrossRef]
- Lera, N.; Torrent, D.; San-Jose, P.; Alvarez, J.V. Valley Hall phases in kagome lattices. Phys. Rev. B 2019, 99, 134102. [Google Scholar] [CrossRef]
- Benalcazar, W.A.; Lia, T.; Hughes, T.L. Quantization of fractional corner charge in C n-symmetric higher-order topological crystalline insulators. Phys. Rev. B 2019, 99, 245151. [Google Scholar] [CrossRef]
- Wang, H.; Liang, L.; Jiang, B.; Hu, J.; Lu, X.; Jiang, J. Higher-order topological phases in tunable C3 symmetric photonic crystals. Photonics Res. 2021, 9, 1854–1864. [Google Scholar] [CrossRef]
- Chen, M.; Jiang, L.; Lan, Z.; Sha, W. Local orbital-angular-momentum dependent surface states with topological protection. Opt. Express 2020, 28, 14428–14435. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Li, Y.; Fan, Y.; Zhao, X.; Ding, L.; Yuan, X.; Ji, B.; Hu, J.; Liu, L.; Su, G.; et al. Directional Excitation of Multi-Dimensional Coupled Topological Photonic States Based on Higher-Order Chiral Source. Photonics 2025, 12, 488. https://doi.org/10.3390/photonics12050488
He J, Li Y, Fan Y, Zhao X, Ding L, Yuan X, Ji B, Hu J, Liu L, Su G, et al. Directional Excitation of Multi-Dimensional Coupled Topological Photonic States Based on Higher-Order Chiral Source. Photonics. 2025; 12(5):488. https://doi.org/10.3390/photonics12050488
Chicago/Turabian StyleHe, Jiangle, Yaxuan Li, Yangyang Fan, Xinwen Zhao, Lin Ding, Xueqi Yuan, Beijia Ji, Junzheng Hu, Lifu Liu, Guangxu Su, and et al. 2025. "Directional Excitation of Multi-Dimensional Coupled Topological Photonic States Based on Higher-Order Chiral Source" Photonics 12, no. 5: 488. https://doi.org/10.3390/photonics12050488
APA StyleHe, J., Li, Y., Fan, Y., Zhao, X., Ding, L., Yuan, X., Ji, B., Hu, J., Liu, L., Su, G., Zhan, P., & Liu, F. (2025). Directional Excitation of Multi-Dimensional Coupled Topological Photonic States Based on Higher-Order Chiral Source. Photonics, 12(5), 488. https://doi.org/10.3390/photonics12050488




