Efficient Generation of Transversely and Longitudinally Truncated Chirped Gaussian Laser Pulses for Application in High-Brightness Photoinjectors
Abstract
:1. Introduction
2. Materials and Methods
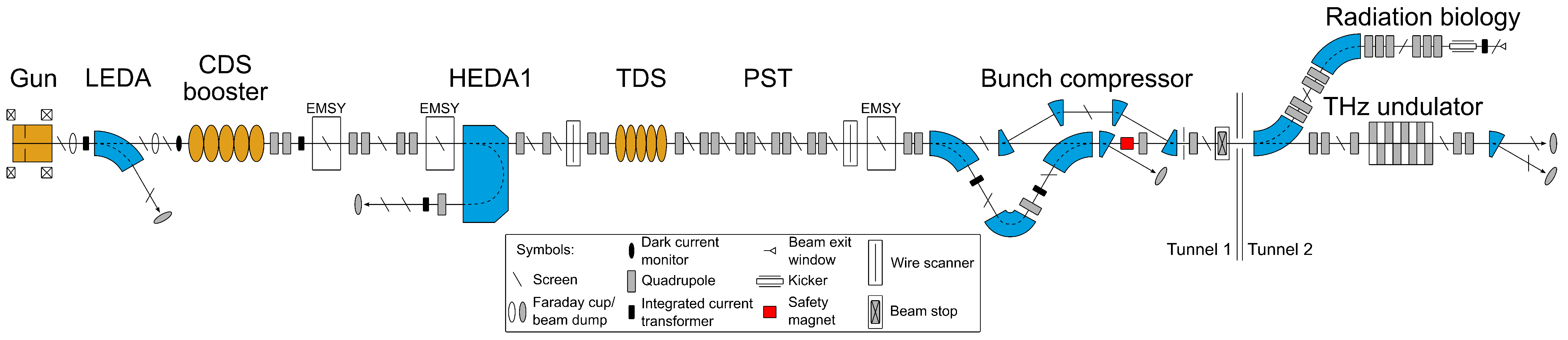
2.1. PITZ Overview
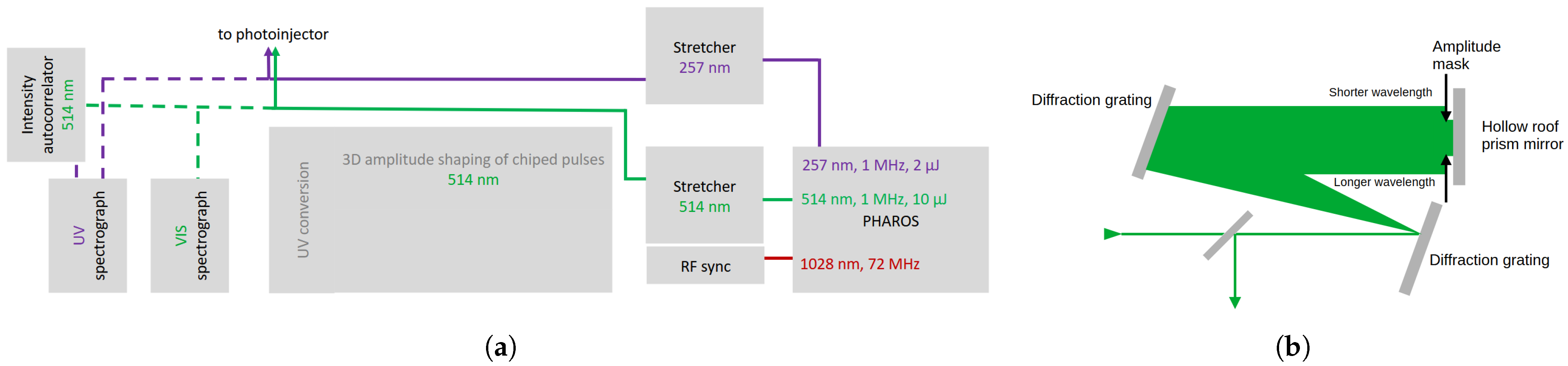
2.2. Laser System and Pulse-Shaping Scheme
2.3. Beam Transport to the Photocathode
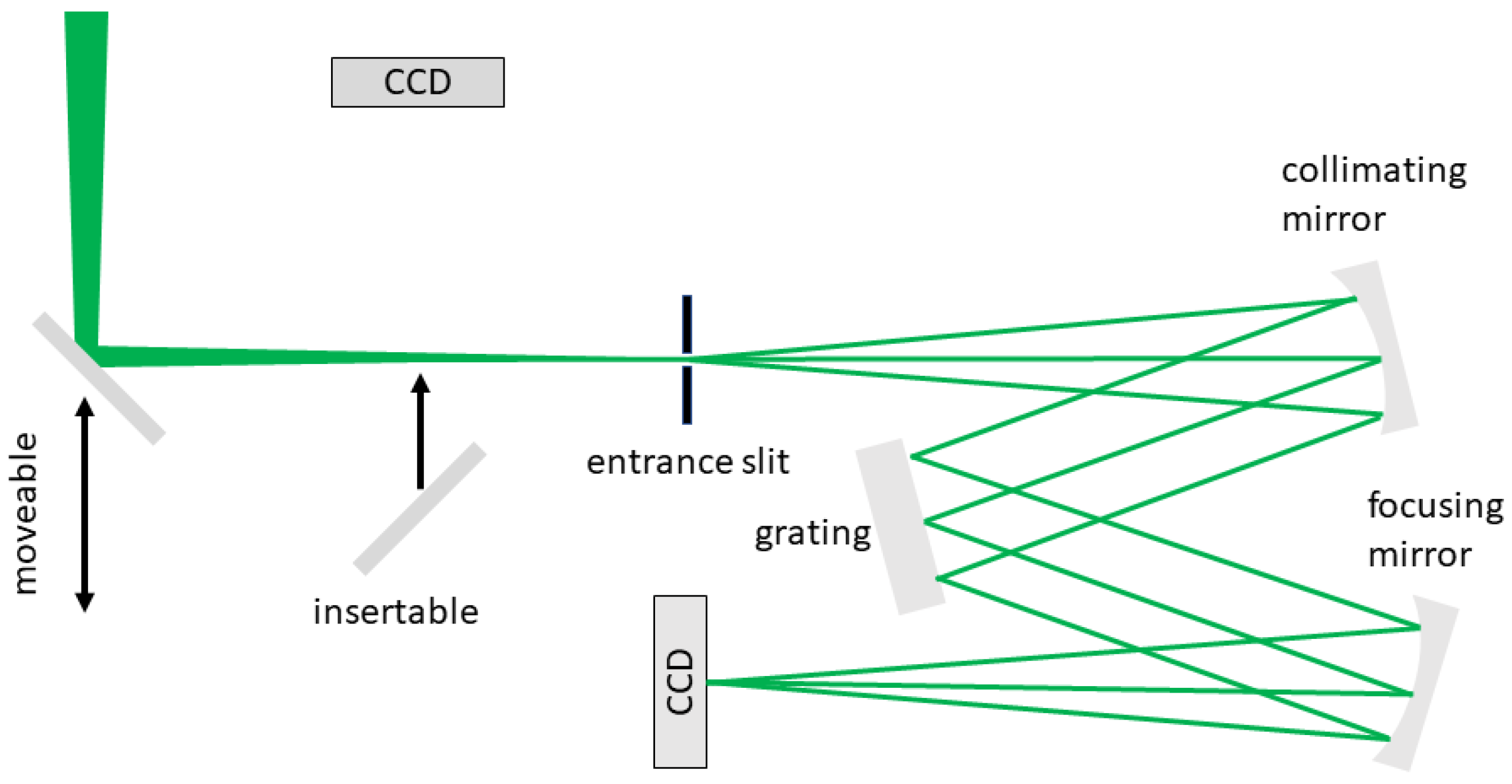
2.4. Diagnostics
3. Results
3.1. Beam Dynamics Simulations
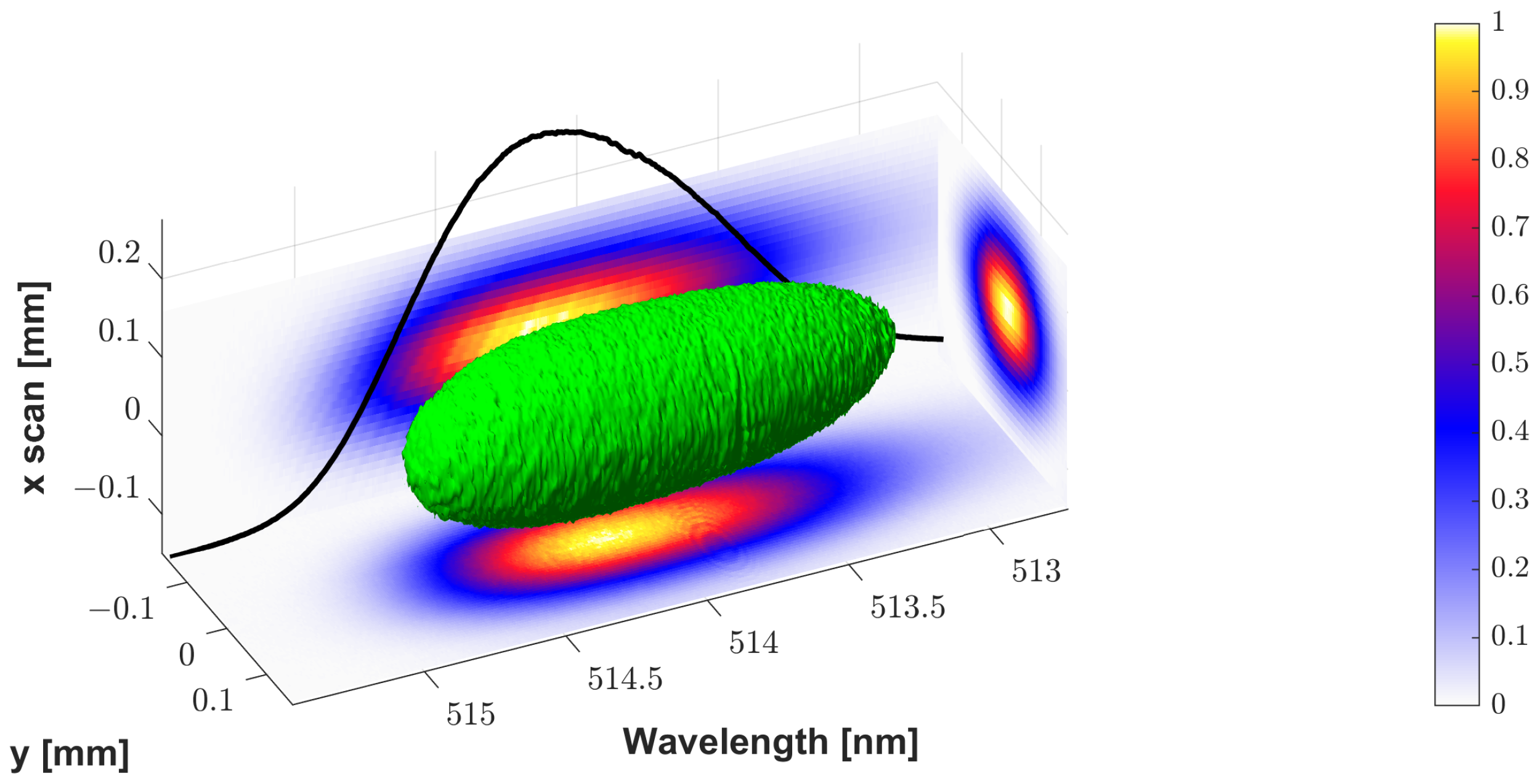
3.2. Experiments at 514 nm
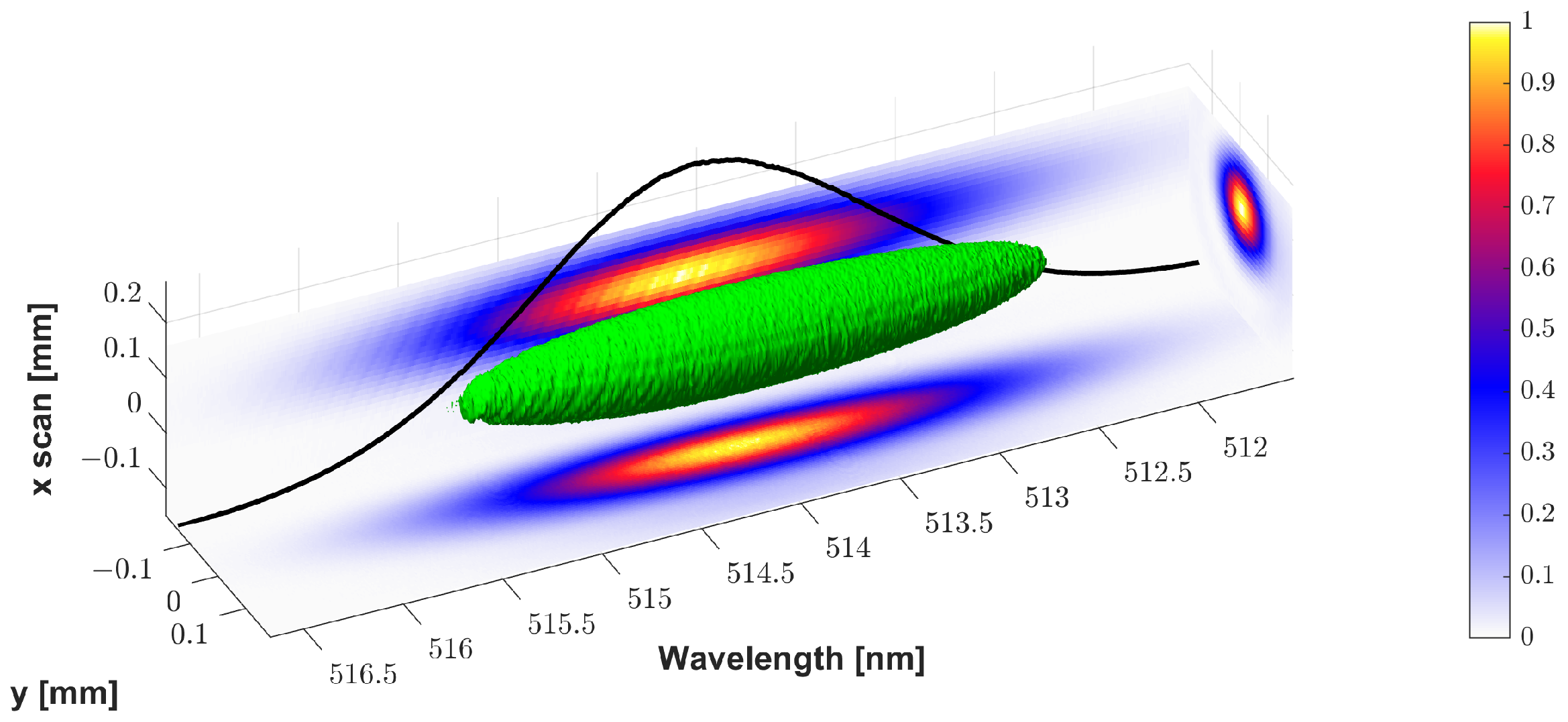
3.2.1. Characterization of Chirped Gaussian Pulses
3.2.2. Characterization of Chirped Truncated Gaussian Pulses
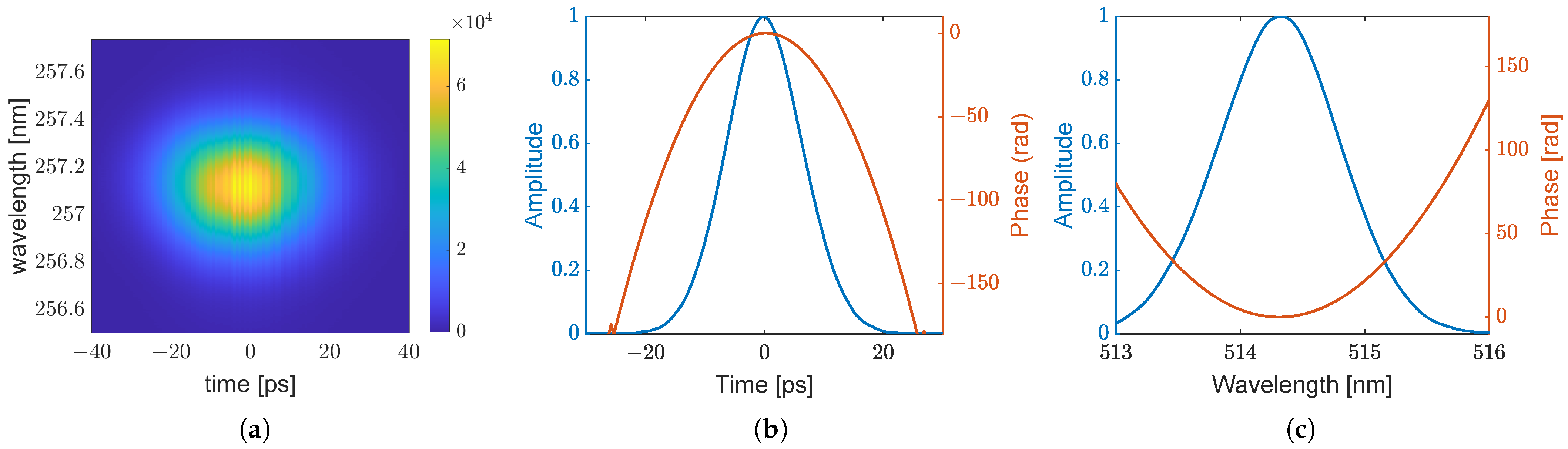
3.3. Experiments at 257 nm
4. Discussion
4.1. Quality of Shaped UV Pulses and Efficiency
4.2. Application in THz Undulators
4.3. Simplification for Alkali Antimonide Photocathodes
4.4. Transfer to Other Photocathode Lasers
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ASTRA | A Space Charge Tracking Algorithm |
| BSA | beam-shaping aperture |
| DESY | Deutsches Elektronen-Synchrotron |
| EMSY | emittance measurement system |
| FEL | free-electron laser |
| FROG | frequency-resolved optical gating |
| PITZ | Photo Injector Test Facility at DESY in Zeuthen |
| RF | radio frequency |
| RMS | root mean square |
| UV | ultraviolet |
| Yb:KGW | ytterbium-doped potassium gadolinium tungstate |
Appendix A

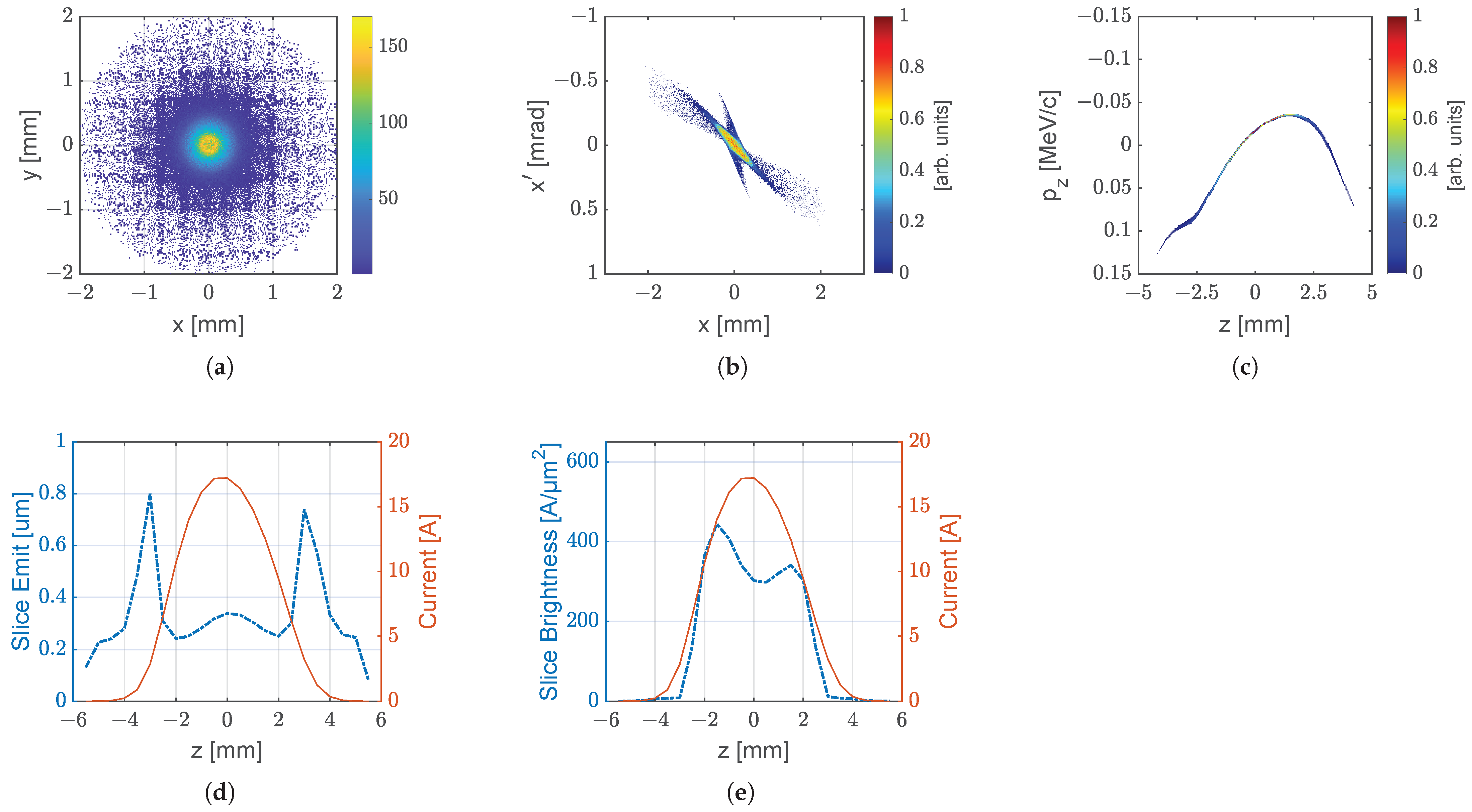
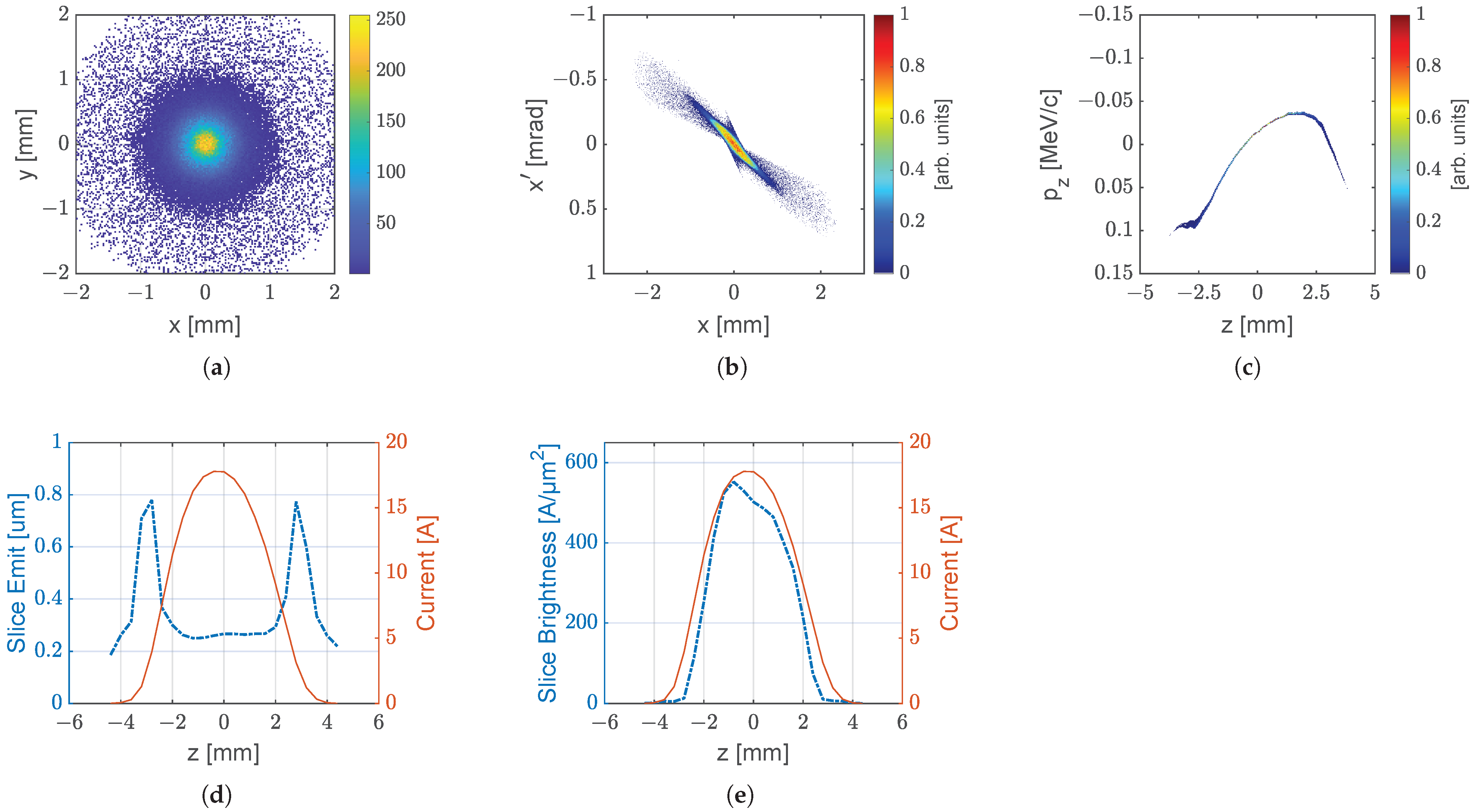
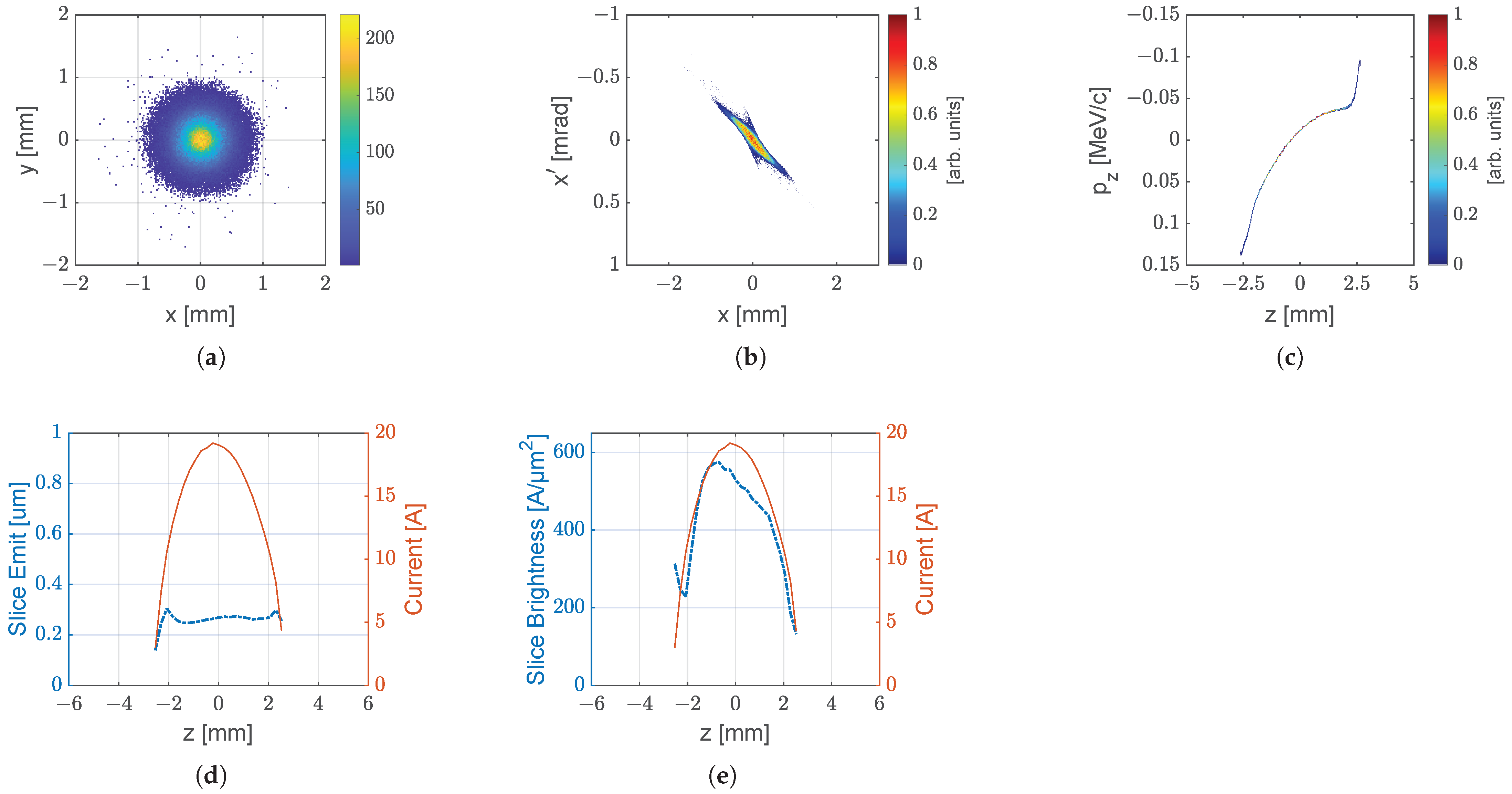
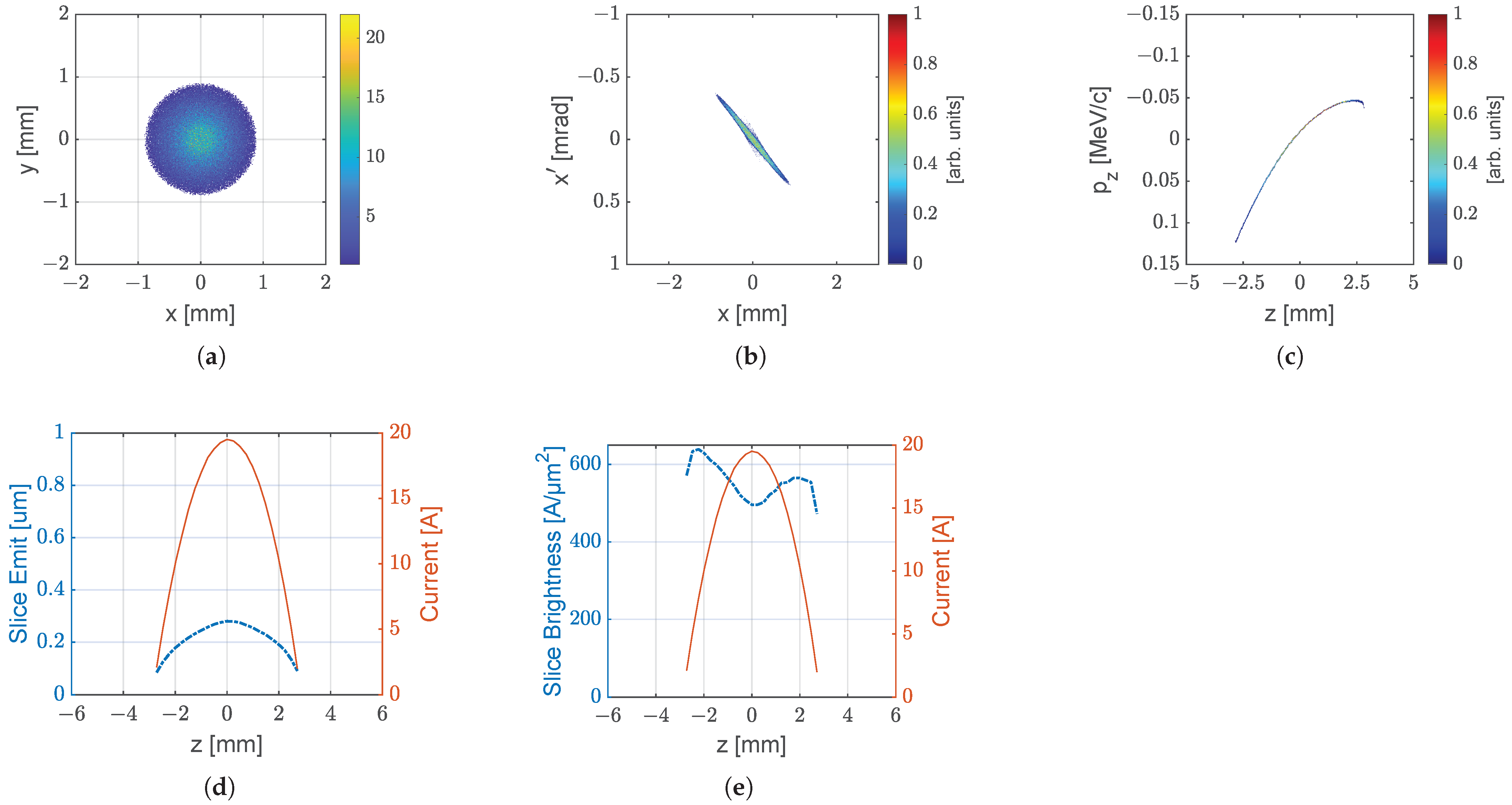
References
- Serafini, L.; Rosenzweig, J.B. Envelope analysis of intense relativistic quasilaminar beams in rf photoinjectors: A theory of emittance compensation. Phys. Rev. E 1997, 55, 7565–7590. [Google Scholar] [CrossRef]
- Limborg-Deprey, C.; Tomizawa, H. Maximizing brightness in photoinjectors. Int. J. Mod. Phys. 2007, 22, 3864–3881. [Google Scholar] [CrossRef]
- Sannibale, F. High-brightness electron injectors for high-duty cycle X-ray free electron lasers. Front. Phys. 2023, 11, 1187346. [Google Scholar] [CrossRef]
- Kapchinskij, I.M.; Vladimirskij, V.V. Limitations Of Proton Beam Current In A Strong Focusing Linear Accelerator Associated with The Beam Space Charge. In Proceedings of the 2nd International Conference on High-Energy Accelerators, Geneva, Switzerland, 14–19 September 1959; pp. 274–287. [Google Scholar]
- Kellogg, O. Foundations of Potential Theory; Reprint from the 1st ed. of 1929; Dover: New York, NY, USA, 1954. [Google Scholar]
- Reiser, M. Theory and Design of Charged Particle Beams; Wiley-VCH: Weinheim, Germany, 2008. [Google Scholar]
- Ha, G.; Kim, K.J.; Power, J.G.; Sun, Y.; Piot, P. Bunch shaping in electron linear accelerators. Rev. Mod. Phys. 2022, 94, 25006. [Google Scholar] [CrossRef]
- Serafini, L. Improving the beam quality of RF guns by correction of RF and space-charge effects. AIP Conf. Proc. 1992, 279, 645–674. [Google Scholar] [CrossRef]
- Luiten, O.J.; van der Geer, S.B.; de Loos, M.J.; Kiewiet, F.B.; van der Wiel, M.J. How to Realize Uniform Three-Dimensional Ellipsoidal Electron Bunches. Phys. Rev. Lett. 2004, 93, 094802. [Google Scholar] [CrossRef]
- Will, I.; Templin, H.I.; Schreiber, S.; Sandner, W. Photoinjector drive laser of the FLASH FEL. Opt. Express 2011, 19, 23770–23781. [Google Scholar] [CrossRef]
- Winkelmann, L.; Choudhuri, A.; Grosse-Wortmann, U.; Hartl, I.; Li, C.; Mohr, C.; Müller, J.; Peters, F.; Pfeiffer, S.; Salman, S. The European XFEL Photocathode Laser. In Proceedings of the 39th in Free Electron Laser Conference, Proc. FEL’19, Hamburg, Germany, 26–30 August 2019; JACoW Publishing: Geneva, Switzerland, 2019; pp. 423–426. [Google Scholar] [CrossRef]
- Li, C.; Akcaalan, O.; Frede, M.; Grosse-Wortmann, U.; Hartl, I.; Mohr, C.; Puncken, O.; Seidel, M.; Tuennermann, H.; Vidoli, C.; et al. Photocathode Laser Development for Superconducting X-ray Free Electron Lasers at DESY. In Proceedings of the 12th in International Particle Accelerator Conference, Proc. IPAC’21, Virtual, 24–28 May 2021; JACoW Publishing: Geneva, Switzerland, 2021; pp. 3599–3601. [Google Scholar] [CrossRef]
- Mironov, S.Y.; Potemkin, A.K.; Gacheva, E.I.; Andrianov, A.V.; Zelenogorskii, V.V.; Krasilnikov, M.; Stephan, F.; Khazanov, E.A. Shaping of cylindrical and 3D ellipsoidal beams for electron photoinjector laser drivers. Appl. Opt. 2016, 55, 1630–1635. [Google Scholar] [CrossRef]
- Koschitzki, C.; Qian, H.; Aboulbanine, Z.; Adhikari, G.; Aftab, N.; Boonpornprasert, P.; Georgiev, G.; Good, J.; Gross, M.; Hoffmann, A.; et al. Chirped Pulse Laser Shaping for High Brightness Photoinjectors. In Proceedings of the 40th International Free Electron Laser Conference, Proc. FEL2022, Trieste, Italy, 22–26 August 2022; JACoW Publishing: Geneva, Switzerland, 2022; pp. 345–348. [Google Scholar] [CrossRef]
- Hoffmann, A.; Good, J.; Gross, M.; Krasilnikov, M.; Stephan, F. Towards Implementation of 3D Amplitude Shaping at 515 nm and First Pulseshaping Experiments at PITZ. Photonics 2024, 11, 6. [Google Scholar] [CrossRef]
- Hoffmann, A.; Good, J.; Gross, M.; Krasilnikov, M.; Stephan, F. Generation of UV Ellipsoidal Pulses by 3D Amplitude Shaping for Application in High-Brightness Photoinjectors. Photonics 2024, 11, 779. [Google Scholar] [CrossRef]
- Galdi, A.; Balajka, J.; DeBenedetti, W.J.I.; Cultrera, L.; Bazarov, I.V.; Hines, M.; Maxson, J.M. Reduction of surface roughness emittance of Cs3Sb photocathodes grown via codeposition on single crystal substrates. Appl. Phys. Lett. 2021, 118, 244101. [Google Scholar] [CrossRef]
- Mohanty, S.K.; Krasilnikov, M.; Oppelt, A.; Stephan, F.; Sertore, D.; Monaco, L.; Pagani, C.; Hillert, W. Development and Characterization of Multi-Alkali Antimonide Photocathodes for High-Brightness RF Photoinjectors. Micromachines 2023, 14, 1182. [Google Scholar] [CrossRef] [PubMed]
- Brinkmann, R.; Schneidmiller, E.; Sekutowicz, J.; Yurkov, M. Prospects for CW and LP operation of the European XFEL in hard X-ray regime. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2014, 768, 20–25. [Google Scholar] [CrossRef]
- Sekutowicz, J.; Ayvazyan, V.; Barlak, M.; Branlard, J.; Cichalewski, W.; Grabowski, W.; Kostin, D.; Lorkiewicz, J.; Merz, W.; Nietubyc, R.; et al. Research and development towards duty factor upgrade of the European X-ray Free Electron Laser linac. Phys. Rev. ST Accel. Beams 2015, 18, 50701. [Google Scholar] [CrossRef]
- Chatterley, A.; Karamatskos, E.; Schouder, C.; Christiansen, L.; Jørgensen, A.; Mullins, T.; Küpper, J.; Stapelfeldt, H. Communication: Switched wave packets with spectrally truncated chirped pulses. J. Chem. Phys. 2018, 148, 221105. [Google Scholar] [CrossRef]
- Kafka, K.; Papernov, S.; Demos, S. Enhanced laser conditioning using temporally shaped pulses. Opt. Lett. 2018, 43, 1239–1242. [Google Scholar] [CrossRef]
- Altucci, C.; Bruzzese, R.; Lisio, C.; Nisoli, M.; Priori, E.; Stagira, S.; Pascolini, M.; Poletto, L.; Villoresi, P.; Tosa, V.; et al. Phase-matching analysis of high-order harmonics generated by truncated Bessel beams in the sub-10-fs regime. Phys. Rev. A 2003, 68, 033806. [Google Scholar] [CrossRef]
- Jin, C.; Lin, C. Comparison of high-order harmonic generation of Ar using truncated Bessel and Gaussian beams. Phys. Rev. A 2012, 85, 033423. [Google Scholar] [CrossRef]
- Worku, N.; Gross, H. Spatially truncated Gaussian pulsed beam and its application in modeling diffraction of ultrashort pulses from hard apertures. J. Opt. Soc. Am. A 2020, 37, 317–326. [Google Scholar] [CrossRef]
- Pan, L.; Lü, B. Spectral behavior of diffracted chirped Gaussian pulses in the far field. Optik 2004, 115, 57–66. [Google Scholar] [CrossRef]
- Rao, T.; Dowell, D. (Eds.) An Engineering Guide To Photoinjectors; CreateSpace Independent Publishing: Charleston, SC, USA, 2013; Available online: https://arxiv.org/abs/1403.7539 (accessed on 10 February 2025).
- Zhou, F.; Brachmann, A.; Emma, P.; Gilevich, S.; Huang, Z. Impact of the spatial laser distribution on photocathode gun operation. Phys. Rev. ST Accel. Beams 2012, 15, 090701. [Google Scholar] [CrossRef]
- Groß, M.; Aftab, N.; Boonpornprasert, P.; Chen, Y.; Georgiev, G.; Good, J.; Koschitzki, C.; Krasilnikov, M.; Li, X.; Lishilin, O.; et al. Characterization of Low Emittance Electron Beams Generated by Transverse Laser Beam Shaping. In Proceedings of the 12th International Particle Accelerator Conference, Proc. IPAC ’21, Campinas, Brazil, 24–28 May 2021; JACoW Publishing: Geneva, Switzerland, 2021; pp. 2690–2692. [Google Scholar] [CrossRef]
- Zhu, X.; Broemmelsiek, D.; Shin, Y. Theoretical and numerical analyses of a slit-masked chicane for modulated bunch generation. J. Instrum. 2015, 10, P10042. [Google Scholar] [CrossRef]
- Muggli, P.; Yakimenko, V.; Babzien, M.; Kallos, E.; Kusche, K. Generation of Trains of Electron Microbunches with Adjustable Subpicosecond Spacing. Phys. Rev. Lett. 2008, 101, 054801. [Google Scholar] [CrossRef] [PubMed]
- Andruszkow, J.; Aune, B.; Ayvazyan, V.; Baboi, N.; Bakker, R.; Balakin, V.; Barni, D.; Bazhan, A.; Bernard, M.; Bosotti, A.; et al. First Observation of Self-Amplified Spontaneous Emission in a Free-Electron Laser at 109 nm Wavelength. Phys. Rev. Lett. 2000, 85, 3825–3829. [Google Scholar] [CrossRef]
- Ackermann, W.; Asova, G.; Ayvazyan, V.; Azima, A.; Baboi, N.; Baehr, J.; Balandin, V.; Beutner, B.; Brandt, A.; Bolzmann, A.; et al. Operation of a free-electron laser from the extreme ultraviolet to the water window. Nat. Photonics 2007, 1, 336–342. [Google Scholar] [CrossRef]
- Altarelli, M.; Brinkmann, R.; Chergui, M.; Decking, W.; Dobson, B.; Düsterer, S.; Grübel, G.; Graeff, W.; Graafsma, H.; Hajdu, J.; et al. XFEL: The European X-ray Free-Electron Laser; Technical Design Report; DESY: Hamburg, Germany, 2006. [Google Scholar] [CrossRef]
- Decking, W.; Abeghyan, S.; Abramian, P.; Abramsky, A.; Aguirre, A.; Albrecht, C.; Alou, P.; Altarelli, M.; Altmann, P.; Amyan, K.; et al. A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator. Nat. Photonics 2020, 14, 391–397. [Google Scholar] [CrossRef]
- Loisch, G.; Chen, Y.; Koschitzki, C.; Qian, H.; Gross, M.; Hannah, A.; Hoffmann, A.; Kalantaryan, D.; Krasilnikov, M.; Lederer, S.; et al. Direct measurement of photocathode time response in a high-brightness photoinjector. Appl. Phys. Lett. 2022, 120, 104102. [Google Scholar] [CrossRef]
- Krasilnikov, M.; Aboulbanine, Z.; Adhikari, G.; Aftab, N.; Boonpornprasert, P.; Bousonville, M.; Brinker, F.; Castro Carballo, M.E.; Georgiev, G.; Good, J.; et al. RF Performance of a Next-Generation L-Band RF Gun at PITZ. In Proceedings of the 31st International Linear Accelerator Conference, LINAC2022, Liverpool, UK, 28 August–2 September 2022; JACoW Publishing: Geneva, Switzerland, 2022; pp. 699–702. [Google Scholar] [CrossRef]
- Krasilnikov, M.; Aboulbanine, Z.; Adhikari, G.; Aftab, N.; Asoyan, A.; Boonpornprasert, P.; Davtyan, H.; Georgiev, G.; Good, J.; Grebinyk, A.; et al. First high peak and average power single-pass THz free-electron laser in operation. Phys. Rev. Accel. Beams 2025, 28, 030701. [Google Scholar] [CrossRef]
- Li, X.; Amirkhanyan, Z.; Grebinyk, A.; Gross, M.; Komar, Y.; Riemer, F.; Asoyan, A.; Boonpornprasert, P.; Borchert, P.; Davtyan, H.; et al. Demonstration of ultra-high dose rate electron irradiation at FLASHlab@PITZ. Phys. Med. Biol. 2025. [Google Scholar] [CrossRef]
- Flöttmann, K. ASTRA—A Space Charge Tracking Algorithm. Available online: https://www.desy.de/~mpyflo/ (accessed on 13 March 2025).
- van der Geer, S.B.; de Loos, M.J. General Particle Tracer (GPT). Available online: https://www.pulsar.nl/gpt/ (accessed on 17 March 2025).
- Qiang, J.; Lidia, S.; Ryne, R.; Limborg-Deprey, C. Three-dimensional quasistatic model for high brightness beam dynamics simulation. Phys. Rev. ST Accel. Beams 2006, 9, 044204. [Google Scholar] [CrossRef]
- Trebino, R.; De Long, K.W.; Fittinghoff, D.N.; Sweetser, J.N.; Krumbügel, M.A.; Richman, B.A.; Kane, D.J. Measuring ultrashort laser pulses in the time-frequency domain using frequency-resolved optical gating. Rev. Sci. Instrum. 1997, 68, 3277–3295. [Google Scholar] [CrossRef]
- Sweetser, J.N.; Fittinghoff, D.N.; Trebino, R. Transient-grating frequency-resolved optical gating. Opt. Lett. 1997, 22, 519–521. [Google Scholar] [CrossRef] [PubMed]
- Krasilnikov, M.; Stephan, F.; Asova, G.; Grabosch, H.J.; Groß, M.; Hakobyan, L.; Isaev, I.; Ivanisenko, Y.; Jachmann, L.; Khojoyan, M.; et al. Experimentally minimized beam emittance from an L-band photoinjector. Phys. Rev. ST Accel. Beams 2012, 15, 100701. [Google Scholar] [CrossRef]
- Will, I. Generation of flat-top picosecond pulses by means of a two-stage birefringent filter. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrom. Detect. Assoc. Equip. 2008, 594, 119–125. [Google Scholar] [CrossRef]
- Liu, F.; Huang, S.; Si, S.; Zhao, G.; Liu, K.; Zhang, S. Generation of picosecond pulses with variable temporal profiles and linear polarization by coherent pulse stacking in a birefringent crystal shaper. Opt. Express 2019, 27, 1467–1478. [Google Scholar] [CrossRef]
- Schmidt, B.; Hacker, M.; Stobrawa, G.; Feurer, T. LAB2—A Virtual Femtosecond Laser Lab. Available online: http://www.lab2.de (accessed on 13 July 2012).



| Longitudinal Shape | Transversal Shape | BSA [mm] | [A] | [mm · mrad] | [ps] | [keV · mm] | Relative Reduction | Improvement | |
|---|---|---|---|---|---|---|---|---|---|
| Gaussian | Radial uniform | 1.1 | 373 | 0.535 | 5.09 | 32.3 | 3447 | 100% | 1 |
| Super-Gaussian | Truncated Gaussian (0.9) | 1.3 | 374 | 0.439 | 4.78 | 25.6 | 4995 | −18% | 1.4 |
| Flattop | Truncated Gaussian (0.9) | 1.3 | 374 | 0.339 | 4.17 | 17.5 | 7162 | −37% | 2.1 |
| Parabolic | Truncated Gaussian (0.9) | 1.3 | 374 | 0.318 | 4.26 | 16.9 | 8909 | −41% | 2.6 |
| Truncated Gaussian (1.5) | Truncated Gaussian (0.9) | 1.1 | 374 | 0.297 | 4.25 | 17.4 | 9647 | −45% | 2.8 |
| Ellipsoidal | Truncated Gaussian (0.9) | 1.1 | 376 | 0.242 | 4.29 | 13.7 | 12,775 | −55% | 3.7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoffmann, A.; Zeeshan, S.; Good, J.; Gross, M.; Krasilnikov, M.; Stephan, F. Efficient Generation of Transversely and Longitudinally Truncated Chirped Gaussian Laser Pulses for Application in High-Brightness Photoinjectors. Photonics 2025, 12, 460. https://doi.org/10.3390/photonics12050460
Hoffmann A, Zeeshan S, Good J, Gross M, Krasilnikov M, Stephan F. Efficient Generation of Transversely and Longitudinally Truncated Chirped Gaussian Laser Pulses for Application in High-Brightness Photoinjectors. Photonics. 2025; 12(5):460. https://doi.org/10.3390/photonics12050460
Chicago/Turabian StyleHoffmann, Andreas, Sumaira Zeeshan, James Good, Matthias Gross, Mikhail Krasilnikov, and Frank Stephan. 2025. "Efficient Generation of Transversely and Longitudinally Truncated Chirped Gaussian Laser Pulses for Application in High-Brightness Photoinjectors" Photonics 12, no. 5: 460. https://doi.org/10.3390/photonics12050460
APA StyleHoffmann, A., Zeeshan, S., Good, J., Gross, M., Krasilnikov, M., & Stephan, F. (2025). Efficient Generation of Transversely and Longitudinally Truncated Chirped Gaussian Laser Pulses for Application in High-Brightness Photoinjectors. Photonics, 12(5), 460. https://doi.org/10.3390/photonics12050460






