Mitigating the Impact of Satellite Vibrations on the Acquisition of Satellite Laser Links Through Optimized Scan Path and Parameters
Abstract
1. Introduction
2. Acquisition, Pointing, and Tracking in Inter-Satellite Laser Links
2.1. Acquisition Schemes
2.1.1. Stare/Stare
2.1.2. Stare/Scan
2.1.3. Scan/Scan
2.1.4. Scan/Stare
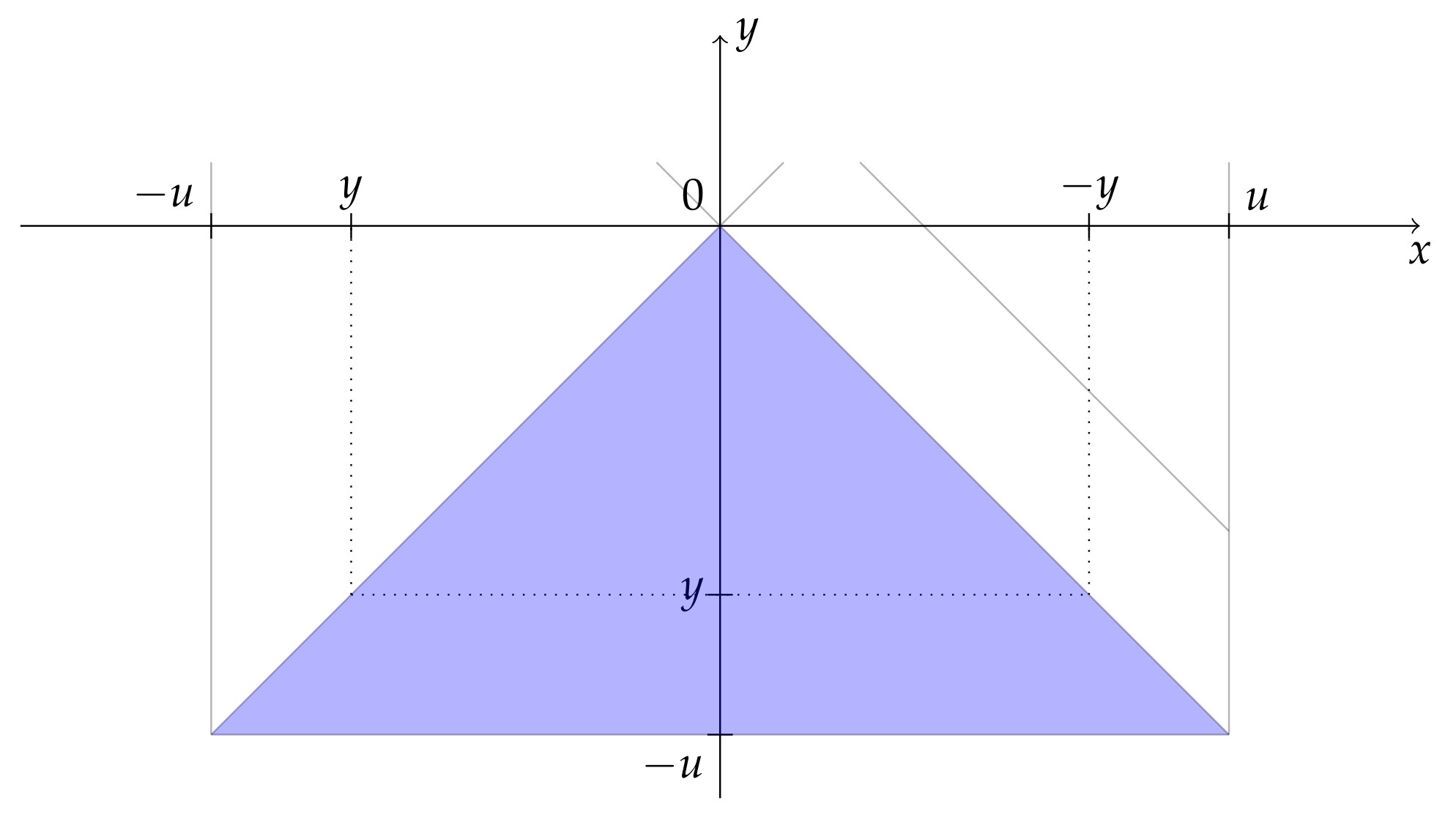
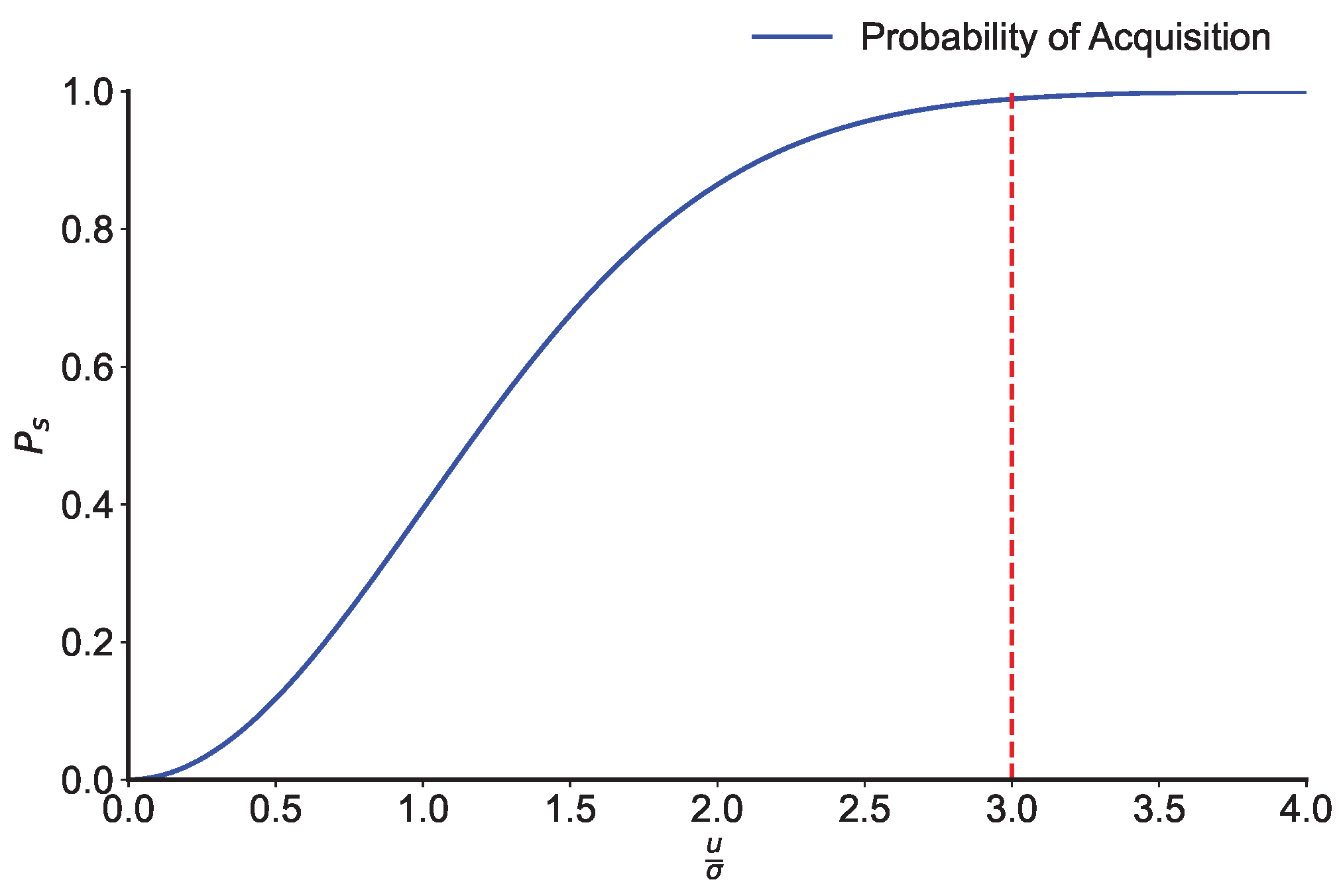
2.2. Receiver Satellite Probability Density Function in the Presence of Pointing Error
3. Types of Scanning Patterns
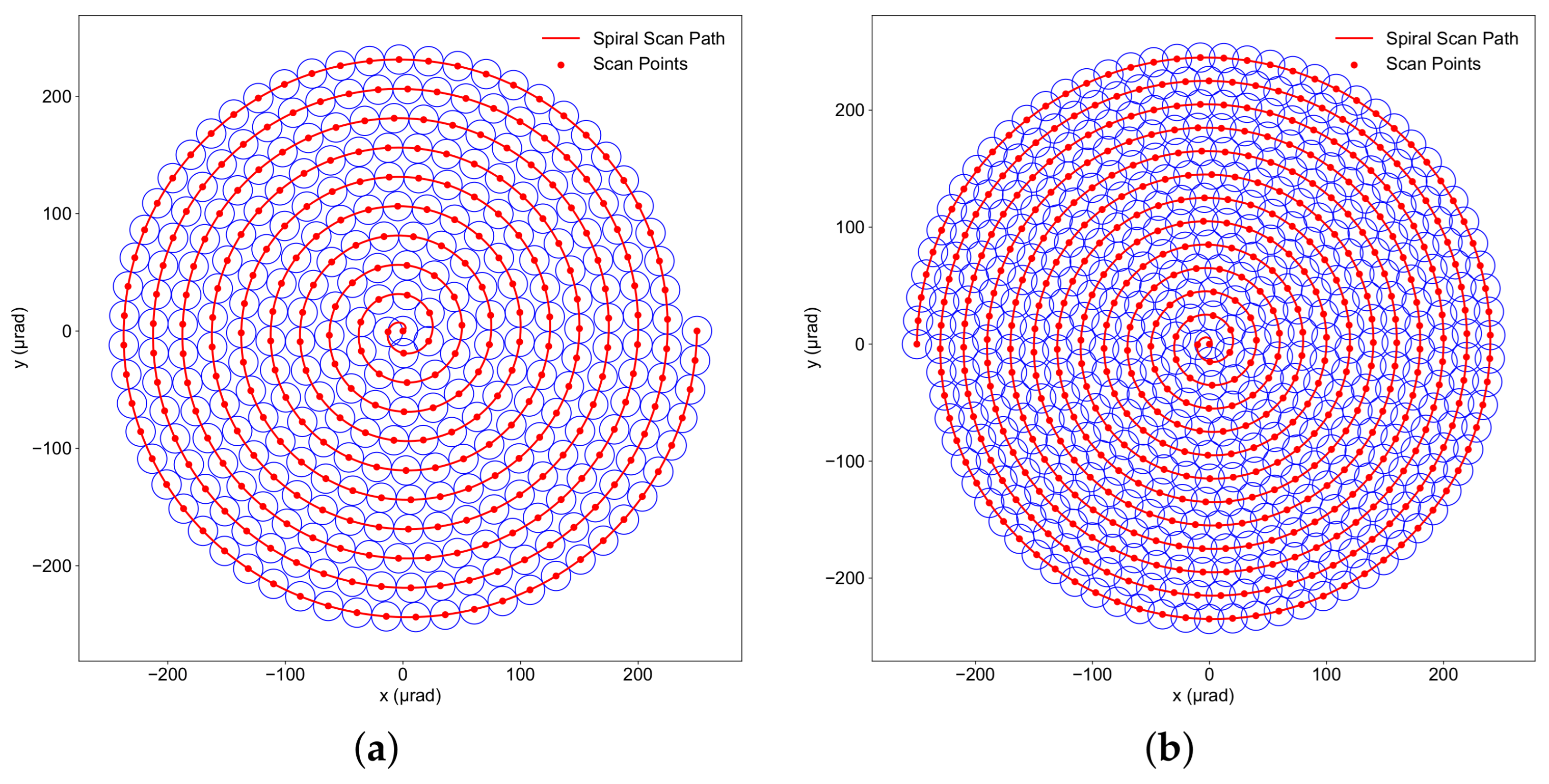
3.1. Spiral Scanning
3.1.1. Spiral Scan Trajectory
3.1.2. Mean Acquisition Time for Spiral Scan
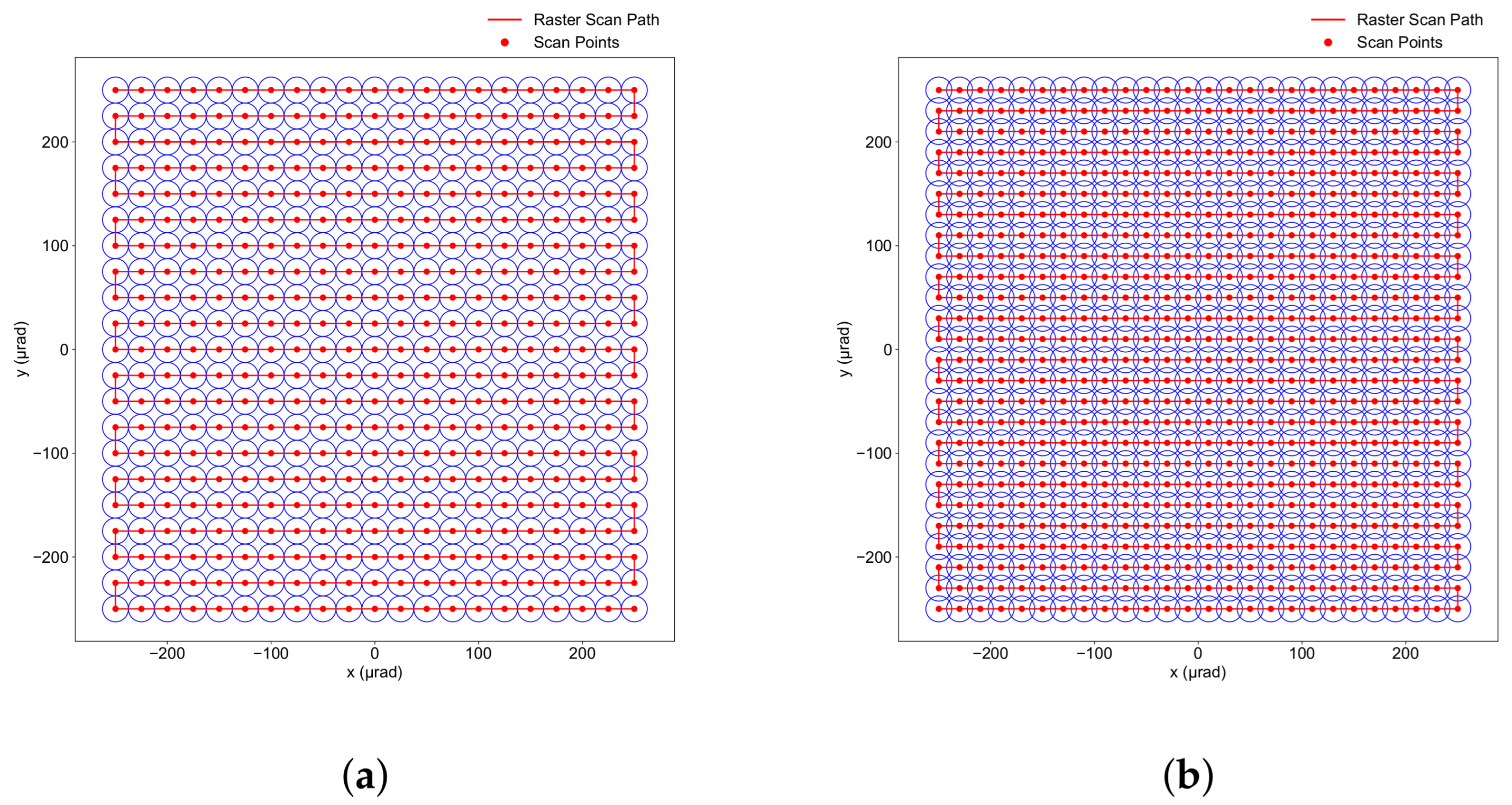
3.2. Raster Scanning
3.2.1. Raster Scan Trajectory
3.2.2. Mean Acquisition Time for Raster Scan
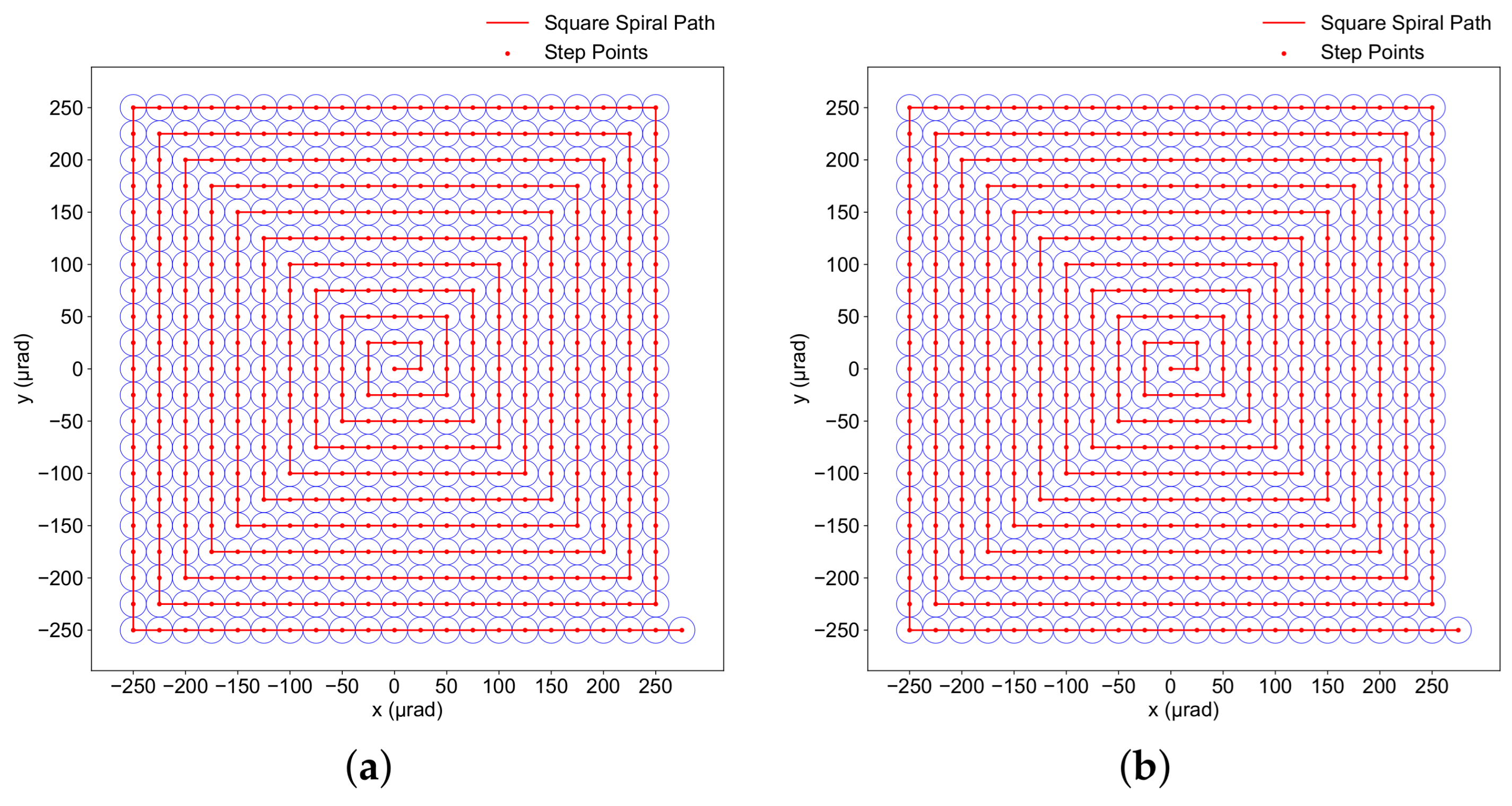
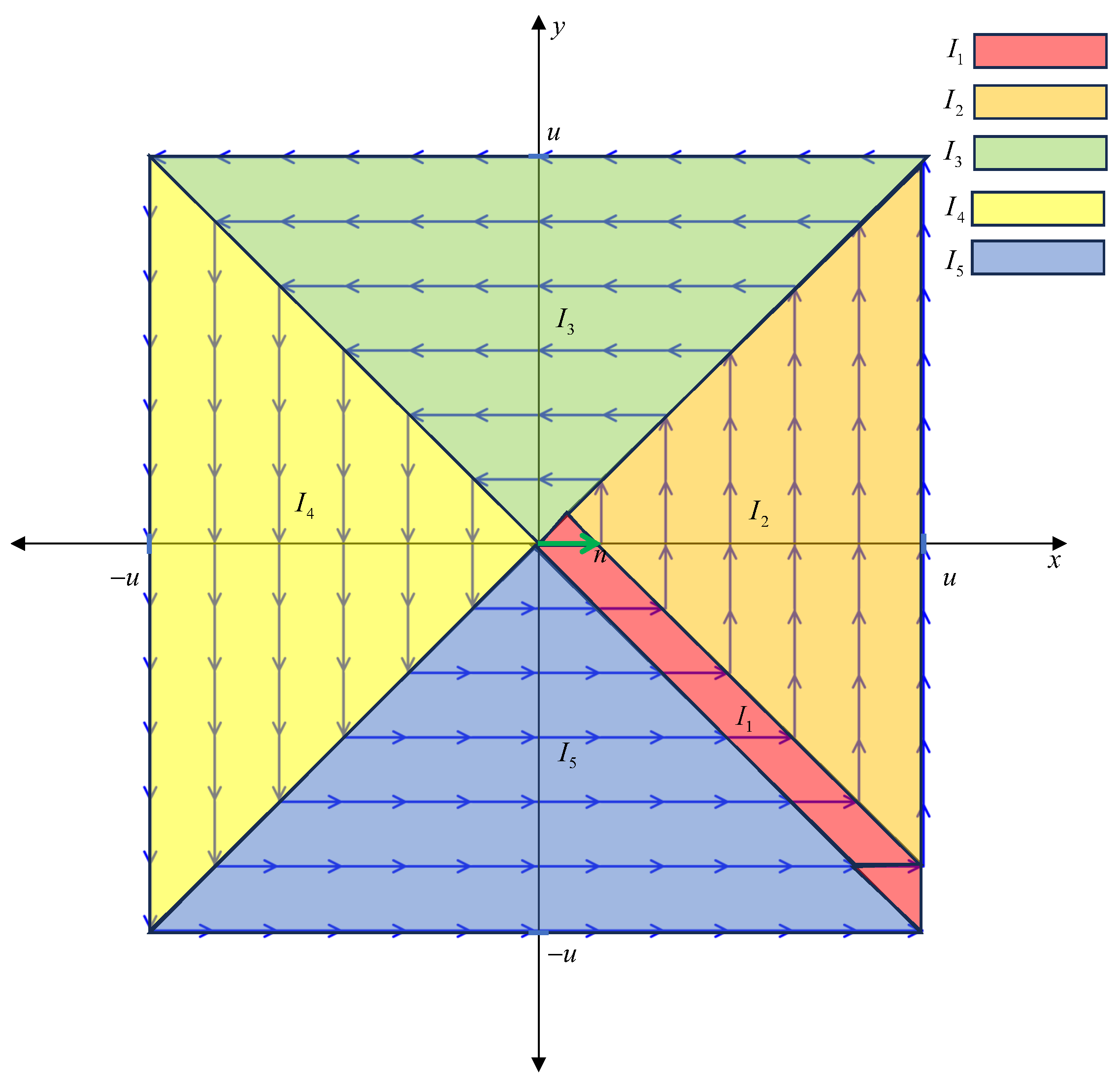
3.3. Square Spiral Scanning
3.3.1. Square Spiral Scan Trajectory
3.3.2. Mean Acquisition Time for Square Spiral
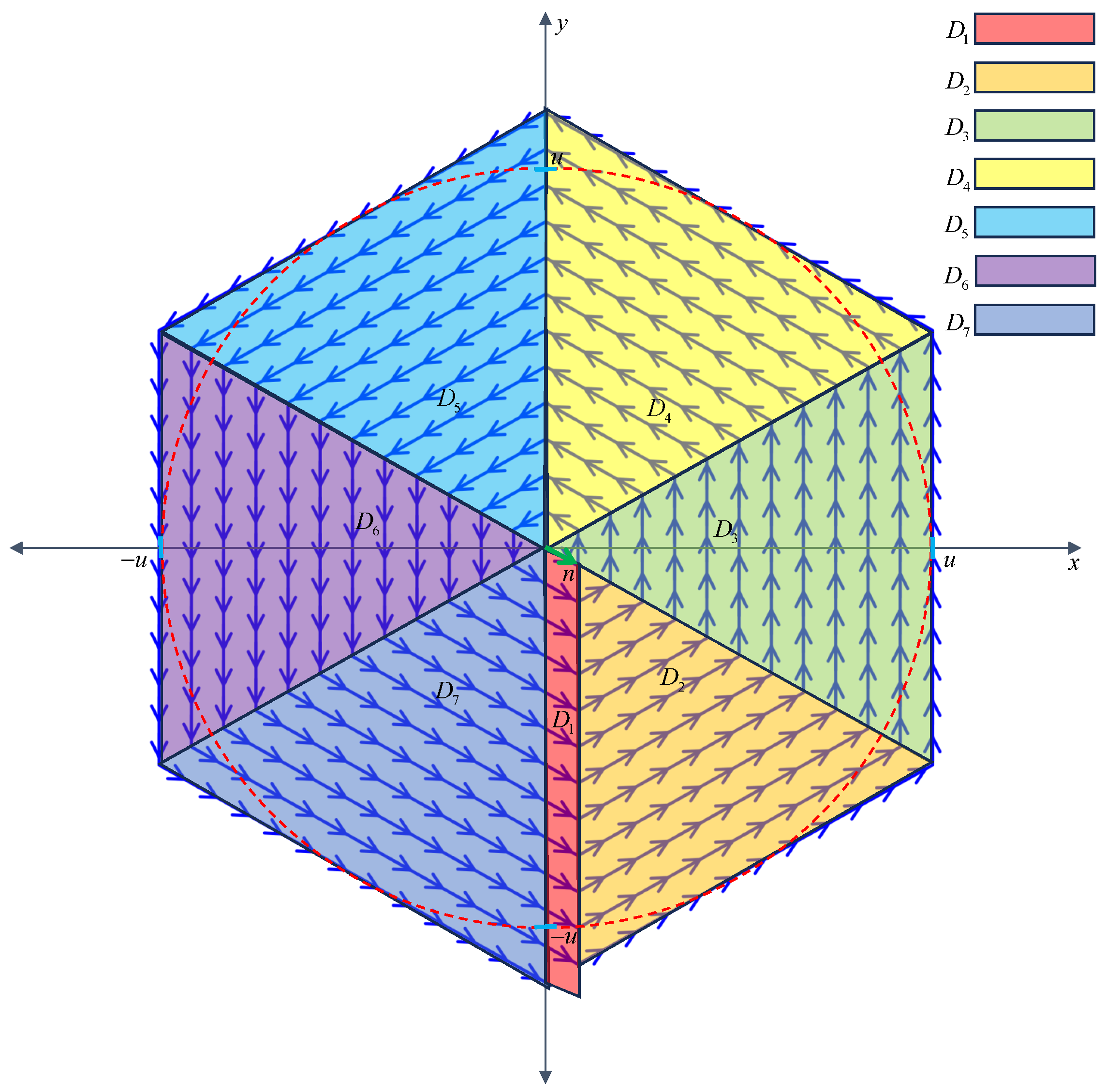
3.4. Hexagon Scanning
3.4.1. Hexagon Scan Trajectory
3.4.2. Mean Acquisition Time for Hexagon Scan
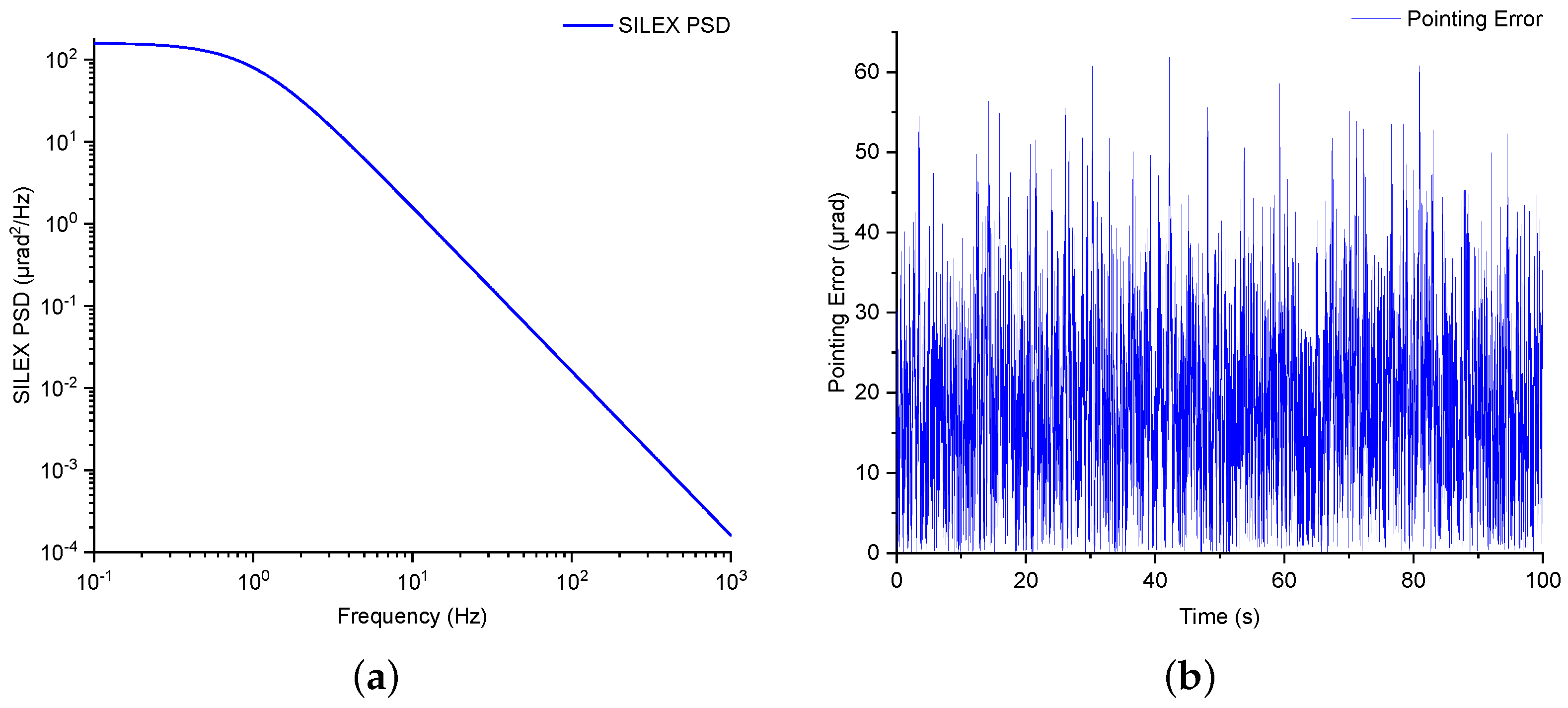
4. Satellite Platform Vibration Spectrum Model
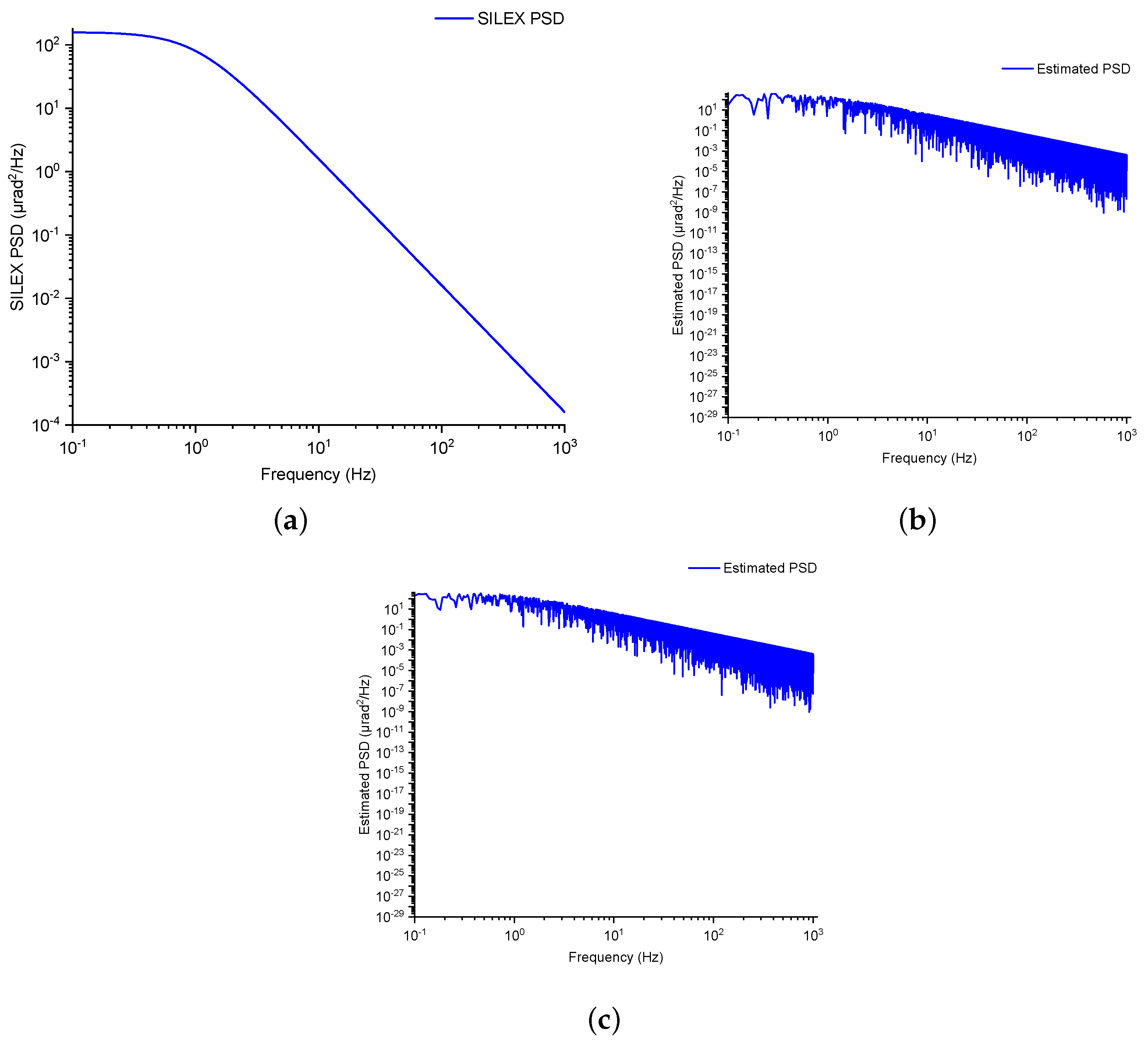
4.1. Power Spectral Density
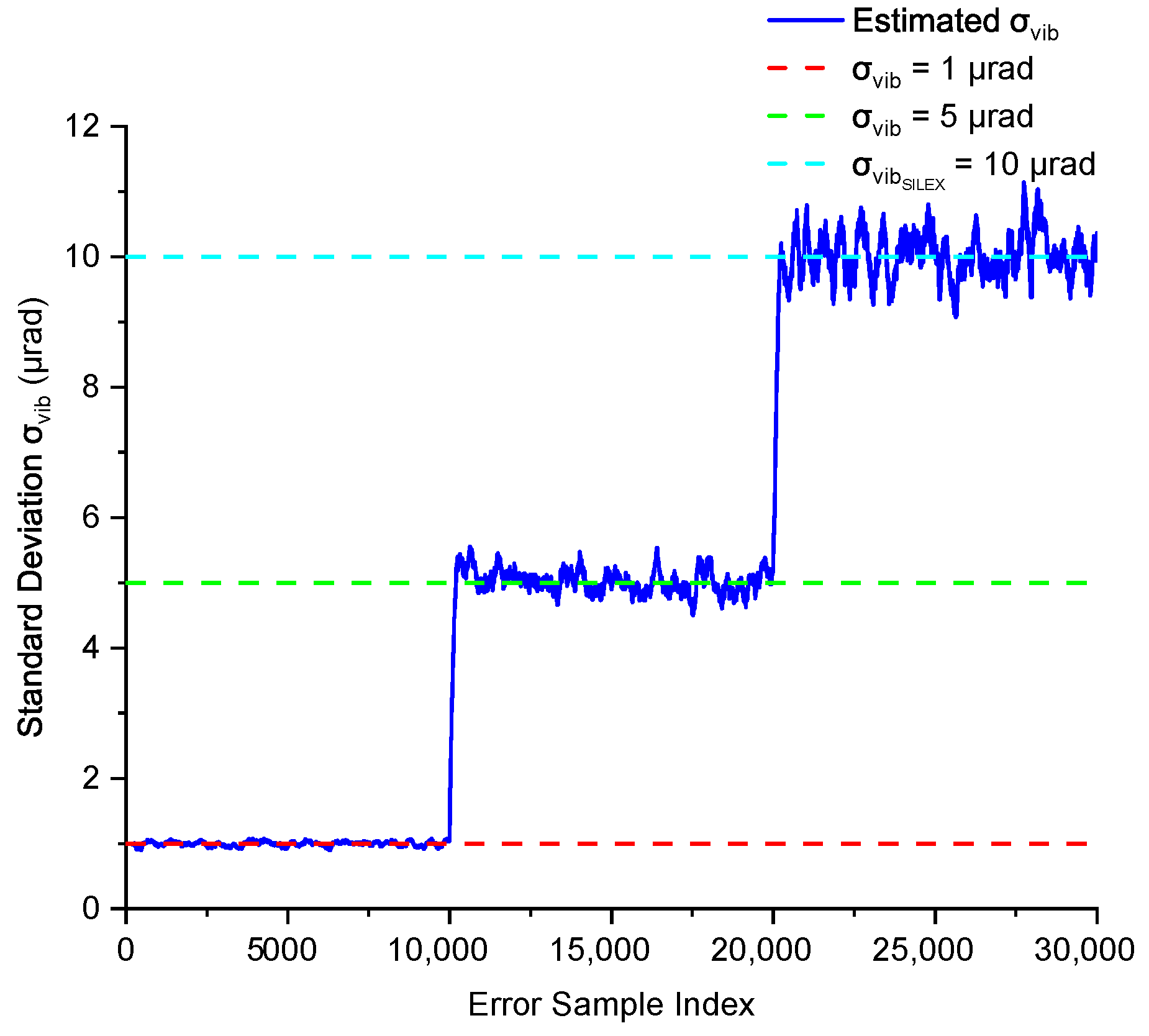
4.2. Maximum Likelihood Estimation (MLE) of Vibration Error
5. Optimization of Scan Parameters
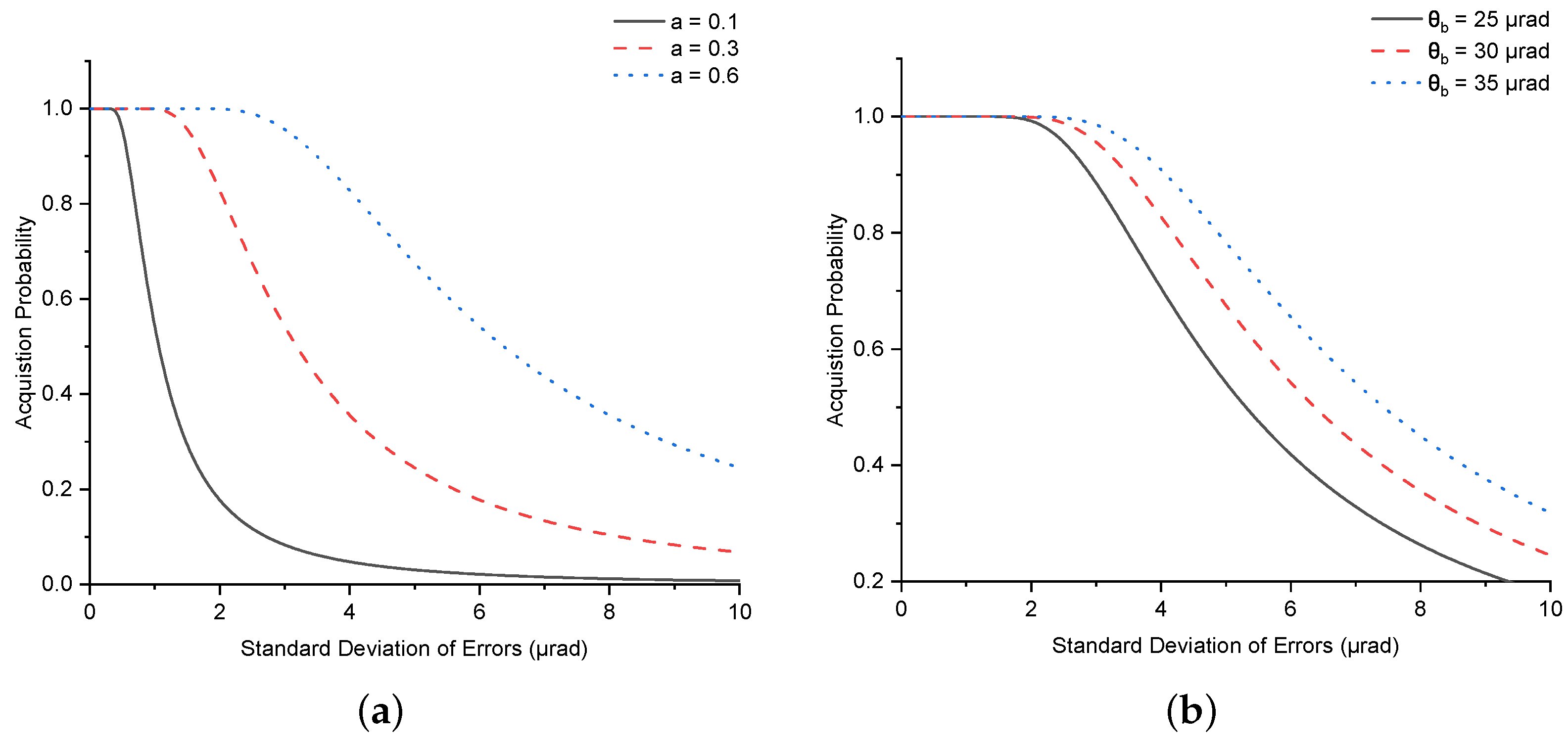
5.1. Overlap Factor
5.2. Beam Divergence
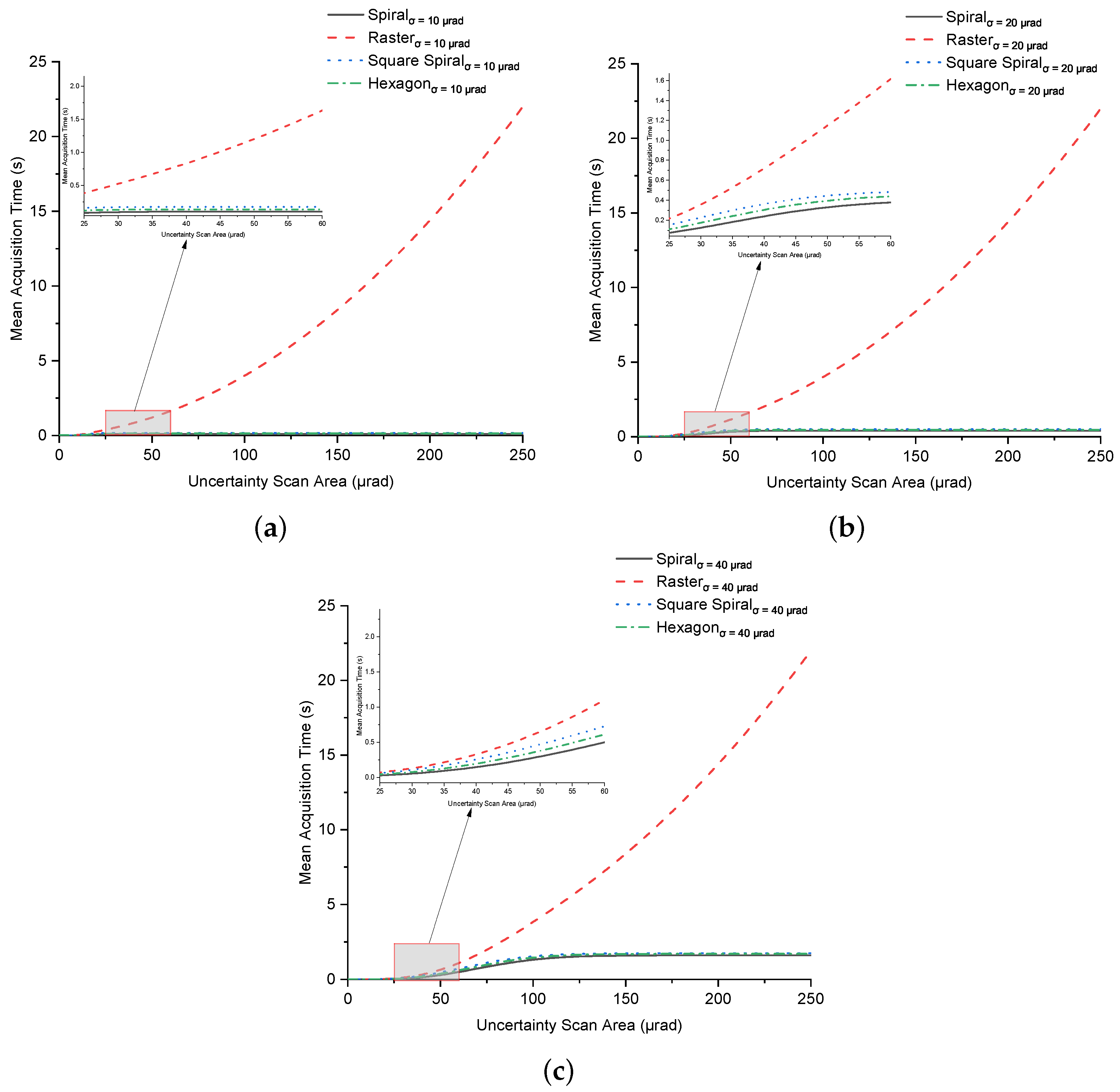
5.3. Uncertainty Area Size
6. Simulation Results and Discussion
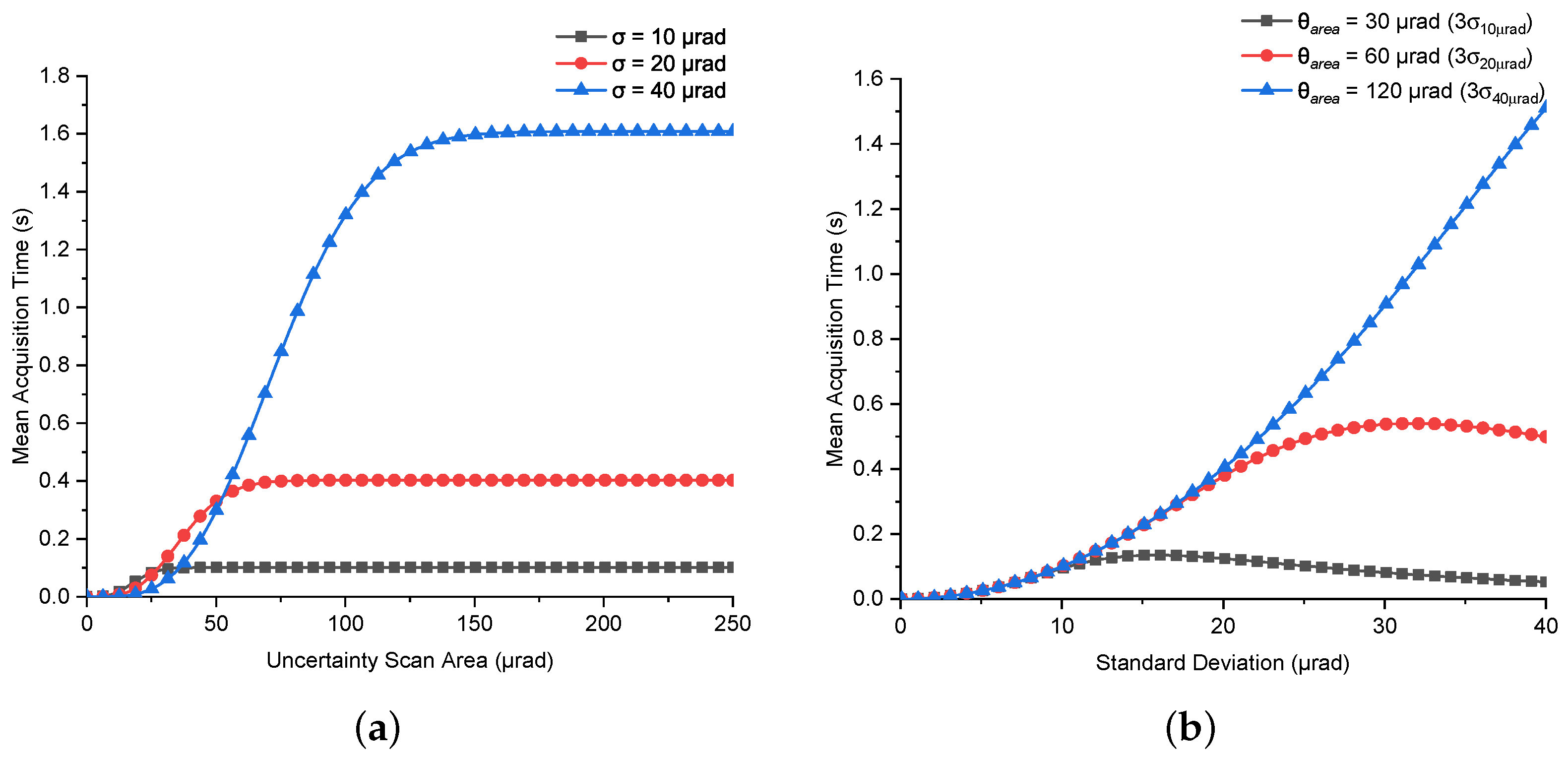
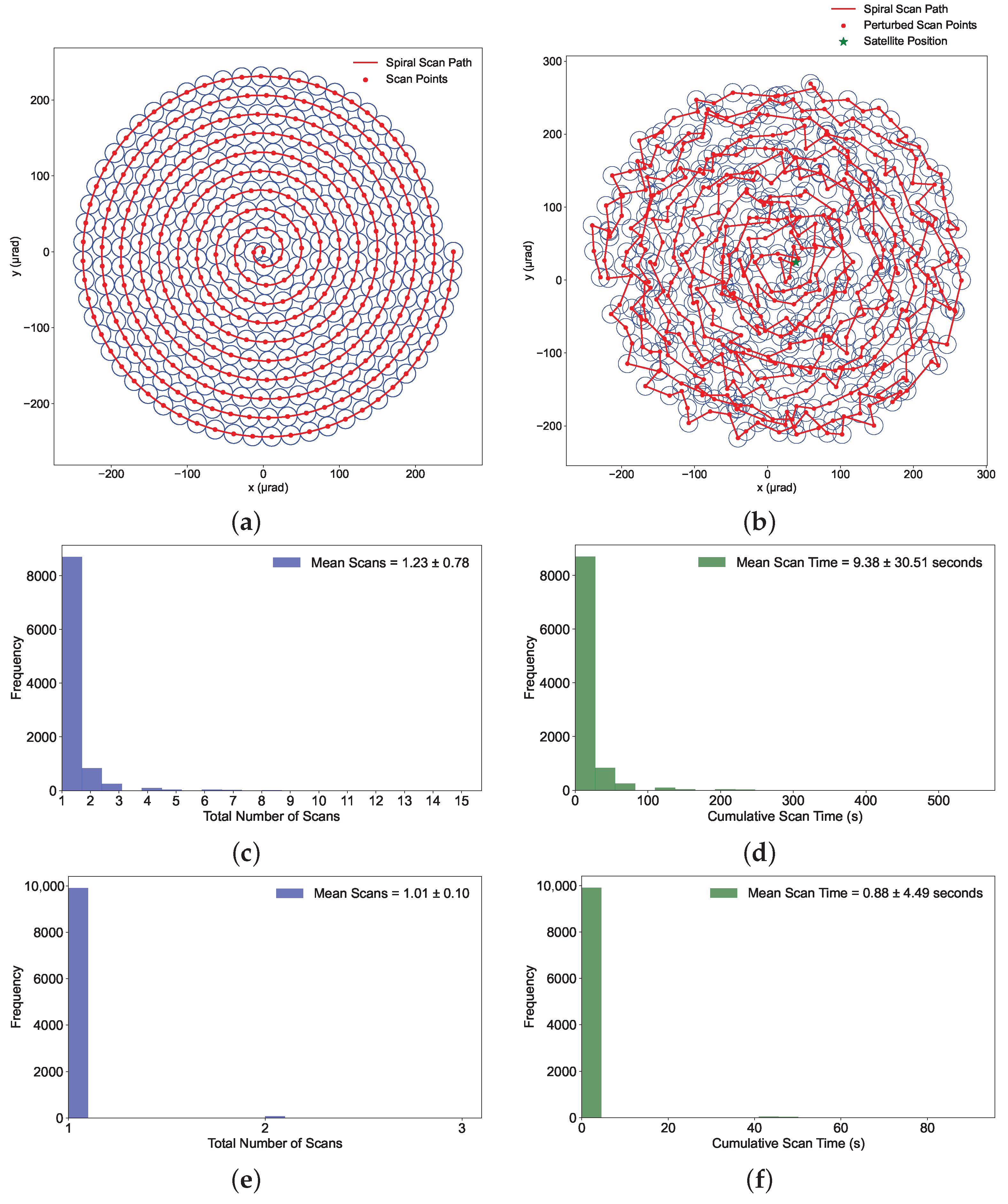
6.1. Mean Acquisition Time Using Spiral Scan
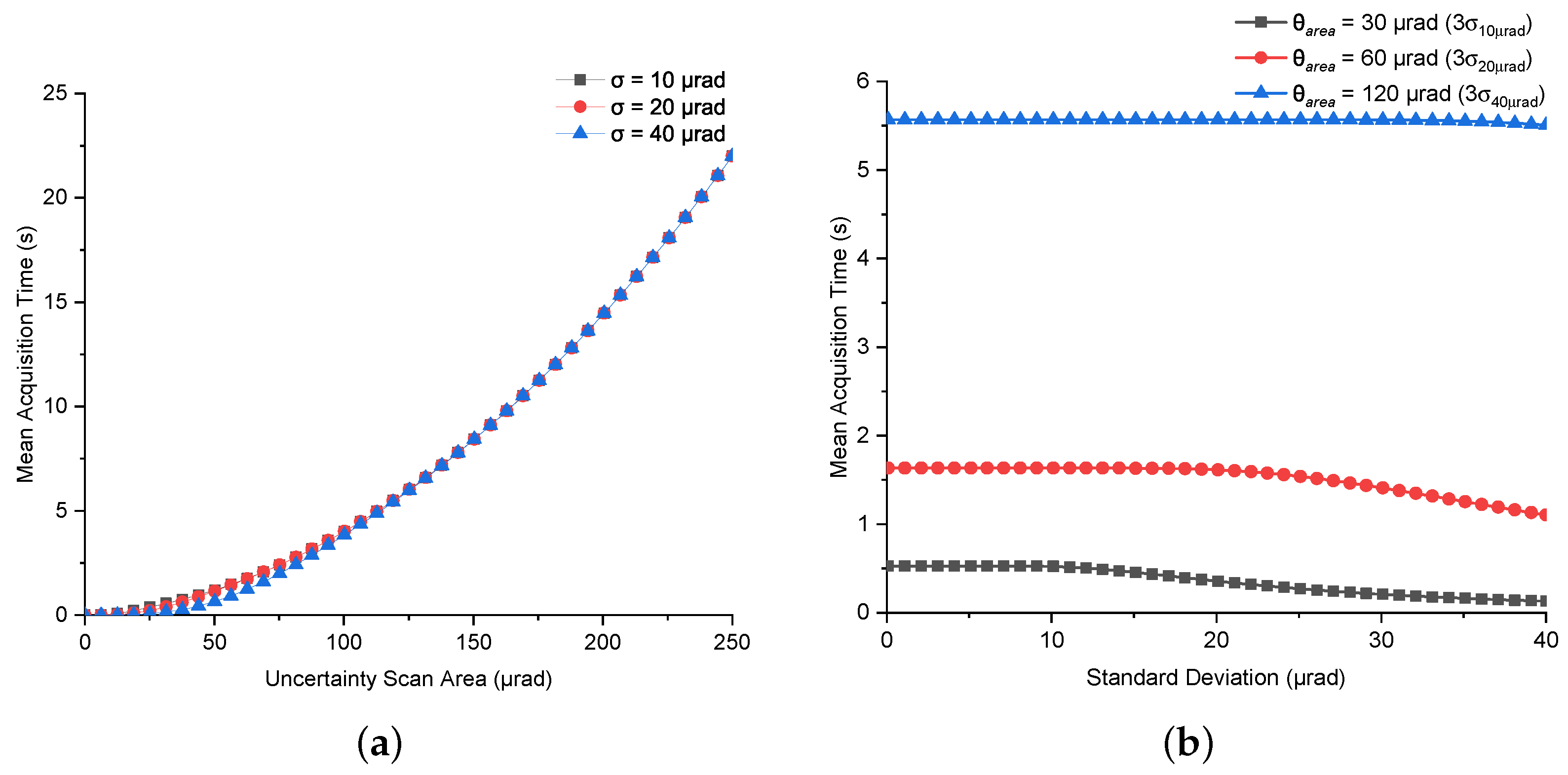
6.2. Mean Acquisition Time Using Raster Scan
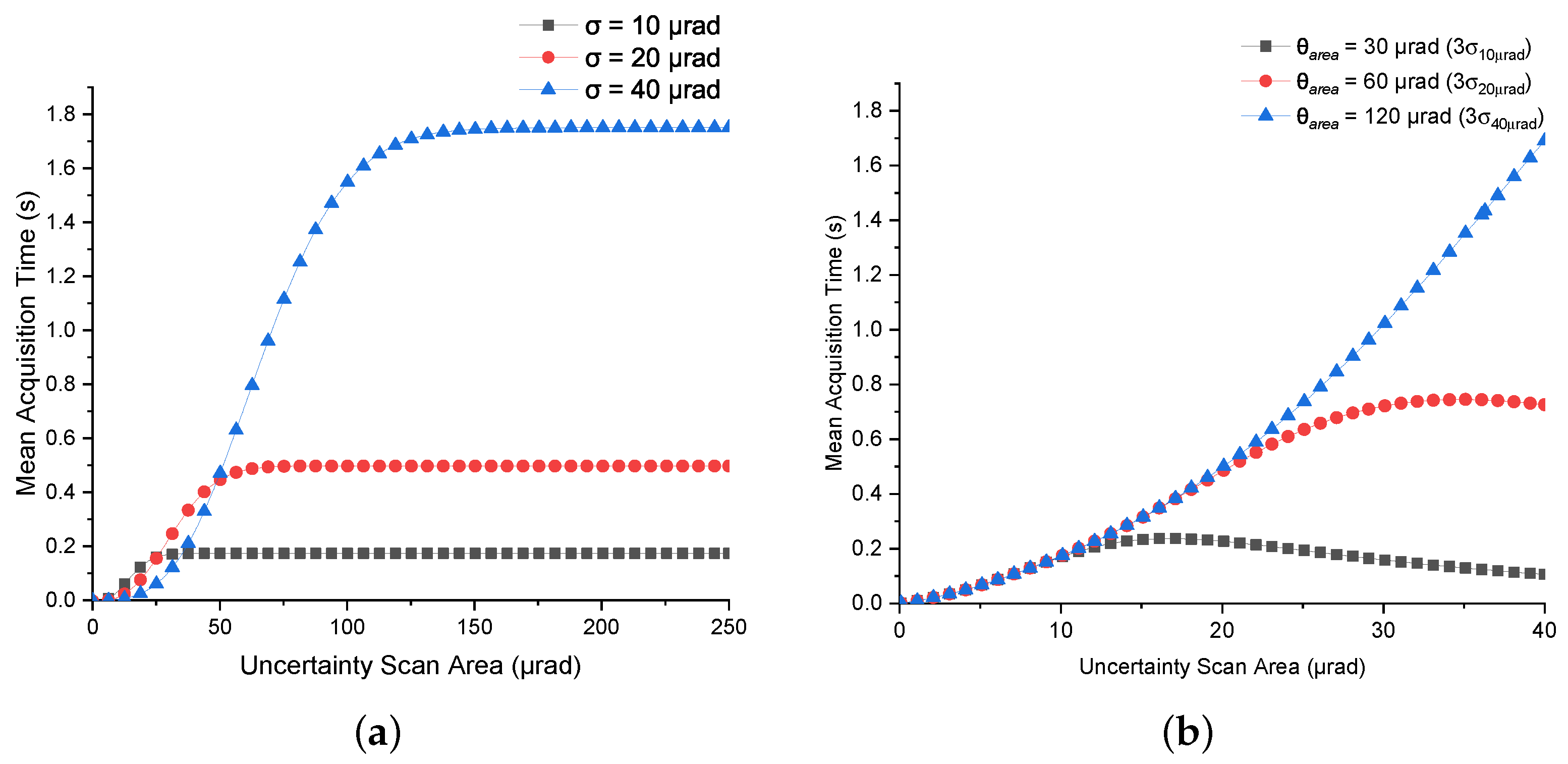
6.3. Mean Acquisition Time Using Square Spiral Scan
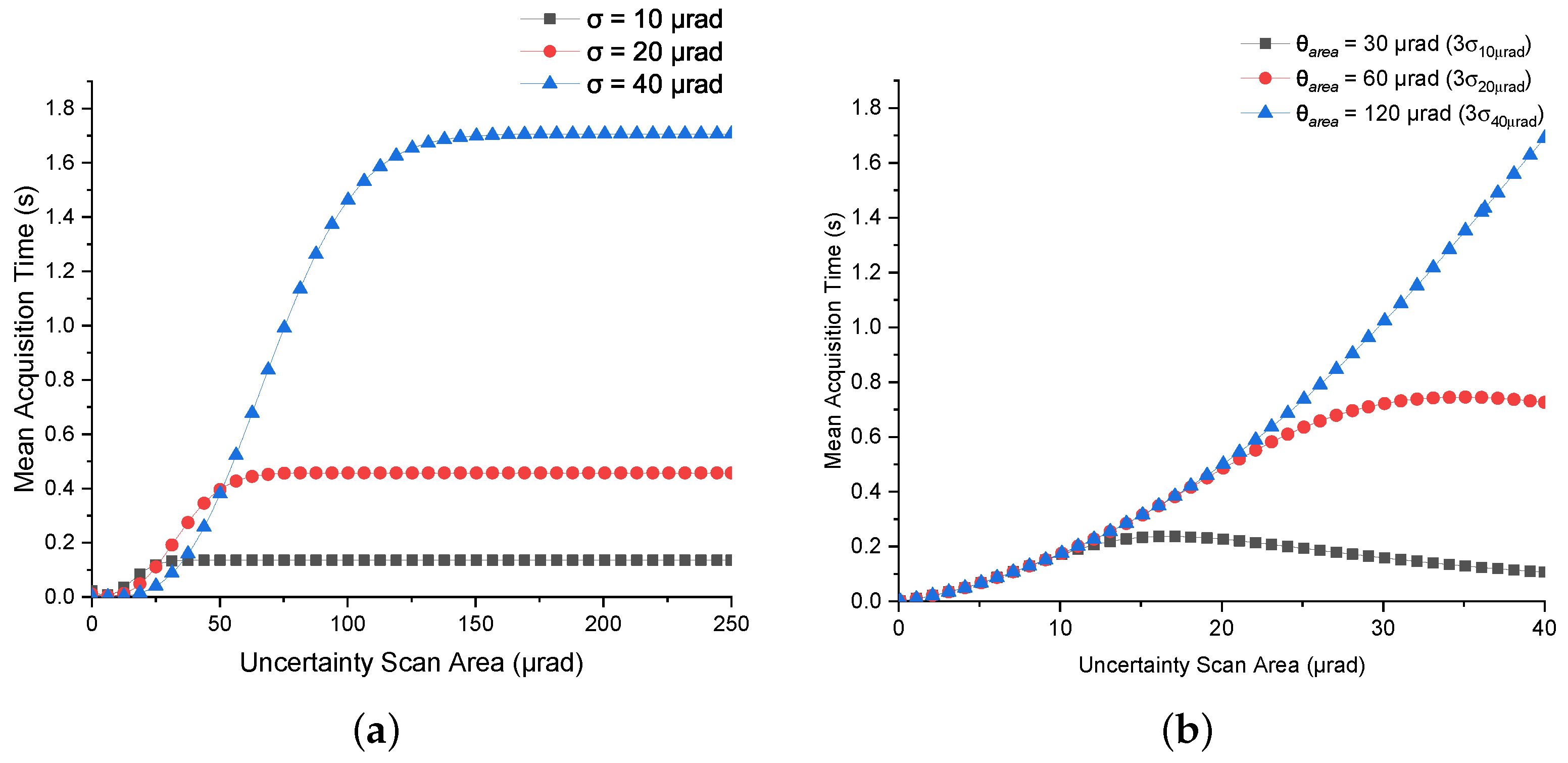
6.4. Mean Acquisition Time Using Hexagon Scan
6.5. Error Estimation for Satellite Vibration Effects
6.6. Impact of Scan Parameters on Acquisition Performance
6.7. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ABC | Adaptive Beam Control |
| LOS | Line-of-sight |
| ESA | European Space Agency |
| GPS | Global Positioning System |
| IoT | Internet of Things |
| MLE | Maximum Likelihood Estimation |
| OWC | Optical Wireless Communication |
| PAA | Point Ahead Angle |
| APT | Acquisition Pointing and Tracking |
| VFL | Variable Focus Lens |
| BER | Bit Error Rate |
| DFT | Discrete Fourier Transform |
| FOU | Field of Uncertainty |
| FOV | Field of View |
| PSD | Power Spectral Density |
| Probability Density Function | |
| RMSE | Root Mean Square Error |
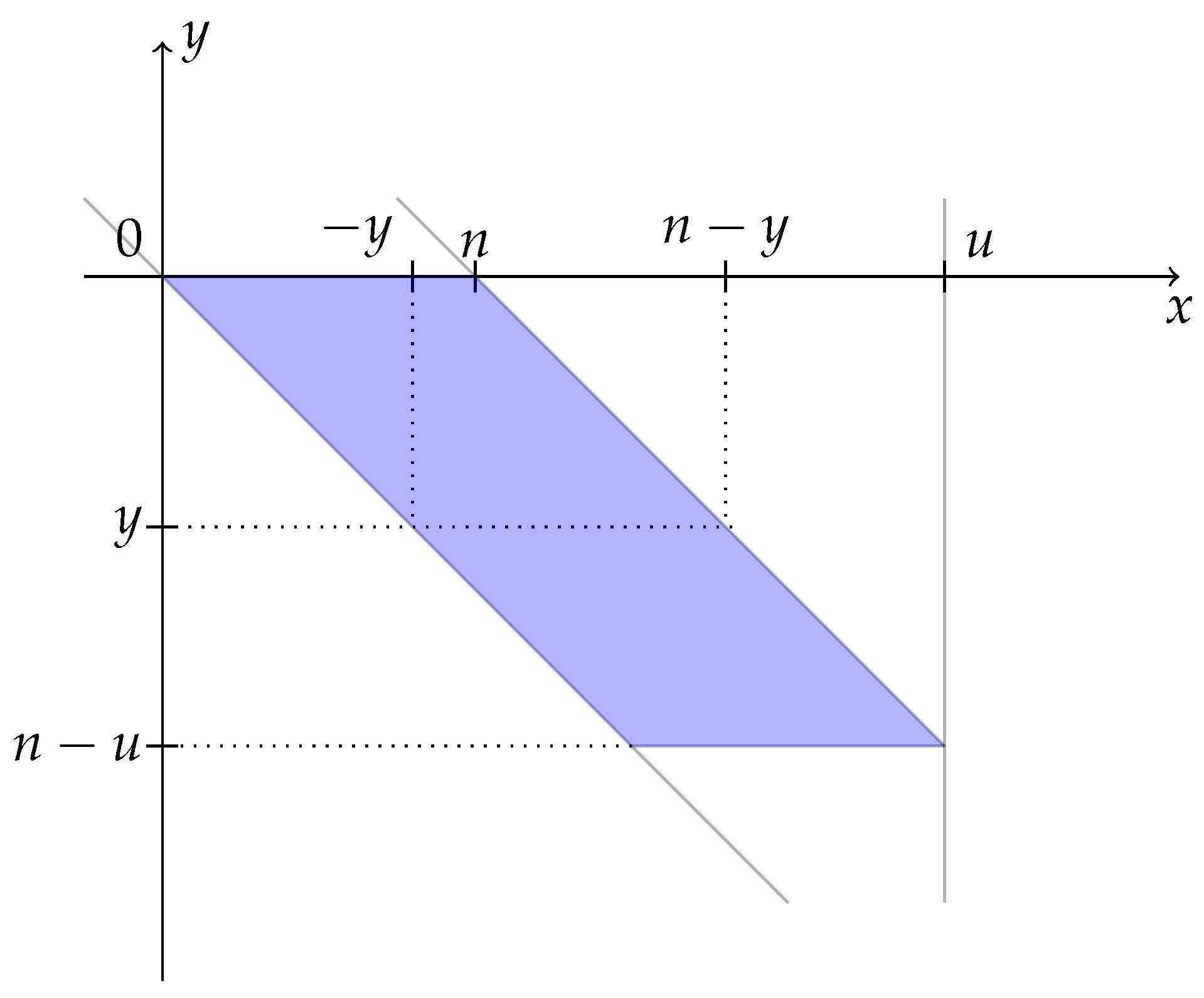
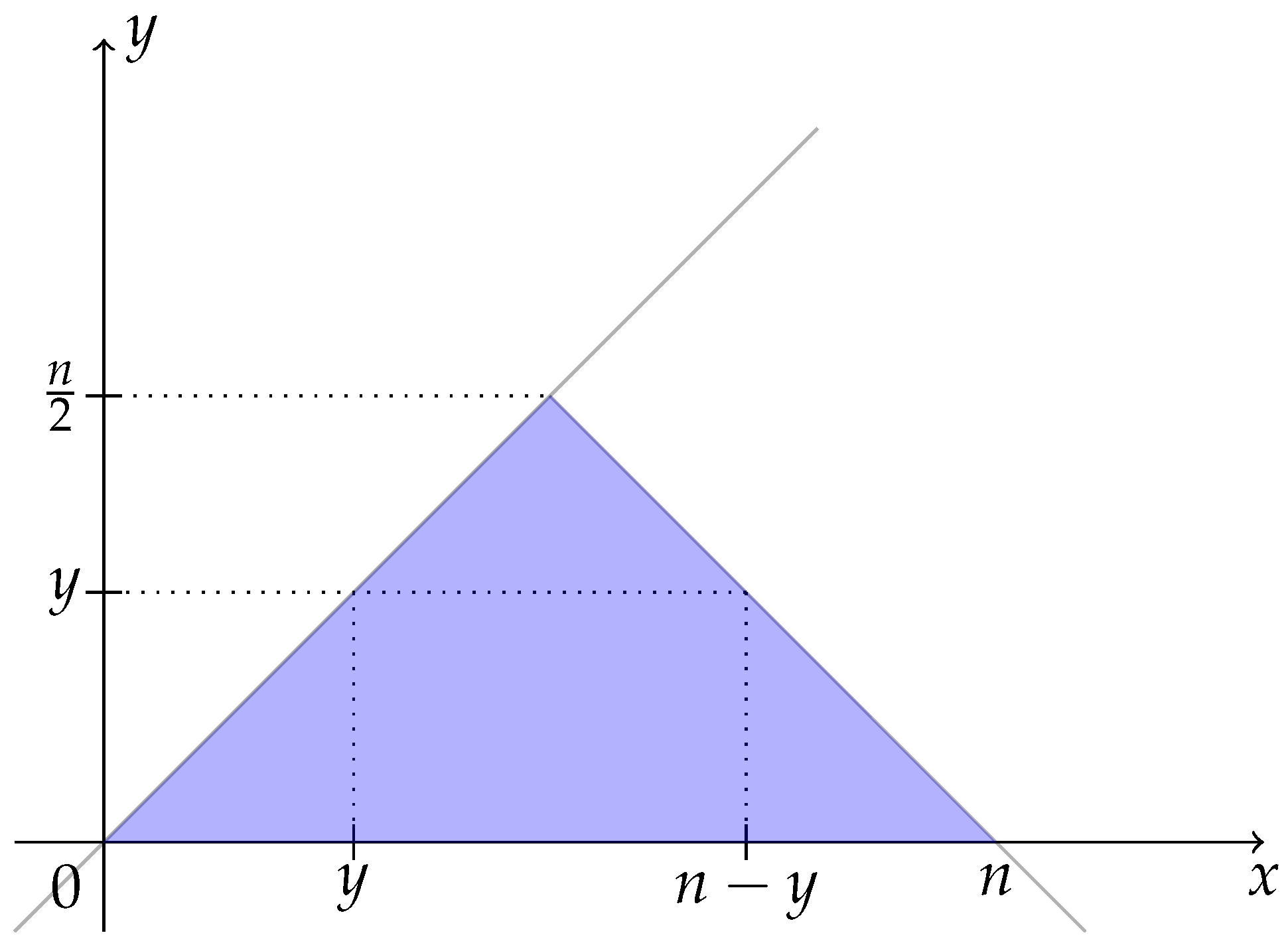
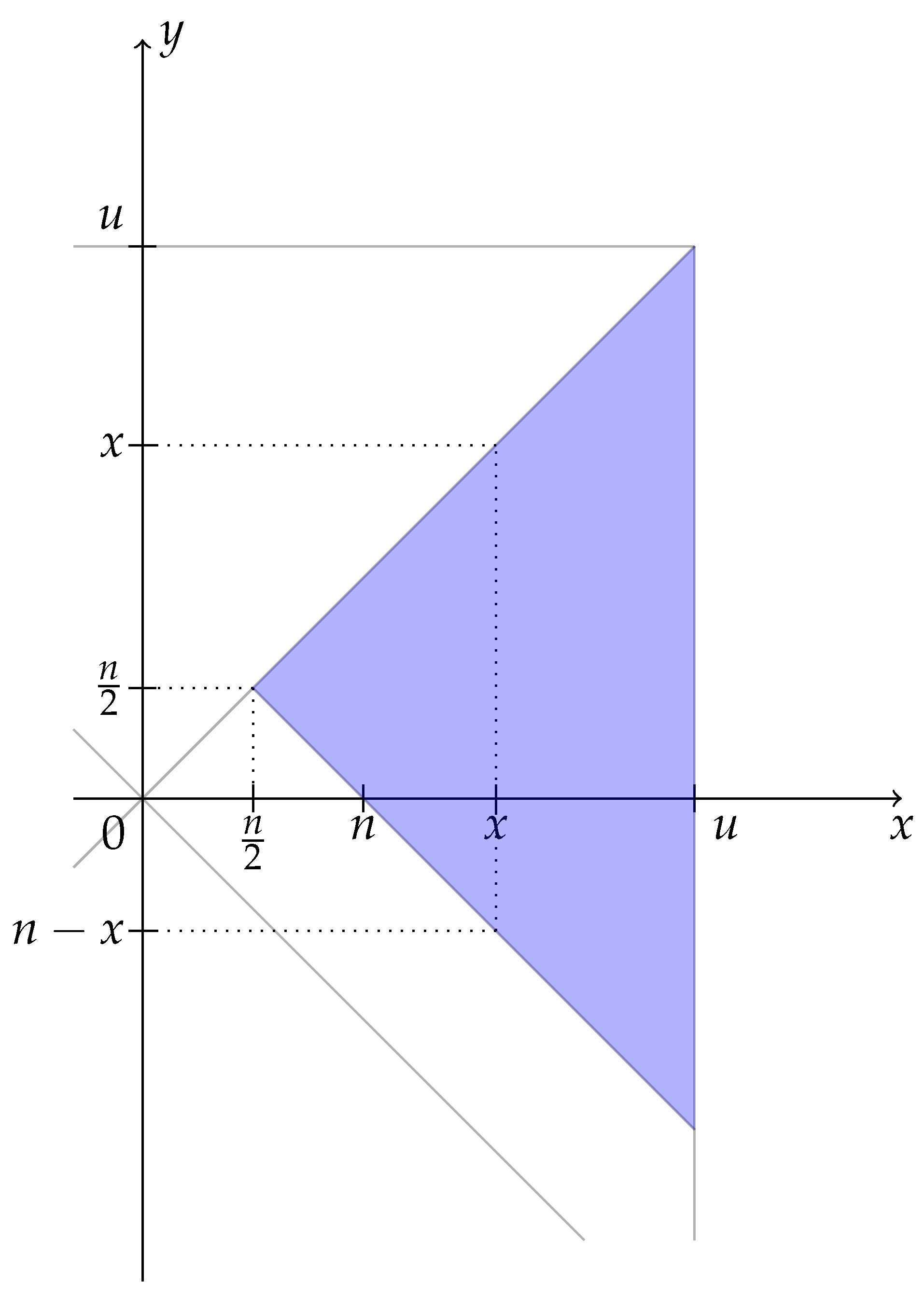
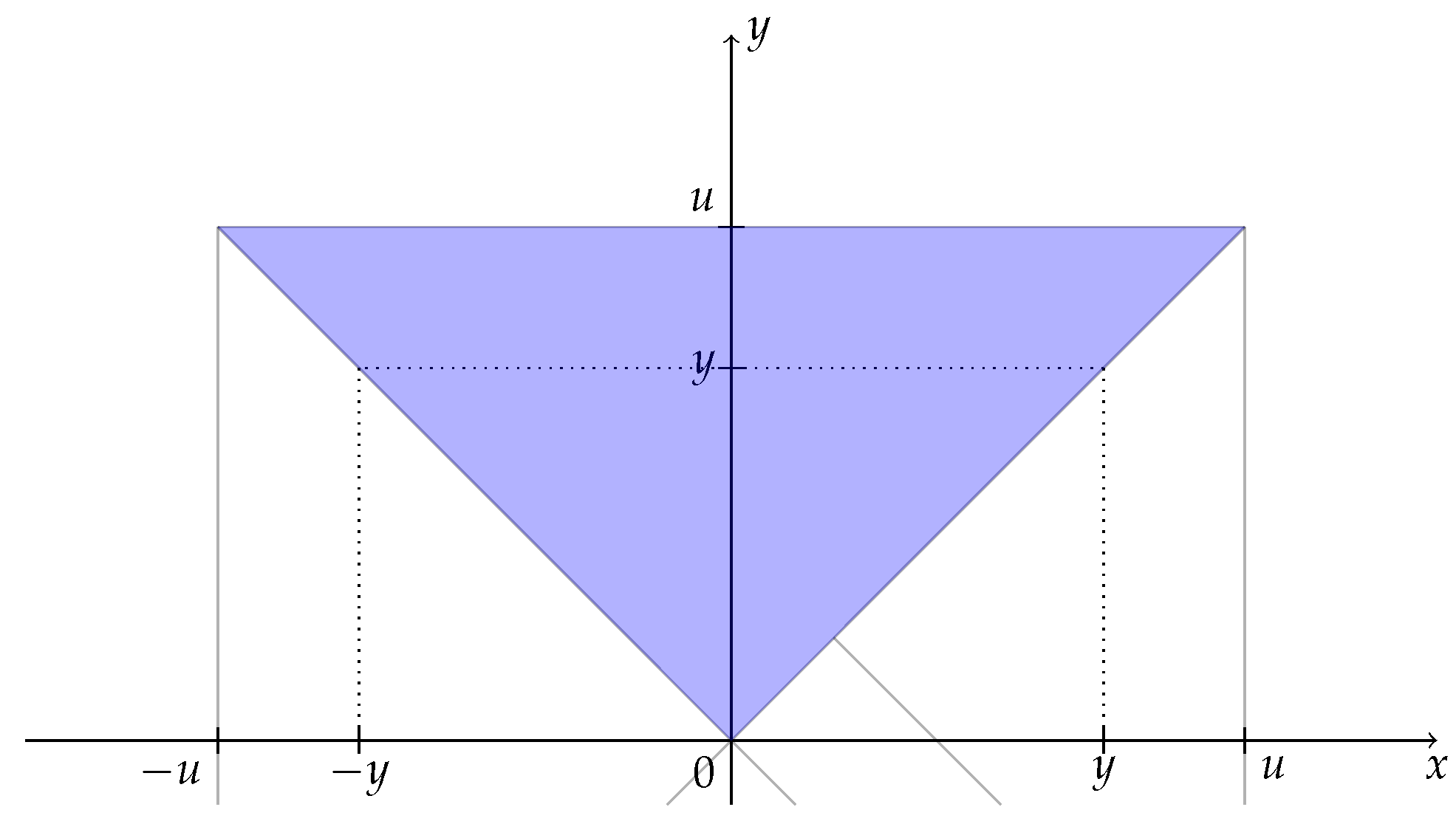
Appendix A


References
- Raj, A.B.; Majumder, A.K. Historical perspective of free space optical communications: From the early dates to today’s developments. IET Commun. 2019, 13, 2405–2419. [Google Scholar] [CrossRef]
- Raj, A.A.B.; Krishnan, P.; Darusalam, U.; Kaddoum, G.; Ghassemlooy, Z.; Abadi, M.M.; Majumdar, A.K.; Ijaz, M. A Review–Unguided Optical Communications: Developments, Technology Evolution, and Challenges. Electronics 2023, 12, 1922. [Google Scholar] [CrossRef]
- Jahid, A.; Alsharif, M.H.; Hall, T.J. A contemporary survey on free space optical communication: Potentials, technical challenges, recent advances and research direction. J. Netw. Comput. Appl. 2022, 200, 103311. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical Communication in Space: Challenges and Mitigation Techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef]
- Zafar, S.; Khalid, H. Free Space Optical Networks: Applications, Challenges and Research Directions. Wirel. Pers. Commun. 2021, 121, 429–457. [Google Scholar] [CrossRef]
- Khalighi, M.A.; Uysal, M. Survey on Free Space Optical Communication: A Communication Theory Perspective. IEEE Commun. Surv. Tutor. 2014, 16, 2231–2258. [Google Scholar] [CrossRef]
- Sova, R.M.; Sluz, J.E.; Young, D.W.; Juarez, J.C.; Dwivedi, A.; Demidovich, N.M., III; Graves, J.E.; Northcott, M.; Douglass, J.; Phillips, J.; et al. 80 Gb/s free-space optical communication demonstration between an aerostat and a ground terminal. In Proceedings of the Free Laser Communication VI, San Diego, CA, USA, 1 September 2006; SPIE: St Bellingham, WA, USA, 2006; Volume 6304, p. 630414. [Google Scholar] [CrossRef]
- Gregory, M. Commercial optical inter-satellite communication at high data rates. Opt. Eng. 2012, 51, 031202. [Google Scholar] [CrossRef]
- Zhang, X.; Klevering, G.; Lei, X.; Hu, Y.; Xiao, L.; Tu, G.H. The Security in Optical Wireless Communication: A Survey. ACM Comput. Surv. 2023, 55, 3594718. [Google Scholar] [CrossRef]
- Kodheli, O.; Lagunas, E.; Maturo, N.; Sharma, S.K.; Shankar, B.; Montoya, J.F.M.; Duncan, J.C.M.; Spano, D.; Chatzinotas, S.; Kisseleff, S.; et al. Satellite Communications in the New Space Era: A Survey and Future Challenges. IEEE Commun. Surv. Tutor. 2021, 23, 70–109. [Google Scholar] [CrossRef]
- Liu, W.; Ding, J.; Zheng, J.; Chen, X.; Lin, C. Relay-Assisted Technology in Optical Wireless Communications: A Survey. IEEE Access 2020, 8, 194384–194409. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Erdogan, E.; Yanikomeroglu, H.; Kurt, G.K.; Hu, P.; Ahmed, K.; Martel, S. Free-Space Optical (FSO) Satellite Networks Performance Analysis: Transmission Power, Latency, and Outage Probability. IEEE Open J. Veh. Technol. 2024, 5, 244–261. [Google Scholar] [CrossRef]
- Dmytryszyn, M.; Crook, M.; Sands, T. Lasers for Satellite Uplinks and Downlinks. Science 2021, 3, 4. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Yanikomeroglu, H. Temporary Laser Inter-Satellite Links in Free-Space Optical Satellite Networks. IEEE Open J. Commun. Soc. 2022, 3, 1413–1427. [Google Scholar] [CrossRef]
- Hamza, A.S.; Deogun, J.S.; Alexander, D.R. Classification Framework for Free Space Optical Communication Links and Systems. IEEE Commun. Surv. Tutor. 2019, 21, 1346–1382. [Google Scholar] [CrossRef]
- Devkota, N.; Maharjan, N.; Kim, B.W. Atmospheric Effects on Downlink Channel of Satellite to Ground Free Space Optical Communications. In Proceedings of the 2022 13th International Conference on Information and Communication Technology Convergence (ICTC), Jeju Island, Republic of Korea, 19–21 October 2022; IEEE: Piscataway, NJ, USA, 2022; Volume 2022, pp. 1335–1340. [Google Scholar] [CrossRef]
- Tiwari, G. A Review on Inter-Satellite Links Free Space Optical Communication. Indian J. Sci. Technol. 2020, 13, 712–724. [Google Scholar] [CrossRef]
- Khalid, M.; Ji, W.; Li, D.; Kun, L. Characterization of Doppler shift in inter-satellite laser link between LEO, MEO, and GEO orbits. Opt. Laser Technol. 2024, 177, 111033. [Google Scholar] [CrossRef]
- Kaushal, H.; Jain, V.K.; Kar, S. Acquisition, Tracking, and Pointing; Springer: Berlin/Heidelberg, Germany, 2017; pp. 119–137. [Google Scholar] [CrossRef]
- Guelman, M.; Kogan, A.; Kazarian, A.; Livne, A.; Orenstein, M.; Michalik, H.; Arnon, S. Acquisition and pointing control for inter-satellite laser communications. IEEE Trans. Aerosp. Electron. Syst. 2004, 40, 1239–1248. [Google Scholar] [CrossRef]
- Liu, C.; Wen, F.; Fan, F. Pointing, acquisition, and tracking (PAT) technology for inter-satellite laser links. In Proceedings of the AOPC 2024: Laser Technology and Applications, Beijing, China, 23–26 July 2024; Zhou, P., Ed.; International Society for Optics and Photonics, SPIE: St Bellingham, WA, USA, 2024; Volume 13492, p. 134920C. [Google Scholar] [CrossRef]
- Kaymak, Y.; Rojas-Cessa, R.; Feng, J.; Ansari, N.; Zhou, M.; Zhang, T. A Survey on Acquisition, Tracking, and Pointing Mechanisms for Mobile Free-Space Optical Communications. IEEE Commun. Surv. Tutor. 2018, 20, 1104–1123. [Google Scholar] [CrossRef]
- Lambert, S.G.; Casey, W.L. Laser Communications in Space; Artech House: Norwood, MA, USA, 1995. [Google Scholar]
- Zhang, J.; Li, J. Laser Inter-Satellite Links Technology; John Wiley & Sons: Hoboken, NJ, USA, 2023. [Google Scholar]
- Swanson, E.; Chan, V. Heterodyne Spatial Tracking System for Optical Space Communication. IEEE Trans. Commun. 1986, 34, 118–126. [Google Scholar] [CrossRef]
- Tsukamoto, K.; Morinaga, N. Heterodyne optical detection/spatial tracking system using spatial field pattern matching between signal and local lights. Electron. Commun. Jpn. Part I Commun. 1994, 77, 73–87. [Google Scholar] [CrossRef]
- Arnon, S.; Rotman, S.; Kopeika, N.S. Beam width and transmitter power adaptive to tracking system performance for free-space optical communication. Appl. Opt. 1997, 36, 6095. [Google Scholar] [CrossRef] [PubMed]
- Hindman, C.; Engberg, B. Atmospheric and Platform Jitter Effects on Laser Acquisition Patterns. In Proceedings of the 2006 IEEE Aerospace Conference, Big Sky, MT, USA, 4–11 March 2006; IEEE: Piscataway, NJ, USA, 2006; Volume 2006, pp. 1–8. [Google Scholar] [CrossRef]
- Sun, J.; Liu, L.; Lu, W.; Yan, A.; Zhou, Y. Acquisition strategy for the satellite laser communications under the laser terminal scanning errors situation. In Proceedings of the Free Atmospheric Laser Communications XI, San Diego, CA, USA, 24–25 August 2011; Majumdar, A.K., Davis, C.C., Eds.; SPIE: St Bellingham, WA, USA, 2011; Volume 8162, p. 81620U. [Google Scholar] [CrossRef]
- Zhang, M.; Li, B.; Tong, S. A New Composite Spiral Scanning Approach for Beaconless Spatial Acquisition and Experimental Investigation of Robust Tracking Control for Laser Communication System with Disturbance. IEEE Photonics J. 2020, 12, 1–12. [Google Scholar] [CrossRef]
- Hechenblaikner, G. Analysis of performance and robustness against jitter of various search methods for acquiring optical links in space: Erratum. Appl. Opt. 2022, 61, 10801. [Google Scholar] [CrossRef]
- Hindman, C.; Robertson, L. Beaconless satellite laser acquisition-modeling and feasability. In Proceedings of the IEEE MILCOM 2004. Military Communications Conference 2004, Monterey, CA, USA, 31 October–3 November 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 1, pp. 41–47. [Google Scholar] [CrossRef]
- Friederichs, L.; Sterr, U.; Dallmann, D. Vibration Influence on Hit Probability During Beaconless Spatial Acquisition. J. Light. Technol. 2016, 34, 2500–2509. [Google Scholar] [CrossRef]
- Scheinfeild, M.; Kopeika, N.S.; Melamed, R. Acquisition system for microsatellites laser communication in space. In Proceedings of the Free-Space Laser Communication Technologies XII, San Jose, CA, USA, 22–28 January 2000; Mecherle, G.S., Ed.; SPIE: St Bellingham, WA, USA, 2000; Volume 3932, pp. 166–175. [Google Scholar] [CrossRef]
- Scheinfeild, M.; Kopeika, N.S.; Shlomi, A. Acquisition time calculation and influence of vibrations for microsatellite laser communication in space. In Proceedings of the Acquis. Tracking, Pointing XV, Orlando, FL, USA, 16–20 April 2001; Masten, M.K., Stockum, L.A., Eds.; SPIE: St Bellingham, WA, USA, 2001; Volume 4365, pp. 195–205. [Google Scholar] [CrossRef]
- Qi, S.; Zhang, Q.; Xin, X.; Tao, Y.; Tian, Q.; Tian, F.; Cao, G.; Shen, Y.; Chen, D.; Gao, Z.; et al. Research on Scanning Method in Satellite Laser Communication. In Proceedings of the 2019 18th International Conference on Optical Communications and Networks (ICOCN), Huangshan, China, 5–8 August 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Zhang, L.Z.; Zhang, R.Q.; Li, Y.H.; Meng, L.X.; Li, X.M. The quick acquisition technique for laser communication between LEO and GEO. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Laser Communication Technologies and Systems, Beijing, China, 25–27 June 2013; Wilson, K.E., Ma, J., Liu, L., Jiang, H., Ke, X., Eds.; SPIE: St Bellingham, WA, USA, 2013; Volume 8906, p. 890621. [Google Scholar] [CrossRef]
- Jia, B.; Jin, F.; Lv, Q.; Li, Y. Improved Target Laser Capture Technology for Hexagonal Honeycomb Scanning. Photonics 2023, 10, 541. [Google Scholar] [CrossRef]
- Jia, Q.; Li, C.; Liu, L.; Chen, T.; Cao, G. Acquisition, Scanning and Control Technology for Inter-satellite Laser Communication. In Proceedings of the 2021 IEEE 16th Conference on Industrial Electronics and Applications (ICIEA), Chengdu, China, 1–4 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1769–1774. [Google Scholar] [CrossRef]
- Wang, X.; Han, J.; Wang, C.; Xie, M.; Liu, P.; Cao, Y.; Jing, F.; Wang, F.; Su, Y.; Meng, X. Beam Scanning and Capture of Micro Laser Communication Terminal Based on MEMS Micromirrors. Micromachines 2023, 14, 1317. [Google Scholar] [CrossRef]
- Wang, J.; Ma, Y.; Zhu, W.H.; Qiang, J. Study of acquisition technology of scanning in satellite-to-ground laser communication. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013: Laser Communication Technologies and Systems, Beijing, China, 25–27 June 2013; Wilson, K.E., Ma, J., Liu, L., Jiang, H., Ke, X., Eds.; SPIE: St Bellingham, WA, USA, 2013; Volume 8906, p. 89060M. [Google Scholar] [CrossRef]
- Lee, K.; Mai, V.; Kim, H. Acquisition Time in Laser Inter-Satellite Link Under Satellite Vibrations. IEEE Photonics J. 2023, 15, 1–9. [Google Scholar] [CrossRef]
- Zhi, X.; Ai, Y.; Lu, M. Acquisition methods for microsatellite laser communication in space. In Proceedings of the Wireless and Mobile Communications II, Shanghai, China, 16–18 October 2002; Wu, H., Vaario, J., Eds.; SPIE: St Bellingham, WA, USA, 2002; Volume 4911, pp. 372–379. [Google Scholar] [CrossRef]
- Li, X.; Song, Q.; Ma, J.; Yu, S.; Tan, L. Spatial acquisition optimization based on average acquisition time for intersatellite optical communications. In Proceedings of the 2010 Academic Symposium on Optoelectronics and Microelectronics Technology and 10th Chinese-Russian Symposium on Laser Physics and Laser Technology Optoelectronics Technology (ASOT), Harbin, China, 28 July–1 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 244–248. [Google Scholar] [CrossRef]
- Arnon, S. Power versus stabilization for laser satellite communication. Appl. Opt. 1999, 38, 3229. [Google Scholar] [CrossRef]
- Li, X.; Yu, S.; Ma, J.; Tan, L. Analytical expression and optimization of spatial acquisition for intersatellite optical communications. Opt. Express 2011, 19, 2381. [Google Scholar] [CrossRef]
- Yu, S.; Gao, H.; Ma, J.; Dong, Y.; Ma, Z. Selection of acquisition scan methods in intersatellite optical communications. Chin. J. Lasers B Engl. Ed. 2002, 11, 364–368. [Google Scholar]
- Arnon, S.; Kopeika, N. Laser satellite communication network-vibration effect and possible solutions. Proc. IEEE 1997, 85, 1646–1661. [Google Scholar] [CrossRef]
- Tan, L.; Wang, Q.; Yu, S.; Ma, J.; Fu, S.; Wang, J. Spectrum characteristics of optical misalignment induced by satellite platform vibration and angle of arrival fluctuation. In Proceedings of the 2010 Academic Symposium on Optoelectronics and Microelectronics Technology and 10th Chinese-Russian Symposium on Laser Physics and Laser Technology Optoelectronics Technology (ASOT), Harbin, China, 28 July–1 August 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 249–252. [Google Scholar] [CrossRef]
- Xue, Z.Y.; Qi, B.; Ren, G. Vibration-induced jitter control in satellite optical communication. In Proceedings of the International Symposium on Photoelectronic Detection and Imaging 2013, Laser Communication Technologies and Systems, Beijing, China, 25–27 June 2013; Wilson, K.E., Ma, J., Liu, L., Jiang, H., Ke, X., Eds.; SPIE: St Bellingham, WA, USA, 2013; Volume 8906, p. 89061X. [Google Scholar] [CrossRef]
- Teng, Y.; Zhang, M.; Tong, S. The Optimization Design of Sub-Regions Scanning and Vibration Analysis for Beaconless Spatial Acquisition in the Inter-Satellite Laser Communication System. IEEE Photonics J. 2018, 10, 2884718. [Google Scholar] [CrossRef]
- Toyoshima, M. In-orbit measurements of spacecraft microvibrations for satellite laser communication links. Opt. Eng. 2010, 49, 083604. [Google Scholar] [CrossRef]
- Edition, F.; Papoulis, A.; Pillai, S.U. Probability, Random Variables, and Stochastic Processes; McGraw-Hill Europe: New York, NY, USA, 2002. [Google Scholar]
- Myung, I.J. Tutorial on maximum likelihood estimation. J. Math. Psychol. 2003, 47, 90–100. [Google Scholar] [CrossRef]
- Toyoshima, M.; Jono, T.; Nakagawa, K.; Yamamoto, A. Optimum divergence angle of a Gaussian beam wave in the presence of random jitter in free-space laser communication systems. J. Opt. Soc. Am. A 2002, 19, 567. [Google Scholar] [CrossRef] [PubMed]
- Mai, V.; Lee, K.; Kim, H. Adaptive Beam Control for Optical Inter-Satellite Communication Systems. In Proceedings of the 2023 21st International Conference on Optical Communications and Networks (ICOCN), Qufu, China, 31 July–3 August 2023; pp. 1–2. [Google Scholar] [CrossRef]
- Lee, K.; Mai, V.; Kim, H. Dynamic Adaptive Beam Control System Using Variable Focus Lenses for Laser Inter-Satellite Link. IEEE Photonics J. 2022, 14, 3183999. [Google Scholar] [CrossRef]
- Mai, V.V.; Kim, H. Adaptive beam control techniques for airborne free-space optical communication systems. Appl. Opt. 2018, 57, 7462–7471. [Google Scholar] [CrossRef]
- Safi, H.; Dargahi, A.; Cheng, J.; Safari, M. Analytical channel model and link design optimization for ground-to-HAP free-space optical communications. J. Light. Technol. 2020, 38, 5036–5047. [Google Scholar] [CrossRef]
- Mai, V.V.; Kim, H. Beam size optimization and adaptation for high-altitude airborne free-space optical communication systems. IEEE Photonics J. 2019, 11, 1–13. [Google Scholar] [CrossRef]
- Song, T.; Wang, Q.; Wu, M.W.; Kam, P.Y. Performance of laser inter-satellite links with dynamic beam waist adjustment. Opt. Express 2016, 24, 11950–11960. [Google Scholar] [CrossRef]
- Do, P.X.; Carrasco-Casado, A.; Vu, T.V.; Hosonuma, T.; Toyoshima, M.; Nakasuka, S. Numerical and analytical approaches to dynamic beam waist optimization for LEO-to-GEO laser communication. OSA Contin. 2020, 3, 3508–3522. [Google Scholar] [CrossRef]
- Heng, K.H.; Zhong, W.D.; Cheng, T.H.; Liu, N.; He, Y. Beam divergence changing mechanism for short-range inter-unmanned aerial vehicle optical communications. Appl. Opt. 2009, 48, 1565–1572. [Google Scholar] [CrossRef] [PubMed]
- Zhou, D.; LoPresti, P.G.; Refai, H.H. Design analysis of a fiber-bundle-based mobile free-space optical link with wavelength diversity. Appl. Opt. 2013, 52, 3689–3697. [Google Scholar] [CrossRef] [PubMed]
- Mai, V.V.; Kim, H. Airborne free-space optical communications for fronthaul/backhaul networks of 5G and beyond. IEEE Future Netw. Tech Focus 2021, 4, 1–5. [Google Scholar]
- Mai, V.V.; Kim, H. Non-mechanical beam steering and adaptive beam control using variable focus lenses for free-space optical communications. J. Light. Technol. 2021, 39, 7600–7608. [Google Scholar] [CrossRef]
- Chen, L.; Ghilardi, M.; Busfield, J.J.; Carpi, F. Electrically tunable lenses: A review. Front. Robot. AI 2021, 8, 678046. [Google Scholar] [CrossRef]
- Leuenberger, D.; Optotune, A.; Voigt, F.F. Focus-tunable lenses enable 3-d microscopy. Biophotonics 2015, 22, 26–27. [Google Scholar]
- Wang, Q.; Tan, L.; Ma, J.; Yu, S.; Jiang, Y. A novel approach for simulating the optical misalignment caused by satellite platform vibration in the ground test of satellite optical communication systems. Opt. Express 2012, 20, 1033. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khalid, M.; Ji, W.; Li, D.; Kun, L. Mitigating the Impact of Satellite Vibrations on the Acquisition of Satellite Laser Links Through Optimized Scan Path and Parameters. Photonics 2025, 12, 444. https://doi.org/10.3390/photonics12050444
Khalid M, Ji W, Li D, Kun L. Mitigating the Impact of Satellite Vibrations on the Acquisition of Satellite Laser Links Through Optimized Scan Path and Parameters. Photonics. 2025; 12(5):444. https://doi.org/10.3390/photonics12050444
Chicago/Turabian StyleKhalid, Muhammad, Wu Ji, Deng Li, and Li Kun. 2025. "Mitigating the Impact of Satellite Vibrations on the Acquisition of Satellite Laser Links Through Optimized Scan Path and Parameters" Photonics 12, no. 5: 444. https://doi.org/10.3390/photonics12050444
APA StyleKhalid, M., Ji, W., Li, D., & Kun, L. (2025). Mitigating the Impact of Satellite Vibrations on the Acquisition of Satellite Laser Links Through Optimized Scan Path and Parameters. Photonics, 12(5), 444. https://doi.org/10.3390/photonics12050444



