Nonlinear Dielectric Metasurfaces for Terahertz Applications
Abstract
1. Introduction
2. Overview
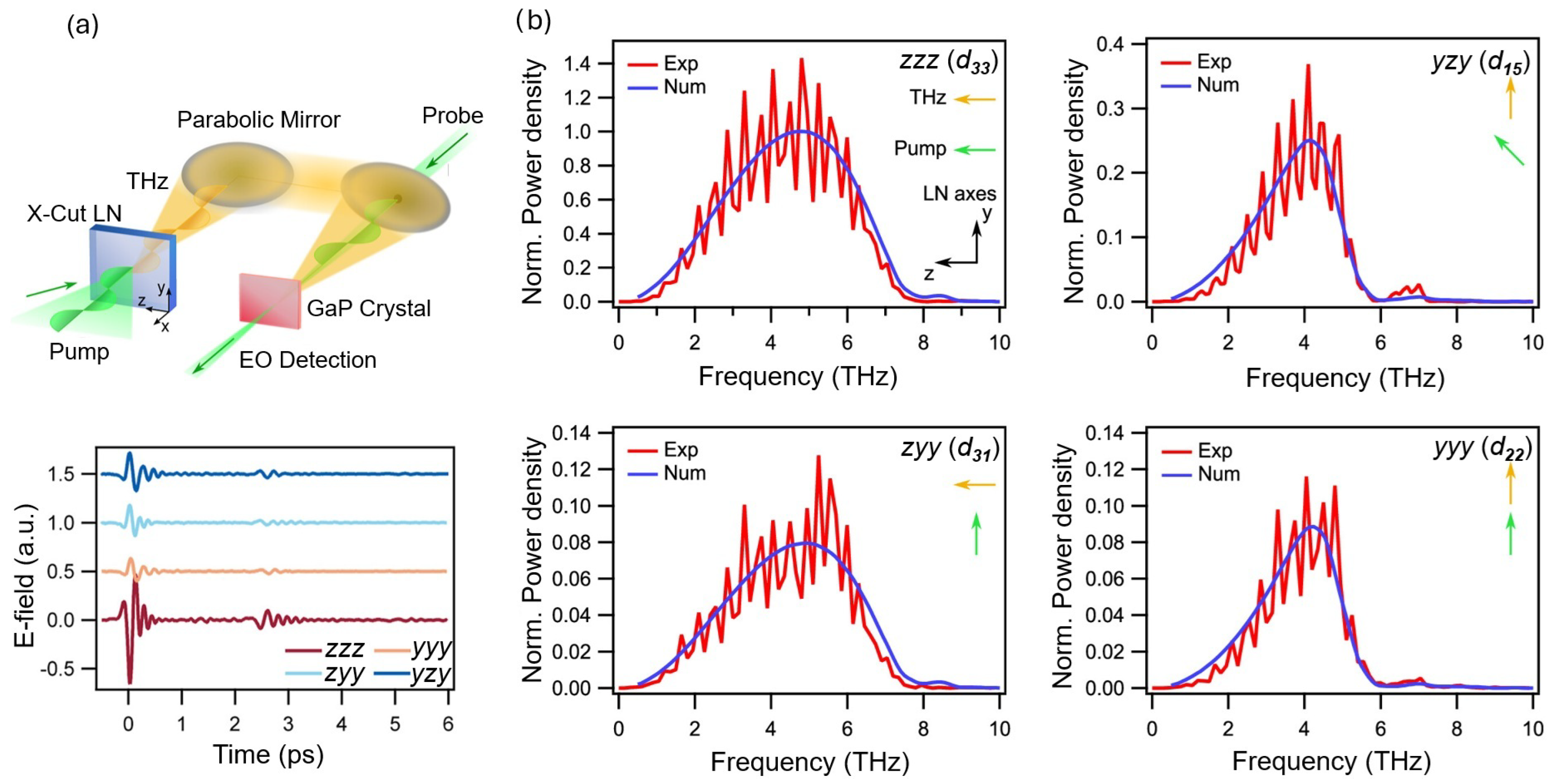
3. THz Generation in Dielectric Slabs
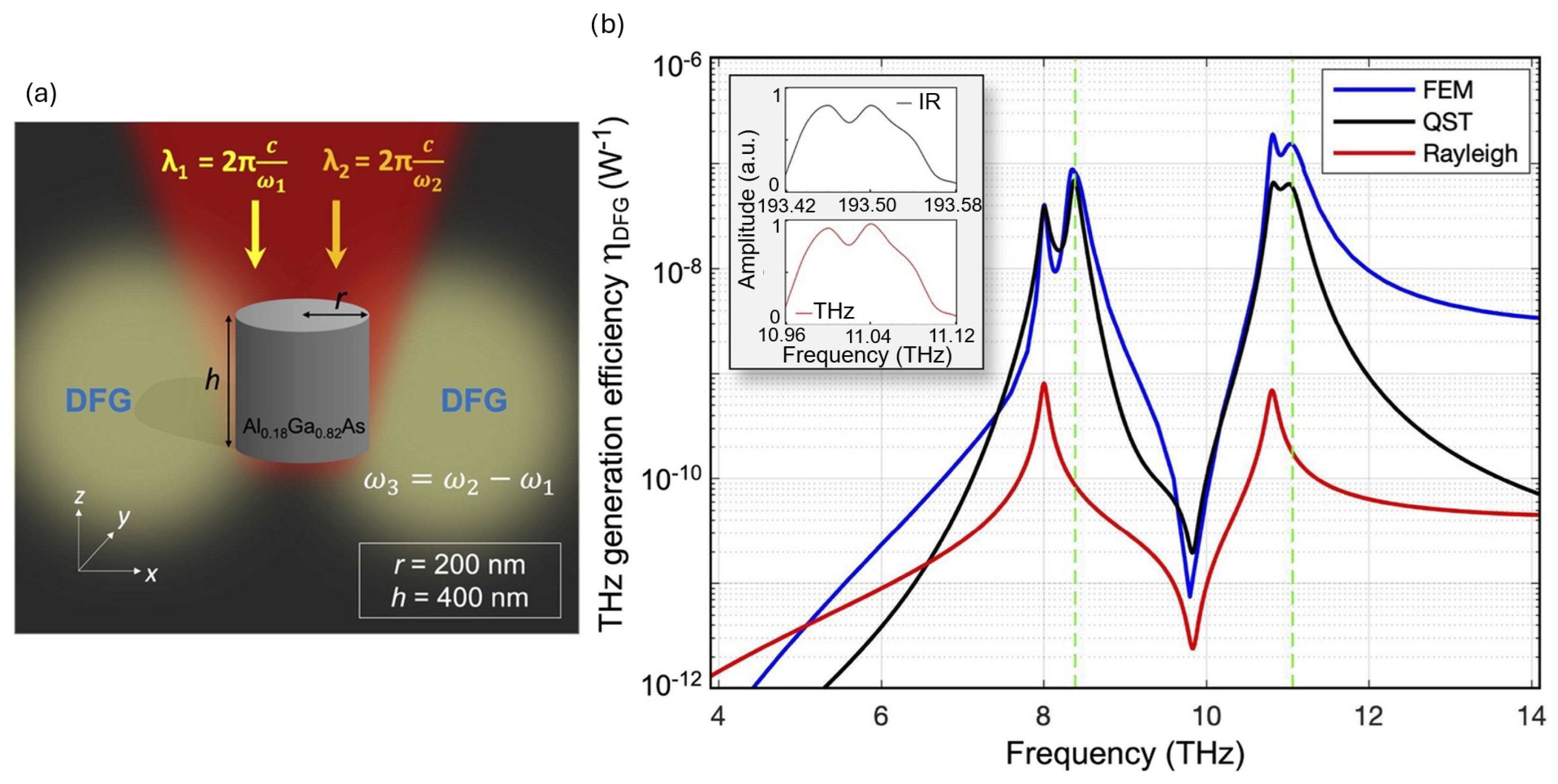
4. THz Generation from Resonant Dielectric Metasurfaces
5. Perspectives
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Davies, G.; Linfield, E. Bridging the terahertz gap. Phys. World 2004, 17, 37. [Google Scholar] [CrossRef]
- Pang, X.; Ozolins, O.; Jia, S.; Zhang, L.; Schatz, R.; Udalcovs, A.; Bobrovs, V.; Hu, H.; Morioka, T.; Sun, Y.T.; et al. Bridging the terahertz gap: Photonics-assisted free-space communications from the submillimeter-wave to the mid-infrared. J. Light. Technol. 2022, 40, 3149–3162. [Google Scholar] [CrossRef]
- Han, R.; Hu, Z.; Wang, C.; Holloway, J.; Yi, X.; Kim, M.; Mawdsley, J. Filling the gap: Silicon terahertz integrated circuits offer our best bet. IEEE Microw. Mag. 2019, 20, 80–93. [Google Scholar] [CrossRef]
- Tzydynzhapov, G.; Gusikhin, P.; Muravev, V.; Dremin, A.; Nefyodov, Y.; Kukushkin, I. New real-time sub-terahertz security body scanner. J. Infrared Millim. Terahertz Waves 2020, 41, 632–641. [Google Scholar] [CrossRef]
- Markl, D.; Ruggiero, M.T.; Zeitler, J.A. Pharmaceutical applications of terahertz spectroscopy and imaging. Eur. Pharm. Rev. 2016, 21, 45–50. [Google Scholar]
- Federici, J.F.; Schulkin, B.; Huang, F.; Gary, D.; Barat, R.; Oliveira, F.; Zimdars, D. THz imaging and sensing for security applications—Explosives, weapons and drugs. Semicond. Sci. Technol. 2005, 20, S266. [Google Scholar] [CrossRef]
- Leon, U.A.; Rocco, D.; Carletti, L.; Peccianti, M.; Maci, S.; Della Valle, G.; De Angelis, C. THz-photonics transceivers by all-dielectric phonon-polariton nonlinear nanoantennas. Sci. Rep. 2022, 12, 4590. [Google Scholar] [CrossRef] [PubMed]
- Arregui Leon, U.; Carletti, L.; Rocco, D.; De Angelis, C.; Della Valle, G. THz Generation via Optical Rectification in Nanomaterials: Universal Modeling Approach and Effective χ(2) Description. Laser Photonics Rev. 2024, 18, 2300669. [Google Scholar] [CrossRef]
- Arregui Leon, U.; Franceschini, P.; Sergaeva, O.; Tognazzi, A.; Rocco, D.; Carletti, L.; de Ceglia, D.; Della Valle, G.; De Angelis, C. Event detection via THz generation with flat nonlinear optics. Opt. Mater. Express 2025, 15, 307–318. [Google Scholar] [CrossRef]
- Zheludev, N.I.; Kivshar, Y.S. From metamaterials to metadevices. Nat. Mater. 2012, 11, 917–924. [Google Scholar] [CrossRef]
- Tao, H.; Bingham, C.; Strikwerda, A.; Pilon, D.; Shrekenhamer, D.; Landy, N.; Fan, K.; Zhang, X.; Padilla, W.; Averitt, R. Highly flexible wide angle of incidence terahertz metamaterial absorber: Design, fabrication, and characterization. Phys. Rev. B Condens. Matter Mater. Phys. 2008, 78, 241103. [Google Scholar] [CrossRef]
- Grady, N.K.; Heyes, J.E.; Chowdhury, D.R.; Zeng, Y.; Reiten, M.T.; Azad, A.K.; Taylor, A.J.; Dalvit, D.A.; Chen, H.T. Terahertz metamaterials for linear polarization conversion and anomalous refraction. Science 2013, 340, 1304–1307. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Zhang, X.; Kenney, M.; Su, X.; Xu, N.; Ouyang, C.; Shi, Y.; Han, J.; Zhang, W.; Zhang, S. Broadband metasurfaces with simultaneous control of phase and amplitude. Adv. Mater. 2014, 26, 5031–5036. [Google Scholar] [CrossRef] [PubMed]
- Keiser, G.; Karl, N.; Liu, P.; Tulloss, C.; Chen, H.T.; Taylor, A.J.; Brener, I.; Reno, J.; Mittleman, D. Nonlinear terahertz metamaterials with active electrical control. Appl. Phys. Lett. 2017, 111, 121101. [Google Scholar] [CrossRef]
- Seren, H.R.; Zhang, J.; Keiser, G.R.; Maddox, S.J.; Zhao, X.; Fan, K.; Bank, S.R.; Zhang, X.; Averitt, R.D. Nonlinear terahertz devices utilizing semiconducting plasmonic metamaterials. Light Sci. Appl. 2016, 5, e16078. [Google Scholar] [CrossRef]
- Lepeshov, S.; Gorodetsky, A.; Krasnok, A.; Rafailov, E.; Belov, P. Enhancement of terahertz photoconductive antenna operation by optical nanoantennas. Laser Photonics Rev. 2017, 11, 1600199. [Google Scholar] [CrossRef]
- Hale, L.L.; Jung, H.; Gennaro, S.D.; Briscoe, J.; Harris, C.T.; Luk, T.S.; Addamane, S.J.; Reno, J.L.; Brener, I.; Mitrofanov, O. Terahertz pulse generation from GaAs metasurfaces. ACS Photonics 2022, 9, 1136–1142. [Google Scholar] [CrossRef]
- Minerbi, E.; Keren-Zur, S.; Ellenbogen, T. Nonlinear metasurface Fresnel zone plates for terahertz generation and manipulation. Nano Lett. 2019, 19, 6072–6077. [Google Scholar] [CrossRef]
- Dong, T.; Li, S.; Manjappa, M.; Yang, P.; Zhou, J.; Kong, D.; Quan, B.; Chen, X.; Ouyang, C.; Dai, F.; et al. Nonlinear THz-nano metasurfaces. Adv. Funct. Mater. 2021, 31, 2100463. [Google Scholar] [CrossRef]
- Tymchenko, M.; Gomez-Diaz, J.S.; Lee, J.; Belkin, M.; Alù, A. Highly-efficient THz generation using nonlinear plasmonic metasurfaces. J. Opt. 2017, 19, 104001. [Google Scholar] [CrossRef]
- McDonnell, C.; Deng, J.; Sideris, S.; Ellenbogen, T.; Li, G. Functional THz emitters based on Pancharatnam-Berry phase nonlinear metasurfaces. Nat. Commun. 2021, 12, 30. [Google Scholar] [CrossRef] [PubMed]
- Dragoman, D.; Dragoman, M. Terahertz fields and applications. Prog. Quantum Electron. 2004, 28, 1–66. [Google Scholar] [CrossRef]
- Pawar, A.Y.; Sonawane, D.D.; Erande, K.B.; Derle, D.V. Terahertz technology and its applications. Drug Invent. Today 2013, 5, 157–163. [Google Scholar] [CrossRef]
- Zhong, S. Progress in terahertz nondestructive testing: A review. Front. Mech. Eng. 2019, 14, 273–281. [Google Scholar] [CrossRef]
- Leitenstorfer, A.; Moskalenko, A.S.; Kampfrath, T.; Kono, J.; Castro-Camus, E.; Peng, K.; Qureshi, N.; Turchinovich, D.; Tanaka, K.; Markelz, A.G.; et al. The 2023 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2023, 56, 223001. [Google Scholar] [CrossRef]
- Jiang, W.; Zhou, Q.; He, J.; Habibi, M.A.; Melnyk, S.; El-Absi, M.; Han, B.; Di Renzo, M.; Schotten, H.D.; Luo, F.L.; et al. Terahertz communications and sensing for 6G and beyond: A comprehensive review. IEEE Commun. Surv. Tutorials 2024, 26, 2326–2381. [Google Scholar] [CrossRef]
- Chen, H.; Sarieddeen, H.; Ballal, T.; Wymeersch, H.; Alouini, M.S.; Al-Naffouri, T.Y. A tutorial on terahertz-band localization for 6G communication systems. IEEE Commun. Surv. Tutorials 2022, 24, 1780–1815. [Google Scholar] [CrossRef]
- Shafie, A.; Yang, N.; Han, C.; Jornet, J.M.; Juntti, M.; Kürner, T. Terahertz communications for 6G and beyond wireless networks: Challenges, key advancements, and opportunities. IEEE Netw. 2022, 37, 162–169. [Google Scholar] [CrossRef]
- Han, C.; Wu, Y.; Chen, Z.; Wang, X. Terahertz communications (TeraCom): Challenges and impact on 6G wireless systems. arXiv 2019, arXiv:1912.06040. [Google Scholar]
- Serghiou, D.; Khalily, M.; Brown, T.W.; Tafazolli, R. Terahertz channel propagation phenomena, measurement techniques and modeling for 6G wireless communication applications: A survey, open challenges and future research directions. IEEE Commun. Surv. Tutor. 2022, 24, 1957–1996. [Google Scholar] [CrossRef]
- Wang, J.; Wang, C.X.; Huang, J.; Chen, Y. 6G THz propagation channel characteristics and modeling: Recent developments and future challenges. IEEE Commun. Mag. 2022, 62, 56–62. [Google Scholar] [CrossRef]
- Alsharif, M.H.; Albreem, M.A.; Solyman, A.A.A.; Kim, S. Toward 6G communication networks: Terahertz frequency challenges and open research issues. Comput. Mater. Contin. 2021, 66, 2831–2842. [Google Scholar] [CrossRef]
- Azari, M.M.; Solanki, S.; Chatzinotas, S.; Bennis, M. THz-empowered UAVs in 6G: Opportunities, challenges, and trade-offs. IEEE Commun. Mag. 2022, 60, 24–30. [Google Scholar] [CrossRef]
- Jepsen, P.U.; Cooke, D.G.; Koch, M. Terahertz spectroscopy and imaging—Modern techniques and applications. Laser Photonics Rev. 2011, 5, 124–166. [Google Scholar] [CrossRef]
- Beard, M.C.; Turner, G.M.; Schmuttenmaer, C.A. Terahertz spectroscopy. J. Phys. Chem. B 2002, 106, 7146–7159. [Google Scholar] [CrossRef]
- Plusquellic, D.F.; Siegrist, K.; Heilweil, E.J.; Esenturk, O. Applications of terahertz spectroscopy in biosystems. ChemPhysChem 2007, 8, 2412–2431. [Google Scholar] [CrossRef]
- Baxter, J.B.; Guglietta, G.W. Terahertz spectroscopy. Anal. Chem. 2011, 83, 4342–4368. [Google Scholar] [CrossRef] [PubMed]
- Globus, T.; Woolard, D.; Khromova, T.; Crowe, T.; Bykhovskaia, M.; Gelmont, B.; Hesler, J.; Samuels, A. THz-spectroscopy of biological molecules. J. Biol. Phys. 2003, 29, 89–100. [Google Scholar] [CrossRef]
- Dexheimer, S.L. Terahertz Spectroscopy: Principles and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Zaytsev, K.; Dolganova, I.; Chernomyrdin, N.; Katyba, G.; Gavdush, A.; Cherkasova, O.; Komandin, G.; Shchedrina, M.; Khodan, A.; Ponomarev, D.; et al. The progress and perspectives of terahertz technology for diagnosis of neoplasms: A review. J. Opt. 2019, 22, 013001. [Google Scholar] [CrossRef]
- Yan, Z.; Zhu, L.G.; Meng, K.; Huang, W.; Shi, Q. THz medical imaging: From in vitro to in vivo. Trends Biotechnol. 2022, 40, 816–830. [Google Scholar] [CrossRef]
- Vafapour, Z.; Keshavarz, A.; Ghahraloud, H. The potential of terahertz sensing for cancer diagnosis. Heliyon 2020, 6, e05623. [Google Scholar] [CrossRef] [PubMed]
- Li, R.; Li, C.; Li, H.; Wu, S.; Fang, G. Study of automatic detection of concealed targets in passive terahertz images for intelligent security screening. IEEE Trans. Terahertz Sci. Technol. 2018, 9, 165–176. [Google Scholar] [CrossRef]
- Cheng, Y.; Qiao, L.; Zhu, D.; Wang, Y.; Zhao, Z. Passive polarimetric imaging of millimeter and terahertz waves for personnel security screening. Opt. Lett. 2021, 46, 1233–1236. [Google Scholar] [CrossRef]
- Choi, M.K.; Bettermann, A.; Van Der Weide, D. Potential for detection of explosive and biological hazards with electronic terahertz systems. Philos. Trans. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci. 2004, 362, 337–349. [Google Scholar] [CrossRef]
- Trofimov, V.A.; Varentsova, S.A. A possible way for the detection and identification of dangerous substances in ternary mixtures using THz pulsed spectroscopy. Sensors 2019, 19, 2365. [Google Scholar] [CrossRef]
- Gowen, A.A.; O’Sullivan, C.; O’Donnell, C.P. Terahertz time domain spectroscopy and imaging: Emerging techniques for food process monitoring and quality control. Trends Food Sci. Technol. 2012, 25, 40–46. [Google Scholar] [CrossRef]
- Wietzke, S.; Jördens, C.; Krumbholz, N.; Baudrit, B.; Bastian, M.; Koch, M. Terahertz imaging: A new non-destructive technique for the quality control of plastic weld joints. J. Eur. Opt.-Soc.-Rapid Publ. 2007, 2, 07013. [Google Scholar] [CrossRef]
- Küter, A.; Reible, S.; Geibig, T.; Nüßler, D.; Pohl, N. THz imaging for recycling of black plastics. Tech. Mess. 2018, 85, 191–201. [Google Scholar] [CrossRef]
- Jelali, M.; Papadopoulos, K. Inline Inspection of Packaged Food Using Microwave/Terahertz Sensing—An Overview with Focus on Confectionery Products. Processes 2024, 12, 712. [Google Scholar] [CrossRef]
- Hao, D.; Liu, J.; Zou, P.; Zhang, Y.; Moro, R.; Ma, L. All-dielectric Metasurfaces and Their Applications in the Terahertz Range. Laser Photonics Rev. 2024, 18, 2301210. [Google Scholar] [CrossRef]
- Tan, L.; Wang, D.; Xu, K.D. Terahertz metamaterials for spectrum modulation: Structural design, materials and applications. Mater. Des. 2024, 244, 113217. [Google Scholar] [CrossRef]
- He, J.; He, X.; Dong, T.; Wang, S.; Fu, M.; Zhang, Y. Recent progress and applications of Terahertz metamaterials. J. Phys. D Appl. Phys. 2022, 55, 123002. [Google Scholar] [CrossRef]
- Lee, W.S.L.; Atakaramians, S.; Withayachumnankul, W. Terahertz Metasurfaces, Metawaveguides, and Applications. In More-Than-Moore Devices and Integration for Semiconductors; Iacopi, F., Balestra, F., Eds.; Springer International Publishing: Cham, Switzerland, 2023; pp. 127–156. [Google Scholar]
- Leng, J.; Peng, J.; Jin, A.; Cao, D.; Liu, D.; He, X.; Lin, F.; Liu, F. Investigation of terahertz high Q-factor of all-dielectric metamaterials. Opt. Laser Technol. 2022, 146, 107570. [Google Scholar] [CrossRef]
- Bai, J.; Shen, P.; Wang, S.; Xu, W.; Shen, W.; Chang, S. A High-Q Terahertz Metamaterials Absorber for Refractive Index Sensing. Phys. Status Solidi B 2023, 260, 2200444. [Google Scholar] [CrossRef]
- Zhou, S.; Shen, Z.; Kang, R.; Ge, S.; Hu, W. Liquid Crystal Tunable Dielectric Metamaterial Absorber in the Terahertz Range. Appl. Sci. 2018, 8, 2211. [Google Scholar] [CrossRef]
- Bi, K.; Yang, D.; Chen, J.; Wang, Q.; Wu, H.; Lan, C.; Yang, Y. Experimental demonstration of ultra-large-scale terahertz all-dielectric metamaterials. Photon. Res. 2019, 7, 457–463. [Google Scholar] [CrossRef]
- Ma, Z.; Hanham, S.M.; Albella, P.; Ng, B.; Lu, H.T.; Gong, Y.; Maier, S.A.; Hong, M. Terahertz All-Dielectric Magnetic Mirror Metasurfaces. ACS Photonics 2016, 3, 1010–1018. [Google Scholar] [CrossRef]
- Kadlec, F.; Kužel, P.; Coutaz, J.L. Optical rectification at metal surfaces. Opt. Lett. 2004, 29, 2674–2676. [Google Scholar] [CrossRef]
- Kadlec, F.; Kužel, P.; Coutaz, J.L. Study of terahertz radiation generated by optical rectification on thin gold films. Opt. Lett. 2005, 30, 1402–1404. [Google Scholar] [CrossRef]
- Ramakrishnan, G.; Planken, P.C. Percolation-enhanced generation of terahertz pulses by optical rectification on ultrathin gold films. Opt. Lett. 2011, 36, 2572–2574. [Google Scholar] [CrossRef]
- Welsh, G.H.; Hunt, N.T.; Wynne, K. Terahertz-pulse emission through laser excitation of surface plasmons in a metal grating. Phys. Rev. Lett. 2007, 98, 026803. [Google Scholar] [CrossRef] [PubMed]
- Welsh, G.H.; Wynne, K. Generation of ultrafast terahertz radiation pulses on metallic nanostructured surfaces. Opt. Express 2009, 17, 2470–2480. [Google Scholar] [CrossRef] [PubMed]
- Berry, C.W.; Wang, N.; Hashemi, M.R.; Unlu, M.; Jarrahi, M. Significant performance enhancement in photoconductive terahertz optoelectronics by incorporating plasmonic contact electrodes. Nat. Commun. 2013, 4, 1622. [Google Scholar] [CrossRef]
- Jin, Y.; Reno, J.L.; Kumar, S. Phase-locked terahertz plasmonic laser array with 2 W output power in a single spectral mode. Optica 2020, 7, 708–715. [Google Scholar] [CrossRef]
- Neu, J.; Schmuttenmaer, C.A. Tutorial: An introduction to terahertz time domain spectroscopy (THz-TDS). J. Appl. Phys. 2018, 124, 231101. [Google Scholar] [CrossRef]
- Reimann, K. Table-top sources of ultrashort THz pulses. Rep. Prog. Phys. 2007, 70, 1597. [Google Scholar] [CrossRef]
- Averitt, R.; Taylor, A.J. Ultrafast optical and far-infrared quasiparticle dynamics in correlated electronmaterials. J. Phys. Condens. Matter 2002, 14, R1357. [Google Scholar] [CrossRef]
- Fang, M.; Niu, K.; Huang, Z.; Sha, W.E.; Wu, X.; Koschny, T.; Soukoulis, C.M. Investigation of broadband terahertz generation from metasurface. Opt. Express 2018, 26, 14241–14250. [Google Scholar] [CrossRef]
- Luo, L.; Chatzakis, I.; Wang, J.; Niesler, F.B.; Wegener, M.; Koschny, T.; Soukoulis, C.M. Broadband terahertz generation from metamaterials. Nat. Commun. 2014, 5, 3055. [Google Scholar] [CrossRef]
- Kowerdziej, R.; Jaroszewicz, L.; Olifierczuk, M.; Parka, J. Experimental study on terahertz metamaterial embedded in nematic liquid crystal. Appl. Phys. Lett. 2015, 106, 092905. [Google Scholar] [CrossRef]
- Khan, M.I.; Fraz, Q.; Tahir, F.A. Ultra-wideband cross polarization conversion metasurface insensitive to incidence angle. J. Appl. Phys. 2017, 121, 045103. [Google Scholar] [CrossRef]
- Tal, M.; Keren-Zur, S.; Ellenbogen, T. Nonlinear plasmonic metasurface terahertz emitters for compact terahertz spectroscopy systems. ACS Photonics 2020, 7, 3286–3290. [Google Scholar] [CrossRef]
- Keren-Zur, S.; Tal, M.; Fleischer, S.; Mittleman, D.M.; Ellenbogen, T. Generation of spatiotemporally tailored terahertz wavepackets by nonlinear metasurfaces. Nat. Commun. 2019, 10, 1778. [Google Scholar] [CrossRef]
- Shcherbakov, M.R.; Neshev, D.N.; Hopkins, B.; Shorokhov, A.S.; Staude, I.; Melik-Gaykazyan, E.V.; Decker, M.; Ezhov, A.A.; Miroshnichenko, A.E.; Brener, I.; et al. Enhanced third-harmonic generation in silicon nanoparticles driven by magnetic response. Nano Lett. 2014, 14, 6488–6492. [Google Scholar] [CrossRef] [PubMed]
- Di Francescantonio, A.; Zilli, A.; Rocco, D.; Vinel, V.; Coudrat, L.; Conti, F.; Biagioni, P.; Duò, L.; Lemaître, A.; De Angelis, C.; et al. All-optical free-space routing of upconverted light by metasurfaces via nonlinear interferometry. Nat. Nanotechnol. 2024, 19, 298–305. [Google Scholar] [CrossRef] [PubMed]
- Liu, S.; Sinclair, M.B.; Saravi, S.; Keeler, G.A.; Yang, Y.; Reno, J.; Peake, G.M.; Setzpfandt, F.; Staude, I.; Pertsch, T.; et al. Resonantly enhanced second-harmonic generation using III–V semiconductor all-dielectric metasurfaces. Nano Lett. 2016, 16, 5426–5432. [Google Scholar] [CrossRef]
- Meng, Y.; Chen, Y.; Lu, L.; Ding, Y.; Cusano, A.; Fan, J.A.; Hu, Q.; Wang, K.; Xie, Z.; Liu, Z.; et al. Optical meta-waveguides for integrated photonics and beyond. Light Sci. Appl. 2021, 10, 235. [Google Scholar] [CrossRef]
- Wang, C.; Li, Z.; Kim, M.H.; Xiong, X.; Ren, X.F.; Guo, G.C.; Yu, N.; Lončar, M. Metasurface-assisted phase-matching-free second harmonic generation in lithium niobate waveguides. Nat. Commun. 2017, 8, 2098. [Google Scholar] [CrossRef]
- Herter, A.; Shams-Ansari, A.; Settembrini, F.F.; Warner, H.K.; Faist, J.; Lončar, M.; Benea-Chelmus, I.C. Terahertz waveform synthesis in integrated thin-film lithium niobate platform. Nat. Commun. 2023, 14, 11. [Google Scholar] [CrossRef]
- Hu, L.; Wang, B.; Guo, Y.; Du, S.; Chen, J.; Li, J.; Gu, C.; Wang, L. Quasi-BIC Enhanced Broadband Terahertz Generation in All-Dielectric Metasurface. Adv. Opt. Mater. 2022, 10, 2200193. [Google Scholar] [CrossRef]
- Sun, G.; Wang, Y.; Cui, Z.; Xie, R.; Zhao, X. Enhanced terahertz high-harmonic generation from high-Q quasi-bound states in the continuum empowered by permittivity-broken metasurface. Appl. Phys. Lett. 2024, 124, 111704. [Google Scholar] [CrossRef]
- Liu, Y.; Xu, Y.; Yu, B.; Liu, W.; Zhang, Z.; Cheng, H.; Chen, S. Terahertz Metasurfaces for Polarization Manipulation and Detection: Principles and Emerging Applications. Adv. Phys. Res. 2025, 4, 2400100. [Google Scholar] [CrossRef]
- Hu, F.; Li, L.; Liu, Y.; Meng, Y.; Gong, M.; Yang, Y. Two-plasmon spontaneous emission from a nonlocal epsilon-near-zero material. Commun. Phys. 2021, 4, 84. [Google Scholar] [CrossRef]
- Weis, R.; Gaylord, T. Lithium niobate: Summary of physical properties and crystal structure. Appl. Phys. A 1985, 37, 191–203. [Google Scholar] [CrossRef]
- Volk, T.; Wöhlecke, M. Polarization Reversal and Ferroelectric Domains in LiNbO3 Crystals. In Lithium Niobate: Defects, Photorefraction and Ferroelectric Switching; Springer: Berlin/Heidelberg, Germany, 2009; pp. 153–212. [Google Scholar]
- Zhu, D.; Shao, L.; Yu, M.; Cheng, R.; Desiatov, B.; Xin, C.; Hu, Y.; Holzgrafe, J.; Ghosh, S.; Shams-Ansari, A.; et al. Integrated photonics on thin-film lithium niobate. Adv. Opt. Photonics 2021, 13, 242–352. [Google Scholar] [CrossRef]
- Hebling, J.; Almasi, G.; Kozma, I.Z.; Kuhl, J. Velocity matching by pulse front tilting for large-area THz-pulse generation. Opt. Express 2002, 10, 1161–1166. [Google Scholar] [CrossRef]
- Hirori, H.; Blanchard, F.; Tanaka, K.J.A.P.L. Single-cycle terahertz pulses with amplitudes exceeding 1 MV/cm generated by optical rectification in LiNbO3. Appl. Phys. Lett. 2011, 98, 091106. [Google Scholar] [CrossRef]
- Jang, D.; Sung, J.H.; Lee, S.K.; Kang, C.; Kim, K.Y. Generation of 0.7 mJ multicycle 15 THz radiation by phase-matched optical rectification in lithium niobate. Opt. Lett. 2020, 45, 3617–3620. [Google Scholar] [CrossRef]
- Boyd, G.; Pollack, M. Microwave nonlinearities in anisotropic dielectrics and their relation to optical and electro-optical nonlinearities. Phys. Rev. B 1973, 7, 5345. [Google Scholar] [CrossRef]
- Carletti, L.; McDonnell, C.; Arregui Leon, U.; Rocco, D.; Finazzi, M.; Toma, A.; Ellenbogen, T.; Della Valle, G.; Celebrano, M.; De Angelis, C. Nonlinear THz generation through optical rectification enhanced by phonon–polaritons in lithium niobate thin films. ACS Photonics 2023, 10, 3419–3425. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, X.C. Free-space electro-optic sampling of terahertz beams. Appl. Phys. Lett. 1995, 67, 3523–3525. [Google Scholar] [CrossRef]
- Yang, J.; Wang, C. Efficient terahertz generation scheme in a thin-film lithium niobate-silicon hybrid platform. Opt. Express 2021, 29, 16477–16486. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Xia, S.; Wang, R.; Ma, R.; Lu, Y.; Zhang, X.; Song, D.; Wu, Q.; Morandotti, R.; Xu, J.; et al. Topologically tuned terahertz confinement in a nonlinear photonic chip. Light Sci. Appl. 2022, 11, 152. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Bai, W.; Feng, J.; Jie, W. The synthesis of large-diameter ZnTe crystal for THz emitting and detection. J. Cryst. Growth 2017, 475, 115–120. [Google Scholar] [CrossRef]
- Wilson, D.J.; Schneider, K.; Hönl, S.; Anderson, M.; Baumgartner, Y.; Czornomaz, L.; Kippenberg, T.J.; Seidler, P. Integrated gallium phosphide nonlinear photonics. Nat. Photonics 2020, 14, 57–62. [Google Scholar] [CrossRef]
- Ponseca, C.S., Jr.; Arlauskas, A.; Yu, H.; Wang, F.; Nevinskas, I.; Duda, E.; Vaicaitis, V.; Eriksson, J.; Bergqvist, J.; Liu, X.K.; et al. Pulsed terahertz emission from solution-processed lead iodide perovskite films. ACS Photonics 2019, 6, 1175–1181. [Google Scholar] [CrossRef]
- Valverde-Chávez, D.A.; Cooke, D.G. Multi-cycle terahertz emission from β-barium borate. J. Infrared Millim. Terahertz Waves 2017, 38, 96–103. [Google Scholar] [CrossRef]
- Balos, V.; Wolf, M.; Kovalev, S.; Sajadi, M. Optical rectification and electro-optic sampling in quartz. Opt. Express 2023, 31, 13317–13327. [Google Scholar] [CrossRef]
- Xu, L.; Zhang, X.C.; Auston, D. Terahertz beam generation by femtosecond optical pulses in electro-optic materials. Appl. Phys. Lett. 1992, 61, 1784–1786. [Google Scholar] [CrossRef]
- Marder, S.R.; Perry, J.W.; Yakymyshyn, C.P. Organic salts with large second-order optical nonlinearities. Chem. Mater. 1994, 6, 1137–1147. [Google Scholar] [CrossRef]
- Pan, F.; Knöpfle, G.; Bosshard, C.; Follonier, S.; Spreiter, R.; Wong, M.; Günter, P. Electro-optic properties of the organic salt 4-N, N-dimethylamino-4′-N′-methyl-stilbazolium tosylate. Appl. Phys. Lett. 1996, 69, 13–15. [Google Scholar] [CrossRef]
- Yang, Z.; Mutter, L.; Stillhart, M.; Ruiz, B.; Aravazhi, S.; Jazbinsek, M.; Schneider, A.; Gramlich, V.; Guenter, P. Large-size bulk and thin-film stilbazolium-salt single crystals for nonlinear optics and THz generation. Adv. Funct. Mater. 2007, 17, 2018–2023. [Google Scholar] [CrossRef]
- Coe, B.J.; Harris, J.A.; Asselberghs, I.; Clays, K.; Olbrechts, G.; Persoons, A.; Hupp, J.T.; Johnson, R.C.; Coles, S.J.; Hursthouse, M.B.; et al. Quadratic Nonlinear Optical Properties of N-Aryl Stilbazolium Dyes. Adv. Funct. Mater. 2002, 12, 110–116. [Google Scholar] [CrossRef]
- Kim, P.J.; Jeong, J.H.; Jazbinsek, M.; Choi, S.B.; Baek, I.H.; Kim, J.T.; Rotermund, F.; Yun, H.; Lee, Y.S.; Günter, P.; et al. Highly Efficient Organic THz Generator Pumped at Near-Infrared: Quinolinium Single Crystals. Adv. Funct. Mater. 2012, 22, 200–209. [Google Scholar] [CrossRef]
- Hu, J.; Bandyopadhyay, S.; Liu, Y.h.; Shao, L.y. A review on metasurface: From principle to smart metadevices. Front. Phys. 2021, 8, 586087. [Google Scholar] [CrossRef]
- Huang, L.; Zhang, S.; Zentgraf, T. Metasurface holography: From fundamentals to applications. Nanophotonics 2018, 7, 1169–1190. [Google Scholar] [CrossRef]
- Deng, Z.L.; Li, G. Metasurface optical holography. Mater. Today Phys. 2017, 3, 16–32. [Google Scholar] [CrossRef]
- Arbabi, A.; Arbabi, E.; Horie, Y.; Kamali, S.M.; Faraon, A. Planar metasurface retroreflector. Nat. Photonics 2017, 11, 415–420. [Google Scholar] [CrossRef]
- Rocco, D.; Locatelli, A.; Carletti, L.; Vincenti, M.A.; De Angelis, C. Nonlinear asymmetric imaging with AlGaAs metasurface. Opt. Express 2024, 32, 11673–11680. [Google Scholar] [CrossRef]
- Qiu, Y.; Yan, D.; Li, X.; Zhang, L.; Li, J. Highly efficient second harmonic generation assisted by the quasi-bound states in the continuum from AlGaAs meta-gratings. Opt. Commun. 2023, 546, 129772. [Google Scholar] [CrossRef]
- Camacho-Morales, R.; Rahmani, M.; Kruk, S.; Wang, L.; Xu, L.; Smirnova, D.A.; Solntsev, A.S.; Miroshnichenko, A.; Tan, H.H.; Karouta, F.; et al. Nonlinear generation of vector beams from AlGaAs nanoantennas. Nano Lett. 2016, 16, 7191–7197. [Google Scholar] [CrossRef] [PubMed]
- Gili, V.F.; Carletti, L.; Locatelli, A.; Rocco, D.; Finazzi, M.; Ghirardini, L.; Favero, I.; Gomez, C.; Lemaître, A.; Celebrano, M.; et al. Monolithic AlGaAs second-harmonic nanoantennas. Opt. Express 2016, 24, 15965–15971. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.; Fang, X.; Xiao, S. Tuning nonlinear second-harmonic generation in AlGaAs nanoantennas via chalcogenide phase-change material. Phys. Rev. B 2021, 104, 195428. [Google Scholar] [CrossRef]
- Marino, G.; Rocco, D.; Gigli, C.; Beaudoin, G.; Pantzas, K.; Suffit, S.; Filloux, P.; Sagnes, I.; Leo, G.; De Angelis, C. Harmonic generation with multi-layer dielectric metasurfaces. Nanophotonics 2021, 10, 1837–1843. [Google Scholar] [CrossRef]
- Liu, S.; Keeler, G.A.; Reno, J.L.; Sinclair, M.B.; Brener, I. III–V Semiconductor Nanoresonators—A New Strategy for Passive, Active, and Nonlinear All-Dielectric Metamaterials; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2016. [Google Scholar]
- Romeira, B.; Borme, J.; Fonseca, H.; Gaspar, J.; Nieder, J.B. Efficient light extraction in subwavelength GaAs/AlGaAs nanopillars for nanoscale light-emitting devices. Opt. Express 2020, 28, 32302–32315. [Google Scholar] [CrossRef]
- Gandolfi, M.; Carletti, L.; Tognazzi, A.; Cino, A.C.; De Angelis, C.; Guasoni, M. Near to short wave infrared light generation through AlGaAs-on-insulator nanoantennas. Opt. Express 2023, 31, 31051–31060. [Google Scholar] [CrossRef]
- Cruciano, C.; Rocco, D.; Genco, A.; Tognazzi, A.; Locatelli, A.; Carletti, L.; Fedorov, A.; Trovatello, C.; Di Blasio, G.; Bargigia, I.; et al. Shaping the Emission Directivity of Single Quantum Dots in Dielectric Nanodisks Exploiting Mie Resonances. ACS Nano 2025, 19, 3500–3509. [Google Scholar] [CrossRef]
- Baboux, F.; Moody, G.; Ducci, S. Nonlinear integrated quantum photonics with AlGaAs. Optica 2023, 10, 917–931. [Google Scholar] [CrossRef]
- Coudrat, L.; Boulliard, G.; Gérard, J.M.; Lemaître, A.; Degiron, A.; Leo, G. Unravelling the nonlinear generation of designer vortices with dielectric metasurfaces. Light Sci. Appl. 2025, 14, 51. [Google Scholar] [CrossRef]
- Gandhi, H.K.; Rocco, D.; Carletti, L.; De Angelis, C. Gain-loss engineering of bound states in the continuum for enhanced nonlinear response in dielectric nanocavities. Opt. Express 2020, 28, 3009–3016. [Google Scholar] [CrossRef]
- Peters, L.; Rocco, D.; Olivieri, L.; Arregui Leon, U.; Cecconi, V.; Carletti, L.; Gigli, C.; Della Valle, G.; Cutrona, A.; Totero Gongora, J.S.; et al. Resonant Fully dielectric metasurfaces for ultrafast Terahertz pulse generation. Adv. Opt. Mater. 2024, 12, 2303148. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, Y.; Xu, X.; Fan, Z.; Khurgin, J.B.; Xiong, Q. Nonlinear optical properties of halide perovskites and their applications. Appl. Phys. Rev. 2020, 7, 041313. [Google Scholar] [CrossRef]
- He, Y.; Li, N.; Feng, Y.; Li, X.; Liu, D.; Huang, J.; Zhou, R.; Wu, M.; Miao, L.; Zhao, C. Broadband nonlinear optical modulator with 2D organic-inorganic hybrid perovskite nanocrystals. IEEE J. Sel. Top. Quantum Electron. 2023, 29, 1–8. [Google Scholar] [CrossRef]
- Marjanowska, A.; El Karout, H.; Guichaoua, D.; Sahraoui, B.; Płóciennik, P.; Zawadzka, A. Topography and nonlinear optical properties of thin films containing iodide-based hybrid perovskites. Nanomaterials 2023, 14, 50. [Google Scholar] [CrossRef]
- Li, H.; Diao, M.; Boukhvalov, D.W.; Ke, Y.; Humphrey, M.G.; Zhang, C.; Huang, Z. Prominent Nonlinear Optical Absorption in SnS2-Based Hybrid Inorganic—Organic Superlattice. Adv. Funct. Mater. 2024, 34, 2400077. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, L.; Yao, Z.; Zhang, L.; He, C.; Zhao, Q.; Bai, J.; Xu, X. Terahertz surface emission from layered MoS2 crystal: Competition between surface optical rectification and surface photocurrent surge. J. Phys. Chem. C 2018, 122, 481–488. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Habibighahfarokhi, F.; Sergaeva, O.; Carletti, L.; Franceschini, P.; Tognazzi, A.; Locatelli, A.; Leon, U.A.; Della Valle, G.; De Angelis, C.; Rocco, D. Nonlinear Dielectric Metasurfaces for Terahertz Applications. Photonics 2025, 12, 370. https://doi.org/10.3390/photonics12040370
Habibighahfarokhi F, Sergaeva O, Carletti L, Franceschini P, Tognazzi A, Locatelli A, Leon UA, Della Valle G, De Angelis C, Rocco D. Nonlinear Dielectric Metasurfaces for Terahertz Applications. Photonics. 2025; 12(4):370. https://doi.org/10.3390/photonics12040370
Chicago/Turabian StyleHabibighahfarokhi, Forouzan, Olga Sergaeva, Luca Carletti, Paolo Franceschini, Andrea Tognazzi, Andrea Locatelli, Unai Arregui Leon, Giuseppe Della Valle, Costantino De Angelis, and Davide Rocco. 2025. "Nonlinear Dielectric Metasurfaces for Terahertz Applications" Photonics 12, no. 4: 370. https://doi.org/10.3390/photonics12040370
APA StyleHabibighahfarokhi, F., Sergaeva, O., Carletti, L., Franceschini, P., Tognazzi, A., Locatelli, A., Leon, U. A., Della Valle, G., De Angelis, C., & Rocco, D. (2025). Nonlinear Dielectric Metasurfaces for Terahertz Applications. Photonics, 12(4), 370. https://doi.org/10.3390/photonics12040370








