Chaos Suppression in Optically Injected Semiconductor Lasers Through an Unequally Spaced Optical Frequency Comb

Abstract

This study theoretically investigates the impact of comb spacing irregularity on the dynamics of optically injected semiconductor lasers using a rate equation model. Bifurcation analysis, time-domain simulations, spectral properties, and Mode Suppression Ratio (MSR) calculations reveal that equal spacing induces strong mode competition and chaos, while unequal spacing suppresses chaos and enhances stability. Interestingly, the Flipped comb exhibits similar behavior to the unequal comb, further supporting the conclusion that relative spacing—not spectral order—governs stability the Arbitrary combs, though lacking structured spacing, demonstrate intermediate suppression, indicating that breaking uniformity mitigates instability, but optimal spacing maximizes stabilization. Extending beyond previous studies on frequency comb injection, this work identifies spacing irregularity as a key mechanism for chaos control, offering new strategies for laser stabilization in optical communications and photonic integration.

1. Introduction

The injection of optical frequency combs into semiconductor lasers has emerged as a critical topic in laser physics, enabling enhanced stability, frequency control, and novel nonlinear dynamics. Optical injection locking has been extensively explored in semiconductor lasers, with foundational studies demonstrating locking conditions, stability properties, and applications in optical communications [1,2,3]. Recent work has extended these concepts to the injection of frequency combs, revealing rich nonlinear dynamics and chaos control mechanisms [4].

Optical frequency combs, characterized by their precisely spaced spectral lines, have found broad applications in optical communications [5], spectroscopy [6], and microwave photonics [7]. The injection of such combs into semiconductor lasers introduces complex interactions, leading to phenomena such as frequency stabilization, linewidth narrowing, and chaos suppression [8,9]. Studies have shown that semiconductor lasers injected with optical frequency combs exhibit diverse dynamical behaviors, including period doubling, quasi-periodicity, and chaos [10,11].

Several experimental and theoretical efforts have focused on understanding the nonlinear dynamics induced by comb injection. Recent numerical investigations have highlighted the effects of injection strengths, detuning, and phase noise on the stability of injected semiconductor lasers [12,13]. Experimental work has demonstrated that cascaded injection locking can generate tunable frequency combs with enhanced coherence and reduced phase noise [14,15]. Additionally, self-injection locking techniques have been explored to stabilize optical frequency combs in semiconductor lasers [16].

In particular, the effect of comb spacing on the stability of injected semiconductor lasers has been a topic of increasing interest. Studies have demonstrated that varying the injection strengths and comb spacing defines regions of stable locking and complex nonlinear dynamics [17]. Numerical investigations further reveal that comb spacing affects the locking bandwidth and the frequency shift of the slave laser, influencing its spectral properties [11]. Experimental research has shown that, under certain conditions, a slave laser injected with a frequency comb can lock to rational harmonics of the injected comb spacing, generating additional comb lines through nonlinear interactions [18]. Additionally, an analysis of chaotic optical frequency combs suggests that comb spacing plays a crucial role in determining the complexity of the laser’s output, quantified through permutation entropy and chaos bandwidth [19]. These findings highlight the importance of frequency comb spacing in shaping the behavior of optically injected semiconductor lasers, affecting their stability, frequency response, and nonlinear characteristics.

Furthermore, studies have demonstrated that the injection of frequency combs into quantum cascade lasers [20] and vertical-cavity surface-emitting lasers (VCSELs) [21] can lead to controlled frequency modulation and mode selection. Injection locking of semiconductor lasers using frequency combs has also been utilized for high-speed optical communication systems, enabling wavelength-division multiplexing and data transmission with enhanced spectral efficiency [12,22].

Recent advancements have also explored the use of optically injected semiconductor lasers for the generation of arbitrary frequency combs [23,24]. These studies have investigated how frequency comb generation can be manipulated through gain switching, optical feedback, and dual-mode injection, leading to new capabilities for precision metrology and high-speed optical networks [25,26].

Despite these advancements, most existing research has focused on the effects of equally spaced frequency combs, while the influence of unequally spaced combs on semiconductor laser dynamics remains largely unexplored. This study builds on these insights by investigating how comb spacing irregularity influences stability and chaos suppression in optically injected semiconductor lasers. Through a theoretical analysis based on rate equations, we systematically explore the role of unequal spectral spacing in controlling nonlinear interactions. Our findings contribute to the ongoing efforts to optimize frequency comb injection for practical applications in photonic integrated circuits, optical communication, and laser stabilization.

2. Materials and Methods

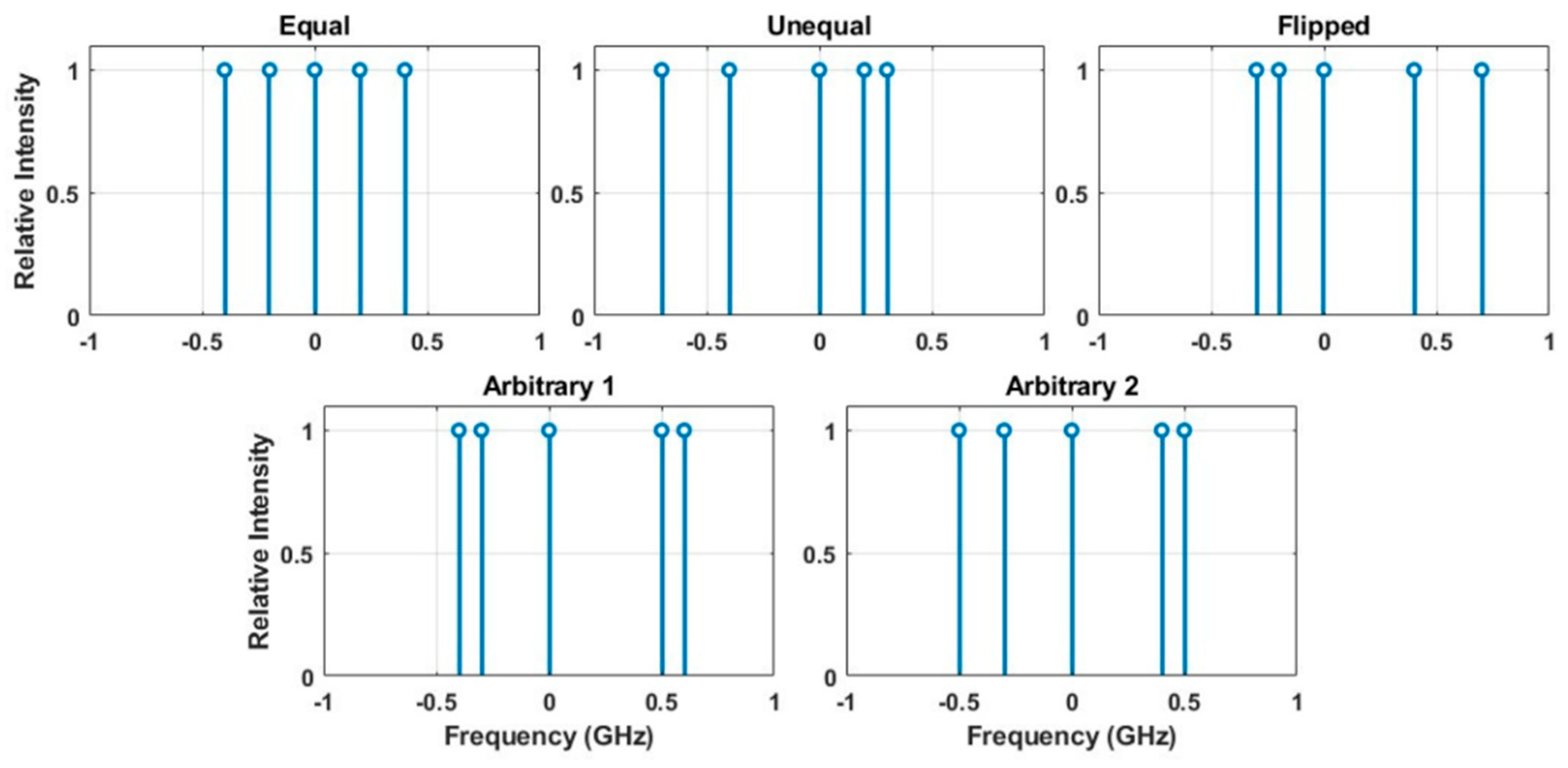
To examine the effect of unequal spacing comb on the dynamics of optically injected semiconductor lasers, we proposed five different combinations of combs, as shown in Figure 1. The first comb is the Equal one, where the spacing of signals is equal (0.2 GHz). The second comb is unequal spacing (from left to right: 0.3, 0.4, 0.2, and 0.1 GHz) while the third one is a flipped version of the previous one (from left to right: 0.1, 0.2, 0.4 and 0.3 GHz). The fourth and fifth combs are both arbitrary (Arbitrary 1: 0.1, 0.3, 0.5, and 0.1 GHz, while Arbitrary 2: 0.2, 0.3, 0.4, and 0.1). These values are listed in

Table 1. Parameters used in this study’s simulation.

Comb Type	Spacing (GHz)
Equal spacing	0.2	0.2	0.2	0.2
Unequal	0.3	0.4	0.2	0.1
Flipped	0.1	0.2	0.4	0.3
Arbitrary 1	0.1	0.3	0.5	0.1
Arbitrary 2	0.2	0.3	0.4	0.1

.

The dynamics of an injected laser can be accurately described by rate equations that govern the evolution of the electric field amplitude, phase, and carrier density, as follows:

$${\displaystyle \frac{d}{dt}}{E}_o(t)={\displaystyle \frac{1}{2}}{G}_N\Delta N(t)E_o(t)+\eta \left[\sum E_m\cos (\Delta t_m)\right]$$

(1)

$${\displaystyle \frac{d}{dt}}{\phi }_o(t)={\displaystyle \frac{1}{2}}\alpha G_N\Delta N(t)+\eta \left[\sum {\displaystyle \frac{E_m}{E_o(t)}}\sin (\Delta t_m)\right]$$

(2)

$${\displaystyle \frac{d}{dt}}N(t)=J-{\displaystyle \frac{N(t)}{{\tau }_s}}-G_N(N(t)-N_o)E_o^2(t)$$

(3)

The key parameters influencing injection locking include the frequency detuning (Δf) and the injection level (K). The frequency detuning represents the difference between the frequency of the master laser (ML), specifically the central line of the frequency comb, and that of the free-running slave laser (SL). The injection level is defined as the ratio of the electric field amplitude of the ML comb to that of the SL, expressed as K = E_m/E_o, where Em corresponds to the electric field of the ML comb at mode index m (ranging from m = 1 to 5), and E_o(t) denotes the electric field of the SL. The SL is assumed to be a single mode laser.

Additional parameters include the gain coefficient of the cavity medium (G_N), the population inversion (ΔN(t) = N − Nth), where N is the carrier density and Nth is the threshold carrier density. The coupling coefficient is denoted as η and m represents the mode order in the frequency comb. The angular frequency detuning between the SL and the m mode of the ML is given by $\Delta {\omega }_m={\omega }_m-{\omega }_o$. The phase of the SL is represented by ϕ_o(t), while α is the linewidth enhancement factor (LEF), also known as Henry’s factor. The carrier density at transparency is denoted by N_o. Furthermore, J represents the injected current density and τ_s is the carrier lifetime associated with spontaneous emission and nonradiative recombination. For simplicity, the central signal of each of the five comb signals (i.e., the third line from each side) is considered the main reference signal in terms of frequency detuning. In other words, the frequency detuning between the slave laser (SL) and the master laser (ML) is defined as the frequency difference between the SL and this central comb signal. Accordingly, this signal is aligned at 0 GHz in the ML spectrum, as shown in Figure 1.

To incorporate spacing irregularity into the model, the spacing of the uniform comb (0.2 GHz) is chosen as the standard value. Multiples or fractions of this value are then randomly added to or subtracted from the ideal spacing to introduce the desired irregularities. The goal is to investigate the impact of spacing irregularities, irrespective of any fine-tuning or optimization. The corresponding angular frequencies of the comb signals are subsequently calculated and incorporated into the model. As previously noted, the frequency detuning is defined as the difference between the SL and the central signal of the comb.

As previously mentioned, the injection level of all comb modes is maintained constant and the dynamic behavior is analyzed as a function of both injection level and detuning. The dynamics are obtained through numerical integration of the rate equations using the Runge–Kutta method within a computational framework. The bifurcation diagrams are obtained from the electric field time series. Finally, the parameters implemented in this simulation are obtained through the experimental characterization of a real semiconductor laser and can be found in [11].

To determine the Mode Suppression Ratio (MSR) from optical spectra, the typical formula used is:

MSR = 10 log₁₀ (P_p/P_n)

(4)

where P_p is the power (intensity) of the dominant mode (the highest peak in the optical spectrum) and P_n is the power of the second strongest mode (the next highest peak in the spectrum).

This formula expresses MSR in decibels (dB), indicating how effectively the primary mode dominates over competing modes. A higher MSR means stronger mode suppression, implying a more stable laser operation with reduced mode competition, whereas a lower MSR suggests multimode operation and potential instability.

3. Results and Discussion

To reveal the effect of the equality of comb spacing, we first generate the bifurcation diagrams of the SL when injected with different comb configurations. Figure 2 shows the bifurcation diagrams as a function of frequency detuning for the five configurations and at five different injection strengths. The rows correspond to different comb spacing configurations, while the columns represent varying injection levels. These diagrams provide insight into the stability, mode competition, and dynamical transitions occurring in the semiconductor laser under different injection conditions. In the case of equal spacing comb (1st row in Figure 1), the dynamics exhibit chaotic behaviors with strong mode competition across most of the detuning and at all injection levels. This aligns with findings from Doumbia et al. [19], where the injection of optical frequency combs into semiconductor lasers resulted in complex nonlinear dynamics, including routes to chaos. The reason is probably that the evenly distributed comb lines allow the laser modes to enhance and synchronize more effectively, leading to the shown chaotic profile.

In contrast, for the unequal spacing comb (2nd row in Figure 2), the mode competition seems to be weaker and the chaotic profiles become more structured. At the negative frequency detuning, the system shows periodic behavior in most cases, proving that the inequality in comb spacing can, in some way, control chaos. This also suggests that unequal spacing disrupts the even mode coupling, preventing strong nonlinear interactions and thus enabling more periodic behavior, particularly at negative detuning.

However, when the comb is horizontally flipped, the Flipped comb configuration appears to exhibit a very similar structure (3rd row in Figure 1) to the unequal one. This suggests that simply flipping the comb spectrum (left to right) does not fundamentally alter the laser’s dynamic response. Instead, the bifurcation structure remains largely unchanged, implying that the key factor influencing the mode competition and chaotic behavior is the spacing itself rather than the absolute frequency ordering. The similarity between the Flipped and unequal combs likely arises because the laser responds to relative spacing rather than absolute frequency order. Since both maintain the same separations, they excite similar internal modes. Additionally, semiconductor lasers often exhibit symmetric responses to frequency inversions, preserving the bifurcation structure. This supports the idea that spacing irregularity, not spectral order, governs mode competition and stability.

Finally, the reduced chaos in both Arbitrary 1 and Arbitrary 2 (4th and 5th rows in the figure), compared to the equal comb, further supports the idea that breaking uniformity in spacing weakens mode competition and stabilizes the laser dynamics. Despite their arbitrary nature, the lack of evenly distributed spectral lines likely prevents strong synchronization between injected modes and the laser’s internal resonances, reducing chaotic interactions. The similarity between the two arbitrary cases suggests that as long as the comb spacing is irregular, the system exhibits more structured behavior, regardless of the exact arrangement. This underscore the conclusion that comb spacing irregularity, rather than absolute frequency positioning, is the dominant factor controlling chaos and stability in optically injected semiconductor lasers.

The bifurcation diagrams as a function of injection level at different frequency detuning for the same comb configurations are shown in Figure 3. The trends observed here closely align with our previous analysis, further reinforcing the role of comb spacing in shaping the laser’s dynamic behavior. By examining how the system evolves under varying injection strengths, we can better understand the interplay between optical injection and comb structure.

For the equal comb (1st row), the bifurcation diagrams confirm the persistence of strong chaotic behavior across all injection levels, similar to what was observed when varying detuning. Higher injection levels lead to increased mode competition, maintaining a broad chaotic region throughout the parameter space. This supports our earlier conclusion that evenly spaced comb lines strongly interact with the laser’s internal modes, leading to persistent instability. The equal spacing enhances synchronization among modes, resulting in complex multimode interactions that drive the system toward chaos.

In contrast, the unequal and Flipped combs (2nd and 3rd) exhibit significantly more structured dynamics, mirroring the results from our detuning-based bifurcation analysis. The strong similarity between these two configurations confirms that flipping the comb spectrum does not fundamentally alter the laser’s response. The reduced chaotic regions and more structured transitions as injection increases suggest that spacing irregularity disrupts strong nonlinear interactions, leading to more stable behavior. This further supports the idea that the key factor influencing chaos control is the nonuniformity in frequency spacing, rather than the absolute order of comb lines.

The Arbitrary 1 and Arbitrary 2 combs (4th and 5th rows) continue to show reduced chaotic tendencies, consistent with previous findings. The transition from stable to chaotic states appears smoother, suggesting that breaking uniformity in spacing limits extreme mode competition. At specific detuning values, these configurations exhibit structured bifurcation patterns, reinforcing the notion that irregular spacing acts as a stabilizing mechanism. This means that any deviation from equal spacing tends to weaken the strong multimode coupling that drives chaotic behavior, making the system more predictable and stable under optical injection.

Overall, the correlation between the two bifurcation analyses (as a function of detuning and injection level) confirms that comb spacing irregularity consistently acts as a stabilizing factor, reducing chaos in both parameter spaces. The persistence of chaos in the equal case and the relative stabilization in the unequal, Flipped, and Arbitrary cases strongly suggest that introducing nonuniform frequency spacing can be an effective strategy for controlling dynamical transitions in optically injected semiconductor lasers. Further analysis of time-domain signals or spectral properties could provide deeper insights, as we are going to discuss.

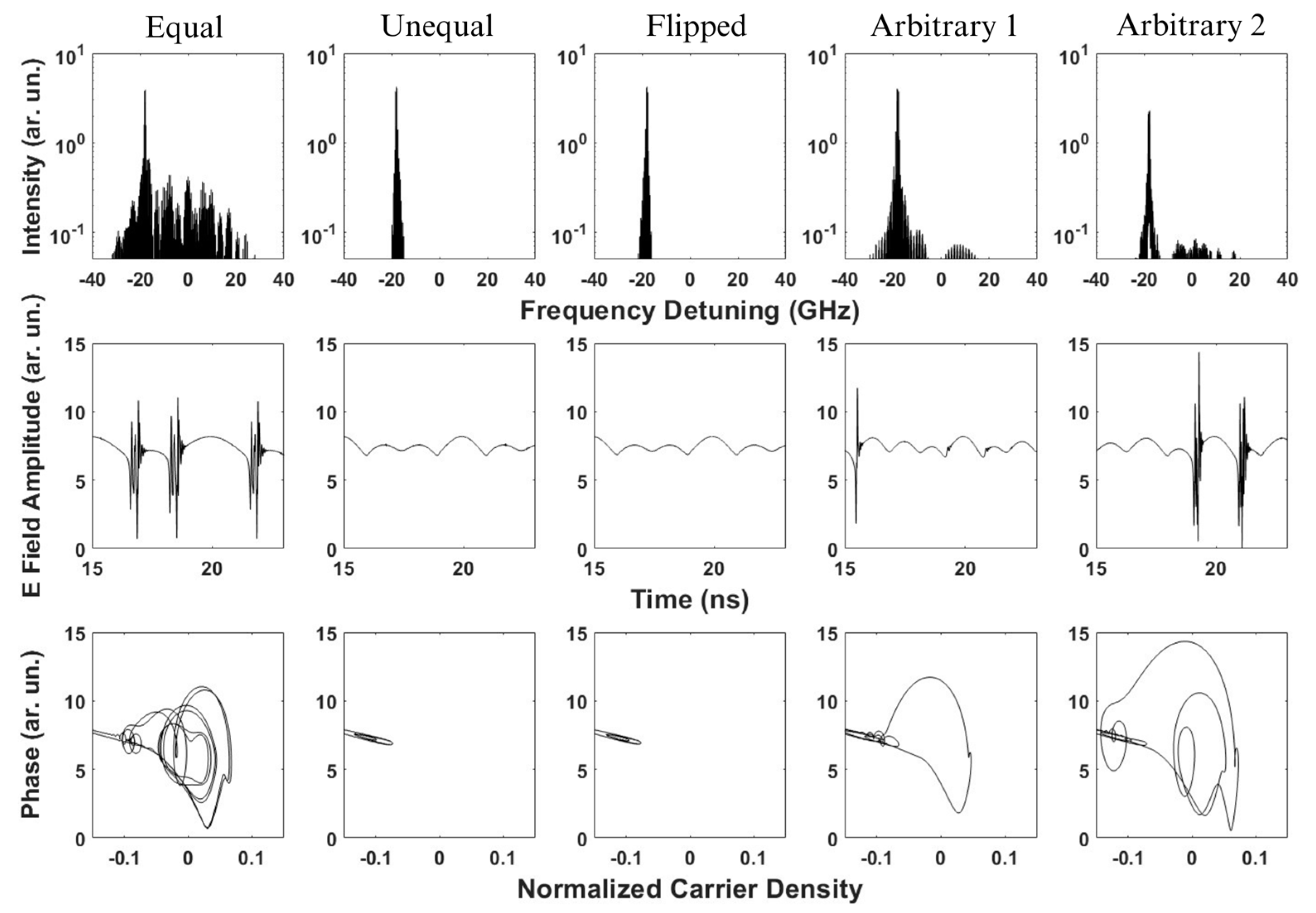
Figure 4 provides critical insights into the laser’s response under different comb configurations by examining the optical spectra (1st row), electric field amplitude time series (2nd row), and phase-space portraits (3rd row). The results further confirm the impact of comb spacing on stability, mode competition, and chaotic behavior, aligning well with our previous bifurcation analysis.

For the equal comb, the optical spectrum exhibits a broad, noisy profile, indicating strong mode competition and chaotic behavior. The time-domain signal shows irregular, high-amplitude oscillations, reflecting instability and significant power fluctuations. The phase-space portrait features a complex, multi-loop attractor, confirming a chaotic regime with strong carrier density variations. These observations reinforce our previous finding that Equal comb spacing enhances nonlinear interactions, leading to persistent chaos.

In contrast, the unequal and Flipped combs exhibit much narrower spectra, indicating reduced mode competition and a more stable dynamic regime. Their time-domain signals display smooth oscillations with low amplitude variations, suggesting a more periodic or stable state. The corresponding phase-space portraits collapse into simple, well-defined attractors, confirming the suppression of chaotic dynamics. The similarity between these two cases reaffirms our earlier conclusion that flipping the comb does not fundamentally change the laser’s response as long as spacing irregularity is maintained. This confirms that breaking equal spacing disrupts strong synchronization effects and reduces chaotic tendencies.

For the Arbitrary 1 and Arbitrary 2 combs, the optical spectra remain broader than the unequal and Flipped cases but still exhibit noticeable peaks, indicating an intermediate stability level. The time-domain signals show a mix of periodic and transient behaviors, while the phase-space portraits feature partially structured attractors with some chaotic elements. These results confirm that breaking uniformity in spacing mitigates chaos but does not necessarily eliminate it, as the exact arrangement of comb lines still influences nonlinear interactions.

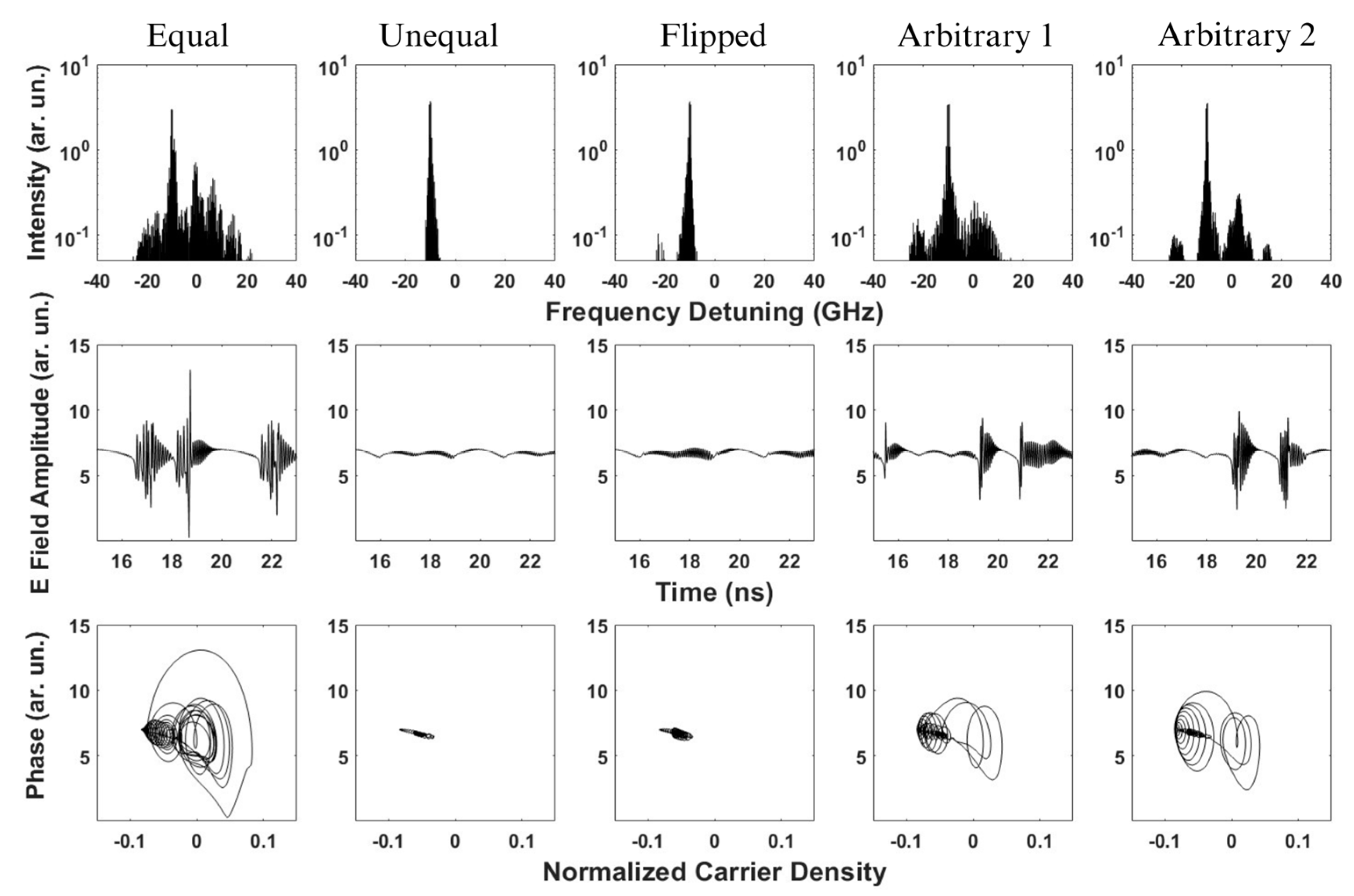
To further confirm our conclusion, we generate the same spectra at different operating points as shown in Figure 5. At this new operating point (injection level of 0.8 and detuning of −20 GHz), the results remain consistent with previous observations, further confirming the impact of comb spacing on laser stability. The equal comb continues to exhibit a broad and noisy spectrum, irregular time-domain oscillations, and a complex phase-space attractor, reinforcing its inherently chaotic nature due to strong mode competition. In contrast, the unequal and Flipped combs display narrow spectral peaks, smooth time-domain oscillations, and well-defined phase-space trajectories, confirming their stability and reduced nonlinear interactions. The Arbitrary 1 and Arbitrary 2 combs again show intermediate behavior, with structured yet slightly broadened spectra, indicating partial chaos suppression. Compared to previous results, increasing the injection level to 0.8 enhances stability in the unequal and Flipped cases while maintaining strong chaotic dynamics in the equal comb. This further aligns with the bifurcation analysis, showing that a higher injection reinforces the stabilizing effect of spacing irregularity while amplifying chaos in uniformly spaced combs.

Although the slave laser is modeled as a single-mode device, the optical spectra in Figure 4 and Figure 5 display multiple peaks and broad profiles that may superficially resemble multimode operation. However, these features do not indicate the presence of multiple longitudinal modes in the laser cavity. Instead, they arise from nonlinear interactions between the injected frequency comb components and the single-mode field of the slave laser. These interactions generate sidebands and complex temporal dynamics—including quasi-periodic and chaotic oscillations—that manifest as spectral broadening and multiple frequency components. Thus, the observed spectral characteristics reflect the dynamical modulation of a single-mode laser rather than true multimode lasing.

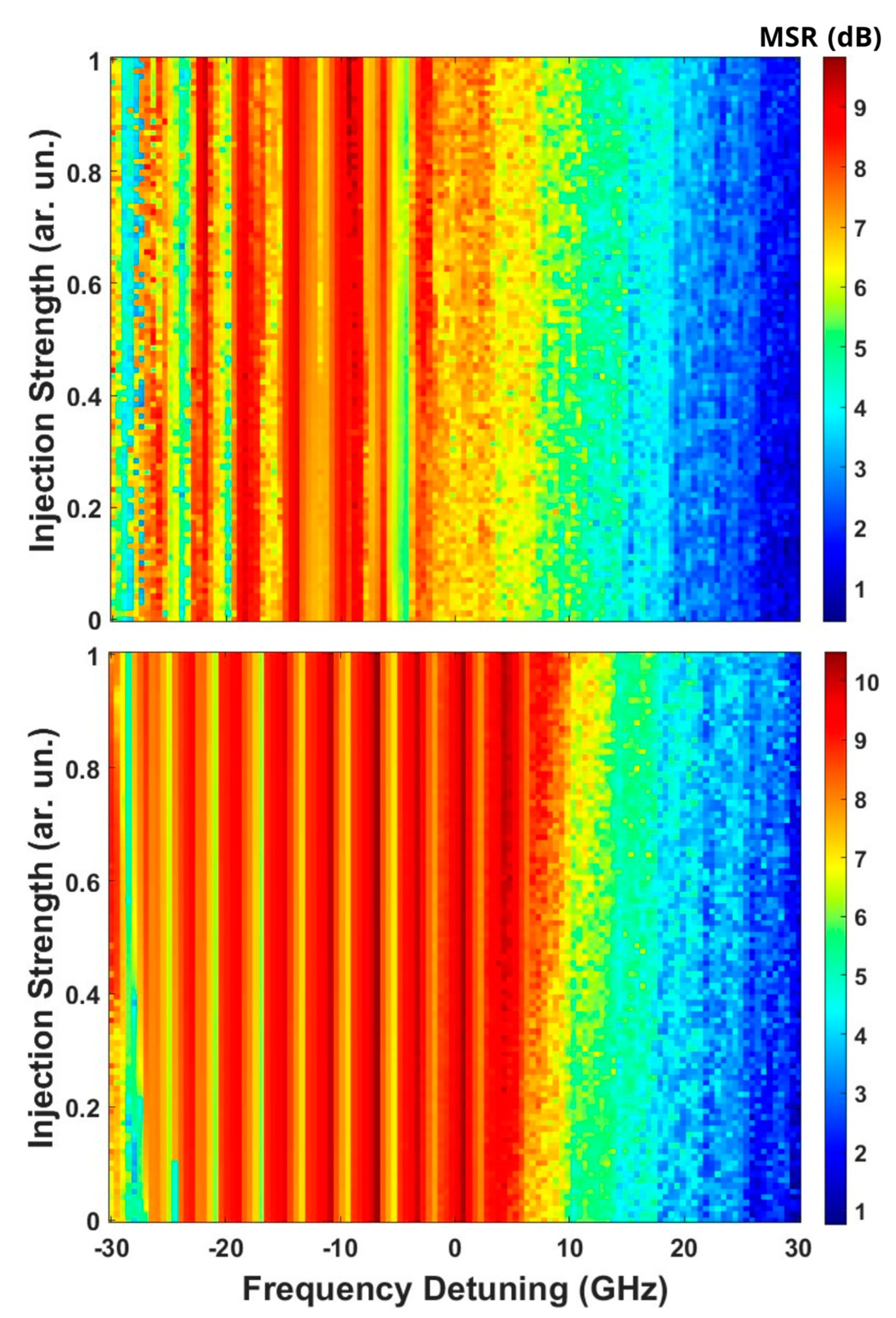
Finally, we used Formula (4) to calculate the Mode Suppression Ratio MSR as shown in Figure 6. This figure presents the MSR as a function of frequency detuning and injection strengths for the equally spaced comb (upper panel) and the unequal comb (lower panel). MSR quantifies how well the dominant mode suppresses competing modes, with higher values (red regions) indicating greater suppression and, consequently, a more stable operation.

The equally spaced comb (upper panel) exhibits lower MSR values overall, with significant blue and cyan regions, particularly at positive detuning and higher injection levels. This indicates weaker mode suppression, suggesting strong mode competition and multimode operation, aligning with our earlier findings that the equal comb induces chaotic dynamics and instability. The lower MSR at high injection strengths also supports previous observations that increasing injection does not stabilize the laser when mode competition is intense. This corresponds well with the broad optical spectra, irregular time-domain oscillations, and complex chaotic phase-space portraits seen earlier for the equal comb.

In contrast, the unequal comb (lower panel) demonstrates consistently higher MSR values, with large red and orange regions, indicating stronger mode suppression. This confirms that irregular spacing helps reduce mode competition, leading to more stable operation. The improved MSR, particularly at negative detuning and moderate-to-high injection strengths, correlates well with our previous observations, where unequal comb spacing resulted in smoother time-domain oscillations, well-defined phase-space trajectories, and narrower optical spectra. The fact that MSR remains high across a broader range of injection levels further supports our conclusion that introducing spacing irregularity disrupts strong synchronization effects, mitigating chaotic behavior and stabilizing laser dynamics.

This MSR analysis strongly supports the bifurcation, spectral, and time-domain results discussed earlier. The equal comb consistently struggles with mode suppression, reinforcing its chaotic and unstable nature, while the unequal comb maintains stronger mode suppression across various detuning values and injection strengths, confirming its role in reducing chaos and promoting stable laser operation. This further emphasizes that comb spacing irregularity is a key factor in controlling laser dynamics, rather than the absolute frequency order of injection modes. Note that the Arbitrary 1 and Arbitrary 2 combs were generated by applying random deviations to the standard equal spacing value (0.2 GHz), as outlined in Section 2. Specifically, these deviations were not optimized or guided by a particular design algorithm but were instead selected to explore generic nonuniform configurations. The intention was to assess whether random spacing irregularities—without any fine-tuned optimization—could still contribute to chaos suppression. This reinforces the idea that breaking uniformity itself is a sufficient mechanism for partial stabilization, even in the absence of a targeted comb design.

Although this study is based on theoretical modeling, the proposed effects of comb spacing irregularity on chaos suppression could be tested experimentally using tunable optical injection setups and integrated photonic platforms. Experimental investigations by Doumbia et al. [4,9] have demonstrated how optical injection of frequency combs into semiconductor lasers can induce wideband chaos and complex nonlinear dynamics, supporting the idea that comb structure critically influences laser behavior. These existing experimental results provide a foundational basis for validating our predictions and suggest that comb spacing irregularity could be a viable tool for stabilizing laser dynamics in practical systems.

4. Conclusions

This study demonstrates that comb spacing irregularity is a key factor in controlling chaos and stability in optically injected semiconductor lasers, rather than the absolute frequency ordering of injected modes. The equally spaced comb induces strong mode competition, leading to chaotic dynamics and low mode suppression, while the unequal comb significantly reduces chaos, exhibiting narrow spectra, smooth oscillations, and high MSR values. The Flipped comb shows similar stabilization effects, confirming that relative spacing—not spectral order—governs laser dynamics. The Arbitrary combs provide partial chaos suppression, reinforcing that any deviation from equal spacing improves stability.

Unlike previous studies on frequency comb and mode interactions, this work uniquely demonstrates that spacing irregularity itself acts as a chaos suppression mechanism by systematically correlating bifurcation behavior, spectral properties, time-domain signals, and MSR trends. These insights offer a novel approach to laser stabilization through comb design.

Strategic comb spacing can enhance optical communications, frequency comb generation, and nonlinear laser applications. Future research should optimize spacing patterns to enhance stability, develop adaptive comb designs, and explore integration into photonic circuits and high-speed transmission systems.