Experimental Study on Fiber Optic Strain Characterization of Overlying Rock Layer Movement Forms and States Using DFOS

Abstract

Mastering the movement laws of hard overlying rock layers is the foundation of the development of coal mining technology and plays an important role in improving coal mine safety production. Therefore, an indoor similar simulation experiment was conducted based on an actual coal mining face to test the strain variations of the pre-embedded optical fibers in the model using distributed fiber optic sensing. Finally, the fiber optic strain distribution curve was used to characterize the movement form and state of the overlying rock layer and fractured rock blocks. The experimental results showed the following. (1) The strain distribution of horizontally laid optical fibers is characterized by an upward trapezoidal convex platform, reflecting the evolution law of various horizontal movement forms of overlying rock layers: voussoir beam → cantilever beam → reverse cantilever beam → voussoir beam. The strain curve of vertically laid optical fibers is characterized by two levels of right-handed trapezoidal protrusions above and below, representing the motion state of the upper voussoir beam–lower cantilever beam structure of the overburden. (2) In addition, as excavation progresses, the range and height of the failure deformation of the overlying rock layers develop in a stepped shape. (3) In the end, the final vertical development heights of the cantilever beam structure and the voussoir beam structure in the overburden were 90.27 m and 24.99 m, respectively. The experimental results are highly consistent with the UDEC numerical simulation and mandatory calculation formulas, thus verifying the feasibility of the experiment. These research results provide theoretical and experimental support for safe coal mining in practical working faces.

1. Introduction

The underground coal mining process can lead to overburden deformation movement, which is an important cause of coal mine water inrush, gas outburst, and roof collapse accidents. It is also the basic cause of the manifestation of mine pressure and the instability of the surrounding rocks ahead of the coal face [1]. Mastering the overburden mining-induced movement laws during mining processes can help solve engineering problems such as mining pressure prediction, water hazard prevention, gas extraction, surrounding rock support, and grouting in isolation zones in underground coal mining, etc., thereby preventing coal mine safety accidents. As is well-known, the destruction of the stable equilibrium mechanical state of the initial overlying strata will inevitably occur during coal-mining progress, causing rupture, and deforming the motion of overlying rock formations. The fractured rock blocks will slide or rotate in the form of cantilever beams or voussouir beams; these fractured and broken rock blocks either lose their mechanical connection with the original rock stratum and fall into the goaf, or maintain their connection with the original rock layer and rotate-sink along the hinge point, which will lead to spatial variations in the movement forms and states of the overburden [2]. The overburden failure deformation range during coal mining is usually divided into various horizontal and vertical zones in space via different rock block movement forms and states.

The “two zones”—comprising the structures of the voussoir beam as well as the cantilever beam in the perpendicular direction [3]—correspond to the distribution ranges of the caving zone and the fracture zone, respectively. The “two zones” are regions where rock blocks in the overlying strata exhibit intense movement and where fractures are fully developed [4,5]. The deformation development laws of the overburden are specifically reflected in the spatiotemporal movement laws of the fractured rock blocks within “two zones”. This has become an important research field in coal mining, and many scholars have conducted various studies for this purpose.

The research methods for overburden deformation movement mainly include theoretical analysis, numerical simulation, the similarity simulation experiment (SSE), machine learning, and on-site testing, etc. [6,7,8,9,10]. Among them, the SSE is the most commonly used and important technology. SSE refers to the construction of an overburden simulation model based on field research, using similar materials and the overburden parameters, and combining the geological structure characteristics in situ, to simulate the overburden mining-induced deformation movement. SSE is an outstanding method for solving geotechnical engineering issues in coal-seam mining. It can not only make up for the shortcomings of theoretical analysis, but also solve some problems that are difficult to solve in the research process of coal-mining sites.

In SSE, the most important thing is how to accurately obtain parameters such as displacement, strain, temperature, stress, and so on within the overburden. However, in traditional SSE, displacement measurement typically relies on close-range photogrammetry, total stations, and dial gauges. For stress–strain monitoring, electromagnetic sensors such as strain gauges, pressure sensors, pressure boxes, and pressure gauges are commonly utilized. However, these conventional measurement methods and sensors are fraught with inherent limitations and drawbacks: (1) they exhibit relatively low accuracy and sensitivity, resulting in significant measurement errors; (2) they are “point-type” measurement tools, which means their layout and operation are complex and prone to missing critical data; (3) they can only monitor the surface displacement deformation and localized stress or strain, thus failing to provide internal distributed monitoring; and (4) continuous and real-time monitoring of the entire model is challenging to achieve. Most critically, the excessive insertion of various “point-type” sensors at different intervals inevitably alters the original state of the tested structure. This leads to deviations in the test results and directly impacts the assessment of the overall stability of the overlying rock mass under mining conditions. Therefore, there is an urgent need to develop a high-precision, real-time, parallel testing method that can achieve distributed and internal monitoring to deformation and stress in the SSE.

Due to the inherent advantages of distributed fiber optic sensing (DFOS), such as high precision, sensitivity, resistance to electromagnetic interference, and resistance to acid and alkali corrosion, DFOS using soft and slender sensing fibers for multi-parameter distributed measurement can accurately address this issue.

DFOS has recently become a hot topic for scholars in many research fields. DFOS has developed rapidly, especially with the improvement in computing power and the advancement of interdisciplinary integration. Machine learning (ML) has propelled DFOS to achieve remarkable progress in both technology and application. For instance, Christos et al. [11] addressed the cross-sensitivity issue between temperature and humidity in DFOS monitoring using ML. They proposed a signal post-processing method based on a convolutional neural network (CNN), which reduced the temperature measurement time of the Brillouin optical frequency domain analyzer (BOFDA) by more than nine times [12]. Additionally, they applied a Bayesian algorithm in ML to resolve the cross-sensitivity problem between temperature and strain in DFOS monitoring [13]. Liu et al. developed a corrosion quantification method based on an ML model for the automatic analysis of strain data measured by DFOS, enabling the simultaneous monitoring of cracks and corrosion [14]. In summary, with the aid of ML, DFOS has achieved smarter data processing, higher resolution, and more accurate predictive modeling. These advancements have expanded the application of DFOS in structural health monitoring, environmental sensing, and industrial monitoring. As ML technology continues to evolve, the integration of artificial intelligence (AI) and DFOS is expected to drive further breakthroughs in sensing technology [15].

With the rapid development of DFOS, DFOS has become a key focus of structural stability monitoring and research in various fields such as geotechnical engineering, geological engineering, civil engineering, and hydraulic engineering. Moreover, it has also garnered widespread attention from scholars for its applications in monitoring the overburden deformation in mining operations. For example, Piao et al. [16] carried out SSE studies on the movement and development of overlying rock layers in goaf based on DFOS monitoring. Cheng et al. [17] developed a spatiotemporal continuous sensing system and conducted the SSE for the failure deformation of overlying rock layers based on DFOS. Yuan et al. [18] proposed a conceptual model for characterizing fiber Bragg gratings and conducted an SSE using DFOS to characterize the overburden mining-induced deformation. Chai et al. [19] presented a partitioning method for overlying rock cavities caused by mining based on DFOS and systematically studied the characteristics of rock cavities through SSE. Zhang et al. [20] conducted an SSE in order to explore the activation rule of the fault where the coal face is located above and below. Du et al. [21] applied DFOS to carry out an SSE for the overlying rock layer failure law and its interior stress development characteristics, and so on.

The author classified and compared the literature on experimental research on overburden mining deformation monitoring with DFOS from 2014 to the present. The comparison was carried out from several aspects including the applied technologies [Brillouin optical time domain reflection (BOTDR), Brillouin optical time domain analysis (BOTDA), Pulse Pre Pump BOTDA (PPP-BOTDA), BOFDA, and optical frequency domain reflection (OFDR)], spatial resolution, application scenarios, technical advantages, limitations, and experimental research content, as shown in

Table 1. Statistical comparison of the main DFOS applied in overburden deformation monitoring.

Methods	Spatial Resolution	Application Scenarios	Research Contents	Number of Papers	Advantage	Limitation
BOTDR	1 m	Field test	Height of WCFZ	12	Single-end testing, no need for loops, good robustness, easy locate breakpoints, long distance (80 km), wide range, excellent adaptability.	Low spatial resolution and strain testing accuracy; difficult to achieve precise measurement.
			Laws of overburden deformation movement	9
			Strata separation	1
			Stress evolution	1
BOTDA	0.5 m	Indoor test	State of overlying strata	2	Measurement accuracy and spatial resolution are significantly higher than BOTDR.	Need testing circuit, with poor environmental adaptability; unable to measure breakpoints.
		Field test	Strata separation	1
BOFDA	0.2 m	Field test	Settlement displacement	1	Higher spatial resolution and strain testing accuracy than BOTDA.	Double-ended testing, unable to measure breakpoints; the on-site layout is quite complex.
		Indoor test	Height of WCFZ	2
			Evolution of voids	1
			Settlement displacement	1
PPP- BOTDA	0.05/0.1 m	Indoor test	Overburden deformation	16	Higher spatial resolution and strain testing accuracy than BOTDA.	Dual-end testing, poor environmental adaptability; the on-site wiring is relatively complex; the failure rate of on-site application instruments is relatively high.
			Height of WCFZ	3
			Coal mine pressure	3
			Evolution of voids and separation	3
			fault activation	2
			Rock- fiber coupling	1
OFDR	0.001 m	Indoor test	Overburden deformation	1	High spatial resolution and strain testing accuracy, high signal-to-noise ratio, low probe light power.	Poor environmental adaptability; complex on-site layout; height failure rate on-site application; smaller range as high-precision measurement.
			Key strata stability	1
			Hinge structure and rotating angle	1
			Void evolution	1

.

As illustrated in Table 1, BOTDR, despite its relatively low spatial resolution of 1 m, is predominantly utilized for on-site testing in coal mines. This preference stems from its notable advantages including single-ended testing, extensive measurement range, and ease of fiber deployment. Both BOFDA and BOTDA offer higher spatial resolutions of 0.2 m and 0.5 m, respectively. They employ dual-end monitoring methods and are suitable for both on-site monitoring and indoor SSE. BOFDA is particularly recognized for its high accuracy in strain measurement. PPP-BOTDA, with a spatial resolution of 0.05 m and a dual-end monitoring mode, is primarily applied in indoor SSE, accounting for 70% of all research content in this field. Therefore, it has emerged as a crucial tool in SSE research.

OFDR currently stands out as the technology with the highest spatial resolution, achieving a resolution of 0.001 m. It is mainly employed for precision measurements in indoor SSE. It is worth noting that OFDR, based on Rayleigh scattering technology, has demonstrated a broad application potential in various sensing fields, such as temperature, strain, vibration, pressure, shape, magnetic field, refractive index, radiation, gas, and flow velocity sensing, due to its high spatial resolution, high sensitivity, and distributed measurement capabilities [22,23,24].

Given that this experimental study focused on the engineering application of DFOS, the primary objective was to measure the deformation of the overlying rock strata. The key concern was the accuracy of fiber optic strain measurement. Considering the limitations of time and experimental conditions, BOFDA, which combines high spatial resolution and high strain measurement accuracy, was selected for this experimental research.

As shown in Table 1, more previously unimaginable scientific discoveries have been achieved with the introduction of DFOS, which greatly improved people’s comprehension and mastery of the “black box” within the overburden. However, research on the DFOS monitoring of overburden mining deformation has primarily focused on the development height of water-conducting fracture zones (WCFZs), the coal mining pressure, the overall deformation status of the overburden, and the evolution laws of rock separation or voids, etc. In contrast, studies on the movement forms and states of fractured rock blocks, and even individual single key strata (KS), are relatively limited.

However, the deformation and movement of the overburden are essentially an integrated manifestation of the motion of the overlying hard KS. As coal mining progresses, these rock layers fracture and form discrete “rock blocks”. Fundamentally, this is a mechanical phenomenon characterized by the movement and interaction of these fractured rock blocks [2]. Furthermore, the movement of these fractured rock blocks is a key cause of underground coal mine accidents. Therefore, it is imperative to conduct thorough and meticulous research on the movement forms and states of both the overlying KS and the fractured rock blocks. Regrettably, in the realm of DFOS research, studies that focus on the movement characteristics of rock blocks are currently few and far between..

This study attempts to characterize the motion patterns and states of overlying hard KS and fractured rock blocks via fiber optic strain distribution by applying the advanced DFOS BOFDA in an SSE and exploring the movement laws of overlying rock blocks in time and space. It is expected to further deepen and enrich the human understanding of the “black box” of overburden mining deformation, which will be more conducive and helpful in improving coal mine safety production.

2. Distributed Fiber Optic Sensing Technology Based on BOFDA

DFOS is a new monitoring technology that accompanied the arrival of the 21st century, which uses optical fibers that originally transmit optical signals to continuously measure the physical measureands over their entire length range [25]. More and more fiber optic sensors are being manufactured by utilizing different optical effects such as Rayleigh, Raman, and Brillouin back scattering or FBG spectra [26]. According to years of in-depth research and data statistics by Bado [27], BOTDR, BOTDA, and BOFDA are the most widely used DFOS technologies based on Brillouin back-scattering light. Among them, BOFDA relies on its high strain measurement accuracy and spatial measurement resolution, which are particularly valuable for precise measurements [28]. In recent years, BOFDA has made significant progress in achieving centimeter level spatial resolution [29], up to 100 km measuring distances [30], and significantly reduced measuring times [31], etc. These improvements have made BOFDA highly respected in the field of DFOS monitoring research, providing a promising exploration and application pathway in various monitoring scenarios.

2.1. The Sensing Principle of BOFDA

BOFDA stems from measuring a complicated baseband transmitting function that is associated with the amplitude of pump light and Stokes light traveling subtendedly along the optical fiber’s whole length [32], as shown in Figure 1.

As soon as the baseband transfer function is determined, it can be subjected to inverse Fourier transform (IFFT) to obtain the impulse response [32,33,34]. By analyzing the transmission pump intensity of probe light and pump light under different frequency differences, the distribution of the fiber optic temperature and strain can be derived [35].

The detailed strain or temperature measurement by BOFDA can be briefly explained through BOFDA’s system configuration diagram, as shown in Figure 2.

As shown in the figure, the cw light of a narrow-linewidth pump laser is coupled into one end of a single-mode fiber. At the other end of the cw light of a narrow-linewidth probe laser is coupled in, whose frequency is downshifted compared with that of the pump laser by an amount that equals the characteristic Brillouin frequency of the fiber. At 1.3 $\mathsf{\mu }\mathrm{m},$ this characteristic frequency has a value of some 13 GHz for standard telecommunication single-mode fibers [36,37]. The light of the probe laser is modulated in amplitude with a variable angular modulation frequency $f_{\mathrm{m}}$. The measurement principle is that for each value of $f_{\mathrm{m}}$, the alternating parts of the modulated probe wave intensity and the modulated pump wave intensity are recorded at the end of the sensor fiber. Here, the probe-induced Brillouin loss of the pump wave is used. The output signals of the photo detectors (PD) are fed to a network analyzer (NWA), which determines the baseband transfer function $H\left(j\omega \right)$ of the test fiber. The output of the NWA is digitized by an analog-to-digital converter (A/D) and fed to a signal processor, which calculates the IFFT. This IFFT is a good approximation of the pulse response $h\left(t,\Delta f_{\mathrm{m}}\right)$ of the test fiber and resembles the temperature and strain distribution along the fiber [38]. Finally, stemming from the relationship between the propagation time and spatial span of light in optical fibers, the specific spatial and frequency shift relationship $h\left(z,\Delta f_{\mathrm{m}}\right)$ in optical fibers can be obtained. The following mathematical formulas provide a comprehensive explanation for all of these processes [28,38,39].

$$H\left(j\mathsf{\omega },\Delta f_{\mathrm{m}}\right)\to h\left(t,\Delta f_{\mathrm{m}}\right)\stackrel{z={\displaystyle \frac{t\times c}{2n}}}{\to }h\left(z,\Delta f_{\mathrm{m}}\right),$$

(1)

In the formula, $H\left(j\mathsf{\omega },\Delta f_{\mathrm{m}}\right)$ represents the baseband transfer function; $h\left(t,\Delta f_{\mathrm{m}}\right)$ represents the temporal pulse response of fiber optic sensors; $h\left(z,\Delta f_{\mathrm{m}}\right)$ represents the spatial pulse response of fiber optic sensors; c represents the light velocity; n denotes the fiber optic refractive index; t is the time it takes for light to be launched and received.

In summary, the key to the entire BOFDA sensing system is the acquisition of the baseband transfer function $H\left(j\omega \right)$. BOFDA can reconstruct the Brillouin gain spectrum (BGS) by performing IFFT with the baseband transfer function of the sensing fiber. Then, based on the spectrum, the Brillouin frequency shift (BFS) can be determined by performing Lorentz curve fitting (LCF) [11,36,38]. In the end, the strain or temperature changes at each position along the fiber optic cable at each measurement moment are obtained, as demonstrated in Figure 3.

The variations in fiber optic temperature T and fiber optic strain $\epsilon$ can be solved by the following formula based on the variation of Brillouin frequency shift $f_B$.

$$[\begin{array}{c}{f}_B\left(\epsilon \right)=f_B\left(0\right)+C_{\epsilon }·\epsilon \\ f_B\left(T\right)=f_B\left(0\right)+C_T·T\end{array},$$

(2)

Here, $C_{\epsilon }$ and $C_T$ are the strain coefficient and temperature coefficient, $C_{\mathrm{T}}=1 \mathrm{MHz}/℃$ and $C_{\mathsf{\epsilon }}=500 \mathrm{MHz}/{\mathsf{\epsilon }}_{ , }\mathrm{respectively} .$ In particular, if the ambient temperature does not change by more than 5$°$, only the effect of fiber optic strain should be considered, and that of temperature can be neglected [20].

Based on the aforementioned analysis, when an optical fiber is subjected to axial tension or compression and experiences strain, the Brillouin frequency monitored by BOFDA will correspondingly increase or decrease. Therefore, when a sensing optical fiber is embedded in the overlying rock strata of a coal-mining face, BOFDA can be utilized to monitor the deformation of the overlying rock during coal extraction. Specifically, the following scenarios can be observed:

(1)

When the rock strata are subjected to shear stress or tensile stress, the buried optical fiber will be stretched, resulting in an increase in the Brillouin frequency value.

(2)

The separation of fractured rock blocks, such as when these blocks detach from the original rock layer and collapse or rotate around it, will also exert tensile effects on the buried optical fibers. Consequently, the Brillouin frequency value will increase.

(3)

Conversely, if the loosely stacked fractured rock blocks are subjected to compaction, the gaps between the rock blocks will gradually decrease. The optical fibers embedded in the original rock layer will be correspondingly compressed axially. The tension previously induced in the fibers by the collapse and rotation of the rock blocks will gradually diminish, inevitably leading to a gradual decrease in the Brillouin frequency value.

2.2. Key Parameters of BOFDA

2.2.1. The Maximum Sensing Distance of BOFDA

The maximum sensing distance of BOFDA can be studied through frequency domain methods. For BOFDA, the reference signal of VNA undergoes modulation frequency scanning step-by-step with the equidistant frequency steps $\Delta f_m$. The reference signal is transformed into the time domain using IFFT, generating a discrete impulse response. The frequency step size $\Delta f_m$ determines the baseband transfer function, while the BOFDA fiber optic sensing length is limited by $\Delta f_m$. The maximum sensing distance is expressed as follows:

$$L_{\max }={\displaystyle \frac{c}{2n}}\cdot {\displaystyle \frac{1}{\Delta f_m}}$$

(3)

In the equation, when the step frequency is 2 kHz, the maximum fiber length is 51.4 km.

2.2.2. Spatial Resolution Accuracy

The spatial resolution of BOFDA, which is two-point resolution, is the minimum distinguishable length between any two event points on the BOFDA sensing fiber, given by the following equation [40]:

$$\Delta z={\displaystyle \frac{c}{2n}}\cdot {\displaystyle \frac{1}{{f_m}^{\max }-{f_m}^{\min }}}$$

(4)

Among them, $f_m^{max}$ and $f_m^{min}$ represent the maximum and minimum modulation frequencies, respectively. Up to now, the highest spatial resolution of BOFDA can arrive at 5 mm [29].

2.3. Measuring Instrument fTB2505 of BOFDA in the Study

The BOFDA demodulator adopted was fTB2505 [34], manufactured by Fibris Terre Systems in Berlin, Germany. The test parameters are illustrated in

Table 2. Test specifications of the BOFDA fTB2505 instrument.

Parameter	Values
Types of optical fiber	Single mode optical fiber
dynamic range	>10 dB
Spatial resolution	0.2 m
Highest sampling resolution	0.05 m
Measuring accuracy	±1 με
Measurement repeatability	≤±2 με
Scope of testing	−15,000 με~15,000 με
Test range	25 km
Data output format	Binary, ASCII
Frequency scanning range	9.9~12.0 GHz
Dynamic testing range/dB	10
Interface	Ethernet
Optical output interface	E-2000/APC
Environmental requirements	Working temperature: 0~−40 °C; Relative humidity: 5–90%; No condensation

.

As can be clearly seen from Table 2, BOFDA features high spatial resolution, high strain resolution, and a large dynamic range, which make it well-suited for advanced indoor experiments that require precise measurements. Therefore, from the perspective of monitoring principles, the measurement specification parameters, and technological advantages, the application of BOFDA in simulating overburden mining-induced deformation experiments could be feasible and effective.

2.4. Theoretical Analysis of BOFDA Characterization

The area of goaf gradually expands during coal mining. When the mechanical balance of the rock formation above the goaf is disrupted, the roof rock formation will fracture. If rock blocks to be fractured are limited in space by the previously broken rock blocks and can only rotate and sink at a small angle, they will develop a stable hinged structure of a voussoir beam located in the fracture zone. Otherwise, they will fall into the goaf at a large angle in a sliding-rotating manner, and adjacent unbroken rock blocks will be a cantilever beam structure within the caving zone of the overlying rock formations. It is obvious that the fractured overburden blocks will exist in two states: the fracture zone and the caving zone, and will present two movement forms: voussoir beams and cantilever beams, which are all depicted in Figure 4.

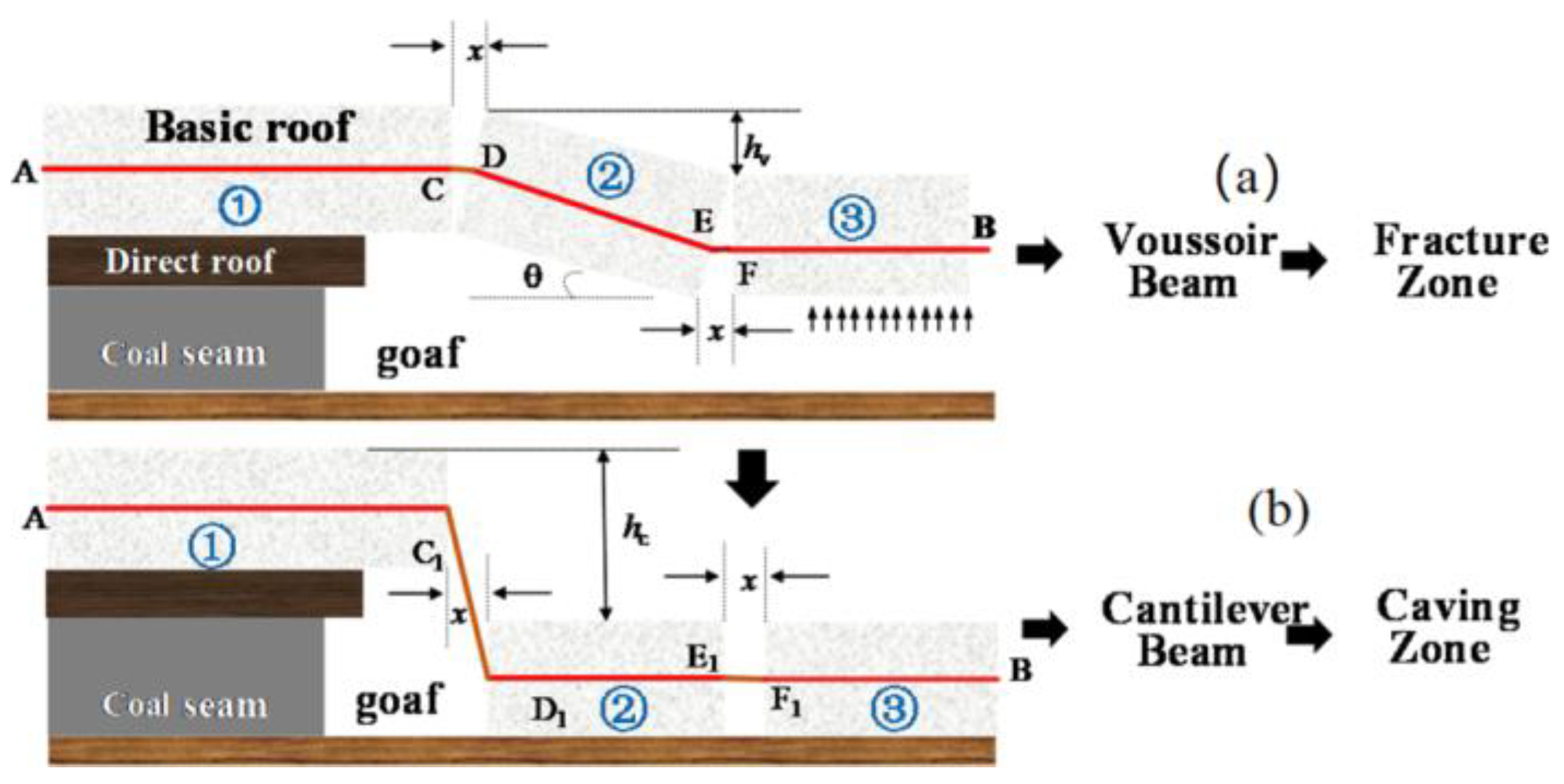
2.4.1. Horizontal Optical Fibers to Characterize Rock Blocks Movement

The basic roof of the coal-mining face is a rock layer that is not only hard, but also thick, which is the sub key stratum (sub1 KS) at the lowest place within the overburden. Assuming a horizontal optical fiber is planted amidst the thickness of the basic roof along the rock formation strike direction, if the basic roof is fractured and deformed due to coal mining, as shown in Figure 5, it will lead to strain variations in the buried horizontal optical fiber.

Based on Figure 5, the following assumptions for the fiber optic strain characterization of rock block movement in the overburden were proposed:

• Assuming the thicknesses of the basic roof is H, the initial crack width with the overburden is ignored.
• The initial stretch of the optical fiber in the basic roof deflection zone CE is $l_{CE}$, which is not less than the spatial resolution of BOFDA (i.e., CE = $l_{CE} \ge 0.2\mathrm{m})$.
• The fiber optic strain of the deformed fiber CE section is $\epsilon$.
• The rotation angle between blocks ①~② and ②~③ is $\theta$; its maximum value is ${\theta }_{max}$.
• The width of the fissure between the fractured blocks is x, and its maximum value is $x_{max}$.
• In the voussoir beam, the settlement displacement of blocks ② and ③ is $h_v$.
• In the cantilever beam, the settlement displacement of blocks ② and ③ is ${\mathrm{h}}_{\mathrm{c}}$.

(1)

Fiber optic strain (FOS) characterizing voussoir beam movement.

As shown in Figure 5a, the width x of the cracks will rise with the enlargement of the rotation angle bit by bit, and the tensile length of the horizontally laid optical fibers within the crack range will also gradually increase, resulting in an increment in FOS of section CE, as demonstrated in Equation (5) below.

$${\mathit{\epsilon }}_F={\displaystyle \frac{x}{l_{CE}}}\approx {\displaystyle \frac{\theta ·H}{l_{CE}}},\therefore {\epsilon }_F\propto \theta \left({\epsilon }_F\propto x\right)$$

(5)

(2)

Characterization of the cantilever beam structure movement

If the revolve angle $\mathit{\theta }$ of key block ② exceeds its limit angle ${\theta }_{max}$, the crack width reaches its maximum value ${\mathrm{x}}_{\max }$, and sliding rotation (S-R) instability will arise within the arch support beam structure, as depicted referring to Figure 5b. At this point, the key block ① is in the movement state of the overhanging beam structure, and key block ② and the rear rock blocks will collapse into the goaf. It can be seen that the tensile increment of section CE is $C_1{\mathrm{E}}_1$, and FOS ${\epsilon }_C$ in the CE section is positively correlated with the horizontal displacement x and caving height $h_{\mathrm{c}}$.

$${\epsilon }_C\approx {\displaystyle \frac{x+\sqrt{x^2+{h_c}^2}}{l_{CE}}}$$

(6)

By comparing ${\epsilon }_C$ and ${\epsilon }_F$, it is evident that ${\epsilon }_C\ge {\epsilon }_F$ in the same rock layer, and the horizontal optical fiber in the cantilever beam motion state (in the caving zone) will exhibit a larger numerical tensile FOS distribution. Therefore, movement forms and states of the overburden can be depicted by horizontal FOS variations: the section with larger FOS values in the same horizontal rock stratum is mostly the movement state of the cantilever beam (mostly belonging to the caving zone), and the smaller section is mostly the movement state of the masonry beam within the fracture zone of overburden.

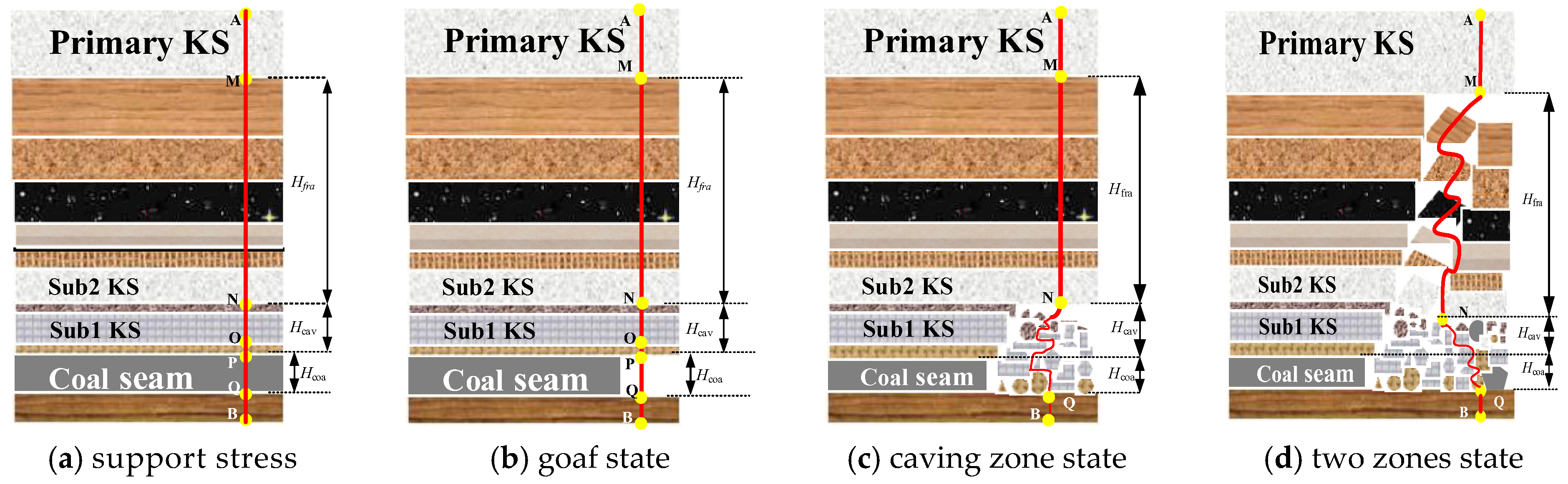
2.4.2. Vertical Optical Fibers to Characterize Rock Block Movement

Assuming there are three KS strata in the overburden, Sub1-KS is the basic roof of the coal face. Fiber optic cables are laid vertically upward from the lower bottom of the coal to be mined into the overburden. The optical fibers in the overburden will be in different states with the processes of coal mining as follows:

(a)

The lower segments of the fiber are situated within bracing stress regions ahead.

(b)

The lower portions of the fiber are in the goaf scope.

(c)

The lower part of the fiber optic cable is in a state affected by rock masses caving, while the upper part is in a state of original rock stress.

(d)

The lower segment of the optical fiber is seated within caving zones affected by the fragmentation and expansion of gangue, while the upper portion is in the range of the fracture zone with the voussoir beam’s movement state, as illustrated in Figure 6.

As shown in the figure, the overburden deformation movement has gone through the instability process of cantilever beams and voussoir beams, and has developed from the initial original rock stress state to the occurrence state of caving zones and fracture zones. Fiber optic strain will undergo the following changes and developments:

(1)

Fiber optic strain (FOS) characterization of the cantilever beam movement forms

When the coal seam is in its initial state without any interference, the optical fiber is merely at the mercy of the gravitational stress of overlying surrounding rock formations, resulting in an initial compressive FOS increasing linearly with the burial depth.

When the excavation approaches the position of the fiber optical cables deployed, the overlying strata ahead of the coal face is in the advanced support stress zone, and the optical fiber is susceptible to the pressure of the forward sustain stress of the coal face. Therefore, the bottom segment of the optical fiber seated ahead of the coal face is in a state of increasing compressive FOS, as shown in Figure 6a. When excavation passes through vertical optical fibers, the basic roof is in a cantilever beam structure state and a goaf will form around the fiber optic cable. The early vertical compressive stress exerted by the overburden is released, causing a sharp decrease in the compressive stress of the optical fiber section and restoring it to its initial pre-stretched state, also known as the incipient strain state, as shown in Figure 6b. This period is usually accompanied by the fracture and caving of weak-thin direct roof rock layers, which may result in an increase in tensile stress, causing the FOS to rapidly shift from compressive to tensile strain.

As illustrated in Figure 6c, with the expansion of the goaf, the suspended area of the cantilever beam structure within the basic roof gradually increases. When Sub1-KS of basic roof experiences rupture and collapse, the fractured rock blocks collapse onto the floor of the goaf. It is obviously the fracture and caving of the rock blocks will cause a sharp tensile effect on the optical fibers, resulting in a suddenly tensile FOS increment in the caving zone. In later stage, the tensile FOS of this section of optical fiber was reduced due to the fragmentation and swelling of the broken gangue in the falling zone.

It is evident that during the breaking and collapsing movements of the cantilever beam structure, the vertical FOS in the stope (caving zone) transitions from compressive strain to initial strain.

(2)

Fiber optic strain (FOS) characterizes the voussoir beam movement

As shown in Figure 6d, the fractured rock blocks of the Sub2-KS layer at a high position cannot collapse due to the vertical support and the horizontal clamping of the fragmented rock blocks below or the early Sub1-KS fractured rock blocks behind them. Therefore, the Sub2-KS layer forms a masonry beam, and the crack zone will develop from the Sub2-KS layer to the primary KS.

The rotational deformation of the rock blocks causes a pulling effect, resulting in the distribution of the tensile FOS curve within the fracture zone. Compared with the overburden thickness, the vertical optical fiber in the voussoir beam is mainly affected by the gravity of the overburden. The larger thickness of the voussoir beam results in a greater gravity effect on the vertical optical fiber. Therefore, the upright optical fiber in the fracture zone will produce a larger numerical tensile FOS curve distribution. At this point, the vertical optical fiber presents two different parts of the tensile FOS curve distributions, with the lower part showing the tensile FOS curves with smaller values in the caving zone and the upper part showing the tensile FOS curves with larger values in the fracture zone, depicted as Equation (7).

$${\epsilon }_{\mathrm{F}}\ge {\epsilon }_{\mathrm{C}}$$

(7)

In summary, the movement law of overburden mining deformation can be characterized by the distribution shape and numerical characteristics of horizontal and vertical FOS variations.

3. Similar Simulation Experiment Based on BOFDA DFOS

The BOFDA DFOS technology measuring the overburden deformation movement is mainly achieved by using the FOS distribution to characterize the movement characteristics of the overburden mining deformation. The BOFDA DFOS experimental processes in this study were as follows:

(1)

Research on fiber optic selection. This process mainly included calibrating the strain coefficient, temperature coefficient, and strain transmission efficiency coefficient.

(2)

Construction of SSE models and layout of the optical fibers.

(3)

Calibration of the fiber optic position. This involved locating the fiber optic position along its length in the spatial position of the experimental model through fiber optic experiments.

(4)

Fiber optic strain testing by BOFDA.

(5)

Other experimental tasks. This mainly included monitoring data acquisition, processing and analysis of the data, and finally, the interpretation of experimental phenomena.

Therefore, the first step is to select the optical fiber and calibrate its corresponding sensing coefficient when applying BOFDA DFOS for the SSE.

3.1. Experimental Study on Fiber Optic Selection

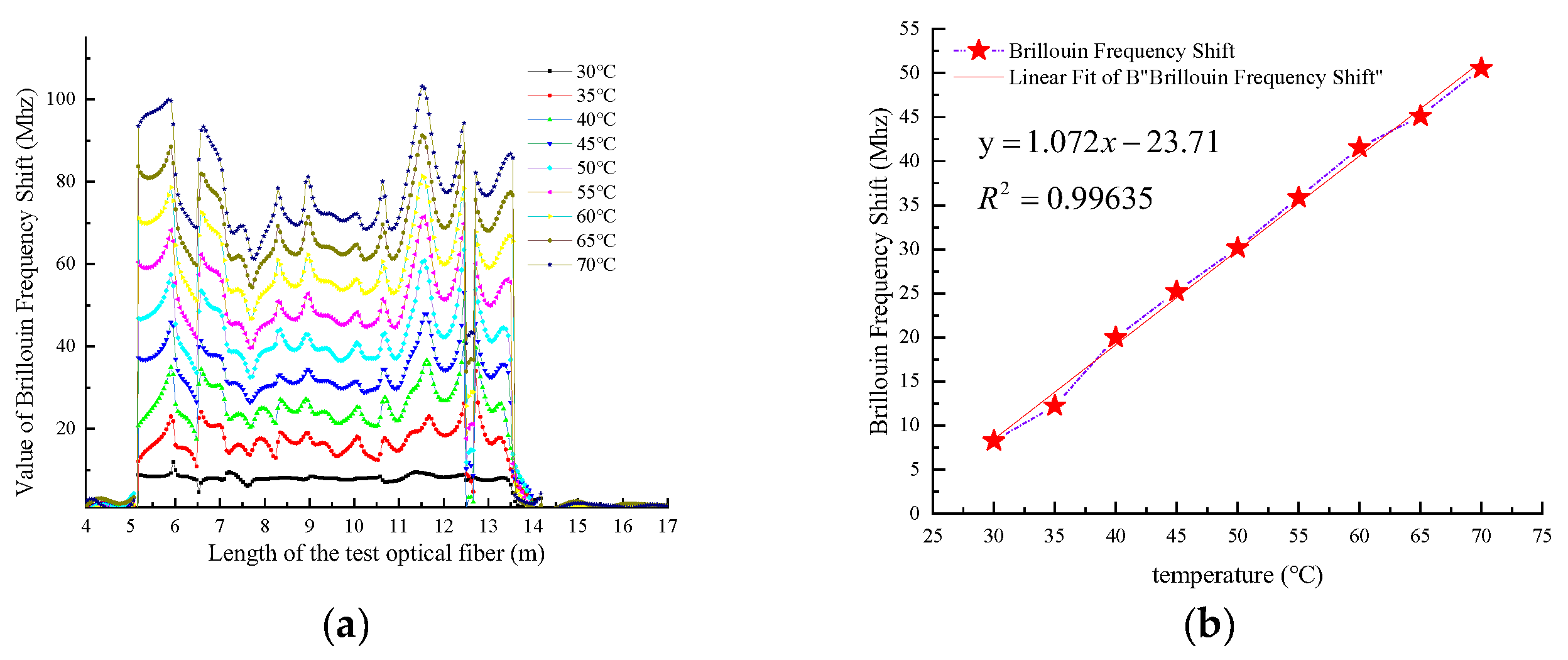
3.1.1. Calibration of Fiber Optic Strain Sensing Coefficient

In this study, a novel 2 mm tight fitting strain fiber designed specifically for strain measurement was selected, as depicted in Figure 7a. This 2 mm fiber has excellent flexibility and can solve the problem of the sheath effect, which is caused by relative sliding between traditional optical fibers and their protective sleeves. The fiber optic strain coefficient calibration device consists of a stretching tube, a manual hydraulic pump, a dial gauge, a fixed fixture, and BOFDA fTB2505. In the test, the dial gauge is used to measure the tensile increment of the optical fiber to calculate its fiber optic strain. Then, the 2 mm fiber’s Brillouin frequency shift after each stretching was measured by BOFDA, and the fiber optic strain changes caused linear changes in the fiber optic frequency, as shown in Figure 7b. Finally, through linear fitting, the strain coefficient was obtained as 0.04954 MHz/$\mathsf{\mu }\mathsf{\epsilon }$, with a standard deviation of 0.99824, as shown in Figure 7c.

3.1.2. Calibration of Fiber Optic Temperature Sensing Coefficient

In this study, relaxed 20 m long 2 mm fibers were placed in a computer-controlled water bath to test the fiber optic BFS values at different water temperatures. The test results in Figure 8a show the fiber optic BFS distribution curves measured at different temperature levels. Obviously, the fiber optic BFS showed a linear trend with temperature variation. Through fitting BFS against the temperature variation, a robust linear correlation was successfully identified, as illustrated in Figure 8b. The temperature coefficient of the 2 mm fiber was obtained as 1.07 MHz/$℃$, with a standard deviation of 0.99635.

3.1.3. Calibration of Fiber Optic Strain Transfer Efficiency

In order to ensure the effectiveness of FOS measurement in the SSE, it is necessary to ensure that the strain changes among the fiber optic and the monitored material matrix are consistent, that is, to ensure a high strain transmission efficiency. In the experiment, a 5 mm steel stranded fiber optic cable (SS cable) was used as the material matrix, and a special bonding agent was used to stick a 2 mm fiber optic cable to the outer surface of the SS cable. The experimental setup and process were the same as those used for the fiber optic strain coefficient calibration. During the tensile process of SS cables via the BFS and FOS, the alterations of two optical fibers were measured and compared, so the strain transfer efficiency of the 2 mm optical fibers could be determined. That is to say, if the strain changes of the SS cable and 2 mm optical fiber under various tensile states are highly consistent, it means that the 2 mm optical fiber has a high strain transmission efficiency, and the FOS obtained through the 2 mm optical fiber is reliable and effective. The strain transmission efficiency curve obtained from the experiment is shown in Figure 9.

Through the analysis of Figure 9a, the strain transfer efficiency of the 2 mm fiber ranged from 0.9937 to 0.9968. The strain differences of the two fibers were essentially identical, as depicted in Figure 9b.

This experimental study referred to the existing experimental research [17] and was based on the study conducted by Cheng et al. Although the principles of the two studies were essentially the same, there were significant differences in the experimental methods. Cheng et al. embedded optical fibers into sandy soil and conducted fiber pull-out tests to investigate the development of stress and strain as the relative displacement between the soil and the sensing fiber gradually increased. They studied the entire process from full coupling to partial coupling and eventually to the fiber slipping and completely detaching, in order to determine the deformation coordination and strain transfer characteristics between the sensing fiber and the surrounding soil. In contrast, the current experimental study involved fully adhering a 2 mm optical fiber to the outer surface of an SS cable. During the pull-out process of the SS cable, the strain changes of the SS cable were obtained by measuring its elongation with a micrometer. Meanwhile, the strain changes of the 2 mm optical fiber were measured using BOTDA (Brillouin optical time domain analysis). By comparing the two sets of strain data, we aimed to determine the ability of the 2 mm optical fiber to characterize the deformation of external structures and its strain transfer efficiency.

As shown in Figure 9a, before the SS cable was stretched by 2 mm, the strain transfer efficiency gradually deteriorated, falling below 0.0975. This indicates that in the initial stage of fiber stretching, due to the effect of pre-tension stress, the fiber cannot effectively reflect the strain changes of the external structure. When the SS cable was stretched by more than 2 mm, the strain changes of the two became increasingly consistent. This suggests that after a 3 mm stretch, the influence of pre-tension strain transfer was essentially eliminated, and the strain transfer coefficient stabilized above 0.99. Additionally, as seen in Figure 9a,b, when the SS cable was stretched to 16 mm, the strain transfer coefficient no longer increased. This may have been due to the effect of sheath slippage, measurement errors from the micrometer, or measurement error from the BOTDA. The experiment showed that before the structural body underwent a strain change of 6000 με, the 2 mm optical fiber had a high strain transfer efficiency and could effectively reflect the strain changes of the external measured structure. Therefore, the strain transfer efficiency of the 2 mm fiber satisfied the testing demands.

3.1.4. The Influence of Temperature on Strain Testing in BOFDA Measurement

The temperature coefficient of the optical fiber studied in this experiment was eliminated by placing the relaxed and strain free optical fiber in a computer-controlled water bath to eliminate the influence of strain. The strain coefficient was obtained by conducting fiber optic tensile experiments under conditions of essentially constant temperature. Although the temperature strain cross sensitivity problem was basically eliminated in this fiber optic strain coefficient calibration experiment, it is difficult to eliminate the temperature strain cross sensitivity problem in actual fiber optic testing.

(1)

When the temperature changes little and remains basically constant.

According to the calibrated fiber temperature coefficient of 1.07 MHz/and strain coefficient of 0.04954 MHz/$℃$ in this article, it can be seen that the influence of temperature on Brillouin frequency was much smaller than that of the strain. Experimental studies have shown that if the temperature change does not exceed 5 °C, the influence of temperature can be ignored, as was our SSE with a controlled constant temperature.

(2)

When temperature changes exceed 5 °C, temperature compensation is necessary for fiber optic strain testing to eliminate errors in strain monitoring caused by temperature fluctuations. Several methods can achieve this:

• Parallel loose tube fiber: Place a loose tube fiber of the same length parallel to the strain fiber. Since the loose tube fiber is minimally affected by strain, it can compensate for temperature effects on the strain data.
• Relaxed fiber section: Reserve a relaxed fiber section of the same type between the strain-testing fiber and the DFOS analyzer under identical temperature conditions. This section, unaffected by strain, allows one to subtract the strain-testing fiber’s Brillouin frequency shift from the relaxed fiber’s average shift for temperature compensation.
• FBG temperature sensors: Connect fiber Bragg grating (FBG) temperature sensors in series with strain-sensing fibers at regular intervals for temperature compensation.
• Machine learning: Apply machine learning and other AI techniques to analyze the monitoring data and eliminate temperature-related influences.

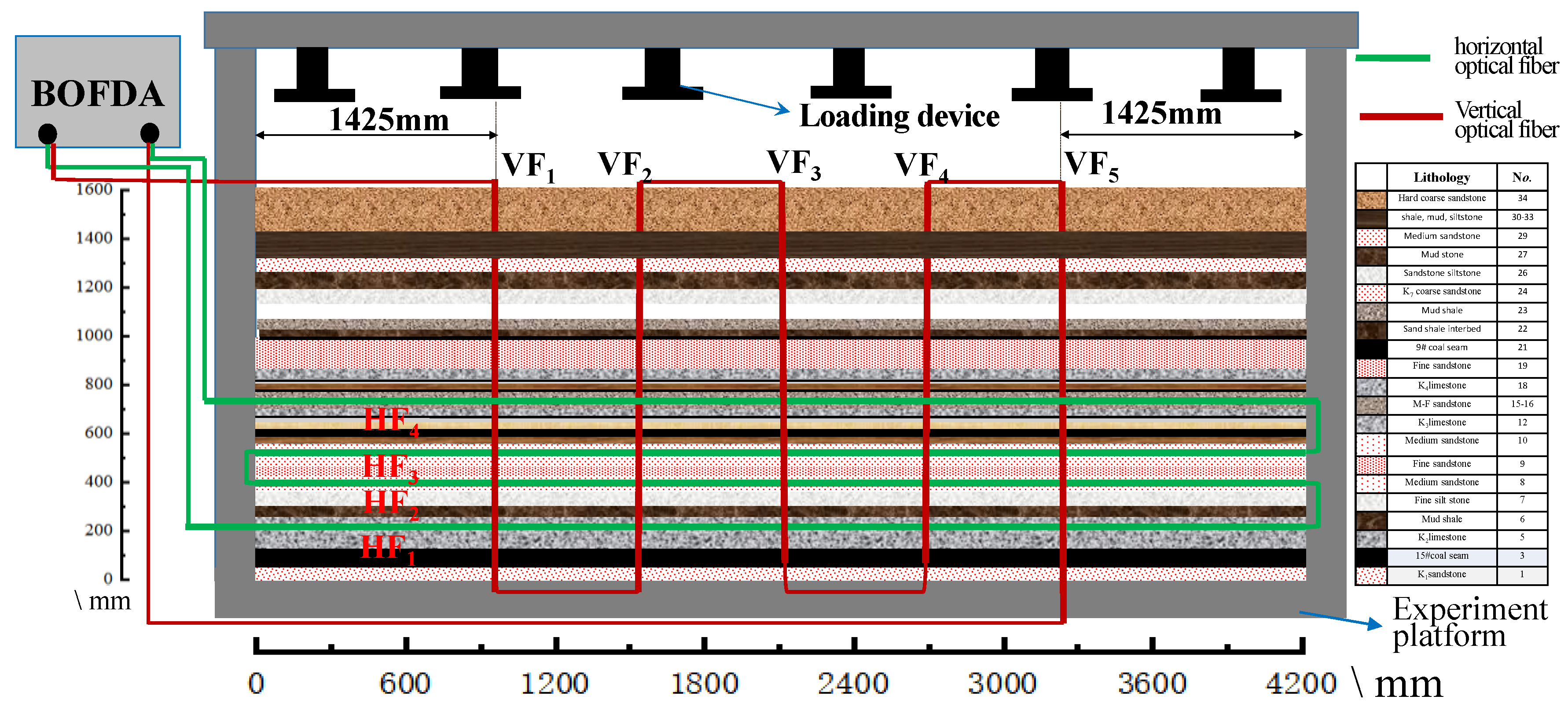
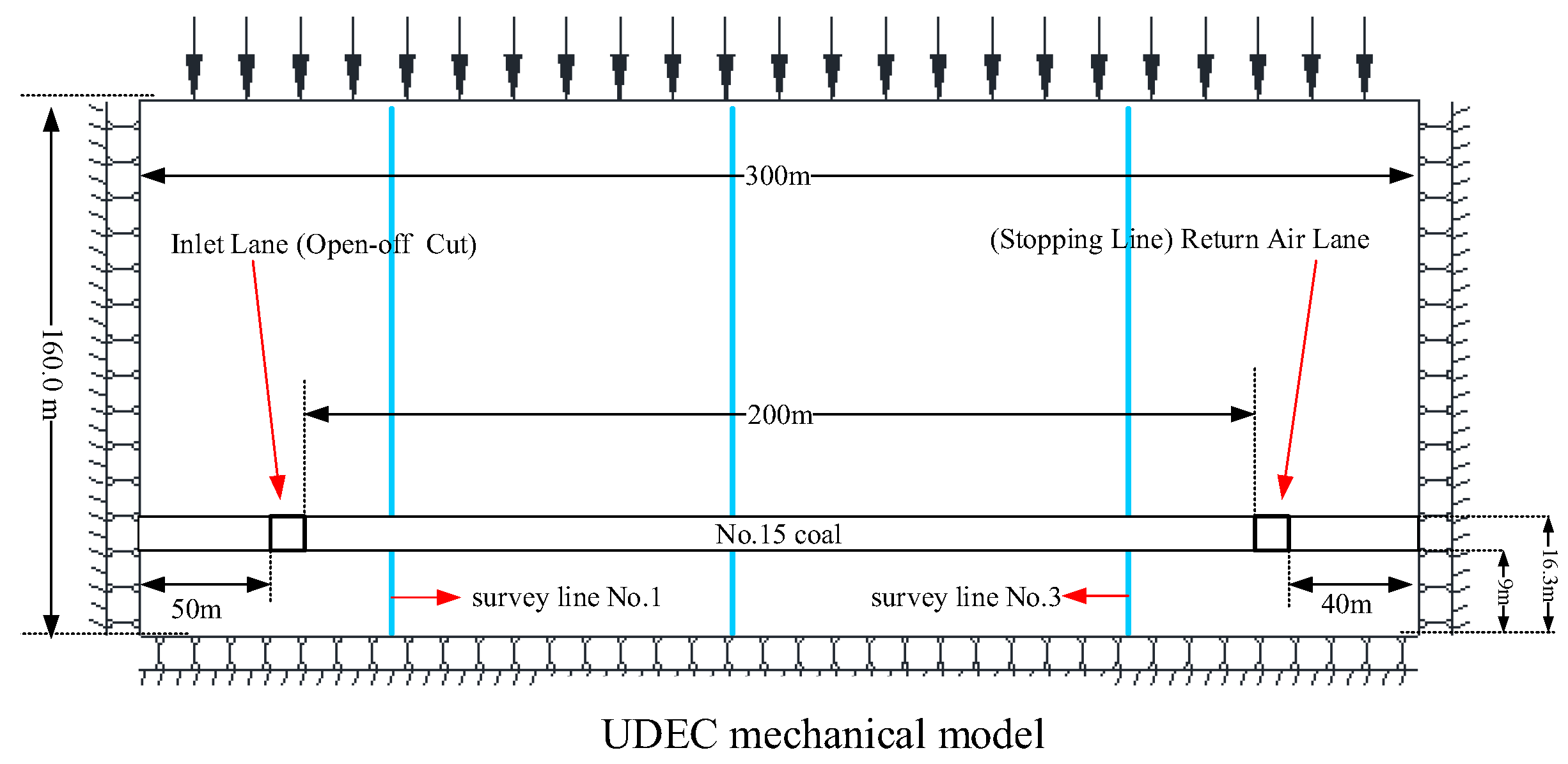
3.2. Construction of Similar Simulation Experiment Model for BOFDA Characterization

This study took the engineering geology, drilling column chart, stratigraphic tectonic, and production design of the actual coal-mining face as the engineering background, and an analogous simulation experiment was conducted based on the production situation of the actual working face. The actual overburden strata structure and its rock mechanical arguments of the studied coal face are described in

Table 3. Rock mass mechanical parameters of the actual working face.

No.	Lithology	Thickness (m)	Bulk Modulus (GPa)	Shear Modulus (GPa)	Density (kg/cm3)	Friction Angle (o)	Cohesion (MPa)	Tensile Strength (MPa)
24	K7 coarse sandstone	110.60	3.58	5.7	2470	43	6	2.00
23	Medium sandstone	104.57	5.2	6.94	2590	40	5.5	2.67
22	No. 9 coal shale	100.07	2.52	4.89	1540	28	1.8	1.00
21	Fine sandstone	95.00	4.08	6.8	2810	35	4	2.17
20	Shale	93.55	13.46	24.78	2660	29	2.2	2.13
19	K4 limestone	80.57	7.19	8.18	2660	33	3.3	1.70
18	Mud stone	78.02	2.61	4.58	2450	28	1.9	0.67
17	Medium sandstone	77.01	5.04	6.45	2600	41	5	1.26
16	Sand shale	75.12	5.67	5.38	2660	39	4.2	1.67
15	No. 12 coal	72.62	2.3	4.98	1390	30	2.1	1.00
14	Medium sandstone	71.12	11.26	20.7	2750	44	5.3	1.69
13	K3 limestone	66.06	6.45	7.9	2800	33	3.3	1.97
12	No. 13 coal	63.11	2.52	5.47	1380	29	2.0	1.00
11	Medium sandstone	61.60	5	6.67	2580	40	5	2.5
10	Fine sandstone	54.11	5.24	7.96	2870	37	4.4	1.67
9	Medium sandstone	49.11	5.21	6.94	2590	42	5	2.67
8	Fine silt stone	41.12	5.62	7.82	2640	36	4.1	2.00
7	Shale	35.12	13.46	24.78	2660	31	2.2	2.13
6	K2 limestone	28.73	29.43	32.23	2720	37	3.5	2.08
5	Mud stone	16.23	12.79	23.55	2540	27	1.3	1.00
4	No. 15 coal	14.81	3.33	7.66	1360	25	1.8	2.41
3	Sand silt stone	7.42	8.76	9.57	2530	29	2.0	1.00
2	Medium sandstone	7.00	5	6.67	2580	38	4.3	2.5
1	K1 coarse sandstone	6.00	18.09	27.45	2640	44	5	2.00

.

When constructing the model, materials such as fine river sand, lime powder, gypsum powder, mica powder, and water were mixed and stirred according to the designed and calculated similar proportions. Black ink was added to simulate coal seams. The dimensions of the completed model were 4200 mm in length, 250 mm in thickness, and 1600 mm in height, as shown in Figure 10. These were used to simulate the overlying strata movement with the mining of No. 15 coal seam in the actual working face.

3.2.1. Fiber Optic Layout for the Similar Simulation Experiment

As shown in Figure 10, four horizontal pre-stretched optical fibers were laid in each KS layer within the overburden. Among them, HF1 was located in the basic roof K2 limestone layer of Sub1-KS, HF2 was located in the middle sandstone layer of the overlying 8th layer of Sub2-KS, HF3 was located in the middle sandstone layer of the overlying 10th layer of Sub3-KS, HF4 was located in the overlying 16th layer of Sub4-KS sandstone layer, and the 24th layer of the K7 coarse sandstone layer was the primary key stratum.

For the layout of vertical optical fibers, firstly, to eliminate boundary effects, a rock boundary with a width of 1425 mm was retained on both sides of the model. Then, five vertically pre-stretched optical fibers were laid out at equal intervals. VF1 was installed at the open-off cut, VF5 was deployed at the stopping line, the vertical distance between VF2 and VF1 was about 337 mm, the vertical distance between VF3 and VF1 was about 675 mm, and the vertical distance between VF4 and the stopping line was about 337 mm.

3.2.2. Position Calibration of the Optical Fibers

In this SSE, we cut two 2 mm optical fibers, each 26 m long, as horizontal and vertical fiber optic cables. For the purpose of accurately correlating the FOS varying points in the BOFDA measurements with specific deformation points in similar material layers of the overburden, this study used the hot pressing method to calibrate the precise position of the optical fibers. This method utilizes the characteristic frequency shift of the central Brillouin frequency under the influence of temperature. Which involves wrapping a hot towel around a small section of fiber optic cable at the designated location and then measuring the BFS to locate the precise position of the optical fiber.

The positioning results of four sections of horizontal fiber HF1, HF2, HF3, and HF4 were located in the interval length of the 26 m fiber, with length sections of 7217–11,388 mm, 11,406–15,494 mm, 15,806–19,964 mm, and 24,693–20,535 mm, respectively. The positioning results of the five segments of vertical optical fibers VF1, VF2, VF3, VF4, and VF5 were the interval lengths of the 26 m optical fiber: 8550~10,150 mm, 10,900~125,00 mm, 14,800~1320 mm, 15,600~17,200 mm, and 20,000~18,400 mm.

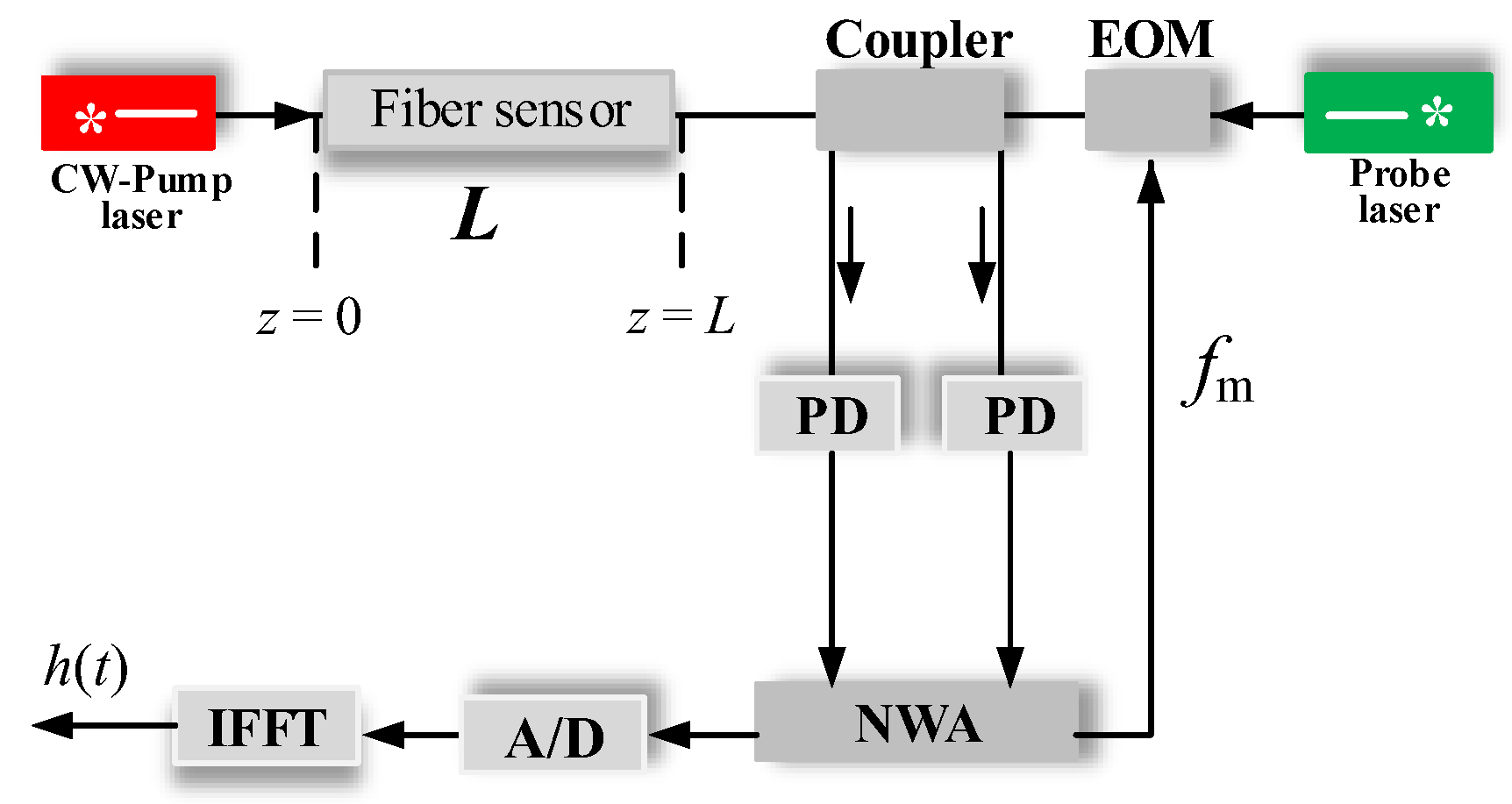
3.2.3. Measuring System for the Similar Simulation Experiment

This study mainly used BOFDA fTB2505 to measure the FOS of pre-laid optical fibers. The instrument is shown in the Figure 11a. To verify the correctness of the BOFDA FOS characterization results, manually marked points were set on the model surface at certain intervals as survey benchmarks, as exhibited in Figure 11b. Therefore, position changes of the survey points were continuously photographed by a DSLR digital camera during the excavation process. Then, by performing geometric arithmetic post-processing on the captured digital images, the settlement variations of the survey points were obtained.

3.3. Distribution of Fiber Optic Strain Variations During Excavation Processes in the SSE

The excavation in this study was designed by the actual daily advancing plan of the actual production, and the time interval of excavation and the excavation step distance were determined by converting the designed time similarity ratio and geometric similarity ratio. Then, we used excavation tools to carry out the simulated excavation. The excavation step spacing for each excavation was set as 30 mm, with a total of 45 excavations and a total excavation length of 1350 mm. After each excavation, BOFDA was used to measure the FOS, and a DSLR digital camera was used to take photos of the displacement situation of the sampling points of the model surface.

During the experiment, two original FOS curves were acquired through BOFDA measurement, each 26 m long, showing the strain distribution of the total horizontally and total vertically laid optical fibers, as shown in Figure 12.

3.3.1. The Overall Horizontal Fiber Optic Strain Distribution

(1)

A trapezoidal boss embodied the FOS distribution features, where the boss height and width decreased progressively from the bottom to the top (that is, from HF1 to HF4).

(2)

The width of the trapezoidal boss platform, which is the range of FOS variation segments gradually increased with the excavation.

(3)

The different shapes of trapezoidal convex platforms reflected the different forms and states of movement of the overlying rocks.

(4)

Simultaneously, it can be seen that the variation of HF1 FOS was the most complex, and the scope of FOS variation was the largest. Most excavation processes have an impact on this.

3.3.2. The Total Vertical Fiber Optic Strain Distribution Curve

(1)

VF1 and VF5 were located at the open-off cut and stopping line positions, respectively, and were minimally affected by mining, resulting in little change in FOS.

(2)

VF2~VF4 FOS curves exhibited a trapezoidal boss, which can be divided into a single trapezoidal boss and a two-level stepped trapezoidal boss.

(3)

The overall width of the boss gradually increased with excavation; the boss heights of VF2, VF3, and VF4 were relatively large.

(4)

In the later stage, heights of the overall boss, that is, the magnitude of the strain value, gradually decreased with excavation due to the influence of the fragmentation and swelling of the fallen gangue.

(5)

The strain curves of VF2, VF3, and VF4 mostly exhibited a stepped trapezoidal convex shape of 1 to 2 levels, representing various rock mass movements. It is obvious that VF2–VF4 are more fully affected by mining and can fully reflect the entire process of overlying rock deformation.

To sum up, due to the longer duration and greater extent of the impacts of excavation on optical fibers HF1 and VF2, they can adequately reflect the movement laws of the overlying rock strata caused by coal mining. Therefore, this study applied HF1 and VF2 to discuss the FOS characterizing methods for rock block movement forms and states.

4. Fiber Optic Strain Characterization of Overlying Rock Movement Features

Drawing from the above investigation, this section intends to not only portray the transverse movement characteristics of the overlying rock blocks in accordance with the fiber optic strain (FOS) distribution of HF1 during excavation, but also characterize the vertical movement characteristics of the overlying rock strata in accordance with the FOS distribution changes of VF2 during excavation.

4.1. Characterization by Horizontally Laid Optical Fibers

This section explores the characterization of horizontal fiber optic strain distribution changes from two aspects: the motion forms and the movement states of the overburden.

The horizontal optical fiber HF1 was installed in the middle of the K2 limestone (the basic roof). With excavation, it has undergone eight major rock movement processes, forming four different types of optical fiber strain distribution curves.

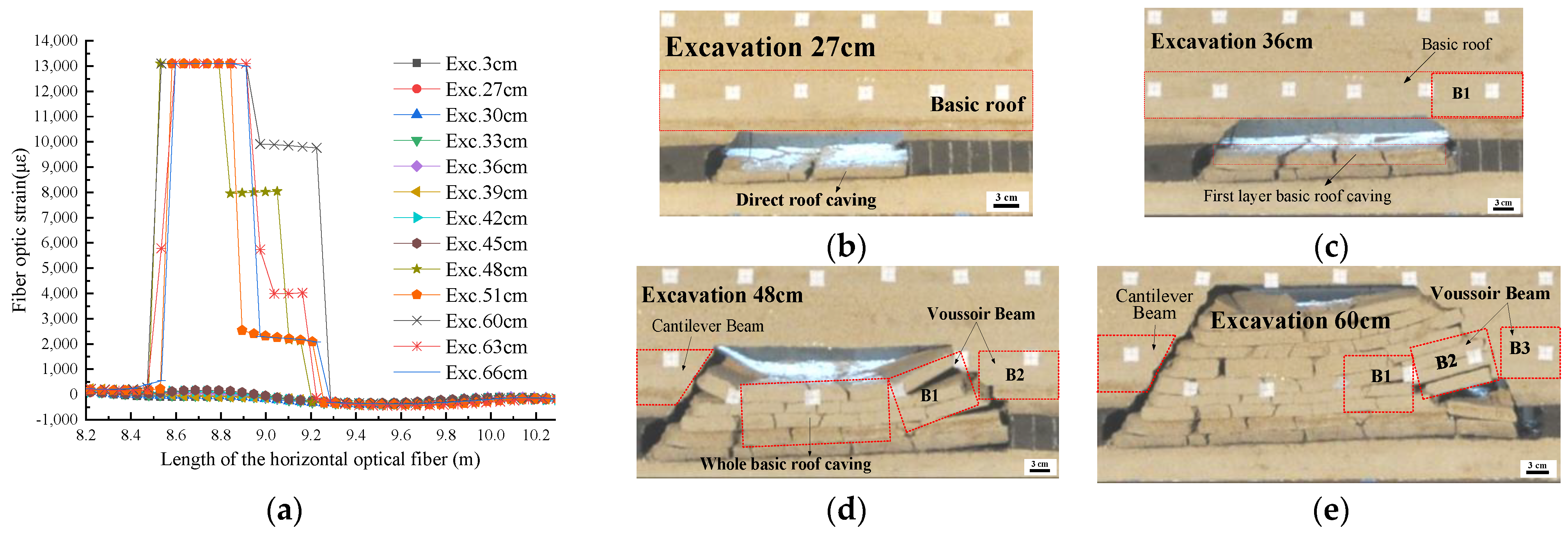
• Excavation of 0–66 cm, the movement form of voussoir beams.

Excavating to 27 cm, the direct roof began caving, as shown in Figure 13b. The first layer of K2 limestone started to collapse as the excavation approached 36–45 cm, but the second layer of the basic roof rock layer where FH1 was buried was in a stable state (Figure 13c), which resulted in FH1 not being influenced by coal mining and the FOS maintaining its initial state (Figure 13a). During the excavation process of 48–66 cm, the FOS curve showed a multi-level trapezoidal boss shape, and the height at the open-off cut side was the highest, reaching 13,000 $\mathsf{\mu }\mathsf{\epsilon }$. The height at the excavation side was comparatively low (2000~10,000 $\mathsf{\mu }\mathsf{\epsilon }$), indicating the basic roof at the open-cut side exhibited the movement characteristics of a cantilever beam, while the basic roof on the sides of the coal-mining face moved in the form of a voussoir beam: the B1 block fractured and rotated to sink into a voussoir beam structure after excavation to 48 cm. After excavation to 60~66 cm, the B2 block also began to fracture-rotate, continuing to sink into a voussoir beam structure, as demonstrated in Figure 13d,e.

• Excavation of 69–102 cm, a cantilever beam movement form.

After excavating to 69 cm, the B2 block changed from inclined rotation to horizontal settlement, causing strong rotation settlement of the B3 block until excavating to 75 cm (Figure 14b). The basic roof retained the movement form of a voussoir beam, which resulted in the disappearance of the stepped shape of the FOS curve, forming a single trapezoidal boss platform to the HF1 FOS curve, which was slightly lower in height (Figure 14a).

As shown in Figure 14, when excavated to 78 cm, the B3 block rotated and settled, causing the B4 block to lose its horizontal clamping effect and form a cantilever beam structure. Subsequently, the B4 block rotated and collapsed (Figure 14c), causing the FOS curve to be an isosceles trapezoid with consistent heights at both ends. This movement continued until the excavation of 87 cm. Excavating to 90 cm, the B5 block underwent strong rotation and collapse at a large angle, and the basic roof overburden exhibited a cantilever beam movement form (Figure 14c). This movement pattern continued until the excavation of 102 cm. The basic roof movement form and intensity were the same, resulting in a single isosceles trapezoidal shape in the FOS curve.

• Excavation of 105–126 cm, a reverse cantilever beam rotating movement form.

Figure 15 shows that when the excavation reached 105 cm, the cantilever beam of the basic roof overburden began to fracture, and the B6 block began to show a reverse rotation collapse. Due to the continuous reverse rotation movement of the B5 and B6 blocks, the stretch deformation of the embedded fibers increased significantly, causing the FOS curve to become a stepped-ladder shape with a larger altitude at the coal-face side. When the excavation reached 117 cm, the basic roof cantilever beam broke again, and the B7 block broke, showing a reverse rotation collapse. The continuous rotation collapse of the three blocks B5~B7 also caused the HF1 FOS curve to show a ladder shape with a larger step height near excavation, as shown in Figure 15a–c.

• Excavation of 129–135 cm, the overburden movement form of the voussoir beam.

In Figure 16a,b, the B8 block fractured under the overlying load of the fractured rock masses. On account of the horizontal restriction of the B7 block, it rotated and sank into a voussoir beam structure. Due to the smaller stretching effect of masonry beams compared with cantilever beams on the optical fiber, the FOS curve became a step shape with a lower ladder height at the coal-face side. Meanwhile, as a consequence of the early influence of the reverse rotation motion of B5~B7, the step height on the coal-face side was only slightly more modest than that on the coal-mining face side, with a height difference of less than 2000 $\mathsf{\mu }\mathsf{\epsilon }.$

As aforementioned, through the study of the sHF1 FOS curve distribution, the various horizontal FOS curve distributions characterized the different spatial movement forms of the basic roof overburden with the excavation, that is: voussoir beam movement → cantilever beam movement → reverse cantilever beam movement → voussoir beam movement, according to their chronological order.

4.2. Characterization of Overburden Deformation Movement by Vertically Laid Optical Fibers

From the perspective of the perpendicular FOS curve, the overall FOS curve showed a rightward trapezoidal boss shape. The boss height gradually increased with excavation. Taking VF2 as an example, features of FOS distribution as excavation were:

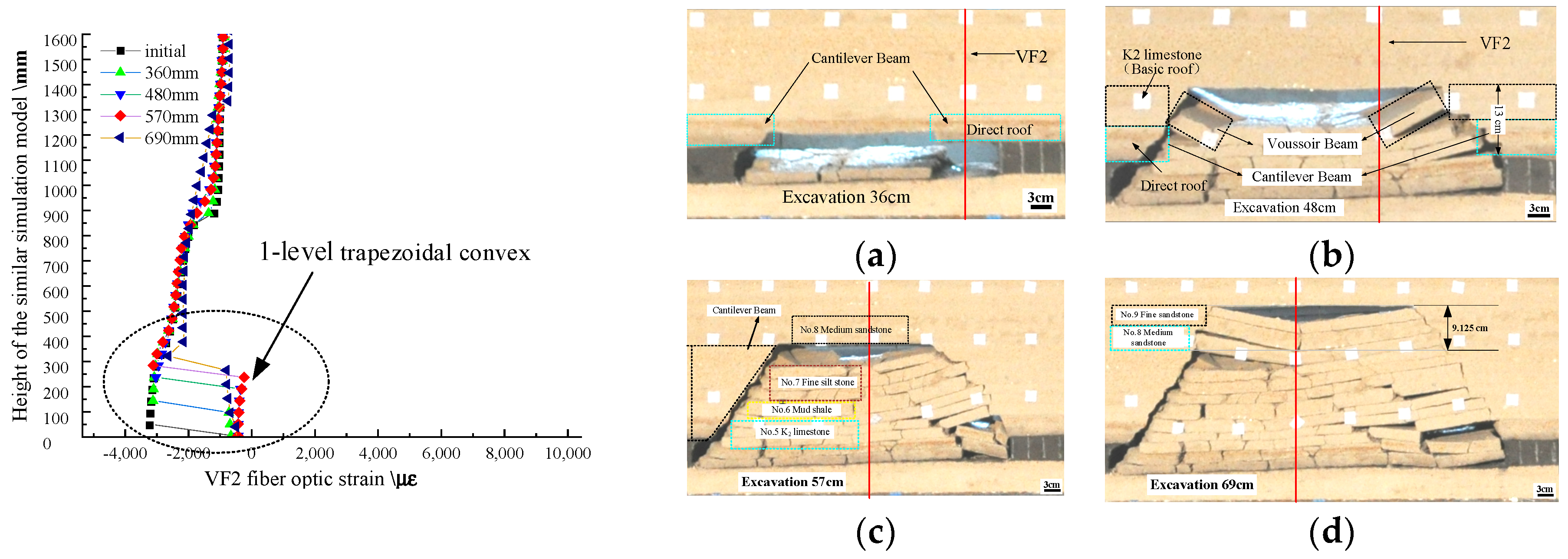
(1)

Initial compressive strain curve.

Before excavating 36 cm, the excavation did not pass through the VF2. The compressive strain of the VF2 increased with the growth in the buried depth of the model, showing a curve shape gradually increasing from −918.53$\mathsf{\mu }\mathsf{\epsilon }$ to −3229.46 $\mathsf{\mu }\mathsf{\epsilon }$, as described in Figure 17 below.

(2)

The 1-level rightward trapezoidal convex shape curve.

As shown in Figure 17, after excavating 36 cm, excavations passed through VF2. The goaf caused the early compressive stress of the VF2 within the goaf to be released. Later, not only the first layer of the basic roof, but also the direct roof collapsed. The VF2 FOS curve in the goaf immediately transformed as a rightward trapezoidal boss under the caving impact effects of broken rock masses, and the FOS (right end of fiber optic strain boss) also increased sharply from −3229.46 $\mathsf{\mu }\mathsf{\epsilon }$ to −700 $\mathsf{\mu }\mathsf{\epsilon }$. The height of the abrupt transition point from the lower boundary of the model was 10.494 cm. Subsequently, the height of the overlying rock layer collapse increased as the excavation progressed.

As shown in Figure 17b, when excavated to 48 cm, the lower segment of the basic roof of K2 limestone showed a cantilever beam structure, which broke and collapsed to the goaf; the upper portion of the basic roof showed a voussoir beam structure, which fractured and rotated. Due to the overall thickness of the cantilever beam and voussoir beam being only 13 cm, which was less than the spatial resolution of BOFDA, the VF2 FOS only exhibited a 1-level rightward-boss like curve, and the height of the fiber transition point (1-level rightward boss height) gradually increased to 20.788 cm.

When the excavation reached 57 cm, all K2 limestone~the 8th fine silt stone overlying rock showed a cantilever beam movement form as a whole on the open-off cut side, which fractured and collapsed. The VF2 FOS curve showed a 1-level rightward boss shape, and the height of the transition point (1-level rightward boss height) increased to 25.985 cm. The caving movement state of the cantilever beam developed to bottom of the 9th medium sandstone overlying, as illustrated in Figure 17c.

When the excavation arrived at 69 cm, the overburden continued to fracture and deform. The 9th medium sandstone and 10th fine sandstone fractured, and the fractured rock blocks did not collapse but maintained contact with the original rock layers through hinge points. The fractured rock blocks rotated and sank, becoming a masonry beam structure; because of the height difference among the rock fracture deformation point and the previous overburden deformation point being only 9.125 cm, which was the whole thickness of the 9th and 10th layers, this was less than the spatial resolution. Furthermore, the overburden near VF2 was in an overall caving state, so the FOS still maintained a 1-level rightward trapezoidal boss curve, and the height of the FOS transition point (1-level boss height) increased to 30.202 cm, as shown in Figure 17d.

(3)

The 2-level rightward trapezoidal boss fiber optic strain curve

As shown in Figure 18, after excavating 96 cm, the rock layers below the 9th overburden showed a cantilever beam collapse movement state, while the 9th and 10th layers of the overburden continued to maintain a stable voussoir beam. Later, during the process of excavation, the overlying 11th medium sandstone~13th K3 limestone layers successively fractured and settled, becoming a part of the voussoir beam. The failure deformation of the overlying rocks on the stope manifested as a clear binary structure: the upper voussoir beam–the lower cantilever beam are all displayed in Figure 18. Simultaneously, the voussoir beam structure’s thickness reached 20.3 cm, the thickness difference exceeded the spatial resolution of BOFDA, and VF2 FOS curve showed outstanding different upper and lower parts. The lower part maintained the original 1-level rightward boss shape, while the upper part suddenly changed to a rightward 2-level trapezoidal tensile boss FOS curve with 8000 $\mathsf{\mu }\mathsf{\epsilon }$. The height of the sudden change-point on the 2-level boss became 51.126 cm, and the height of the sudden change-point below the 2-level boss (i.e., the change-point on the 1-level boss) was 33.116 cm.

As shown in Figure 18b, at the excavation to 105 cm, the 21th fine sandstone and the underlying soft rock layers underwent overall rotational settlement deformation and were attached as a whole load to the voussoir beam formed by the 9th medium sandstone. The elevation difference from the upper border to the lower border of the whole masonry beam structure reached 37.92 cm. The top of the VF2 FOS curve presented a rightward 2-level trapezoidal boss tensile strain curve with a positive value of 7000 $\mathsf{\mu }\mathsf{\epsilon }$. The height of the abrupt change-point on the 2-level boss suddenly increased to about 60.126 cm, and the height of the lower change-point below the boss was the same as above.

When the excavation arrived at 117 cm, the thickness of the voussoir beam structure developed by 38.18 cm, and the failure deformed rock layer developed to the bottom of the 22th shale interbedded layer (Figure 18c). The upper VF2 FOS curve showed a rightward 2-level trapezoidal boss tensile FOS curve with a positive value of 5000–6000 $\mathsf{\mu }ϵ$. The height of the sudden change-point on the 2-level boss suddenly changed to 63.059 cm, and the height of the lower sudden change-point below the convex platform (i.e., the change-point on the 1-level boss) decreased to 27.116 cm.

Finally, when excavating 135 cm, the voussoir beam thickness developed to 45.76 cm, and the overlying 23th medium grained sandstone layer began to settle and deform. The development height of the fissure development zone eventually remained at the bottom of the No. 24 K7 coarse sandstone layer (Figure 18d). The VF2 curve showed a rightward 2-level trapezoidal boss tensile FOS curve in its upper portion with a positive value of about 2000 $\mathsf{\mu }\mathsf{\epsilon }$. The height of the sudden change-point on the 2-level boss suddenly changed to about 70.053 cm, and the height of the sudden change-point below the convex platform did not change, which was also about 27.116 cm.

In summary, as excavation progresses, when the excavation passes through the fiber burial location and the thickness of the overburden movement is greater than the BOFDA spatial resolution, the strain exhibits a two-level double trapezoidal boss curve distribution, with the upper 2-level boss representing the movement state of the voussoir beam, and its upper boundary height representing that of the fracture zone. The lower 1-level boss height reflects the movement state of the cantilever beam, and its height reflects that of the collapse zone.

4.3. Characterization of Overburden Movement Law by Fiber Optic Strain Curve Distribution

• Transverse movement forms and states of rock blocks

The FOS curve distribution of the upward trapezoidal boss with horizontally buried optical fibers indicates that:

(1)

Both the left inflection points and the right inflection points of the boss represent broken points of overlying strata, and the width of the boss is also the lateral scope of the overburden failure deformation.

(2)

The FOS curves of all horizontal optical fibers represent the deformation movement mode of the uneven trapezoidal boss of overlying rocks. The development of the width of the boss indicates that the transverse range of the overlying rock movement gradually increases with excavation.

(3)

The various shapes with the trapezoidal boss represent different movement forms of the rock blocks. As the excavation advanced, these are: voussoir beams → cantilever beams → reverse cantilever beam → voussoir beams, respectively.

• Vertical movement forms and states of the overlying rock strata

The FOS curve distribution of the rightward trapezoidal boss with vertically buried optical fibers indicates that:

(1)

When the excavation did not pass through the VF2 optical fiber, the fiber optic strain was the initial stress–strain curve.

(2)

After excavating through VF2, the overlying rock near the stope showed cantilever beam movement, causing the VF2 FOS to exhibit a 1-level rightward trapezoidal boss shape, and the height of the abrupt change-point of the boss gradually increased with excavation, which represents the caving zone height.

(3)

As the excavations advanced, the overlying hard and thick rock strata fractured and exhibited a state of rotation and sinking of the voussoir beams. When the thickness of the voussoir beam was less than the spatial resolution of BOFDA, the VF2 FOS curve reflects the height of the overall overburden failure deformation, presenting a 1-level rightward trapezoidal boss curve. At this time, the height of the inflection point is that of the overburden deformation, which gradually rises with the excavation.

(4)

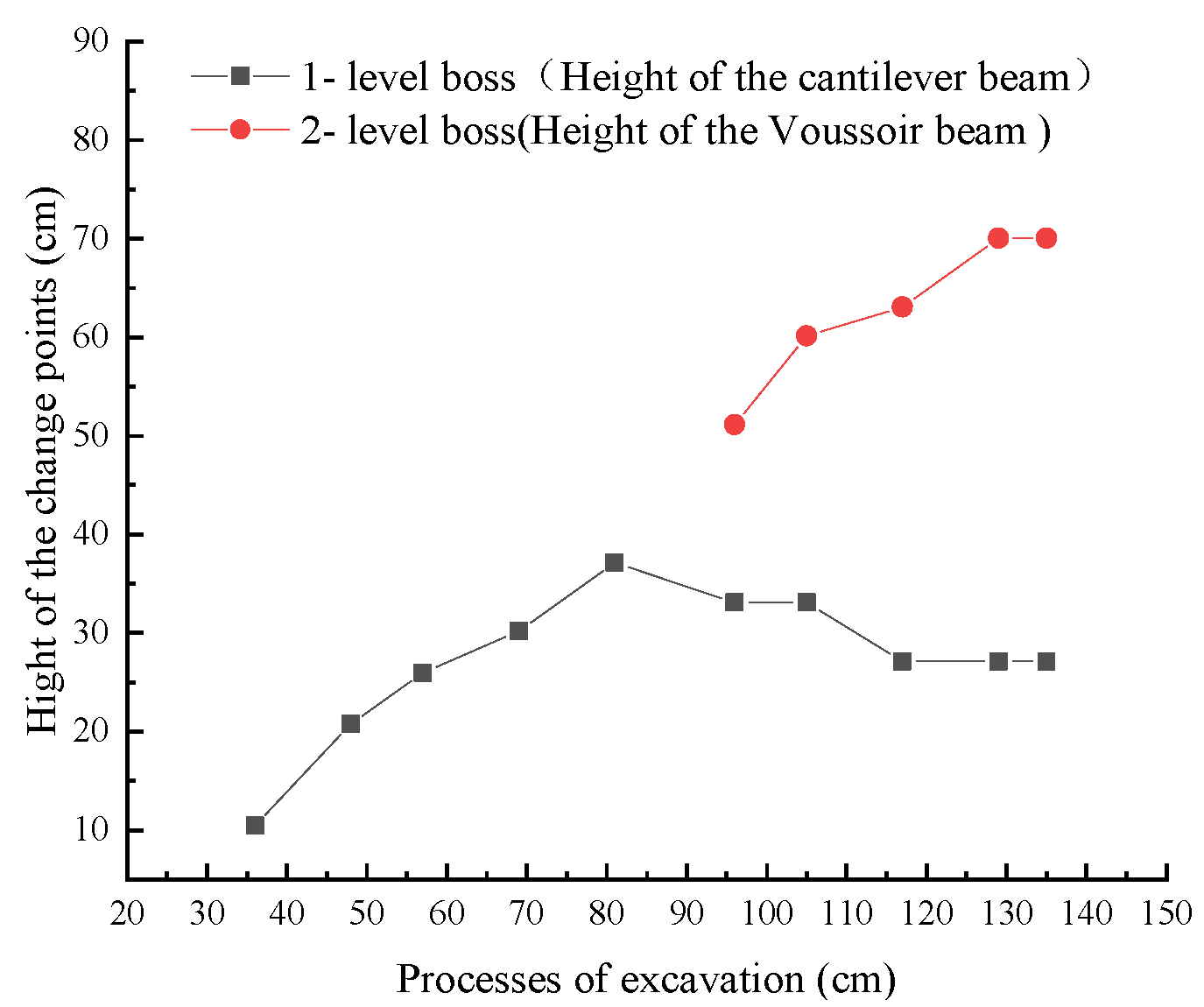
When the thickness of the voussoir beam was bigger than the spatial resolution of BOFDA, the VF2 FOS curve exhibited two distinct shapes of the upper and lower rightward trapezoidal bosses, with the upper part being a larger rightward tensile strain 2-level trapezoidal boss curve, whose vertical height is equal to that of the voussoir beam. Elevation of the lower boss is that of the cantilever beam. The variation curves of the position height of the upper inflection point of the 1-level trapezoidal boss and the 2-level boss in the time dimension are shown in Figure 19.

As displayed in Figure 19, the cantilever beam structure height during the movement of the cantilever beam gradually increased with excavation, reaching a maximum value of 37 mm at an excavation distance of 87 cm, and then gradually decreased with excavation; after excavating to 117 cm, the height remained stable at 27 cm above the bottom of the similar material model.

After excavation reached 96 cm, a 2-level trapezoidal FOS boss appeared, and the fracture zone was formed in the voussoir beam structure of the overlying rock, with its height gradually increasing with excavation. After excavating to 129 cm, the height remained stable at 70.05 cm above the model bottom.

Because the ratio of dimension of the similar model to the actual coal face was 1:150, and the altitude of the coal roof from the bottom of the K1 sandstone stratum in the actual coal face was 14.805 m, cantilever beams’ ultimate height was calculated to be 25.77 m over the coal seam roof; the voussoir beam structure’s height was 90.27 m over the coal seam roof.

5. UDEC Numerical Simulation Verification of BOFDA Characterization

To confirm the correctness of the SSE and the effectiveness of the BOFDA FOS distribution in characterizing the overburden mining-induced movement, this study used UDEC6.0 software to simulate the overlying rock layers’ movement in the actual studied coal-mining face, and verified the deformation movement forms, movement states, and the development height of the overburden failure movement.

UDEC is mainly used to study the progressive failure of rocks and the evaluation of the influence of joints, fissures, faults, and rock layers on underground engineering and rock foundations. By cutting the blocks, the deformed material is separated into discrete sets of blocks to represent discontinuous media. For UDEC 6.0, when slip occurs on the contact surface, the contact surface stress satisfies the Mohr–Coulomb criterion:

$${\mathit{\tau }}_{xy} =-\left({\mathit{\sigma }}_{y}tan\mathit{\phi }+\mathit{C}\right)$$

(8)

In the formula, ${\mathit{\tau }}_{\mathit{x}\mathit{y}}$ is the tangential stress experienced by the coal body in the vicinity of the contact surface, MPa; ${\mathit{\sigma }}_{\mathit{y}}$ is the vertical stress (plastic zone) experienced by the coal body in the vicinity of the contact surface, MPa; $\mathit{\phi }$ is the friction angle within the contact surface;$C$ is the cohesive force within the contact surface, MPa.

In the UDEC numerical calculation process, the bulk modulus K and shear modulus G can be obtained using the following formula:

$$K={\displaystyle \frac{E}{3\left(1-2\nu \right)}}, G={\displaystyle \frac{E}{2\left(1+\nu \right)}}$$

(9)

where the elastic modulus is presented as E, and the Poisson’s ratio is presented as v.

Assume that the virginal stress of the rock blocks is mainly given rise by the gravitational stress of the overlying rock strata. By constructing a UDEC model and inputting the geological and geostress parameters, the overlying rock blocks’ movements were monitored as coal mining in the UDEC simulation, and the movement law of overlying strata was analyzed as shown in the equation below:

$$R=C·\cos \mathsf{\phi }+{\displaystyle \frac{1}{2}}\left({\sigma }_1+{\sigma }_3\right)sin\phi$$

(10)

In the formula, ${\mathit{\sigma }}_{\mathbf{1}}$ is the maximum principal stress; ${\mathit{\sigma }}_{\mathbf{3}} \mathrm{is}$ the minimum principal stress; R is the stress circle radius.

5.1. Construction of Numerical Model

We developed a UDEC model based on not only the strata tectonic of the coal seam to be mined, but also the actual situation of the coal face. The numerical calculation model was constructed based on the actual prototype on site at a 1:1 ratio. Considering the influence of the boundary effects and optimizing the calculation time of the model reasonably, the entire prototype was length $\times$ width = 300 m $\times$ 160 m, and the width of the intake and return airways was set to 5 m. On both sides of the mining layer, a 50 m coal pillar was left nearby the intake airway, and a 40 m protective coal column was kept adjacent to the stopping line in the return airway.

The boundary and loading conditions for the numerical simulation software were determined as follows: ① Equal force horizontal constraints were applied to the left and right boundaries of the UDEC model, so the horizontal displacement of the boundaries was zero; ② the bottom boundary of the UDEC model was fixed with zero displacement; and ③ the top boundary of the UDEC model was set as a free boundary. The material failure of the model conformed to the Mohr–Coulomb strength criterion. This UDEC simulation was calculated according to the UDEC default convergence criterion (i.e., the convergence threshold of the equivalent force is 10⁻⁵).

The grid setting of the UDEC model is shown in Figure 20, and the mining coal seam and its overlying rock layer adopted the strategy of infill grid, and the upward grid was gradually thinned.

In the UDEC simulation, the actual excavation length was 200 m, and the coal bed and overlying strata were nearly horizontal. The model established a total of 26 rock layers, and the accumulated simulated rock strata thickness was set as 160 m. Because the mining depth was simulated merely at 400 m, the load on the upper rock layer was simplified as uniformly distributed in order to simplify the model. The geostatic stress of the overlying rock layers was imposed to the upper model boundary. Ground on the physical properties of the rock formation in the actual coal face, as detailed in Table 2, the numerical model constructed is shown in Figure 21.

When conducting the numerical simulations, three vertical measuring lines, numbered No. 1–No. 3 were put up to display the settlement of overburden rock blocks, located at 80 m, 120 m, and 160 m to the left boundary of the model, respectively.

5.2. Analysis of Numerical Simulation Results

5.2.1. Overburden Mining-Induced Deformation Movement Contour Map

To analyze the failure movement of the rock blocks in the course of excavations, model excavation diagrams and displacement contour diagrams were selected as examples when the working face advanced 60 m, 120 m, and 200 m; these are illustrated in Figure 21 and Figure 22.

The UDEC numerical simulation process showed the overburden failure deformation as coal mining. When the excavation distance reached the maximum span of the basic roof, the basic roof fractures and the overburden deformed with excavation.

(1)

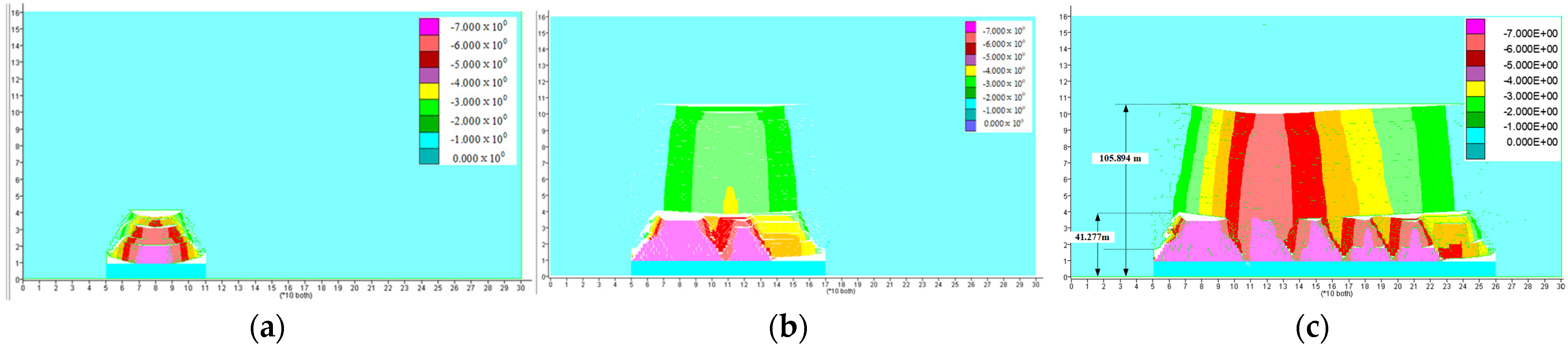
The range of the horizontal rock layers’ collapse expanded with excavation. When the excavation advanced to 60 m, the overburden collapsed on a large scale, and the rock layers showed a movement state of voussoir beams (Figure 22a), followed by a collapse state of cantilever beams in the later stage. As the excavation progressed, the cantilever beam presented the normal caving and reversal caving (Figure 22b,c), and at the end of the excavations, the basic roof presented a voussoir beam movement state.

Finally, at the excavation of 200 m, the overlying strata had been fully excavated, and the width of the overburden failure movement also reached a stable state, ultimately forming a trapezoidal shape as a whole, as in Figure 22 and Figure 23.

(2)

The vertical overburden collapse showed obvious stage features. At the beginning of excavation, only a cantilever beam movement was presented, and its height gradually rose. By the time of excavation at 60 m, the height reached the model height of about 41.277 m, and obviously, large horizontal cracks appeared above the collapse areas. Afterward, the rock strata within the collapse band showed a complete caving and a cantilever beam movement state; later, a voussoir beam structure appeared in the overlying rock blocks of collapse zones, as depicted in Figure 22b,c. A distinct fracture zone developed above the voussoir beam structure, with its height increasing progressively as excavation advanced. By the time 120 m of excavation had been completed, the fracture zone had reached the full model height of 105.894 m, as illustrated in Figure 22 and Figure 23.

A height of 89.62 m for the voussoir beam structure (fracture zone) and the height of 24.99 m for the cantilever beam structure (caving zone) above the No. 15 coal are obtained by deducting the altitude of the coal layer from that of overlying rock blocks failure movement, which are the actual elevation of the fracture zone as well as the caving zone in the actual studied working face; all are depicted in Figure 22c and Figure 23c.

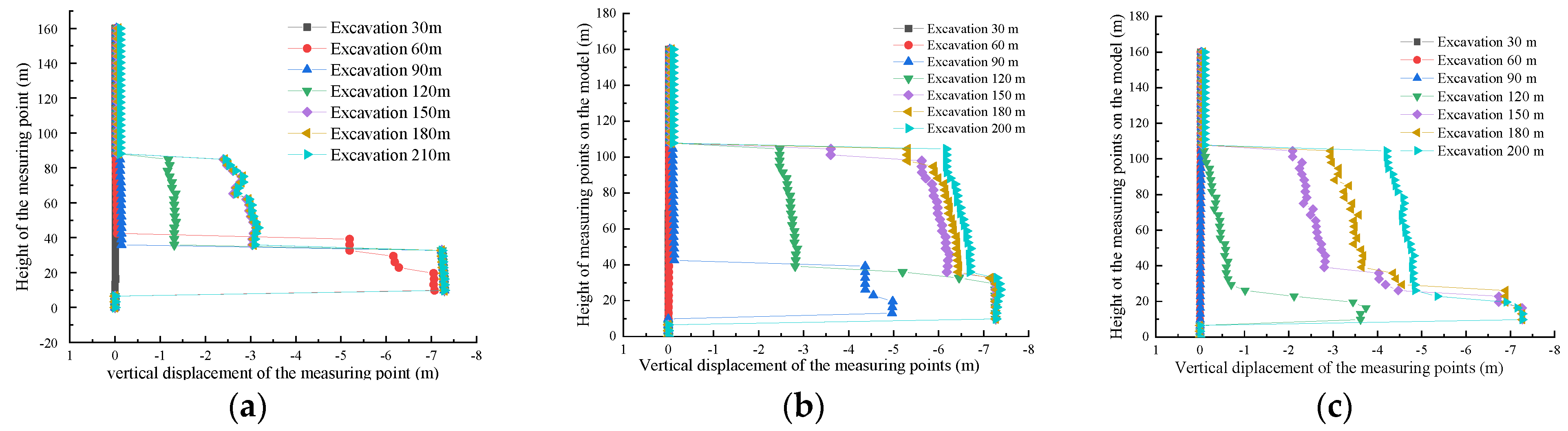
5.2.2. Vertical Survey Lines Displacement in the UDEC Simulation

To accurately calculate the amount of vertical movement of overlying rock blocks, three plummet lines set in the numerical simulation were monitored. The settlement displacement curves to the three plummet lines are illustrated in Figure 24.

The settlement amount of survey lines showed that the elevation of the overburden failure deformation rose with excavation. After the coal face advanced 90 m, the overburden settlement increased quickly. As soon as the coal face advanced to 120 m, the settlement displacement arrived at the utmost values. The largest height of the overburden deformation (fracture zone) stabilized at a model height of 105.896 m That is to say, at 89.62 m over the coal seam. In the meantime, the caving zone height also developed to its maximum, where the caving zone’s height was 24.99 m over the coal to be mined.

5.3. UDEC Numerical Simulation Conclusions

The movement law of overburden mining deformation was obtained through UDEC numerical simulation

(1)

Horizontally. The overlying rocks’ movement scope gradually expanded. The basic roof overburden failure deformation initially presented as the rotating-sinking movement of the voussoir beam, later changed to the sliding-rotating movement of the cantilever beam, then developed into the sliding-caving of the reversal cantilever beam, and finally evolved into the rotating-sinking movement of the voussoir beam.

(2)

Vertically. The failure height of the overburden gradually increased as excavation progressed. The deformation caused by the mining-induced overburden movement exhibited distinct upper and lower bimodal stepwise stages as the lower overburden formed a collapse zone with the cantilever beam movement state, and overlying rock formations formed a fracture zone with the rotating and sinking movement state of voussoir beam structures. Based on the altitude of the coal seam roof, the fracture zone height was 89.69 m, and the caving zone height was 24.99 m.

As demonstrated above, the UDEC numerical simulation results were not only consistent with the BOFDA FOS characterization of the overburden deformation movement in the horizontal direction, but also aligned well with the bimodal structural states (lower cantilever beam and upper voussoir beam) of the overburden deformation characterized by the vertical FOS. Additionally, the simulated and measured heights of the fracture zone and caving zone exhibited a high degree of consistency.

6. Exploration on Characterization of Fiber Optic Strain Curves Distribution

Through the aforementioned BOFDA FOS characterization, digital images processing of the manual-marked survey points, and UDEC simulation, the development law of overburden mining deformation movement in both the lateral and upright directions was basically consistent. That is to say, the range of overburden failure movement gradually expanded as the working face advanced, showing an unequal trapezoidal boss development. The rock block movement forms of the basic roof manifested in the sequence of voussoir beam → cantilever beam → reversal cantilever beam → voussoir beam movement over time. Vertically, the lower part overburden exhibited a developing state of the caving zone like the movement form of a cantilever beam, and the overlying rock formation exhibited an existence state of the fracture zone in the movement form of a voussoir beam. However, there was a slight difference in the fracture zone height and that of the caving zone they represented.

Therefore, this study introduced the empirical formulas stipulated by the state as the standard for analyzing and discussing the ultimate development height of overburden mining damage and deformation. In light of the empirical formulas for compulsory enforcement [41], the final caving zone height, which is the height of the lower part cantilever beam structure within the overburden, was 25.82 m, and the final fracture zone height in the range of the voussoir beam development was obtained as 91.11 m. The calculation formulas are listed below.

$$\{\begin{array}{c}{H}_C={\displaystyle \frac{100{\displaystyle \sum }M}{2.1{\displaystyle \sum }M}}\pm 2.5=20.81~25.82\left(M\right), Max\left(H_C\right)=25.82\left(\mathrm{m}\right)\\ H_{\mathrm{F}}=30\sqrt{{\displaystyle \sum }M}+10=91.11\left(\mathrm{m}\right)\end{array}$$

(11)

By comprehensively comparing the various research methods outlined in this study, discrepancies were determined between the height of the overlying strata’s deformation movement and that indicated by the BOFDA DFOS, as presented in

Table 4. Vertical failure height of the overburden failure movement.

Research Method	Caving Zone Height (m)	Errors (%)	Fracture Zone Height (m)	Errors (%)
Fiber optic strain	25.77	-	90.27	-
UDEC simulation	24.99	3.026	89.69	0.643
Empirical formula	25.82	0.194	91.11	0.931

.

Comparative analysis showed that the vertical height of overburden failure movement represented by FOS had good consistency with the calculation of the UDEC numerical simulations and empirical formulas required by the national mandatory regulations. The consistency of the fracture zone height was relatively high, with an error of less than 1%. It is feasible to use the FOS characterized height to represent the actual fracture zone height, which was 90.27 m.

The maximum error of the caving zone was 3.026%, mainly due to the possible errors between the block division in the UDEC simulation and the actual situation. The numerical simulation was calculated based on the ideal rock state and could not fully reproduce the occurrence state of the rock layer in situ. This problem can be solved by obtaining detailed drilling data and the actual production geological reports as much as possible during the model establishment period, and by using more detailed and rich data to model, the in-situ overburden occurrence can be maximally reproduced.

Furthermore, by averaging the results obtained from the three methods and subtracting the BOFDA characterization from the mean, the error caused by BOFDA with a spatial resolution of 0.2 m in the deformation measurement could be approximately quantified. That is, the error in the height of the caving zone was 0.944%, and the error in the height of the fracture zone was 0.096%. This is consistent with the results of the comparison above. It is believed that if higher spatial resolution DFOS testing techniques, such as OFDR, etc., are used in the future, more satisfactory results will be achieved.

Given that the caving zone height characterized by DFOS is essentially consistent with the theoretical calculations and UDEC numerical simulation, the FOS characterization outcomes can be reliably applied to determine the failure height of the cantilever beam structure (caving zone) in actual coal-mining faces. This approach ensures a high level of safety redundancy and meets the stringent requirements of coal mine safety production. Therefore, it is reasonable to use 25.77 m to represent the caving zone height in actual coal faces. This also validates the feasibility and effectiveness of applying BOFDA DFOS to understand the behavior of the movement forms and states of the overlying blocks in this study.

7. Conclusions

To investigate the overburden mining-induced deformation movement laws, an actual coal mining face was used as the engineering background, and a similar simulation experiment was conducted using BOFDA DFOS technology. This study employed FOS curves to portray the failure movement forms and movement states of the overlying rock blocks. The following conclusions were drawn from the research:

(1)

The BOFDA fiber optic strain exhibited a trapezoidal boss curve due to the specifications and sensing parameters of BOFDA as the work advanced.

(2)

The multi-level trapezoidal boss of the horizontally embedded fiber optic strain curves continuously developed upward and rightward with excavation. The stepped shape of the trapezoidal boss represented the sequential movement forms of the basic roof strata: voussoir beam → cantilever beam → reverse cantilever beam → voussoir beam.

(3)

The vertically embedded FOS curves exhibited a two-level rightward trapezoidal boss shape, representing the bi-mode structure of the overburden deformation: the upper part boss represented the movement state of the voussouir beam, with its height indicating the fracture zone height; and the bottom fiber strain boss represented the movement state of the cantilever beam, with its height indicating the caving zone height.

(4)

The final development altitude of the caving zone with cantilever beam movement states was ascertained to be 25.77 m using BOFDA DFOS characterization, and the final altitude of the fracture zone developing was 90.27 m.

The BOFDA FOS characterizing results were in good agreement with the UDEC numerical simulation results and the results calculated from the national mandatory empirical formulas. This not only demonstrates the feasibility and effectiveness of using BOFDA DFOS in SSE for the overburden mining-induced deformation, but also provides a theoretical and experimental basis for distributed fiber optic monitoring of overburden deformation in production on site.