Electron-Ion Radiative Recombination Assisted by Bicircular Laser Pulses
Abstract
1. Introduction
2. Theoretical Method
3. Numerical Illustrations and Discussion
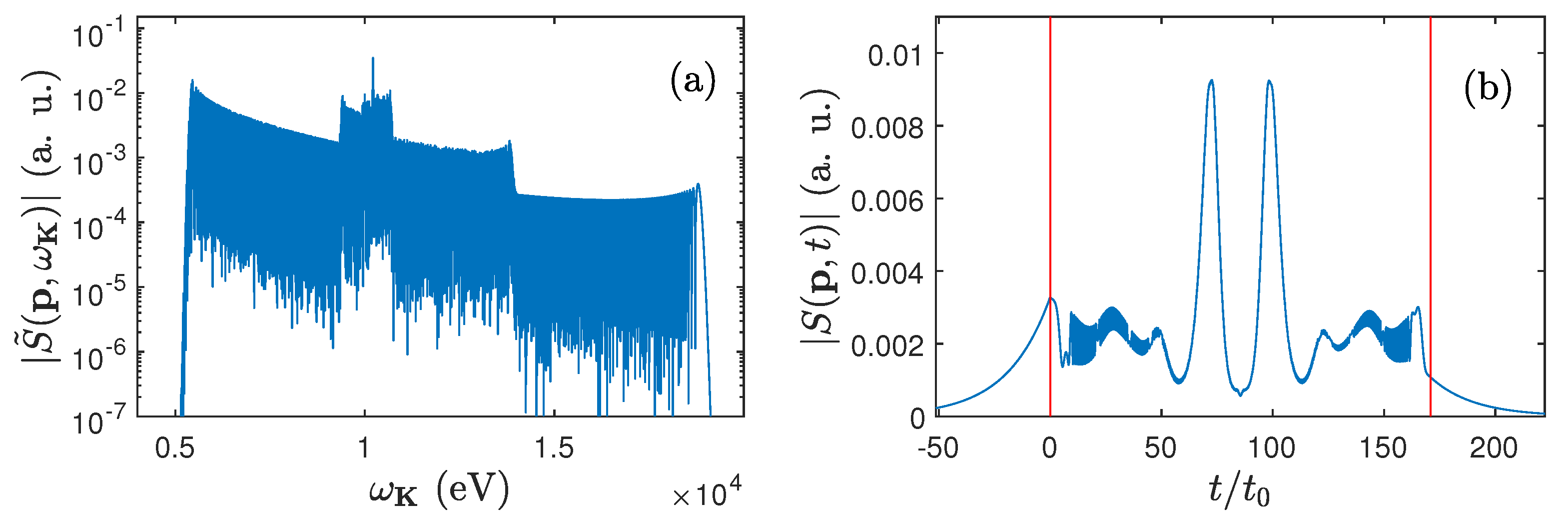
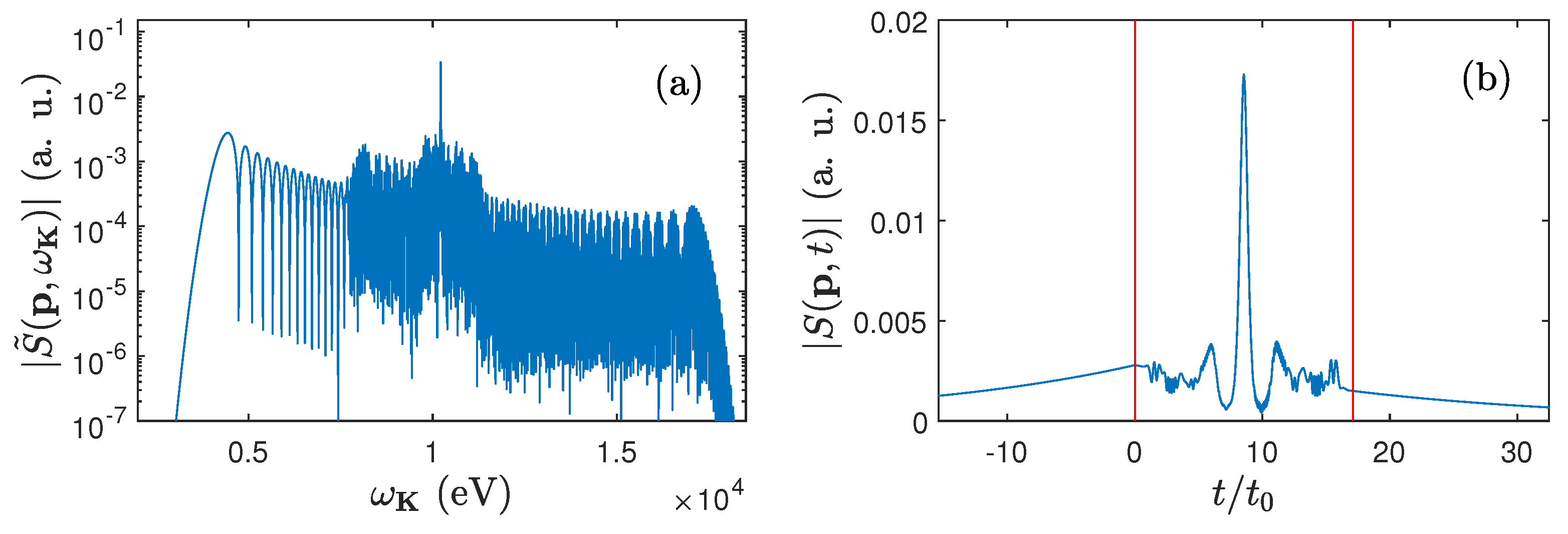
3.1. Energy Distributions of LARR Radiation
3.2. Synthesis of Attosecond Pulses
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Nobel Prize in Physics 2023. Available online: https://www.nobelprize.org/prizes/physics/2023/summary/ (accessed on 17 February 2025).
- Smeenk, C.T.L.; Arissian, L.; Zhou, B.; Mysyrowicz, A.; Villeneuve, D.M.; Staudte, A.; Corkum, P.B. Partitioning of the Linear Photon Momentum in Multiphoton Ionization. Phys. Rev. Lett. 2011, 106, 193002. [Google Scholar] [CrossRef] [PubMed]
- Ludwig, A.; Maurer, J.; Mayer, B.W.; Phillips, C.R.; Gallmann, L.; Keller, U. Breakdown of the Dipole Approximation in Strong-Field Ionization. Phys. Rev. Lett. 2014, 113, 243001. [Google Scholar] [PubMed]
- Wang, M.-X.; Chen, S.-G.; Liang, H.; Peng, L.-Y. Review on non-dipole effects in ionization and harmonic generation of atoms and molecules. Chin. Phys. B 2020, 29, 013302. [Google Scholar]
- Maurer, J.; Keller, U. Ionization in intense laser fields beyond the electric dipole approximation: Concepts, methods, achievements and future directions. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 094001. [Google Scholar]
- Kanti, D.; Majczak, M.M.; Kamiński, J.Z.; Peng, L.-Y.; Krajewska, K. Laser-assisted radiative recombination beyond the dipole approximation. Phys. Rev. A 2024, 110, 043112. [Google Scholar]
- Jaroń, A.; Kamiński, J.Z.; Ehlotzky, F. Stimulated radiative recombination and X-ray generation. Phys. Rev. A 2000, 61, 023404. [Google Scholar]
- Kuchiev, M.Y.; Ostrovsky, V.N. Multiphoton radiative recombination of electron assisted by a laser field. Phys. Rev. A 2000, 61, 033414. [Google Scholar]
- Jaroń, A.; Kamiński, J.Z.; Ehlotzky, F. Bohr’s correspondence principle and x-ray generation by laser-stimulated electron-ion recombination. Phys. Rev. A. 2001, 63, 055401. [Google Scholar]
- Milošević, D.B.; Ehlotzky, F. Rescattering effects in soft-X-ray generation by laser-assisted electron-ion recombination. Phys. Rev. A 2002, 65, 042504. [Google Scholar]
- Bivona, S.; Bonanno, G.; Burlon, R.; Leone, C. Polarization and angular distribution of the radiation emitted in laser-assisted recombination. Phys. Rev. A 2007, 76, 031402. [Google Scholar]
- Zheltukhin, A.N.; Flegel, A.V.; Frolov, M.V.; Manakov, N.L.; Starace, A.F. Resonant phenomena in laser-assisted radiative attachment or recombination. J. Phys. B At. Mol. Opt. Phys. 2012, 45, 081001. [Google Scholar] [CrossRef]
- Jaroń, A.; Kamiński, J.Z.; Ehlotzky, F. Coherent phase control in laser-assisted radiative recombination and X-ray generation. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 1221–1232. [Google Scholar] [CrossRef]
- Bivona, S.; Burlon, R.; Ferrante, G.; Leone, C. Control of multiphoton radiative recombination through the action of two low-frequency fields. Laser Phys. Lett. 2004, 1, 118–123. [Google Scholar]
- Odžak, S.; Milošević, D.B. Bicircular-laser-field-assisted electron-ion radiative recombination. Phys. Rev. A 2015, 92, 053416. [Google Scholar] [CrossRef]
- Čerkić, A.; Busuladžić, M.; Milošević, D.B. Electron-ion radiative recombination assisted by a bichromatic elliptically polarized laser field. Phys. Rev. A 2017, 95, 063401. [Google Scholar]
- Tutmić, A.; Čerkić, A.; Busuladžić, M.; Milošević, D.B. Role of the relative phase and intensity ratio in electron-ion recombination assisted by a bicircular laser field. Eur. Phys. J. D 2019, 73, 231. [Google Scholar] [CrossRef]
- Hu, S.X.; Collins, L.A. Intense laser-induced recombination: The inverse above-threshold ionization process. Phys. Rev. A 2004, 70, 013407. [Google Scholar] [CrossRef]
- Kamiński, J.Z.; Ehlotzky, F. Time-frequency analysis of X-ray generation by recombination in short laser pulses. Phys. Rev. A 2005, 71, 043402. [Google Scholar] [CrossRef]
- Bivona, S.; Burlon, R.; Ferrante, G.; Leone, C. Radiative recombination in the presence of a few cycle laser pulse. Opt. Express 2006, 14, 3715–3723. [Google Scholar]
- Bivona, S.; Burlon, R.; Leone, C. Controlling laser assisted radiative recombination with few-cycle laser pulses. Laser Phys. Lett. 2007, 4, 44–49. [Google Scholar]
- Čerkić, A.; Milošević, D.B. Few-cycle-laser-pulse-assisted electron-ion radiative recombination. Phys. Rev. A 2013, 88, 023414. [Google Scholar]
- Kanti, D.; Kamiński, J.Z.; Peng, L.-Y.; Krajewska, K. Laser-assisted electron-atom radiative recombination in short laser pulses. Phys. Rev. A 2021, 104, 033112. [Google Scholar] [CrossRef]
- Eichmann, H.; Egbert, A.; Nolte, S.; Momma, C.; Wellegehausen, B.; Becker, W.; Long, S.; McIver, J.K. Polarization-dependent high-order two-color mixing. Phys. Rev. A 1995, 51, R3414–R3417. [Google Scholar] [CrossRef] [PubMed]
- Milošević, D.B.; Becker, W.; Kopold, R. Generation of circularly polarized high-order harmonics by two-color coplanar field mixing. Phys. Rev. A 2000, 61, 063403. [Google Scholar] [CrossRef]
- Fleischer, A.; Kfir, O.; Diskin, T.; Sidorenko, P.; Cohen, O. Spin angular momentum and tunable polarization in high-harmonic generation. Nat. Photon. 2014, 8, 543–549. [Google Scholar] [CrossRef]
- Medišauskas, L.; Wragg, J.; van der Hart, H.; Ivanov, M.Y. Generating Isolated Elliptically Polarized Attosecond Pulses using Bichromatic Counterrotating Circularly Polarized Laser Fields. Phys. Rev. Lett. 2015, 115, 153001. [Google Scholar]
- Fan, T.; Grychtol, P.; Knut, R.; Hernández-García, C.; Hickstein, D.D.; Zusin, D.; Gentry, C.; Dollar, F.J.; Mancuso, C.A.; Hogle, C.W.; et al. Bright circularly polarized soft X-ray high harmonics for X-ray magnetic circular dichroism. Proc. Natl. Acad. Sci. USA 2015, 112, 14206–14211. [Google Scholar]
- Baykusheva, D.; Ahsan, M.S.; Lin, N.; Wörner, H.J. Bicircular High-Harmonic Spectroscopy Reveals Dynamical Symmetries of Atoms and Molecules. Phys. Rev. Lett. 2016, 116, 123001. [Google Scholar]
- Frolov, M.V.; Manakov, N.L.; Minina, A.A.; Vvedenskii, N.V.; Silaev, A.A.; Ivanov, M.Y.; Starace, A.F. Control of Harmonic Generation by the Time Delay Between Two-Color, Bicircular Few-Cycle Mid-IR Laser Pulses. Phys. Rev. Lett. 2018, 120, 263203. [Google Scholar] [CrossRef]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamics, 2nd ed.; Pergamon Press: Oxford, UK, 1982; pp. 137–140. [Google Scholar]
- Newton, R.G. Scattering Theory of Waves and Particles, 2nd ed.; Springer: New York, NY, USA, 1982; pp. 424–427. [Google Scholar]
- Allegre, H.; Broughton, J.J.; Klee, T.; Li, Y.; Kowalczyk, K.M.; Thatte, N.; Lim, D.; Marangos, J.P.; Matthews, M.M.; Tisc, J.W.G. Extension of high-harmonic generation cutoff in solids to 50 eV using MgO. Opt. Lett. 2025, 50, 1492–1495. [Google Scholar]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kanti, D.; Kamiński, J.Z.; Peng, L.-Y.; Krajewska, K. Electron-Ion Radiative Recombination Assisted by Bicircular Laser Pulses. Photonics 2025, 12, 320. https://doi.org/10.3390/photonics12040320
Kanti D, Kamiński JZ, Peng L-Y, Krajewska K. Electron-Ion Radiative Recombination Assisted by Bicircular Laser Pulses. Photonics. 2025; 12(4):320. https://doi.org/10.3390/photonics12040320
Chicago/Turabian StyleKanti, Deeksha, Jerzy Z. Kamiński, Liang-You Peng, and Katarzyna Krajewska. 2025. "Electron-Ion Radiative Recombination Assisted by Bicircular Laser Pulses" Photonics 12, no. 4: 320. https://doi.org/10.3390/photonics12040320
APA StyleKanti, D., Kamiński, J. Z., Peng, L.-Y., & Krajewska, K. (2025). Electron-Ion Radiative Recombination Assisted by Bicircular Laser Pulses. Photonics, 12(4), 320. https://doi.org/10.3390/photonics12040320