Incoherent Optical Neural Networks for Passive and Delay-Free Inference in Natural Light
Abstract
1. Introduction
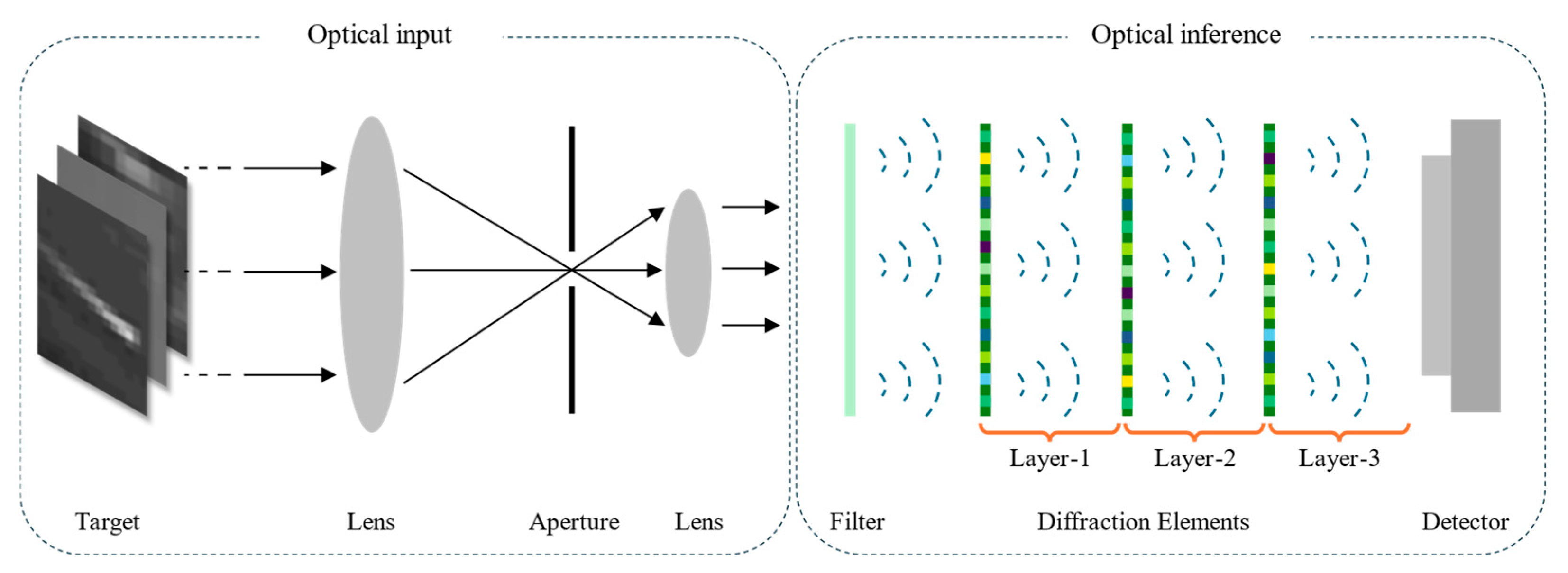
2. Methods
2.1. Subsection
2.2. Principle of ICONN
3. Simulation and Experiment Results
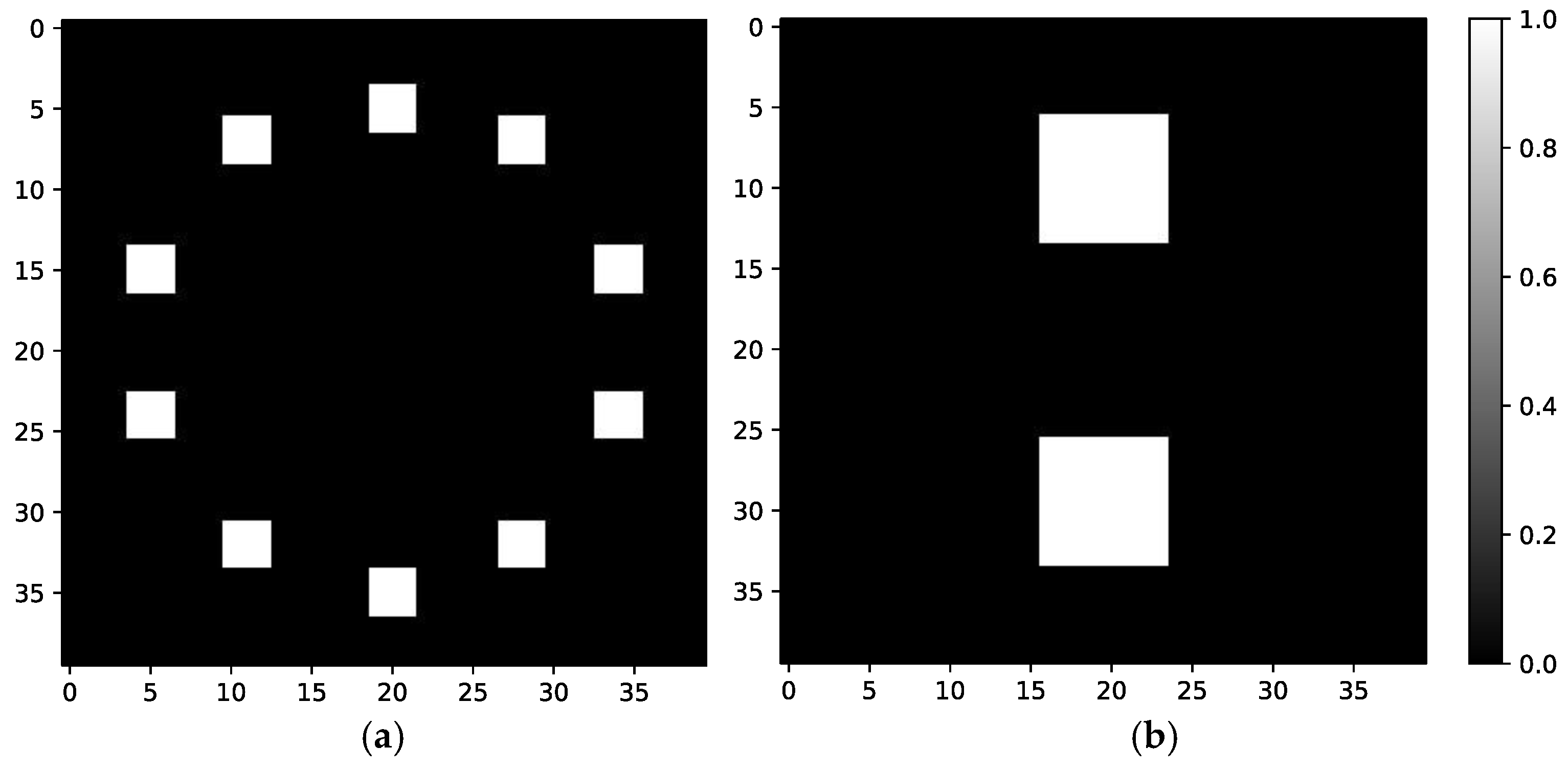
3.1. Simulation Strategy
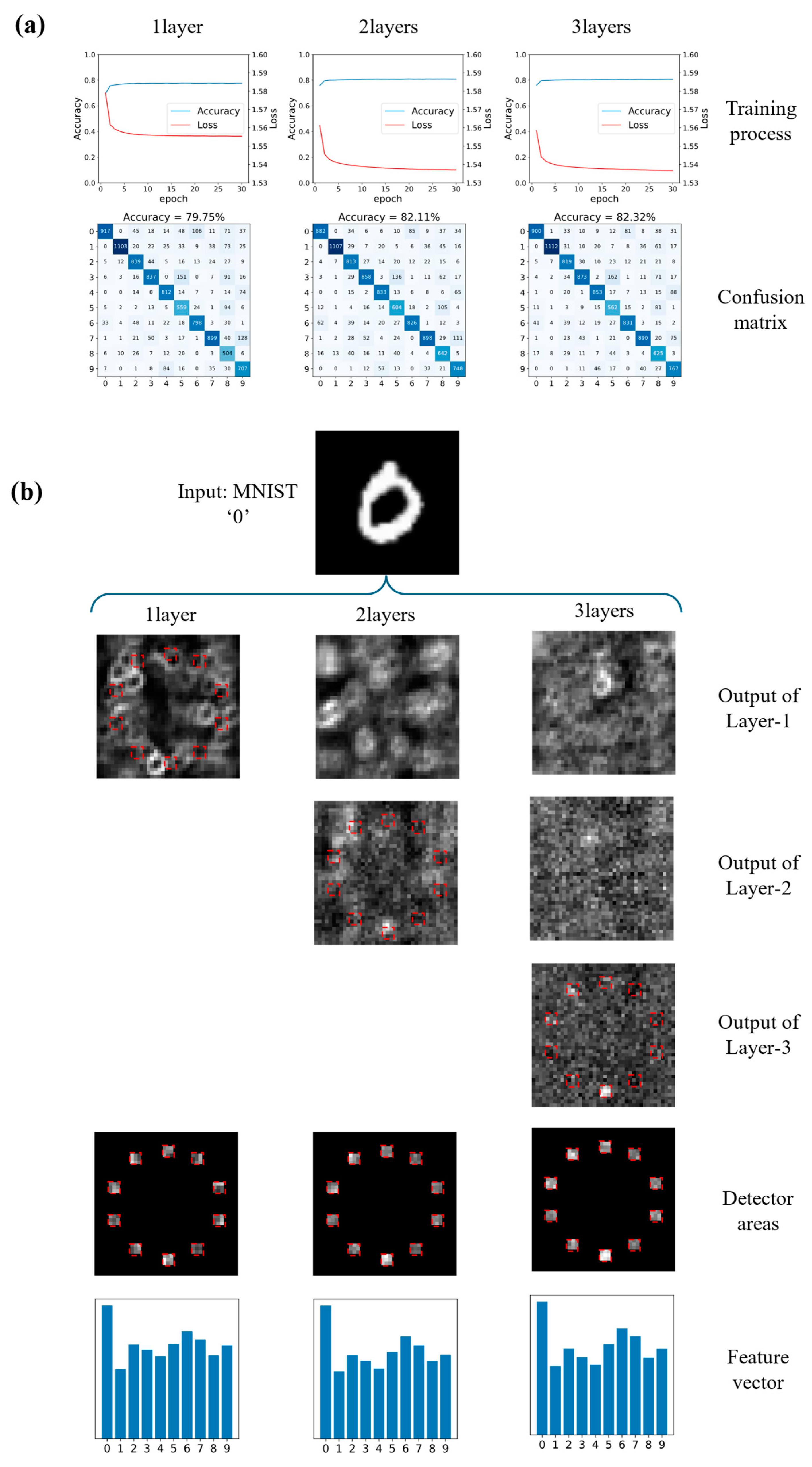
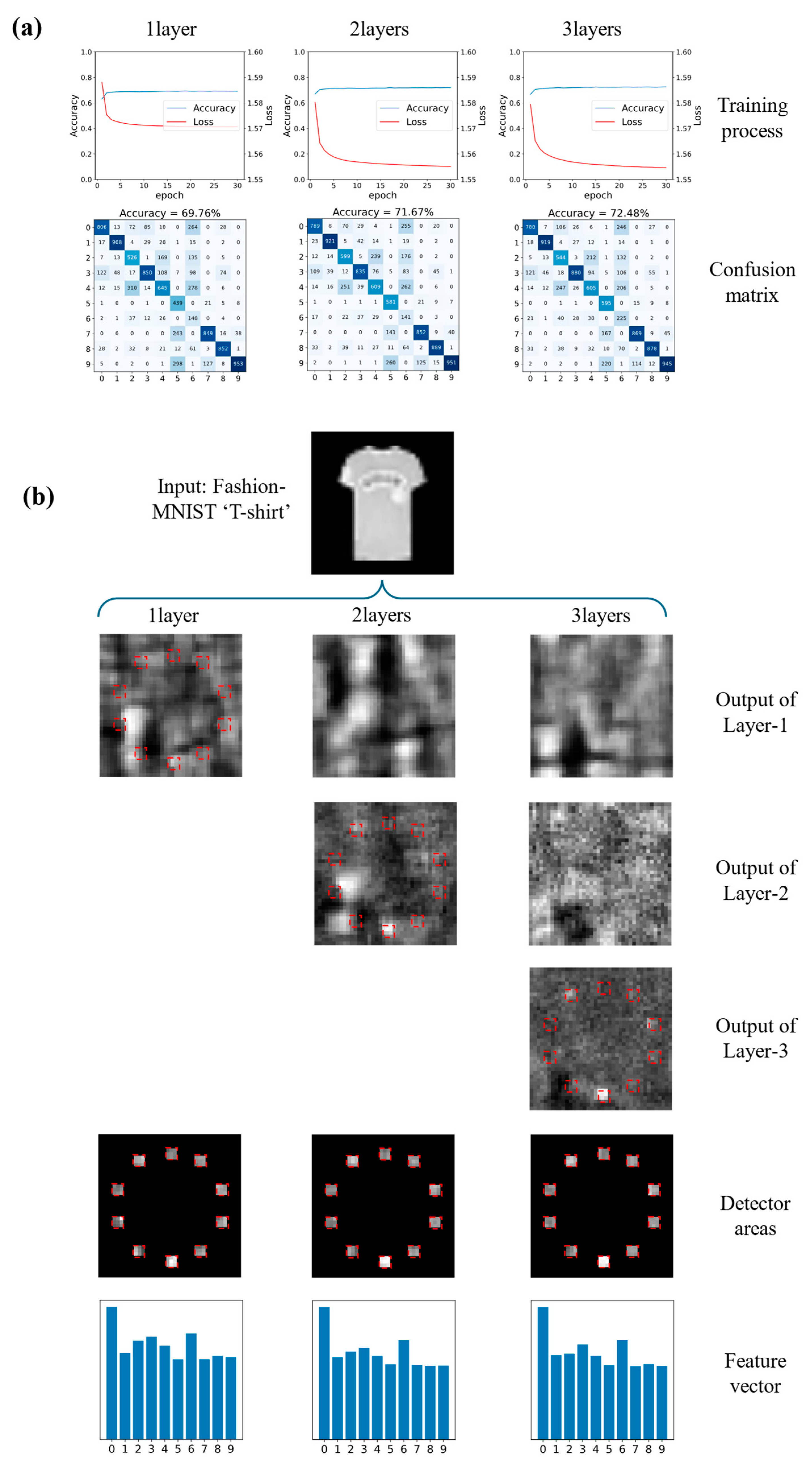
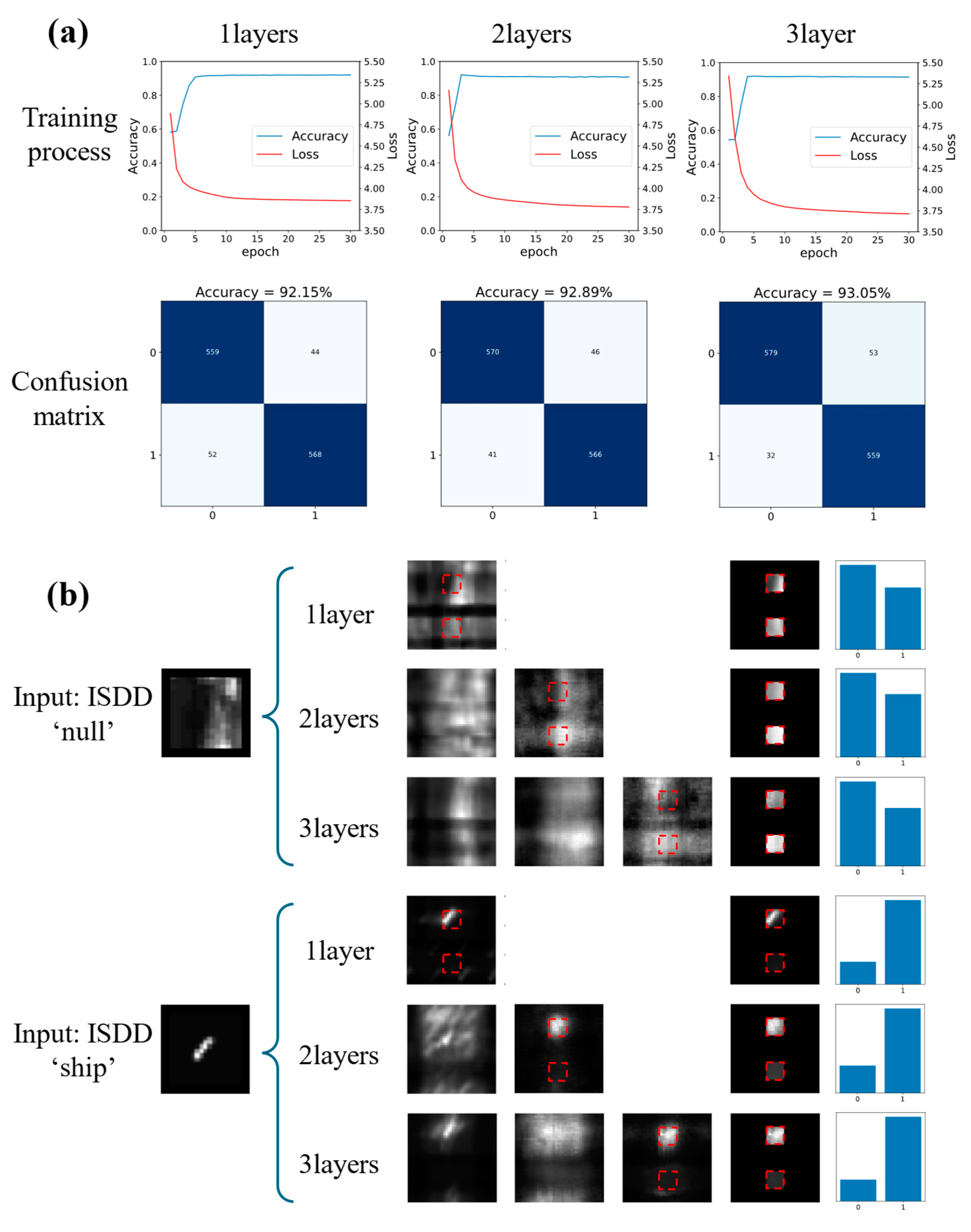
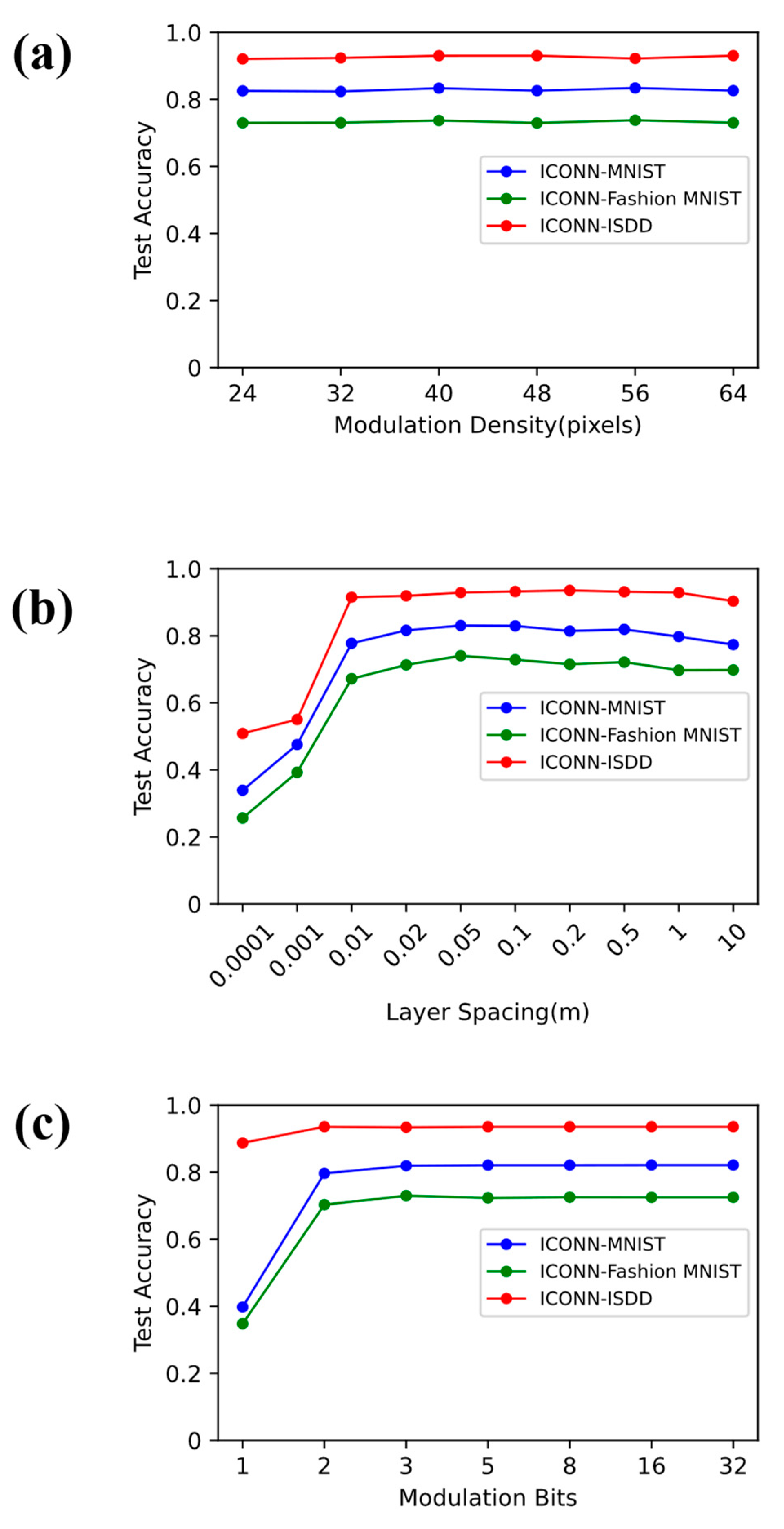
3.2. Simulation Result and Analysis
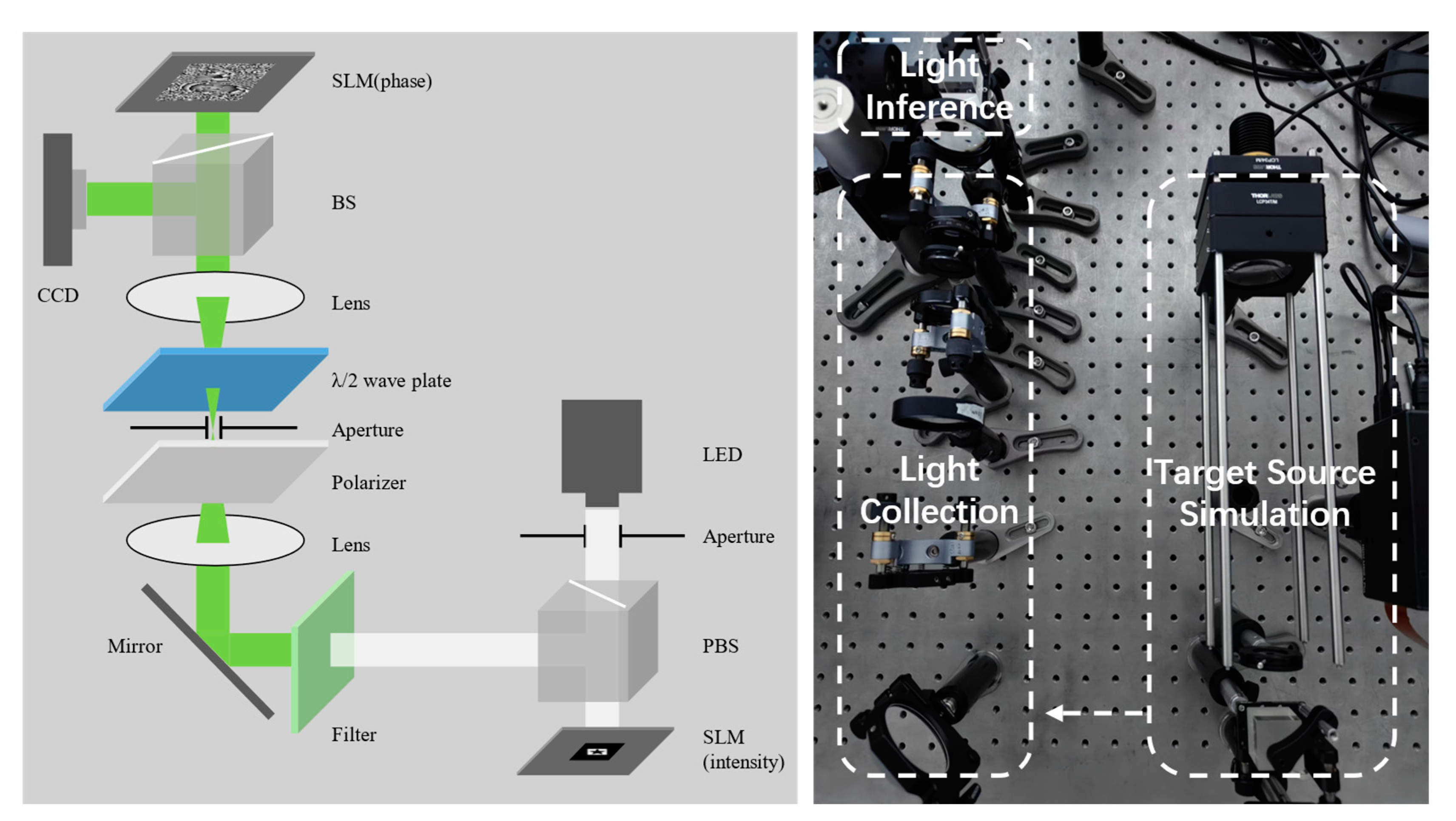
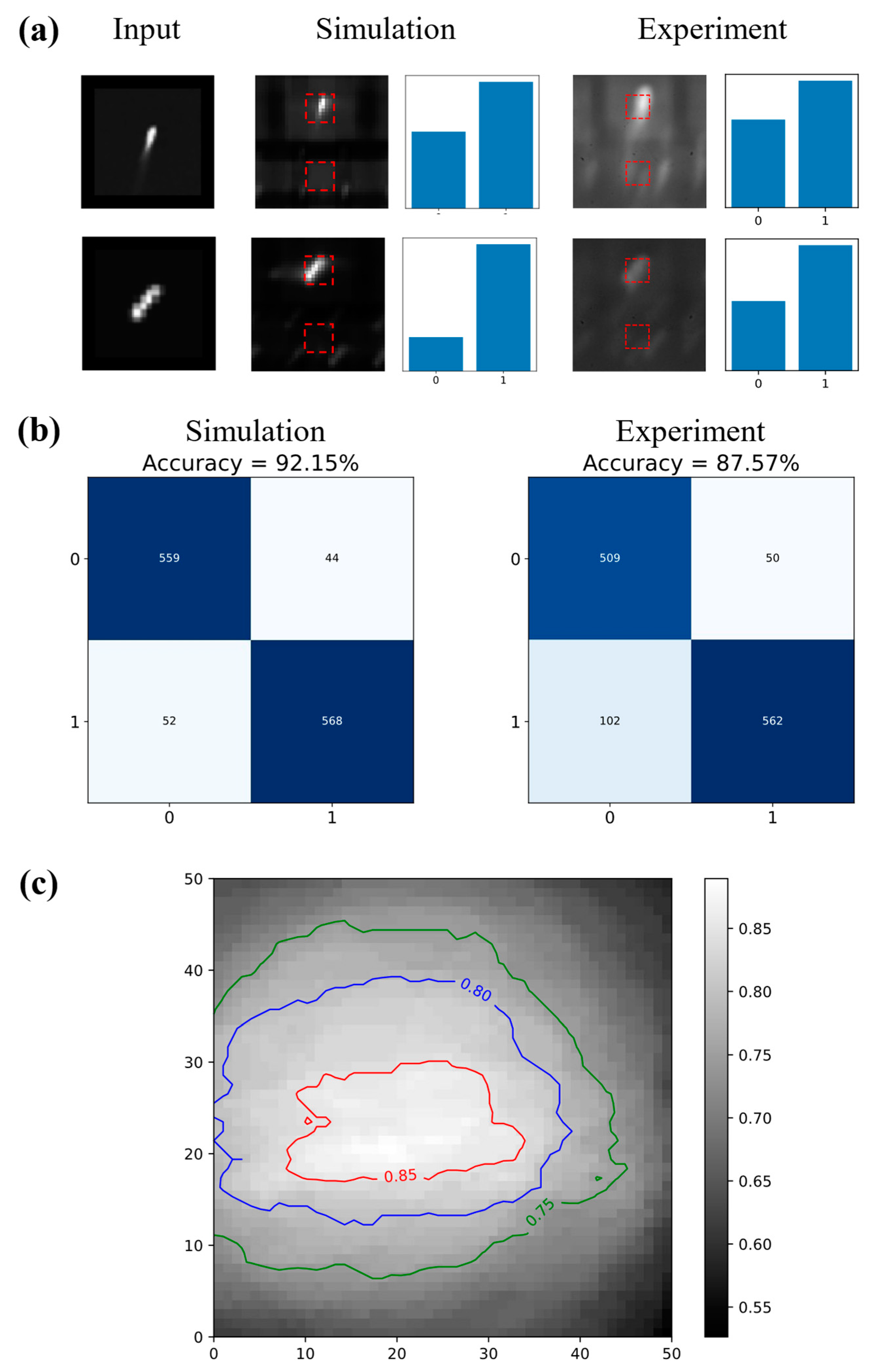
3.3. Experiment Result and Analysis
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Amani, M.; Ghorbanian, A.; Ahmadi, S.A.; Kakooei, M.; Moghimi, A.; Mirmazloumi, S.M.; Moghaddam, S.H.A.; Mahdavi, S.; Ghahremanloo, M.; Parsian, S. Google earth engine cloud computing platform for remote sensing big data applications: A comprehensive review. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 5326–5350. [Google Scholar] [CrossRef]
- Ye, B.; Tian, S.; Ge, J.; Sun, Y. Assessment of WorldView-3 Data for Lithological Mapping. Remote Sens. 2017, 9, 1132. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Chen, H.; Lou, S.; Wang, Q.; Huang, P.; Duan, H.; Hu, Y. Diffractive deep neural networks: Theories, optimization, and applications. Appl. Phys. Rev. 2024, 11, 021332. [Google Scholar] [CrossRef]
- Fu, T.; Zhang, J.; Sun, R.; Huang, Y.; Xu, W.; Yang, S.; Zhu, Z.; Chen, H. Optical neural networks: Progress and challenges. Light Sci. Appl. 2024, 13, 263. [Google Scholar] [CrossRef]
- Hu, J.; Mengu, D.; Tzarouchis, D.C.; Edwards, B.; Engheta, N.; Ozcan, A. Diffractive optical computing in free space. Nat. Commun. 2024, 15, 1525. [Google Scholar] [CrossRef]
- Yu, H.; Huang, Z.; Lamon, S.; Wang, B.; Ding, H.; Lin, J.; Wang, Q.; Luan, H.; Gu, M.; Zhang, Q. All-optical image transportation through a multimode fibre using a miniaturized diffractive neural network on the distal facet. Nat. Photonics 2025. [Google Scholar] [CrossRef]
- Chang, J.; Sitzmann, V.; Dun, X.; Heidrich, W.; Wetzstein, G. Hybrid optical-electronic convolutional neural networks with optimized diffractive optics for image classification. Sci. Rep. 2018, 8, 12324. [Google Scholar] [CrossRef]
- Lin, X.; Rivenson, Y.; Yardimci, N.T.; Veli, M.; Luo, Y.; Jarrahi, M.; Ozcan, A. All-optical machine learning using diffractive deep neural networks. Science 2018, 361, 1004–1008. [Google Scholar] [CrossRef]
- Dou, H.; Deng, Y.; Yan, T.; Wu, H.; Lin, X.; Dai, Q. Residual D2NN: Training diffractive deep neural networks via learnable light shortcuts. Opt. Lett. 2020, 45, 2688–2691. [Google Scholar] [CrossRef]
- Li, W.; Liu, X.; Zhang, W.; Ruan, N. The Application of Deep Learning in Space-Based Intelligent Optical Remote Sensing. Spacecr. Recovery Remote Sens. 2020, 41, 56–65. [Google Scholar]
- Liu, C.; Ma, Q.; Luo, Z.J.; Hong, Q.R.; Xiao, Q.; Zhang, H.C.; Miao, L.; Yu, W.M.; Cheng, Q.; Li, L.; et al. A programmable diffractive deep neural network based on a digital-coding metasurface array. Nat. Electron. 2022, 5, 113–122. [Google Scholar] [CrossRef]
- Wang, T.; Sohoni, M.M.; Wright, L.G.; Stein, M.M.; Ma, S.-Y.; Onodera, T.; Anderson, M.G.; McMahon, P.L. Image sensing with multilayer nonlinear optical neural networks. Nat. Photonics 2023, 17, 408–415. [Google Scholar] [CrossRef]
- Bai, B.; Yang, X.; Gan, T.; Li, J.; Mengu, D.; Jarrahi, M.; Ozcan, A. Pyramid diffractive optical networks for unidirectional image magnification and demagnification. Light Sci. Appl. 2024, 13, 178. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Shi, W.; Wu, S.; Wang, Y.; Yang, S.; Chen, H. Pre-sensor computing with compact multilayer optical neural network. Sci. Adv. 2024, 10, eado8516. [Google Scholar] [CrossRef]
- Li, J.; Li, Y.; Gan, T.; Shen, C.-Y.; Jarrahi, M.; Ozcan, A. All-optical complex field imaging using diffractive processors. Light Sci. Appl. 2024, 13, 120. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Ozcan, A. Nonlinear encoding in diffractive information processing using linear optical materials. Light Sci. Appl. 2024, 13, 173. [Google Scholar] [CrossRef]
- Xue, Z.; Zhou, T.; Xu, Z.; Yu, S.; Dai, Q.; Fang, L. Fully forward mode training for optical neural networks. Nature 2024, 632, 280–286. [Google Scholar] [CrossRef]
- Hamerly, R.; Bernstein, L.; Sludds, A.; Soljacic, M.; Englund, D. Large-Scale Optical Neural Networks Based on Photoelectric Multiplication. Phys. Rev. X 2019, 9, 021032. [Google Scholar] [CrossRef]
- Wang, Q.; Yu, H.; Huang, Z.; Gu, M.; Zhang, Q. Two-photon nanolithography of micrometer scale diffractive neural network with cubical diffraction neurons at the visible wavelength. Chin. Opt. Lett. 2024, 22, 102201. [Google Scholar] [CrossRef]
- Plöschner, M.; Tyc, T.; Čižmár, T. Seeing through chaos in multimode fibres. Nat. Photonics 2015, 9, 529–535. [Google Scholar] [CrossRef]
- Yildirim, M.; Dinc, N.U.; Oguz, I.; Psaltis, D.; Moser, C. Nonlinear processing with linear optics. Nat. Photonics 2024, 18, 1076–1082. [Google Scholar] [CrossRef]
- Li, Y.; Luo, Y.; Mengu, D.; Bai, B.; Ozcan, A. Quantitative phase imaging (QPI) through random diffusers using a diffractive optical network. arXiv 2023, arXiv:2301.07908. [Google Scholar]
- Liu, Z.; Wang, L.; Meng, Y.; He, T.; He, S.; Yang, Y.; Wang, L.; Tian, J.; Li, D.; Yan, P. All-fiber high-speed image detection enabled by deep learning. Nat. Commun. 2022, 13, 1433. [Google Scholar] [CrossRef] [PubMed]
- Lu, K.; Chen, Z.; Chen, H.; Zhou, W.; Zhang, Z.; Tsang, H.K.; Tong, Y. Empowering high-dimensional optical fiber communications with integrated photonic processors. Nat. Commun. 2024, 15, 3515. [Google Scholar] [CrossRef]
- Xu, X.; Tan, M.; Corcoran, B.; Wu, J.; Boes, A.; Nguyen, T.G.; Chu, S.T.; Little, B.E.; Hicks, D.G.; Morandotti, R.; et al. 11 TOPS photonic convolutional accelerator for optical neural networks. Nature 2021, 589, 44–51. [Google Scholar] [CrossRef]
- Wang, T.; Ma, S.-Y.; Wright, L.G.; Onodera, T.; Richard, B.C.; McMahon, P.L. An optical neural network using less than 1 photon per multiplication. Nat. Commun. 2022, 13, 123. [Google Scholar] [CrossRef]
- Zheng, M.; Shi, L.; Zi, J. Optimize performance of a diffractive neural network by controlling the Fresnel number. Photonics Res. 2022, 10, 2667–2676. [Google Scholar] [CrossRef]
- Zhu, H.H.; Zou, J.; Zhang, H.; Shi, Y.Z.; Luo, S.B.; Wang, N.; Cai, H.; Wan, L.X.; Wang, B.; Jiang, X.D.; et al. Space-efficient optical computing with an integrated chip diffractive neural network. Nat. Commun. 2022, 13, 123. [Google Scholar] [CrossRef]
- Chen, Y.; Nazhamaiti, M.; Xu, H.; Meng, Y.; Zhou, T.; Li, G.; Fan, J.; Wei, Q.; Wu, J.; Qiao, F.; et al. All-analog photoelectronic chip for high-speed vision tasks. Nature 2023, 623, 48–57. [Google Scholar] [CrossRef]
- Cheng, J.; Huang, C.; Zhang, J.; Wu, B.; Zhang, W.; Liu, X.; Zhang, J.; Tang, Y.; Zhou, H.; Zhang, Q. Multimodal deep learning using on-chip diffractive optics with in situ training capability. Nat. Commun. 2024, 15, 6189. [Google Scholar] [CrossRef]
- Dai, T.; Ma, A.; Mao, J.; Ao, Y.; Jia, X.; Zheng, Y.; Zhai, C.; Yang, Y.; Li, Z.; Tang, B. A programmable topological photonic chip. Nat. Mater. 2024, 23, 928–936. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Liu, W.; Wang, F.; Peng, X.; Choi, D.-Y.; Cheng, H.; Cai, Y.; Chen, S. Ultra-robust informational metasurfaces based on spatial coherence structures engineering. Light Sci. Appl. 2024, 13, 131. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Hu, J.; Morandi, A.; Nardi, A.; Xia, F.; Li, X.; Savo, R.; Liu, Q.; Grange, R.; Gigan, S. Large-scale photonic computing with nonlinear disordered media. Nat. Comput. Sci. 2024, 4, 429–439. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Z.; Wang, H.; Liu, Q.; Fu, X. Photonic diffractive generators through sampling noises from scattering media. Nat. Commun. 2024, 15, 10643. [Google Scholar] [CrossRef]
- Cui, K.; Rao, S.; Xu, S.; Huang, Y.; Cai, X.; Huang, Z.; Wang, Y.; Feng, X.; Liu, F.; Zhang, W. Spectral convolutional neural network chip for in-sensor edge computing of incoherent natural light. Nat. Commun. 2025, 16, 81. [Google Scholar] [CrossRef]
- Fei, Y.; Sui, X.; Gu, G.; Chen, Q. Zero-power optical convolutional neural network using incoherent light. Opt. Lasers Eng. 2023, 162, 107410. [Google Scholar] [CrossRef]
- Kleiner, M.; Michaeli, L.; Michaeli, T. Coherence Awareness in Diffractive Neural Networks. In Proceedings of the CLEO 2024, Charlotte, NC, USA, 5 May 2024; p. FW4Q.5. [Google Scholar]
- Rahman, M.S.S.; Yang, X.; Li, J.; Bai, B.; Ozcan, A. Universal linear intensity transformations using spatially incoherent diffractive processors. Light Sci. Appl. 2023, 12, 195. [Google Scholar] [CrossRef]
- Rahman, M.S.S.; Gan, T.; Deger, E.A.; Işıl, Ç.; Jarrahi, M.; Ozcan, A. Learning diffractive optical communication around arbitrary opaque occlusions. Nat. Commun. 2023, 14, 6830. [Google Scholar] [CrossRef]
- Chen, R.; Ma, Y.; Zhang, C.; Xu, W.; Wang, Z.; Sun, S. All-optical perception based on partially coherent optical neural networks. Opt. Express 2025, 33, 1609–1624. [Google Scholar] [CrossRef]
- van Cittert, P.H.J.P. Die wahrscheinliche Schwingungsverteilung in einer von einer Lichtquelle direkt oder mittels einer Linse beleuchteten Ebene. Physica 1934, 1, 201–210. [Google Scholar] [CrossRef]
- Zernike, F. The concept of degree of coherence and its application to optical problems. Physica 1938, 5, 785–795. [Google Scholar] [CrossRef]
- Wolf, E. New theory of partial coherence in the space-frequency domain. Part II: Steady-state fields and higher-order correlations. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 1986, 3, 76–85. [Google Scholar] [CrossRef]
- Yan, T.; Wu, J.; Zhou, T.; Xie, H.; Xu, F.; Fan, J.; Fang, L.; Lin, X.; Dai, Q. Fourier-space Diffractive Deep Neural Network. Phys. Rev. Lett. 2019, 123, 023901. [Google Scholar] [CrossRef] [PubMed]
- Liao, K.; Chen, Y.; Yu, Z.; Hu, X.; Wang, X.; Lu, C.; Lin, H.; Du, Q.; Hu, J.; Gong, Q. All-optical computing based on convolutional neural networks. Opto-Electron. Adv. 2021, 4, 200060. [Google Scholar] [CrossRef]
- Wolf, E. Unified theory of coherence and polarization of random electromagnetic beams. Phys. Lett. A 2003, 312, 263–267. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Ma, Y.; Wang, Z.; Sun, S. Incoherent Optical Neural Networks for Passive and Delay-Free Inference in Natural Light. Photonics 2025, 12, 278. https://doi.org/10.3390/photonics12030278
Chen R, Ma Y, Wang Z, Sun S. Incoherent Optical Neural Networks for Passive and Delay-Free Inference in Natural Light. Photonics. 2025; 12(3):278. https://doi.org/10.3390/photonics12030278
Chicago/Turabian StyleChen, Rui, Yijun Ma, Zhong Wang, and Shengli Sun. 2025. "Incoherent Optical Neural Networks for Passive and Delay-Free Inference in Natural Light" Photonics 12, no. 3: 278. https://doi.org/10.3390/photonics12030278
APA StyleChen, R., Ma, Y., Wang, Z., & Sun, S. (2025). Incoherent Optical Neural Networks for Passive and Delay-Free Inference in Natural Light. Photonics, 12(3), 278. https://doi.org/10.3390/photonics12030278



