0.4 THz Broadband Terahertz Noise Source Based on Photoconductive Antennas
Abstract
:1. Introduction
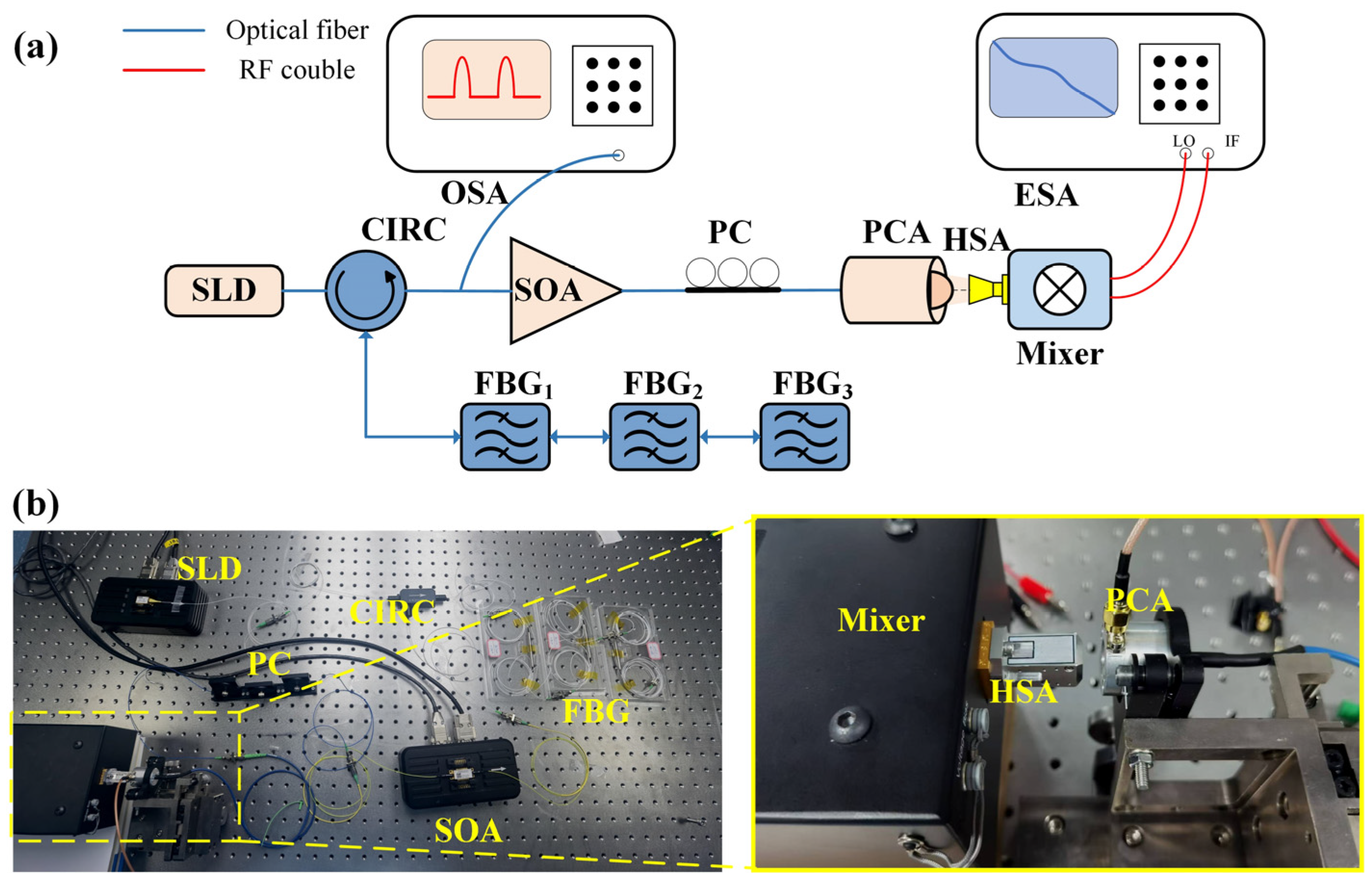
2. Diagram of Experimental and Theoretical Principle
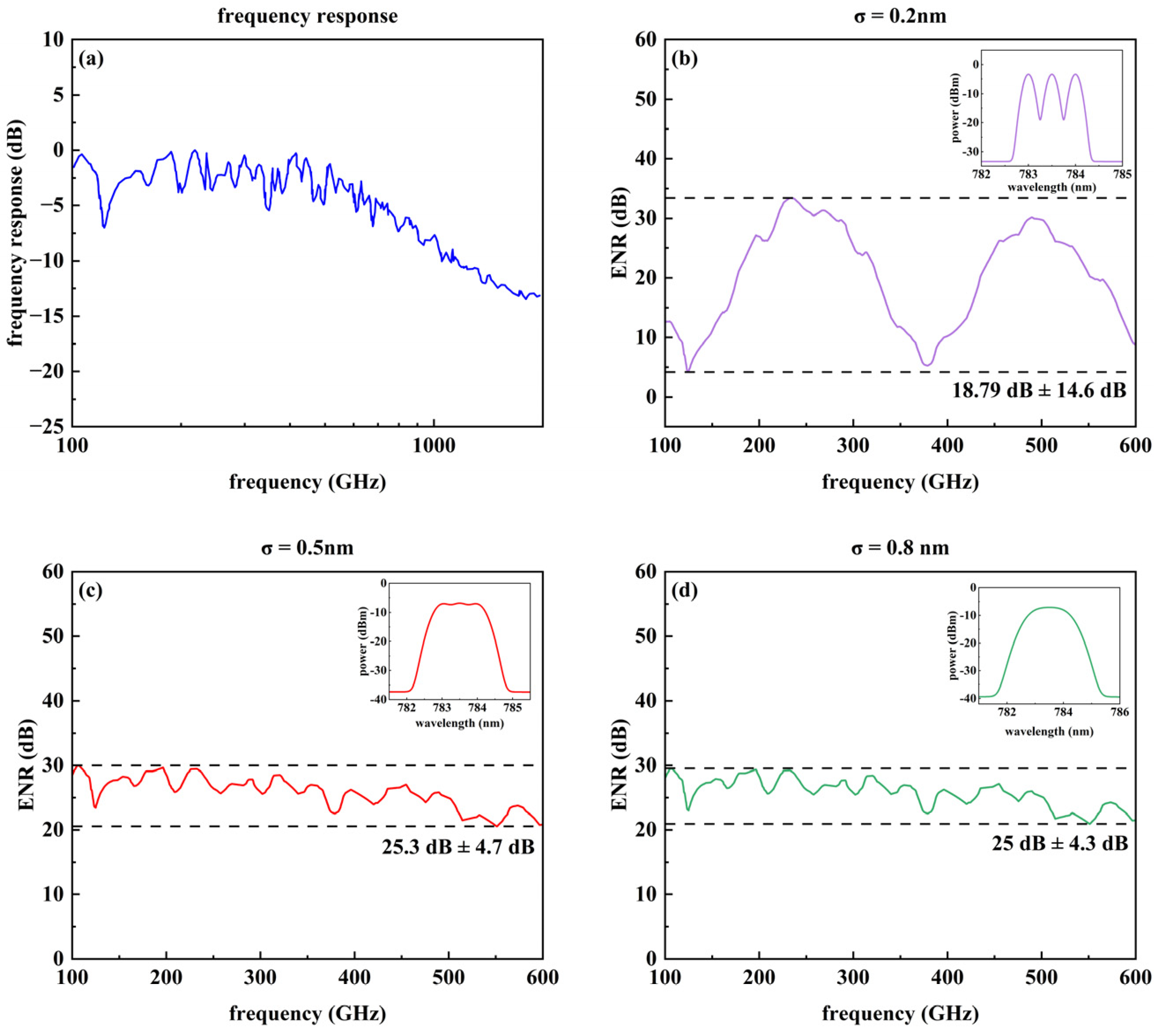
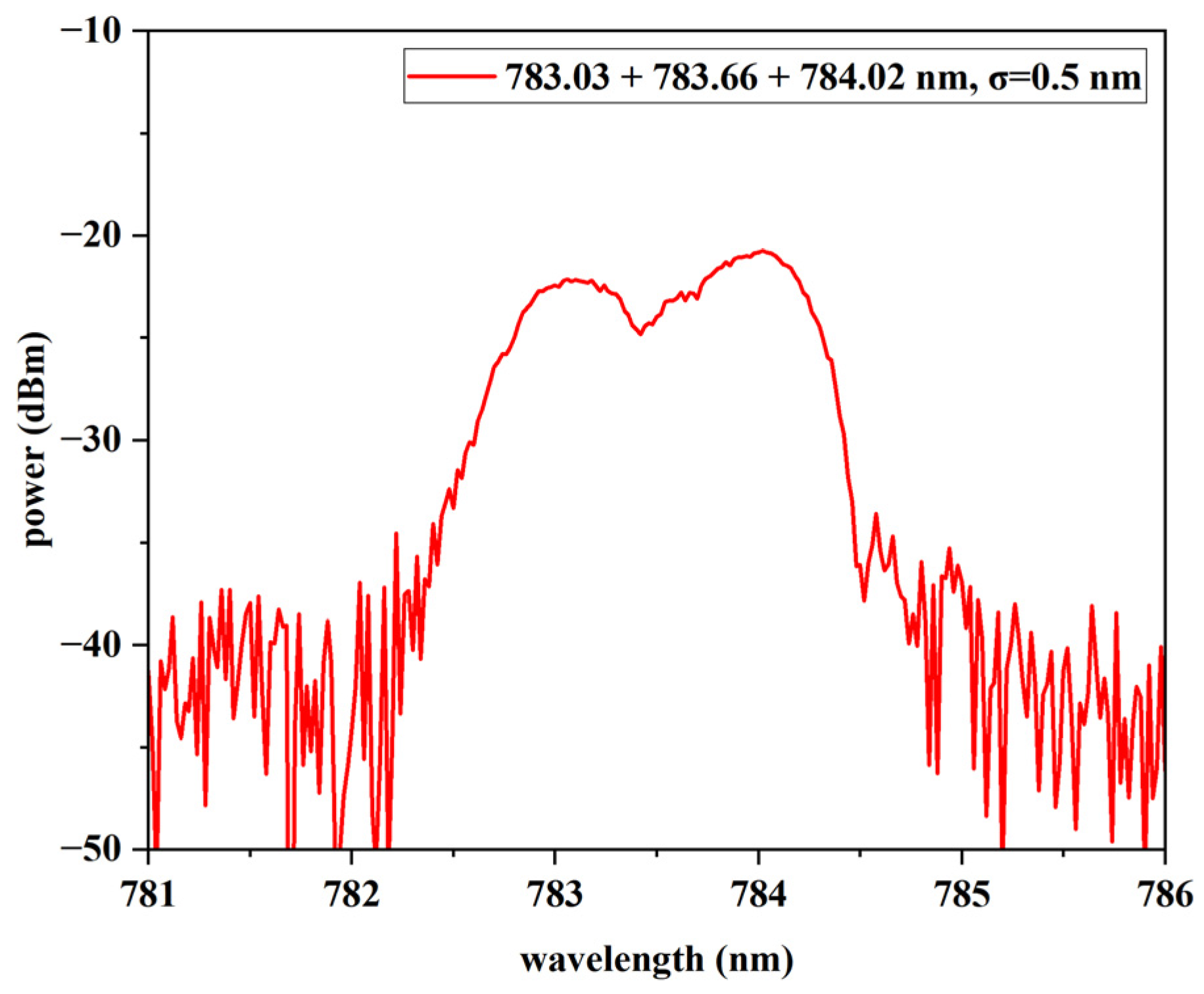
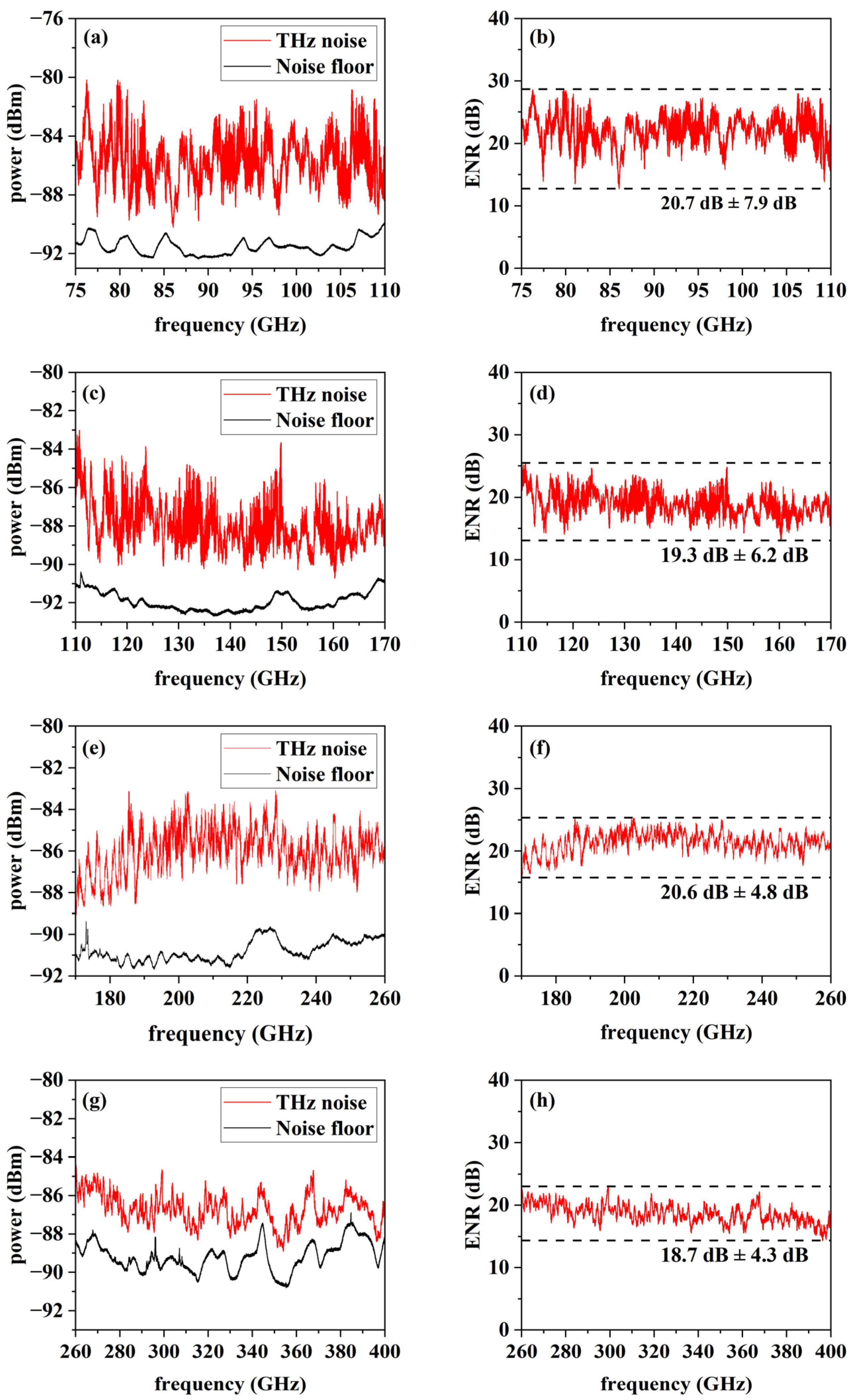
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Fattinger, C.; Grischkowsky, D. Terahertz beams. Appl. Phys. Lett. 1989, 54, 490–492. [Google Scholar] [CrossRef]
- Brown, S.T.; Desai, S.; Wenwen, L.; Tanner, A.B. On the Long-Term Stability of Microwave Radiometers Using Noise Diodes for Calibration. IEEE Trans. Geosci. Remote Sens. 2007, 45, 1908–1920. [Google Scholar] [CrossRef]
- Porranzl, M.; Wagner, C.; Jaeger, H.; Stelzer, A. On-Wafer Noise Characterization of an Automotive Monostatic Radar Transceiver with Self-Interference Evaluation. IEEE Trans. Microw. Theory Tech. 2019, 67, 3494–3505. [Google Scholar] [CrossRef]
- Diebold, S.; Weissbrodt, E.; Massler, H.; Leuther, A.; Tessmann, A.; Kallfass, I. A W-band monolithic integrated active hot and cold noise source. IEEE Trans. Microw. Theory Tech. 2014, 62, 623–630. [Google Scholar] [CrossRef]
- Azevedo Goncalves, J.C.; Ghanem, H.; Bouvot, S.; Gloria, D.; Lepilliet, S.; Ducournau, G.; Gaquiere, C.; Danneville, F. Millimeter-Wave Noise Source Development on SiGe BiCMOS 55-nm Technology for Applications up to 260 GHz. IEEE Trans. Microw. Theory Tech. 2019, 67, 3732–3742. [Google Scholar] [CrossRef]
- Alawar, M.; Fiorese, V.; Lépilliet, S.; Gloria, D.; Ducournau, G.; Dubois, E. A G-Band Glass Interposer Technology for the Integration of an Amplified Noise Source based on SiGe BiCMOS 55-nm Technology. In Proceedings of the 2024 IEEE Radio Frequency Integrated Circuits Symposium (RFIC), Washington, DC, USA, 16–18 June 2024; pp. 31–34. [Google Scholar]
- Ghanem, H.; Azevedo Goncalves, J.C.; Chevalier, P.; Alaji, I.; Aouimeur, W.; Lepilliet, S. Modeling and Analysis of a Broadband Schottky Diode Noise Source up to 325 GHz Based on 55-nm SiGe BiCMOS Technology. IEEE Trans. Microw. Theory Tech. 2020, 68, 2268–2277. [Google Scholar] [CrossRef]
- Song, H.J.; Shimizu, N.; Furuta, T.; Wakatsuki, A.; Nagatsuma, T. Subterahertz noise signal generation using a photodetector and wavelength-sliced optical noise signals for spectroscopic measurements. Appl. Phys. Lett. 2008, 93, 241113. [Google Scholar] [CrossRef]
- Sun, Y.H.; Chen, Y.X.; Li, P.; Zinsou, R.; Wang, A.B.; Wang, Y.C. Flat Millimeter-Wave Noise Generation by Optically Mixing Multiple Wavelength-Sliced ASE Lights. IEEE Photonics Technol. Lett. 2021, 33, 1270–1273. [Google Scholar] [CrossRef]
- Liu, J.B.; Liu, W.J.; Sun, Y.H.; Guo, Y.; Zhang, Y.W.; Xu, L.M.; Wang, Y.C. Generation of broadband flat millimeter-wave white noise using rectangular ASE slices mixing. Opt. Commun. 2022, 530, 129106. [Google Scholar] [CrossRef]
- Chen, T.X.; Liu, W.J.; Tao, X.Y.; Lu, D.; Sun, Y.H.; Liu, J.B.; Jia, Z.W.; Wang, Y.C. Millimeter-wave noise generation based on a monolithically integrated dual-mode chaotic laser. Opt. Lett. 2023, 48, 4649–4652. [Google Scholar] [CrossRef] [PubMed]
- Molter, D.; Kolano, M.; Freymann, G.V. Terahertz Cross-Correlation Spectroscopy Driven by Incoherent Light from a Superluminescent Diode. Opt. Express 2019, 27, 12659–12665. [Google Scholar] [CrossRef] [PubMed]
- Bai, Z.C.; Liu, X.; Ding, J.; Cui, H.L.; Su, B.; Zhang, C.L. Terahertz Generation and Detection of 1550-nm-Excited LT-GaAs Photoconductive Antennas. J. Mod. Opt. 2021, 68, 824–829. [Google Scholar] [CrossRef]
- Taghinejad, M.; Xia, C.Y.; Hrton, M.; Lee, K.; Kim, A.; Li, Q.; Guzelturk, B.; Kalousek, R.; Xu, F.; Cai, W.S.; et al. Terahertz radiation of plasmonic hot carriers. In Proceedings of the Photonic and Phononic Properties of Engineered Nanostructures XIV, San Francisco, CA, USA, 29 January–1 February 2024; p. 1289602. [Google Scholar]
- Burford, N.M.; El-Shenawee, M.O. Review of terahertz photoconductive antenna technology. Opt. Eng. 2017, 56, 010901. [Google Scholar] [CrossRef]
- Preu, S.; Döhler, G.H.; Malzer, S.; Wang, L.J.; Gossard, A.C. Tunable, continuous-wave Terahertz photomixer sources and applications. J. Appl. Phys. 2011, 109, 061301. [Google Scholar] [CrossRef]
- Kuwashima, F.; Jarrahi, M.; Cakmakyapan, S.; Morikawa, O.; Shirao, T.; Iwao, K.; Kurihara, K.; Kitahara, H.; Furuya, T.; Wada, K.; et al. Evaluation of High-Stability Optical Beats in Laser Chaos by Plasmonic Photomixing. Opt. Express 2020, 28, 24833–24844. [Google Scholar] [CrossRef] [PubMed]
- Oeuvrard, S.; Lampin, J.F.; Ducournau, G.; Lepilliet, S.; Danneville, F. On wafer silicon integrated noise source characterization up to 110 GHz based on germanium-on-silicon photodiode. In Proceedings of the 2014 International Conference on Microelectronic Test Structures (ICMTS), Udine, Italy, 24–27 March 2014; pp. 150–154. [Google Scholar]
- Gregory, I.S.; Baker, C.; Tribe, W.R.; Bradley, I.V.; Evans, M.J.; Linfield, E.H.; Davies, A.G.; Missous, M. Optimization of photomixers and antennas for continuous-wave terahertz emission. IEEE J. Quantum Electron. 2005, 41, 717–728. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, Z.; Zhang, Y.; Zhang, S.; Duan, X.; Li, Y. Design and Implementation of 50GHz-110GHz Ultra-Broadband Noise Source. In Proceedings of the 2022 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Harbin, China, 12–15 August 2022; pp. 1–3. [Google Scholar]
- Ghanem, H.; Lepilliet, S.; Danneville, F.; Ducournau, G. 300-GHz Intermodulation/Noise Characterization Enabled by a Single THz Photonics Source. IEEE Microw. Wirel. Compon. Lett. 2020, 30, 1013–1016. [Google Scholar] [CrossRef]
- Taghinejad, M.; Xia, C.Y.; Hrton, M.; Lee, K.; Kim, A.; Li, Q.; Guzelturk, B.; Kalousek, R.; Xu, F.; Cai, W.S.; et al. Determining hot-carrier transport dynamics from terahertz emission. Science 2023, 382, 299–305. [Google Scholar] [CrossRef] [PubMed]

| Year | Generating Technology | Device | Frequency (GHz) | ENR (dB) | Flatness (dB) | Ref |
|---|---|---|---|---|---|---|
| 2022 | Electronics | GaAs Schottky Diodes | 50~110 | 7~19 | ±6 | [20] |
| 2024 | Electronics | Si Schottky Diodes | 140~170 | 20~24 | ±2 | [6] |
| 2014 | Photonics | GeHSPD | 75~110 | 35 | ±3 | [18] |
| 2020 | Photonics | UTC-PD | 260~320 | 28 | ±2.5 | [21] |
| 2023 | Photonics | UTC-PD | 237~281 | 47 | - | [11] |
| 2022 | Photonic mixing | UTC-PD | 130~170 | - | ±1.75 | [10] |
| 2025 | Photonic mixing | PCA | 75~400 | 18.7~20.7 | ±7.9 | This work |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.; Qin, F.; Liu, L.; Zhao, Z.; Li, P.; Sun, Y.; Liu, W.; Wang, Y. 0.4 THz Broadband Terahertz Noise Source Based on Photoconductive Antennas. Photonics 2025, 12, 252. https://doi.org/10.3390/photonics12030252
Chen Y, Qin F, Liu L, Zhao Z, Li P, Sun Y, Liu W, Wang Y. 0.4 THz Broadband Terahertz Noise Source Based on Photoconductive Antennas. Photonics. 2025; 12(3):252. https://doi.org/10.3390/photonics12030252
Chicago/Turabian StyleChen, Yinwei, Feifei Qin, Lijuan Liu, Zeyu Zhao, Pu Li, Yuehui Sun, Wenjie Liu, and Yuncai Wang. 2025. "0.4 THz Broadband Terahertz Noise Source Based on Photoconductive Antennas" Photonics 12, no. 3: 252. https://doi.org/10.3390/photonics12030252
APA StyleChen, Y., Qin, F., Liu, L., Zhao, Z., Li, P., Sun, Y., Liu, W., & Wang, Y. (2025). 0.4 THz Broadband Terahertz Noise Source Based on Photoconductive Antennas. Photonics, 12(3), 252. https://doi.org/10.3390/photonics12030252





