Design of an Aperiodic Optical Phased Array Based on the Multi-Strategy Enhanced Particle Swarm Optimization Algorithm
Abstract
1. Introduction
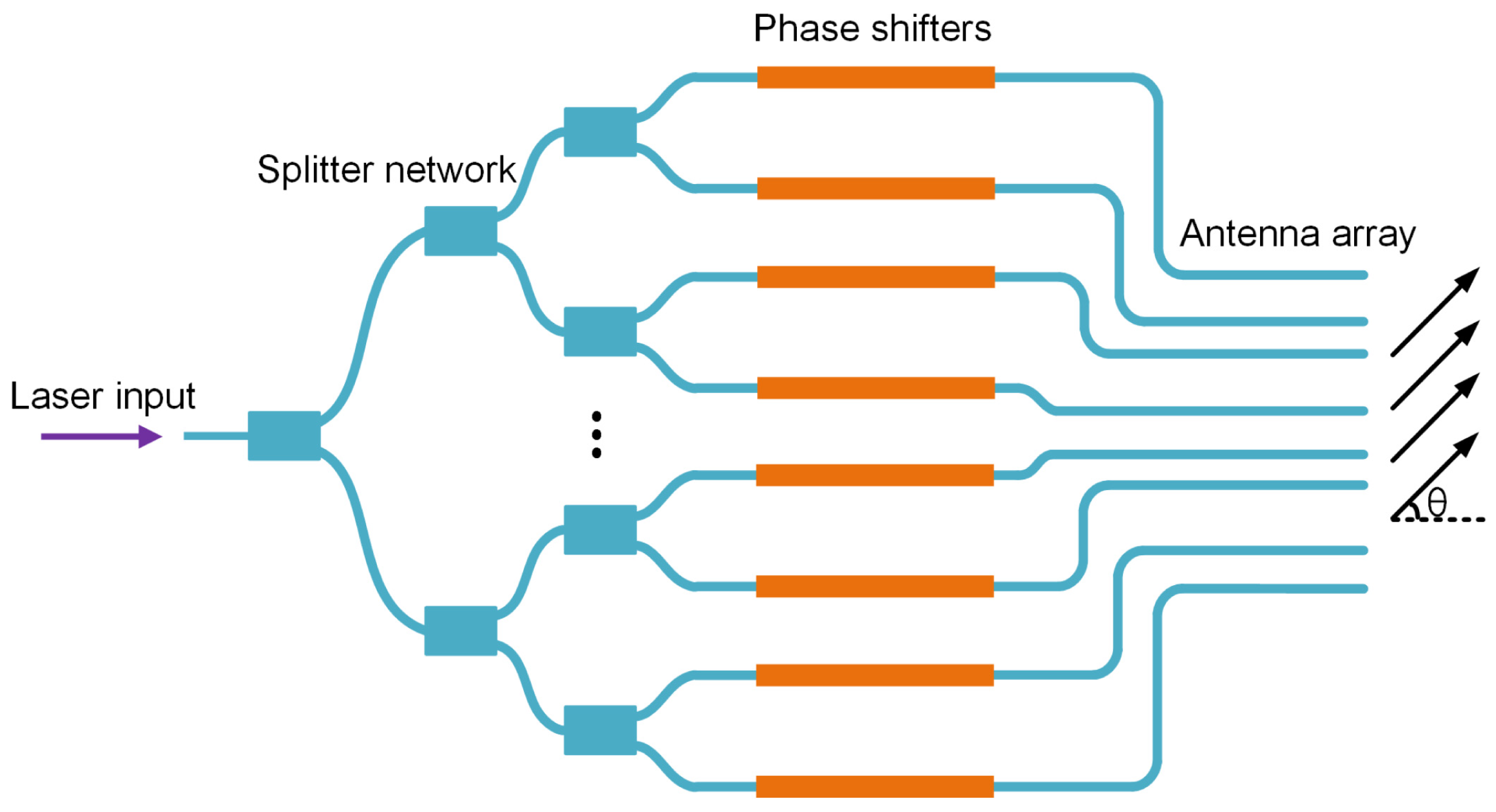
2. Principle of the Aperiodic OPA
3. Aperiodic Antenna Array Optimization
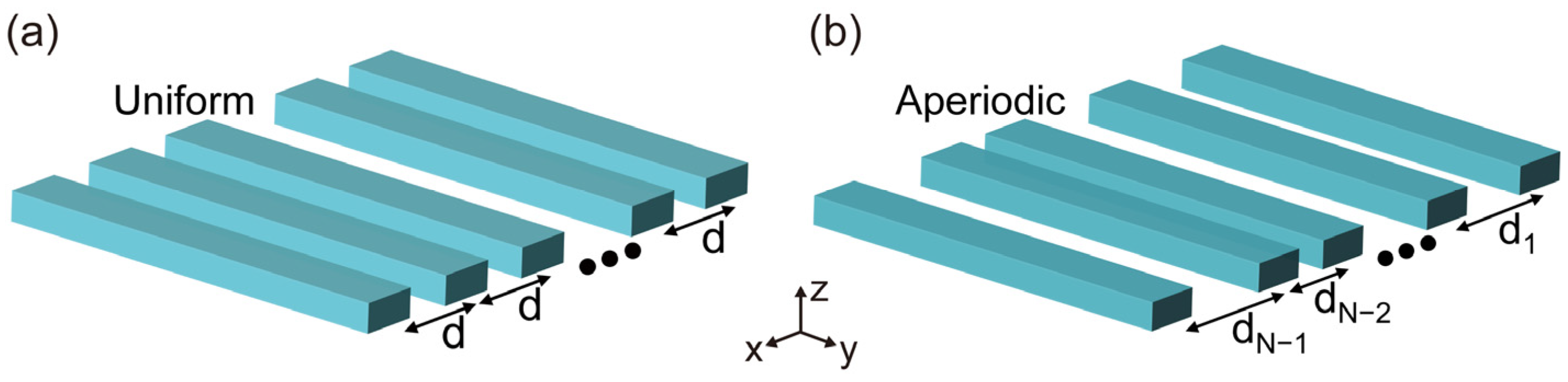
3.1. Principle of Spacing Distribution Optimization
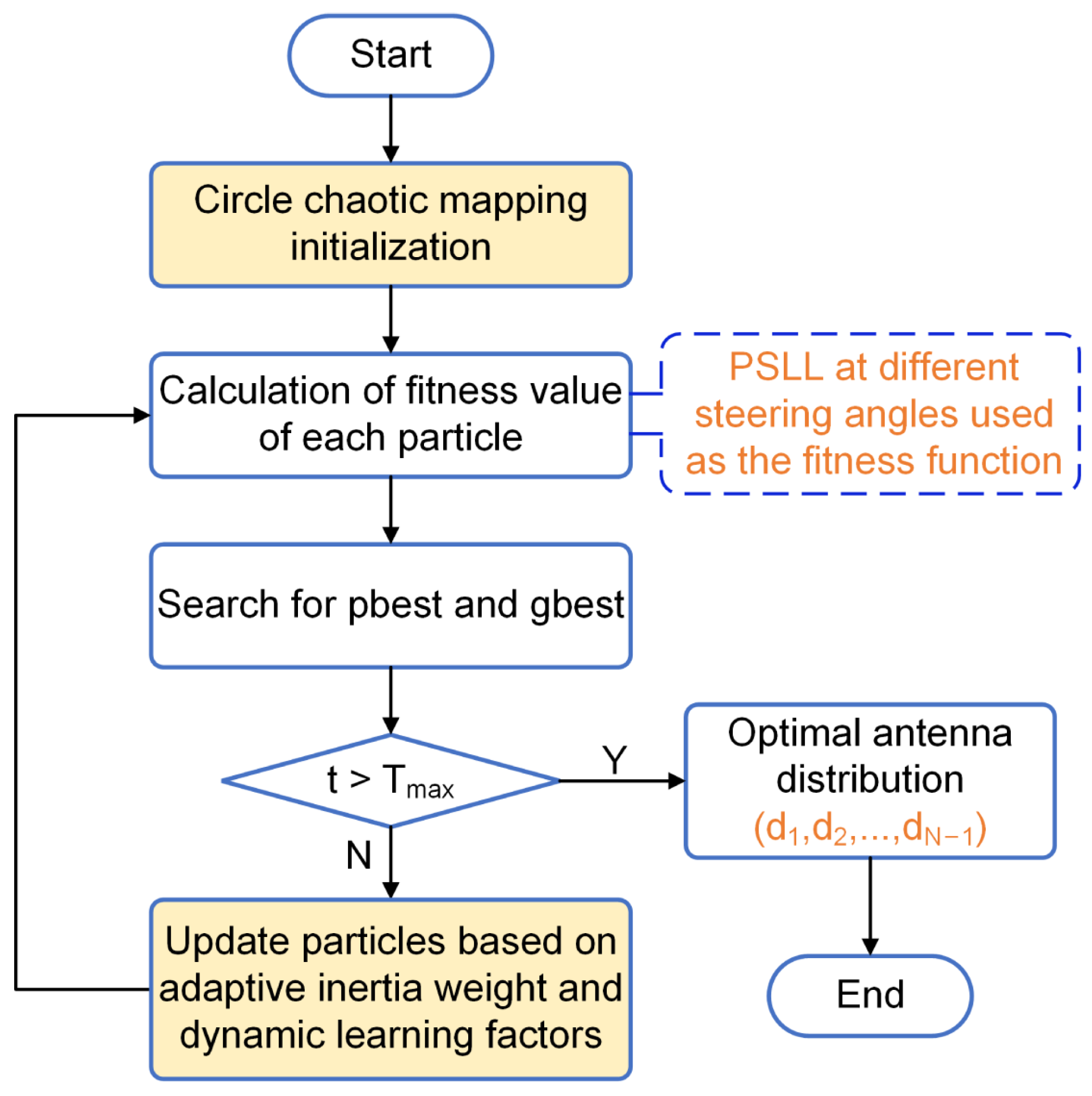
3.2. Algorithm Optimization Process
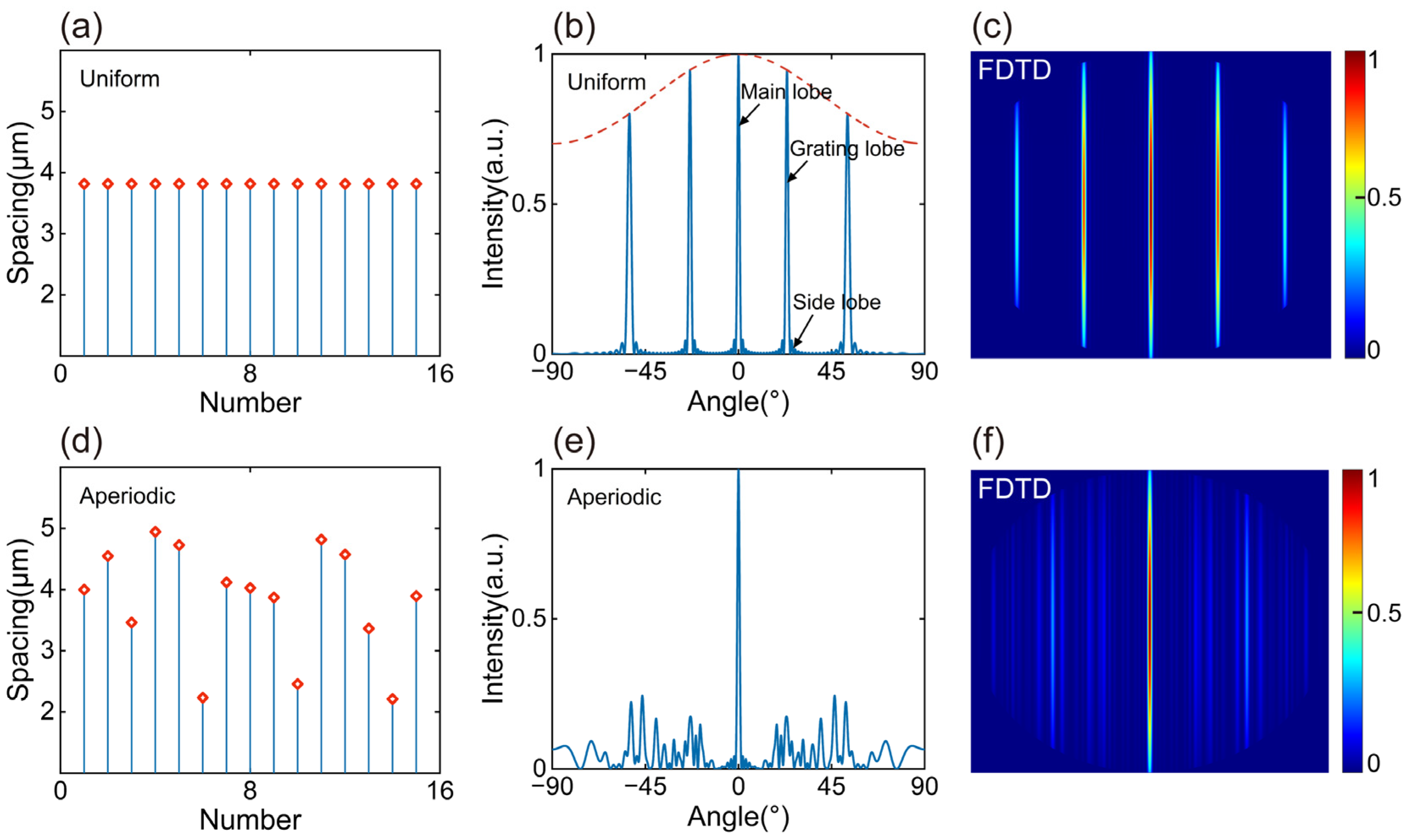
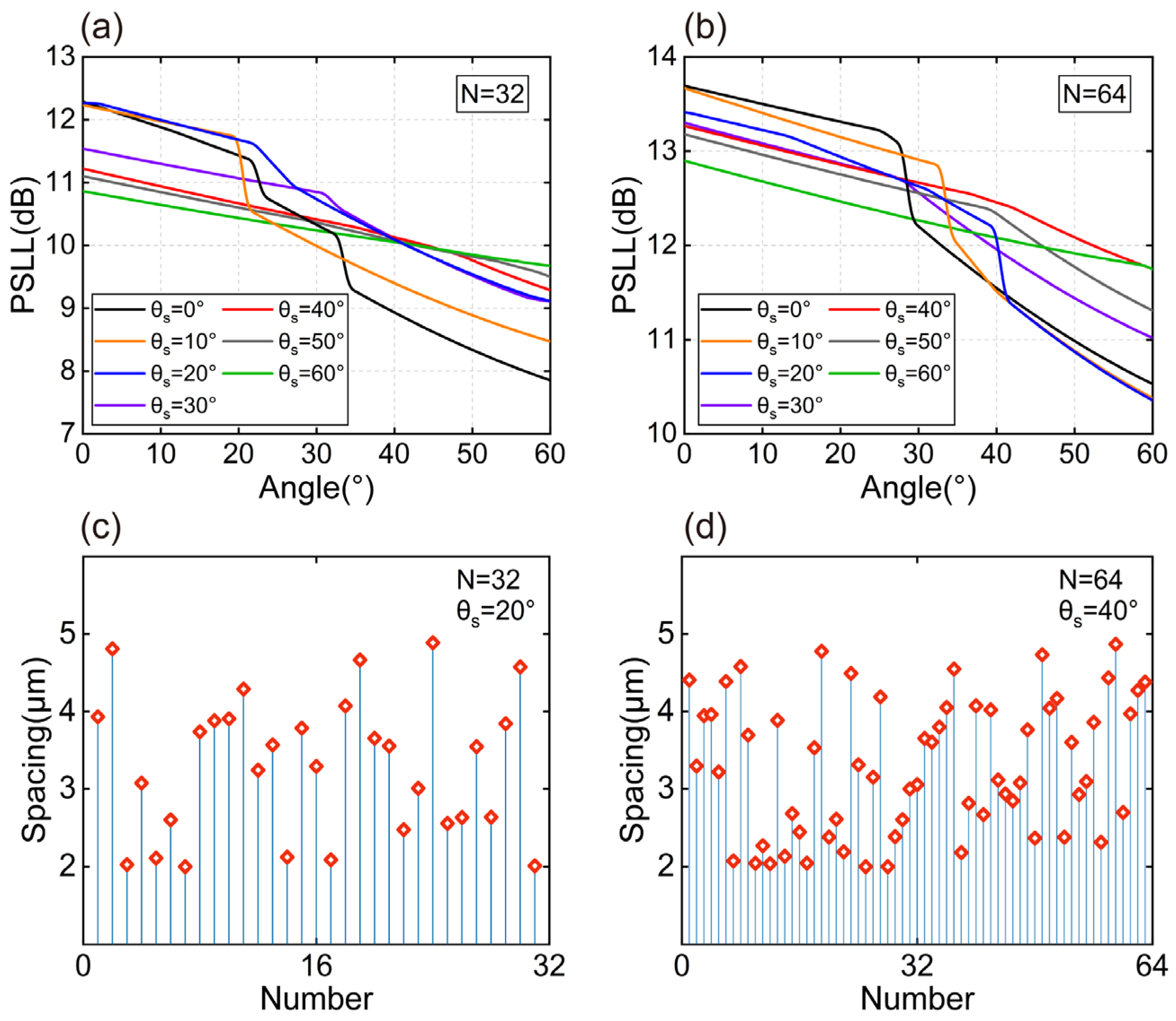
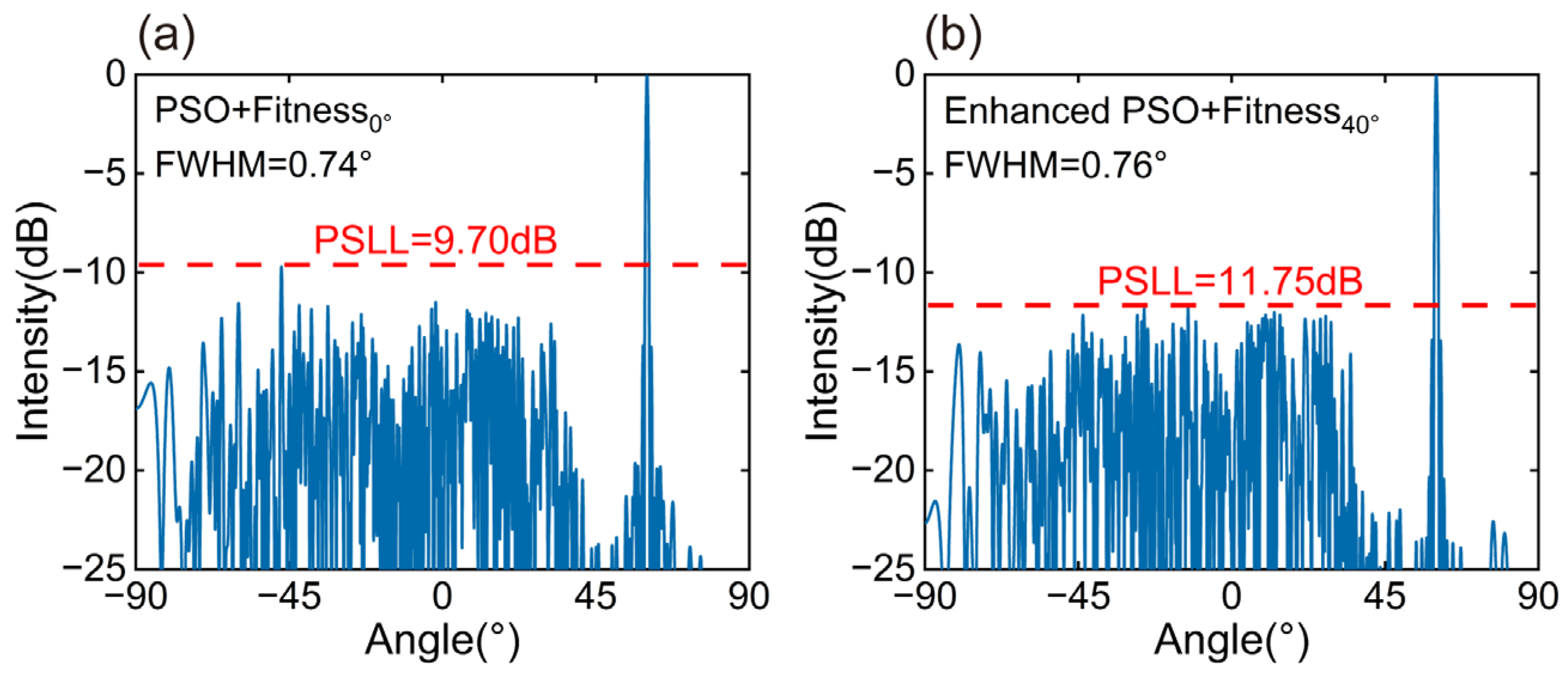
3.3. Optimization Results
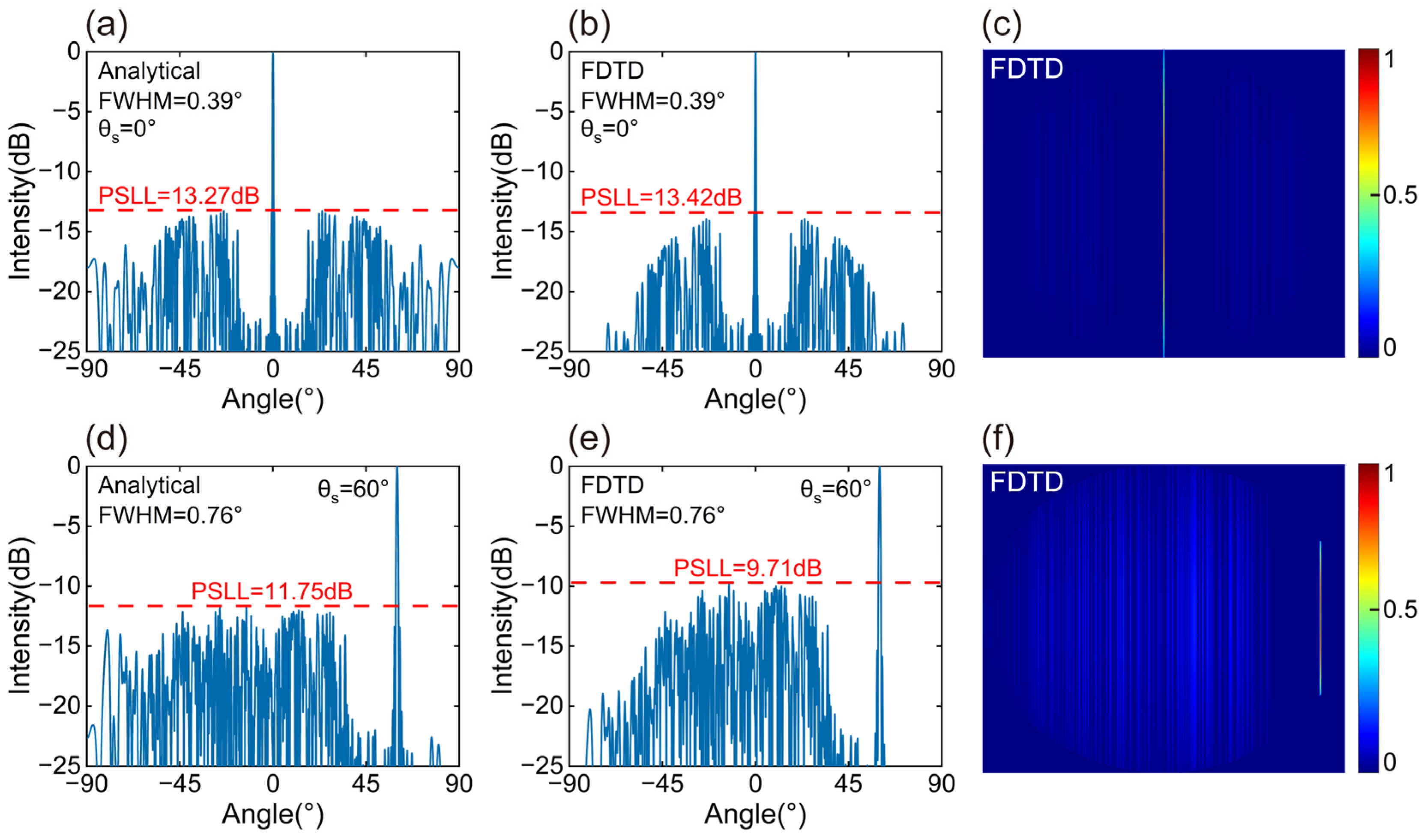
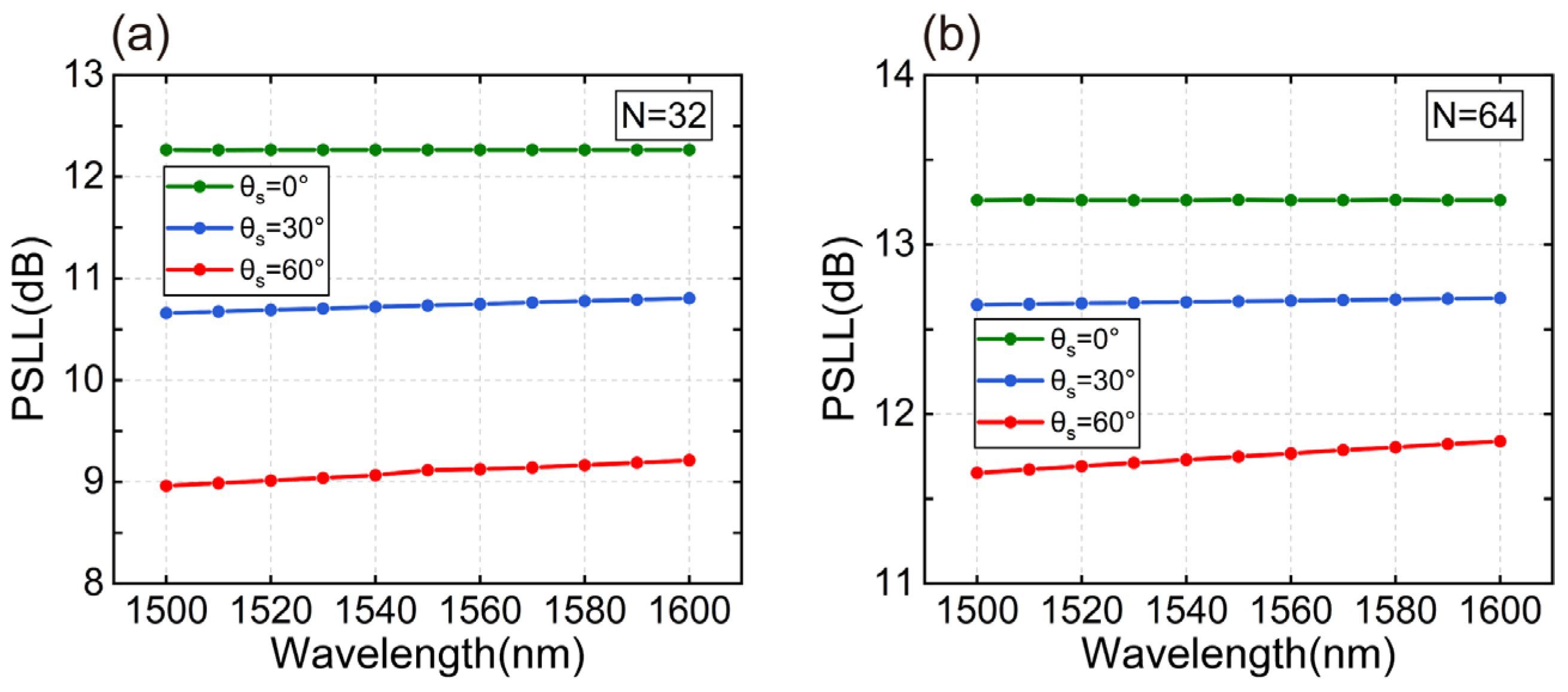
4. Error Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xie, W.; Komljenovic, T.; Huang, J.; Tran, M.; Davenport, M.; Torres, A.; Pintus, P.; Bowers, J. Heterogeneous silicon photonics sensing for autonomous cars [Invited]. Opt. Express 2019, 27, 3642–3663. [Google Scholar] [CrossRef]
- Zhuang, D.; Zhang, L.; Han, X.; Li, Y.; Li, Y.; Liu, X.; Gao, F.; Song, J. Omnidirectional beam steering using aperiodic optical phased array with high error margin. Opt. Express 2018, 26, 19154–19170. [Google Scholar] [CrossRef] [PubMed]
- Yi, Y.; Wu, D.; Kakdarvishi, V.; Yu, B.; Zhuang, Y.; Khalilian, A. Photonic integrated circuits for an optical phased array. Opt. Express 2024, 11, 243. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Zhao, Z.; Yan, P. Multi-beam steering with low grating lobes using optimized unequally spaced phased array. Opt. Commun. 2018, 427, 48–53. [Google Scholar] [CrossRef]
- Wang, Z.; Ma, P.; Yang, Y.; Cui, L.; Yu, L.; Luo, G.; Wang, P.; Pan, J.; Su, Y.; Zhang, Y. Non-uniform optical phased array with a large steering angle and high side mode suppression ratio. Appl. Opt. 2022, 61, 10788–10793. [Google Scholar] [CrossRef]
- Raptakis, A.; Lymperakis, G.; Gounaridis, L.; Weigel, M.; Kleinert, M.; Tsokos, C.; Groumas, P.; Andrianopoulos, E.; Keil, N.; Avramopoulos, H.; et al. Sparse aperiodic optical phased arrays on polymer integration platform. IEEE Photonics Technol. Lett. 2024, 36, 469–472. [Google Scholar] [CrossRef]
- Elsheikh, O.E.; Swillam, M.A. Wide-angle non-uniform optical phased array using compact and efficient antenna design. Sci. Rep. 2024, 14, 3780. [Google Scholar] [CrossRef]
- Du, Y.; Qiu, Y.; Zheng, S.; Zhao, X.; Dong, Y.; Zhong, Q.; Hu, T. Non-uniform distributed silicon optical phased array for high directionality and a wide steering range. Appl. Opt. 2024, 63, 1522–1528. [Google Scholar] [CrossRef]
- Du, K.; Wang, R.; Guo, J.; Jiang, R.; Kan, D.; Zhang, Y. Design of a sparse array for a one-dimensional non-uniform optical phased array. J. Opt. Soc. Am. B 2022, 39, 1141–1146. [Google Scholar] [CrossRef]
- Ye, M.; Chen, Y.; Li, J.; Deng, Y.; Chen, J.; Zhang, W.; Li, Y.; Hu, K.; Xu, C.; Liu, L.; et al. Large steering range and low-loss integrated optical phased array with SiN-Si dual-layer non-uniform antenna. Opt. Express 2023, 31, 44564–44574. [Google Scholar] [CrossRef] [PubMed]
- Yang, B.; Chen, H.; Yang, S.; Chen, M. An improved aperiodic OPA design based on large antenna spacing. Opt. Commun. 2020, 475, 125852. [Google Scholar] [CrossRef]
- Wu, Y.; Shao, S.; Che, D. Fast and low grating lobe multi-beam steering with a subarray level unequally spaced optical phased array. J. Opt. Soc. Am. B 2021, 38, 3417–3424. [Google Scholar] [CrossRef]
- He, J.; Dong, T.; Xu, Y. Review of photonic integrated optical phased arrays for space optical communication. IEEE Access 2020, 8, 188284–188298. [Google Scholar] [CrossRef]
- Komljenovic, T.; Helkey, R.; Coldren, L.; Bowers, J.E. Sparse aperiodic arrays for optical beam forming and LIDAR. Opt. Express 2017, 25, 2511–2528. [Google Scholar] [CrossRef] [PubMed]
- He, X.; Dong, T.; He, J.; Xu, Y. A design approach of optical phased array with low side lobe level and wide angle steering range. Photonics 2021, 8, 63. [Google Scholar] [CrossRef]
- Wang, J.; Song, R.; Li, X.; Yue, W.; Cai, Y.; Wang, S.; Yu, M. Beam steering technology of optical phased array based on silicon photonic integrated chip. Micromachines 2024, 15, 322. [Google Scholar] [CrossRef] [PubMed]
- Tan, S.; Dai, X.; Lou, J.; Song, L.; Liu, C.; Gu, Y.; Chen, Q.; Jiang, C.; Yu, X.; Lu, Q.; et al. Low-power consumption InP-based optical phase arrays with non-uniformly spaced output waveguides. Opt. Express 2023, 31, 3199–3211. [Google Scholar] [CrossRef] [PubMed]
- Dong, T.; He, J.; He, X.; Xu, Y.; Zhou, J. Hybrid design approach of optical phased array with wide beam steering range and low side-lobe level. Opt. Lett. 2022, 47, 806–809. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Yu, L.; Yang, Y.; Ma, P.; Cui, L.; Luo, S.; Ji, Z.; Song, Z.; Su, Y.; Pan, J.; et al. Wide field of view optical phased array with a high-directionality antenna. Opt. Express 2023, 31, 21192–21199. [Google Scholar] [CrossRef]
- De Cea, M.; Ram, R.J. Critical evaluation of non-uniform optical phased arrays for real-world beam-steering applications. Opt. Express 2024, 32, 26561–26582. [Google Scholar] [CrossRef] [PubMed]
- Deng, W.; Zhao, H.; Zou, L.; Li, G.; Yang, X.; Wu, D. A novel collaborative optimization algorithm in solving complex optimization problems. Soft Comput. 2017, 21, 4387–4398. [Google Scholar] [CrossRef]
- Liu, T.; Meng, X. Hybrid strategy improved sparrow search algorithm in the field of intrusion detection. IEEE Access 2023, 11, 32134–32151. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, F.; Pan, S. Grating-lobe-suppressed optical phased array with optimized element distribution. Opt. Commun. 2018, 419, 47–52. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zang, Z.; Wu, J.; Huang, Q. Design of an Aperiodic Optical Phased Array Based on the Multi-Strategy Enhanced Particle Swarm Optimization Algorithm. Photonics 2025, 12, 210. https://doi.org/10.3390/photonics12030210
Zang Z, Wu J, Huang Q. Design of an Aperiodic Optical Phased Array Based on the Multi-Strategy Enhanced Particle Swarm Optimization Algorithm. Photonics. 2025; 12(3):210. https://doi.org/10.3390/photonics12030210
Chicago/Turabian StyleZang, Zhuangzhuang, Junjie Wu, and Qingzhong Huang. 2025. "Design of an Aperiodic Optical Phased Array Based on the Multi-Strategy Enhanced Particle Swarm Optimization Algorithm" Photonics 12, no. 3: 210. https://doi.org/10.3390/photonics12030210
APA StyleZang, Z., Wu, J., & Huang, Q. (2025). Design of an Aperiodic Optical Phased Array Based on the Multi-Strategy Enhanced Particle Swarm Optimization Algorithm. Photonics, 12(3), 210. https://doi.org/10.3390/photonics12030210




