Next Article in Journal
Laser Linewidth Measurement Using an FPGA-Based Delay Self-Homodyne System
Previous Article in Journal
Controllable Burst-Mode Nd3+:YAG/Cr4+:YAG Laser Pumped by 808 nm Polarization-Combined Laser Diodes
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Photonics
Volume 12
Issue 3
10.3390/photonics12030204
photonics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

Probing nS/nD Rydberg States via 6P3/2 Intermediate Level Using Electromagnetically Induced Transparency in 87Rb

by
Donghao Li
1,2,
Beining Xu
1,
Keyu Qin
1,
Xin Jia
1,
Changtao Zhao
1,
Yaoting Zhou
1 and
Zhongxiao Xu
1,2,*
1
State Key Laboratory of Quantum Optics Technologies and Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China
2
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China
*
Author to whom correspondence should be addressed.
Photonics 2025, 12(3), 204; https://doi.org/10.3390/photonics12030204
Submission received: 23 January 2025 / Revised: 15 February 2025 / Accepted: 25 February 2025 / Published: 26 February 2025
Browse Figures
Review Reports Versions Notes

Abstract

We perform precise measurements of the 87Rb Rydberg excitation spectrum by using electromagnetically induced transparency (EIT) in a ladder system. We utilize a two-photon excitation configuration with the probe and control lasers at 420 nm and 1013 nm, respectively. In this work, we employ 6 P 3 / 2 , F′ = 3 as an intermediate state to excite the high-lying Rydberg states of the n S and n D series, with principal quantum numbers ranging from n = 35 to n = 70 . To improve the signal-to-noise ratio (SNR) in this inverted level scheme ( λ p < λ c ), we apply a 100 kHz chopping to the control beam, which is followed by a demodulation operated with a lock-in amplifier. Additionally, we verify the ionization energies and determine the quantum defects for the n S and n D series, respectively. Our work offers a database for applications of large-scale quantum simulation and quantum computation with the 87Rb atom array.

1. Introduction

The array of neutral atoms emerges as an ideal platform for large-scale quantum computation and simulation [1,2,3,4,5], attributed to their reconfigurable geometries [6,7], single-atom addressability [8], and arbitrary connectivity [9]. Central to this system is the excitation of Rydberg states [10]. Rydberg atoms, being in a highly excited state, exhibit a significant increase in atomic electric dipole moment, leading to long-range interactions that can extend over micrometer scales. This provides a powerful tool for implementing two-qubit entangled gates in quantum circuits [11,12,13] and exploring interacting many-body dynamics [14,15,16] and quantum phase [17].
Conventionally, a two-photon excitation associated with transitions 5 S 1 / 2 → 5 P 3 / 2 → n S / n D is applied to prepare the Rydberg states of 87Rb atoms, wherein lasers at 780 nm and 480 nm are used. Consequently, the Rydberg excitation of neutral atoms in large-scale arrays necessitates substantial laser power at 480 nm, due to the scaling of power requirements with array size. In practice, the generation of the 480 nm-laser is based on frequency doubling. However, the limited seeds power and low conversion efficiency, due to serious absorption and the heating effect with blue light, impede the production of the high-power 480 nm laser. To address this issue, the inverted scheme of two-photon excitation was proposed, involving the transitions 5 S 1 / 2 → 6 P 3 / 2 → n S / n D driven by 420 nm and 1013 nm lasers [18]. In this case, the requirement of the high-power 1013 nm laser can be fulfilled by using a doped fiber amplifier. Yet, the data associated with this transition has never been reported in any publications. In particular, the poor signal-to-noise ratio (SNR) of the corresponding electromagnetically induced transparency (EIT) spectrum further restricts the laser frequency reference in such an inverted configuration.
In this study, we investigate the Rydberg excitation spectrum with the 420 nm–1013 nm two-photon transition in hot 87Rb atomic vapor. Concretely, the ladder-type EIT is utilized to illustrate the excitation, and we use 6 P 3 / 2 as the intermediate state. Here, the 420 nm ( λ p ) laser is emitted by a frequency doubler with the seeds from a Ti:sapphire laser, while the external cavity diode laser (ECDL) provides a frequency tunable 1013 nm ( λ c ) laser for fiber optic amplification, enabling the EIT spectrum scanning. Furthermore, we leverage a modulation–demodulation protocol to obtain the high-performance EIT spectrum with principal quantum numbers ranging from n = 35 to n = 70 . In combination with the ionization energy calculation, our result thus provides the full information of 420 nm–1013 nm two-photon Rydberg excitation, which can be directly applied to scalable quantum information processing with 87Rb atoms.

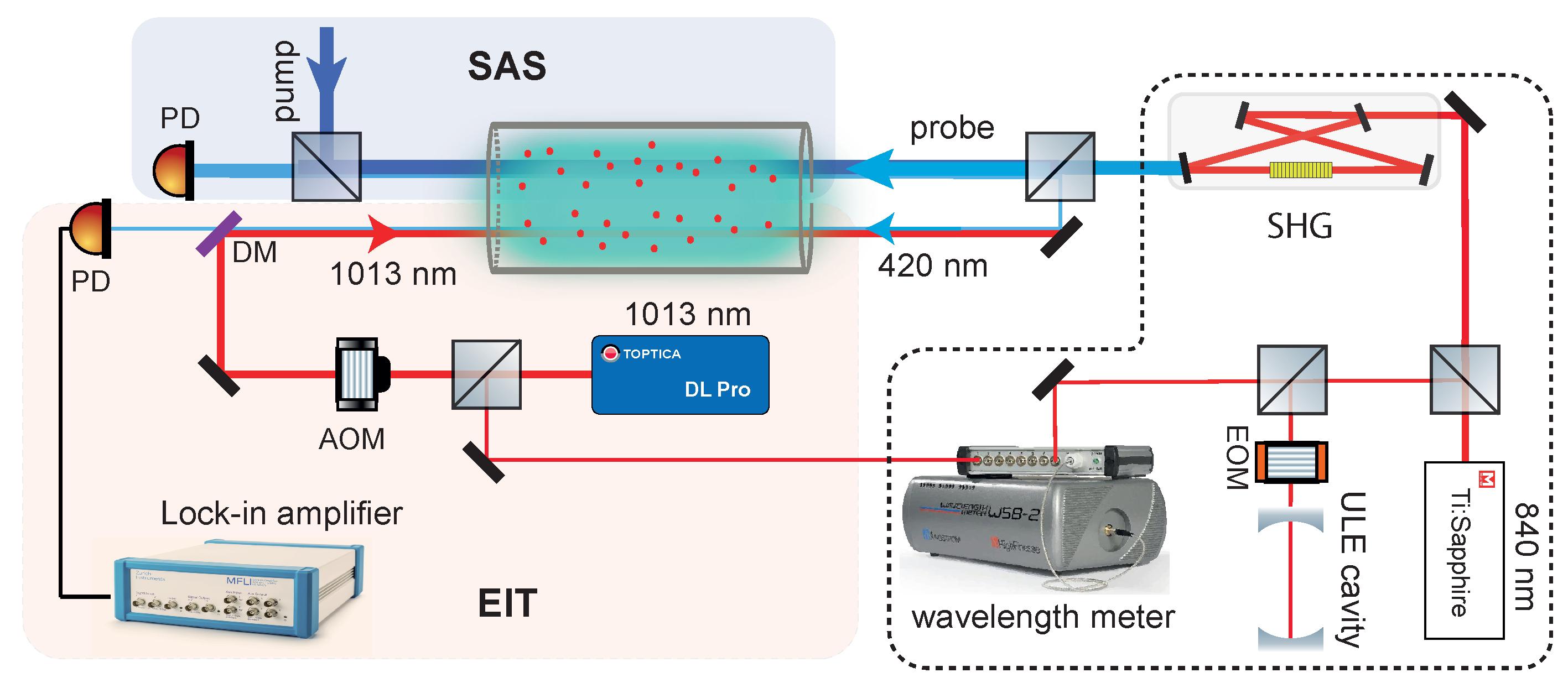
2. Experimental Setup

The schematic of EIT measurement is outlined in Figure 1. Our experiment is performed with an isotopically enriched 87Rb vapor cell maintained at the operation temperature of 60 °C. This cylindrical cell, with diameter of 2.5 cm and length of 7.5 cm, resides inside a single-layer magnetic shielding to screen out the ambient magnetic field.
In this 420 nm–1013 nm two-photon excitation scheme (Figure 2a), a 420 nm laser is generated by frequency-doubled via second harmonic generation (SHG). In order to prepare such a beam, we use a seed laser at 840 nm emitted by a frequency tunable Ti:Sapphire laser (M Square), which provides high output power and narrow linewidth light source. This seed laser is frequency-locked to an ultra-low expansion (ULE) cavity (fineness∼40,000) through the sideband Pound-Drever-Hall (PDH) locking technique, ensuring the SHG-generated 420 nm laser is resonant to the transition between 5 S 1 / 2 , F = 2 and 6 P 3 / 2 , F′ = 3 of 87Rb atoms. In experiments, we expand the beam size to 4 mm in diameter by utilizing a pair of plano-convex lenses, and we set the power ratio of the probe to pump beams to approximately 1:10 to enhance the SAS signal [19]. The associated result of saturated absorption spectroscopy (SAS) is displayed in Figure 2b.
The control light at 1013 nm driving the transition 6 P 3 / 2 , F′ = 3 to Rydberg state n S / n D is emitted by a ECDL (Toptica, DL pro). The counter-propagating probe (420 nm) and control (1013 nm) fields set up the Rydberg EIT process. The transmitted light of 420 nm is separated from the 1013 nm beam with a dichroic mirror (DM) and subsequently detected by a photodetector (PD). When scanning the frequency of the 1013 nm laser, i.e., single-photon detuning corresponding to the transition 6 P 3 / 2 , F′ = 3 to the Rydberg state n S / n D , the EIT spectrum is extracted by using a lock-in amplifier with a demodulation frequency at 100 kHz. In addition, the laser frequencies of 420 nm and 1013 nm are continuously monitored by a wavelength meter (Highfinesse, WS8-2) to accurately record the two-photon transition frequencies.

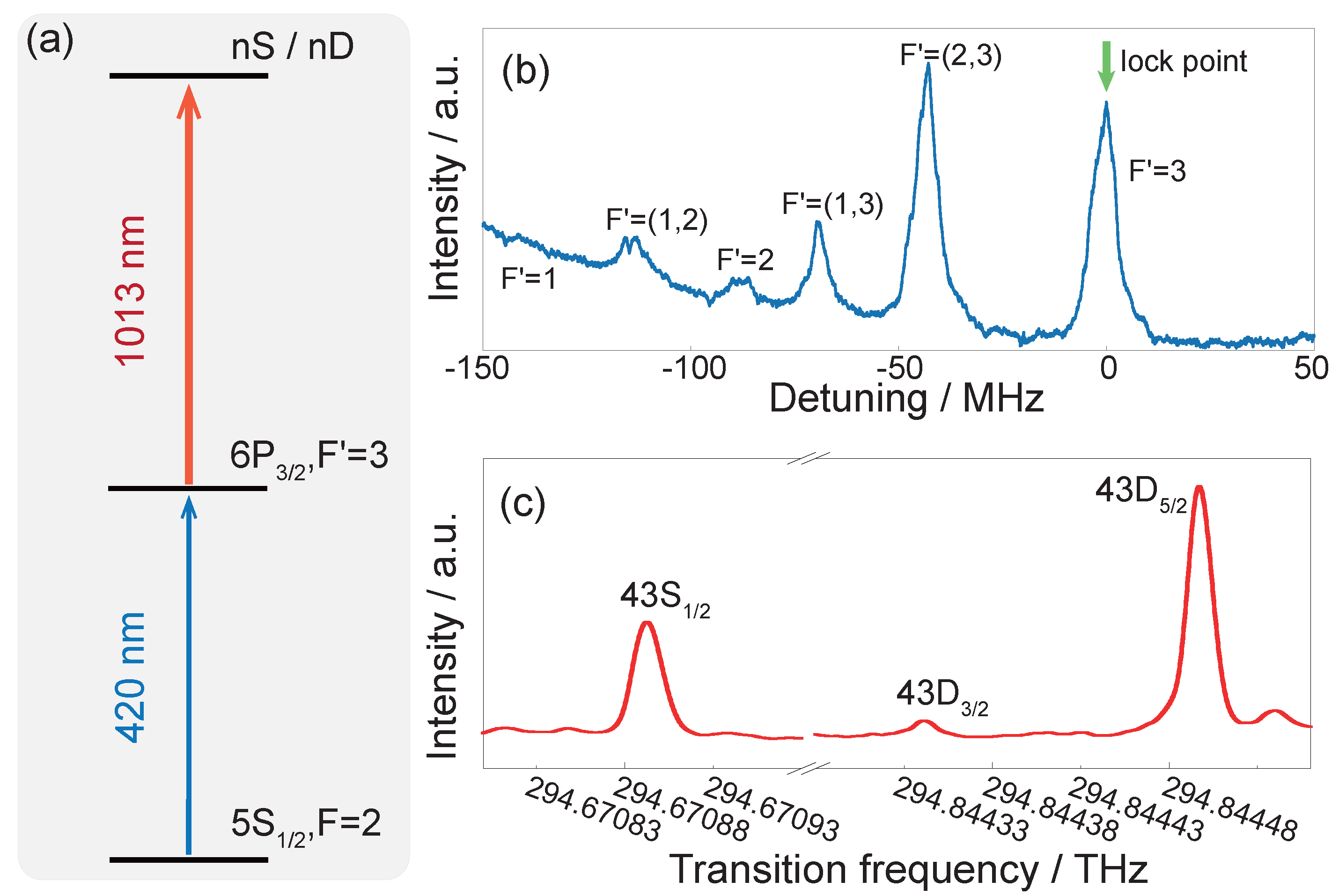
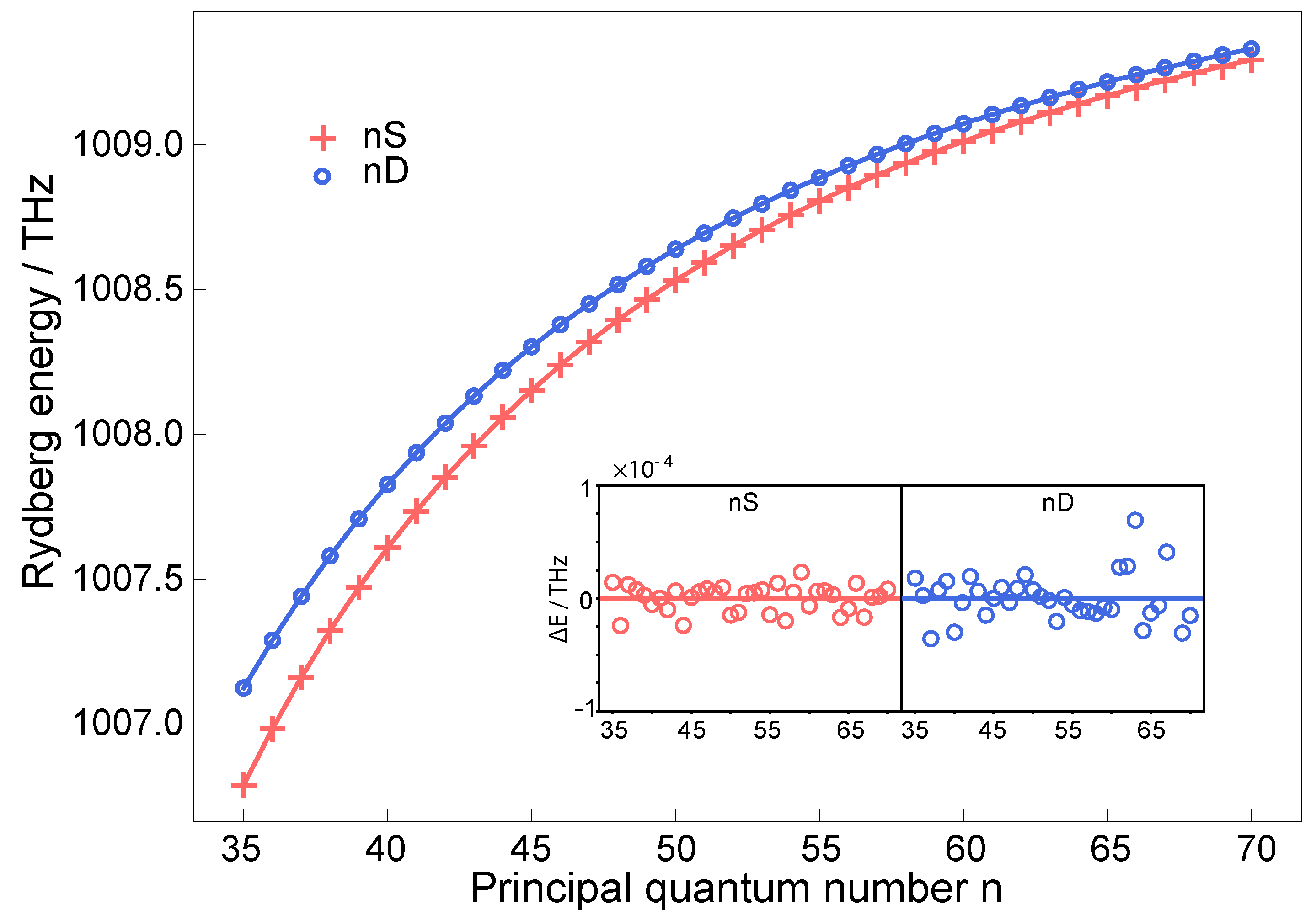
3. Results

In our experiment, we adopt the configuration with λ p < λ c to address the issue of high power requirement on the blue laser. However, in this inverted scheme, the Doppler shifts for both the one-photon, − k p v , and two-photon, − ( k p v − k c v ) , have the same sign, and thus the transparency window vanishes [20,21,22]. As a consequence, given the Doppler averaged absorption, the magnitude of the EIT structure is significantly reduced by many orders with respect to the case that the probe wavelength is longer than the coupling wavelength.
In order to improve the SNR of the EIT signal, we apply a 100 kHz intensity modulation with the periodical rectangular pulses and 50% duty cycle. Meanwhile, the beam size of 420 nm is reduced to 200 μm to increase the Rabi frequency between 5 S 1 / 2 and 6 P 3 / 2 . The relative frequencies for the transitions from 6 P 3 / 2 to n S and n D states are measured by scanning the 1013 nm laser.
By using this method, we investigate the spectrum of high-lying Rydberg excited states, including the n S and n D series, with principal quantum numbers ranging from n = 35 to n = 70 . Figure 2c displays the EIT spectrum associated with the transition from the state 6 P 3 / 2 to Rydberg states 43 S 1 / 2 / 43 D 3 / 2 / 43 D 5 / 2 . Notably, the signal associated with the D 5 / 2 state transitions is significantly stronger than that of the D 3 / 2 state transitions in the observed spectrum. The relative intensities of n D 3 / 2 and n D 5 / 2 are determined by the geometric part of the electric dipole transition matrix element.
To ensure the accuracy of our frequency measurements, we utilize a wavelength meter that is consistently calibrated in real-time using a Rubidium atomic clock (Highfinesse Stabilized Laser Reference, SLR780), which is operated at 384.228115 THz. This calibration approach guarantees that our measurements are in line with the highest precision benchmarks set by atomic clock standards. The transition of 5 S 1 / 2 , F = 2 → 6 P 3 / 2 , F′ = 3 is observed at a frequency of 713.281710(5) THz. The value, however, exhibits a difference of 30 MHz, with the result reported in Ref. [23]. We repeat the measurement several times to obtain this resonant frequency, and the deviation is much less than the 30 MHz. It shows that a stable offset can occur when there a substantial wavelength disparity exists between the calibration laser (780 nm) and the target laser.
By fixing this resonant transition, we further measure the transition frequency from 6 P 3 / 2 , F′ = 3 to the Rydberg state n S / n D via scanning the frequency of a 1013 nm laser. The measured transition frequencies are summarized in Table 1. In this process, the measured mean deviation of several measurements is approximately 10 MHz. Here, the external field interferenceis effectively mitigated by enclosing the vapor in a single-layer μ -metal shield, rendering its impact negligible. Thus, the main factors of measurement uncertainty are attributed to systematic vibrations, which induce spectral line shifts, and the thermal drift of the wavelength meter. Furthermore, we find that there is a significant discrepancy of approximately 300 MHz between the experimental data and the theoretical values of the transition frequency, which is larger than the measurement uncertainty (around 10 MHz). This difference primarily arises from the idealized model employed and the initial values selected for the quantum defects in ARC. The similar discrepancies have also been reported in Refs. [24,25].
Building upon the measured results, we can determine the ionization energy and quantum defect of 87Rb. The ionization energy for a given Rydberg level, characterized by quantum numbers n, l, and j, is described by the following relation [26]:
E n , l , j = E ∞ − E h f s − R y ( n − δ n , l , j ) 2 ,
where E n , l , j represents energy levels of the Rydberg states. The term E ∞ denotes the ionization energy threshold. The hyperfine splitting between the ground state sublevels 5 S 1 / 2 , F = 1 and 5 S 1 / 2 , F = 2 is represented by E h f s , and R y = h · 3289.82119466(2) THz is the Rydberg constant, corrected for the reduced electron mass in 87Rb [27], where h is Planck’s constant.
Table 1. Measured transition frequencies between the intermediate state 6 P 3 / 2 , F′ = 3 and Rydberg state n S / n D series in theory and experiment. Here, n is principal quantum number and the theoretical value of the transition is calculated by Ref. [28].
Table 1. Measured transition frequencies between the intermediate state 6 P 3 / 2 , F′ = 3 and Rydberg state n S / n D series in theory and experiment. Here, n is principal quantum number and the theoretical value of the transition is calculated by Ref. [28].
nnS1/2 (THz)nD3/2 (THz)nD5/2 (THz)
TheoryExpTheoryExpTheory Exp
35293.501710293.501345(10)293.836011293.835671(10)293.836291293.835947(10)
36293.695816293.695414(10)294.001250294.000881(10)294.001506294.001141(10)
37293.872984293.872618(10)294.152780294.152374(10)294.153016294.152608(10)
38294.035129294.034759(10)294.292079294.291713(10)294.292296294.291928(10)
39294.183901294.183527(10)294.420428294.420057(10)294.420627294.420266(10)
40294.320733294.320351(10)294.538944294.538536(10)294.539129294.538721(10)
41294.446868294.446492(10)294.648608294.648222(10)294.648779294.648397(10)
42294.563394294.563008(10)294.750279294.749911(10)294.750438294.750079(10)
43294.671262294.670892(10)294.844716294.844341(10)294.844864294.844492(10)
44294.771309294.770909(10)294.932589294.932204(10)294.932727294.932334(10)
45294.864273294.863898(10)295.014493295.014115(10)295.014621295.014244(10)
46294.950807294.950437(10)295.090955295.090595(10)295.091075295.090708(10)
47295.031492295.031124(10)295.162449295.162065(10)295.162561295.162182(10)
48295.106842295.106471(10)295.229394295.229027(10)295.229500295.229134(10)
49295.177317295.176951(10)295.292170295.291818(10)295.292269295.291916(10)
50295.243330295.242940(10)295.351114295.350753(10)295.351207295.350842(10)
51295.305249295.304861(10)295.406534295.406158(10)295.406621295.406251(10)
52295.363406295.363035(10)295.458703295.458331(10)295.458785295.458413(10)
53295.418100295.417729(10)295.507872295.507479(10)295.507949295.507560(10)
54295.469600295.469232(10)295.554266295.553897(10)295.554339295.553972(10)
55295.518150295.517760(10)295.598090295.597706(10)295.598159295.597787(10)
56295.563971295.563609(10)295.639531295.639158(10)295.639596295.639219(10)
57295.607264295.606868(10)295.678758295.678381(10)295.678820295.678443(10)
58295.648212295.647842(10)295.715926295.715547(10)295.715985295.715607(10)
59295.686980295.686628(10)295.751177295.750806(10)295.751232295.750861(10)
60295.723722295.723339(10)295.784640295.784269(10)295.784693295.784321(10)
61295.758575295.758206(10)295.816434295.816095(10)295.816485295.816151(10)
62295.791667295.791298(10)295.846669295.846337(10)295.846717295.846385(10)
63295.823115295.822743(10)295.875445295.875142(10)295.875490295.875200(10)
64295.853025295.852633(10)295.902854295.902471(10)295.902897295.902509(10)
65295.881497295.881113(10)295.928981295.928611(10)295.929022295.928651(10)
66295.908622295.908259(10)295.953905295.953542(10)295.953944295.953581(10)
67295.934482295.934090(10)295.977699295.977379(10)295.977737295.977421(10)
68295.959155295.958781(10)296.000430296.000057(10)296.000466296.000089(10)
69295.982713295.982340(10)296.022161296.021778(10)296.022195296.021809(10)
70296.005225296.004855(10)296.042948296.042575(10)296.042982296.042611(10)
To accurately describe the quantum defects associated with the Rydberg states, we employ the Rydberg–Ritz equation [27]:
δ n , l , j ≈ δ 0 + δ 2 ( n − δ 0 ) 2 + δ 4 ( n − δ 0 ) 4 + …
The dominant dependence of the quantum defect lies in the l, with negligible contributions from higher-order terms in j and n for Rydberg states. For the n > 20, we consider only the first two terms of the equation, which provides an approximation for the quantum defect. This correction accounts for deviations from the energy levels predicted by the classical calculation of the hydrogen wavefunction. Here, δ 0 and δ 2 represent fitting parameters, whose values are determined by optimizing the agreement with experimental data from Table 1 [29,30].
Figure 3 illustrates the dependence of Rydberg energy levels on the principal quantum number n, whereby the experimental data are fitted with Equation (1). These fitting results tell us that the ionization energy levels E ∞ / h for n S , n D 3 / 2 , and n D 5 / 2 are 1010.0291339(12) THz, 1010.0291784(15) THz and 1010.0291709(18) THz, respectively. The value for n S states agrees well with the results in Ref. [27]. Additionally, the parameters δ 0 and δ 2 in the Rydberg–Ritz formula have been extracted from our fitting data, and the ionization energy E ∞ / h c is displayed in Table 2.

4. Conclusions

We report the precise measurement of the 87Rb Rydberg excitation spectrum in an inverted ladder-type EIT configuration. This setup couples the 5 S 1 / 2 ground state with the n S or n D Rydberg states via the 6 P 3 / 2 intermediate state, overcoming the shortcoming of the high power requirement in the 780 nm–480 nm two-photon excitation. Furthermore, by using a modulation–demodulation protocol we extract the EIT features from the noisy backgrounds. Importantly, we measure the Rydberg transition frequencies for the principal quantum number n = 35 to n = 70 , and we calculate the Rydberg energy. By fitting the data, we obtained the corresponding ionization energies and quantum defects. Our results provide the experimental data reference for applications on large-scale quantum information processing with 87Rb Rydberg atoms and promote novel experiments related to Rydberg atoms with long-range dipole-dipole interactions.

Author Contributions

Conceptualization, D.L. and K.Q; methodology and formal analysis, D.L.; data curation, B.X.; investigation, B.X., K.Q., X.J., C.Z. and Y.Z.; writing—original draft, D.L. and B.X.; writing—review and editing, D.L. and Z.X.; experimental setup, B.X. and K.Q.; and project administration and supervision, D.L. and Z.X. All authors have read and agreed to the published version of the manuscript.

Funding

This work was funded by National Key R&D Program of China (Grant No. 2020YFA0309400), the National Natural Science Foundation of China (Grant No. 12222409, 12204289), and the Key Research and Development Program of Shanxi Province (Grant No. 202101150101025).

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The original contributions presented in the study are included in the article; further inquiries can be directed to the corresponding author.

Conflicts of Interest

The authors declare no conflicts of interest.

References

  1. Bluvstein, D.; Evered, S.J.; Geim, A.A. Logical quantum processor based on reconfigurable atom arrays. Nature 2024, 626, 58–65. [Google Scholar] [CrossRef] [PubMed]
  2. Henriet, L.; Beguin, L.; Signoles, A. Quantum computing with neutral atoms. Quantum 2020, 4, 327. [Google Scholar] [CrossRef]
  3. Sunami, S.; Tamiya, S.; Inoue, R. Scalable Networking of Neutral-Atom Qubits: Nanofiber-Based Approach for Multiprocessor Fault-Tolerant Quantum Computer. arXiv 2024, arXiv:2407.11111. [Google Scholar] [CrossRef]
  4. Bornet, G.; Emperauger, G.; Chen, C. Scalable spin squeezing in a dipolar Rydberg atom array. Nature 2023, 621, 728–733. [Google Scholar] [CrossRef]
  5. Scholl, P.; Schuler, M.; Williams, H.J. Quantum simulation of 2D antiferromagnets with hundreds of Rydberg atoms. Nature 2021, 595, 233–238. [Google Scholar] [CrossRef]
  6. Barredo, D.; Lienhard, V.; De Leseleuc, S.; Lahaye, T.; Browaeys, A. Synthetic three-dimensional atomic structures assembled atom by atom. Nature 2018, 561, 79–82. [Google Scholar] [CrossRef]
  7. Maskara, N.; Ostermann, S.; Shee, J. Programmable Simulations of Molecules and Materials with Reconfigurable Quantum Processors. arXiv 2023, arXiv:2312.02265. [Google Scholar] [CrossRef]
  8. Endres, M.; Bernien, H.; Keesling, A. Atom-by-atom assembly of defect-free one-dimensional cold atom arrays. Science 2016, 354, 1024–1027. [Google Scholar] [CrossRef]
  9. Nguyen, M.; Jin-Guo, L.; Wurtz, J. Quantum Optimization with Arbitrary Connectivity Using Rydberg Atom Arrays. PRX Quantum 2023, 4, 010316. [Google Scholar] [CrossRef]
  10. Saffman, M. Quantum computing with atomic qubits and Rydberg interactions: Progress and challenges. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 2020001. [Google Scholar] [CrossRef]
  11. Evered, S.J.; Bluvstein, D.; Kalinowski, M. High-fidelity parallel entangling gates on a neutral-atom quantum compute. Nature 2023, 622, 268–272. [Google Scholar] [CrossRef] [PubMed]
  12. Graham, T.M.; Song, Y.; Scott, J. Multi-qubit entanglement and algorithms on a neutral-atom quantum computer. Nature 2022, 604, 457–462. [Google Scholar] [CrossRef] [PubMed]
  13. Crescimanna, V.; Taylor, J.; Goldberg, A.Z. Quantum Control of Rydberg Atoms for Mesoscopic Quantum State and Circuit Preparation. Phys. Rev. Appl. 2023, 20, 034019. [Google Scholar] [CrossRef]
  14. Serbyn, S.; Abanin, D.A.; Papić, Z. Quantum many-body scars and weak breaking of ergodicity. Nat. Phys. 2021, 17, 675–685. [Google Scholar] [CrossRef]
  15. Lee, J.Y.; Ramette, J.; Metlitski, M.A. Landau-Forbidden Quantum Criticality in Rydberg Quantum Simulators. Phys. Rev. Lett. 2023, 131, 083601. [Google Scholar] [CrossRef]
  16. Browaeys, A.; Thierry, L. Many-body physics with individually controlled Rydberg atoms. Nat. Phys. 2020, 16, 132–142. [Google Scholar] [CrossRef]
  17. Ebadi, S.; Wang, T.T.; Ha Levine, A. Quantum phases of matter on a 256-atom programmable quantum simulator. Nature 2021, 595, 227–232. [Google Scholar] [CrossRef]
  18. Bernien, H.; Schwartz, S.; Keesling, A. Probing many-body dynamics on a 51-atom quantum simulator. Nature 2017, 551, 227–232. [Google Scholar] [CrossRef]
  19. Das, R.C.; Khan, S.; Ravi, T.; Pandey, K. Direct spectroscopy of Rubidium using a narrow-line transition at 420 nm. Eur. Phys. J. D 2024, 78, 40. [Google Scholar] [CrossRef]
  20. Urvoy, A.; Carr, C.; Ritter, R.; Adams, C.S.; Weatherill, K.J.; Löw, R. Optical coherences and wavelength mismatch in ladder systems. J. Phys. B: At. Mol. Opt. Phys. 2013, 46, 245001. [Google Scholar] [CrossRef]
  21. Xu, W.; DeMarco, B. Velocity-selective electromagnetically-induced-transparency measurements of potassium Rydberg states. Phys. Rev. A 2016, 93, 011801. [Google Scholar] [CrossRef]
  22. Zhu, Y.; Ghosh, S.; Cahn, S.B. Electromagnetically-induced-transparency spectroscopy of high-lying Rydberg states in 39K. Phys. Rev. A 2022, 105, 042808. [Google Scholar] [CrossRef]
  23. Glaser, C.; Karlewski, F.; Kluge, J. Absolute frequency measurement of rubidium 5S-6P transitions. Phys. Rev. A 2020, 102, 012804. [Google Scholar] [CrossRef]
  24. Wu, M.; Bao, X.; Yu, S. Electromagnetically Induced Transparency Spectra of 6Li Rydberg Atoms. Photonics 2023, 10, 1367. [Google Scholar] [CrossRef]
  25. Li, D.; Bian, G.; Miao, J. Rydberg excitation spectrum of 40K ultracold Fermi gases 5S-6P transitions. Phys. Rev. A 2021, 103, 063305. [Google Scholar] [CrossRef]
  26. Li, B.; Li, M.; Jiang, X.; Qian, J.; Li, X.; Liu, L.; Wang, Y. Optical spectroscopy of nP Rydberg states of 87Rb atoms with a 297-nm ultraviolet laser. Phys. Rev. A 2019, 99, 042502. [Google Scholar] [CrossRef]
  27. Mack, M.; Karlewski, F.; Hattermann, H. Measurement of absolute transition frequencies of 87Rb to nS and nD Rydberg states by means of electromagnetically induced transparency. Phys. Rev. A 2011, 83, 052515. [Google Scholar] [CrossRef]
  28. Šibalić, N.; Pritchard, J.D.; Adams, C.S. ARC: An open-source library for calculating properties of alkali Rydberg atoms. Comput. Phys. Commun. 2017, 220, 319–331. [Google Scholar] [CrossRef]
  29. Li, W.; Mourachko, I.; Noel, M.W. Millimeter-wave spectroscopy of cold Rb Rydberg atoms in a magneto-optical trap: Quantum defects of the ns, np, and nd series. Phys. Rev. A 2003, 67, 05250. [Google Scholar] [CrossRef]
  30. Han, J.; Jamil, Y.; Noruml, D.V.L. Rb nf quantum defects from millimeter-wave spectroscopy of cold 85Rb Rydberg atoms. Phys. Rev. A 2006, 74, 054502. [Google Scholar] [CrossRef]
Photonics 12 00204 g001
Figure 1. Schematic of the experimental setup for Rydberg excitation spectrum measurement in 87Rb atomic vapor. A Ti:Sapphire laser operating at 840 nm is frequency-doubled to generate the 420 nm light. The 840 nm seed laser is locked to an ultra-low expansion (ULE) cavity, overcoming the frequency drift caused by temperature variation. A small portion of the 420 nm is used for saturated absorption spectroscopy (SAS). By tuning the sideband frequency, the 420 nm laser can be scanned. The 1013 nm laser is produced by a Toptica laser and counter-propagated with the 420 nm laser for realizing the Rydberg spectrum measurement. An acoustic optical modulator (AOM) is employed for chopping the 1013 nm light. The transmitted 420 nm passes through the dichroic mirror (DM) and is sent to a lock-in amplifier to extract the weak EIT signal. A wavelength meter (Highfinesse, WS8-2) continuously monitors the frequencies of all lasers. The vapor cell, 7.5 cm in length and 2.5 cm in diameter, is heated to 60 °C for both SAS and EIT detection. SHG: second harmonic generation, EOM: electro-optic modulator, and PD: photodetector.
Figure 1. Schematic of the experimental setup for Rydberg excitation spectrum measurement in 87Rb atomic vapor. A Ti:Sapphire laser operating at 840 nm is frequency-doubled to generate the 420 nm light. The 840 nm seed laser is locked to an ultra-low expansion (ULE) cavity, overcoming the frequency drift caused by temperature variation. A small portion of the 420 nm is used for saturated absorption spectroscopy (SAS). By tuning the sideband frequency, the 420 nm laser can be scanned. The 1013 nm laser is produced by a Toptica laser and counter-propagated with the 420 nm laser for realizing the Rydberg spectrum measurement. An acoustic optical modulator (AOM) is employed for chopping the 1013 nm light. The transmitted 420 nm passes through the dichroic mirror (DM) and is sent to a lock-in amplifier to extract the weak EIT signal. A wavelength meter (Highfinesse, WS8-2) continuously monitors the frequencies of all lasers. The vapor cell, 7.5 cm in length and 2.5 cm in diameter, is heated to 60 °C for both SAS and EIT detection. SHG: second harmonic generation, EOM: electro-optic modulator, and PD: photodetector.
Photonics 12 00204 g001
Photonics 12 00204 g002
Figure 2. (a) Energy−level diagram of Rydberg excitation via two-photon transitions. (b) SAS of the 5 S 1 / 2 , F = 2 to 6 P 3 / 2 , F′ = 3 at 420 nm. The peak of F′ = ( m , n ) corresponds to the crossover resonance peak resulting from the F′ = m and F′ = n peaks. (c) Recorded EIT signals for the 6 P 3 / 2 to n S 1 / 2 , n D 3 / 2 , and n D 5 / 2 transitions at the principal quantum number n = 43 , showcasing the characteristic transparency peaks associated with each state.
Figure 2. (a) Energy−level diagram of Rydberg excitation via two-photon transitions. (b) SAS of the 5 S 1 / 2 , F = 2 to 6 P 3 / 2 , F′ = 3 at 420 nm. The peak of F′ = ( m , n ) corresponds to the crossover resonance peak resulting from the F′ = m and F′ = n peaks. (c) Recorded EIT signals for the 6 P 3 / 2 to n S 1 / 2 , n D 3 / 2 , and n D 5 / 2 transitions at the principal quantum number n = 43 , showcasing the characteristic transparency peaks associated with each state.
Photonics 12 00204 g002
Photonics 12 00204 g003
Figure 3. Energies of Rydberg states for n S (red plus) and n D (blue circle) corresponding to principal quantum numbers ranging from n = 35 to n = 70 . The solid lines depict the fitted curves corresponding to n S and n D series, respectively. The insets display the difference Δ E between the data and the fit for each series. The residual squared (R2) differs from 1 by 10−10 and 10−9 for the n S and n D 3 / 2 series, respectively. Here, only the n D 3 / 2 series is plotted, due to the small energy difference between the n D 3 / 2 and n D 5 / 2 levels.
Figure 3. Energies of Rydberg states for n S (red plus) and n D (blue circle) corresponding to principal quantum numbers ranging from n = 35 to n = 70 . The solid lines depict the fitted curves corresponding to n S and n D series, respectively. The insets display the difference Δ E between the data and the fit for each series. The residual squared (R2) differs from 1 by 10−10 and 10−9 for the n S and n D 3 / 2 series, respectively. Here, only the n D 3 / 2 series is plotted, due to the small energy difference between the n D 3 / 2 and n D 5 / 2 levels.
Photonics 12 00204 g003
Table 2. Determination of quantum defects δ 0 and δ 2 for the n S and n D Rydberg states of 87Rb. The ionization frequency from the ground state 5 S 1 / 2 , F = 1 is calculated on basis of the fit result in this work and compared with the result reported in Ref. [27].
Table 2. Determination of quantum defects δ 0 and δ 2 for the n S and n D Rydberg states of 87Rb. The ionization frequency from the ground state 5 S 1 / 2 , F = 1 is calculated on basis of the fit result in this work and compared with the result reported in Ref. [27].
This WorkRef. [27]
n S 1 / 2 δ 0 3.1311650(8)3.1311807(8)
δ 2 0.2119(2)0.1787(2)
n D 3 / 2 δ 0 1.3493698(11)1.3480948(11)
δ 2 −1.8656(4)−0.6054(4)
n D 5 / 2 δ 0 1.3474759(11)1.3464622(11)
δ 2 −1.5901(4)−0.5940(4)
E ∞ , 5 S 1 / 2 , F = 1 / h c 33,690.94541(6) cm−133,690.94644(1) cm−1
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content.

Share and Cite

MDPI and ACS Style

Li, D.; Xu, B.; Qin, K.; Jia, X.; Zhao, C.; Zhou, Y.; Xu, Z. Probing nS/nD Rydberg States via 6P3/2 Intermediate Level Using Electromagnetically Induced Transparency in 87Rb. Photonics 2025, 12, 204. https://doi.org/10.3390/photonics12030204

AMA Style

Li D, Xu B, Qin K, Jia X, Zhao C, Zhou Y, Xu Z. Probing nS/nD Rydberg States via 6P3/2 Intermediate Level Using Electromagnetically Induced Transparency in 87Rb. Photonics. 2025; 12(3):204. https://doi.org/10.3390/photonics12030204

Chicago/Turabian Style

Li, Donghao, Beining Xu, Keyu Qin, Xin Jia, Changtao Zhao, Yaoting Zhou, and Zhongxiao Xu. 2025. "Probing nS/nD Rydberg States via 6P3/2 Intermediate Level Using Electromagnetically Induced Transparency in 87Rb" Photonics 12, no. 3: 204. https://doi.org/10.3390/photonics12030204

APA Style

Li, D., Xu, B., Qin, K., Jia, X., Zhao, C., Zhou, Y., & Xu, Z. (2025). Probing nS/nD Rydberg States via 6P3/2 Intermediate Level Using Electromagnetically Induced Transparency in 87Rb. Photonics, 12(3), 204. https://doi.org/10.3390/photonics12030204

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop