Laser Linewidth Measurement Using an FPGA-Based Delay Self-Homodyne System

Abstract

Narrow-linewidth lasers play a crucial role in nonlinear optics, atomic physics, optical metrology, and high-speed coherent optical communications. Precise linewidth measurement is essential for assessing laser noise characteristics; however, conventional methods are often bulky, costly, and unsuitable for integrated applications. This paper presents a compact and cost-effective delay self-homodyne system for laser linewidth measurement, leveraging a field-programmable gate array (FPGA)-based data acquisition circuit. By employing fast Fourier transform (FFT) analysis, the system achieves high-precision linewidth measurement in the kHz range. Additionally, by optimizing the fiber length, the system effectively suppresses low-frequency and 1/f noise, providing an integrated and efficient solution for advanced laser characterization with enhanced performance and reduced cost.

1. Introduction

Narrow-linewidth lasers, renowned for their high-frequency stability and signal-to-noise ratio, find extensive applications in fields such as communications, sensing, monitoring, and advanced physics research [1,2,3,4,5,6]. Their remarkable performance stems from their low noise characteristics and high coherence, which, while advantageous, also present significant challenges for precise linewidth measurement [7,8,9,10]. In engineering applications, laser linewidth is a critical parameter that directly impacts system performance, influencing factors such as the sensitivity of sensing systems, the channel capacity of communication networks, and the accurate calculation of effective gain in nonlinear optical processes [11,12,13,14]. Therefore, precise linewidth measurement is essential to advancing high-coherence lasers from laboratory research to a diverse array of industrial applications and cutting-edge scientific pursuits.

In the field of narrow-linewidth laser measurement (~kHz or narrower), two methods are commonly used—Voigt fitting and the beat frequency method based on delay structures—each with distinct advantages. The Voigt fitting method is characterized by its simplicity, low cost, and minimal environmental requirements, making it straightforward to set up and operate. However, its measurement accuracy is limited by the amount of data collected and the efficiency of the fitting algorithm. When measuring ultra-narrow-linewidth lasers, this method requires large data sets and is susceptible to deviations under high noise conditions [15,16]. Currently, the beat frequency method based on delay structures has become the predominant approach for measuring the linewidth of narrow-linewidth lasers, offering accurate results even in the kHz range [17,18]. This technique employs a Mach–Zehnder interferometer, where a fixed fiber delay is introduced in one branch to modify the light’s phase, and a coupler is used for light distribution and combination. A variation of this method, the delay self-heterodyne structure, incorporates an acousto-optic frequency shifter to induce frequency changes in the branch [19,20,21,22]. These methods are highly accurate, offer some degree of noise suppression, and are adaptable to multi-wavelength and variable power ranges. Researchers have continually refined these measurement techniques to overcome their limitations. For example, the envelope calculation method under sub-coherent conditions addresses a key issue in traditional setups: the requirement for delay lines is significantly longer than the coherence length of the light source. This innovation reduces excessive fiber lengths and mitigates frequency noise, contributing to further optimization of laser systems. However, despite these advancements, the reliance on bulky equipment such as spectrum analyzers continues to hinder the portability and integration of these measurement systems.

In recent years, researchers have revisited the potential of various devices as alternatives to spectrum analyzers, with digital oscilloscopes standing out as a notable option [23,24,25]. While these devices have improved experimental accuracy and reduced costs to some extent, their bulkiness remains a significant barrier to achieving integration in practical applications. Advances in technology have brought field-programmable gate array (FPGA) systems into the spotlight due to their high-speed processing capabilities, compact size, and versatility [26,27,28,29], making them a promising solution for replacing bulky equipment and enabling highly integrated linewidth measurement systems.

In this paper, we propose an FPGA-based linewidth measurement system that integrates a time–frequency conversion program to address the limitations of traditional measurement methods. Compared to other compact circuit devices, this FPGA-based approach offers superior anti-interference capabilities, exceptional flexibility, high-speed processing, and real-time performance. Because the measurement data from heterodyne systems predominantly resides in the high-frequency domain—posing significant challenges for hardware under the constraints of the Nyquist theorem—we optimized the conventional delay self-heterodyne system to eliminate the reliance on spectrum analyzers. This optimization not only reduces device costs but also enhances system portability and integration. By employing the sub-coherent envelope linewidth calculation method, we successfully measured the linewidth of a commercial laser, demonstrating the system’s effectiveness in practical applications.

2. Experimental Setup and Principles

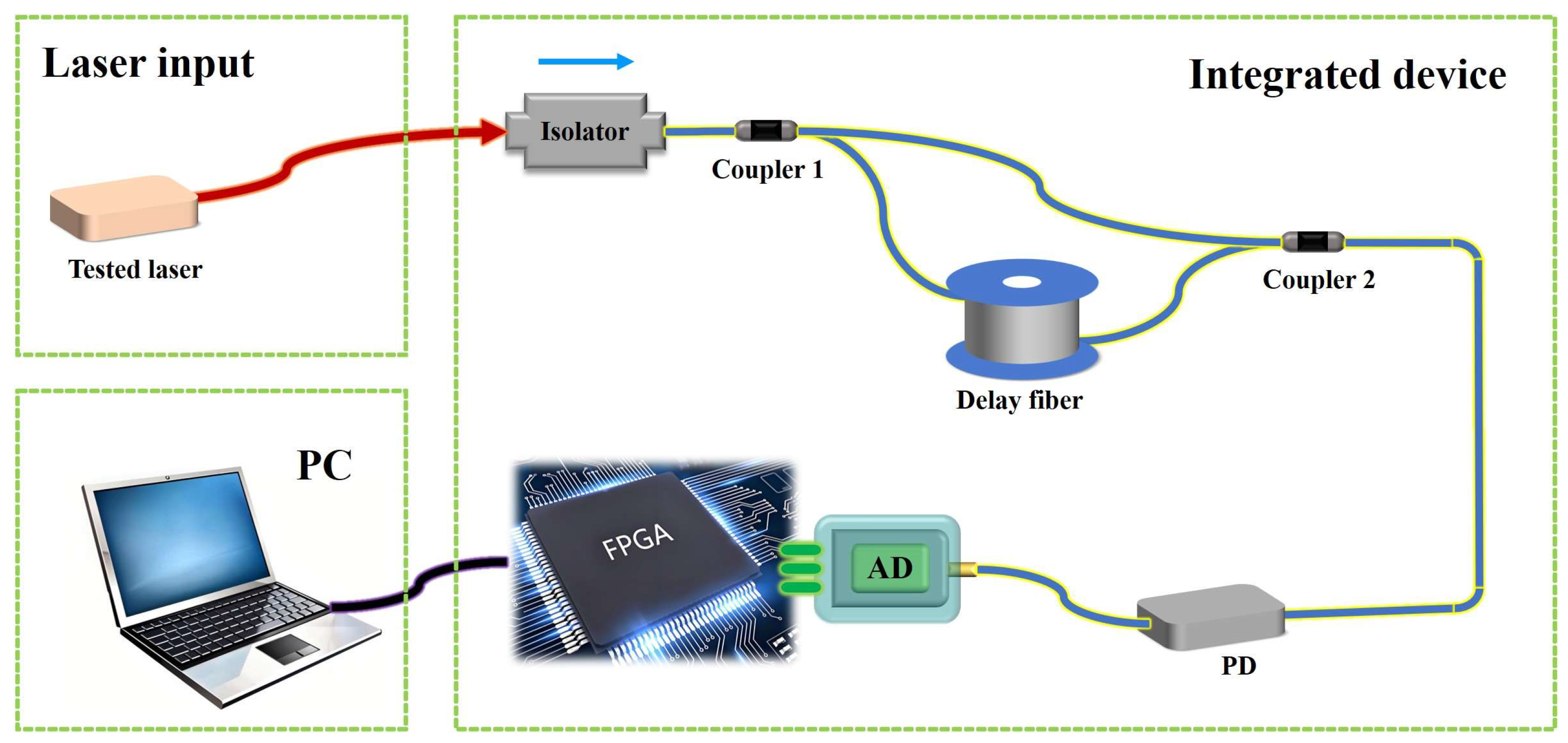
The integrated system designed in this study is illustrated in Figure 1. Measurement of the laser was accomplished using three components: the laser under test, a portable measurement module, and a personal computer (PC) for signal processing. The portable measurement module consists of a delay self-homodyne measurement device and an FPGA-based data acquisition circuit. The delay self-homodyne device will be considered in conjunction with short delay optical fibers and a sub-coherent envelope algorithm, which can not only significantly reduce the redundancy of the device but can also achieve more precise linewidth measurements compared to traditional schemes. After passing through the delay self-homodyne system, the laser signal is converted into an analog electrical signal by the photodetector (PD). The FPGA data acquisition system collects the signal data and transmits them to the PC. The FPGA’s analog-to-digital converter (ADC) performs data collection, analog-to-digital conversion, and transmission. The PC is used to process and analyze the data using fast Fourier transform (FFT) to display the power spectral density (PSD) of the signal, ultimately allowing for the measurement of the laser linewidth. The entire system boasts an extremely fast response speed. The combination of the measurement optical path and FPGA architecture enables near-instantaneous acquisition of the laser source’s characteristics upon connection, streamlining subsequent frequency power spectrum calculations and analysis.

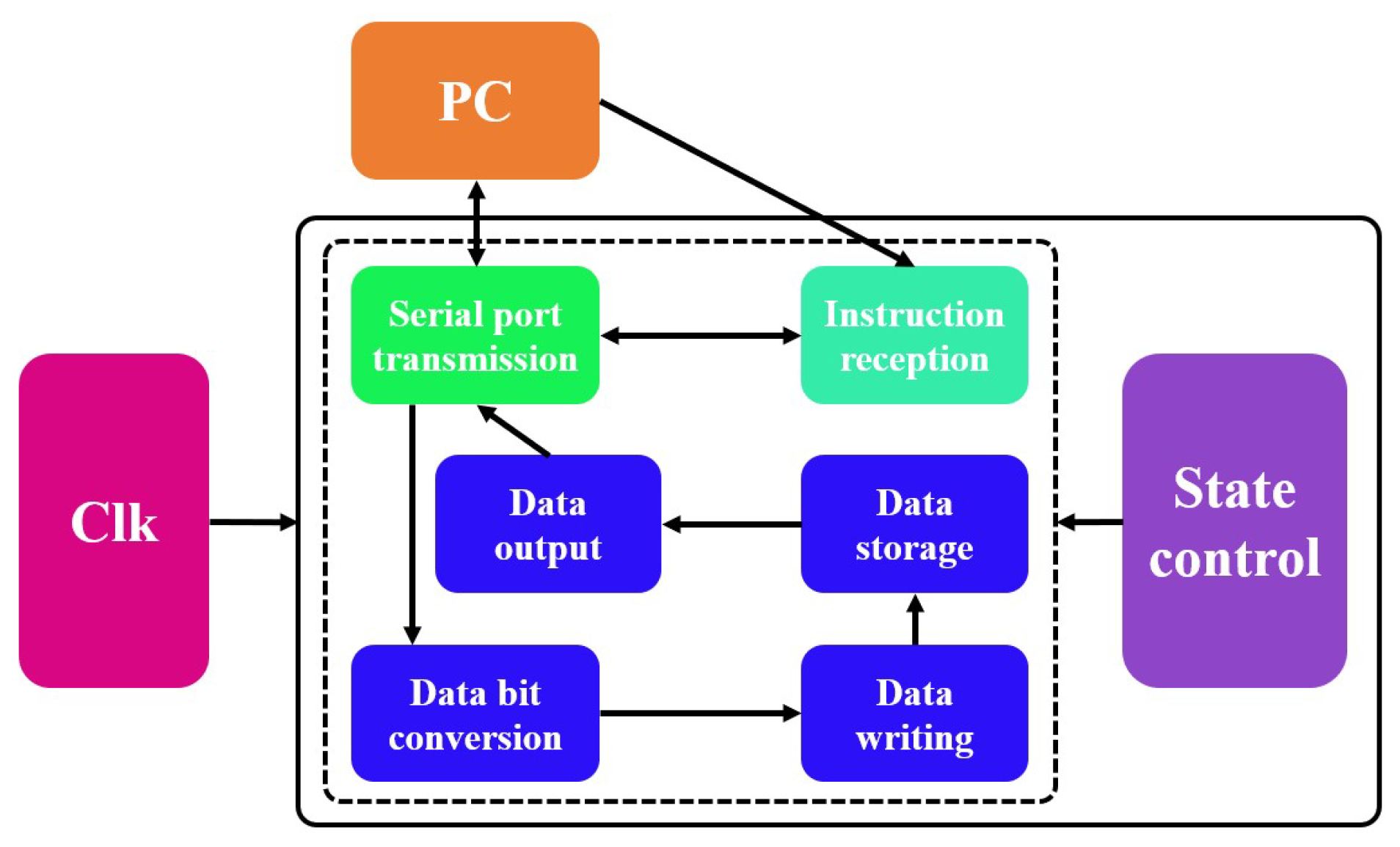
The main components of the program design are illustrated in Figure 2. The external PC interfaces with the FPGA system via a serial port, enabling both program uploads and command transmission through serial communication. The FPGA development board is connected to an analog-to-digital converter (ADC), which receives signals from the photodetector for data acquisition. Because the PC processes and stores data in 8-bit or 16-bit formats and the acquired data is in a 10-bit format, a conversion from 10-bit to 16-bit is required for proper storage. Once the data are converted, they are written into the onboard register for buffering. After data acquisition is completed, the stored data are transmitted back to the PC via the serial port for further processing and analysis. To ensure seamless operation, the entire program design incorporates a state machine module to coordinate control among different functional modules. Additionally, a clock module manages the timing control of the entire system, ensuring precise synchronization and efficient data processing.

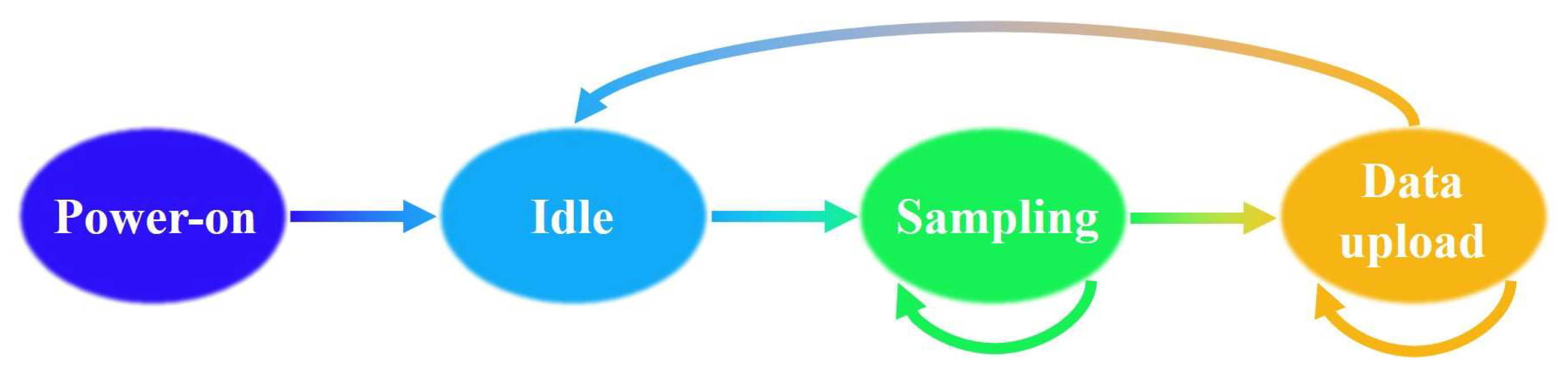
The state transitions in the program design are categorized into four main stages: power-on, idle, sampling, and serial data upload, as illustrated in Figure 3. Upon powering on, the system enters the idle state, where it awaits commands sent via the serial port. At this stage, users can configure parameters such as the number of samples and the sampling frequency, as well as issue the start sampling command. Once the FPGA receives the sampling start command, it transitions to the ADC sampling state, where the acquired data are stored on the development board. The system remains in this state until the specified number of samples is collected. Upon completion of data acquisition, the system moves to the serial port upload state, where the stored data are transmitted to the PC. If the upload process is incomplete, the system will remain in this state until all data are successfully transferred. After the upload is finalized, the system returns to the idle state, ready to receive new commands.

3. Experimental Results and Analysis

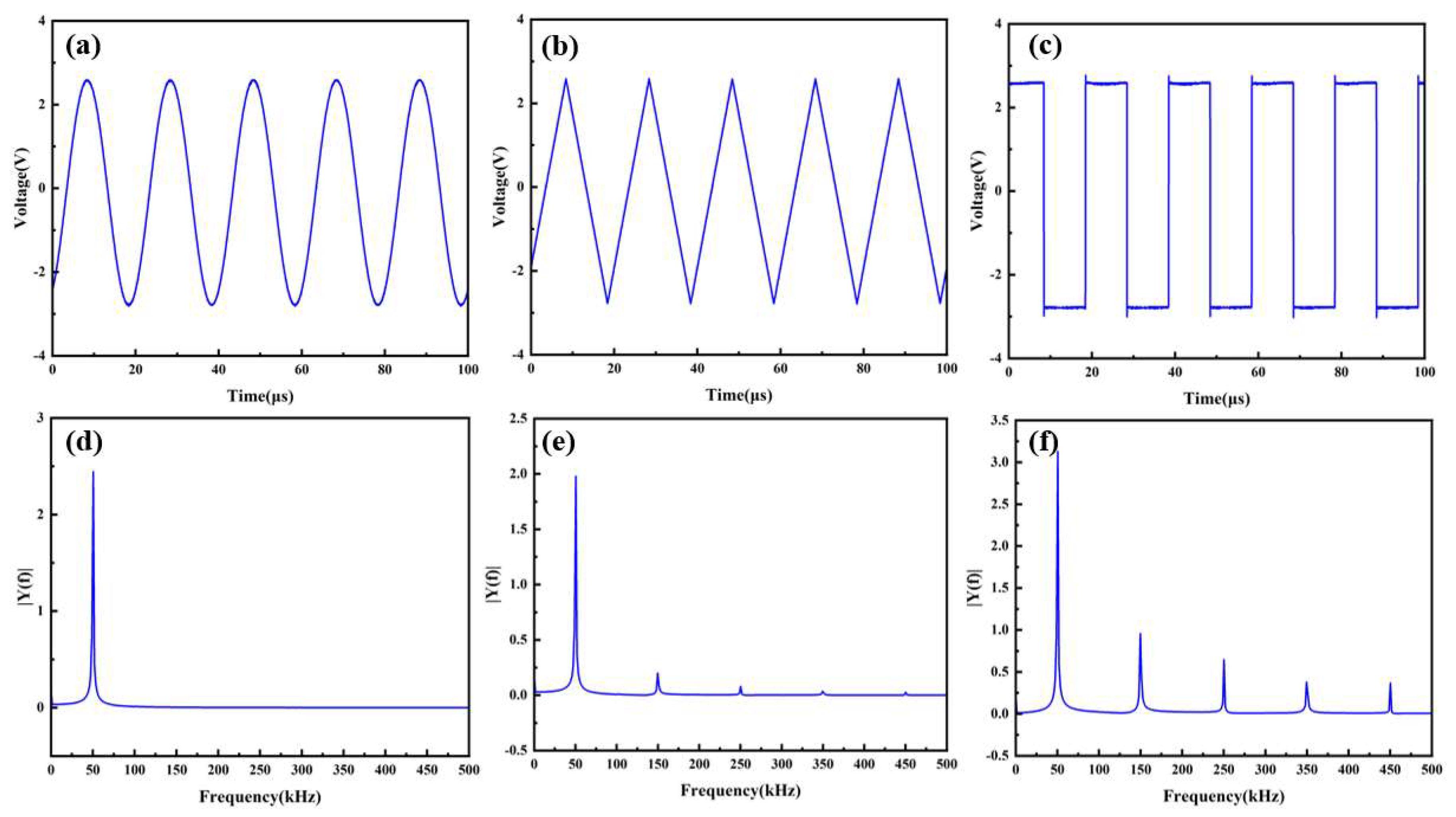
To validate the feasibility and accuracy of the designed FPGA-based data acquisition system and time–frequency conversion program, we first conducted a verification experiment using standard test signals before processing the laser signal. A signal generator was used to produce voltage signals of a specific frequency, which were then acquired by the FPGA data acquisition circuit. The collected data were processed on a PC to reconstruct the time-domain voltage waveforms, while the designed time–frequency conversion program was employed to analyze their spectral characteristics. In this experiment, the signal generator produced three types of voltage waveforms: a sine wave, a triangle wave, and a square wave, each with a peak-to-peak voltage (Vpp) of 5 V and a frequency of 50 kHz. The reconstructed voltage waveforms for the sine, triangle, and square waves are shown in Figure 4a, Figure 4b, and Figure 4c, respectively, while the corresponding spectra obtained using the time–frequency conversion program are displayed in Figure 4d–f. Theoretically, all three waveforms should exhibit a dominant spectral peak at 50 kHz. The sine wave’s spectrum is primarily concentrated at this frequency, while the spectra of the triangle and square waves include odd harmonics, with amplitudes gradually decreasing as frequency increases [30]. The obtained spectral results closely match theoretical expectations, confirming the accuracy and reliability of the proposed system design.

In this study, traditional delay self-heterodyne and self-homodyne schemes utilize long optical fibers and depend on Lorentzian linear spectra for linewidth estimation. However, the use of long fibers can introduce 1/f noise and other detrimental effects, ultimately reducing measurement accuracy [31,32]. To enhance measurement precision and improve system integration, we implemented a short optical fiber in combination with a sub-coherent envelope algorithm for linewidth calculation. The core formula is given by [8,21,33,34,35]:

$$\begin{gathered} \Delta s=10{log}_{10}{S}_H-10{log}_{10}{S}_L=10{log}_{10}{\displaystyle \frac{S\left[f_1+\frac{\left(m+2\right)c}{2nL}\right]}{S\left[f_1+\frac{\left(k+2\right)c}{2nL}\right]}} \\ =10{log}_{10}{\displaystyle \frac{\left[\mathsf{\Delta }{f}^2+{\left[\frac{\left(k+2\right)c}{2nL}\right]}^2\right]}{\left[\mathsf{\Delta }{f}^2+{\left[\frac{\left(m+2\right)c}{2nL}\right]}^2\right]}}{\displaystyle \frac{[1-exp\left(-2\pi \frac{nL}{c}\mathsf{\Delta }f\right)cos\left[\left(m+2\right)\pi \right]]}{[1-exp\left(-2\pi \frac{nL}{c}\mathsf{\Delta }f\right)cos\left[\left(k+2\right)\pi \right]]}}, \end{gathered}$$

(1)

where n is the refractive index of the delay optical fiber, $c$ is the speed of light, L is the length of the delay optical fiber, $\mathsf{\Delta }f$ is the laser linewidth, $f_1$ is the center frequency of the PSD, $S_H$ is the larger value of the adjacent extremum pairs, and $S_L$ is the smaller value. m and k are natural numbers with the condition k ≠ m. As the selected extremum points are adjacent, the constraint |m − k = 1| must be satisfied. This method consists of two key steps: first, identifying adjacent extremum point pairs and computing their amplitude difference; second, incorporating the amplitude difference data into the calculation formula to determine the laser linewidth [21].

The laser under test in this study is a narrow-linewidth semiconductor laser (RIO0175-5-07-1) manufactured by RIO, with a reported linewidth of 5.1 kHz according to the test report. Experimental observations revealed that adjusting the laser’s output power within the safe operating range of the measuring device did not significantly affect the spectral characteristics. Additionally, the amplitude difference measured in dB is a relative value, eliminating the need to consider the impact of laser power on linewidth measurement [21]. Three representative lengths of delay optical fibers 100 m, 1000 m, and 5000 m were selected for linewidth measurement studies.

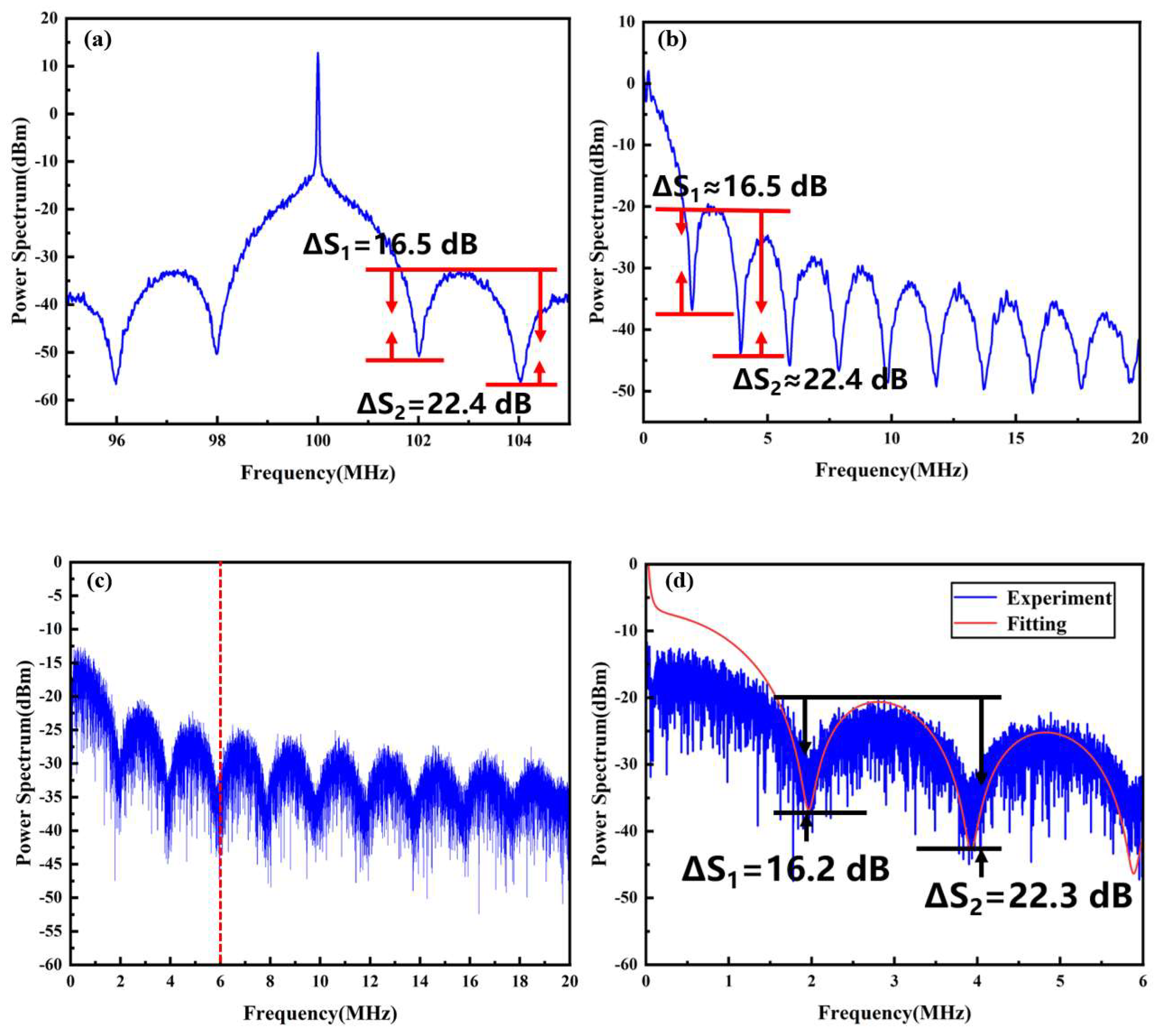
In the measurement system, the delay optical fiber length in the delay self-homodyne system is initially set to 100 m. The frequency power spectrum of the laser under test is obtained and analyzed using both a spectrum analyzer and the designed FPGA data acquisition system in conjunction with the time–frequency conversion program. Simultaneously, a delay self-heterodyne system is utilized for comparative analysis. The frequency power spectrum measured by the spectrum analyzer in the delay self-heterodyne system is shown in Figure 5a. In this heterodyne spectrum, the amplitude differences of the first and second peak-valley pairs are recorded as 16.5 dB and 22.4 dB, respectively. Based on Formula (1), the corresponding calculated linewidths are 6.20 kHz and 6.38 kHz, which are highly consistent with the nominal linewidth of the laser. In the delay self-homodyne system, the frequency power spectrum measured by the spectrum analyzer is shown in Figure 5b. Compared to the heterodyne spectrum, the self-homodyne spectrum is affected by low-frequency noise near zero frequency. However, within the coherent envelope region, the peak-valley differences closely match those obtained using the heterodyne method, with the impact of low-frequency noise significantly reduced. The frequency power spectrum obtained using the integrated system designed in this study is shown in Figure 5c. The spectral results align closely with those from the spectrum analyzer, validating the effectiveness of the proposed system. For the low-frequency portion of the frequency power spectrum (the region to the left of the red dashed line in Figure 5c), a numerical fitting procedure was performed to compare the theoretical model with the experimental data, as illustrated in Figure 5d. The red curve represents the theoretical fit. It is evident that in the low-frequency region, the actual spectrum deviates from the theoretical prediction due to low-frequency noise interference, leading to suboptimal fitting performance. However, within the envelope spectrum region, the experimental and theoretical spectra exhibit high consistency, demonstrating excellent fitting accuracy. Analyzing the envelope region, the amplitude differences of the first and second peak-valley pairs are 16.2 dB and 22.3 dB, respectively. Using the coherent envelope amplitude difference algorithm, the measured linewidths are determined to be 6.65 kHz and 6.53 kHz. These values are highly consistent with both the laser’s nominal linewidth and the measurements obtained from the heterodyne system, further confirming the validity and reliability of the proposed method.

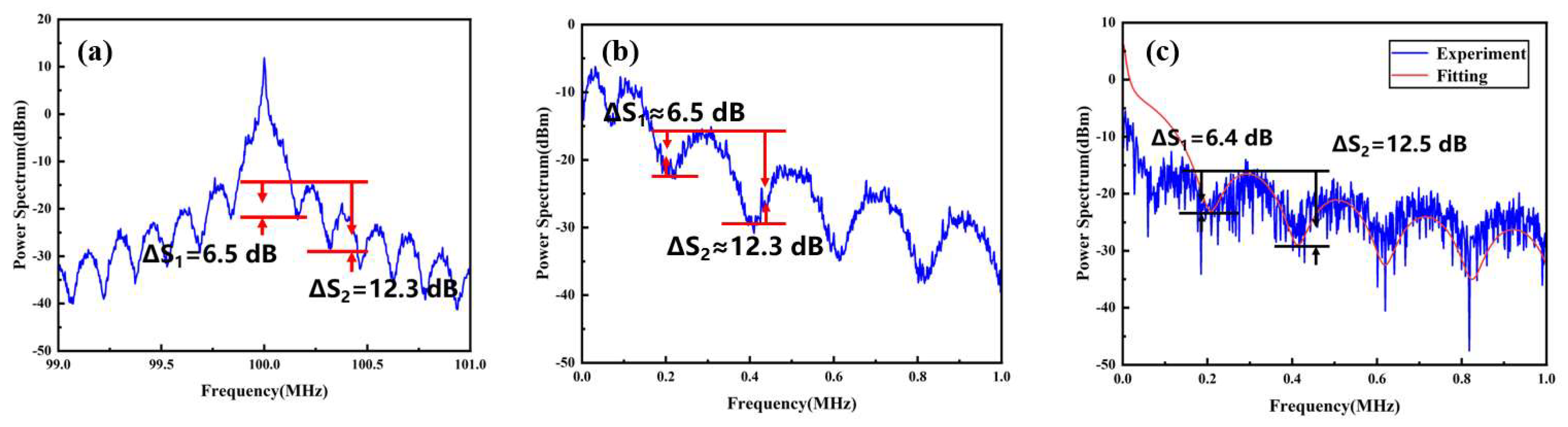
Next, the length of the delay optical fiber in the measurement system was increased from 100 m to 1000 m, and the aforementioned procedures were repeated. The frequency power spectrum obtained from the heterodyne system is shown in Figure 6a, where the amplitude differences of the first and second peak-valley pairs were measured as 6.5 dB and 12.3 dB, respectively, corresponding to calculated linewidths of 6.23 kHz and 6.55 kHz. Figure 6b presents the frequency power spectrum acquired from the spectrum analyzer in the self-homodyne system, while Figure 6c displays the spectrum obtained from the integrated system designed in this study. The spectral characteristics of both are consistent with the previous analysis. By applying theoretical spectral simulation fitting, represented by the red curve in Figure 6c, the amplitude differences of the first and second peak-valley pairs were determined to be 6.4 dB and 12.5 dB, respectively, resulting in measured linewidths of 6.37 kHz and 6.25 kHz. These results confirm that even after increasing the delay fiber length, the measurement remains accurate and reliable. Therefore, employing a short optical fiber in a delay self-homodyne system for linewidth measurement is both feasible and effective, and the integrated system proposed in this study demonstrates high accuracy and reliability. It is worth noting that at a delay fiber length of 1000 m, the actual spectral profile deviates more significantly from the ideal theoretical spectrum in the zero-frequency region and becomes more susceptible to low-frequency noise. However, this deviation does not significantly impact the envelope region, thus exerting minimal influence on the final measurement results, which can be safely disregarded. This highlights the advantage of the coherent envelope algorithm over other methods [21,33].

The linewidth values measured using the delay self-homodyne system exhibit distinct patterns compared to those obtained from the delay self-heterodyne system. Specifically, due to the influence of the noise floor, the linewidth measured from the second peak-valley pair in the heterodyne system is slightly larger than that from the first peak-valley pair [8]. In contrast, in the self-homodyne system, the linewidth measured from the second peak-valley pair is smaller than that from the first peak-valley pair, indicating that the second peak-valley measurement in the self-homodyne system is more accurate and reliable. This discrepancy arises because, in the self-homodyne system, low-frequency noise has a more significant impact than the noise floor. Furthermore, in the more distant third peak-valley and subsequent envelope regions, most spectral features are heavily affected by the noise floor, leading to a substantial decline in measurement accuracy. Therefore, when employing a short optical fiber in a delay self-homodyne system combined with the coherent envelope algorithm for linewidth measurement, selecting the second peak-valley pair in the envelope spectrum for linewidth calculation and analysis is the most accurate and reasonable approach. This selection effectively minimizes the influence of both low-frequency noise and the noise floor on the measurement results [33].

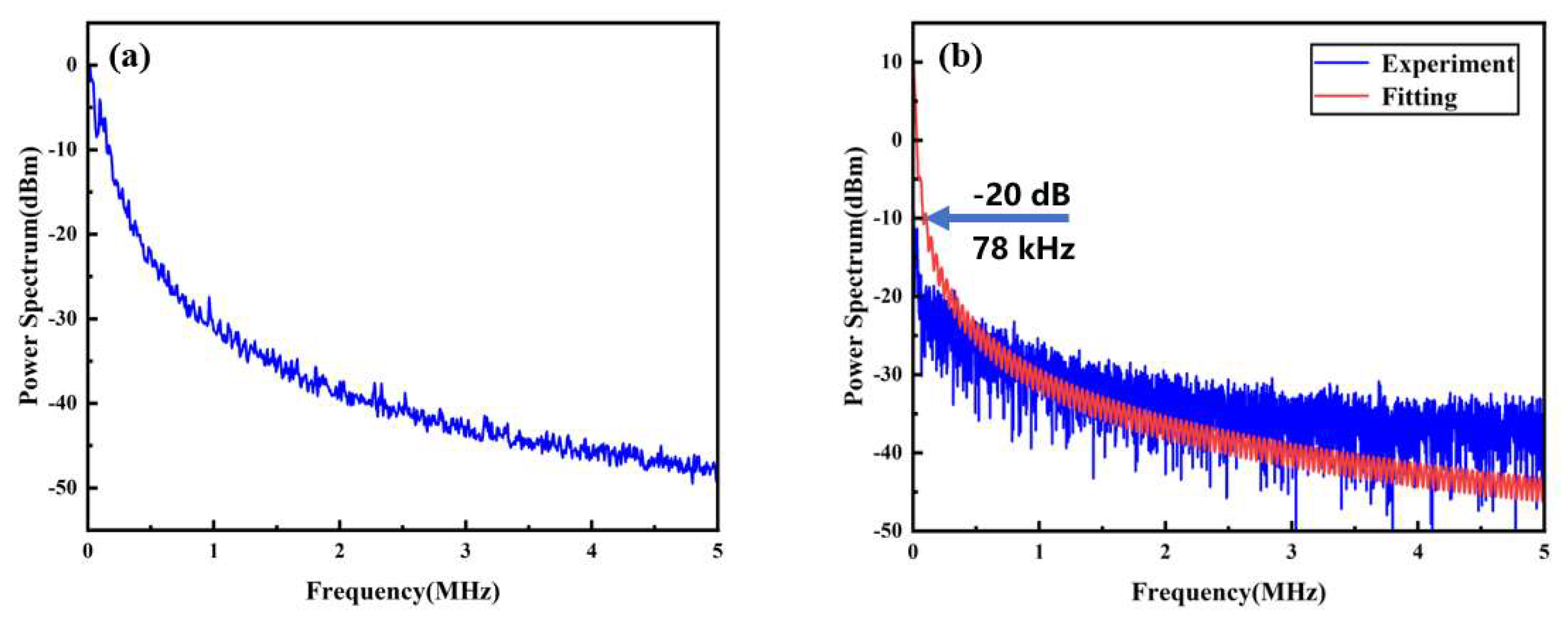
Finally, the length of the delay optical fiber in the delay self-homodyne system was increased to 5000 m for linewidth measurement. The frequency power spectra obtained from both the spectrum analyzer and the integrated system designed in this study are shown in Figure 7a and Figure 7b, respectively. When the optical fiber length was extended to 5 km, a significant degradation in the coherence characteristics of the frequency-domain power spectral density was observed, resulting in a spectrum that closely resembled a Lorentzian shape. The theoretical spectrum was simulated and fitted to the experimentally obtained spectrum, as indicated by the red curve in Figure 7b. However, due to the combined effects of low-frequency noise and 1/f noise, the fitting accuracy of the spectral line was significantly reduced. Given the poor coherence and high sensitivity to low-frequency noise at this fiber length, the Lorentzian spectrum relation was used to estimate the linewidth. The measured spectrum exhibited a −20 dB half-width of approximately 78 kHz, corresponding to an actual linewidth of about 7.8 kHz [21,31]. This value deviates considerably from both the nominal linewidth and the previously obtained measurement results. Therefore, in the system designed in this study, utilizing a short delay optical fiber in combination with the sub-coherent envelope algorithm effectively mitigates the impact of low-frequency noise, 1/f noise, and the noise floor, thereby enhancing the accuracy of linewidth measurements.

4. Conclusions

In conclusion, this study presents the design of a linewidth measurement system for narrow-linewidth lasers based on an FPGA system using the delay self-homodyne approach. By employing the developed FPGA data acquisition circuit and time–frequency conversion program, the frequency power spectrum of the laser under test is efficiently reconstructed, offering an alternative to traditional spectrum analyzers. This approach enhances both the portability and integration of the measurement device. Additionally, by selecting an optimal short delay optical fiber (preferably under 1000 m), the system minimizes the effects of low-frequency noise in the delay self-homodyne method and reduces 1/f noise introduced by long optical fibers. The integrated measurement system proposed in this work provides a novel solution for combining optoelectronic systems, enabling efficient data acquisition and processing through a cost-effective and compact FPGA-based circuit. This innovation overcomes some limitations of traditional spectrum analyzers and holds considerable significance for advancing narrow-linewidth laser measurement techniques. Moreover, this optoelectronic measurement system demonstrates great potential and broad application prospects, particularly in areas such as laser noise spectrum analysis.