Theoretical and Experimental Analysis of Optical Frequency Combs Synchronized to a Microwave Reference Achieving 10−19-Level Additional Stability
Abstract
1. Introduction
2. Theoretical Model and Experimental Implement
2.1. Theoretical Model
2.1.1. Model of Additional Phase Noise and Frequency Stability
2.1.2. Model of the n-th Harmonic Locking
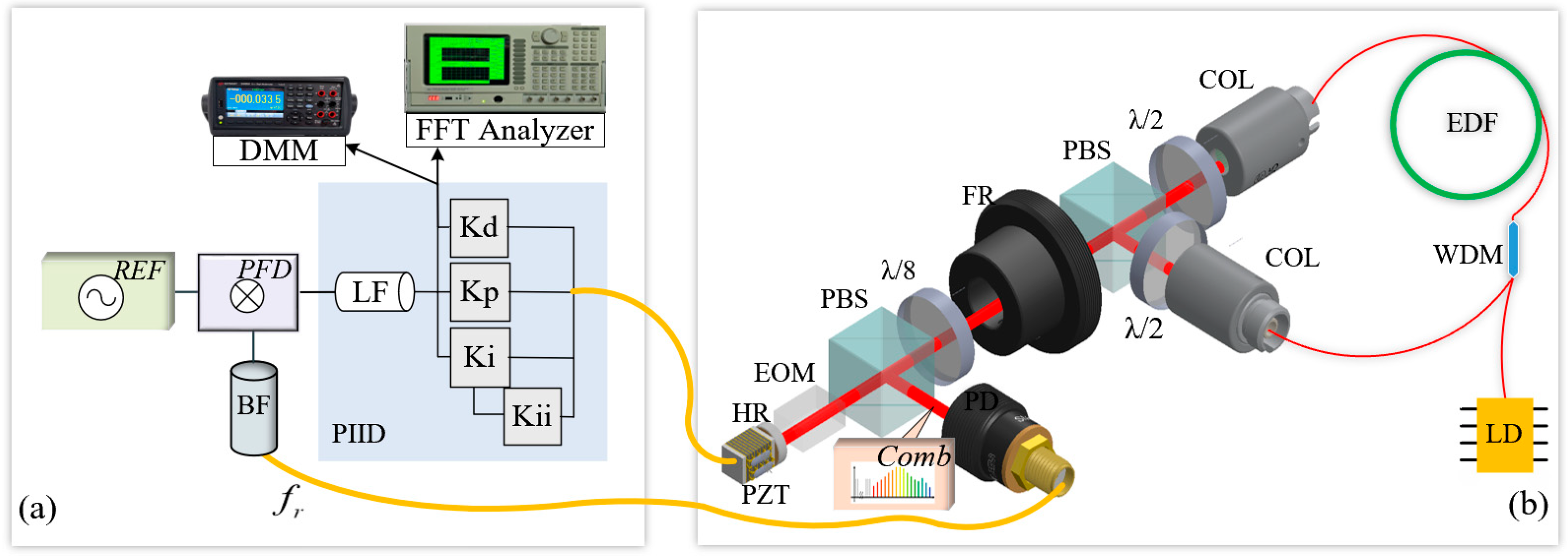
2.2. Experimental Implement
- Measured the OFC background phase noise SFree(f) utilizing a phase noise meter and the corresponding background frequency stability utilizing a frequency meter (Figure 2a);
- Simulated phase noise SLocked(f) and stability using Formulas (2) and (4) in the locked mode.
- Connected both PFD inputs to REF and measured the output voltage with a DMM (Figure 2b);
- Simulated the equivalent PFD background phase noise SPDF(f) and frequency stability via Formulas (A10)–(A12).
- Combine SFree(f), , SPDF(f), and in Formulas (5)–(6) to simulated overall additional phase noise Soverall(f) and frequency stability ;
- For n-th harmonic locking, simulated the overall additional phase noise Sn-overall(f) and frequency stability via Formulas (8)–(9).
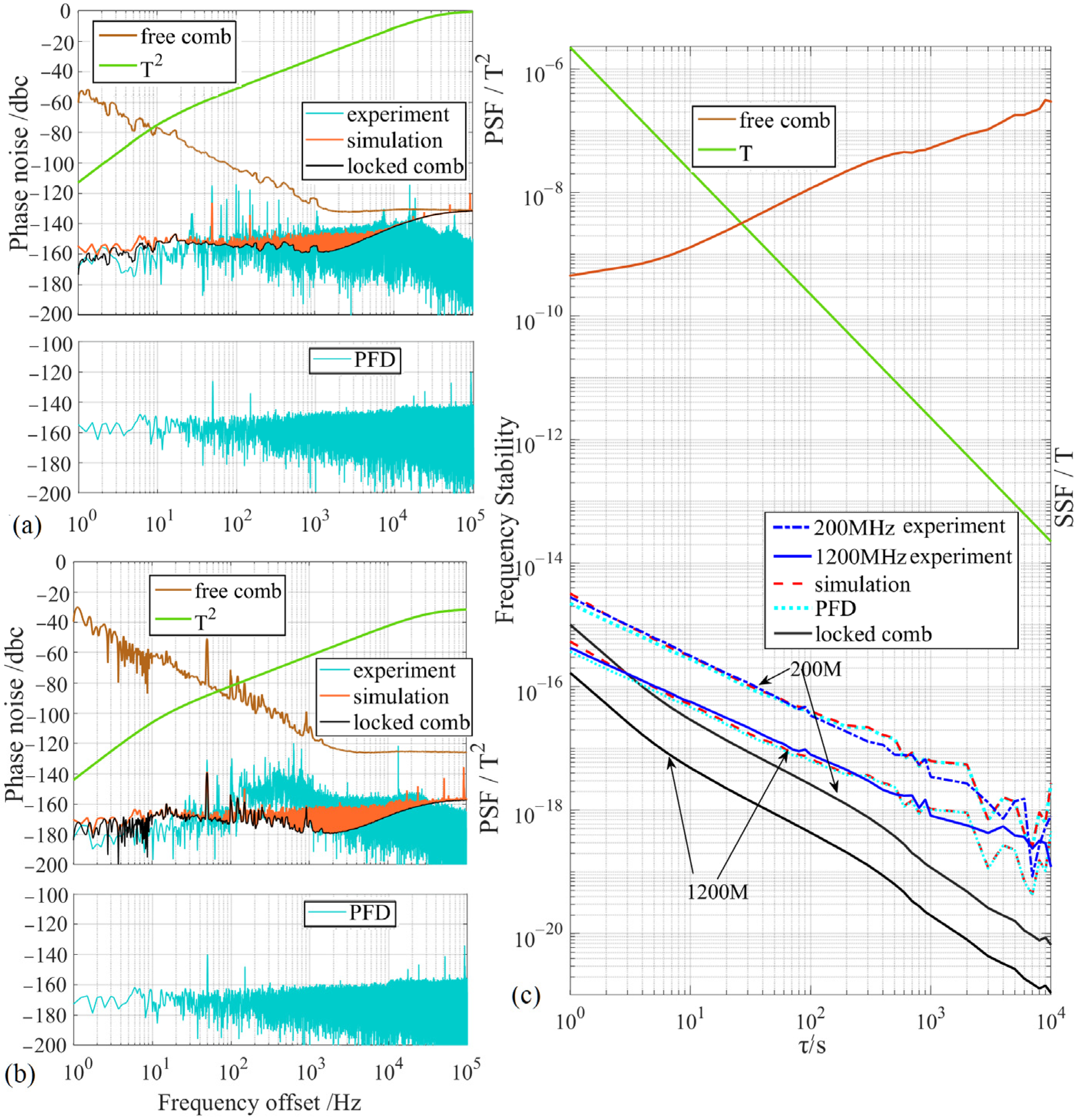
3. Experimental Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| OFCs | Optical frequency combs |
| PLL | Phase-locked loop |
| PFD | Phase frequency detector |
| PIID | A phase frequency detector and a proportional, first-order integer, second-order integer, first-order differential controller |
| PSF | Phase noise suppression factor |
| SSF | Stability suppression factor |
| REF | Radio frequency |
| RF | Microwave reference |
| SNR | Signal-to-noise ratio |
| NALM | Nonlinear amplification loop mirror |
Appendix A
Appendix A.1
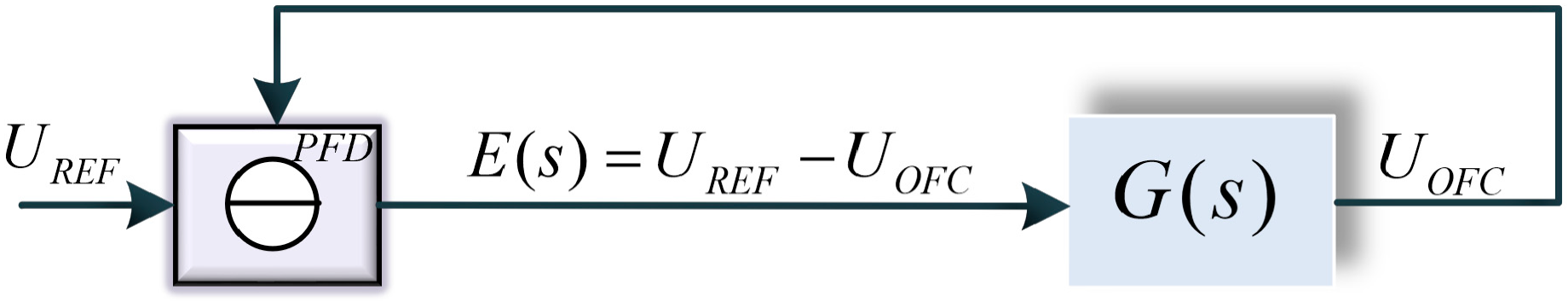
Appendix A.2
References
- Niering, M.; Holzwarth, R.; Reichert, J.; Pokasov, P.; Udem, T.; Weitz, M.; Hänsch, T.W.; Lemonde, P.; Santarelli, G.; Abgrall, M.; et al. Measurement of the Hydrogen 1s–2s Transition Frequency by Phase Coherent Comparison with a Microwave Cesium Fountain Clock. Phys. Rev. Lett. 2000, 84, 5496–5499. [Google Scholar] [CrossRef] [PubMed]
- Fortier, T.; Baumann, E. 20 years of developments in optical frequency comb technology and applications. Commun. Phys. 2019, 2, 153. [Google Scholar] [CrossRef]
- Zheng, X.; Sun, Y.R.; Chen, J.J.; Jiang, W.; Pachucki, K.; Hu, S.M. Measurement of the Frequency of the 23S-23P Transition of 4He. Phys. Rev. Lett. 2017, 119, 263002. [Google Scholar] [CrossRef] [PubMed]
- Picqué, N.; Hänsch, T.W. Frequency comb spectroscopy. Nat. Photonics 2019, 13, 146–157. [Google Scholar] [CrossRef]
- Lu, H.; Li, Z.; Wang, J.; Meng, H.; Zhao, J. Two-Way Optical Time and Frequency Transfer Over a 20-km Fiber Link Based on Optical Frequency Combs. IEEE Photonics J. 2019, 11, 1–7. [Google Scholar] [CrossRef]
- Shen, Q.; Guan, J.-Y.; Zeng, T.; Lu, Q.-M.; Huang, L.; Cao, Y.; Chen, J.-P.; Tao, T.-Q.; Wu, J.-C.; Hou, L.; et al. Experimental simulation of time and frequency transfer via an optical satellite–ground link at 10-18 instability. Optica 2021, 8, 471–476. [Google Scholar] [CrossRef]
- Jung, K.; Kim, J. Subfemtosecond synchronization of microwave oscillators with mode-locked Er-fiber lasers. Opt. Lett. 2012, 37, 2958–2960. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Yu, D.; Lu, G.; Zhang, Y.; Yu, S.; Luo, B.; Guo, H. Dual-comb-enhanced microwave clock synchronization over commercial fiber. Optica 2024, 11, 1268–1276. [Google Scholar] [CrossRef]
- Bahmanian, M.; Scheytt, J.C. A 2–20-GHz Ultralow Phase Noise Signal Source Using a Microwave Oscillator Locked to a Mode-Locked Laser. IEEE Trans. Microw. Theory Tech. 2021, 69, 1635–1645. [Google Scholar] [CrossRef]
- Yan, L.; Zhao, W.; Zhang, Y.; Zhang, P.; Zhao, C.; Zhang, X.; Guo, W.; Zhang, S.; Jiang, H. Ultra-Stable Microwave Signal Generation with Er: Fiber-Based Optical Frequency Comb. In Proceedings of the 2019 Joint Conference of the IEEE International Frequency Control Symposium and European Frequency and Time Forum (EFTF/IFC), Orlando, FL, USA, 14–18 April 2019; pp. 1–3. [Google Scholar]
- Heinecke, D.C.; Bartels, A.; Fortier, T.M.; Braje, D.A.; Hollberg, L.; Diddams, S.A. Optical frequency stabilization of a 10 GHz Ti:sapphire frequency comb by saturated absorption spectroscopy inr87ubidium. Phys. Rev. A 2009, 80, 053806. [Google Scholar] [CrossRef]
- Minamikawa, T.; Hayashi, K.; Mizuguchi, T.; Hsieh, Y.-D.; Abdelsalam, D.G.; Mizutani, Y.; Yamamoto, H.; Iwata, T.; Yasui, T. Real-Time Determination of Absolute Frequency in Continuous-Wave Terahertz Radiation with a Photocarrier Terahertz Frequency Comb Induced by an Unstabilized Femtosecond Laser. J. Infrared Millim. Terahertz Waves 2016, 37, 473–485. [Google Scholar] [CrossRef]
- Jun, Y.; Schnatz, H.; Hollberg, L.W. Optical frequency combs: From frequency metrology to optical phase control. IEEE J. Sel. Top. Quantum Electron. 2003, 9, 1041–1058. [Google Scholar] [CrossRef]
- Kim, K.; Diddams, S.A.; Westbrook, P.S.; Nicholson, J.W.; Feder, K.S. Improved stabilization of a 1.3 µm femtosecond optical frequency comb by use of a spectrally tailored continuum from a nonlinear fiber grating. Opt. Lett. 2006, 31, 277–279. [Google Scholar] [CrossRef] [PubMed]
- Leopardi, H.; Davila-Rodriguez, J.; Quinlan, F.; Olson, J.; Sherman, J.A.; Diddams, S.A.; Fortier, T.M. Single-branch Er:fiber frequency comb for precision optical metrology with 10−18 fractional instability. Optica 2017, 4, 879–885. [Google Scholar] [CrossRef]
- Ning, K.; Hou, L.; Fan, S.-T.; Yan, L.-L.; Zhang, Y.-Y.; Rao, B.-J.; Zhang, X.-F.; Zhang, S.-G.; Jiang, H.-F. An All-Polarization-Maintaining Multi-Branch Optical Frequency Comb for Highly Sensitive Cavity Ring-Down Spectroscopy. Chin. Phys. Lett. 2020, 37, 064202. [Google Scholar] [CrossRef]
- Pang, L.; Han, H.; Zhao, Z.; Liu, W.; Wei, Z. Ultra-stability Yb-doped fiber optical frequency comb with 2 × 10−18/s stability in-loop. Opt. Express 2016, 24, 28993–29000. [Google Scholar] [CrossRef] [PubMed]
- Shao, X.; Han, H.; Wang, H.; Ma, J.; Hu, Y.; Li, C.; Teng, H.; Chang, G.; Wang, B.; Wei, Z. High power optical frequency comb with 10−19 frequency instability. Opt. Express 2023, 31, 32813–32823. [Google Scholar] [CrossRef] [PubMed]
- Deng, Z.; Liu, Y.; Zhu, Z.; Luo, D.; Gu, C.; Zhou, L.; Xie, G.; Li, W. Ultra-precise optical phase-locking approach for ultralow noise frequency comb generation. Opt. Laser Technol. 2021, 138, 106906. [Google Scholar] [CrossRef]
- Zhang, P.; Zhang, Y.-Y.; Li, M.-K.; Rao, B.-J.; Yan, L.-L.; Chen, F.-X.; Zhang, X.-F.; Chen, Q.-F.; Jiang, H.-F.; Zhang, S.-G. All polarization-maintaining Er:fiber-based optical frequency comb for frequency comparison of optical clocks. Chin. Phys. B 2022, 31, 054210. [Google Scholar] [CrossRef]
- Briles, T.C.; Stone, J.R.; Drake, T.E.; Spencer, D.T.; Fredrick, C.; Li, Q.; Westly, D.; Ilic, B.R.; Srinivasan, K.; Diddams, S.A.; et al. Interlocking Kerr-microresonator frequency combs for microwave to optical synthesis. Opt. Lett. 2018, 43, 2933–2936. [Google Scholar] [CrossRef] [PubMed]
- Li, M.; Yang, X.; Rao, B.; Yan, L.; Chen, X.; Yuan, R.; Zhang, P.; Zhang, Y.; Liu, T. A low phase noise high power Er-fiber frequency comb synchronized to the hydrogen maser clock by harmonic phase locking. Front. Phys. 2023, 11, 1044842. [Google Scholar] [CrossRef]
- Fortier, T.M.; Kirchner, M.S.; Quinlan, F.; Taylor, J.; Bergquist, J.C.; Rosenband, T.; Lemke, N.; Ludlow, A.; Jiang, Y.; Oates, C.W.; et al. Generation of ultrastable microwaves via optical frequency division. Nat. Photonics 2011, 5, 425–429. [Google Scholar] [CrossRef]
- Best, R.E. Phase-Locked Loops: Design, Simulation, and Applications; McGraw-Hill Education: New York, NY, USA, 2003. [Google Scholar]
- Paschotta, R. Noise of mode-locked lasers (Part I): Numerical model. Appl. Phys. B 2004, 79, 153–162. [Google Scholar] [CrossRef]
- Sauvage, G. Phase Noise in Oscillators: A Mathematical Analysis of Leeson’s Model. IEEE Trans. Instrum. Meas. 1977, 26, 408–410. [Google Scholar] [CrossRef]
- Behzad, R. A Simple Model of Feedback Oscillator Noise Spectrum. In Monolithic Phase-Locked Loops and Clock Recovery Circuits: Theory and Design; IEEE: New York, NY, USA, 1996; pp. 180–181. [Google Scholar]
- Rubiola, E. Phase Noise and Frequency Stability in Oscillators; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Tan, W.K.; Wong, H.-Y.; Kelly, A.E.; Sorel, M.; Marsh, J.H.; Bryce, A.C. Temperature Behaviour of Pulse Repetition Frequency in Passively Mode-Locked InGaAsP/InP Laser Diode—Experimental Results and Simple Model. IEEE J. Sel. Top. Quantum Electron. 2007, 13, 1209–1214. [Google Scholar] [CrossRef]
| Locking Strategy | 1 Hz | 1 Hz (Harmonic) |
|---|---|---|
| PFD + PIID | −168.7 dBc/Hz | −182.3 dBc/Hz Δ |
| Multiplier + PI [22] | −96 dBc/Hz | −138 dBc/Hz * |
| Improvement ratio | 72.7 dB | 44.3 dB |
| Locking Strategy | τ = 1 s | τ = 8000 s | τ = 1 s (Harmonic) | τ = 8000 s (Harmonic) |
|---|---|---|---|---|
| PFD + PIID | 2.81 × 10−15 | 2.72 × 10−19 | 4.25 × 10−16 Δ | 2.80 × 10−19 Δ |
| Multiplier + PI [22] | 4.54 × 10−14 | 1.67 × 10−16 | 1.46 × 10−14 * | 4.85 × 10−17 * |
| Improvement ratio | 16.2 | 614.0 | 34.4 | 173.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Li, M.; Rao, B.; Yang, X.; Hu, Z.; Dong, R.; Zhang, S.; Zhang, P. Theoretical and Experimental Analysis of Optical Frequency Combs Synchronized to a Microwave Reference Achieving 10−19-Level Additional Stability. Photonics 2025, 12, 195. https://doi.org/10.3390/photonics12030195
Chen X, Li M, Rao B, Yang X, Hu Z, Dong R, Zhang S, Zhang P. Theoretical and Experimental Analysis of Optical Frequency Combs Synchronized to a Microwave Reference Achieving 10−19-Level Additional Stability. Photonics. 2025; 12(3):195. https://doi.org/10.3390/photonics12030195
Chicago/Turabian StyleChen, Xin, Mingkun Li, Bingjie Rao, Xiguang Yang, Zhenyuan Hu, Ruifang Dong, Shougang Zhang, and Pan Zhang. 2025. "Theoretical and Experimental Analysis of Optical Frequency Combs Synchronized to a Microwave Reference Achieving 10−19-Level Additional Stability" Photonics 12, no. 3: 195. https://doi.org/10.3390/photonics12030195
APA StyleChen, X., Li, M., Rao, B., Yang, X., Hu, Z., Dong, R., Zhang, S., & Zhang, P. (2025). Theoretical and Experimental Analysis of Optical Frequency Combs Synchronized to a Microwave Reference Achieving 10−19-Level Additional Stability. Photonics, 12(3), 195. https://doi.org/10.3390/photonics12030195





