Abstract
An analysis is performed of the response of arrays of semiconductor nano-lasers to phase-conjugate optical feedback. A comparison is made of their response to conventional mirror feedback. It is shown that phase-conjugate feedback induces a quasi-periodic route to chaos. The impact of the Purcell-enhanced spontaneous emission, which is a salient feature of nano-lasers, is also delineated for both phase-conjugate and conventional mirror feedback.
1. Introduction
The dynamical behaviour of electrically pumped semiconductor nano-lasers has been explored in some detail. Early attention was given to single semiconductor nano-lasers [1], where the effects of direct current modulation, optical injection and regular and phase-conjugate optical feedback were categorized. Attention has also been given to the phenomena which arise in coupled nano-lasers. More recently, research efforts have been directed at three-element arrays of nano-lasers, where the behaviours of linear and triangular arrays were compared and contrasted. Due to inter-element coupling, interesting dynamics arises in stand-alone three-element arrays [2], whilst arrays that are subject to external perturbation display a variety of dynamics. To date, attention has been given to three-element arrays that are subject to direct modulation, optical injection and optical feedback. The present contribution aims to explore yet another external perturbation of such arrays: phase-conjugate optical feedback (PCF).
The two key physical effects which impact the topic under exploration in the present paper are Purcell cavity-enhanced spontaneous emission [3] and phase-conjugate optical feedback. Purcell cavity-enhanced spontaneous emission is a well-established phenomenon which may have particular significance for micro- and nano-lasers [4,5]. Phase-conjugate optical feedback has also been extensively explored [6]. The salient feature of such feedback is the elimination of the optical phase change which is acquired in regular optical feedback, where the laser emission makes a round-trip of the external cavity. In general, the physical effects which are used to generate a phase-conjugate signal imply that there is a sluggishness in the response of the phase-conjugate mirror. In the present case, it is assumed that the phase-conjugate response is instantaneous.
2. Model
Figure 1 shows a schematic diagram of the semiconductor nano-laser array under phase-conjugate feedback, containing ternary linear and triangular arrays, respectively. It is assumed that an ideal phase-conjugated mirror is available, which has an instantaneous phase-conjugate response without any frequency shift in the reflected light. Based on the traditional Lang–Kobayashi (L-K) coupled-rate equations, the dynamics model of the semiconductor nano-laser array with phase-conjugate feedback is extended to include a Purcell-enhanced spontaneous emission factor F and spontaneous emission coupling factor β. In particular, the effects of the Purcell factor and spontaneous emission coupling coefficient on the spontaneous emissivity are shown by Equations (1) and (3), respectively. In contrast, the phase Equation (2) is based on the laser gain. Therefore, it is not affected by enhanced spontaneous emission. The gain compression term is not included in the equations, because the gain saturation caused by spectral hole burning is symmetrically distributed around the emission frequency.
where the subscripts ‘j’ and ‘m’ represent the jth and mth laser, respectively. M is the number of lasers in the array. t is the time. S(t) is the photon density, ϕ(t) is the optical phase, and N(t) is the carrier density. Γ is the confinement factor, τn is the carrier lifetime, gn is the differential gain, N0 is the transparency carrier density, τp is the photon lifetime, k is the coupling rate between the two lasers, α is the linewidth enhancement factor, Δω is the frequency detuning between the two lasers, I is the injection current, e is the elementary charge, and Va is the volume of the active region. The external cavity round-trip delay time is τ = 2 Lext/c. Lext is the distance from the laser surface to the phase-conjugate mirror. The feedback strength κ is defined as the rate at which the proportion of optical field is reflected back into the laser, which is derived as follows (5):
where η is the fraction of the reflected field which couples back into the lasing mode and is varied in the simulations that determine the feedback rate κ. r1 = 0.95 and r2 = 0.85 are the power reflectivities of the phase-conjugate mirror and the front laser facet, respectively. c is the speed of light in free space, n is the refractive index, and Lin = 1.39 μm is the semiconductor nano-laser internal cavity length. The structure of the nano-laser is described in [7]. The array could be two or more nano-lasers that are closely arranged with evanescent coupling from underneath the nano-lasers. The wavelength is around 1550 nm. Equations (1)–(3) were solved numerically using a fourth-order Runge–Kutta integration method. The dynamics of the nano-lasers were analysed using the device parameters given in Table 1.
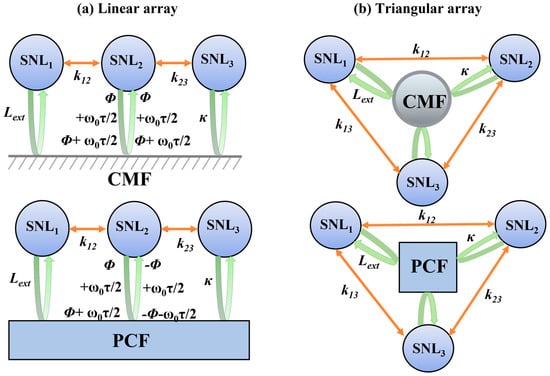
Figure 1.
A schematic diagram of the semiconductor nano−laser array subjected to conventional mirror feedback (CMF) and phase-conjugate feedback. (a) Linear array; (b) triangular array.

Table 1.
Physical meaning and value of symbols in (1)–(3).
3. Results
In order to provide a thorough portrayal of the dynamics of nano-laser arrays that are subject to phase-conjugate optical feedback, in Figure 2, we show a bifurcation diagram which characterizes a three-element linear array when subjected to increasing phase-conjugate optical feedback. It is shown that the output is successively stable (S), periodic (P), quasi-periodic (QP) and chaotic (C). The insets in Figure 2 are representative time series of the laser dynamics in the relevant regimes.
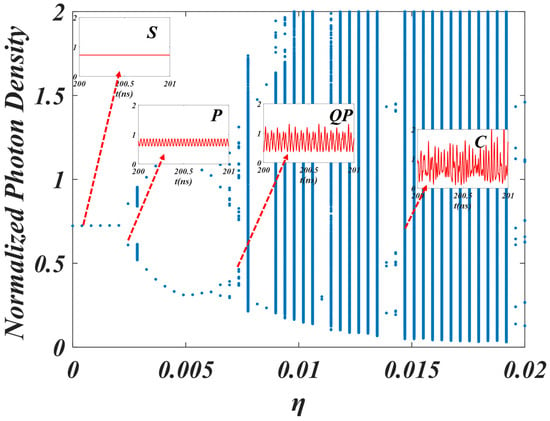
Figure 2.
The bifurcation diagram of nano-laser 2 in linear (when k12 = k23 = 5 × 108) nano-laser 3-element arrays with phase-conjugate feedback when F = 5, I = 2 Ith and Lext = 1500 μm.
In order to demonstrate the clear differences between the response of a linear three-element nano-laser array when subjected to conventional and phase-conjugate mirror feedback, Figure 3 displays the responses to both forms of feedback. Phase-conjugate feedback is shown in blue and conventional mirror feedback is shown in red. For both cases, the time series and power spectrum are shown.
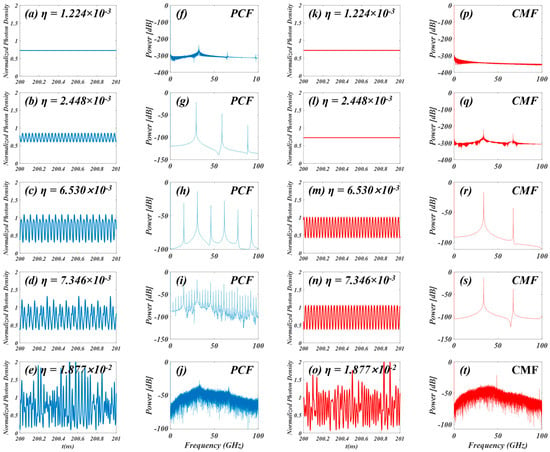
Figure 3.
Time series and corresponding spectrum of nano−laser 2 in a linear array (when k12 = k23 = 5 × 108) and nano−laser 3−element arrays with (a–j) phase-conjugate feedback (PCF) and (k–t) traditional mirror feedback (CMF) when F = 5, I = 2 Ith and Lext = 1500 μm.
From Figure 3, it can be seen that when η is small, e.g., η = 1.224 × 10−3, the nano-laser is stable for both PCF and CMF. This stability can also be confirmed by the power spectrum (Figure 3f), in which there are small and broad components at around 32 GHz, which is amplified by comparing them to the relaxation oscillation frequency of the solitary semiconductor nano-lasers, typically about 6–10 GHz.
With an increase in η to, e.g., η = 2.448 × 10−3, the semiconductor nano-laser enters the unstable region, and the photon density undergoes periodic oscillations for PCF (Figure 3b,h). The frequency of the peak in the spectrum becomes sharper.
With a further increase in η to η = 7.346 × 10−3 for PCF, the photon density exhibits quasi-periodic dynamics (Figure 3d), as evidenced by the appearance of many prominent peaks in the spectrum (Figure 3i).
When the feedback coupling factor increases to a higher value, i.e., η = 1.877 × 10−2, the peaks in the spectrum for PCF are broadened, and the floor level increases (Figure 3j) compared with the cases of stable, periodic oscillations and quasi-periodic oscillations. These two phenomena indicate the occurrence of chaos (Figure 3e).
Based on the results in Figure 3, it can be seen that for PCF, nano-laser 2 in the array follows a quasi-periodic route to chaos as the feedback strength increases, while for CMF, the nano-laser follows a period-doubling route.
As indicated above, a key feature of nano-laser behaviour is Purcell cavity-enhanced spontaneous emission. In Figure 4 and Figure 5, two-dimensional diagrams are used to characterize the dynamics when both the Purcell factor and phase-conjugate feedback strength are varied. Figure 4 presents a linear three-element array, whilst Figure 5 addresses the effects in a triangular array. Again, both figures incorporate the results for phase-conjugate and conventional mirror feedback.
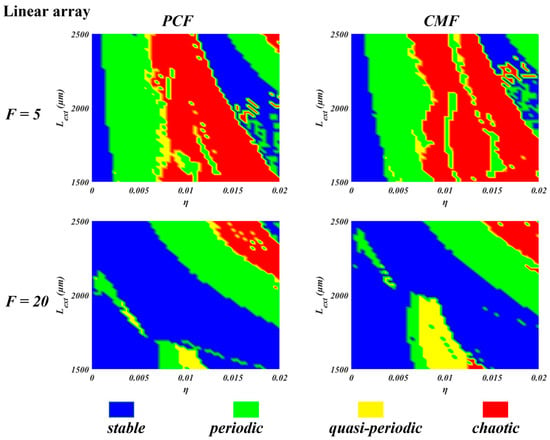
Figure 4.
The two-dimensional dynamics diagram for nano-laser 2 in the linear (when k12 = k13 = 5 × 108) array for PCF and CMF when the Purcell factor F = 5 and 20, and I = 2 Ith.
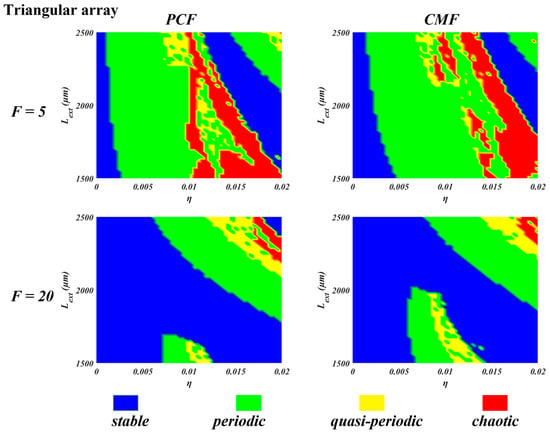
Figure 5.
The two-dimensional dynamics diagram of nano-laser 2 in the triangular (when k12 = k23 = k13 = 5 × 108) array for PCF and CMF when the Purcell factor F = 5 and 20, and I = 2 Ith.
As would be expected, Figure 4 incorporates the principal dynamical regimes which were revealed by the bifurcation diagram in Figure 2. The salient effect of increasing the strength of the Purcell enhancement is to dampen the dynamics, resulting in expanded domains of stability. For the smaller value, 5, of the Purcell factor, there is a relatively small difference in the PCF and CMF responses. The principal distinction between PCF and CMF for the larger value of the Purcell factor, 20, is the suppression of the quasi-periodic behaviour, which is prominent in the case of CMF.
Considering the case of a triangular array in Figure 5, the dominant feature is expanded areas of periodic behaviour relative to that found for linear arrays. It is also seen that chaotic regimes are relatively more easily accessed under PCF in the case of a lower Purcell factor, but otherwise, there are strong similarities between PCF and CMF. For the larger Purcell factor, enlarged regions of stability are again apparent, and, as in the case of linear arrays, there appears to be a lower propensity for quasi-periodic behaviour under PCF with the larger Purcell factor.
4. Conclusions
It has been shown that the application of phase-conjugate optical feedback to arrays of nano-lasers induces dynamical scenarios which are distinct from those appearing when conventional optical feedback is applied to such arrays. In particular, it was found that, subject to phase-conjugate optical feedback, a quasi-periodic route to chaos is followed. With respect to the influence of Purcell-enhanced spontaneous emission, a distinguishing feature of nano-lasers, it was found that its primary effect is to broaden the regions of stability. The experimental demonstration of the effects explored here is contingent on the availability of electrically pumped nano-lasers, and hence, early confirmations of the present predictions are not anticipated.
Author Contributions
Conceptualization, K.A.S.; methodology, Y.F. and K.A.S.; software, J.Z.; validation, J.Z. and K.A.S.; formal analysis, Y.F. and K.A.S.; investigation, Y.F. and K.A.S.; resources, Y.F.; data curation, J.Z.; writing—original draft preparation, Y.F. and K.A.S.; writing—review and editing, Y.F., J.Z. and K.A.S.; visualization, J.Z.; supervision, K.A.S.; project administration, Y.F.; funding acquisition, Y.F. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Key Research and Development Program of Zhejiang Province under Grant No. 2025C01197(SD2).
Institutional Review Board Statement
Not applicable.
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Jiang, P.; Zhou, P.; Li, N.; Mu, P.; Li, X. Optically Injected Nano-lasers for Time-Delay Signature Suppression and Communications. Opt. Express 2020, 28, 26421. [Google Scholar] [CrossRef] [PubMed]
- Fan, Y.; Shore, K.A.; Shao, X. Dynamics of Electrically Pumped Semiconductor Nano-Laser Arrays. Photonics 2023, 10, 1249. [Google Scholar] [CrossRef]
- Purcell, E.M. Spontaneous emission probabilities at radio frequencies. Phys. Rev. 1946, 69, 681. [Google Scholar]
- Gu, Q.; Slutsky, B.; Vallini, F.; Smalley, J.S.; Nezhad, M.P.; Frateschi, N.C.; Fainman, Y. Purcell effect in sub-wavelength semiconductor lasers. Opt. Express 2013, 21, 15603–15617. [Google Scholar] [CrossRef] [PubMed]
- Romeira, B.; Fiore, A. Purcell Effect in the Stimulated and Spontaneous Emission Rates of Nanoscale Semiconductor Lasers. IEEE J. Quantum Electron. 2018, 54, 2000412. [Google Scholar] [CrossRef]
- Agrawal, G.P.; Gray, G.R. Effect of phase-conjugate feedback on the noise characteristics of semiconductor lasers. Phys. Rev. A 1992, 46, 5890–5898. [Google Scholar] [CrossRef] [PubMed]
- Gu, Q.; Shane, J.; Vallini, F.; Wingad, B.; Smalley, J.S.; Frateschi, N.C.; Fainman, Y. Amorphous Al2O3 shield for thermal management in electrically pumped metallo-dielectric nanolasers. IEEE J. Quantum Electron. 2014, 50, 499–509. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).