High-Efficiency Hemispherical Short-Cavity Continuous-Wave Yb:YAG Laser by High-Intensity Pumping
Abstract
1. Introduction
2. Materials and Methods
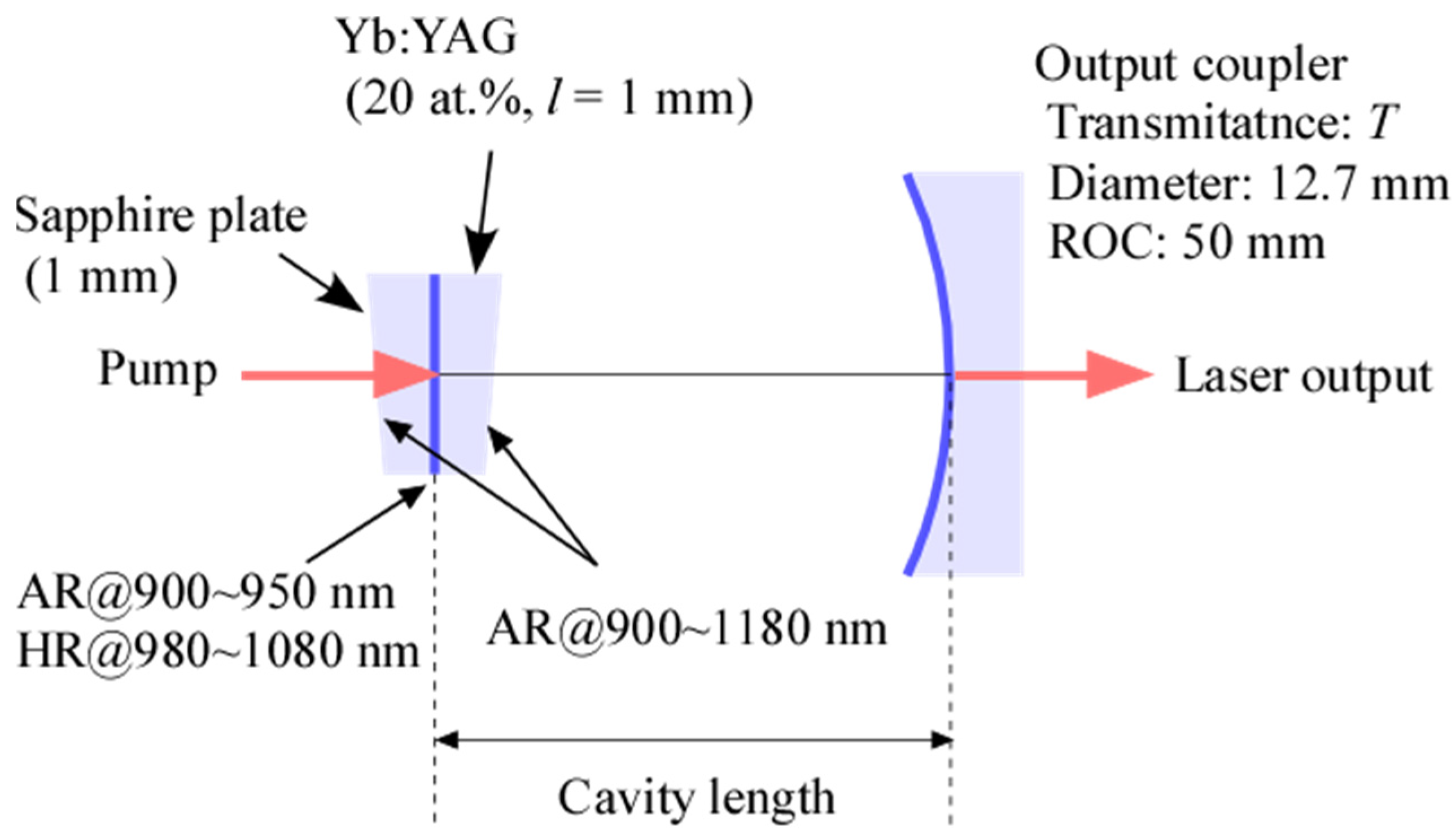
2.1. Experiment with the Hemispherical Short-Cavity Yb:YAG Laser
2.2. Quasi-Four-Level Laser Theory Including the Spatial Distribution of Pump and Laser Modes
3. Results
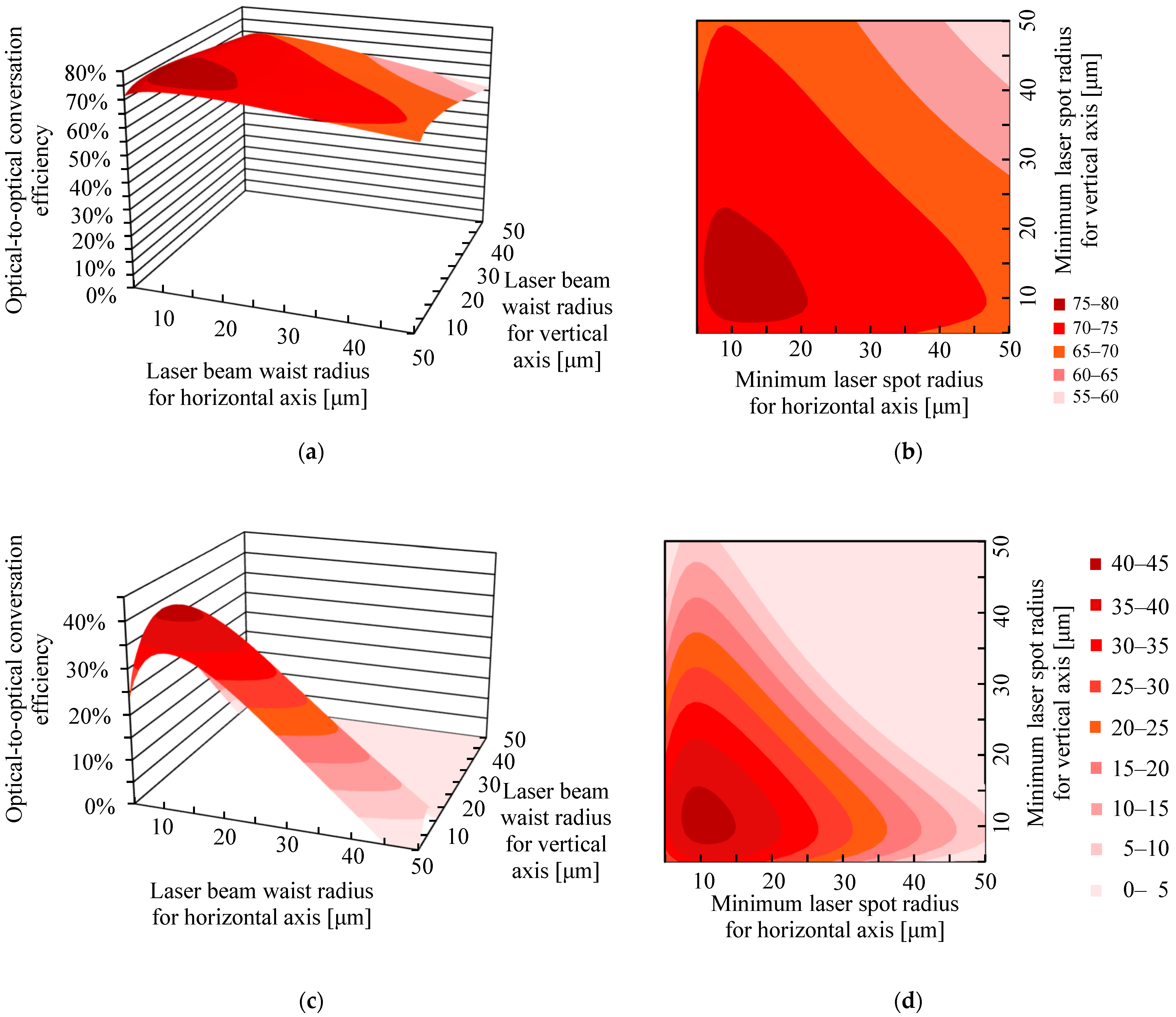
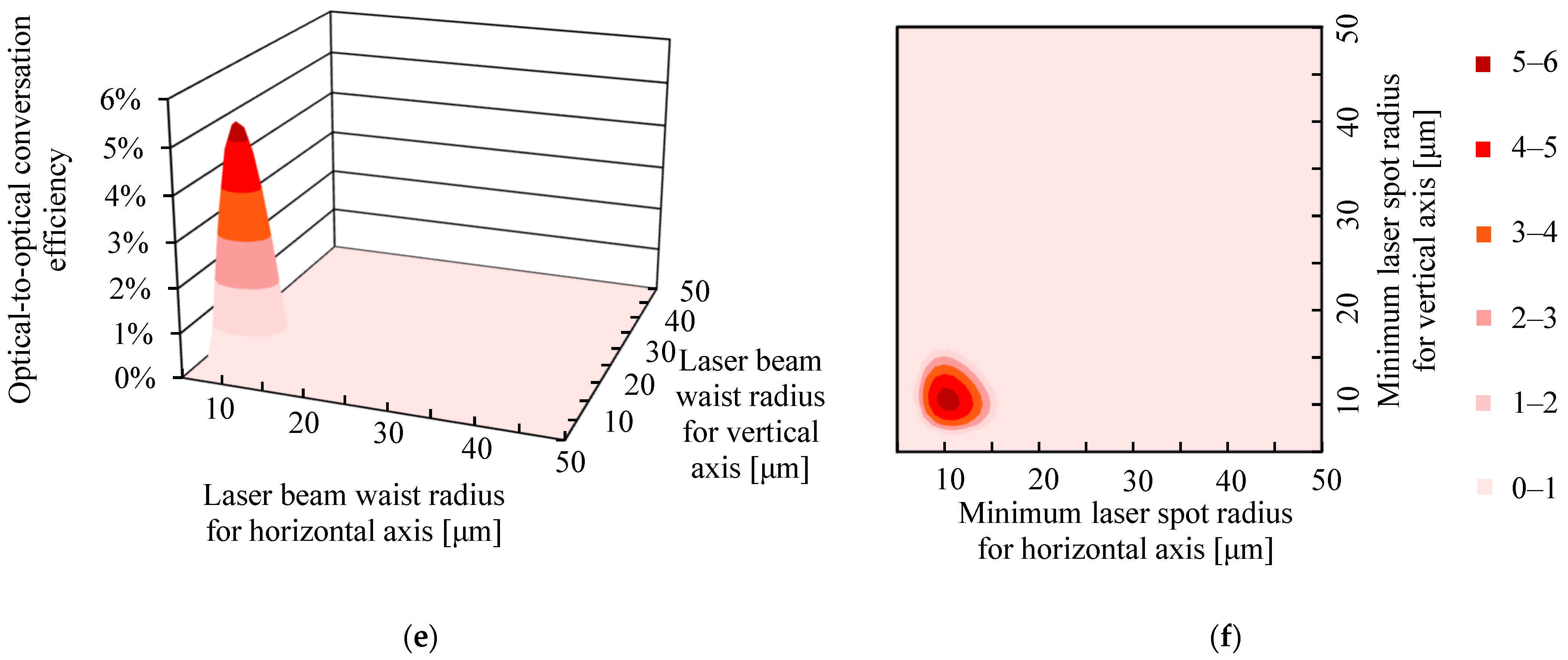
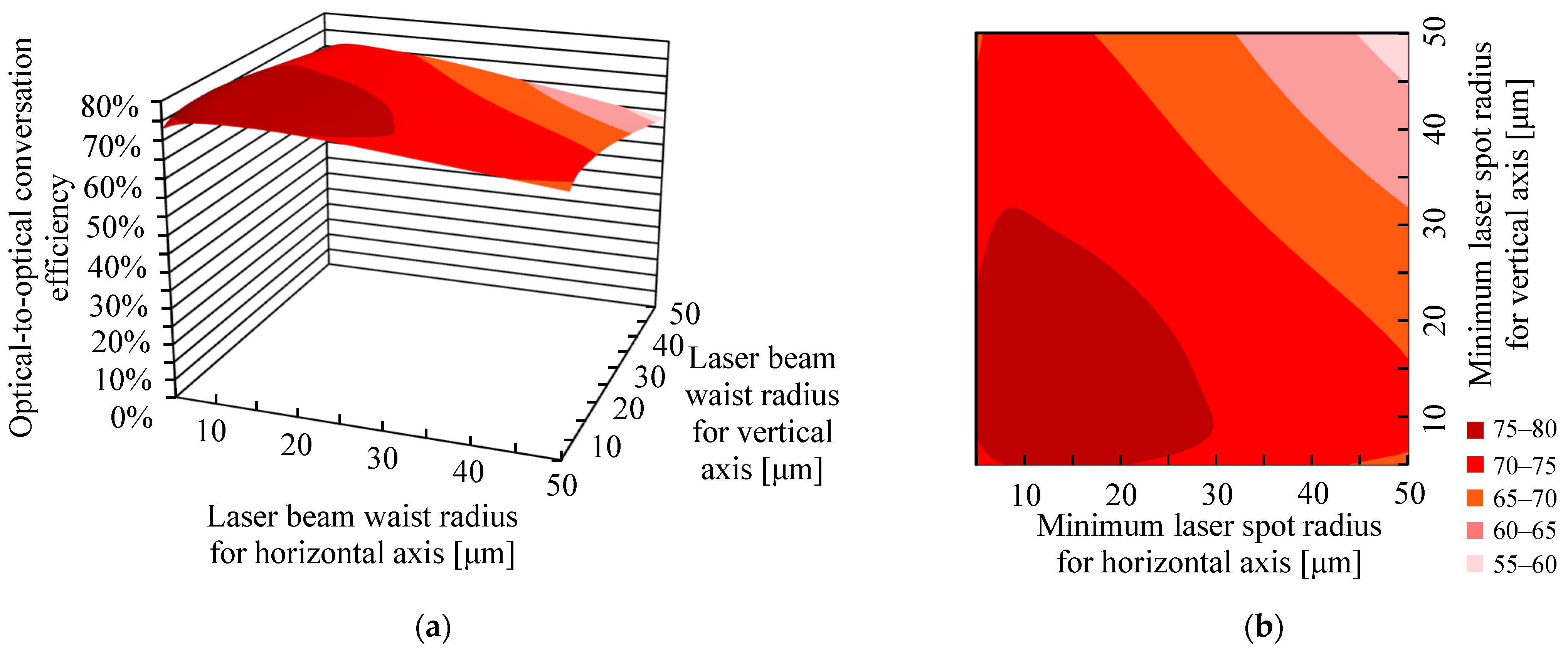
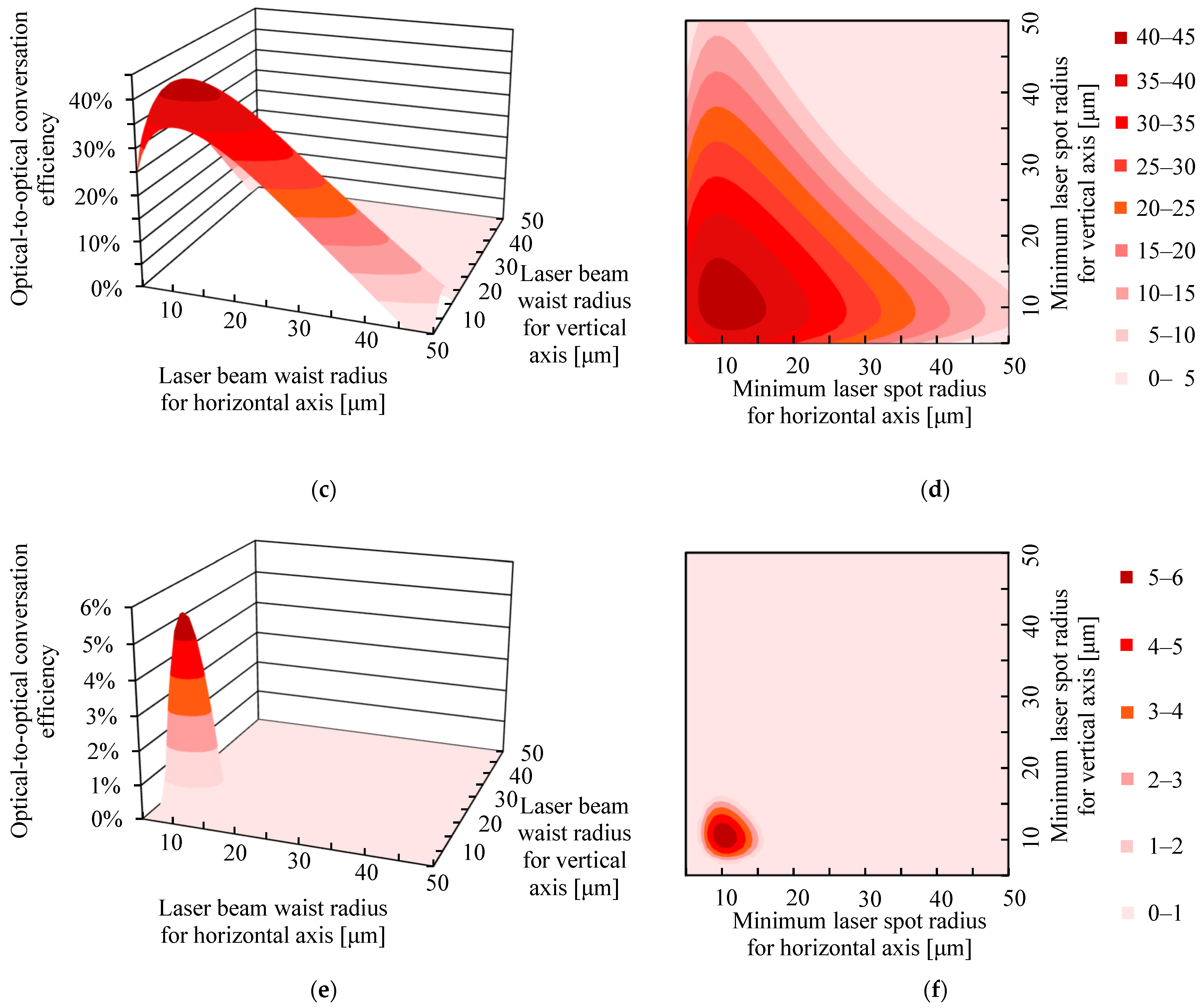
3.1. Theoretical Results for the Dependence of the Optical-to-Optical Conversion Efficiency on the Laser Beam Waist Radii
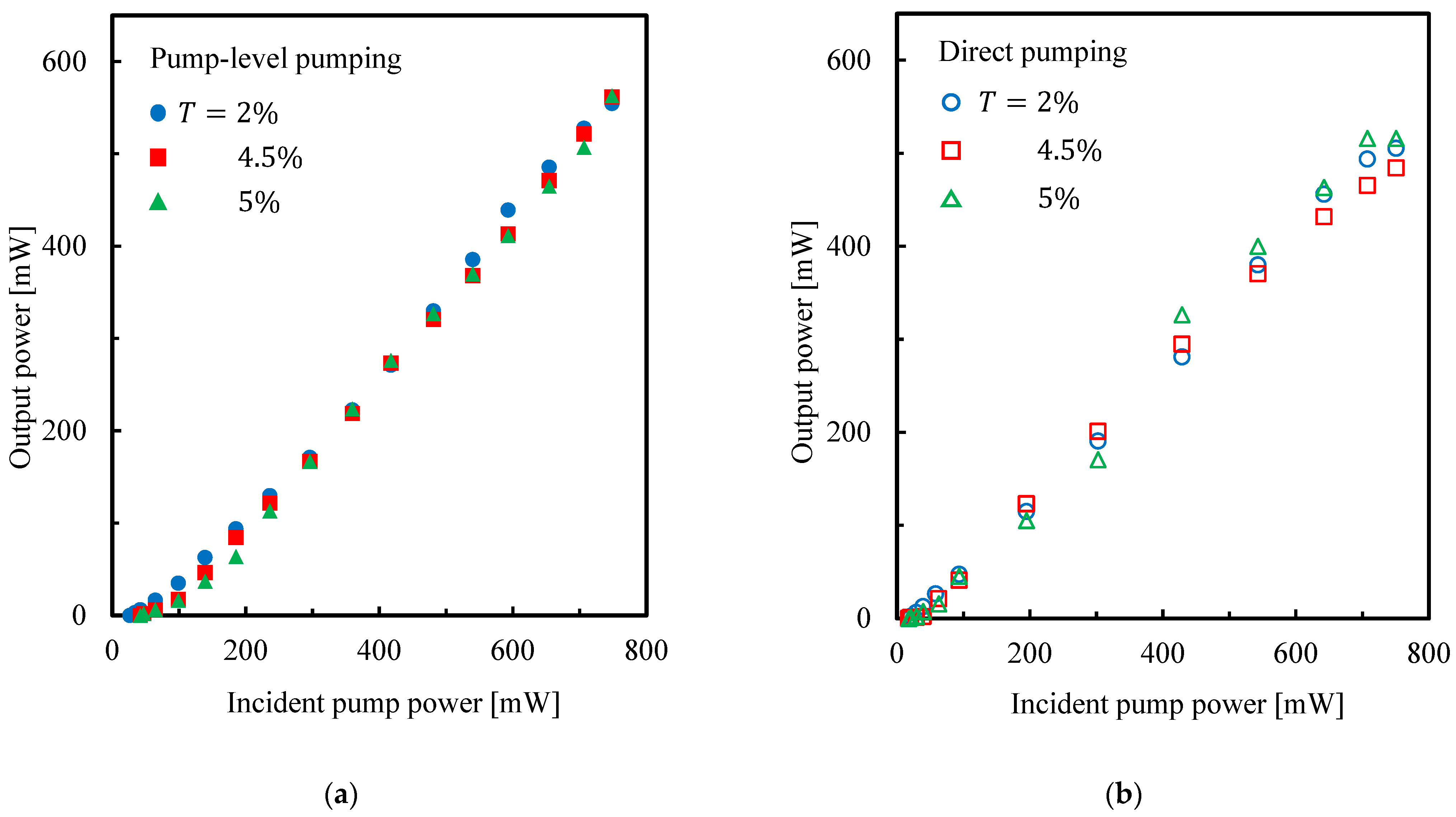
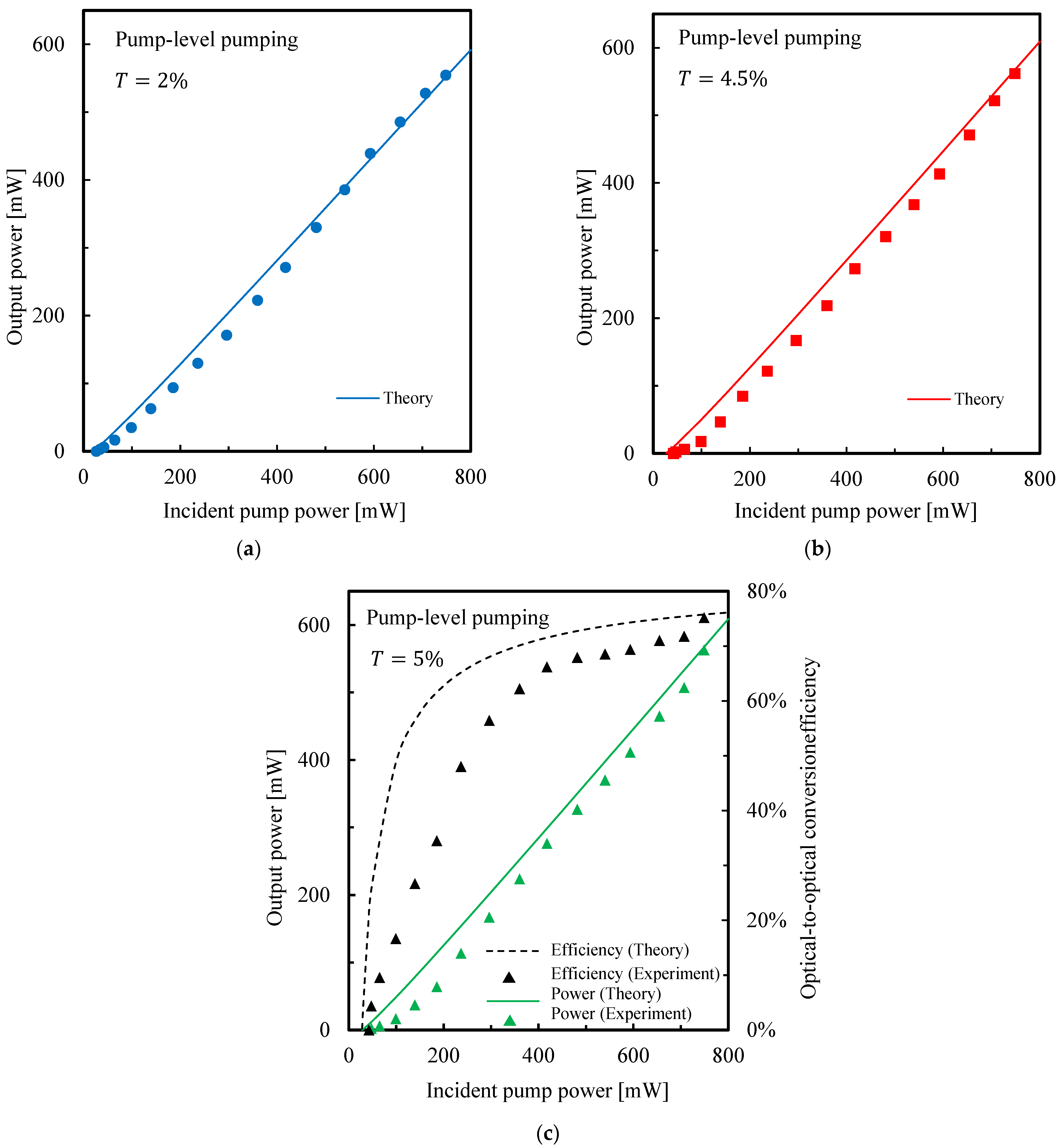
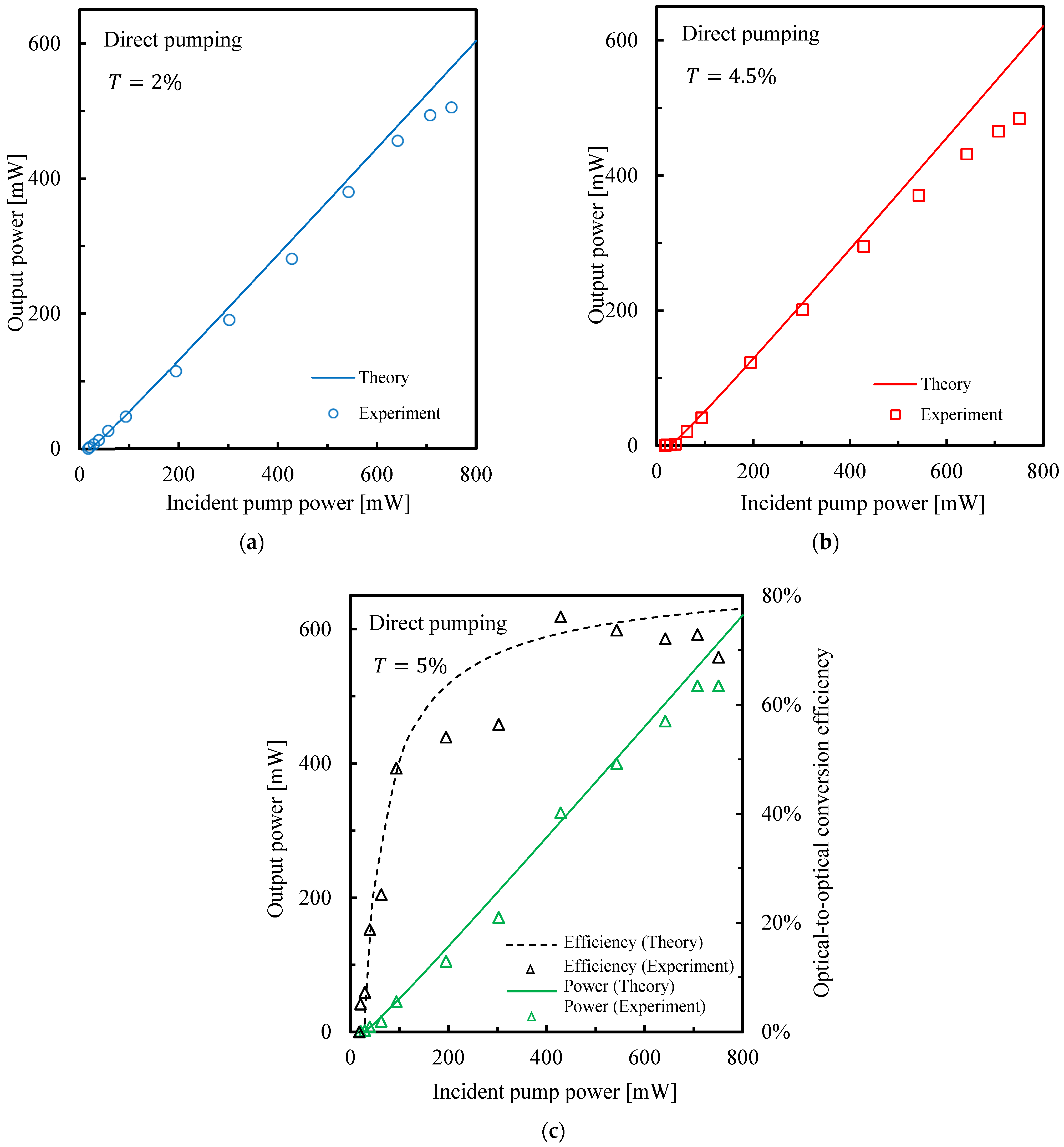
3.2. Experimental Results for Input–Output Characteristics
4. Discussion
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Johnson, L.F.; Geusic, J.E.; Van Uitert, L.G. Coherent oscillations from Tm3+, Ho3+, Yb3+ and Er3+ ions in yttrium aluminum garnet. Appl. Phys. Lett. 1965, 7, 127–129. [Google Scholar] [CrossRef]
- Reinberg, A.R.; Riseberg, L.A.; Brown, R.M.; Wacker, R.W.; Holton, W.C. GaAs: Si LED Pumped Yb-Doped YAG Laser. Appl. Phys. Lett. 1971, 19, 11–13. [Google Scholar] [CrossRef]
- Lacovara, P.; Choi, H.K.; Wang, C.A.; Aggarwal, R.L.; Fan, T.Y. Room-temperature diode-pumped Yb:YAG laser. Opt. Lett. 1991, 16, 1089–1091. [Google Scholar] [CrossRef] [PubMed]
- Taira, T. Yb solid state lasers. Jpn. J. Opt. 1999, 28, 435–442. [Google Scholar]
- Pavel, N.; Saikawa, J.; Taira, T. Radial-Pumped Microchip High-Power Composite Yb:YAG laser: Design and Power Charac-teristics. Jpn. J. Appl. Phys. 2001, 40, 146–152. [Google Scholar] [CrossRef]
- Shoji, T.; Tokita, S.; Kawanaka, J.; Fujita, M.; Izawa, Y. Quantum-defect-limited operation of diode-pumped Yb:YAG laser at low temperature. Jpn. J. Appl. Phys. 2004, 43, L496–L498. [Google Scholar] [CrossRef]
- Ripin, D.J.; Ochoa, J.R.; Aggarwal, R.L.; Fan, T.Y. 165-W cryogenically cooled Yb:YAG laser. Opt. Lett. 2004, 29, 2154–2156. [Google Scholar] [CrossRef]
- Giesen, A.; Hügel, H.; Voss, A.; Wittig, K.; Brauch, U.; Opower, H. Scalable concept for Diode-Pumped High-Power Solid-state Lasers. Appl. Phys. B 1994, 58, 365–372. [Google Scholar] [CrossRef]
- Peters, R.; Kränkel, C.; Petermann, K.; Huber, G. Broadly tunable high-power Yb:Lu2O3 thin disk laser with 80% slope efficiency. Opt. Express 2007, 15, 7075–7082. [Google Scholar] [CrossRef]
- Stolzenburg, C.; Voss, A.; Graf, T.; Larionov, M.; Giesen, A. Advanced pulsed thin disk laser sources. Soc. Photo-Opt. Instrum. Eng. 2008, 6871, 137–150. [Google Scholar] [CrossRef]
- Hanna, D.C.; Percival, R.M.; Perry, I.R.; Smart, R.G.; Suni, P.J.; Townsend, J.E.; Tropper, A.C. Contiuous-wave oscillation of a monomode ytterbium-doped fiber laser. Electron. Lett. 1988, 24, 1111–1113. [Google Scholar] [CrossRef]
- Armitage, J.R.; Wyatt, R.; Ainslie, B.J.; Craig-Ryan, S.P. Efficient 980-nm Operation of a Yb3+-Doped Silica Fiber Laser. In Advanced Solid State Lasers; OSA Proceedings Series 1989; Optica Publishing Group: Washington, DC, USA, 1989; p. JJ2. [Google Scholar] [CrossRef]
- Jeong, Y.; Sahu, J.K.; Payne, D.N.; Nilsson, J. Ytterbium-doped large-core fiber laser with 1.36 kW continuous-wave output power. Opt. Express 2004, 12, 6088–6092. [Google Scholar] [CrossRef] [PubMed]
- Matsubara, S.; Ueda, T.; Kawato, S.; Kobayashi, T. Highly Efficient Continuous-Wave Laser Oscillation in Microchip Yb:YAG Laser at Room Temperature. Jpn. J. Appl. Phys. 2007, 46, L132–L134. [Google Scholar] [CrossRef]
- Takama, M.; Matsubara, S.; Ueda, T.; Inoue, M.; Tanaka, M.; Otani, K.; Kawato, S.; Kobayashi, T. Highly efficient nanosecond-pulse Yb:YAG laser. Smart Process. Technol. 2007, 2, 281–283. [Google Scholar]
- Kawato, S.; Kadoya, H.; Sugiki, F.; Kobayashi, R.; Kanetake, T.; Nakajima, N.; Kataoka, S. Laser efficiency improvement on hemispherical short cavity lasers by high intensity pumping. In Proceedings of the EMN Angkor Meeting & CC Physical Chemistry, Ankor, Cambodia, 12–13 March 2018; p. A14. [Google Scholar]
- Kawato, S. Influence of High-Intensity Pumping on Gain Medium Temperature Increase and Laser Mode Tunability in a Hemispherical Short Cavity. Photonics 2023, 10, 1239. [Google Scholar] [CrossRef]
- Newman, R. Excitation of the Nd3+ Fluorescence in CaWO4 by Recombination Radiation in GaAs. J. Appl. Phys. 1963, 34, 437. [Google Scholar] [CrossRef]
- Fan, T.Y.; Byer, R.L. Diode Laser-Pumped Solid-State Lasers. IEEE J Quantum Electron. 1988, 24, 895–912. [Google Scholar] [CrossRef]
- Loiko, P.; Serres, J.M.; Mateos, X.; Xu, X.; Xu, J.; Jambunathan, V.; Navratil, P.; Lucianetti, A.; Mocek, T.; Zhang, X.; et al. Microchip Yb:CaLnAlO_4 lasers with up to 91% slope efficiency. Opt. Lett. 2017, 42, 2431–2434. [Google Scholar] [CrossRef]
- Liu, J.; Griebner, U.; Petrov, V.; Zhang, H.; Zhang, J.; Wang, J. Efficient continuous-wave and Q-switched operation of a diode-pumped Yb:Klu(WO4)2Yb:Klu(WO4)2 laser with self-Raman conversion. Opt. Lett. 2005, 30, 2427–2429. [Google Scholar] [CrossRef]
- Kawato, S.; Kobayashi, T. Design of End-Pumped Thin Rod Yb:YAG Laser Amplifiers. Jpn. J. Appl. Phys. 2003, 42, 2705–2710. [Google Scholar] [CrossRef]
- Kubodera, K.; Otsuka, K. Single-transverse-mode LiNdP4O12 slab waveguide laser. J. Appl. Phys. 1979, 50, 653–659. [Google Scholar] [CrossRef]
- Fan, T.Y.; Byer, R.L. Medeling and CW Operation of a Quasi-Three-Level 946 nm Nd:YAG Laser. IEEE J. Quantum Electron. 1987, 23, 605–612. [Google Scholar] [CrossRef]
- Risk, W.P. Modeling of longitudinally pumped solid-state lasers exhibiting reabsorption losses. J. Opt. Soc. Am. 1988, 5, 1412–1423. [Google Scholar] [CrossRef]
- Taira, T.; Tuloch, M.W.; Byer, L.R. Modeling of quasi-three-level lases and operation of cw Yb:YAG lasers. Appl. Opt. 1997, 20, 1867–1874. [Google Scholar] [CrossRef]
- Sumida, S.D.; Fan, Y.T. Effect of radiation trapping on fluorescence lifetime and emission cross section measurements in solid-state laser media. Opt. Lett. 1994, 19, 1343–1345. [Google Scholar] [CrossRef]
- Krupke, F.W. Ytteribium Solid-State Lasers—The First Decate. IEEE J. Quantum Electron. 2000, 6, 1287–1296. [Google Scholar] [CrossRef]
- Koechner, W. Section 2.6. Yb:YAG. Solid State Laser Engineering, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 97–101. [Google Scholar]
- Findlay, D.; Clay, R.A. The Measument of internal losses in 4-level lasers. Phys. Lett. 1966, 20, 277–278. [Google Scholar] [CrossRef]
- Koechner, W. Sections 5.1.3. Resonator Configurations—5.1.4. Stability of Laser Resonators Solid State Laser Engineering, 6th ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 217–222. [Google Scholar]
- Yariv, A.; Yeh, P. Section 4.4. Mode Stability Criteria. In Photonics, Optical Electronics in Mordern Communications, 6th ed.; Oxford University Press: New York, NY, USA, 2007; pp. 176–177. [Google Scholar]
- Oezisik, M.N. Heat Conduction, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 1993; p. 10. [Google Scholar]
- Whitaker, S. Elementary Heat Transfer Analysis; Pergamon Unified Engineering Series; Pergamon Press Inc.: New York, NY, USA, 1976; p. 4. [Google Scholar]
- Russbueldt, P.; Mans, T.; Rotarius, G.; Weitenberg, J.; Hoffmann, H.D.; Poprawe, R. 400W Yb:YAG Innoslab fs-Amplifier. Opt. Express 2009, 17, 12230–12245. [Google Scholar] [CrossRef]
- Sueda, K.; Takahashi, H.; Kawato, S.; Kobayashi, T. High-efficiency laser-diodes-pumped microthickness Yb:Y3Al5O12 slab laser. Appl. Phys. Lett. 2005, 87, 151110. [Google Scholar] [CrossRef]
- Chenais, S.; Balembois, F.; Druon, F.; Lucas-Leclin, G.; Georges, P. Thermal lensing in diode-pumped ytterbium Lasers-Part I: Theoretical analysis and wavefront measurements. IEEE J. Quantum Electron. 2004, 40, 1217–1234. [Google Scholar] [CrossRef]
- Chénais, S.; Druon, F.; Forget, S.; Balembois, F.; Georges, P. On thermal effects in solid-state lasers: The case of ytterbium-doped materials. Prog. Quantum Electron. 2006, 30, 89–126. [Google Scholar] [CrossRef]
- Dong, J.; Shirakawa, A.; Ueda, K.; Kaminskii, A. Effect of ytterbium concentration on cw Yb:YAG microchip laser performance at ambient temperature—Part I: Experiments. Appl. Phys. B 2007, 89, 359–365. [Google Scholar] [CrossRef]
- Pirri, A.; Toci, G.; Alderighi, A.; Vannini, M. Effects of the excitation density on the laser output of two different doped Yb:YAG ceramics. Opt. Express 2010, 18, 17262–17272. [Google Scholar] [CrossRef] [PubMed]
- Brauch, U.; Röcker, C.; Graf, T.; Ahmed, M.A. High-power, high-brightness solid-state laser architectures and their characteristics. Appl. Phys. B 2022, 128, 58. [Google Scholar] [CrossRef]
- Shang, P.; Bai, L.; Wang, S.; Cai, D.; Li, B. Research progress on thermal effect of LD pumped solid state laser. Opt. Laser Technol. 2023, 157, 108640. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kawato, S. High-Efficiency Hemispherical Short-Cavity Continuous-Wave Yb:YAG Laser by High-Intensity Pumping. Photonics 2025, 12, 174. https://doi.org/10.3390/photonics12030174
Kawato S. High-Efficiency Hemispherical Short-Cavity Continuous-Wave Yb:YAG Laser by High-Intensity Pumping. Photonics. 2025; 12(3):174. https://doi.org/10.3390/photonics12030174
Chicago/Turabian StyleKawato, Sakae. 2025. "High-Efficiency Hemispherical Short-Cavity Continuous-Wave Yb:YAG Laser by High-Intensity Pumping" Photonics 12, no. 3: 174. https://doi.org/10.3390/photonics12030174
APA StyleKawato, S. (2025). High-Efficiency Hemispherical Short-Cavity Continuous-Wave Yb:YAG Laser by High-Intensity Pumping. Photonics, 12(3), 174. https://doi.org/10.3390/photonics12030174




