Research on the High Tolerance Flexible Support Structure for the Primary Mirror in Cassegrain Optical Systems

Abstract

Conventional mirror support structures often fail to meet optical system tolerances due to inadequate mitigation of the installation stresses caused by machining-induced surface irregularities and inclinations. This study proposes a novel single-point central support using an arc-shaped flexible hinge. Materials for the mirror and support structure are carefully selected based on their properties, and the optimal dimensions are determined through stiffness analysis. The new flexible support structure is detailed in this work. Simulations show that the mirror assembly achieves a first-order frequency of 296.66 Hz. Under separate triaxial gravitational and thermal loads at −40 °C and 50 °C, the mirror’s surface figure accuracy RMS remains better than λ/45 (λ = 632.8 nm). With a 0.008 mm forced displacement applied to the installation surface, the RMS change in the mirror’s surface figure is less than λ/200, meeting structural design specifications. In practical assembly tests, even when surface irregularities exceed tolerances by more than double, the RMS change in the mirror’s surface figure is only 7 nm. This design effectively ensures high-precision surface quality while significantly reducing assembly difficulty and installation surface precision requirements, achieving a large-tolerance assembly. It provides a valuable reference for mirror support design in imaging optical systems.

1. Introduction

Amidst the burgeoning advancement in optical technology, optical systems have come to occupy a pivotal position in fields as diverse as national production, astronomical exploration, and the earth sciences [1,2,3,4,5]. Mirrors, as integral components of optical systems, are subject to increasingly stringent requirements. Typically, the form tolerance of mirrors needs to meet the demands of a few micrometers or several arcseconds, and the surface figure error of optical lenses usually needs to be maintained within a fraction or even a few percent of the operating wavelength. However, in the actual use of optical instruments, mirrors are inevitably affected by external environmental factors such as temperature changes, impact, vibration, and overload, causing changes in their position and surface figure, which in turn leads to the degradation of the system’s optical performance [6,7]. Therefore, it is necessary to consider the impact of force and thermal environments on the mirror assembly. Statics mainly involve stiffness deformation and mirror figure deformation under the influence of gravity and temperature changes, while dynamics mainly consider the first-order vibration frequency of the assembly to determine whether it is within the operating frequency range, avoiding resonance that could arise from a too-low first-order frequency. The flexible joint, serving as the connection channel between the mirror and the main structure of the camera, can effectively eliminate the impact of the above-mentioned environments through its own deformation and is a key technology in the design of mirror assemblies.

Scholars at home and abroad have conducted extensive research on the design and optimization of mirrors and their supports. Zhongyao Zhu et al. designed a novel dual-axis arc-shaped flexible support structure that reduces the impact of temperature on mirror assemblies while enhancing structural stiffness. For each gravity acceleration of 1 g, within the temperature range from 16 to 24 °C, carrying a forced displacement of 5 µm, the RMS value of the mirror component can reach 1/55λ (λ = 632.8 nm), and the first-order mode reached 179.6 Hz [8]. Jiaqi Zhang et al. proposed a method of bonding and inlaying pieces after mirror processing and coating, and studied the parameters of the adhesive layer. Under 1 g gravity and within a temperature range of −40 °C to 60 °C, the RMS value of the mirror was better than λ/20, and the first-order mode reached 242 Hz [9]. Ruijing Liu et al., based on the requirements of large aspect ratio mirrors for space telescopes, proposed an “L” shaped dual-axis flexible hinge structure. After dimensional optimization, under the action of 1 g gravity, the surface accuracy RMS in the x and y directions were 4.97 nm and 2.91 nm, respectively, and the first-order mode was 228.27 Hz [10]. B. Liu et al. proposed an adjustable two-foot bending body for circular mirrors, which can effectively reduce the astigmatism caused by gravity on the optical axis by adjusting the distance between the two feet, with a surface RMS value of 8.1 nm [11]. Ning Xu et al., in response to the challenge of supporting mirrors in aviation optical systems, used a three-point backplate support for a ϕ 232 mm mirror, combining a cross hinge with an orthogonal hinge to design a new composite hinge form. After assembly, the mirror surface accuracy was better than λ/50, the mass was less than 2 kg, and the first-order mode was 645 Hz [12]. Wansha Wen et al. proposed a support force scheme through the center of gravity of the prism and, based on this, used a multi-island genetic algorithm to optimize the position parameters of the prism’s main cross-section support pads. Under the coupled conditions of gravity at temperatures of 2 °C and 42 °C, the RMS values were 107.8 nm and 69.5 nm, respectively, and the first-order frequency was 69.61 Hz [13]. Xiaohan Liu et al. conducted an optimized design for the large-aperture main mirror of a space camera with a diameter of ϕ 610 mm, combining the flange with the main mirror body. Under conditions of 1 g gravity, a 4 °C temperature rise, and a 0.01 mm assembly error, the RMS surface error was less than λ/50, the mass of the main mirror was 8.66 kg, and the maximum displacement of the main mirror assembly was less than 10 µm, with the maximum tilt angle being less than 5″ [14]. The summary is shown in

Table 1. Comparison of mirror support structure.

Reference	Mirror Size	Eigenfrequency	Mirror Surface Accuracy (RMS)
Zhongyao Zhu et al. [8]	550 mm × 450 mm	179.6 Hz	1 g gravity, 16 °C~24 °C and a 5 µm assembly error: better than 1/55 λ
Jiaqi Zhang et al. [9]	not mentioned	242 Hz	1 g gravity and −40 °C~60 °C: better than λ/20
Ruijing Liu [10]	not mentioned	228.27 Hz	1 g gravity load: better than 4.97 nm
B. Liu [11]	1200 mm	188.7 Hz	1 g gravity load: better than 8.1 nm
Ning Xu [12]	ϕ 232 mm	645 Hz	Under assembly conditions: better than λ/50
Wansha Wen [13]	ϕ 1460 mm	69.61 Hz	gravity coupling at temperatures of 2 °C and 42 °C: better than 107.8 nm
Xiaohan Liu [14]	ϕ 610 mm	203.74 Hz	1 g gravity, a 4 °C temperature rise and a 0.01 mm assembly error: better than λ/50

.

Currently, there is a scarcity of research on the design optimization of aerial mirrors and their support structures, with the majority of lightweight mirror and support structure optimizations focusing on spaceborne or ground-based telescopes. Due to the different operating environments of airborne and spaceborne mirrors, there are also differences in design approaches and indicators.

This paper addresses the support scheme and completes the structural design for a ϕ 240 mm airborne pod coaxial mirror, considering its specific usage environment and surface figure precision requirements. The camera’s requirements for the mirror are as follows: under the separate actions of three-directional gravity; 50 °C high temperature, and −40 °C low temperature; the root mean square (RMS) value of the mirror surface figure accuracy should be ≤λ/40 (λ = 632.8 nm); when there is a forced displacement of 0.008 mm on any installation surface, the RMS value of the mirror surface figure accuracy should be ≤λ/200 (λ = 632.8 nm); and the first-order eigenfrequency of the mirror assembly should be greater than 100 Hz to avoid resonance phenomena [15]. The above target surface errors are obtained after deducting polishing errors from the total error budget. Therefore, while ensuring the system is lightweight, compact, and highly stable, a flexible support structure suitable for medium and small-sized mirrors has been studied. The actual environment was simulated using Patran/Nastran finite element software, and the simulation results were surface figure fitted using Sigfit2020. Finally, actual detection was conducted to compare the mirror surface figure accuracy before and after installation, proving the feasibility of the design. This effectively reduces the impact of environmental factors and assembly conditions, demonstrating a certain level of environmental adaptability.

2. Mirror Assembly Design

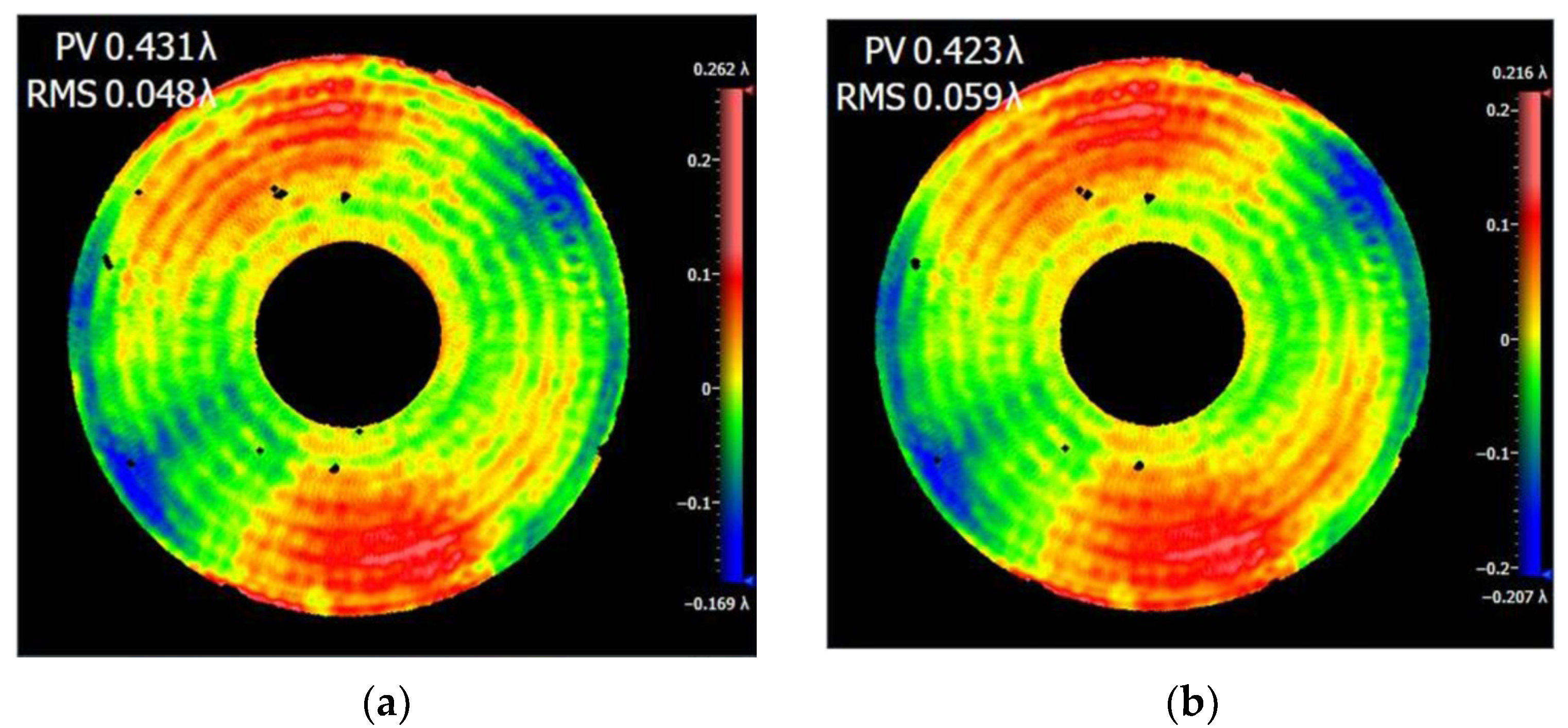
2.1. Mirror Support Scheme

Mirror support structures can be categorized based on the location of contact points into peripheral, side, central, and back supports [16]. Peripheral support is often used for small-sized mirrors, using the surface or edge of the lens as a reference, and the lens is secured to the frame or seat using a pressure ring for system positioning. Side support uses the side edge of the mirror as a reference for positioning, connecting the mirror to the system via screw fastening or adhesive bonding, which is a relatively common method of fixing mirrors. Central support is widely used in medium and small-aperture mirrors, often employed in optical systems with a central hole, and is a support method that uses the central position of the mirror as a reference for positioning. The support structure is fixed to the central hole of the mirror through adhesive bonding, offering advantages such as small structural size, simple structure, and ease of design. Back support is commonly used in medium-to-large-aperture mirrors, positioning and supporting the mirror through blind holes on the back of the mirror connected to a cone sleeve and flexible joint. The most classic of these support methods is the three-point back support, which, based on the principle of three-point positioning, can be evolved into six-point, nine-point, eighteen-point, and twenty-seven-point support configurations [17].

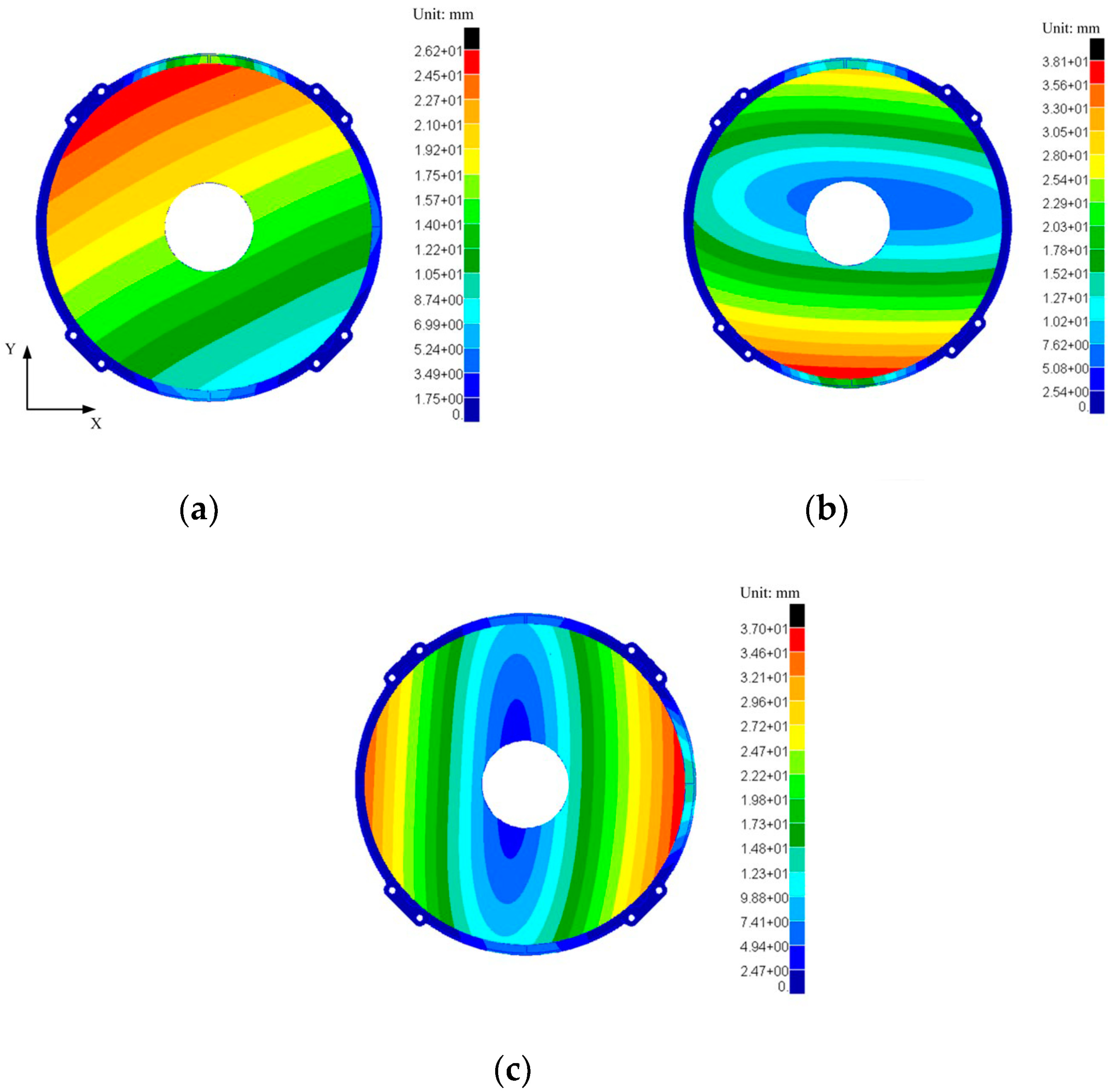
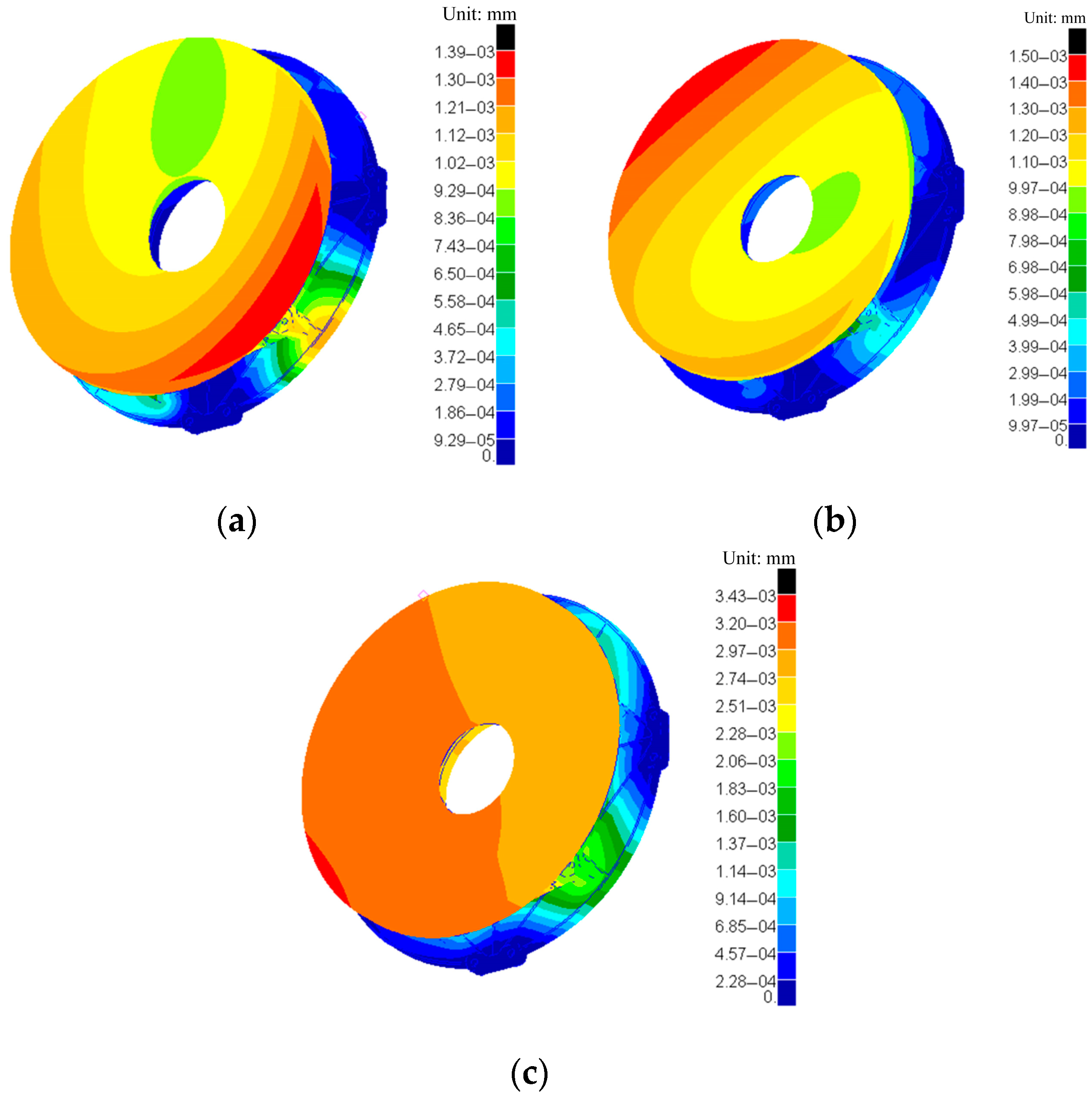
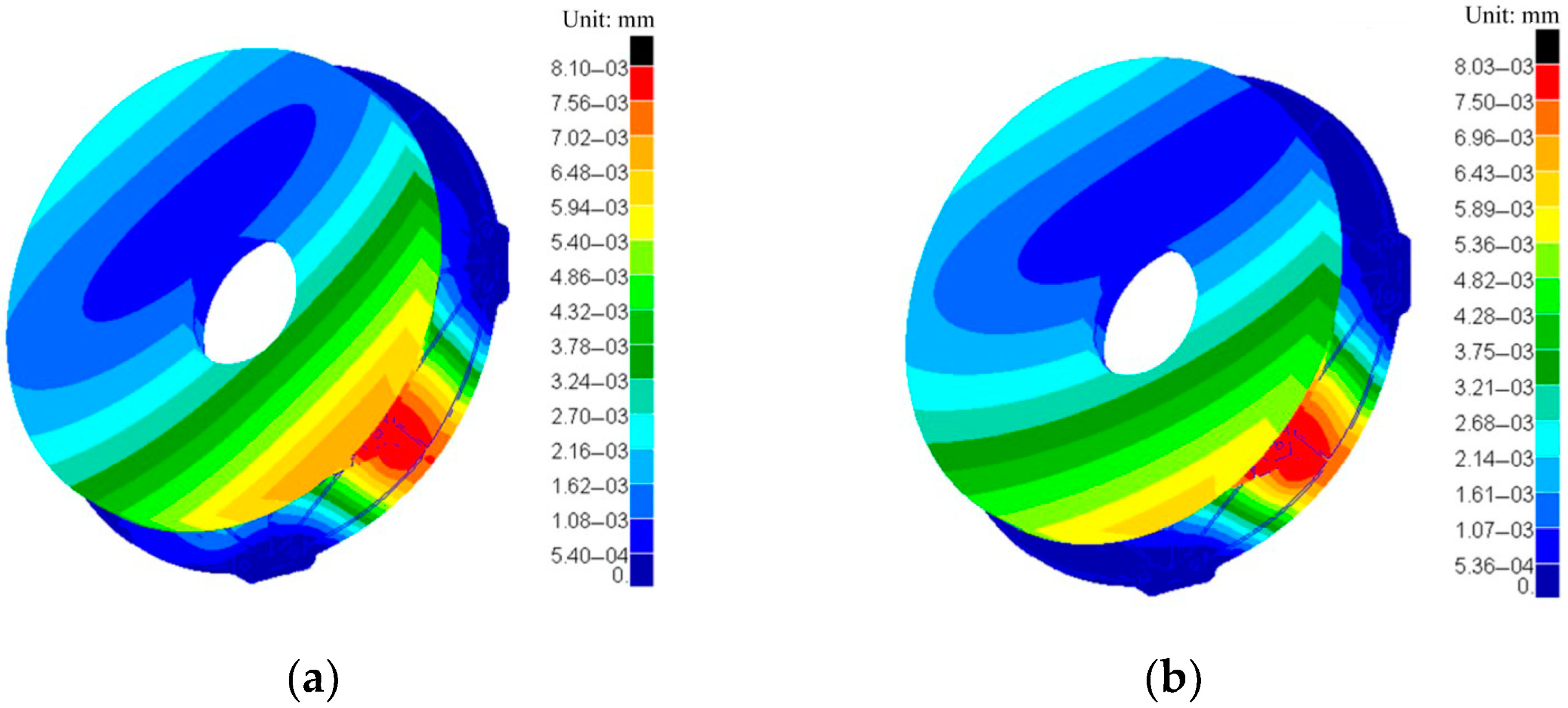
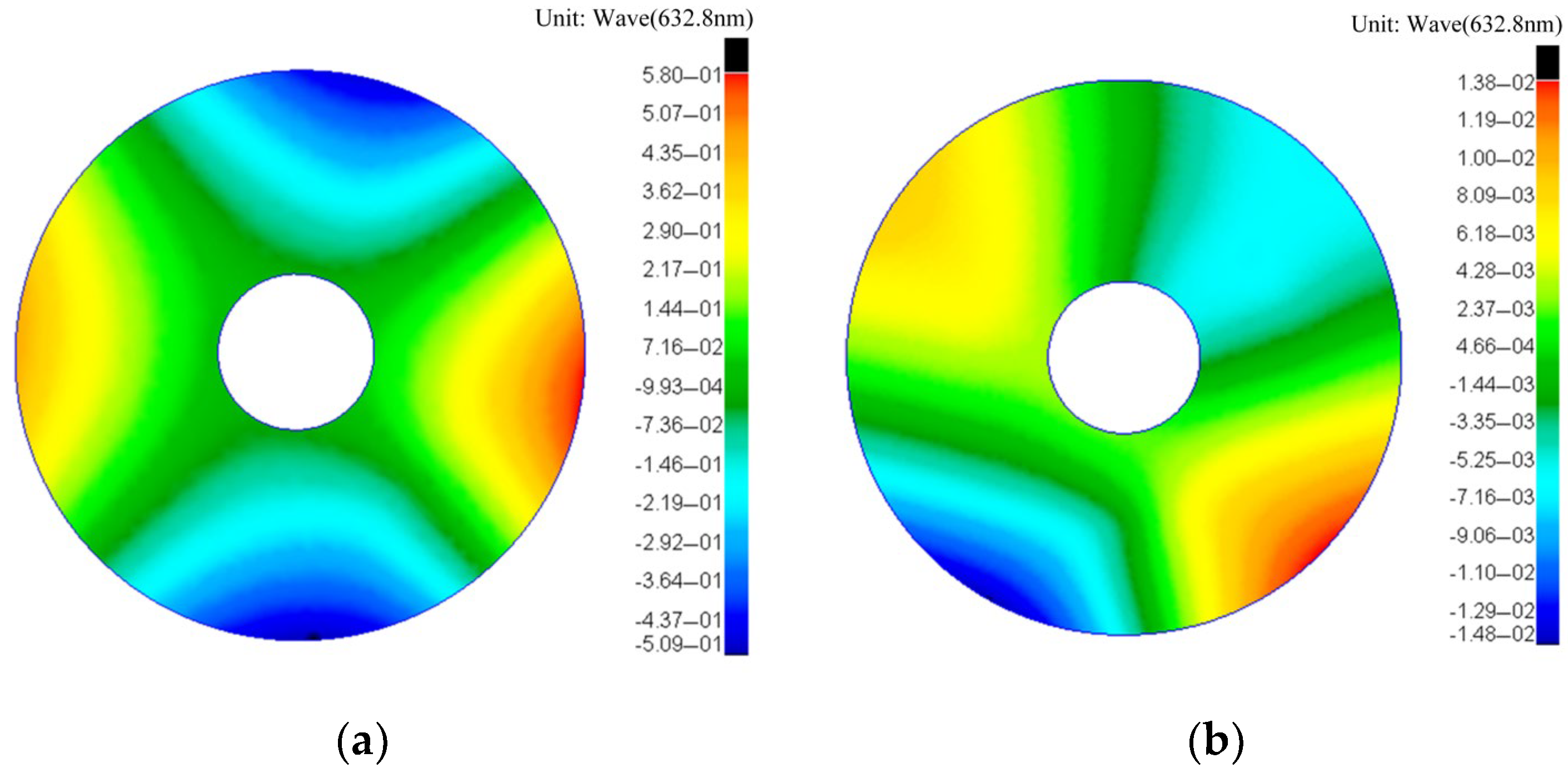
This system is a pre-research device, and there is a potential need for mass production in the future. Therefore, manufacturability and the time and economic costs are important considerations. In the selection of the mirror support scheme, central support is less complex in terms of assembly and adjustment compared to side and back support, and it does not introduce over-constraint, making it easier to achieve assembly. The mirror has a diameter of 240 mm, classifying it as a medium-to-small-aperture mirror, and it features a central control structure. To meet the rigid body displacement requirements of the component, and considering manufacturability, cost, and assembly complexity, central support was ultimately chosen as the support scheme for the mirror. The mirror assembly consists of three parts: the mirror, the flexible flange, and the backplate. The circular “tail” at the back of the mirror is adhesively bonded to the inner ring of the flexible flange, which is then connected to the backplate via bolts. 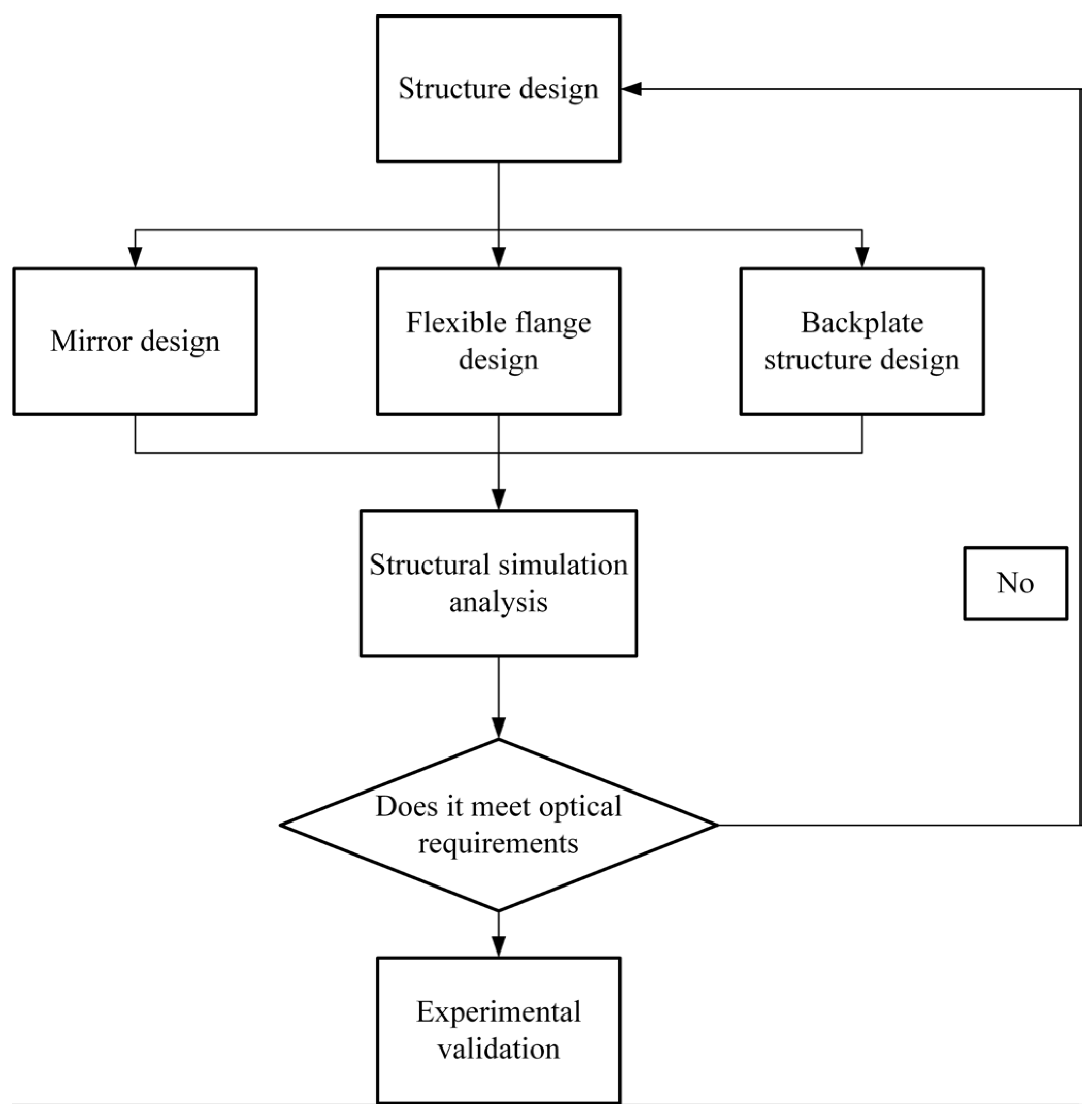Finally, the backplate is connected to the main optical system using four sets of installation surfaces with bolts, as shown in Figure 1. The design process is primarily divided into three parts, as illustrated in Figure 2: structural design of the assembly, finite element simulation analysis, and experimental validation.

2.2. Mirror Design

Mirrors, composed of a rigid body, place greater emphasis on their physical properties to ensure the spatial position of the reflective surface and the surface figure of the mirror. Therefore, the selection of mirror materials requires consideration of the mechanical properties and thermal stability of the mirror blank, as well as good machinability.

The commonly used mirror materials and their characteristics are shown in

Table 2. Characteristics of commonly used materials for mirrors.

Material	Density/ ρ (g·cm−1)	Young’s Modulus/E (Gpa)	Thermal Conductivity/ (W·m−1·K−1)	CTE/ (10−6·K−1)	(E/ρ)/ (106 m)
SiC	2.80	310	120	2.5	11.07
Al	2.68	78	167	23.6	2.91
ULE	2.21	67	1.31	0.03	3.03
Zerodur	2.53	91	1.64	0.05	3.57

, it can be observed that SiC material has a higher elastic modulus and stiffness compared to ULE, Zerodur, and Al, offering advantages such as high thermal conductivity, high specific stiffness, and excellent thermal stability. However, it also has significant drawbacks, including high material hardness, difficulty in processing, high cost, and long processing cycles. Al, as a commonly used structural material, has a larger coefficient of thermal expansion and a lower stiffness compared to other materials, making it suitable for optical systems with minimal environmental temperature changes and lower precision requirements. ULE can be applied to closed-back structures, which significantly increases the stiffness of the mirror compared to Zerodur, leading to a greater lightweighting ratio, but its production cost is high and the processing cycle is long, typically used for large-aperture space mirrors. The ϕ 240 mm aperture mirror in this project is categorized as a medium-to-small aperture. Although ULE exhibits similar performance to Zerodur, its manufacturability is inferior to that of Zerodur, resulting in longer processing times and higher costs. Considering the manufacturability, time and economic costs, as well as the potential for future mass production, ULE is not suitable as the material for the mirror. Zerodur is readily available, has relatively low cost, mature technology, and a shorter surface figure polishing cycle, making it particularly suitable for mass production when it meets usage requirements. After a comprehensive comparison of the aforementioned materials, Zerodur is chosen as the mirror material.

Compared to solid structure mirrors, porous sandwich structures are a more efficient form and are commonly used as lightweight structural types. By removing materials that contribute little to the overall stiffness of the structure, the specific stiffness of the structure is increased, and the structural form becomes more rational. However, this form of lightweighting has a longer processing cycle, higher processing costs, and is highly prone to mechanical processing residual stresses [18]. Therefore, in this paper, lightweighting is only achieved by slightly altering the contour of the mirror’s back substrate. Due to the use of central support, the mirror substrate is shaped into a single-arch form. In single-arch mirrors, the center of gravity is located near or in front of the top point of the mirror surface, making the surface figure of the single-arch mirror susceptible to the influence of gravity. Adjusting the center of gravity below the reflective surface can reduce this impact.

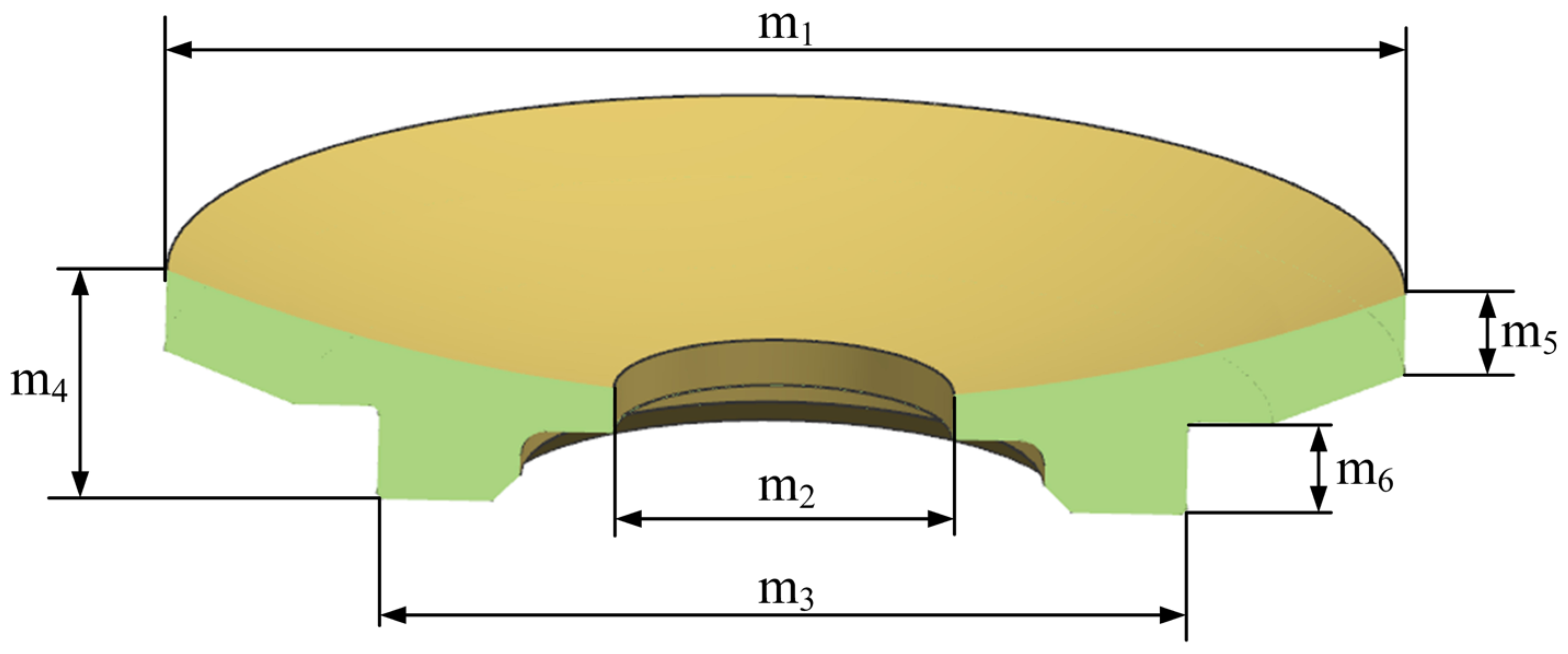
Thus, unlike the traditional single-arch mirror structure, this design includes a “tail” at the bottom of the mirror with a thickness of t. This design serves two purposes: on one hand, to adjust the center of gravity of the mirror so that it is as much as possible below the reflective surface, reducing the impact of gravity on the surface figure accuracy; on the other hand, to meet the needs of the mirror’s adhesive area. The mirror’s design takes into account factors such as the support structure form, lightweighting, and mirror surface processing technology. Through engineering analysis and optimization of the mirror’s diameter, body thickness, and single-arch shape dimensions, the actual shape of the mirror is designed as shown in Figure 3. The diameter of the main mirror is ϕ 240 mm, the diameter of the central hole is ϕ 68 mm, the thickness of the mirror m₄ = 50 mm, the thickness of the edge of the mirror m₅ = 17 mm, the thickness of the cementation m₆ = 19.5 mm, and the radius of the cementation m₃ = 162 mm. The circumference of the “tail” on the back of the mirror is the bonding surface with the support structure.

2.3. Flexible Flange Design

The complex thermal environment within aerial pods leads to significant temperature variations, causing thermal elastic deformation of the camera, which, in turn, leads to deviations in the optical surface figure of mirrors and changes in spacing, degrading the imaging quality of the optical system. Additionally, during ground assembly and testing, the influence of gravity orientation changes and assembly stresses resulting from manufacturing errors also affect the imaging quality of the system. Therefore, to meet the specifications for surface figure and rigid body displacement of the mirror under force and thermal environments, a support form combining inner and outer rings with circular arc-shaped flexible hinges is proposed. This design reduces the strain energy of the mirror body through its own deformation, thereby reducing the surface figure error of the mirror. While ensuring the rigidity and strength requirements of the component itself and the overall camera, increasing the flexibility of the flexible flange eliminates the stresses produced by temperature changes and gravity orientation changes, and also eliminates the impact of assembly stresses.

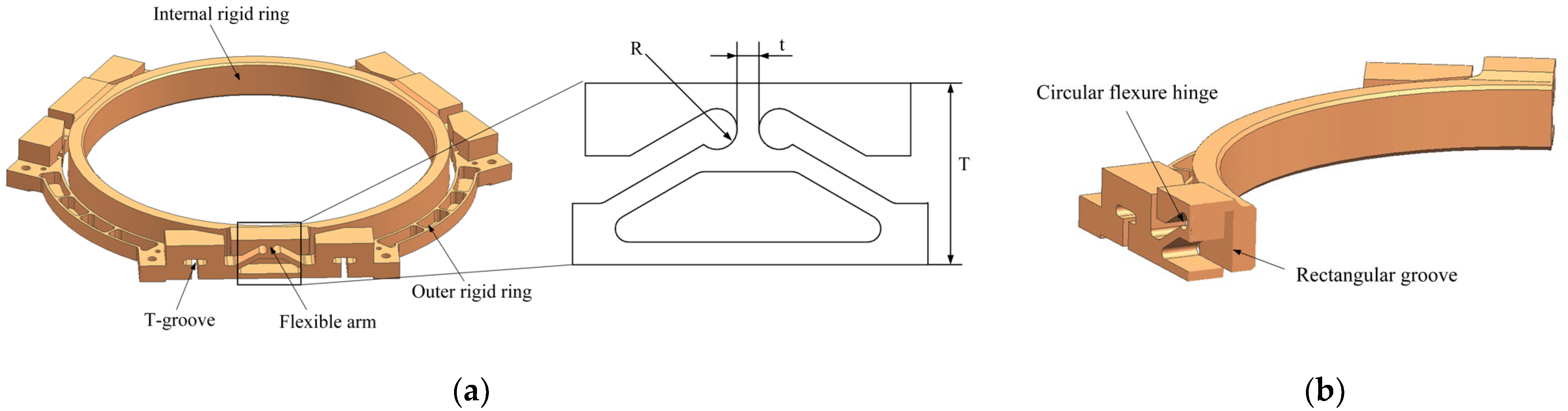
To meet the system’s wide temperature range usage conditions of −40 °C to 50 °C and compensate for thermal stress, the linear thermal expansion coefficient of the flexible support structure material must be matched with the microcrystalline material used for processing the mirror, as mentioned earlier. Although 4J32 Invar steel has a lower specific stiffness, its thermal expansion coefficient is closest to that of microcrystalline glass material, making it the material of choice for the flexible support structure. As shown in Figure 4, the structure mainly consists of an internal rigid ring, an outer rigid ring, and flexible arms; the total thickness is 21 mm. The internal rigid ring is in the form of a ring structure, with its inner wall adhesively bonded to the circular “tail” on the back of the mirror body, and the diameter of the inner ring is ϕ 162, which matches the size of the main mirror; the outer rigid ring extends three sets of evenly distributed mechanical interfaces outward from the ring structure to connect with the backplate, with T-shaped grooves at the mechanical interface parts, which can appropriately increase the radial flexibility of the support structure. Through its own elastic deformation, it absorbs external loads and releases installation stresses. The structure adopts a lightweight design, with a number of reinforcing ribs left in the circumferential direction of the ring and the rest of the parts removed. A rectangular groove is made between the internal and outer rigid rings to avoid rigid connection between the internal and outer rings, and connected by three evenly distributed flexible arms in a circular manner. Since the circular arc-shaped flexible hinge has higher rotation precision compared to the straight beam-type, circular arc-type, and elliptical flexible hinges, the center of rotation does not shift significantly during rotation. This design reduces the floating of the hinge center, thus providing good comprehensive performance. Therefore, the circular arc-shaped flexible hinge is used as the structural form of the flexible arm, effectively reducing the impact of the uneven installation surface of the mirror assembly on the mirror surface figure. As shown in the figure, the slot radius of the flexible arm R = 2.25 mm, the thinnest thickness t = 3.4 mm, and the hinge thickness b = 10 mm; these are explained in detail in the following article.

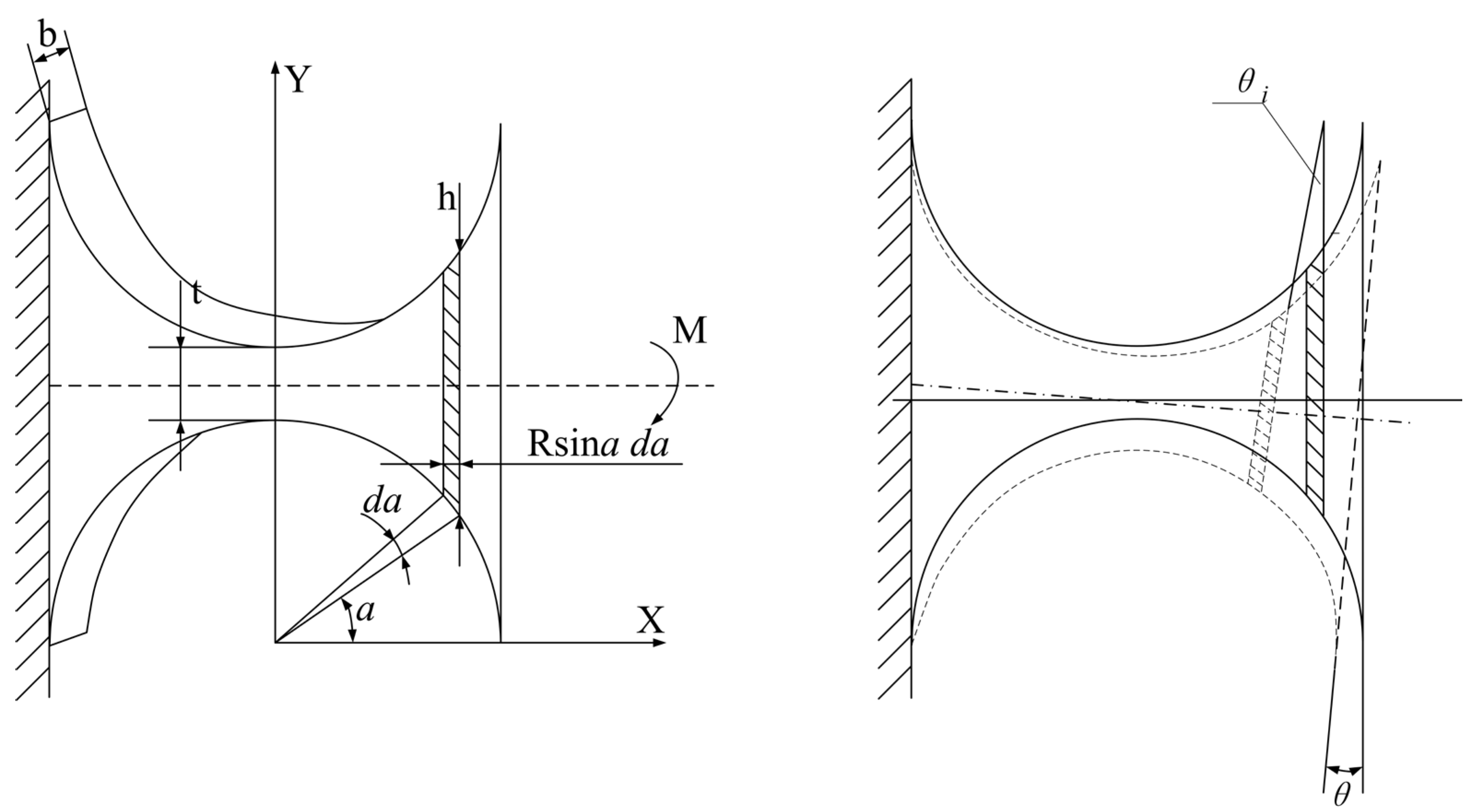
Figure 5 illustrates the schematic diagram of an arc-shaped flexible hinge, with geometric dimension parameters including the central angle, the cutting circle radius R, width b, height h, and minimum thickness t, among others. The calculation method for the rotational stiffness of the hinge under the action of a bending moment M is analyzed. The formula for the rotation angle of the flexible hinge in the support structure, after simplification, is as follows:

Consider a point (x, y) on the flexible joint, which undergoes angular displacement under the action of the moment M. Since the angular displacement is small, it can be considered $\theta =tan\theta$ and is expressed by the following formula [19]:

$${\theta }_i=tan{\theta }_i={\displaystyle \frac{dy}{dx}}$$

(1)

According to the theory of mechanics of materials, the curvature at an infinitesimal element dx of the structure is given by:

$${\displaystyle \frac{1}{\rho \left(x\right)}}={\displaystyle \frac{M}{EJ\left(x\right)}}$$

(2)

In the equation mentioned above, ${\displaystyle \frac{1}{\rho \left(x\right)}}$ represents the curvature at the infinitesimal element dx after deformation, E is the elastic modulus of the material for the arc-shaped flexible hinge structure, M is the bending moment at the infinitesimal element dx after deformation, and J(x) is the moment of inertia at the infinitesimal element dx.

According to the curvature formula, the curvature at any point on the curve y = f(x) can be calculated using the following formula:

$${\displaystyle \frac{1}{\rho \left(x\right)}}={\displaystyle \frac{\frac{d^{2}y}{d{x}^2}}{{[1+{\left(\frac{dy}{dx}\right)}^2]}^{\frac{3}{2}}}}$$

(3)

That is to say:

$${\displaystyle \frac{M}{EJ\left(x\right)}}={\displaystyle \frac{\frac{d^{2}y}{d{x}^2}}{{[1+{\left(\frac{dy}{dx}\right)}^2]}^{\frac{3}{2}}}}$$

(4)

Given that the angular displacement of the flexible hinge is very small, the square terms can be neglected, thus simplifying Equation (4) to:

$${\displaystyle \frac{M}{EJ\left(x\right)}}={\displaystyle \frac{d^{2}y}{d{x}^2}}$$

(5)

Combining Equations (1) and (5), we obtain:

$$\theta ={\displaystyle \frac{dy}{dx}}=\int {\displaystyle \frac{d^{2}y}{d{x}^2}}dx+C=\int {\displaystyle \frac{M}{EJ\left(x\right)}}dx+C$$

(6)

Given that the primary focus of stiffness analysis is the functional relationship between structural parameters and stiffness, the constants in Equation (6) can be disregarded. Transforming the Cartesian coordinates in Equation (6) into polar coordinates, we have the following relationships:

$$dx=Rsin\alpha d\alpha ,$$

(7)

$$h=2R+t-2Rsin\alpha ,$$

(8)

$$J\left(x\right)={\displaystyle \frac{b{h}^3}{12}}={\displaystyle \frac{b{(2R+t-2Rsin\alpha )}^3}{12}}$$

(9)

Considering the central angle of the arc-shaped flexible hinge to be 180°, and integrating within the interval [0, π], the rotational angle formula for the support structure’s flexible hinge is given by:

$$\theta ={\int }_0^{\mathrm{\pi }}{\displaystyle \frac{M}{EJ\left(x\right)}}Rsin\alpha d\alpha ={\int }_0^{\mathrm{\pi }}{\displaystyle \frac{12Rsin\alpha M}{Eb{(2R+t-2Rsin\alpha )}^3}}d\alpha$$

(10)

The rotational angle θ of the flexible hinge is determined using the method of integration, and the rotational stiffness under the action of the bending moment M is derived as:

$$K={\displaystyle \frac{M}{\theta }}={\displaystyle \frac{1}{{\int }_0^{\mathrm{\pi }}\frac{12Rsin\alpha }{Eb{(2R+t-2Rsin\alpha )}^3}d\alpha }}$$

(11)

In the equation, b is the width of the hinge; R is the radius of the arc of the flexible hinge; and t is the minimum thickness of the flexible hinge. Using the above formula, the stiffness value K of the arc-shaped hinge can be calculated for different dimensional parameters, thereby designing an arc-shaped flexible support structure that meets the requirements.

By analyzing the impact of different dimensions of R, t, and b on the rotational stiffness K of the flexible hinge through the aforementioned formula, the variation curves of the rotational stiffness with respect to the hinge structural parameters are obtained as shown in Figure 6 and Figure 7. It can be observed from the figures that the hinge width b has a linear relationship with the rotational stiffness, while the minimum thickness t of the flexible hinge significantly affects the rotational stiffness K. As t increases, the rotational stiffness increases in a quadratic manner. The influence of the radius R on stiffness becomes more pronounced; conversely, as R increases, the rotational stiffness decreases, indicating that the impact of R on the flexibility of the hinge is minimal. Concurrently, the rotational stiffness of the flexible flange exhibits a monotonically increasing relationship with the hinge parameters. However, as the parameters increase, the system stiffness becomes greater, rendering the system more rigid. This results in reduced buffering capacity and a corresponding decrease in flexibility. Consequently, the system’s surface deformation tends to deteriorate under the influence of mechanical and thermal loads. Nevertheless, this relationship is difficult to fully describe using a mathematical expression. Therefore, we selected an appropriate dimension and obtained satisfactory results through finite element analysis. Therefore, in the actual design process, the values of R and b should be determined based on the structural requirements, followed by the determination of the minimum thickness t to ensure the rotational stiffness of the flexible hinge. Integrating the aforementioned design theory, this paper proposes a flexible support structure suitable for medium and small-sized mirrors, taking into account the requirements for axial stiffness and radial flexibility, as well as structural design constraints. Ultimately, the following dimensions were determined: slotting radius R = 2.25 mm, minimum thickness t = 3.4 mm, and hinge thickness b = 10 mm.

2.4. Backplate Design

The backplate serves as the connecting structure between the mirror assembly and the camera frame. To prevent stress due to thermal expansion at different rates between parts, Invar 4J32, which is the same material as the flexible flange, is selected. In terms of structural design, to reduce the weight of the mirror assembly, a lightweight design is adopted for the backplate, with a number of reinforcing ribs left and the rest of the parts removed. The lightweighting rate can reach 67.9%. The final optimized structure of the backplate is shown in Figure 8.

3. Simulation Analysis

3.1. Modal Analysis

Aircraft experience forced vibrations during flight, and when the vibration frequency approaches the eigenfrequency of the equipment, resonance can occur, potentially damaging the equipment. Therefore, in the design process, it is essential to ensure that the first-order eigenfrequency of the mirror assembly is greater than the excitation frequency of the aircraft to avoid resonance. To analyze the natural frequencies and mode shapes of the mirror assembly, the component model was imported into Hypermesh for meshing and then subjected to modal analysis using Patran/Nastran. To analyze the natural frequencies and vibration modes of the mirror assembly, the assembly model was imported into Hypermesh for mesh generation. This study employs second-order tetrahedral meshes, with the maximum element size being 4 mm and the minimum size being 0.8 mm. Owing to the presence of fillets in the model, the mesh size varies with curvature. Ultimately, a total of 228,342 elements and 357,299 nodes are generated. At the same time, we verify that the finite element model is convergent by modifying the element mesh size. The installation holes are used as boundary conditions. The finite element model after meshing is shown in Figure 9.

Modal analysis was performed using Patran/Nastran without applying any boundary conditions. The results of the first six finite element modal analyses for the mirror assembly are presented in

Table 3. Results of modal analysis of mirror assembly.

Mode No	Eigenfrequency/Hz	Mode No	Eigenfrequency/Hz
1	296.66	4	519.79
2	308.98	5	550.81
3	324.79	6	697.00

, and the vibration modes of the first three orders are illustrated in Figure 10, the first-order mode corresponds to vibrations along the optical axis, the second-order mode corresponds to rotations about the x-axis, and the third-order mode corresponds to rotations about the y-axis. The displacement in Figure 10 involves three directions, rather than a single projection in a certain direction, which is relatively complex and cannot be simply explained as mirror shape error. The same applies to the subsequent displacement diagram. From the table, it can be seen that the first mode of the mirror assembly designed in this study is 296.66 Hz, which is significantly higher than the required 100 Hz, meeting the design and usage requirements.

3.2. Gravity Analysis

Taking into account the impact of gravitational orientation changes during the manufacturing process and the actual working environment on the mirror’s surface figure, a self-weight simulation analysis was conducted on the mirror assembly. The mirror was subjected to 1 g gravitational loads along the X-axis, Y-axis, and Z-axis. The deformation plots and surface figure plots of the mirror assembly are depicted in Figure 11 and Figure 12, respectively.

In the field of optics, the surface figure is commonly evaluated using RMS (Root Mean Square) values and PV (Peak-to-Valley) values. This study employs Sigfit software to extract the strain values at the mirror nodes under three different gravitational fields. The RMS values, PV values, and rigid body displacement values of the mirror under these three gravitational fields were calculated, as shown in

Table 4. Different gravity surface types of mirror components.

Load Specification Items		Gx	Gy	Gz
Linear Displacement (nm)	X-axis	967	−1.32	−117
	Y-axis	−1.67	998	197
	Z-axis	−98	160	2970
Inclination Angle (″)	X-axis	0.465	1.165	−0.129
	Y-axis	−0.943	−0.418	−0.330
	Z-axis	0.260	0.145	0.006
Surface Shape Error (nm)	PV	39.2	39.5	57.1
	RMS	8.63	8.76	13.6

. The maximum relative tilt angle of the mirror is 1.165 arcseconds, the maximum relative displacement is 2970 nm, and the maximum surface figure error RMS value is 13.6 nm, which meets the usage requirements.

After fitting with Sigfit2020 software, the nod file was imported into Patran, yielding the mirror surface figure as depicted in Figure 11.

3.3. Temperature Adaptability Analysis

The finite element model was subjected to temperature field loads of 50 °C and −40 °C to simulate the extreme working environment of the mirror assembly. The analysis of the mirror surface figure under the influence of temperature loads is presented in Figure 13 and Figure 14.

The surface figure nodes of the mirror were extracted from the aforementioned simulation results, and the changes in the mirror’s surface figure under temperature loads were calculated using Sigfit software. The analysis results are presented in

Table 5. High and low temperature surface types of mirror component.

Load Specification Items		Th	Tl
Mirror rigid body displacement (nm)	X-axis	−6.27	12.5
	Y-axis	22.8	−45.7
	Z-axis	2.58	−5.15
Maximum mirror inclination (″)	X-axis	0.026	0.158
	Y-axis	0.023	0.139
	Z-axis	−0.001	−0.007
Profile accuracy (nm)	PV	0.490	0.980
	RMS	0.096	0.191

. “T_h” represents the high-temperature load condition, and “T_l” represents the low-temperature load condition. The changes in the mirror’s surface figure are significantly smaller than the design specifications, meeting the design requirements. This is primarily due to the fact that both the flexible flange and the backplate in this study are made of Invar material, which has the same coefficient of thermal expansion as the microcrystalline material. Consequently, under high and low temperature loads, the expansion rates of the mirror and its support structure are nearly identical. Additionally, the arc-shaped flexible hinges in the flexible flange absorb a portion of the thermal deformation, providing a certain degree of buffering effect. Therefore, the surface figure of the mirror under temperature loads is far less than the design specifications require.

3.4. Forced Displacement Analysis

Due to the unevenness of contact surfaces between parts, mechanical assembly generates assembly stress or forced displacement of optical components, which in turn causes changes in the surface figure of the mirrors in the optical system. Therefore, in the simulation process, we simulate the deformation of optical elements during assembly by applying forced displacements. The mechanical interface designed in this scheme for the flexible flange and backplate consists of six evenly distributed through-holes around the outer rigid ring of the flexible flange, meaning there are six installation surfaces. A forced displacement of 0.008 mm is applied to each set of installation surfaces to observe the impact of surface unevenness on the mirror’s surface figure. To compare the large-tolerance performance of the mirror support structure in this scheme, the flexible hinge of the mirror support structure is removed, and the same load simulation analysis is applied to the mirror assembly. Figure 15 illustrates the structural diagram with the flexible joints removed. Figure 16 shows the simulation results of the mirror assembly with and without the flexible hinge, where Figure 16a (left) is the deformation pseudocolour map of the mirror assembly without the flexible hinge, and Figure 16b (right) is the deformation pseudocolour map of the mirror assembly with the flexible hinge.

The surface figure nodes of the mirror were extracted from the aforementioned simulation results, and the changes in the mirror’s surface figure under forced displacement were calculated using Sigfit software. The mirror’s surface figure is depicted in Figure 17, with Figure 17a (left) showing the surface figure without the flexible hinge, and Figure 17b (right) showing the surface figure with the flexible hinge. When the mirror lacks a flexible hinge, the PV value of the mirror’s surface figure is 690 nm, and the RMS value is 145 nm. In contrast, with the arc-shaped flexible hinge support structure, the PV value is 14.2 nm, and the RMS value is 2.85 nm, with the mirror’s surface figure change being less than 1/200λ (λ = 632.8 nm). The RMS value is only 1.97% of the non-flexible link, and the PV value is only 2.06% of the non-flexible link. It is evident that this mirror support structure effectively suppresses the impact of forced displacement on the installation surface, resulting in a mirror surface figure that meets the design requirements.

4. Experimental Validation

To validate the adaptability of the mirror assembly to forced displacements as per this scheme, the plan involves simulating installation errors by assessing the unevenness of the installation surface. Prior to mirror installation, the mirror assembly is not subjected to forced displacements due to the unevenness of the installation surface. Following installation, the support structure comes into direct contact with the backplate, inducing forced displacements that mimic the assembly stresses resulting from co-planarity errors of the assembly surface, thereby evaluating the assembly’s adaptability to the assembly surface. Two surface figure inspections were conducted using a Zygo interferometer, with the mirror surface figure inspection schematic illustrated in Figure 18. The assembly was maintained in a horizontal optical axis position during inspection, with the surface figure being inspected twice, before and after mirror installation. During the trial assembly phase, a preliminary test was conducted to assess the impact of the mirror support structure’s installation surface flatness on the surface figure.

A coordinate measuring machine was employed to evaluate the planarity of the installation surfaces of the flexible flange and the backplate. The measurements indicated that the surface irregularity of the flexible flange was 0.024 mm, and that of the backplate was 0.004 mm, both of which significantly exceed the geometric tolerance specifications for the mirror assembly. The RMS values of the mirror surface figure under various installation conditions are presented in Figure 19. The RMS of the primary mirror surface figure was 0.048λ (λ = 632.8 nm) before mirror installation and 0.059λ (λ = 632.8 nm) after installation, indicating a difference of less than 7 nm between the pre- and post-installation states of the optical surface. Since the unevenness of the installation surface cannot be accurately determined by simple addition or subtraction of the two surfaces, this inspection only serves to demonstrate the impact of surface irregularity on the mirror assembly. It shows that the proposed design can mitigate the influence of surface unevenness on the mirror figure accuracy and enhance the system’s tolerance capabilities.

5. Summary

This paper presents a flexible support structure for medium and small-aperture mirrors developed for an airborne infrared targeting and laser ranging co-axial optical system. The total mass of the mirror assembly is considered a limiting factor in the structural design, which aims to enhance the tolerance characteristics of the assembly while meeting a wide temperature range and reducing the interference of external factors on its performance. Through the rational design of the mirror support structure, a ϕ 240 mm aperture mirror assembly has been achieved.

Modal analysis was conducted on the design via finite element simulation, revealing that the first-order frequency of the assembly is 296.66 Hz, which significantly exceeds the design requirement. The design was subjected to gravitational loads in three directions and temperature loads of −40 °C and 50 °C. The extracted surface figure values of the mirror under different gravitational and temperature fields showed RMS values less than λ/45, angular changes less than 1.165″ (arc seconds), and maximum displacements less than 2970 nm. Forced displacement analysis of the mirror assembly indicated that the primary mirror surface figure deformation was less than 1/200 λ when a 0.008 mm forced displacement was applied to any installation surface. Zygo interferometry was used to inspect the mirror surface figure before and after installation, simulating the actual installation state of the mirror assembly. The inspection results showed a change of 0.011λ in the mirror surface figure between the two states, demonstrating that the mirror assembly can maintain its surface figure well, confirming that it possesses certain tolerance characteristics and can effectively resist external interference.

Combining the aforementioned simulations and inspections, the single-point central support mirror assembly structure designed in this paper meets the design specifications. It can ensure the rigid body displacement and mirror surface figure of the mirror assembly under three-directional gravitational loads and extreme high and low temperature environments. Moreover, it can effectively reduce the requirements for installation surface precision, decrease the difficulty of mirror alignment and adjustment, and is suitable for engineering use requirements.