Research Progress and Applications of Single-Pixel Imaging Technology

Abstract

Single-pixel imaging is a computational optical imaging technique that uses a single-pixel detector to obtain scene information and reconstruct the image. Compared with traditional imaging techniques, single-pixel imaging has the advantages of high sensitivity and a wide dynamic range, etc., which make it have broad application prospects in special frequency band imaging and scattering media imaging. This paper mainly introduces the history of development and the characteristics of the single-pixel detector, focuses on the typical applications of single-pixel imaging in coded aperture, transverse scanning, and longitudinal scanning systems, and gives an account of the application of deep learning technology in single-pixel imaging. At the end of this paper, the development of single-pixel imaging is summarized and future trends forecasted.

1. Introduction

Single-pixel imaging (SPI) is a computational optical imaging technique that has developed rapidly in recent years, showing significant potential for various applications. The concept of SPI originated from experiments in which a single-point detector was used to capture modulated light after optical field modulation. These experiments date back to the 1880s and involved imaging based on point-by-point scanning. Specifically, British researchers developed a scanning-based electronic visual display technique using a selenium cell to detect light intensities that passed through the holes of a Nipkow disk from different spatial locations at different times [1]. As research on area array detectors was not advanced at that time, this technique became one of the primary methods for obtaining two-dimensional images of objects. In 2005, Sen et al. [2] from Stanford University proposed an image acquisition method called dual-photography, which utilized a single-pixel detector to measure the intensity of modulated light. This method can be considered a prototype of SPI. Since then, SPI has evolved into an imaging method characterized by high sensitivity, low noise, a large dynamic range, and low cost. The technique enables high-quality image reconstruction in low-light conditions, acquiring full image information using only one detector. SPI can be divided into pre-modulation SPI and post-modulation SPI according to different light field modulation methods [3]; the specific imaging principle is shown in Figure 1. Although there are some differences between the two imaging methods in the optical path, the imaging principle and reconstruction algorithm are basically similar, so they are both included in the category of SPI techniques.

SPI offers several advantages: (1) It breaks through the limitations of conventional imaging methods by employing an innovative non-imaging approach. Rather than relying on a complete image reconstruction, it directly measures light intensity in the scene using a single-pixel detector. This allows the rapid acquisition of the geometrical moments of the target object, facilitating fast focusing. (2) Single-point detectors used in SPI outperform array detectors in detection efficiency, sensitivity, and performance [3]. By capturing the total light intensity across the scene, they are particularly effective for capturing low-light signals. These detectors also exhibit a broad spectral response, making them suitable for specialized bands such as infrared [4] and terahertz regions [5,6,7]. (3) The incorporation of advanced signal processing techniques [8], including compressed sensing and deep learning, enhances imaging efficiency compared to traditional point-by-point scanning. (4) SPI is highly robust to noise, particularly in low signal-to-noise ratio conditions, where the integration of optical signals using a single-pixel detector effectively suppresses noise. This robustness ensures stable performance in autofocusing technology even in high-noise environments.

As research has progressed, SPI has addressed several challenges associated with conventional imaging [9], including imaging under low-light conditions and imaging through turbid media. SPI is particularly advantageous in scenarios where pixelated detectors are unsuitable, such as X-ray imaging [10,11], fluorescence imaging [12], and real-time terahertz imaging [7]. Furthermore, SPI shows broad application potential in areas such as hyperspectral imaging [13,14], optical encryption [15,16], remote sensing and tracking [17,18], 3D imaging technology [19,20], and ultrafast imaging [21]. The current mainstream mechanisms of SPI can be broadly categorized into three types: coded aperture, transverse scanning, and longitudinal scanning.

This study begins by introducing single-pixel detectors, followed by a detailed discussion of the typical applications of SPI within the frameworks of coded aperture, transverse scanning, and longitudinal scanning mechanisms. The applications of SPI in coded aperture mechanisms include X-ray coded aperture imaging and ghost imaging. In transverse scanning mechanisms, SPI is applied in optical coherence tomography (OCT) and single-photon light detection and ranging (LiDAR), while in longitudinal scanning mechanisms, it is employed in Fourier transform infrared (FTIR) spectrometry and intensity interferometry. Subsequently, this study provides an overview of the integration of deep learning (DL) techniques in SPI applications. Finally, the study summarizes the existing challenges in key SPI techniques and discusses potential directions for the future development of SPI.

2. Single-Pixel Detectors

Single-photon detectors (SPDs) are essential devices for single-photon detection, offering the capability to capture and convert the energy of individual photons due to their ultra-high sensitivity. SPDs are widely utilized for detecting signals with intensity levels equivalent to the energy of only a few photons. Their detection principle is based on the photoelectric effect, and their primary function is to convert optical signals into electrical signals.

The earliest photodetector, the photomultiplier tube (PMT), is a device based on the external photoelectric effect. It was first successfully applied to single-photon detection in 1949 and was primarily used for low-light detection [22]. In 1964, Haitz’s research team [23] introduced the avalanche photodiode (APD), a device that responds to single photons and utilizes the internal photoelectric effect, unlike the PMT. APDs can operate in two modes: Geiger mode and linear mode. When operating in Geiger mode, APDs are referred to as single-photon avalanche diodes (SPADs) [24]. The key difference between these modes lies in their operating voltage. In 1998, Golovin and Sadygov [25] proposed the multi-pixel silicon photomultiplier (SiPM). Later, in 2001, Gol’tsman et al. [26] developed the superconducting nanowire single-photon detector (SNSPD) and successfully detected photon response signals using this device. The main characteristics of selected detectors are summarized in

Table 1. Main characteristics of selected detectors.

	Quantum Efficiency	Spectral Range	Major Advantages	Major Drawbacks
Photomultiplier (PMT)	Up to 40%	160–1700 nm	Large photosensitive area; high gain, high sensitivity	Low quantum efficiency; limited time resolution; complex structure; high-pressure environment required; large size and weight
Avalanche photodiode (APD)	50–70%	200–1550 nm	High internal gain and frequency response characteristics	Extremely low detection efficiency in infrared band
Single-photon avalanche diode (SPAD)	50–70%	200–1550 nm	Wide spectral range; low power consumption; small size; low production cost	Large time jitter; semiconductor materials with narrow forbidden bands required
Silicon photomultiplier (SiPM)	50–70%	250–950 nm	High dynamic range and linear response; high degree of integration; anti-jamming capability	Lower detection efficiency in near-infrared band; small detection area
SNSPD	Up to 98%	400–1997 nm	Low noise-equivalent power; high detection efficiency; low time jitter; no peripheral gating circuit required	Refrigeration equipment required; high cost and large size

.

Owing to increasingly complex application scenarios and stringent detection standards, detectors are now subject to new requirements and challenges, particularly in terms of the dynamic range, response speed, signal-to-noise ratio, and other critical aspects. Consequently, extensive research has been conducted in recent years to promote advancements in detector technologies. The development trend for detectors emphasizes achieving high photon detection efficiency, low dark count rates, a broad spectral range, high count rates, and other enhanced technical specifications. Future research directions include the following: (1) improving detector structures to increase the photosensitive interval and maximize detection capabilities [27]; (2) refining production processes to reduce the influence of interference factors and enhance detector stability [28]; and (3) enhancing the photoelectric performance of SPDs through the application of new photoelectric materials [29].

3. Coded Aperture-Based SPI

The target undergoes wavefront phase modulation via a phase mask, resulting in a coded and modulated image. The detector captures the coded and modulated two-dimensional image, enabling the establishment of the relationship between the point spread function (PSF) and the distance, thus forming a three-dimensional image of the target. Typical applications of coded aperture-based SPI include X-ray coded aperture imaging and ghost imaging.

3.1. Fundamentals of Coded Aperture Imaging

Coded aperture imaging originates from pinhole imaging. While smaller pinhole apertures yield higher imaging resolutions, they significantly reduce the amount of light passing through, necessitating long exposure times. Additionally, excessively small apertures may result in diffraction effects, leading to imaging failure.

The coded aperture technique [30] involves integrating a specifically shaped mask into a conventional camera and adjusting the transmittance of light such that part of the light passes through while the rest is blocked. The shape and arrangement of the apertures in the coded mask are regular rather than random, with alterations in their shape or arrangement influencing the system’s resolution.

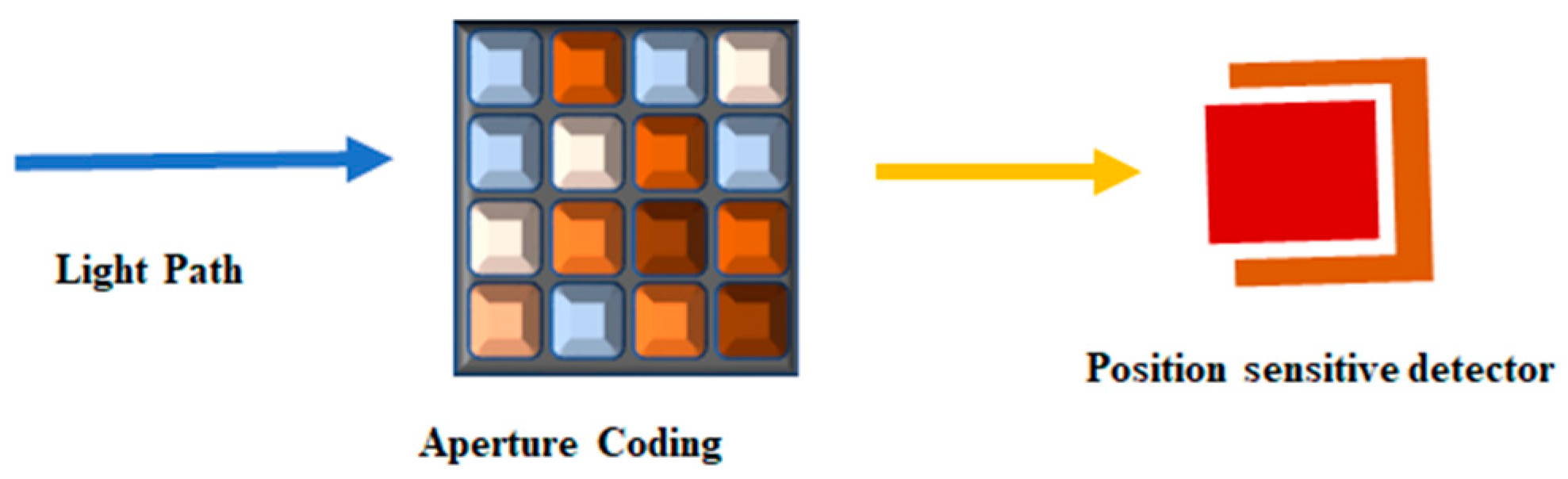
Typically, a coded aperture imaging system comprises a coded aperture and a position-sensitive detector (PSD), as illustrated in Figure 2. The PSD may include components such as a scintillation screen or fiber optic array coupled to a position-sensitive PMT, a charge-coupled device (CCD) camera, an SiPM array, or other semiconductor devices.

For an $n\times n$ square mask, the coding process [31] in a coded aperture system can be modeled as follows:

$$g=Mx+\eta \mathrm{restricted} \mathrm{by} x\ge 0$$

(1)

where g is the coded image reshaped into an $k\times 1$ column vector; M is a $k\times n^2$ measurement matrix derived from the PSF; x represents the reshaped source distribution with a dimension of ${\mathrm{n}}^2\times 1$; and $\eta$ is a $k\times 1$ noise term vector.

3.2. X-Ray Coded Aperture Imaging

To address the low light collection efficiency and signal-to-noise ratio of single-pinhole imaging, coded aperture imaging, an imaging technique that does not require a conventional lens, was first introduced in X-ray transmission imaging systems in 1961 [32]. Compared to single-pinhole imaging cameras, this technique significantly increases the optical system’s throughput, thereby improving its signal-to-noise efficiency. Various coded aperture modalities have been developed for X-ray imaging recently [33], including Fresnel zone plates, random arrays, non-redundant arrays (NRAs), uniformly redundant arrays (URAs), and ring apertures, the main features are shown in

Table 2. Main characteristics of selected coded aperture modalities.

	Major Advantages	Major Drawbacks	Application Scenarios
Fresnel zone plate	Higher throughput; higher resolution and flexibility	High manufacturing precision; production of artifacts; short object distance	X-ray micro-imaging
Random array	High throughput; high signal-to-noise ratio	Low image contrast; production of artifacts	Astronomical X-ray imaging
Non-redundant array	Limited throughput; high signal-to-noise ratio	Failure to image weakly radiating targets	Inertial confinement fusion experiment
Uniformly redundant array	High throughput; no correlated noise; capacity to image weak radiation sources	Production of artifacts; high system complexity	Far-field imaging, localization of possible hot spots of weak radioactivity
Annular aperture	High light collection efficiency; simple structure; low cost; high signal-to-noise ratio and resolution	Pinholes produce optical diffraction, so appropriate ring widths should be selected	Plasma diagnostics

. However, coded images must be decoded using optical or digital image processing methods to reconstruct the image accurately via the reconstruction algorithm, which inevitably increases the complexity and cost of the system.

Fresnel zone plates [34] offer higher throughput than single pinholes, enabling improved resolution and flexibility. However, these plates demand high manufacturing precision to ensure that the ring width, spacing, and thickness are maintained within a high tolerance range, allowing for the coherent superposition of light waves. Artifacts generated during production can significantly reduce the signal-to-noise ratio. Moreover, Fresnel zone plates generally require short object distances, limiting the placement of other detectors. These limitations have restricted the broader application of Fresnel zone plates.

Random arrays, whose distribution is determined by a random number table [35], have the advantage of high throughput, with light transmission through the coding plate reaching up to 50%. However, their drawbacks include an overly strong background, low image contrast, and the production of artifacts. Consequently, random arrays are primarily suitable for imaging isolated point objects, such as in astronomical X-ray imaging.

NRAs [36] provide high resolution and flexibility. However, their pass area is relatively small, limiting the amount of light received. Therefore, NRAs are not suitable for imaging weakly radiating targets.

A URA [37,38] is a two-dimensional random aperture array with an entrance pupil area that accounts for approximately half of the total area of the coding plate [39]. This design offers significant advantages, including high throughput, the absence of correlated noise, good background characteristics, and the ability to image weak radiation sources.

Ring apertures [40] feature a single annular opening. Compared with Fresnel zone plates, ring apertures have lower machining precision requirements, a simpler structure, and lower production costs. Additionally, ring apertures can achieve high resolution while maintaining the necessary light collection efficiency and signal-to-noise ratio, making them suitable for applications such as plasma diagnosis.

3.3. Ghost Imaging

3.3.1. Basic Theory

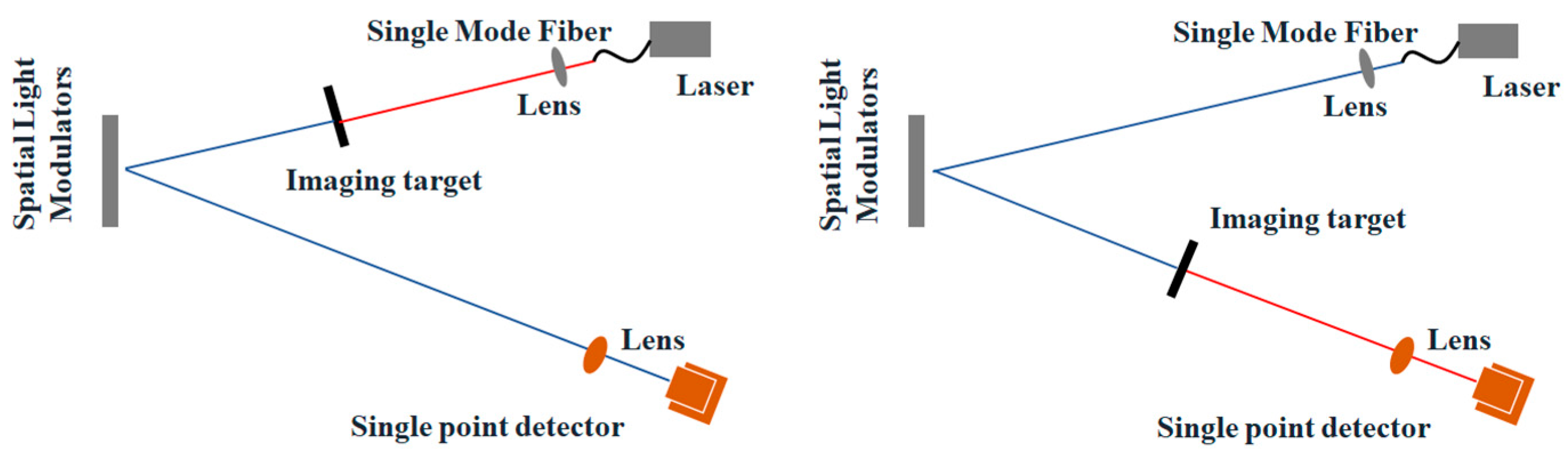
In 1995, Pittman et al. [41] experimentally demonstrated two-photon imaging, reconstructing the two-dimensional intensity information of a target by correlating measurements from the signal and reference optical paths. In 2005, Valencia et al. [42] achieved two-photon imaging using thermal light generated by a pseudo-thermal source, as shown in Figure 3. Later, in 2008, Shapiro et al. [43] introduced lensless computational ghost imaging, which eliminated the need for the reference light path traditionally required in two-beam systems.

The fundamental principle of computational ghost imaging involves the following steps: A laser source generates a beam that is encoded by a spatial light modulator (SLM). This encoded beam is projected onto a scene or object using a lens, encoding and modulating the scene’s information. The modulated light is then captured by a single-pixel detector, which measures the light intensity. Finally, a reconstruction algorithm is applied to recover the scene image from the acquired intensity data.

3.3.2. Coded Sampling Method

To reduce the computational cost of reconstruction algorithms and address hardware limitations, Aßmann et al. [44] proposed a compressive adaptive ghost imaging technique in 2013. By employing a wavelet basis, this method reconstructs high-quality images from low-resolution images by automatically detecting regions with large coefficients and increasing image resolution. Subsequently, in 2014, Yu et al. [45] developed another compressive adaptive ghost imaging approach based on wavelets, designed to enable real-time ghost imaging and produce high-quality images in noisy environments. This method is adaptable for imaging applications across a range of wavelengths.

Noiselets, which are highly incoherent with Haar wavelets, were introduced by Anna et al. [46] in 2016 as measurement and compression matrices for compressed sensing ghost imaging. This method leverages complex-valued, nonbinary noiselet functions for object sampling in systems illuminated by incoherent light, achieving high-quality image reconstruction at low sampling rates. Gaussian white noise was incorporated into the theoretical model to enhance reconstruction quality. However, this method has notable drawbacks, including high computational costs and extended recovery times.

Hadamard basis patterns, which are binary and have a mosaic-like discrete form, are particularly well suited for error-free quantization and display on high-speed binary spatial light modulators such as digital micromirror devices (DMDs). This makes Hadamard basis patterns highly robust to noise in reconstructed images. In 2015, Edgar M. P. [4] and colleagues designed a real-time video system for simultaneous imaging in visible and short-wave infrared wavelengths. Their system employed Hadamard basis patterns for real-time sampling and iterative reconstruction, using an optimization algorithm to achieve higher-quality real-time video imaging.

In contrast to Hadamard basis patterns, Fourier basis patterns are sparser and more efficient for sampling most natural scenes. Fourier basis patterns, which are grayscale fringe patterns, can be modulated using time-division multiplexing on DMDs. Although they can also be displayed on other spatial light modulators, their modulation rate is significantly reduced in such cases. In 2015, Zhang et al. [47] proposed using Fourier basis patterns to reconstruct high-quality, recognizable images with fewer measurements. These patterns were displayed in binary form via a DMD. To further enhance imaging speed, the same research team [48] developed a fast computational ghost imaging approach using Fourier basis patterns in 2017. This approach significantly improved illumination rates compared to the original grayscale patterns.

4. Transverse Scanning-Based SPI

A two-dimensional (2D) dataset is constructed by performing multiple axial scans at different transverse locations, integrating orientation information with depth information at each location of the target. This process ultimately forms a three-dimensional (3D) image of the scene from a series of two-dimensional datasets. Typical applications of transverse scanning in SPI include OCT and single-photon LiDAR.

4.1. OCT

4.1.1. OCT Imaging Theory

OCT is a non-invasive optical imaging technology that utilizes the low-coherence property of a broad-spectrum light source (usually near-infrared light) to process the collected scattered light signals to obtain an interferogram, which is used to show the structural characteristics of and pathological changes in biological tissues [49,50]. OCT plays an important role in early detection and diagnosis in dermatology [51], dentistry [52,53], ophthalmology [54,55,56], and other fields.

Most current OCT systems (as shown in Figure 4) utilize two-beam interferometers (e.g., Michelson interferometers) to achieve short coherence lengths by employing broadband light sources. The basic model of OCT [50] can be expressed as

$$I(\tau )=2\mathrm{Re}\{\Gamma (\tau )*f(\tau )\}$$

(2)

where $\tau$ denotes the time delay, $\mathrm{Re}$ is the real component operator, $*$ is the convolution operator, $f(\tau )$ denotes the impulse response function, and $\Gamma (\tau )$ denotes the coherence function of the light source of the OCT. $\Gamma (\tau )$ is equivalent to the longitudinal PSF of the OCT system, which can be expressed as follows:

$$K_{\mathrm{longitudinal}}=\Gamma (t)=\exp [-{({\displaystyle \frac{\pi c\Delta \lambda \tau }{2\sqrt{\ln 2{\lambda }_0^2}}})}^2]\exp [-i({\displaystyle \frac{2\pi c\tau }{{\lambda }_0}})]$$

(3)

where ${\lambda }_0$ denotes the central wavelength, $c$ is the speed of light, and $\Delta \lambda$ denotes the bandwidth of the light source used in the OCT system. The light sources generally follow a Gaussian distribution. Additionally, the spatial amplitude distribution of the light source is modeled as the longitudinal PSF of the OCT system. The transverse PSF or the amplitude distribution of a Gaussian-distributed beam can be expressed as

$$K_{\mathrm{transverse}}=\exp (-2{\displaystyle \frac{x^2+y^2}{W_z^2}})$$

(4)

where $W_z$ represents the beam radius at which the beam intensity drops to $1/e^2$ of its central value. The radius is given by the following equation:

$$W_z=W_0{[1+{({\displaystyle \frac{z}{z_R}})}^2]}^{1/2}$$

(5)

where $W_0$ denotes the minimum value of $W_z$, $z$ is the vertical coordinate, $z_R$ denotes the boundary of the confocal region, and $\lambda$ denotes the wavelength of the light source.

4.1.2. Scanning OCT Imaging System

Time-domain OCT (TD-OCT) represents the first generation of OCT imaging systems [57], utilizing low-coherence interferometry to obtain scanning intensity distributions. This process involves splitting the light and directing it toward a reference mirror and a sample. Intensity information, in the form of depth reflectivity profiles, is extracted from the resulting interferometric profiles. Adjusting the position of the reference mirror allows the detection of backscattered tissue intensity levels from varying depths within the tissue sample. However, the image acquisition speed of TD-OCT is constrained by mechanical limitations, with a maximum achievable speed of 400 scans/s [58].

Fourier-domain OCT (FD-OCT) represents the next generation of OCT imaging, featuring key advancements such as a stationary reference mirror, the simultaneous measurement of the reflected light spectrum, and the conversion of the frequency domain to the time domain using a Fourier transform. FD-OCT is further divided into spectral-domain OCT (SD-OCT) and swept-source OCT (SS-OCT) [57]. In SD-OCT, signals are recorded via spatial encoding using a line array camera, whereas SS-OCT records spectral signals sequentially over time using a single-point detector. The two techniques also differ in their central wavelengths: SD-OCT commonly employs a wavelength of 850 nm, while SS-OCT uses 1050 nm [59]. Longer wavelengths, such as those used in SS-OCT, provide superior penetration, making SS-OCT particularly effective for imaging deeper structures [60]. Scan acquisition speeds for SD-OCT can reach approximately 100,000 scans per second, while SS-OCT can exceed 200,000 scans per second [59]. These techniques enhance sensitivity, improve signal-to-noise ratios, and deliver higher-quality scans, including 3D imaging capabilities.

Table 3. Characteristics of each OCT technique.

	Light Source	Major Advantages	Major Drawbacks
TD-OCT (time domain)	Near-infrared broadband light source	Intensity information acquired in the time domain; the measurement depth determined by the sweep range of the reference mirror.	Need to move the reference mirror; noisy; slow imaging speed, failing to realize real-time imaging
SD-OCT (spectral domain)	Near-infrared broadband light source	No need to move the reference mirror; higher sensitivity than TD-OCT; high sweep speed and axial resolution achieved.	Sensitivity decreases with the depth of detection; the light source has a short wavelength, and many samples exhibit strong scattering effects
SS-OCT (swept frequency)	Swept-frequency near-infrared broadband light source	No need to move the reference mirror; better spectral resolution and lower sensitivity attenuation than TD-OCT; very high sweep speed can be obtained.	Operating at long wavelengths (λ = 1–1.3 μm); lower axial resolution than TD-OCT; high cost

outlines the specific characteristics of each OCT technique.

4.2. Single-Photon LiDAR

LiDAR technology is capable of precisely measuring the position, motion, and shape of a target, as well as tracking it. The narrow wavelength range of light waves allows for highly accurate detection. A typical LiDAR system consists of three main components: a laser source, a photodetector (see Table 1), and a signal processing module. Based on different scanning modalities, LiDAR systems are generally classified into three categories: mechanical, semi-solid, and solid-state [61]. Mechanical LiDAR achieves scanning through a rotating mechanical mechanism; however, its application is often limited by factors such as reliability, size, and cost [62]. To address these limitations, semi-solid and solid-state LiDAR systems have been developed, offering higher reliability and compactness (shown in

Table 4. Different kinds of LiDAR.

Type	Major Advantages	Major Drawbacks
Mechanical	Wide range of field of view	Bulky; rotating structure is prone to wear
Semi-solid	Microelectromechanical system (MEMS)-based LiDAR	Compact	MEMS mirror design must be considered
Solid-state	Flash-based LiDAR	Faster data acquisition; good reliability	Resolution limited by photodetector array
	Optical phased array (OPA)-based LiDAR	Compact; low manufacturing costs	Low power threshold; slow modulation rate

).

4.2.1. Detection Principles

With advancements in single-photon detection technology, single-photon LiDARs have emerged and rapidly gained prominence. Compared with conventional LiDAR systems, single-photon LiDARs provide higher resolution, improved sensitivity, and enhanced anti-jamming capabilities. These advantages make them particularly suitable for low signal-to-noise environments and applications requiring high-precision target information. Additionally, single-photon LiDARs outperform conventional systems in terms of size, weight, power consumption, and complexity.

(1)

Time-correlated single-photon counting (TCSPC)

In photon-counting LiDAR systems employing TCSPC [63], the Poisson response of an SPD to photons within a given time interval, $(t_1,t_2)$, is modeled as follows:

$$P(k,t_1,t_2)={\displaystyle \frac{1}{k!}}{[M(t_1,t_2)]}^k\exp [-M(t_1,t_2)]$$

(6)

$$M(t_1,t_2)={\displaystyle \underset{t1}{\overset{t2}{\int }}\frac{P_r}{J_P}}(t-\tau )d\tau$$

(7)

In the aforementioned equations, $P_r$ is the echo signal energy, and $J_P$ is the energy of a single photon. $P(k,t_1,t_2)$ represents the probability of detecting k photon events in $(t_1,t_2)$ time.

(2)

Time-of-flight (TOF) method

The TOF method measures distance by utilizing a laser that emits laser pulses. The system begins measuring time when the pulses leave the laser and records the stop signal upon receiving the reflected pulses from the target.

The TOF of a photon ${\tau }_{tof}$ can be obtained as follows [64]:

$${\tau }_{tof}={\displaystyle \frac{d_{tot}}{c}}={\displaystyle \frac{d_{in}+2d_{obj}}{c}}={\tau }_0+{\displaystyle \frac{2d_{obj}}{c}}$$

(8)

In the aforementioned equation, c is the speed of light, $d_{tot}$ is the sum of the distance inside the measuring device $d_{in}$ and the distance from the laser to the object $d_{obj}$, and ${\tau }_o$ is the offset time inside the measuring device.

4.2.2. Reconstruction Algorithms

Point Cloud Reconstruction

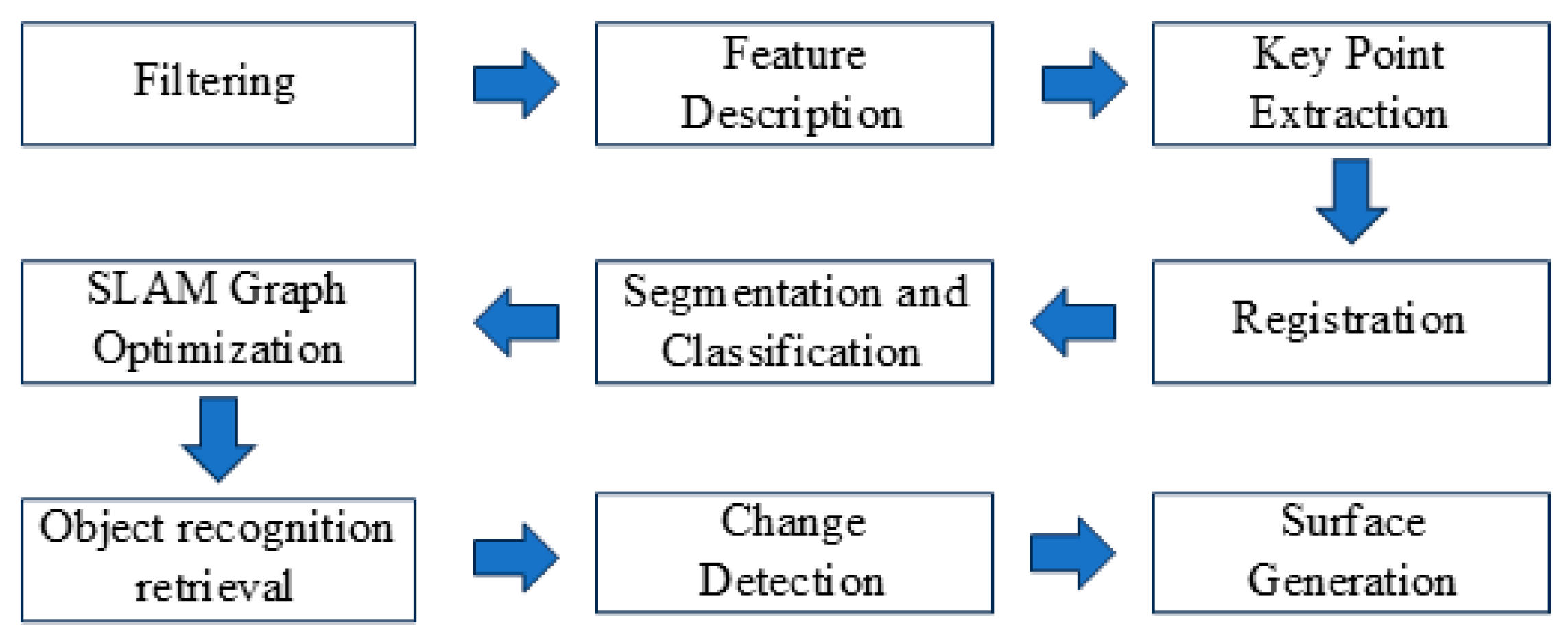
LiDAR systems capture extensive 3D sample points, forming datasets known as point clouds. A point cloud contains the x, y, and z coordinates of the object’s surface relative to the sensor’s position. In some cases, additional information such as color and echo signal intensity is included. Point clouds can accurately describe the geometric characteristics and spatial locations of objects. The basic steps for processing point clouds [65] are illustrated in Figure 5. Point cloud-based surface reconstruction algorithms [66] are presented in the following section, including the Poisson surface reconstruction algorithm and the ball-pivoting surface reconstruction algorithm.

(1)

Poisson surface reconstruction algorithm

The Poisson surface reconstruction algorithm is used to construct a smooth surface with the aid of an indicator function $\psi$ (defined as 1 for a voxel inside the body M and 0 for a voxel outside M) [67]. The vector field $v(x)\in R^3$ is determined from the data sample S. The algorithm aims to determine the scalar function $\psi (x)$ by minimizing the following equation:

$${\epsilon }_1(\psi )={\displaystyle \underset{\Omega }{\int }\left|\right|}\nabla \psi (x)-v(x)|{|}_2^{2}dx$$

(9)

where $x\in \Omega$ and $\Omega \subset R^3$. ∂ is the gradient operator, and $\left|\right|\cdot |{|}_2$ is the inner product of $L_2$. Through the application of the divergence operator to form the Poisson equation, the governing equation is expressed as

$$\Delta \psi =\nabla \cdot v$$

(10)

where $\Delta$ and $\nabla \cdot$ denote the Laplace and divergence operators, respectively. The vector field v is defined by convolving the normal field with the Dirac function $\delta$.

$$v(x)={\displaystyle \underset{\partial M}{\int }\delta (x-p)n(p)dp\approx {\displaystyle \sum _{p\in S}\delta (x-p)n(p)}}$$

(11)

In this equation, $n(p)$ is the inward surface normal vector at the point $p\in S$, $\delta$ is the Dirac function, and $\partial M$ is the boundary of the solid M. Solving Equation (10) provides the solution $\psi$. The reconstructed surface S is then defined as the semi-equivalent surface of the scalar function $\psi$.

(2)

Ball-pivoting surface reconstruction algorithm

The ball-pivoting algorithm is a surface reconstruction method that generates boundary shapes using $\alpha$ shapes [68]. The $\alpha$ shapes ($\varnothing$) are selected from the data sample S to form the boundary shape, where the boundary is determined by a positive parameter $\alpha$:

$$\varnothing =F(S,\alpha )$$

(12)

Here, $\alpha$ is defined as the reciprocal of the planar Euclidean distance between the current point and its next neighboring point.

$$\alpha ={\displaystyle \frac{1}{dist(S_i,S_j)}}$$

(13)

Here, the function $dist(S_i,S_j)$ is used to calculate the planar Euclidean distance between $S_i$ and $S_j$. In this method, spheres of varying radii roll over the sample points to create triangles. If three consecutive points touched by the rolling sphere do not contain any additional points within the sphere, a new triangle is formed.

Frequency-Domain Reconstruction

Frequency-domain reconstruction is based on the Fourier transform of discrete signals. The method generates high-resolution images by encoding spatial information into the frequency domain by irradiating the object with the light of different spatial frequency structures and then converting the frequency-domain information back to the spatial domain.

Spatial frequency-domain fringes generated by light incident on an object are expressed as follows:

$$P_{\phi }(x,y;f_x,f_y)=a+b\cos (2\pi f_{x}x+2\pi f_{y}y+\phi )$$

(14)

Here, $a$ is the DC component of the incident light, $b$ is the contrast, and $\phi$ is the initial phase.

The total intensity of reflected light $I(f_x,f_y)$ is given by

$$I(f_x,f_y)={\displaystyle \underset{s}{\iint }O(x,y)P_{\phi }}(x,y;f_x,f_y)dxdy$$

(15)

where $s$ is the illumination area, and $O(x,y)$ is the position distribution of the object.

The total reflected light intensity measured by the detector, $B_{\phi }(f_x,f_y)$, is given by

$$B_{\phi }(f_x,f_y)=B_n+\gamma \cdot (f_x,f_y)$$

(16)

Here, $B_n$ is the optical noise intensity, and γ is the detector gain.

Following the four-step phase-shift algorithm, the spectrum of the object, $C(f_x,f_y)$, is expressed as follows:

$$C(f_x,f_y)=2b\gamma F\{O(x,y)\}$$

(17)

Here, $F\left\{\right\}$ is the Fourier transform.

Subsequently, image reconstruction is achieved through the equation:

$$O(x,y)={\displaystyle \frac{1}{2b\gamma }}{F}^{-1}\{C(f_x,f_y)\}$$

(18)

In the above equation, $F^{-1}\left\{\right\}$ is the Fourier transform.

4.2.3. Applications

(1)

Autonomous driving

Compared to multi-sensor approaches, single-photon LiDAR does not rely on complex algorithms, operates more efficiently, responds faster, and performs robustly under various lighting conditions. It enables vehicles to acquire remote, high-resolution 3D images of their surroundings, even in challenging environments such as low light or turbid media (e.g., rain, fog, snow, and dust) [69,70]. In 2022, Wu et al. [71] at East China Normal University developed a single-photon LiDAR system capable of high-quality imaging in dense fog with a transmittance of 0.023. This innovation offers a practical solution for imaging in turbid media. Moreover, the system significantly reduces energy consumption, contributing to energy conservation and emission reduction.

(2)

Remote sensing imaging of complex scenes

The long-range and high-resolution capabilities of single-photon LiDAR provide valuable data for applications such as monitoring forest changes, assessing water resources, and managing wildlife habitats [72]. In 2005, the United States Lincoln Laboratory developed the Jigsaw airborne single-photon LiDAR system, which successfully achieved the three-dimensional imaging of vehicles and buildings under tree canopies [73]. These LiDAR systems can also be utilized to inspect structural safety distances in infrastructure such as bridges, dams, and power lines.

(3)

Space exploration

When a ground-based laser irradiates into space, atmospheric attenuation and other factors result in only a small number of photons being sent back via diffuse reflection, making it challenging to detect and extract the target photons. In 2016, Chinese scientists utilized an SNSPD system to successfully measure a target satellite located 3000 km away [74]. With further optimization and advancements in single-photon LiDAR technology, higher range accuracy and the ability to detect smaller space debris are expected in the future.

5. Longitudinal Scanning-Based SPI

In Fourier space scans, the energy of the object is concentrated in the low-frequency region, enabling the encoding of information from other objects into the medium- and high-frequency regions. This approach provides additional degrees of freedom and allows for three-dimensional imaging. Typical applications of longitudinal scanning-based SPI include Fourier transform infrared (FTIR) spectrometry and intensity interferometry.

5.1. FTIR Spectrometry

5.1.1. FTIR Spectrometry Based on Michelson Interferometer

An FTIR spectrometer differs from traditional spectroscopic methods, such as prism or grating spectroscopy, by employing a Michelson interferometer (as shown in Figure 6) to generate an interferogram. The interferogram, which varies with time, is converted into a frequency-dependent spectrogram using a Fourier transform. The incident light is split into two beams by a beam splitter: one beam is directed toward a fixed mirror, while the other is reflected by a movable mirror. The two beams are recombined at the beam splitter, producing interference signals that are detected by a photodetector [75].

When the sample absorbs a specific wavelength, the interference signal I(δ) can be expressed as [75]

$$I(\delta )={\displaystyle {\int }_{-\infty }^{+\infty }B(v)\cos (2\pi \delta v)}dv$$

(19)

where $\delta$ is the optical path difference, $v$ is the wave number, and $B(v)$ is the spectral power density. $B(v)$ can be obtained by performing a Fourier transform on $I(\delta )$ according to the following equation:

$$B(v)={\displaystyle {\int }_{-\infty }^{+\infty }I(\delta )}{e}^{-i2\pi \delta }d\delta$$

(20)

The theoretical spectral resolution $\Delta \sigma$ is given by the following equation:

$$\Delta \sigma ={\displaystyle \frac{1}{2\times \Delta Z_{\max }}}={\displaystyle \frac{1}{{\delta }_{\max }}}$$

(21)

where $\Delta Z_{\max }$ is the maximum displacement of the movable mirror. As shown in Equation (21), the spectral resolution is determined by the displacement of the movable micromirror. The resolution increases with the extension of the displacement. However, the movable mirror must remain well aligned during movement.

5.1.2. Characteristics and Applications of FTIR Spectrometers

An FTIR spectrometer [76] is a universal instrument used to study the infrared optical response of solid-, liquid-, and gas-phase samples. Infrared spectroscopy not only identifies different types of materials (qualitative analysis) but also quantifies the amount of material present (quantitative analysis). FTIR spectrometers offer a variety of advantages (see

Table 5. Main characteristics of FTIR spectrometers.

	Main Characteristics	Details
1	High signal-to-noise ratio	The system has fewer optical components, which reduces the loss of light in propagation, and the light signal can be enhanced by interference, so the detector detects a strong signal
2	High reproducibility	The Fourier transform processes the light signal and avoids the errors associated with motor-driven grating spectroscopy
3	Fast sweep speed	The system can scan a complete infrared spectrogram in one second or a few seconds
4	Large spectral measurement range	The entire infrared spectrum can be measured by simply replacing the beam splitter and light source

for specific performance metrics), such as a high signal-to-noise ratio, good reproducibility, a large spectral measurement range, the use of a single photodetector, and fast sweep speed. These features make them highly applicable in various industries, including pharmaceuticals, chemicals, energy, environmental sciences, and semiconductors.

The rapid development and commercialization of portable spectrometers are gaining significant traction. One common solution for the miniaturization of Fourier transform infrared (FTIR) spectrometers involves replacing the removable mirror modules in conventional Michelson interferometer-based FTIR systems with MEMS micromirrors. So far, three main types of MEMS micromirrors have been employed for FTIR miniaturization: electrostatic [77,78], electromagnetic [79], and electrothermal [80].

5.2. Intensity Interferometry

5.2.1. Basic Principles

Intensity interferometry has not seen significant advancements since the 1970s due to the potential loss of phase information. However, with the advent of technologies such as SPDs and signal digital correlators, it has re-emerged as a high-resolution observational technique in astronomy [81]. Intensity interferometry utilizes different optical telescopes or detectors to measure fluctuations in the light intensity of celestial objects and records the temporal correlation between the arrival times of photons at different locations. The correlation function of the measured light intensity $I(t)$ is expressed as [82]

$$\langle I_1(t)\cdot I_2(t)\rangle =\langle I_1(t)\rangle \langle I_2(t)\rangle (1+|{\gamma }_{12}{|}^2)$$

(22)

Here, $\langle \rangle$ denotes averaging over time, ${\gamma }_{12}$ denotes the cross-correlation function between SPDs 1 and 2, and $\left|{\gamma }_{12}\right|$ is the absolute value of the cross-correlation function.

5.2.2. Large Space Telescopes (LSTs)

The Cherenkov Telescope Array (CTA) [83] is a ground-based observatory designed for the study of ultra-high-energy gamma rays. It comprises multiple LSTs at the array’s center. Each LST is equipped with a fast PMT camera.

The PMT camera consists of thousands of pixels, with each pixel being a combination of a high-quantum-efficiency PMT and a condenser. This setup enables unprecedented high resolution and sensitivity, along with the capability to detect extreme radiation. Consequently, the CTA holds great research potential in the field of astronomy.

The European Extremely Large Telescope (E-ELT), built by the European Southern Observatory (ESO), is another ground-based optical telescope [84]. To address the limited temporal resolution of conventional CCD detectors, Dravins et al. [85] proposed the QuantEYE instrument project. This project was successfully applied to the E-ELT for high-temporal-resolution astronomical observations by segmenting the primary mirror of the Overwhelmingly Large (OWL) telescope into 100 pupil segments and placing a SPAD detector on each segment.

6. Application of DL Techniques in SPI

One of the primary challenges in SPI is the need for large amounts of measurement data. Over the years, various approaches have been developed to reduce the sampling rate. DL, as an emerging technology, has shown significant potential in recovering high-quality images even at very low sampling rates [86]. The following sections discuss three approaches: data-driven DL, physically augmented DL, and physically driven DL.

6.1. Data-Driven DL

In 2017, Lyu et al. [87] introduced the first data-driven DL method and applied it to ghost imaging, marking a foundational development in the application of DL in SPI. This method enhances the quality of reconstructed images while predicting low-noise images, thereby increasing the signal-to-noise ratio of the images. Building on this, Wang et al. [88] proposed an end-to-end neural network capable of directly obtaining one-dimensional bucket signals. Wu et al. [89] further improved image reconstruction quality by integrating dense connection blocks and attention mechanisms. However, data-driven methods rely on large datasets to train neural networks, making the training process time-intensive and less suitable for practical applications.

6.2. Physically Augmented DL

To address the limitations of data-driven DL, Wang et al. [90] proposed a physically augmented DL-based SPI method for image reconstruction in 2022. This approach incorporates physical information layers and model-driven fine-tuning into the neural network. By imposing strong physical model constraints, the method enhances the network’s generalization ability and improves reconstruction accuracy. However, the method still needs to be trained on datasets.

6.3. Physically Driven DL

In 2023, Li et al. [91] proposed an SPI method based on an untrained reconstruction network, utilizing a physical model to construct a network that maps the data and reconstructs the image. The network parameters are optimized through interactions between the neural networks and physical constraints. Unlike previous methods, this approach does not require training on tens of thousands of labeled datasets, thereby eliminating the need for extensive pre-preparation. Moreover, the method is highly generalizable and interpretable, surpassing the aforementioned approaches in image reconstruction quality and noise immunity. However, the method relies on iterative processes, and its imaging time and quality are influenced by the number of iterations.

7. Conclusions and Prospects

This paper reviews and summarizes the SPI technique. Starting from the single-pixel detector, this paper introduces the typical application of SPI technology under different imaging systems and some applications of deep learning techniques in SPI at this stage. The following is a brief summary of the typical applications introduced in the previous sections of this paper, as shown in

Table 6. Development status and future trends of main applications.

	Development Status	Details	Future Trends
X-ray coded aperture imaging	Compared with traditional X-ray projection imaging, both the light-gathering efficiency and the SNR are improved.	The light-gathering efficiency is 10 times or more that of a single pinhole, and the highest SNR can reach 70 times that of a single pinhole.	Obtain high-resolution and high-contrast images using modern image processing technology; explore new coded aperture methods.
Ghost imaging	This method solves the problems of acquisition time and reconstruction quality by using orthogonal matrices; it combines deep learning to improve imaging efficiency.	It can increase the sampling speed by 4 times using orthogonal matrices; it can reconstruct images at a sampling rate of 20% by combining deep learning.	Combine some characteristics of controlled light beam with ghost imaging.
Optical coherence tomography	OCT is divided into TD-OCT and FD-OCT, with relatively fast acquisition speed and the capability of realizing 3D imaging.	Up to 200,000 scans per second can be achieved during acquisition; it can obtain the blood flow velocity inside tissues.	Further improve acquisition speed, sensitivity, and SNR; realize large-field-of-view imaging.
Single-photon LiDAR	The detection sensitivity reaches the single-photon level; 3D reconstruction is possible under weak signals.	The single pulse energy is 1μJ for the laser imaging of a 50 m target.	Improve photon utilization rate and anti-noise ability of detection system; high-performance single-photon imaging algorithms.
Fourier transform infrared spectrometer	Its advantages are multiplexing, a high SNR, fast scanning speed, and a large spectral measurement range.	Only one second or several seconds are required for one scan; the spectral range from 1 μm to 1000 μm can be measured.	Miniaturize FTIR integration; improve accuracy and repeatability of spectral acquisition.
Intensity interferometry	It can achieve micro-arcsecond imaging under extremely long baselines; it shows good robustness to atmospheric turbulence and optical defects.	The CTA spatial resolution may reach close to 30 μas.	Improve sensitivity and SNR to achieve astronomical observations of high-resolution faint targets.

.

SPI, as a notable computational imaging technique, has achieved significant advancements and exhibits distinct advantages in low-light imaging and specialized bands, such as near-infrared and terahertz bands. The technique is gradually being applied in practical scenarios. However, several limitations must still be addressed: (1) Image reconstruction quality—when acquiring complex physical images, only limited information can be obtained, making it challenging to completely reconstruct the physical information and resulting in poor imaging results. (2) Limited imaging efficiency—the light source fails to respond quickly to the system, and the sample collection time is long. (3) Limited range of technical applications—the technique is applicable only in small field-of-view imaging, and it fails to ensure real-time imaging while obtaining a high resolution. (4) Imaging process errors have a significant impact—adding modulation and demodulation steps to the imaging process increases the complexity of the system while obtaining more information, and process errors have a significant impact on the final results.

With the continuous advancement of related technologies, SPI is likely to evolve in the following directions: (1) Some image processing steps can be completed during the sampling process, reducing information redundancy in the transmission channel and saving computing resources and time used in image processing. (2) Given SPI’s diverse imaging mechanisms, it may be possible to achieve faster, higher-resolution imaging by combining multiple mechanisms. (3) In the current era of rapid artificial intelligence development, DL technologies hold tremendous potential for quality enhancement, efficiency improvement, and robustness. Further exploration of DL could yield more effective solutions for increasingly complex scenarios and disruptive factors. (4) Focus on the integration, miniaturization, and on-chip implementation of detection systems is expected. It is believed that in the near future, SPI will develop into a dazzling nova in the field of computational imaging to better adapt to the needs of different scenarios.