Propagation Properties of Laguerre–Gaussian Beams with Three Variable Coefficient Modulations in the Fractional Schrödinger Equation
Abstract
1. Introduction
2. Theoretical Model
3. Numerical Simulation Results and Analysis
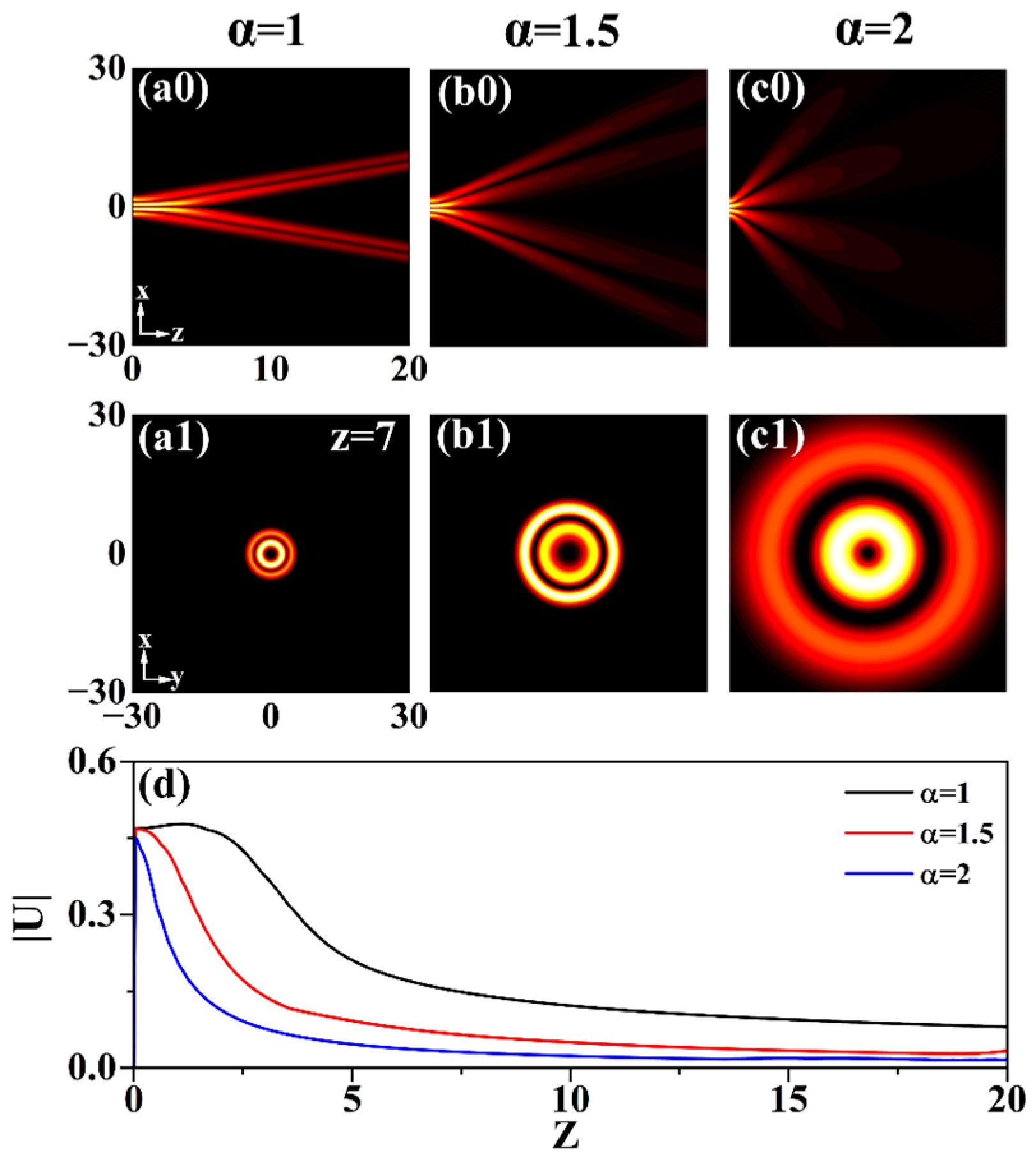
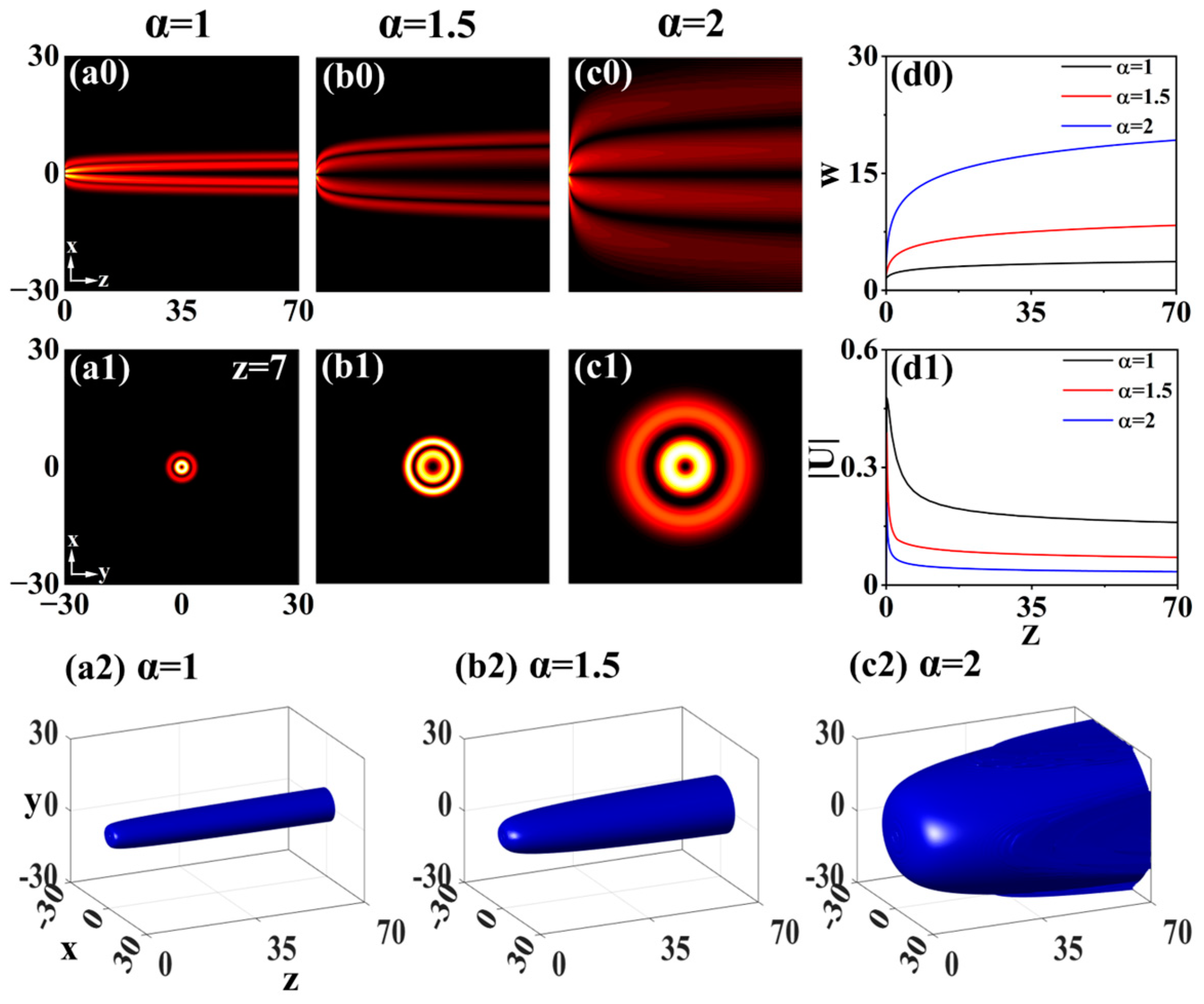
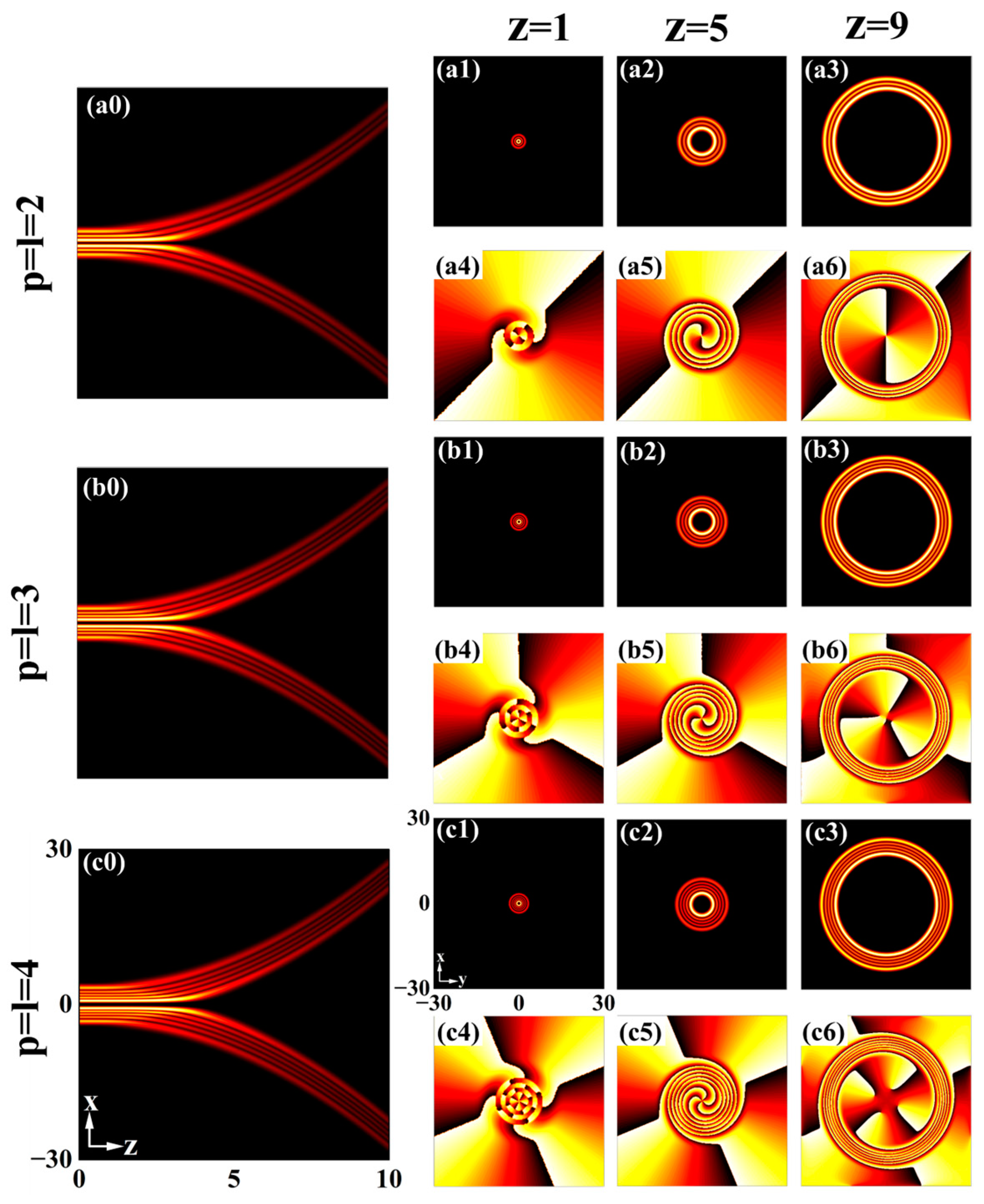
3.1. Without Modulation
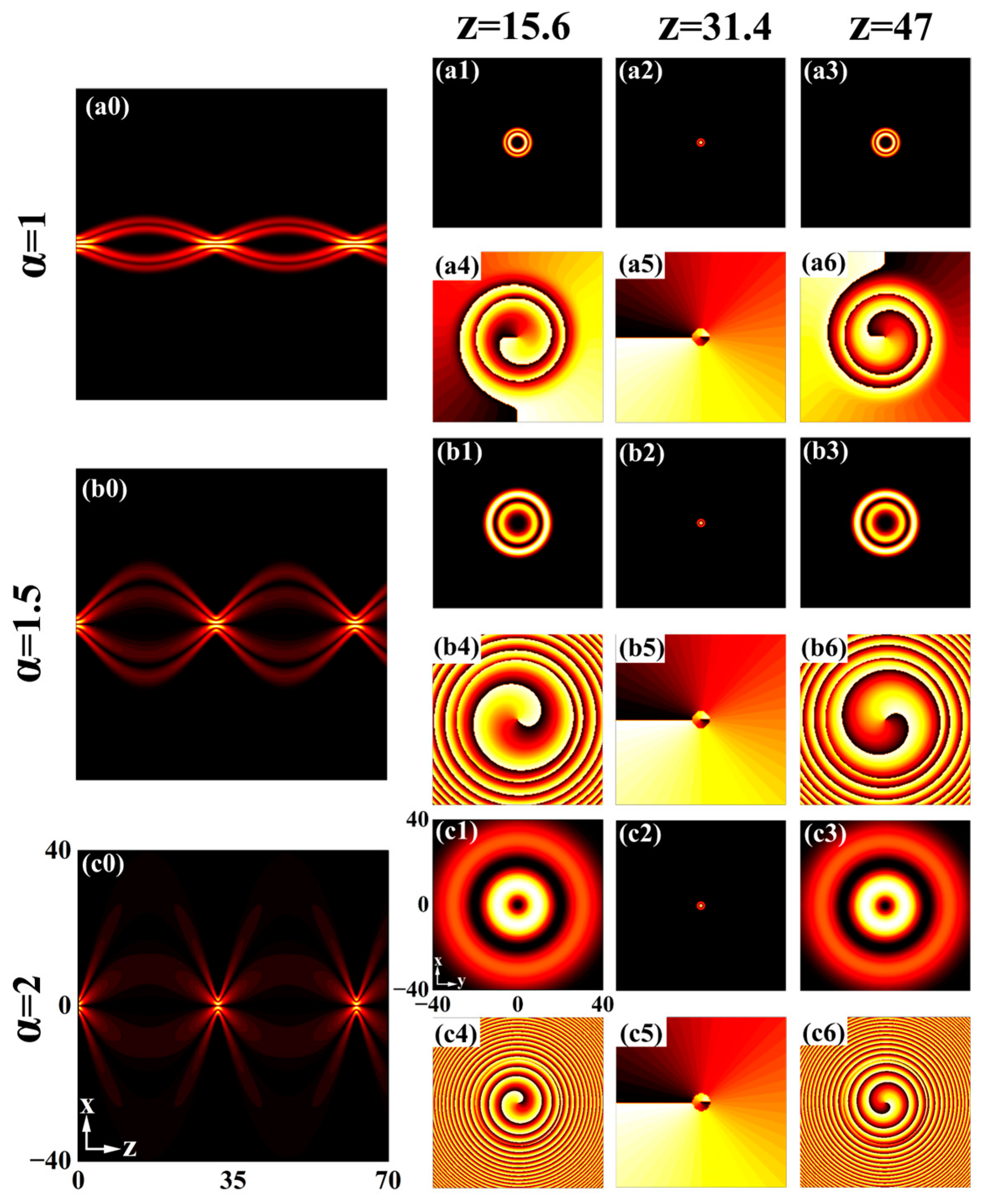
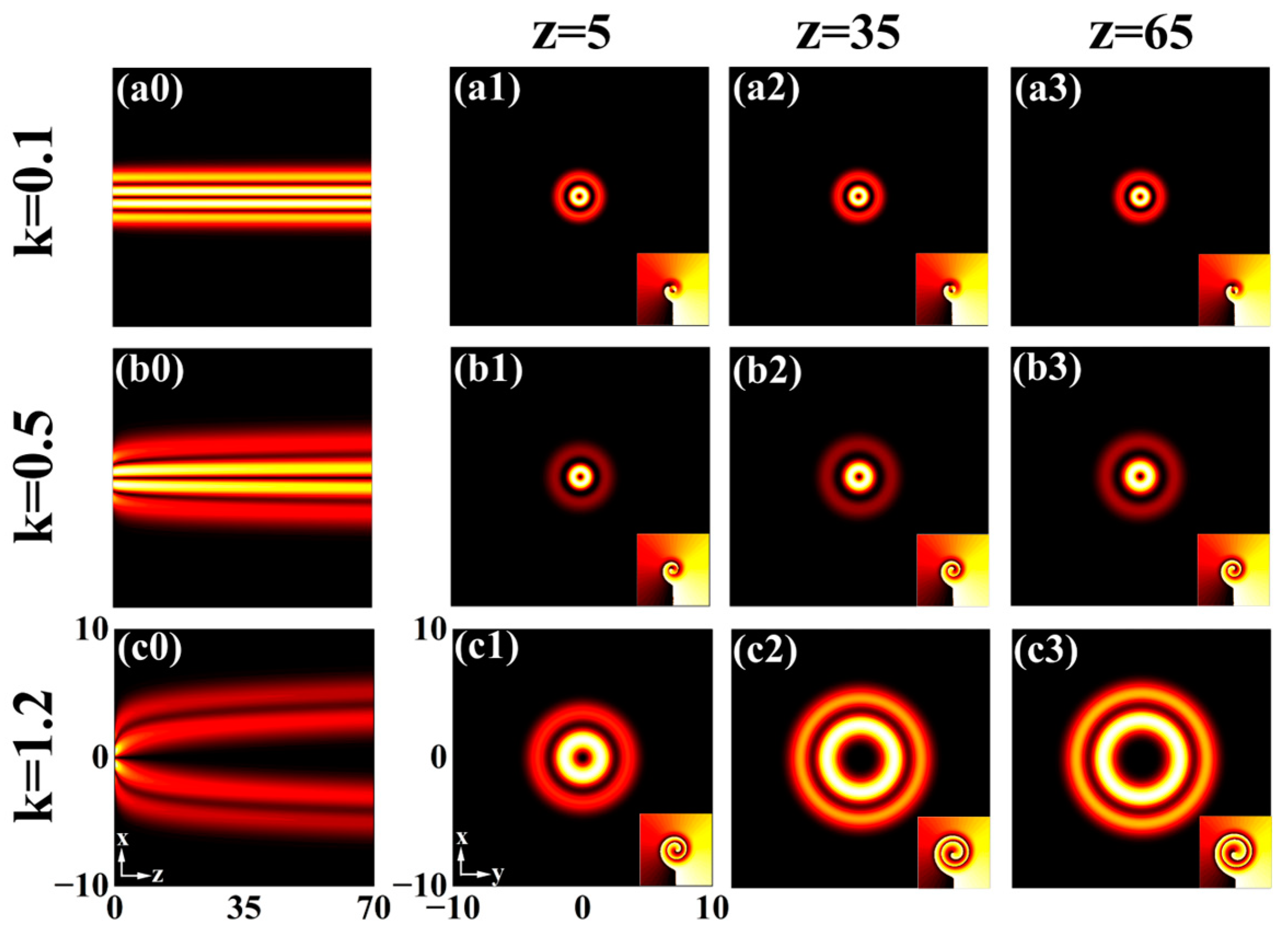
3.2. With Cosine Modulation
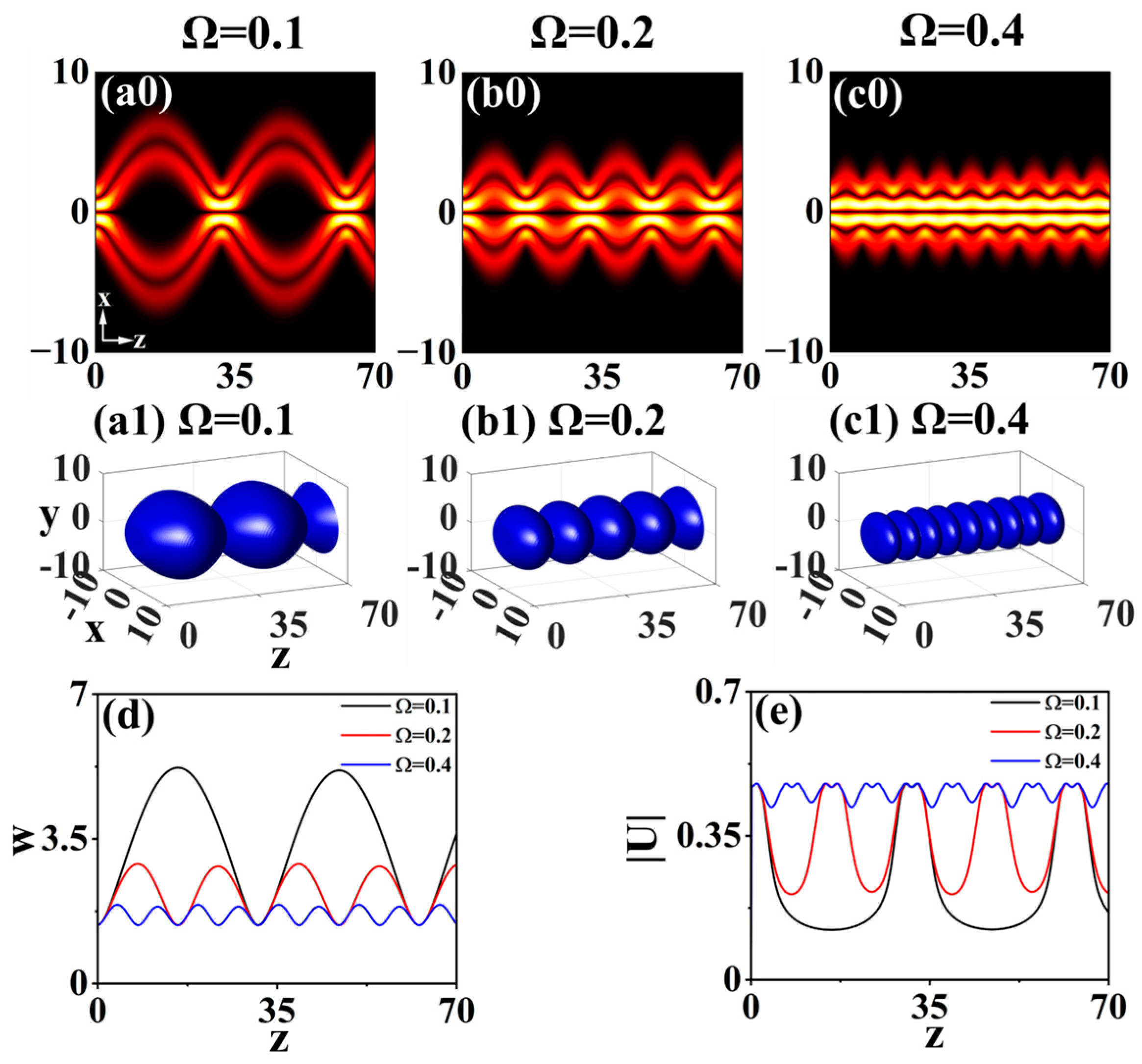
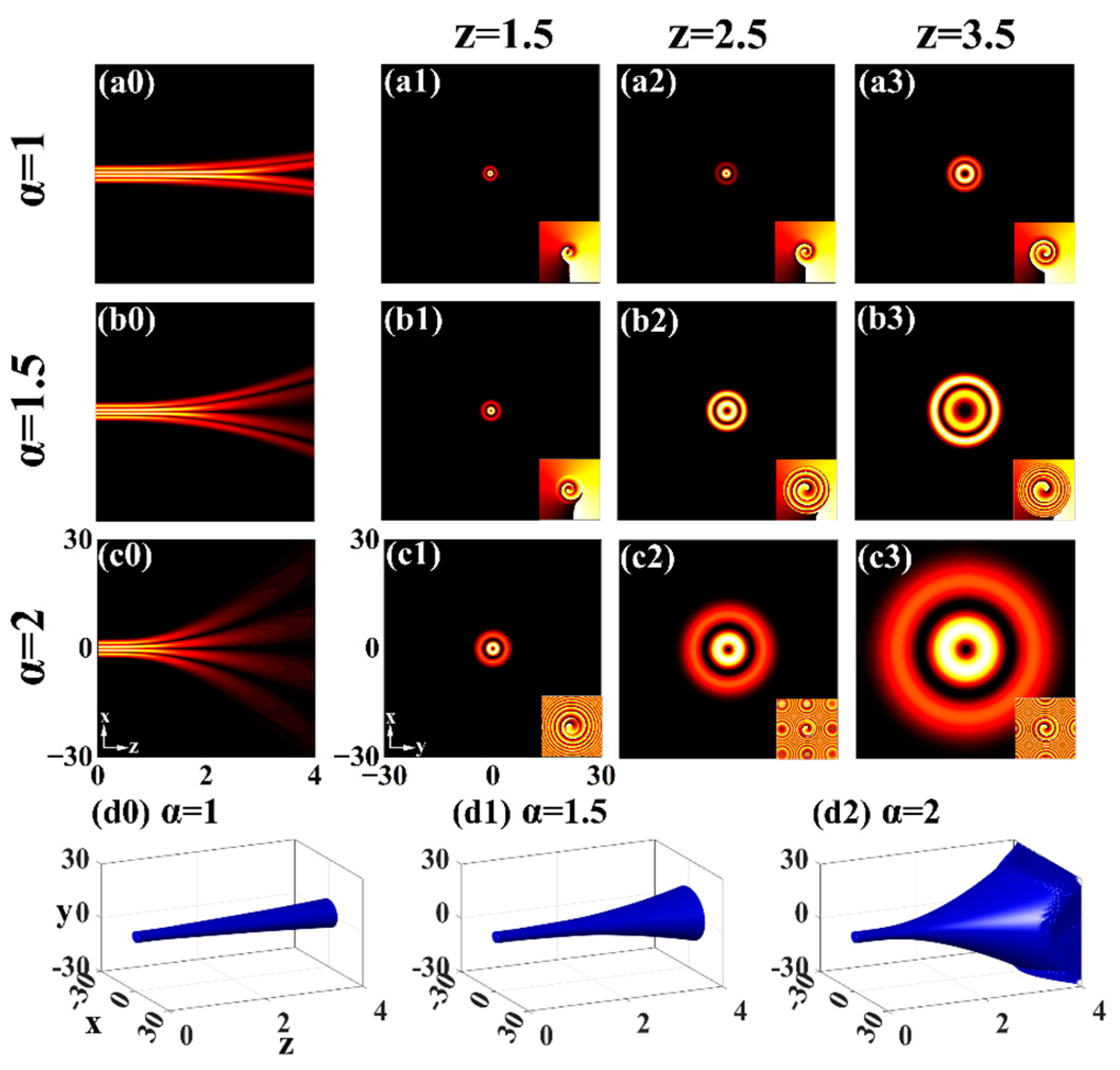
3.3. With Power Function Modulation
3.4. With Linear Modulation
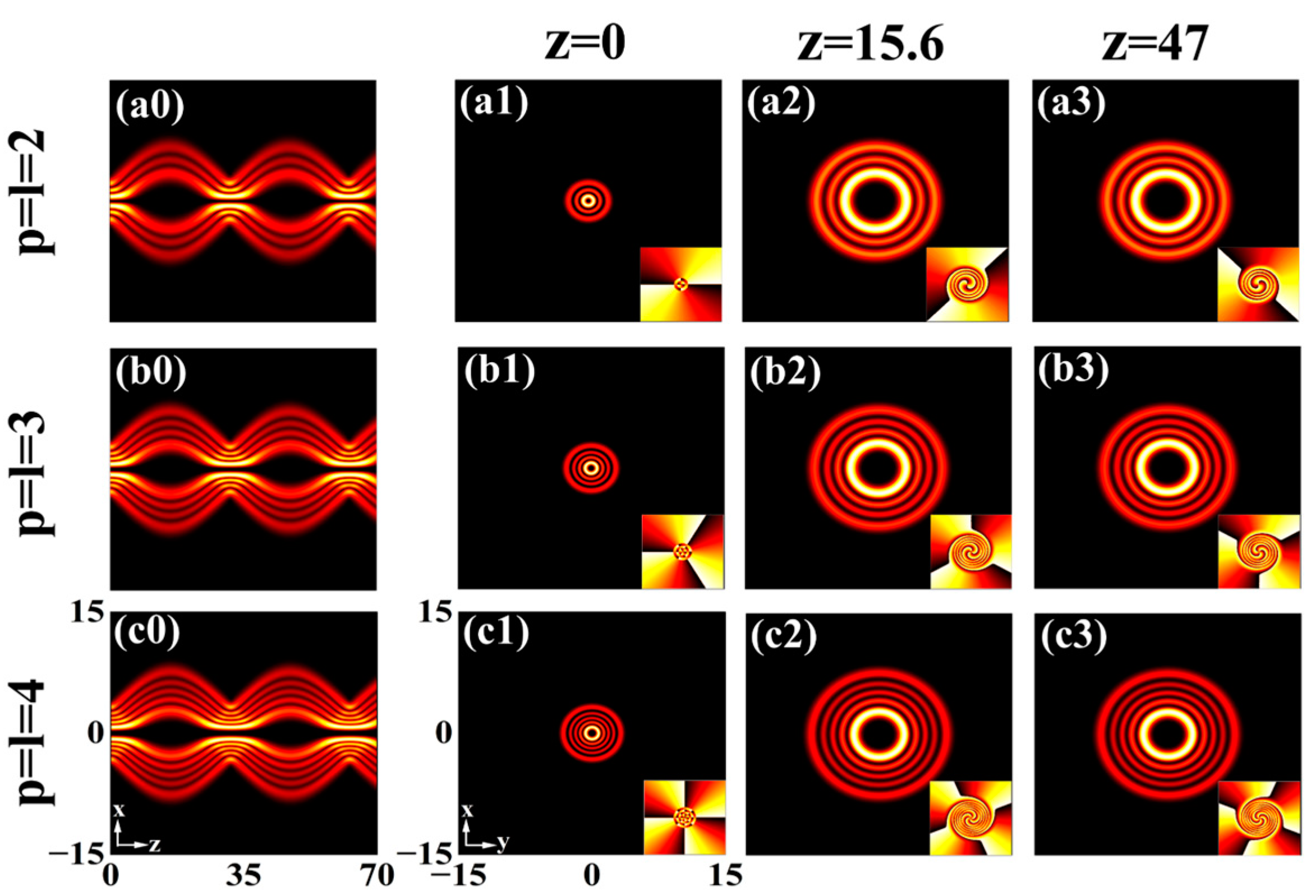
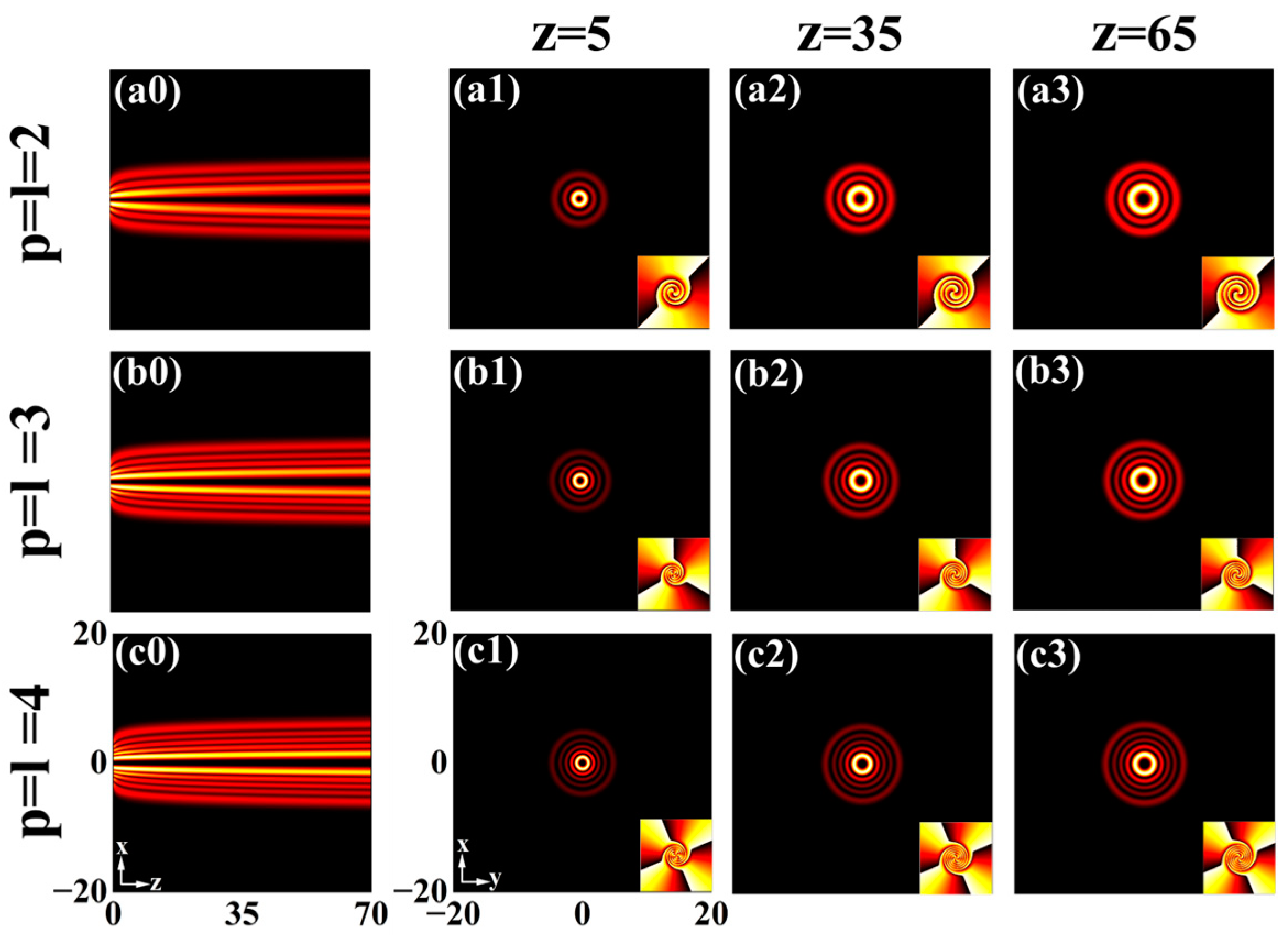
3.5. With Different Modulations ()
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tian, Y.; Wang, L.; Duan, G.; Yu, L. Multi-trap optical tweezers based on composite vortex beams. Opt. Commun. 2021, 485, 126712. [Google Scholar] [CrossRef]
- Avramov-Zamurovic, S.; Watnik, A.T.; Lindle, J.R.; Judd, K.P. Designing laser beams carrying OAM for a high-performance underwater communication system. J. Opt. Soc. Am. A 2020, 37, 876–887. [Google Scholar] [CrossRef] [PubMed]
- Ali, R.; Su, W.; Ullah, U.; Muhammad, A.; Rahman, A.U.; Akbar, J.; Usman, M. Amplification of rotary photon drag using Laguerre-Gaussian beam of control field. Opt. Quantum Electron. 2024, 56, 1443. [Google Scholar] [CrossRef]
- Peng, B.; Zhong, K.; Li, Z. Influence of topological charge on turbid underwater propagation of Laguerre-Gaussian vortex beams. Acta Opt. Sin. 2017, 37, 50–56. [Google Scholar]
- Wang, M.; Yu, W.; Huang, C. Transmission characteristics of underwater Laguerre-Gaussian vortex Beam and its superposition states. Acta Opt. Sin. 2023, 43, 317–325. [Google Scholar]
- Zhao, L.; Xu, Y.; Dan, Y. Evolution properties of partially coherent radially polarized Laguerre–Gaussian vortex beams in an anisotropic turbulent atmosphere. Opt. Express 2021, 29, 34986–35002. [Google Scholar] [CrossRef] [PubMed]
- Abramochkin, E.G.; Kotlyar, V.V.; Kovalev, A.A.; Stafeev, S.S. Generalized Asymmetric Hermite–Gaussian and Laguerre–Gaussian Beams. Photonics 2023, 10, 606. [Google Scholar] [CrossRef]
- Wang, Y.; Bai, L.; Xie, J.; Huang, C.; Guo, L. Radial spectrum spread of Laguerre-Gaussian beam transmission in weak compressible turbulence. Opt. Commun. 2024, 554, 126819. [Google Scholar] [CrossRef]
- Badás, M.; Piron, P.; Bouwmeester, J.; Loicq, J. On the optimum far-field irradiance distribution using Laguerre-Gaussian beams for intersatellite free-space optical communications. Opt. Express 2024, 32, 31597–31620. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Ma, Y.; Yuan, Q.; Chen, W.; Wang, L.; Zhao, S. Properties of focused Laguerre-Gaussian beam propagating in anisotropic ocean turbulence. Chin. Phys. B 2024, 33, 024208. [Google Scholar] [CrossRef]
- Zhang, Y.; Lin, Q.; Zhuang, Z.; Lin, F.; Hong, L.; Che, Z.; Zhuo, L.; Li, Y.; Zhang, L.; Zhao, D. Dynamics of dual-orbit rotations of nanoparticles induced by spin–orbit coupling. Nanophotonics 2025. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, S.; Qi, Y.; Lü, J.-Q.; Liu, Z.; Li, J.; Lin, X.; Lu, Z. On-demand spatial modes and vortex beams from a visible Pr: YLF orbital Poincaré laser with a hybrid pumping scheme. Opt. Express 2025, 33, 1952–1961. [Google Scholar] [CrossRef] [PubMed]
- Laskin, N. Fractional quantum mechanics. Phys. Rev. E 2000, 62, 3135–3145. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Sun, Z.-Z.; Hao, Z.-P. A fourth-order compact ADI scheme for two-dimensional nonlinear space fractional Schrödinger equation. SIAM J. Sci. Comput. 2014, 36, 2865–2886. [Google Scholar] [CrossRef]
- Longhi, S. Fractional Schrödinger equation in optics. Opt. Lett. 2015, 40, 1117–1120. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Li, C.; Zhong, H.; Xu, C.; Lei, D.; Li, Y.; Fan, D. Propagation dynamics of super Gaussian beams in fractional Schrödinger equation: From linear to nonlinear regimes. Opt. Express 2016, 24, 14406–14418. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Liang, Y.; Zou, M.; Lei, T.; Liu, M. The control for multiple kinds of solitons generated in the nonlinear fractional Schrödinger optical system based on Hermite-Gaussian beams. Commun. Nonlinear Sci. Numer. Simul. 2024, 140, 108375. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Wu, H.; Li, C.; Pierangeli, D.; Gao, Y.; Fan, D. Anomalous interaction of Airy beams in the fractional nonlinear Schrödinger equation. Opt. Express 2019, 27, 27936–27945. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; He, Z.; Conti, C.; Wang, Z.; Hu, Y.; Lei, D.; Li, Y.; Fan, D. Modulational instability in fractional nonlinear Schrödinger equation. Commun. Nonlinear Sci. Numer. Simul. 2017, 48, 531–540. [Google Scholar] [CrossRef]
- He, S.; Malomed, B.A.; Mihalache, D.; Peng, X.; Yu, X.; He, Y.; Deng, D. Propagation dynamics of abruptly autofocusing circular Airy Gaussian vortex beams in the fractional Schrödinger equation. Chaos Solitons Fractals 2021, 142, 110470. [Google Scholar] [CrossRef]
- He, S.; Zhou, K.; Malomed, B.A.; Mihalache, D.; Zhang, L.; Tu, J.; Wu, Y.; Zhao, J.; Peng, X.; He, Y.; et al. Airy-Gaussian vortex beams in the fractional nonlinear-Schrödinger medium. J. Opt. Soc. Am. B 2021, 38, 3230–3236. [Google Scholar] [CrossRef]
- Wang, J.; Jin, Y.; Gong, X.; Yang, L.; Chen, J.; Xue, P. Generation of random soliton-like beams in a nonlinear fractional Schrödinger equation. Opt. Express 2022, 30, 8199–8211. [Google Scholar] [CrossRef] [PubMed]
- Zhou, W.; Liu, A.; Huang, X.; Bai, Y.; Fu, X. Propagation dynamics of Laguerre-Gaussian beams in the fractional Schrödinger equation with noise disturbance. J. Opt. Soc. Am. A 2022, 39, 736–743. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Li, J.; Li, T.; Huang, X.; Bai, Y.; Fu, X. Dynamics of Airyprime beams with higher-order spectral phase modulation in the fractional Schrödinger equation. Laser Phys. 2024, 34, 095001. [Google Scholar] [CrossRef]
- Tan, C.; Liang, Y.; Zou, M.; Lei, T.; Tang, P.; Liu, M. Propagation dynamics of the Hermite-Gaussian beam in the fractional Schrödinger equation with different potentials. J. Opt. Soc. Am. B 2024, 41, 921–930. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Malomed, B.A.; Karimi, E. Experimental realisations of the fractional Schrödinger equation in the temporal domain. Nat. Commun. 2023, 14, 222. [Google Scholar] [CrossRef]
- Liu, S.; Zhang, Y.; Virally, S.; Karimi, E.; Malomed, B.A.; Seletskiy, D.V. Experimental emulator of pulse dynamics in fractional nonlinear Schrödinger equation. Laser Photonics Rev. 2025, 2401714. [Google Scholar] [CrossRef]
- Zang, F.; Wang, Y.; Li, L. Dynamics of Gaussian beam modeled by fractional Schrödinger equation with a variable coefficient. Opt. Express 2018, 26, 23740–23750. [Google Scholar] [CrossRef]
- Xin, W.; Song, L.; Li, L. Propagation of Gaussian beam based on two-dimensional fractional Schrödinger equation. Opt. Commun. 2021, 480, 126483. [Google Scholar] [CrossRef]
- Li, P.; Wei, Y.; Malomed, B.A.; Mihalache, D. Stabilization of axisymmetric Airy beams by means of diffraction and nonlinearity management in two-dimensional fractional nonlinear Schrödinger equations. Symmetry 2022, 14, 2664. [Google Scholar] [CrossRef]
- Tan, C.; Lei, T.; Zou, M.; Liang, Y.; Chen, L.; Tang, P.; Liu, M. Manipulating circular Airy beam dynamics with quadratic phase modulation in fractional systems under some diffraction modulations and potentials. Opt. Express 2024, 32, 25261–25275. [Google Scholar] [CrossRef] [PubMed]
- Tan, C.; Liang, Y.; Zou, M.; Lei, T.; Chen, L.; Tang, P.-H.; Liu, M.-W. Controlling Hermite-Gaussian beams dynamics with quadratic phase modulation in fractional systems based on different variable coefficients and potentials. Acta Phys. Sin. 2024, 73, 134205. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, X.; Yu, P.; Ge, X.-L.; Chen, C.; Man, Z.; Deng, D. Space–time dispersive symmetric Pearcey-Pearcey wave packets in the fractional Schrödinger equation. Opt. Lett. 2024, 49, 4681–4684. [Google Scholar] [CrossRef]
- He, S.; Peng, X.; He, Y.; Shan, C.; Deng, D. Propagation dynamics of the second-order chirped circular Pearcey Gaussian vortex beam in the fractional nonlinear Schrödinger equation. Chaos Solitons Fractals 2024, 189, 115734. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, X.; Liang, Y.; Zou, M.; Zhong, B.; Tan, C. Propagation Properties of Laguerre–Gaussian Beams with Three Variable Coefficient Modulations in the Fractional Schrödinger Equation. Photonics 2025, 12, 163. https://doi.org/10.3390/photonics12020163
Hao X, Liang Y, Zou M, Zhong B, Tan C. Propagation Properties of Laguerre–Gaussian Beams with Three Variable Coefficient Modulations in the Fractional Schrödinger Equation. Photonics. 2025; 12(2):163. https://doi.org/10.3390/photonics12020163
Chicago/Turabian StyleHao, Xinru, Yong Liang, Min Zou, Bin Zhong, and Chao Tan. 2025. "Propagation Properties of Laguerre–Gaussian Beams with Three Variable Coefficient Modulations in the Fractional Schrödinger Equation" Photonics 12, no. 2: 163. https://doi.org/10.3390/photonics12020163
APA StyleHao, X., Liang, Y., Zou, M., Zhong, B., & Tan, C. (2025). Propagation Properties of Laguerre–Gaussian Beams with Three Variable Coefficient Modulations in the Fractional Schrödinger Equation. Photonics, 12(2), 163. https://doi.org/10.3390/photonics12020163




