A Long-Period Grating Based on Double-Clad Fiber for Multi-Parameter Sensing

Abstract

This paper proposes a long-period grating (LPG) based on double-clad fibers (DCFs) for multi-parameter sensing. The sensor consists of cascaded-input single-mode fibers (SMF), DCF, and output SMF. Multi-parameter detection is realized by utilizing the different sensing characteristics of the resonance peak under different physical parameters. The experiment results show that within the temperature range of 30–100 °C, the maximum sensitivity is 66.37 pm/°C. For the refractive index (RI) measurement, the tested range is 1.3309–1.3888 and the maximum sensitivity is −45.84 nm/RIU. Regarding curvature detection, the tested range is 0.6928–1.6971 m⁻¹ and the maximum sensitivity is −2.022 nm/m⁻¹. In addition, the sensor has a symmetrical structure, so its measurement is not restricted by the incident direction of light, thus having flexibility in practical use. This research not only contributes to the advancement of optical fiber sensor technology but also has significant implications for practical applications in industry, the environment, and healthcare.

1. Introduction

In many scenarios, multiple parameters often interact with each other. Therefore, comprehensive monitoring of them is crucial for a full understanding of the system under study. For example, in industrial process control, parameters like temperature, pressure, and strain can significantly influence the quality and efficiency of production [1,2]. In the biomedical field, the simultaneous measurement of physiological parameters like temperature, strain, and biochemical substances can provide more comprehensive information for disease diagnosis and treatment [3]. Therefore, the development of multi-parameter sensors capable of detecting multiple analytes simultaneously not only simplifies the sensing system but also improves the accuracy and reliability of measurement results [4,5].

Long-period grating (LPG) is a type of optical fiber device that couples the core mode of an optical fiber to the cladding modes at specific wavelengths [6]. The coupling condition is highly sensitive to changes in the surrounding environment, such as refractive index (RI), temperature, and strain [7,8]. The mode-coupling capability of LPG is further expanded in Few-Mode Fibers (FMF) or ring-core fibers [7]. Studies also show that adding nanocomposites to the fiber surface can enhance the control of structural parameters while improving the detection sensitivity to target parameters [8,9]. Traditional ultraviolet laser writing technology is of great significance in improving the precision of grating processing. However, the introduction of CO₂ laser and femtosecond laser writing technologies has made more complex grating designs possible [10]. These technologies can not only achieve more precise modulation of grating periods but also generate micro/nano structures in optical fibers [11]. The sensitivity to temperature and RI can be further enhanced through micro-hole structuring [12,13].

When LPFG is used for multi-parameter detection, how to achieve efficient multi-parameter signal decoupling is a key issue in design optimization [14]. Existing studies have shown that by introducing tilted long-period fiber gratings, the spectral differentiation of the influence distribution of multiple parameters can be achieved using the dual-mode or multi-mode coupling characteristics of optical fibers, thereby realizing independent detection of multiple parameters [15]. Resonance peak dynamic adjustment technology further enhances the adaptability of LPFG to the complex external environment. The interactive coupling between temperature and RI can reduce signal interference by optimizing the mode field diameter [8,16]. Double-clad optical fibers are highly suitable for applications in the field of optical fiber sensing due to their unique inner–outer cladding structure [17,18,19]. Double-clad fibers (DCF) consist of an inner core, an inner cladding, and an outer cladding. The unique structure of DCFs allows for efficient coupling of light between different regions. This structure provides additional degrees of freedom for light manipulation and sensing applications [19].

In this paper, we propose and demonstrate a novel long-period grating for a multi-parameter optical fiber sensor based on DCF, which is shown in Figure 1. At the grating, the core mode is coupled to the co-propagating cladding modes. The cladding modes transmitted in the double-clad fiber are coupled to the single-mode fiber at the output end through the second waist-enlarged taper. The waist-enlarged taper is a structure that achieves efficient mode coupling between different optical fibers by locally tapering the optical fiber through high-temperature melting and expanding the diameter of the waist. Multi-parameter detection is realized by utilizing the different sensing characteristics of the resonance peak under different physical parameters. Utilizing the unique inner and outer cladding structure of DCFs, the cladding mode not only senses the change in environmental RI through the radiation mode, but also enhances the response through the co-directional coupling mechanism of LPG, thus solving the problem of the insufficient RI-sensing sensitivity of traditional DCF sensors. We aim to explore the sensing principles of this integrated sensor for various parameters, including temperature, RI, and curvature.

2. Materials and Methods

2.1. Principle

The LPG exhibits several loss peaks over a wide wavelength range. The number and extinction ratio of these loss peaks depend on the coupling between the fundamental mode and co-propagating cladding modes of different orders. The phase-matching condition of the LPG can be expressed as

$${\lambda }_{LPG}=\left(n_{eff}^{co}-n_{eff}^{cl}\right)\mathrm{\Lambda }$$

(1)

where $n_{eff}^{co}$ and $n_{eff}^{cl}$ represent the effective RIs of the core and the cladding mode, respectively, and the Λ is the grating period. When the external environmental parameters change, the effective RI difference between the core and the cladding, as well as the grating geometry, changes, leading to a shift in the resonant wavelength. By detecting the displacement of the characteristic wavelength, information about the changes in external environmental variables can be obtained.

When physical quantities such as the external temperature, strain, RI, and curvature of the sensor change, the refractive indices of the core and cladding of the LPG change, and the grating period also changes accordingly, causing the loss peak to drift. Considering the influence of waveguide dispersion, the wavelength drift is

$${\displaystyle \frac{d\lambda }{d\xi }}=\left({\displaystyle \frac{d{n}_{eff}^{co}}{d\xi }}-{\displaystyle \frac{d{n}_{eff}^{cl}}{d\xi }}\right)\mathrm{\Lambda }+\left(n_{eff}^{co}-n_{eff}^{cl}\right){\displaystyle \frac{d\mathrm{\Lambda }}{d\xi }}$$

(2)

where ξ represents physical quantities such as strain, temperature, RI, and curvature.

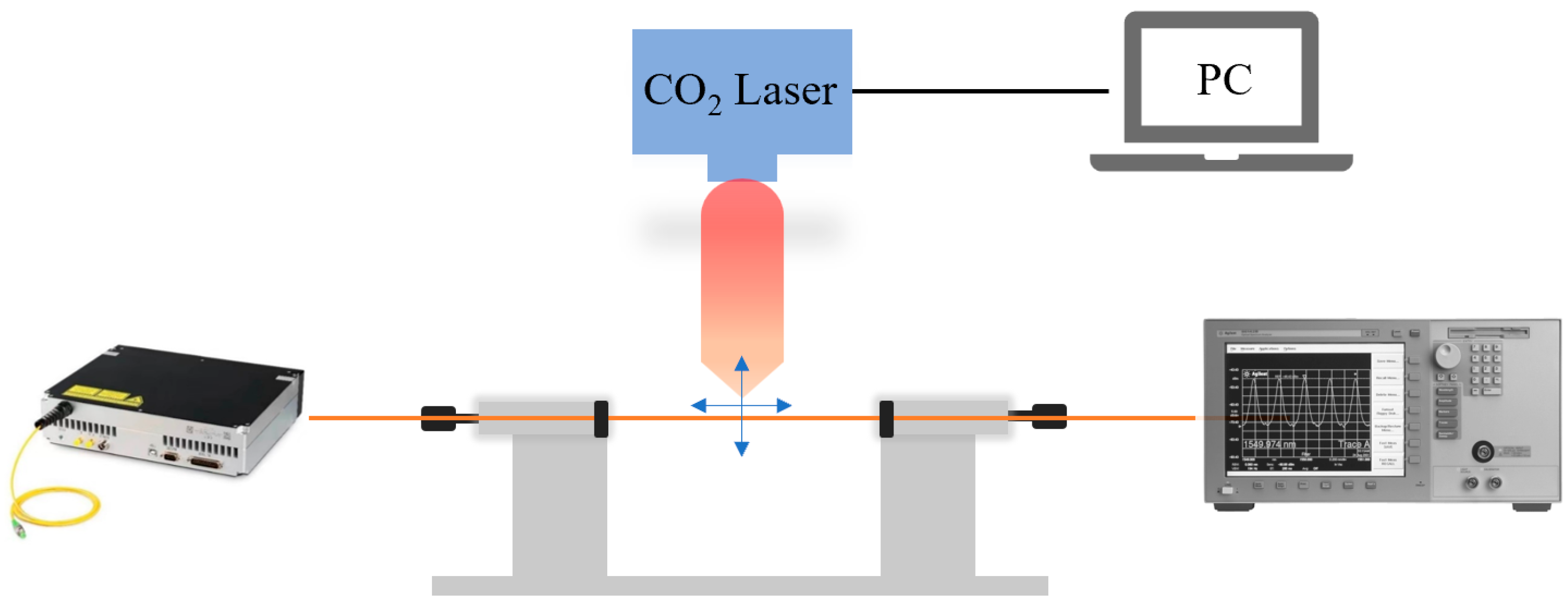
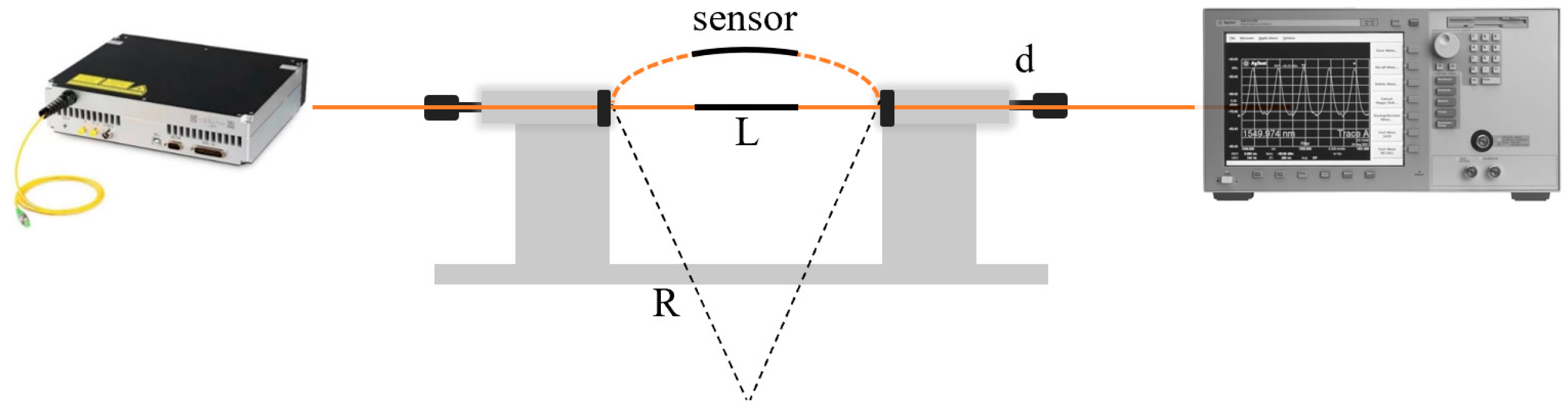
2.2. Fabrication

The experimental setup for fabricating LPG using a CO₂ laser is illustrated in Figure 2. A segment of DCF is taken, and its coating is stripped off with fiber strippers. The two ends of the fiber are then fixed on translation stages, and the bare fiber section is aligned with the CO₂ laser output port by moving the stages. The program parameters are as follows: the grating period is set to Λ, and the number of gratings is N. One of the requirements for achieving simultaneous multi-parameter measurement is the need for multiple independent resonance peaks with different response characteristics, and the distance between adjacent resonance peaks should not be too small.

To determine the optimal sensor structural parameters for multi-parameter measurement, four types of sensors with different parameters were fabricated. First, the transmission spectra of the sensors under initial environmental conditions were measured. The input end of each sensor was connected to a supercontinuum source, and the output end to a spectrometer. The transmission spectra are shown in Figure 3. Within the wavelength range of 1420–1650 nm, the sensor with a sensor length of 13 mm and n = 20 exhibited high fringe contrast, smooth spectral quality, a wide free spectral range, and a compact structure. Therefore, this sensor was selected for multi-parameter sensing research. In subsequent experiments, dipA at 1446 nm, dipB at 1502 nm, and dipC at 1596 nm were chosen as markers for sensor performance analysis.

A fast Fourier transform was performed on its transmission spectrum to obtain the spatial frequency distribution, and the results are shown in Figure 4. It can be seen from the figure that the main modes are the fundamental mode and the cladding mode with a frequency value of 0.02717 nm⁻¹. The other weaker peaks represent interference between higher-order modes, and their presence slightly modulates the transmission spectrum. Since the effective RI difference between LP01 and LP11 is closer to 0.02717, the interference mainly occurs between the fundamental mode and the cladding mode LP11.

3. Results

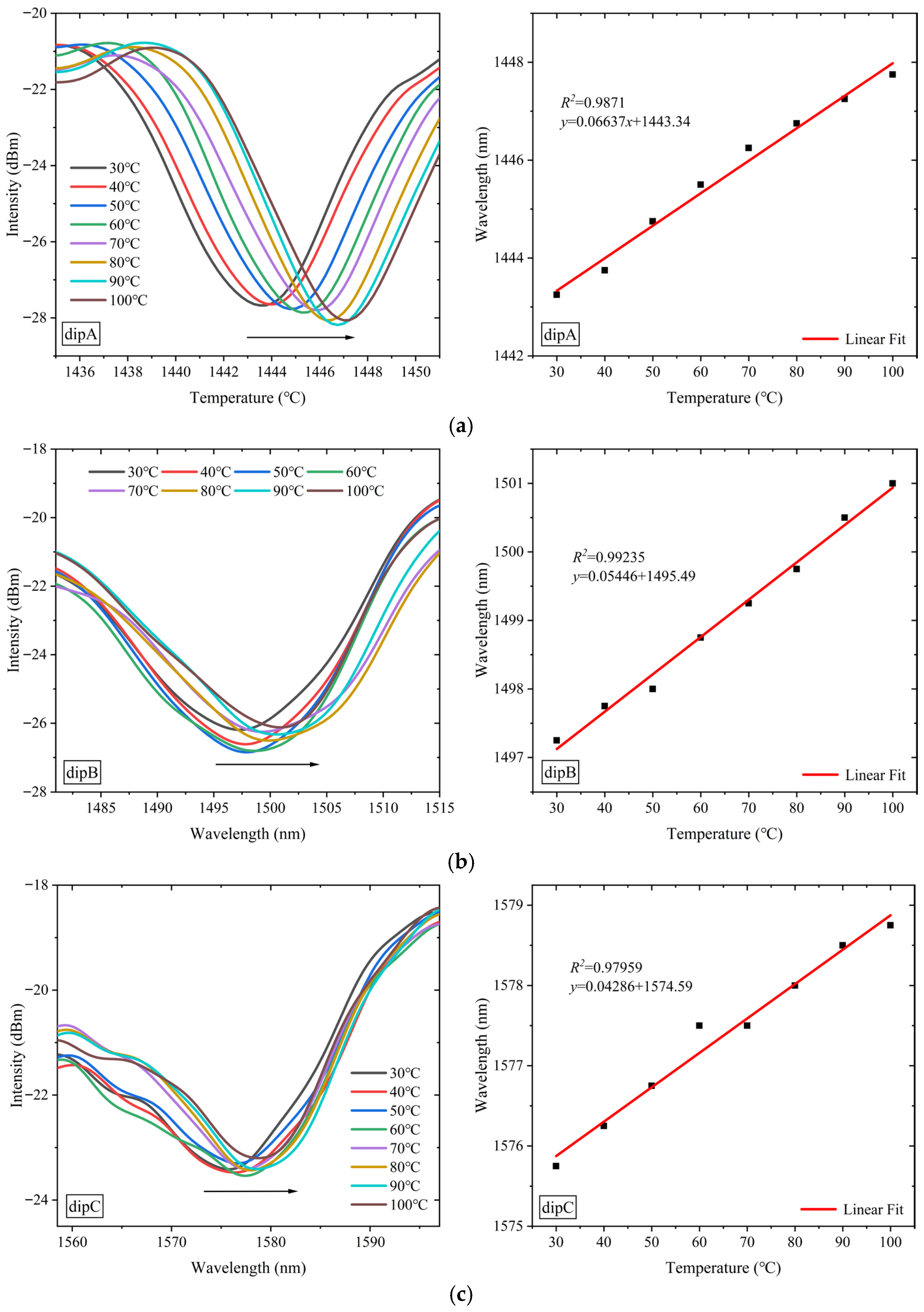
3.1. Results of Temperature Sensing

For the experiment, a supercontinuum light source (Wuhan, China, YSL Photonics SC-5-FC) was employed, while the transmission spectrum was detected using an optical spectrum analyzer (OSA, Beijing, China, Agilent 86142B) with a minimum resolution of 0.06 nm. As illustrated in Figure 5, the two ends of the sensor were connected to the light source and the OSA, respectively. Prior to initiating the temperature-dependent measurements, the sensor was first mounted flat on the heating platform, and the heating experiment was conducted with a temperature increment of 10 °C per step. After each temperature rise, we waited for the spectrum to stabilize before recording the spectral data. The transmission spectra of the resonance peaks dipA, dipB, and dipC of the sensor within the temperature range of 30 °C to 100 °C are shown in Figure 6.

It can be seen from Figure 6 that during the process of temperature rise, the central wavelengths of the resonance peaks dipA, dipB, and dipC all undergo a red shift, with the corresponding central wavelength shifts being 4.5 nm, 3.75 nm, and 3 nm, respectively. When the temperature changes, both the thermo-optic effect and the thermal expansion effect exist simultaneously, but the thermo-optic coefficient is much larger than the thermal expansion coefficient, so the thermo-optic effect is dominant. When the temperature increases, under the thermo-optic effect, the effective RI of the optical fiber will increase. Given that the thermo-optic coefficient of the fiber core exceeds that of the cladding, the change in the effective RI of the fundamental mode will be more significant than that of the cladding. This enlarged difference in effective RI between the two components results in a wavelength increase—specifically, the central wavelength of the resonance peak shifts toward the long-wave region as the temperature rises.

From the linear fitting results in Figure 6, it can be seen that the temperature sensitivity of resonance peak dipA is 66.37 pm/°C with a linear correlation coefficient R² of 0.9871; the temperature sensitivity of resonance peak dipB is 54.46 pm/°C with a linear correlation coefficient R² of 0.9924; and the temperature sensitivity of resonance peak dipC is 42.86 pm/°C with a linear correlation coefficient R² of 0.9796. The obtained sensitivities indicate that the proposed sensor is fairly sensitive to fluctuations in temperature. In addition, all three resonance peaks have a linear correlation coefficient greater than 0.9 with temperature, showing a good linear relationship. The linear correlation between the drift of resonance peaks’ central wavelengths and temperature fluctuations indicates that the sensor can realize ambient temperature measurement.

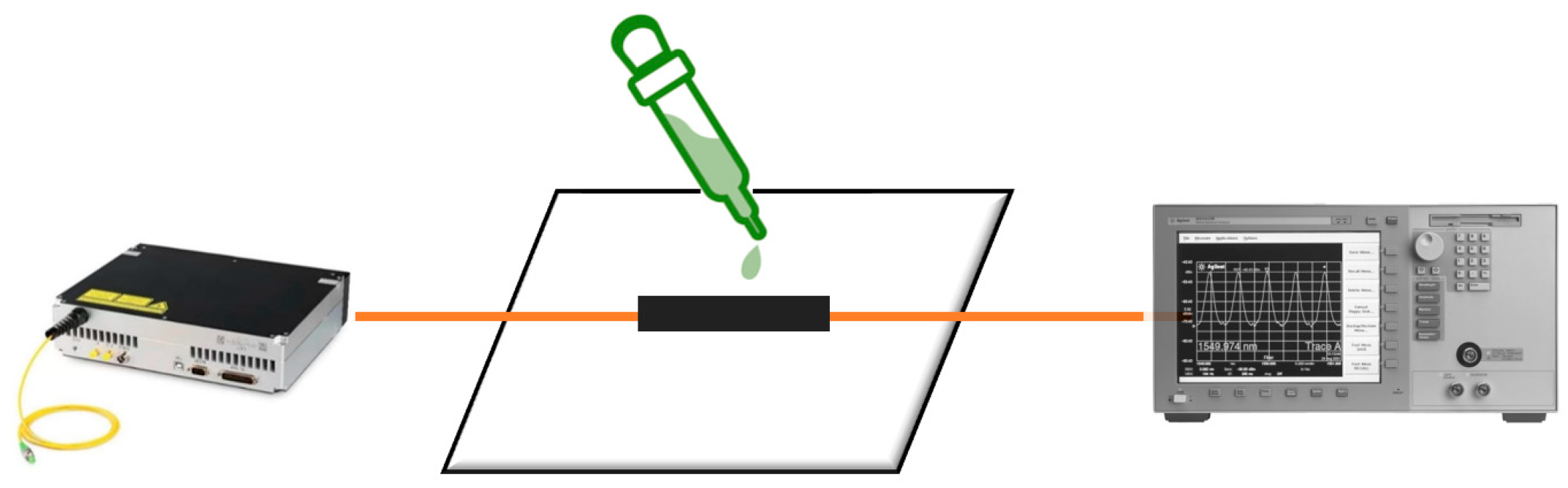
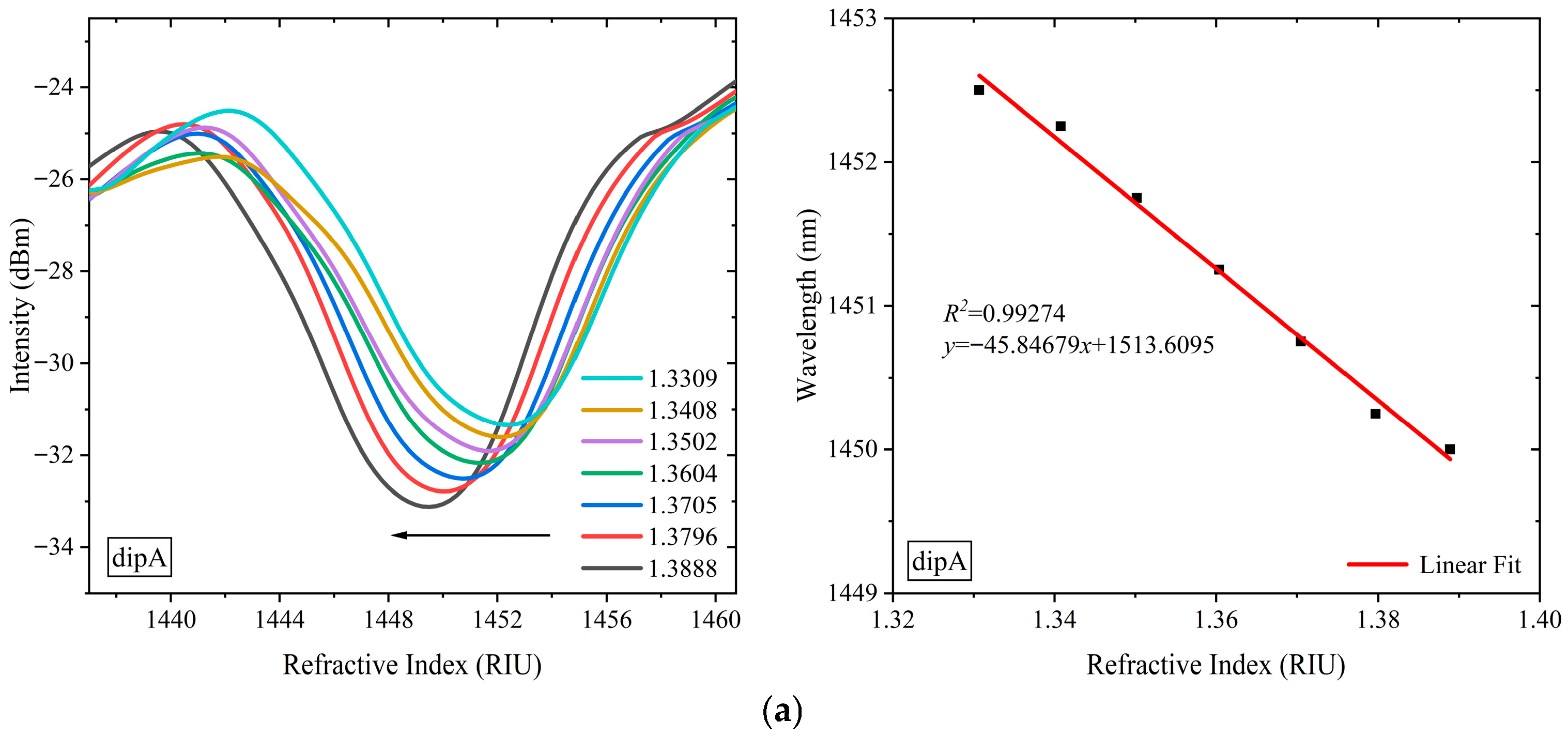
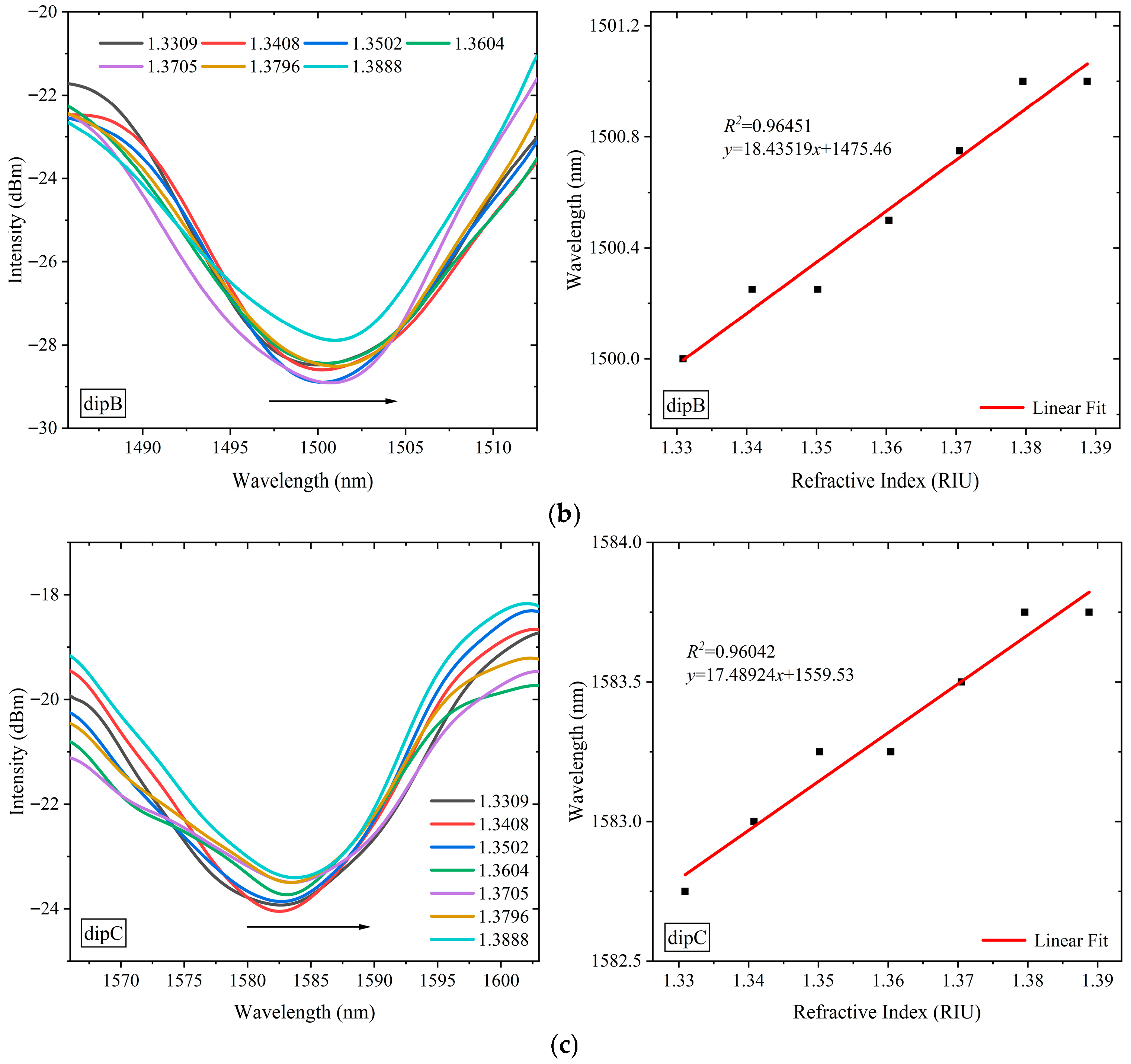
3.2. Results of Refractive Index Sensing

DCF has a two-cladding structure. The modes propagating in the core and inner cladding are protected by the outer cladding, so changes in the RI in the external environment hardly directly affect the effective refractive indices of the inner cladding and the core. On the one hand, more light waves leak into the outer cladding through the thick taper structure, and the change in the environmental RI is sensed through the radiation mode. The cladding mode radiation mode is a mode in which part of the energy in the cladding mode overflows outside the optical fiber and can directly interact with the environmental medium, which is key to sensing changes in the external RI. On the other hand, by using an LPG in the DCF, the sensing mechanism of co-directional coupling between the core mode and the cladding mode allows the cladding to come into contact with the environmental RI medium. The modes propagating in the cladding are more sensitive to changes in the RI of the external medium, enabling RI measurement.

The RI measurement setup is shown in Figure 7. Under room-temperature conditions, the sensor was mounted flat on a clean glass slide. A dropper was utilized to dispense the solution, fully submerging the sensor in the NaCl solution. After the spectrum stabilizes, the OSA data is recorded. Upon completing measurements of a NaCl solution with a specific concentration, the sensor was rinsed with deionized water and thoroughly dried, and then the subsequent experiment was carried out. The RI spanned from 1.3309 to 1.3888, and the recorded transmission spectra of each resonance peak are depicted in Figure 8a–c.

As observed in Figure 8, with the RI increasing from 1.3309 to 1.3888, the central wavelength of resonance peak dipA exhibits a blue shift, whereas those of dipB and dipC undergo a red shift. The dipA blue-shifts, and its light intensity gradually decreases. One possible reason is that when the LPG satisfies the phase-matching condition, the effective RI of the excited forward-propagating cladding mode must be smaller than that of the fiber core’s fundamental mode. Since the RI range of the NaCl solution used in the experiment is closer to the effective RI of the cladding mode, when the RI increases, the coupling efficiency between the core mode and the cladding mode decreases, and part of the cladding mode is converted into a radiation mode, resulting in a decrease in light intensity. In addition, the increase in RI causes the effective RI of the cladding mode to rise. However, the effective RI of the core mode shows almost no variation. The reduction in the difference between their effective RIs leads to the wavelength shifting towards the short wavelength direction. The main reason for the red shift in the central wavelengths of the resonance peaks dipB and dipC is that the RI of the surrounding medium has a greater impact on higher-order modes. A rise in the external RI induces an increase in the effective RI of higher-order modes, which in turn drives the resonance peak’s central wavelength to drift toward the longer wavelength range.

When the RI of the NaCl solution increases from 1.3309 to 1.3888, the resonance peaks dipA, dipB, and dipC shift by −2.5 nm, 1 nm, and 1 nm, respectively. A linear fitting was performed between the wavelengths of the three resonance peaks and their corresponding refractive indices in nanometers. From the fitting results, it can be seen that the RI sensitivities of the three resonance peaks dipA, dipB, and dipC are −45.84679 nm/RIU, 18.43519 nm/RIU, and 17.48924 nm/RIU, respectively, and the linear correlation coefficients R² are 0.99274, 0.96451, and 0.96042, respectively. From the comparison of RI sensitivities, it is known that the resonance peak dipA is more sensitive to changes in the ambient RI and has a larger linear correlation coefficient. Therefore, the spectral characteristics of the resonance peak dipA can mainly be used to detect changes in the ambient RI.

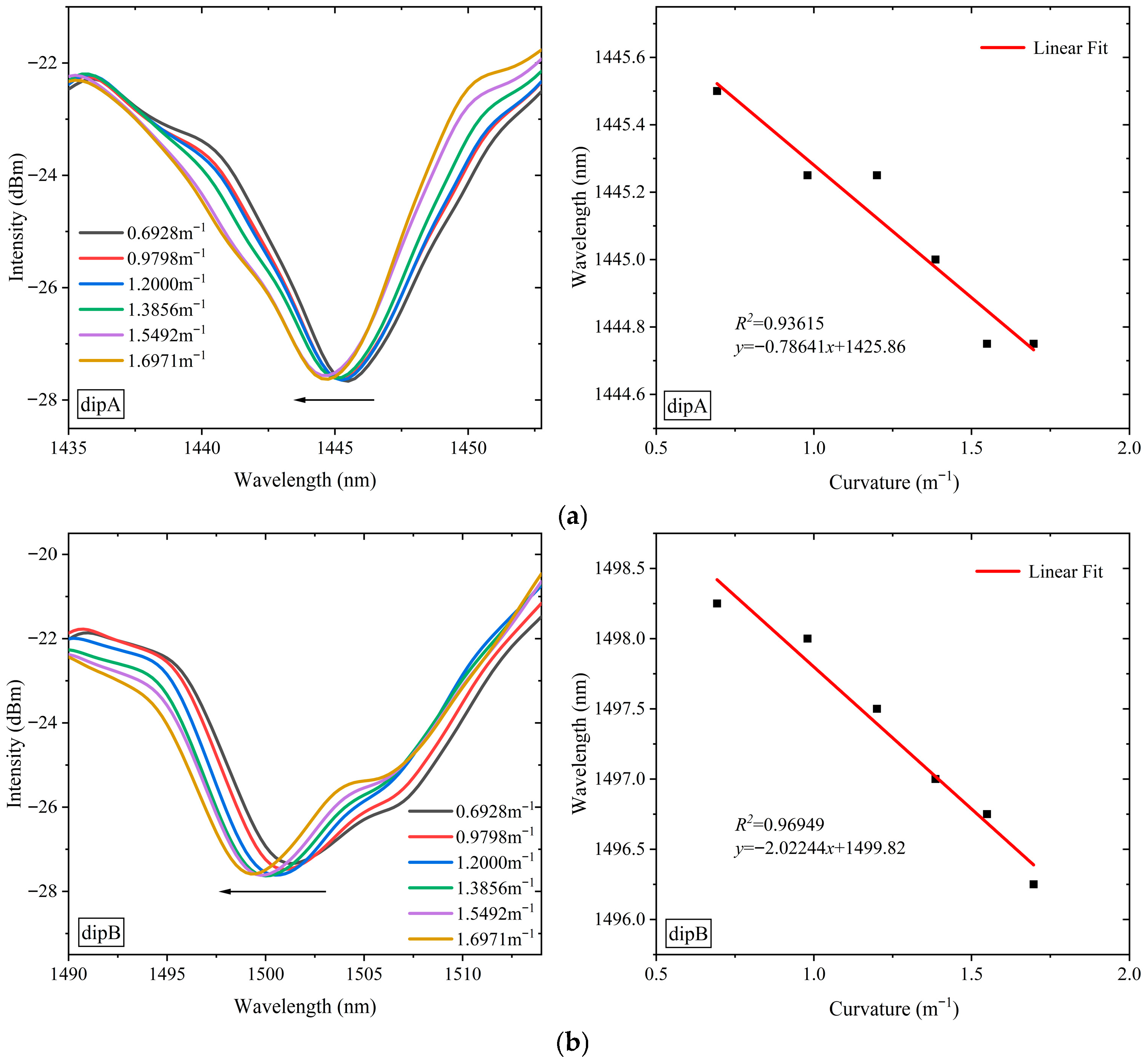
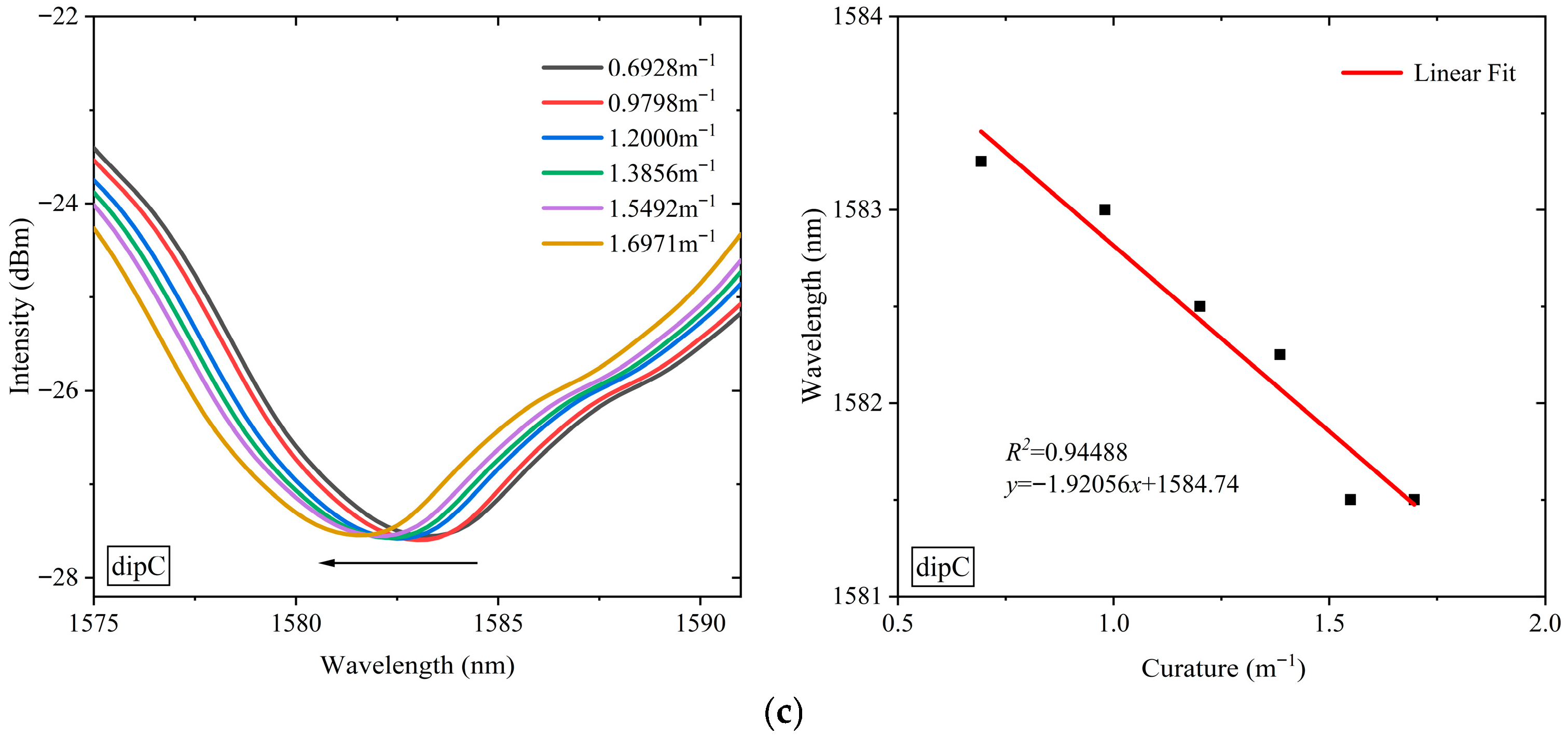
3.3. Results of Curvature Sensing

A schematic diagram of the curvature measurement experimental device is shown in Figure 9. Two optical fiber clamps are, respectively, fixed on the three-dimensional moving platforms on both sides. The three-dimensional moving platform on the right is adjusted so that the two optical fiber clamps are at the same height and in the same straight line. Then, the optical fiber sensor is fixed on an elastic metal plate, with its left and right ends placed in the optical fiber clamps. The lateral displacement position of the platform is precisely controlled through the spiral micrometer of the right displacement platform, thereby applying a curvature effect to the sensor. During the experiment, it is necessary to ensure that the fiber optic clamp, the fiber optic sensor, and the elastic metal plate are always aligned in a straight line.

The sensor located between the two optical fiber clamps approximates a circular shape under lateral compression. Therefore, the curvature C applied to the sensing structure can be calculated as follows:

$$C={\displaystyle \frac{1}{R}}\approx \sqrt{{\displaystyle \frac{24d}{L^3}}}$$

(3)

where L = 10 cm is the length between the two optical fiber clamps when no bending is applied to the optical fiber structure; d = 0.02 mm means that each rotation of the micrometer by 2 scales causes the displacement platform to move linearly inward by 0.02 mm each time until it moves to 0.12 mm; and R denotes the radius of curvature.

Figure 10a–c show the spectral changes in resonance peaks dipA, dipB, and dipC under the influence of different curvatures and their linear fitting results. As the curvature increases, the central wavelengths of the resonance peaks dipA, dipB, and dipC all undergo blue shift. When the curvature changes from 0.6928 m⁻¹ to 1.6971 m⁻¹, the central wavelength shifts in the dipA, dipB, and dipC are −0.75 nm, −2 nm, and −1.75 nm, respectively.

The linear fitting shows that the curvature sensitivity of the resonance peak dipA is −0.7864 nm/m⁻¹, and the corresponding linear correlation coefficient R² amounts to 0.9362; the curvature sensitivity of the resonance peak dipB is −2.022 nm/m⁻¹, with a linear correlation coefficient R² of 0.9695; the curvature sensitivity of the resonance peak dipC is −1.921 nm/m⁻¹, and the corresponding linear correlation coefficient R² amounts to 0.9449. These sensitivities indicate that the sensor proposed in this section is very sensitive to bending changes within a small curvature range. In addition, all three resonance peaks have a linear correlation coefficient greater than 0.9 with curvature. Based on the linear relationship between the change in the central wavelength of the resonance peak and the change in curvature, this sensor can be used to measure tiny curvatures.

4. Discussion

4.1. Cross-Sensitivity of the Sensor

The LPG sensor exhibits high and regular characteristic responses at wavelengths of 1446 nm, 1502 nm, and 1596 nm, affected by external physical parameters such as temperature, RI, and curvature. Therefore, these three independent resonance peaks can be used as the characterization parameters of the sensor to achieve the measurement of three parameters. When concurrent changes occur in the temperature, RI, and curvature of the sensor’s surrounding environment, the relationship between each resonance peak’s wavelength and the aforementioned three parameters can be extracted based on the sensitivity matrix. With pm as the unit, substituting the temperature, RI, and curvature sensitivities corresponding to the three resonance peaks results in

$$\left[\begin{array}{c}\Delta T\\ \Delta n\\ \Delta c\end{array}\right]={\left[\begin{array}{ccc}66.37& -45846& -0.7864\\ 54.46& 18435& -2.022\\ 42.86& 17489& -1.921\end{array}\right]}^{-1}\left[\begin{array}{c}\Delta {\lambda }_1\\ \Delta {\lambda }_2\\ \Delta {\lambda }_3\end{array}\right]$$

(4)

As the characterization parameter chosen is wavelength and the wavelength error is determined by the spectrometer, the central wavelength drift errors of the three resonance peaks are all deemed to be uniform values. The resolution of the OSA is 60 pm, so the sensor’s temperature resolution is 0.231 °C, the RI resolution is 0.7065 RIU, and the curvature resolution is 0.7405 m⁻¹. In practical applications, temperature, RI, and curvature measurements can be realized simply by monitoring the shifts in the central wavelengths of the sensor’s different resonance peaks.

The strain-sensing performance of the sensor is studied, too. When the axial strain increases from 250 με to 2500 με, the central wavelength shifts in the resonance peaks dipA, dipB, and dipC are all less than 1 nm. According to the linear fitting of the central wavelength shift and the strain variation, the strain sensitivity of resonance peak dipA is −0.532 pm/με, with a linear correlation coefficient R² of 0.817; the strain sensitivity of resonance peak dipB is −0.484 pm/με, with a linear correlation coefficient R² of 0.637; the strain sensitivity of resonance peak dipC is −0.375 pm/με, with a linear correlation coefficient R² of 0.832. It can be seen from the strain sensitivities of the three resonance peaks that under the action of 1 με, the central wavelength shifts in the three resonance peaks in the sensor’s transmission spectrum are all lower than 1 pm, indicating that the central wavelengths of the sensor’s resonance peaks exhibit low strain sensitivity within the strain range of 250–2500 με. In addition, the linear correlation coefficient is lower than 0.9, indicating that the sensor structure does not form a regular response to strain, which fully shows that the designed sensor is insensitive to changes in external environmental strain and is not suitable for strain-sensing detection. This is a characteristic of the sensor: under the action of strain, the wavelength shift in the sensor’s resonance peak is extremely small, meaning the sensor is minimally affected by strain interference. The inner cladding diameter of DCFs (125 μm) is larger than that of traditional single-mode fibers. Under axial strain, the elastic deformation of the inner cladding has minimal impact on the effective RI difference between the core mode and the cladding mode. Additionally, the period of the LPG used by the CO₂ laser is less affected by the stretching effect of axial strain (experimental measurements show that when the strain is 2500 με, the change rate of the grating period is less than 0.1%), resulting in an insignificant wavelength shift in the resonance peak. Considering this phenomenon from an alternative perspective, most existing multi-parameter sensors have the problem of cross-interference between strain, curvature, and temperature. This design can achieve strain anti-interference without additional packaging, making it more suitable for complex industrial environments.

4.2. Application Scenarios and Challenges

At present, the application environment of the proposed sensor is under ideal conditions in the laboratory. On the one hand, in industrial scenarios, stainless steel casing packaging can be tried, which is both resistant to high temperatures and mechanical impact. On the other hand, in medical body fluid detection, a parylene coating can be applied to the surface of the optical fiber, which can improve biocompatibility while preventing protein adsorption. In conclusion, when applied in actual scenarios, optical fiber sensors need to be packaged differently, and the performance of the packaged sensors needs to be further tested.

5. Conclusions

This paper proposes a sensor based on LPG in DCF for multi-parameter measurement. The sensing characteristics of the LPFG under the action of various physical quantities such as temperature, RI, and curvature were verified through experiments. The maximum temperature sensitivity is 66.37 pm/°C, the maximum RI sensitivity is −45.85 nm/RIU, and the maximum curvature sensitivity is −2.022 nm/m⁻¹. In addition, the sensor has a symmetrical structure, so it is not restricted by the light incident direction during measurement and has flexibility in practical use.