Liouvillian Superoperator and Maxwell–Bloch Dynamics Under Optical Feedback via the Self-Mixing Effect in Terahertz Quantum Cascade Lasers
Abstract
1. Introduction
2. Theoretical Model
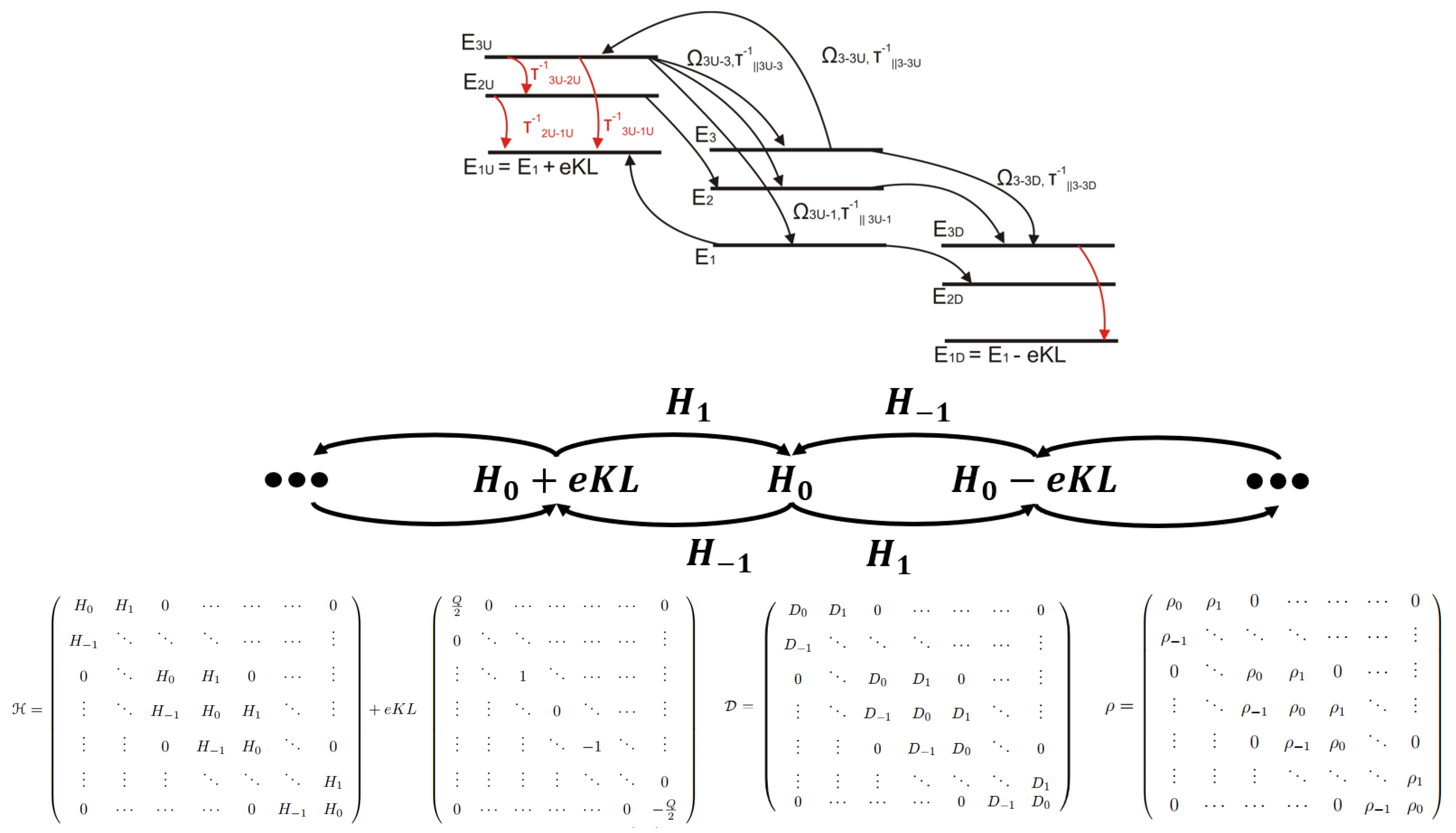
2.1. Transport Model
2.2. Maxwell–Bloch Model
3. Numerical Results
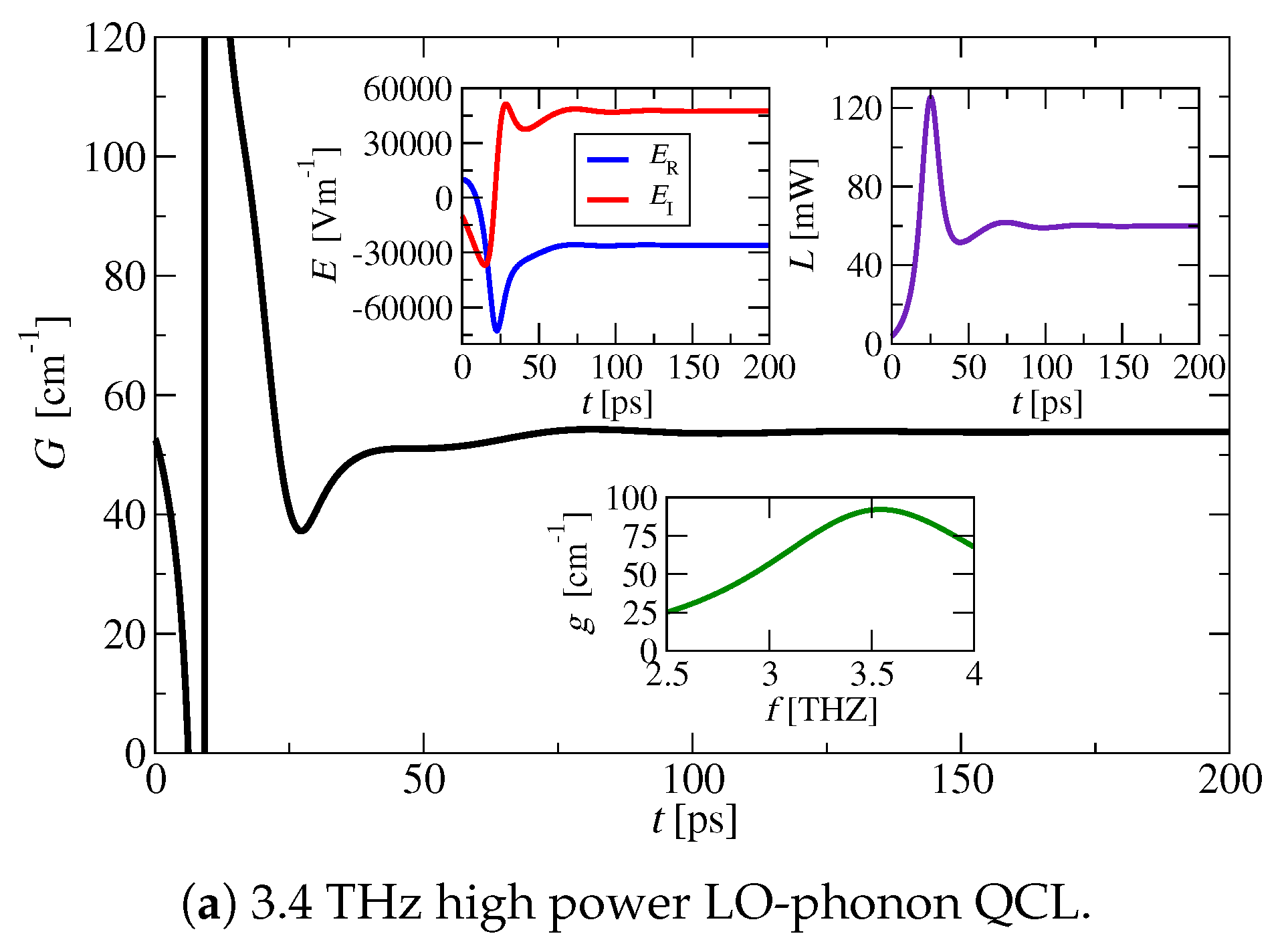
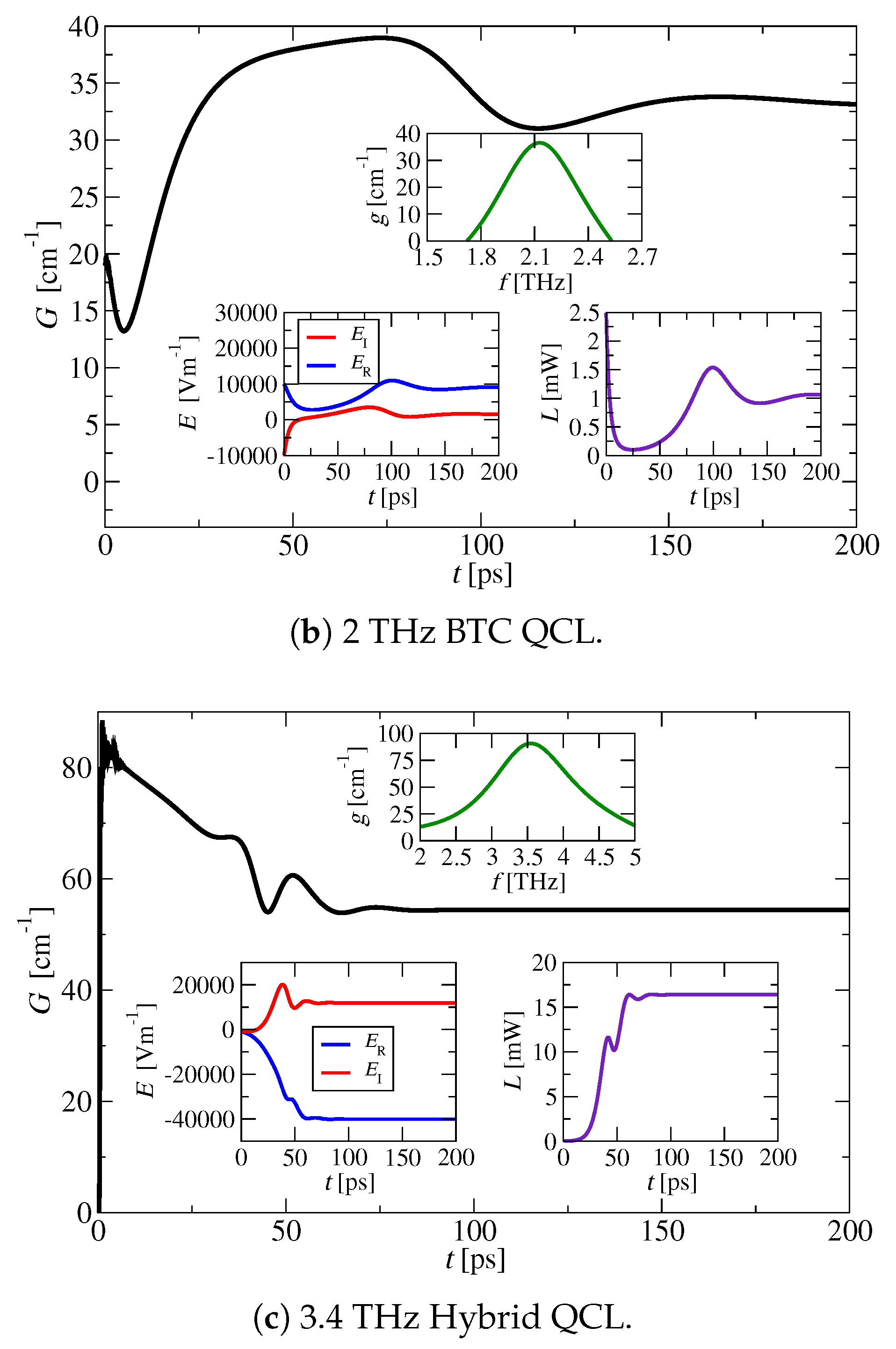
3.1. THz QCL Dynamics Without Optical Feedback
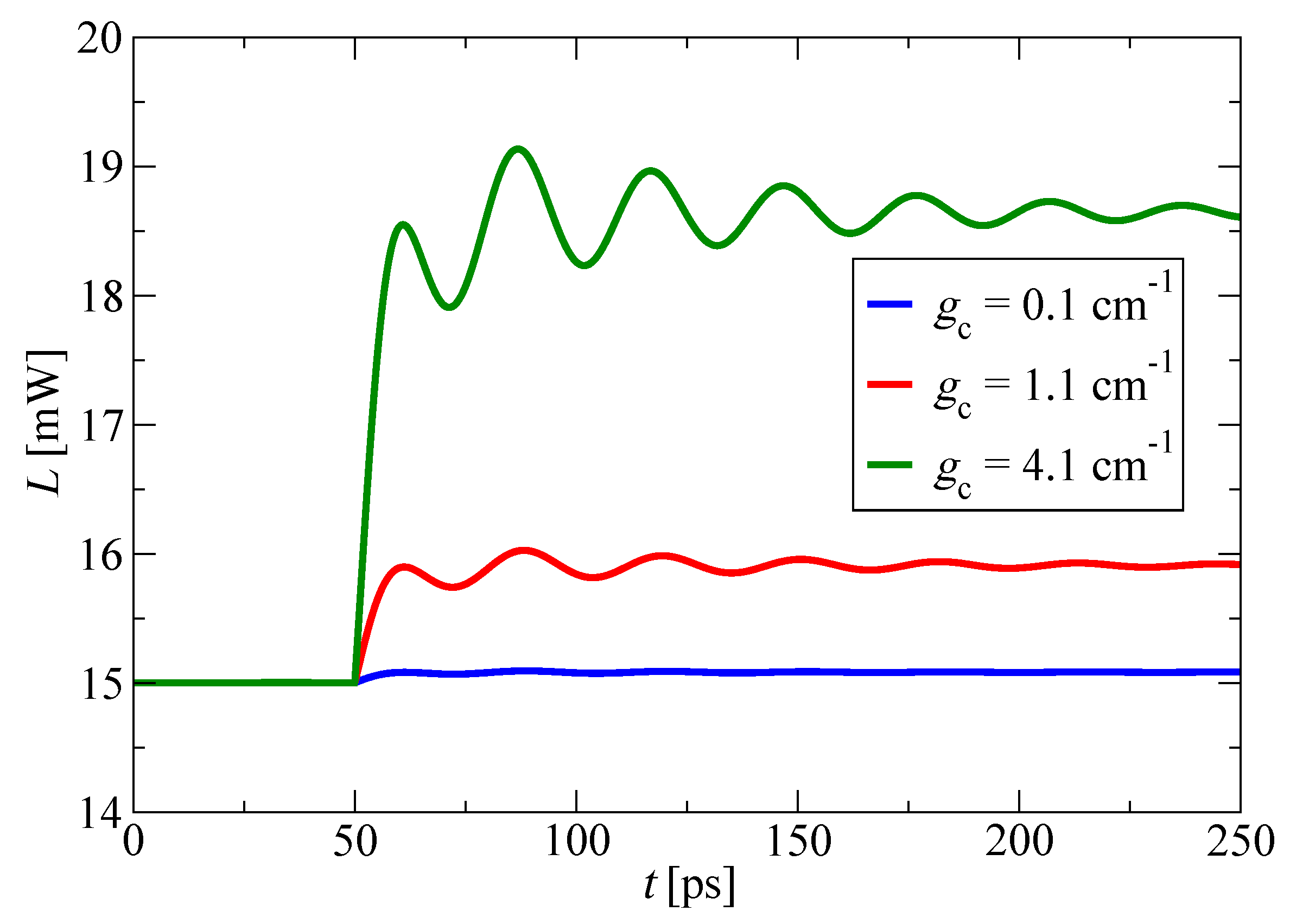
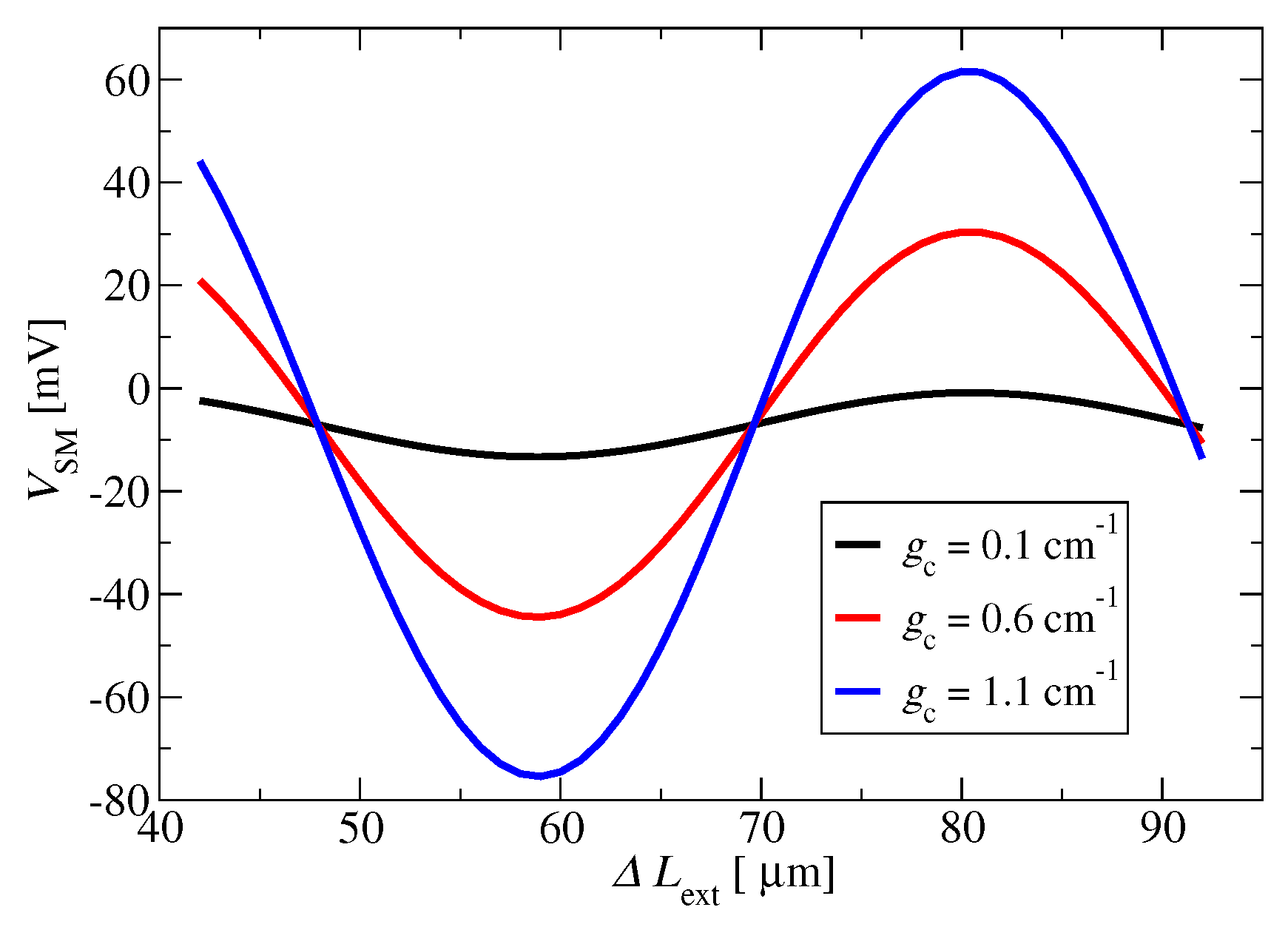
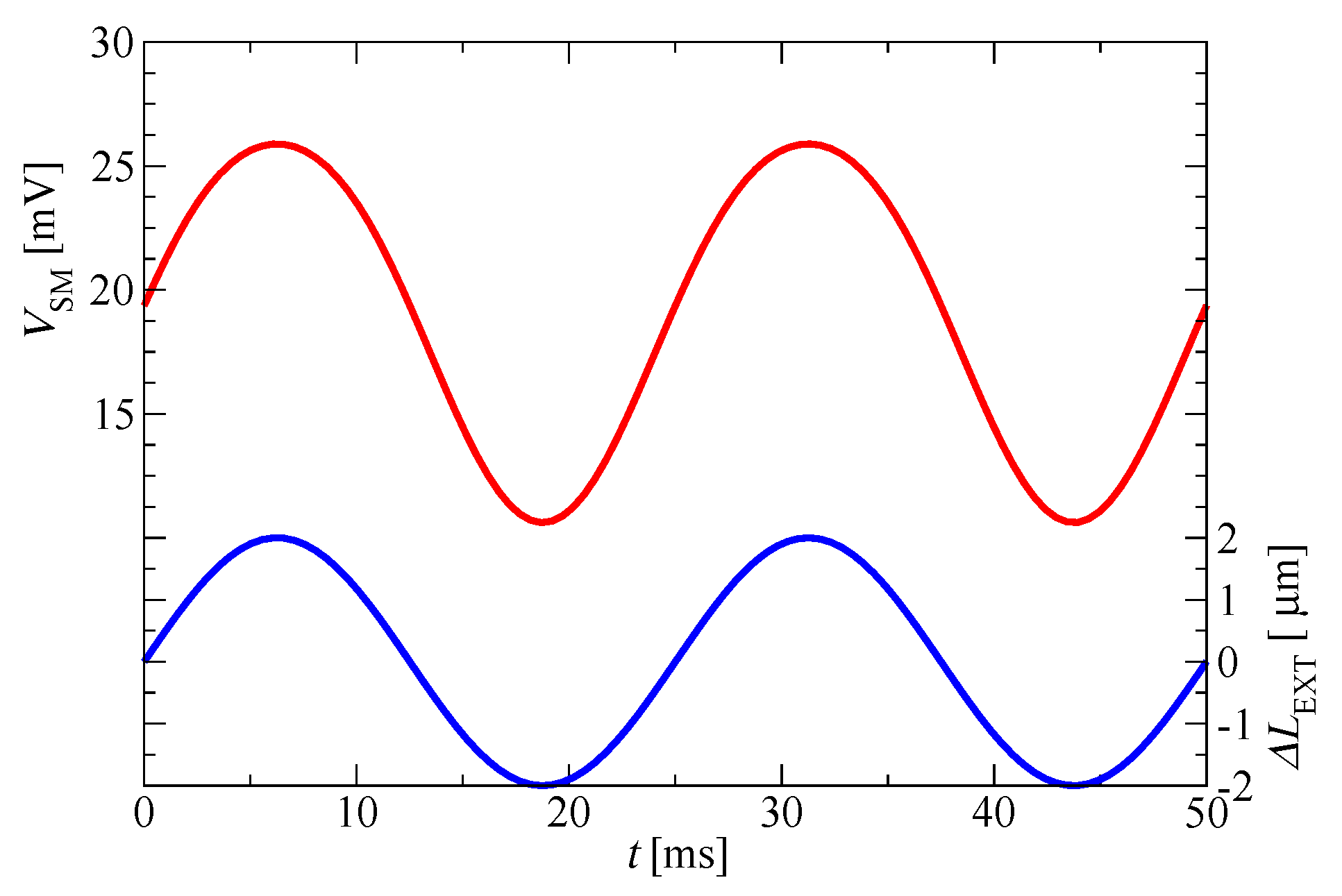
3.2. Self-Mixing Effect
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Liouvilian Superoperator Linearization
- is a partitioned matrix, where each partition is an identity matrix I. It can be algebraically formed as .
- is a partitioned matrix, obtained by applying the rule in Equation (A5), treating this matrix as purely imaginary, since it contains an additional imaginary unit in Equation (A3). This also causes the sign change in front of this term. Simply put, is a block-diagonal matrix with on the main diagonal.
- is a column vector consisting of the stacked vectorized elements:
Appendix B. Linearization of AXT B
Appendix C. Normalization of DM Superoperator
- The same column is subtracted from the columns corresponding to the and variables.
- Rows and are deleted from the system.
- Columns and (after the previous removal) are also deleted from the system and stored in column vectors and , respectively.
- Each column that targets the real part of diagonal elements , is subtracted by column .
- Each column that targets the imaginary part of diagonal elements , is subtracted by column .
- Column is added as a free term to the system (note that is not added, since in that case in Equation (A18)).
References
- King, P.; Steward, G. Metrology with an optical maser. New Sci. 1963, 17, 14. [Google Scholar]
- Ashby, D.E.T.; Jephcott, D. Measurement of plasma density using a gas laser as an infrared interferometer. Appl. Phys. Lett. 1963, 3, 13–16. [Google Scholar] [CrossRef]
- Crowe, J.; Craig, R., Jr. GaAs laser linewidth measurements by heterodyne detection. Appl. Phys. Lett. 1964, 5, 72–74. [Google Scholar] [CrossRef]
- Seko, A.; Mitsuhashi, Y.; Morikawa, T.; Shimada, J.; Sakurai, K. Self-quenching in semiconductor lasers and its applications in optical memory readout. Appl. Phys. Lett. 1975, 27, 140–141. [Google Scholar] [CrossRef]
- Mitsuhashi, Y.; Morikawa, T.; Sakurai, K.; Seko, A.; Shimada, J. Self-coupled optical pickup. Opt. Commun. 1976, 17, 95–97. [Google Scholar] [CrossRef]
- Otsuka, K. Highly sensitive measurement of Doppler-shift with a microchip solid-state laser. Jpn. J. Appl. Phys. 1992, 31, L1546–L1548. [Google Scholar] [CrossRef]
- Okamoto, S.; Takeda, H.; Kannari, F. Ultrahighly sensitive laser-Doppler velocity meter with a diode-pumped Nd: YVO4 microchip laser. Rev. Sci. Instruments 1995, 66, 3116–3120. [Google Scholar] [CrossRef]
- Nerin, P.; Puget, P.; Besesty, P.; Chartier, G. Self-mixing using a dual-polarisation Nd: YAG microchip laser. Electron. Lett. 1997, 33, 491–492. [Google Scholar] [CrossRef]
- Blaize, S.; Bérenguier, B.; Stéfanon, I.; Bruyant, A.; Lérondel, G.; Royer, P.; Hugon, O.; Jacquin, O.; Lacot, E. Phase sensitive optical near-field mapping using frequency-shifted laser optical feedback interferometry. Opt. Express 2008, 16, 11718–11726. [Google Scholar] [CrossRef]
- Hao, H.; Guo, D.; Wang, M.; Xia, W.; Ni, X. Micro-displace sensor based on self-mixing interference of the fiber laser with phase modulation. Photonic Sens. 2014, 4, 379–384. [Google Scholar] [CrossRef]
- Han, D.; Wang, M.; Zhou, J. Self-mixing speckle in an erbium-doped fiber ring laser and its application to velocity sensing. IEEE Photonics Technol. Lett. 2007, 19, 1398–1400. [Google Scholar]
- Wang, M.; Xia, W.; Dai, X.; Zhao, Y. Self-mixing interference in fiber ring laser and its multiplexing. In Proceedings of the 21st International Conference on Optical Fiber Sensors, Ottawa, ON, Canada, 15–19 May 2011; International Society for Optics and Photonics: Bellingham, WA, USA, 2011; Volume 7753, p. 77531Z. [Google Scholar]
- Von Staden, J.; Gensty, T.; Elsäßer, W.; Giuliani, G.; Mann, C. Measurements of the α factor of a distributed-feedback quantum cascade laser by an optical feedback self-mixing technique. Opt. Lett. 2006, 31, 2574–2576. [Google Scholar] [CrossRef]
- Green, R.P.; Xu, J.H.; Mahler, L.; Tredicucci, A.; Beltram, F.; Giuliani, G.; Beere, H.E.; Ritchie, D.A. Linewidth enhancement factor of terahertz quantum cascade lasers. Appl. Phys. Lett. 2008, 92, 071106. [Google Scholar] [CrossRef]
- Dean, P.; Lim, Y.L.; Valavanis, A.; Kliese, R.; Nikolić, M.; Khanna, S.P.; Lachab, M.; Indjin, D.; Ikonić, Z.; Harrison, P.; et al. Terahertz imaging through self-mixing in a quantum cascade laser. Opt. Lett. 2011, 36, 2587–2589. [Google Scholar] [CrossRef] [PubMed]
- Dean, P.; Valavanis, A.; Keeley, J.; Bertling, K.; Leng Lim, Y.; Alhathlool, R.; Chowdhury, S.; Taimre, T.; Li, L.H.; Indjin, D.; et al. Coherent three-dimensional terahertz imaging through self-mixing in a quantum cascade laser. Appl. Phys. Lett. 2013, 103, 181112. [Google Scholar] [CrossRef]
- Dean, P.; Valavanis, A.; Keeley, J.; Bertling, K.; Lim, Y.; Alhathlool, R.; Burnett, A.; Li, L.; Khanna, S.; Indjin, D.; et al. Terahertz imaging using quantum cascade lasers—a review of systems and applications. J. Phys. D Appl. Phys. 2014, 47, 374008. [Google Scholar] [CrossRef]
- Dean, P.; Mitrofanov, O.; Keeley, J.; Kundu, I.; Li, L.; Linfield, E.H.; Giles Davies, A. Apertureless near-field terahertz imaging using the self-mixing effect in a quantum cascade laser. Appl. Phys. Lett. 2016, 108, 091113. [Google Scholar] [CrossRef]
- Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Indjin, D.; Rakić, A.D. Methodology for materials analysis using swept-frequency feedback interferometry with terahertz frequency quantum cascade lasers. Opt. Express 2014, 22, 18633–18647. [Google Scholar] [CrossRef]
- Bertling, K.; Lim, Y.; Taimre, T.; Indjin, D.; Dean, P.; Weih, R.; Höfling, S.; Kamp, M.; Von Edlinger, M.; Koeth, J.; et al. Demonstration of the self-mixing effect in interband cascade lasers. Appl. Phys. Lett. 2013, 103, 231107. [Google Scholar] [CrossRef]
- Köhler, R.; Tredicucci, A.; Beltram, F.; Beere, H.E.; Linfield, E.H.; Davies, A.G.; Ritchie, D.A.; Iotti, R.C.; Rossi, F. Terahertz semiconductor-heterostructure laser. Nature 2002, 417, 156–159. [Google Scholar] [CrossRef]
- Williams, B.S. Terahertz quantum-cascade lasers. Nat. Photonics 2007, 1, 517. [Google Scholar] [CrossRef]
- Kumar, S. Recent Progress in Terahertz Quantum Cascade Lasers. IEEE J. Sel. Top. Quantum Electron. 2011, 17, 38–47. [Google Scholar] [CrossRef]
- Walther, C.; Fischer, M.; Scalari, G.; Terazzi, R.; Hoyler, N.; Faist, J. Quantum cascade lasers operating from 1.2 to 1.6 THz. Appl. Phys. Lett. 2007, 91, 131122. [Google Scholar] [CrossRef]
- Scalari, G.; Walther, C.; Fischer, M.; Terazzi, R.; Beere, H.; Ritchie, D.; Faist, J. THz and sub-THz quantum cascade lasers. Laser Photon. Rev. 2009, 3, 45–66. [Google Scholar] [CrossRef]
- Chan, C.W.I.; Hu, Q.; Reno, J.L. Ground state terahertz quantum cascade lasers. Appl. Phys. Lett. 2012, 101, 151108. [Google Scholar] [CrossRef]
- Wienold, M.; Röben, B.; Lü, X.; Rozas, G.; Schrottke, L.; Biermann, K.; Grahn, H.T. Frequency Dependence of the Maximum Operating Temperature for Quantum-cascade Lasers up to 5.4 THz. Appl. Phys. Lett. 2015, 107, 202101. [Google Scholar] [CrossRef]
- Li, L.; Chen, L.; Zhu, J.; Freeman, J.; Dean, P.; Valavanis, A.; Davies, A.; Linfield, E. Terahertz Quantum Cascade Lasers with >1 W Output powers. Electron. Lett. 2014, 50, 309–311. [Google Scholar] [CrossRef]
- Khalatpour, A.; Tam, M.C.; Addamane, S.J.; Reno, J.; Wasilewski, Z.; Hu, Q. Enhanced operating temperature in terahertz quantum cascade lasers based on direct phonon depopulation. Appl. Phys. Lett. 2023, 122, 161101. [Google Scholar] [CrossRef]
- Wienold, M.; Röben, B.; Schrottke, L.; Sharma, R.; Tahraoui, A.; Biermann, K.; Grahn, H.T. High-temperature, continuous-wave operation of terahertz quantum-cascade lasers with metal-metal waveguides and third-order distributed feedback. Opt. Express 2014, 22, 3334–3348. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-edge terahertz technology. Nat. Photonics 2007, 1, 97. [Google Scholar] [CrossRef]
- Gmachl, C.; Capasso, F.; Sivco, D.L.; Cho, A.Y. Recent progress in quantum cascade lasers and applications. Rep. Prog. Phys. 2001, 64, 1533. [Google Scholar] [CrossRef]
- Kosterev, A.A.; Tittel, F.K. Chemical sensors based on quantum cascade lasers. IEEE J. Quantum Electron. 2002, 38, 582–591. [Google Scholar] [CrossRef]
- Wysocki, G.; Lewicki, R.; Curl, R.F.; Tittel, F.K.; Diehl, L.; Capasso, F.; Troccoli, M.; Hofler, G.; Bour, D.; Corzine, S.; et al. Widely tunable mode-hop free external cavity quantum cascade lasers for high resolution spectroscopy and chemical sensing. Appl. Phys. B 2008, 92, 305–311. [Google Scholar] [CrossRef]
- McManus, J.B.; Shorter, J.H.; Nelson, D.D.; Zahniser, M.S.; Glenn, D.E.; McGovern, R.M. Pulsed quantum cascade laser instrument with compact design for rapid, high sensitivity measurements of trace gases in air. Appl. Phys. B 2008, 92, 387. [Google Scholar] [CrossRef]
- Woolard, D.L.; Loerop, W.R.; Shur, M. Terahertz Sensing Technology: Emerging Scientific Applications & Novel Device Concepts; World Scientific: Singapore, 2003; Volume 2. [Google Scholar]
- Leng Lim, Y.; Dean, P.; Nikolić, M.; Kliese, R.; Khanna, S.P.; Lachab, M.; Valavanis, A.; Indjin, D.; Ikonić, Z.; Harrison, P.; et al. Demonstration of a self-mixing displacement sensor based on terahertz quantum cascade lasers. Appl. Phys. Lett. 2011, 99, 081108. [Google Scholar] [CrossRef]
- Rakić, A.D.; Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Indjin, D.; Ikonić, Z.; Harrison, P.; Valavanis, A.; Khanna, S.P.; et al. Swept-frequency feedback interferometry using terahertz frequency QCLs: A method for imaging and materials analysis. Opt. Express 2013, 21, 22194–22205. [Google Scholar] [CrossRef]
- Lim, Y.L.; Taimre, T.; Bertling, K.; Dean, P.; Indjin, D.; Valavanis, A.; Khanna, S.P.; Lachab, M.; Schaider, H.; Prow, T.W.; et al. High-contrast coherent terahertz imaging of porcine tissue via swept-frequency feedback interferometry. Biomed. Opt. Express 2014, 5, 3981–3989. [Google Scholar] [CrossRef]
- Agnew, G.; Grier, A.; Taimre, T.; Lim, Y.L.; Nikolić, M.; Valavanis, A.; Cooper, J.; Dean, P.; Khanna, S.P.; Lachab, M.; et al. Efficient prediction of terahertz quantum cascade laser dynamics from steady-state simulations. Appl. Phys. Lett. 2015, 106, 161105. [Google Scholar] [CrossRef]
- Agnew, G.; Grier, A.; Taimre, T.; Lim, Y.L.; Bertling, K.; Ikonić, Z.; Valavanis, A.; Dean, P.; Cooper, J.; Khanna, S.P.; et al. Model for a pulsed terahertz quantum cascade laser under optical feedback. Opt. Express 2016, 24, 20554–20570. [Google Scholar] [CrossRef]
- Valavanis, A.; Dean, P.; Lim, Y.L.; Alhathlool, R.; Nikolic, M.; Kliese, R.; Khanna, S.P.; Indjin, D.; Wilson, S.J.; Rakic, A.D.; et al. Self-mixing interferometry with terahertz quantum cascade lasers. IEEE Sens. J. 2012, 13, 37–43. [Google Scholar] [CrossRef]
- Lang, R.; Kobayashi, K. External optical feedback effects on semiconductor injection laser properties. IEEE J. Quantum Electron. 1980, 16, 347–355. [Google Scholar] [CrossRef]
- Jirauschek, C.; Kubis, T. Modeling techniques for quantum cascade lasers. Appl. Phys. Rev. 2014, 1, 011307. [Google Scholar] [CrossRef]
- Indjin, D.; Harrison, P.; Kelsall, R.W.; Ikonic, Z. Self-consistent scattering model of carrier dynamics in GaAs-AlGaAs terahertz quantum-cascade lasers. IEEE Photonics Technol. Lett. 2003, 15, 15–17. [Google Scholar] [CrossRef]
- Demić, A.; Grier, A.; Ikonić, Z.; Valavanis, A.; Evans, C.A.; Mohandas, R.; Li, L.; Linfield, E.H.; Davies, A.G.; Indjin, D. Infinite-Period Density-Matrix Model for Terahertz-Frequency Quantum Cascade Lasers. IEEE Trans. Terahertz Sci. Technol. 2017, 7, 368–377. [Google Scholar] [CrossRef]
- Yasuda, H.; Kubis, T.; Vogl, P.; Sekine, N.; Hosako, I.; Hirakawa, K. Nonequilibrium Green’s function calculation for four-level scheme terahertz quantum cascade lasers. Appl. Phys. Lett. 2009, 94, 151109. [Google Scholar] [CrossRef]
- Wacker, A.; Lindskog, M.; Winge, D.O. Nonequilibrium Green’s Function Model for Simulation of Quantum Cascade Laser Devices Under Operating Conditions. IEEE J. Sel. Top. Quantum Electron. 2013, 19, 1–11. [Google Scholar] [CrossRef]
- Demić, A.; Ikonić, Z.; Kelsall, R.W.; Indjin, D. Density matrix superoperator for periodic quantum systems and its application to quantum cascade laser structures. AIP Adv. 2019, 9, 095019. [Google Scholar] [CrossRef]
- Burnett, B.A.; Williams, B.S. Density matrix model for polarons in a terahertz quantum dot cascade laser. Phys. Rev. B 2014, 90, 155309. [Google Scholar] [CrossRef]
- Burnett, B.A.; Pan, A.; Chui, C.O.; Williams, B.S. Robust density matrix simulation of terahertz quantum cascade lasers. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 492–501. [Google Scholar] [CrossRef]
- Jonasson, O.; Karimi, F.; Knezevic, I. Partially coherent electron transport in terahertz quantum cascade lasers based on a Markovian master equation for the density matrix. J. Comput. Electron. 2016, 15, 1192–1205. [Google Scholar] [CrossRef]
- Jirauschek, C. Density matrix Monte Carlo modeling of quantum cascade lasers. J. Appl. Phys. 2017, 122, 133105. [Google Scholar] [CrossRef]
- Harrison, P.; Valavanis, A. Quantum Wells, Wires and Dots: Theoretical and Computational Physics of Semiconductor Nanostructures; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Pan, A.; Burnett, B.A.; Chui, C.O.; Williams, B.S. Density matrix modeling of quantum cascade lasers without an artificially localized basis: A generalized scattering approach. Phys. Rev. B 2017, 96, 085308. [Google Scholar] [CrossRef]
- Jonasson, O.; Knezevic, I. Dissipative transport in superlattices within the Wigner function formalism. J. Comput. Electron. 2015, 14, 879–887. [Google Scholar] [CrossRef]
- Freeman, J.R.; Marshall, O.; Beere, H.E.; Ritchie, D.A. Improved wall plug efficiency of a 1.9 THz quantum cascade laser by an automated design approach. Appl. Phys. Lett. 2008, 93, 191119. [Google Scholar] [CrossRef]
- Tzenov, P.; Burghoff, D.; Hu, Q.; Jirauschek, C. Time domain modeling of terahertz quantum cascade lasers for frequency comb generation. Opt. Express 2016, 24, 23232–23247. [Google Scholar] [CrossRef] [PubMed]
- Boyd, R.W. Nonlinear Optics; Academic Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Castin, Y.; Mo, K. Maxwell-Bloch equations: A unified view of nonlinear optics and nonlinear atom optics. Phys. Rev. A 1995, 51, R3426. [Google Scholar] [CrossRef] [PubMed]
- Van Tartwijk, G.; Lenstra, D. Semiconductor lasers with optical injection and feedback. Quantum Semiclassical Opt. J. Eur. Opt. Soc. Part B 1995, 7, 87. [Google Scholar] [CrossRef]
- Riesch, M.; Jirauschek, C. mbsolve: An open-source solver tool for the Maxwell-Bloch equations. Comput. Phys. Commun. 2021, 268, 108097. [Google Scholar] [CrossRef]
- Silvestri, C.; Qi, X.; Taimre, T.; Rakić, A.D. Multimode dynamics of terahertz quantum cascade lasers: Spontaneous and actively induced generation of dense and harmonic coherent regimes. Phys. Rev. A 2022, 106, 053526. [Google Scholar] [CrossRef]
- Lindblad, G. On the generators of quantum dynamical semigroups. Commun. Math. Phys. 1976, 48, 119–130. [Google Scholar] [CrossRef]
- Kossakowski, A. On quantum statistical mechanics of non-Hamiltonian systems. Rep. Math. Phys. 1972, 3, 247–274. [Google Scholar] [CrossRef]
- Gorini, V.; Kossakowski, A.; Sudarshan, E.C.G. Completely positive dynamical semigroups of N-level systems. J. Math. Phys. 1976, 17, 821–825. [Google Scholar] [CrossRef]
- Banks, T.; Susskind, L.; Peskin, M.E. Difficulties for the evolution of pure states into mixed states. Nucl. Phys. B 1984, 244, 125–134. [Google Scholar] [CrossRef]
- Siegman, A. Lasers; University Science Books: Melville, NY, USA, 1986. [Google Scholar]
- Evans, C.A.; Indjin, D.; Ikonic, Z.; Harrison, P.; Vitiello, M.S.; Spagnolo, V.; Scamarcio, G. Thermal modeling of terahertz quantum-cascade lasers: Comparison of optical waveguides. IEEE J. Quantum Electron. 2008, 44, 680–685. [Google Scholar] [CrossRef]
- Qi, X.; Bertling, K.; Taimre, T.; Agnew, G.; Lim, Y.L.; Gillespie, T.; Robinson, A.; Brünig, M.; Demić, A.; Dean, P.; et al. Observation of optical feedback dynamics in single-mode terahertz quantum cascade lasers: Transient instabilities. Phys. Rev. A 2021, 103, 033504. [Google Scholar] [CrossRef]
- Kane, D.M.; Shore, K.A. Unlocking Dynamical Diversity: Optical Feedback Effects on Semiconductor Lasers; John Wiley & Sons: Hoboken, NJ, USA, 2005. [Google Scholar]
- Grier, A. Modelling the Optical and Electronic Transport Properties of AlGaAs and AlGaN Intersubband Devices and Optimisation of Quantum Cascade Laser Active Regions. Ph.D. Thesis, University of Leeds, Leeds, UK, 2015. [Google Scholar]
- Galassi, M.; Davies, J.; Theiler, J.; Gough, B.; Jungman, G.; Alken, P.; Booth, M.; Rossi, F.; Ulerich, R. GNU Scientific Library; Network Theory Limited Godalming: Godalming, UK, 2002. [Google Scholar]
- Demić, A.; Ikonić, Z.; Dean, P.; Indjin, D. Dual resonance phonon–photon–phonon terahertz quantum-cascade laser: Physics of the electron transport and temperature performance optimization. Opt. Express 2020, 28, 38788–38812. [Google Scholar] [CrossRef]
- Rubino, P. Near-Field Imaging Using Self Mixing in Terahertz frequency Quantum Cascade Lasers. Ph.D. Thesis, University of Leeds, Leeds, UK, 2019. Available online: http://etheses.whiterose.ac.uk/25163/ (accessed on 26 October 2025).
- Barbieri, S.; Maineult, W.; Dhillon, S.S.; Sirtori, C.; Alton, J.; Breuil, N.; Beere, H.E.; Ritchie, D.A. 13 GHz direct modulation of terahertz quantum cascade lasers. Appl. Phys. Lett. 2007, 91, 143510. [Google Scholar] [CrossRef]
- Green, R.P.; Tredicucci, A.; Vinh, N.Q.; Murdin, B.; Pidgeon, C.; Beere, H.E.; Ritchie, D.A. Gain recovery dynamics of a terahertz quantum cascade laser. Phys. Rev. B 2009, 80, 075303. [Google Scholar] [CrossRef]
- Bacon, D.R.; Freeman, J.R.; Mohandas, R.A.; Li, L.; Linfield, E.H.; Davies, A.G.; Dean, P. Gain recovery time in a terahertz quantum cascade laser. Appl. Phys. Lett. 2016, 108, 081104. [Google Scholar] [CrossRef]
- Derntl, C.G.; Scalari, G.; Bachmann, D.; Beck, M.; Faist, J.; Unterrainer, K.; Darmo, J. Gain dynamics in a heterogeneous terahertz quantum cascade laser. Appl. Phys. Lett. 2018, 113, 181102. [Google Scholar] [CrossRef]
- Taimre, T.; Nikolić, M.; Bertling, K.; Lim, Y.L.; Bosch, T.; Rakić, A.D. Laser feedback interferometry: A tutorial on the self-mixing effect for coherent sensing. Adv. Opt. Photon. AOP 2015, 7, 570–631. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Demić, A.; Ikonić, Z.; Dean, P.; Qi, X.; Taimre, T.; Bertling, K.; Rakić, A.D.; Indjin, D. Liouvillian Superoperator and Maxwell–Bloch Dynamics Under Optical Feedback via the Self-Mixing Effect in Terahertz Quantum Cascade Lasers. Photonics 2025, 12, 1134. https://doi.org/10.3390/photonics12111134
Demić A, Ikonić Z, Dean P, Qi X, Taimre T, Bertling K, Rakić AD, Indjin D. Liouvillian Superoperator and Maxwell–Bloch Dynamics Under Optical Feedback via the Self-Mixing Effect in Terahertz Quantum Cascade Lasers. Photonics. 2025; 12(11):1134. https://doi.org/10.3390/photonics12111134
Chicago/Turabian StyleDemić, Aleksandar, Zoran Ikonić, Paul Dean, Xiaoqiong Qi, Thomas Taimre, Karl Bertling, Aleksandar D. Rakić, and Dragan Indjin. 2025. "Liouvillian Superoperator and Maxwell–Bloch Dynamics Under Optical Feedback via the Self-Mixing Effect in Terahertz Quantum Cascade Lasers" Photonics 12, no. 11: 1134. https://doi.org/10.3390/photonics12111134
APA StyleDemić, A., Ikonić, Z., Dean, P., Qi, X., Taimre, T., Bertling, K., Rakić, A. D., & Indjin, D. (2025). Liouvillian Superoperator and Maxwell–Bloch Dynamics Under Optical Feedback via the Self-Mixing Effect in Terahertz Quantum Cascade Lasers. Photonics, 12(11), 1134. https://doi.org/10.3390/photonics12111134






