High-Sensitivity Broadband Acoustic Wave Detection Using High-Q, Undercoupled Optical Waveguide Resonators
Abstract
1. Introduction
2. Principle
2.1. Optical Waveguide Resonators
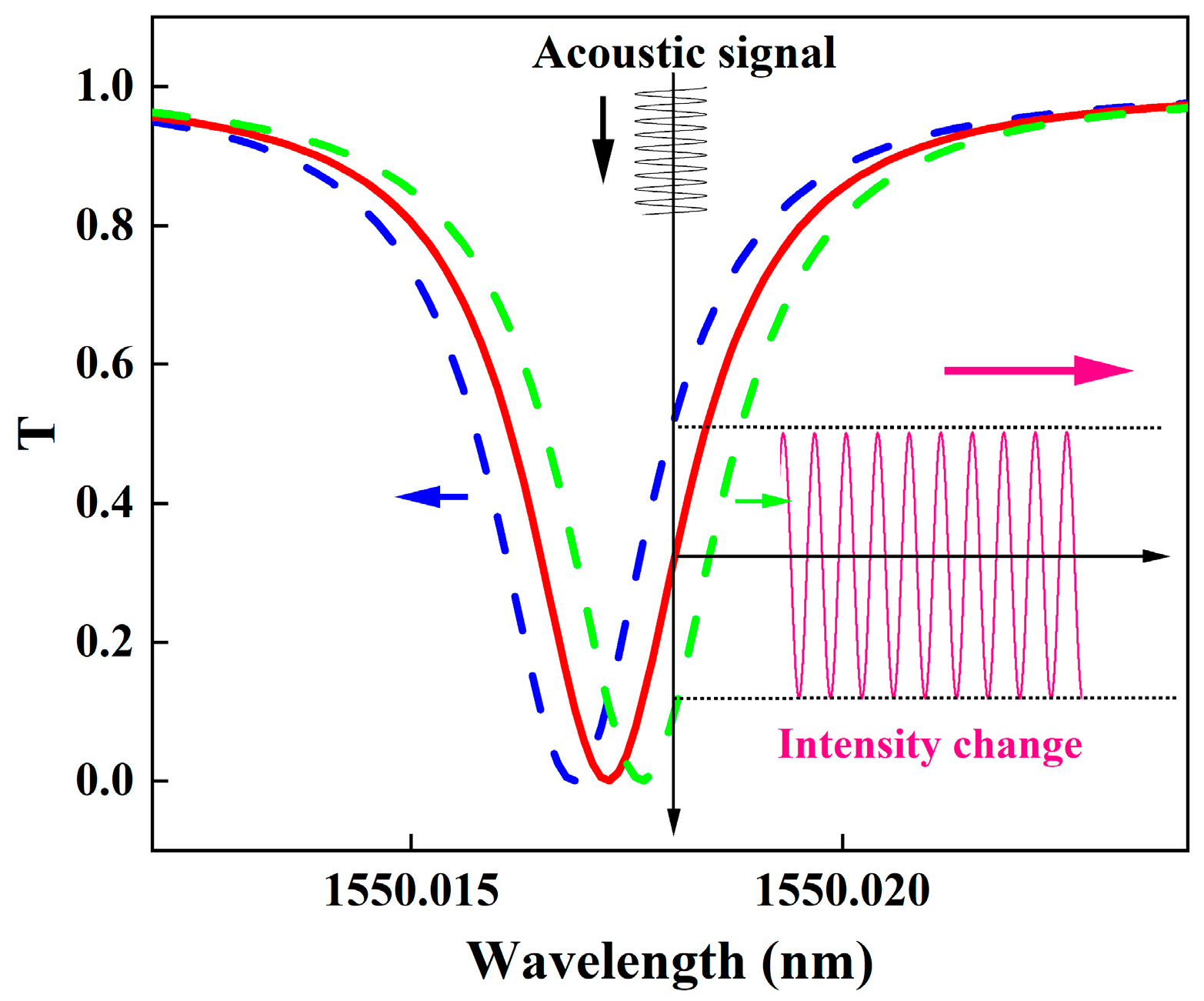
2.2. Principle of Acoustic Detection
3. Design and Fabrication
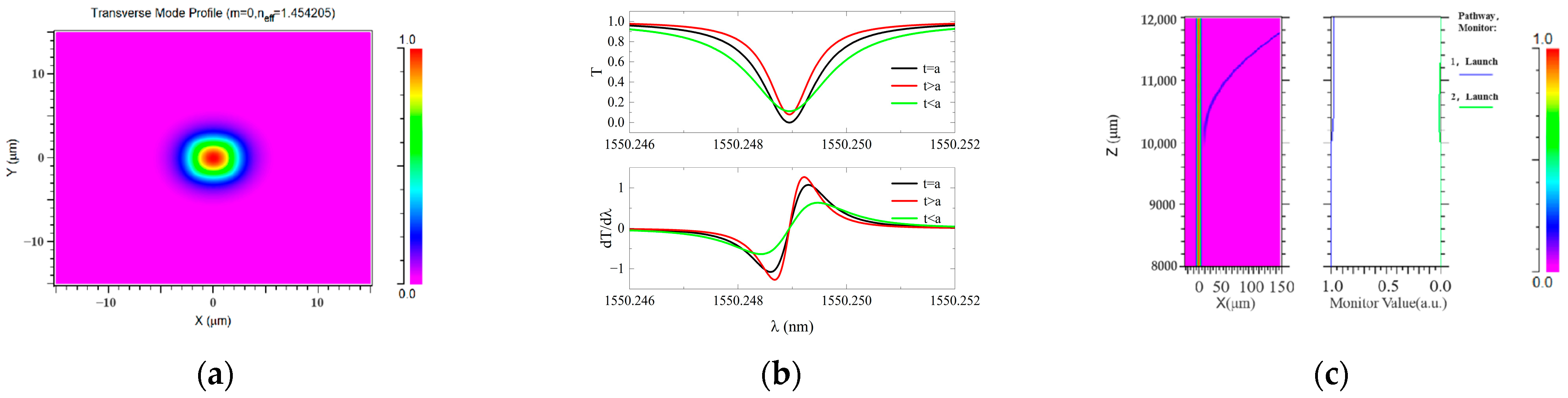
3.1. Design of the Resonator
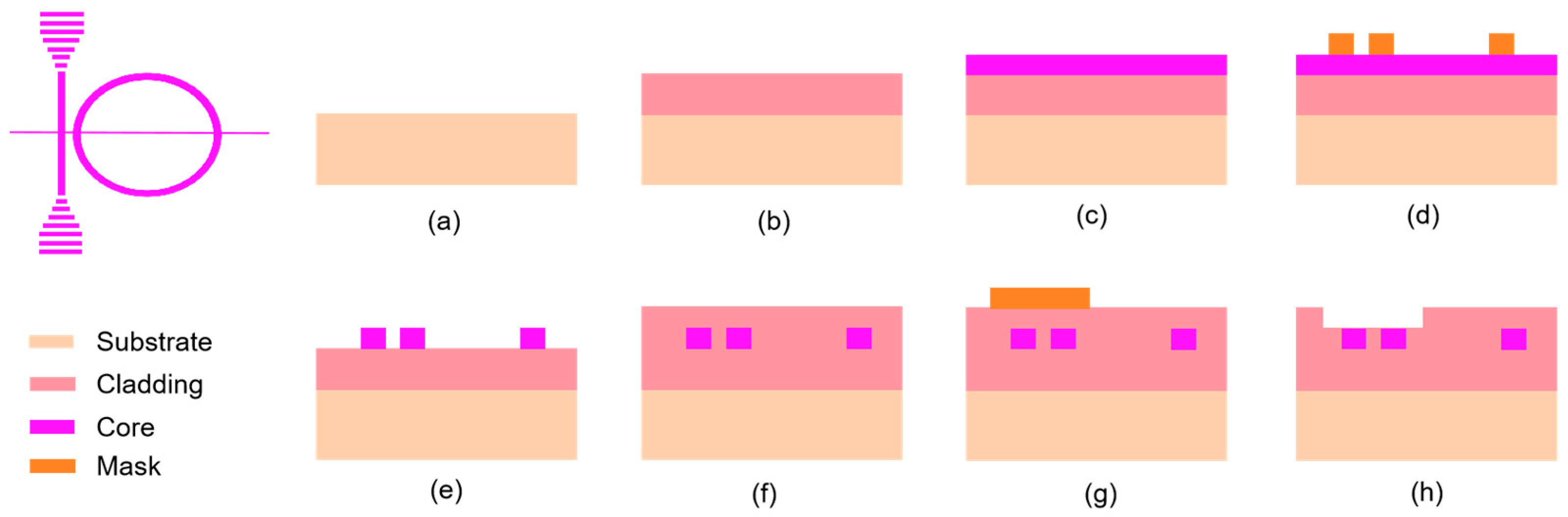
3.2. Fabrication of the Resonator
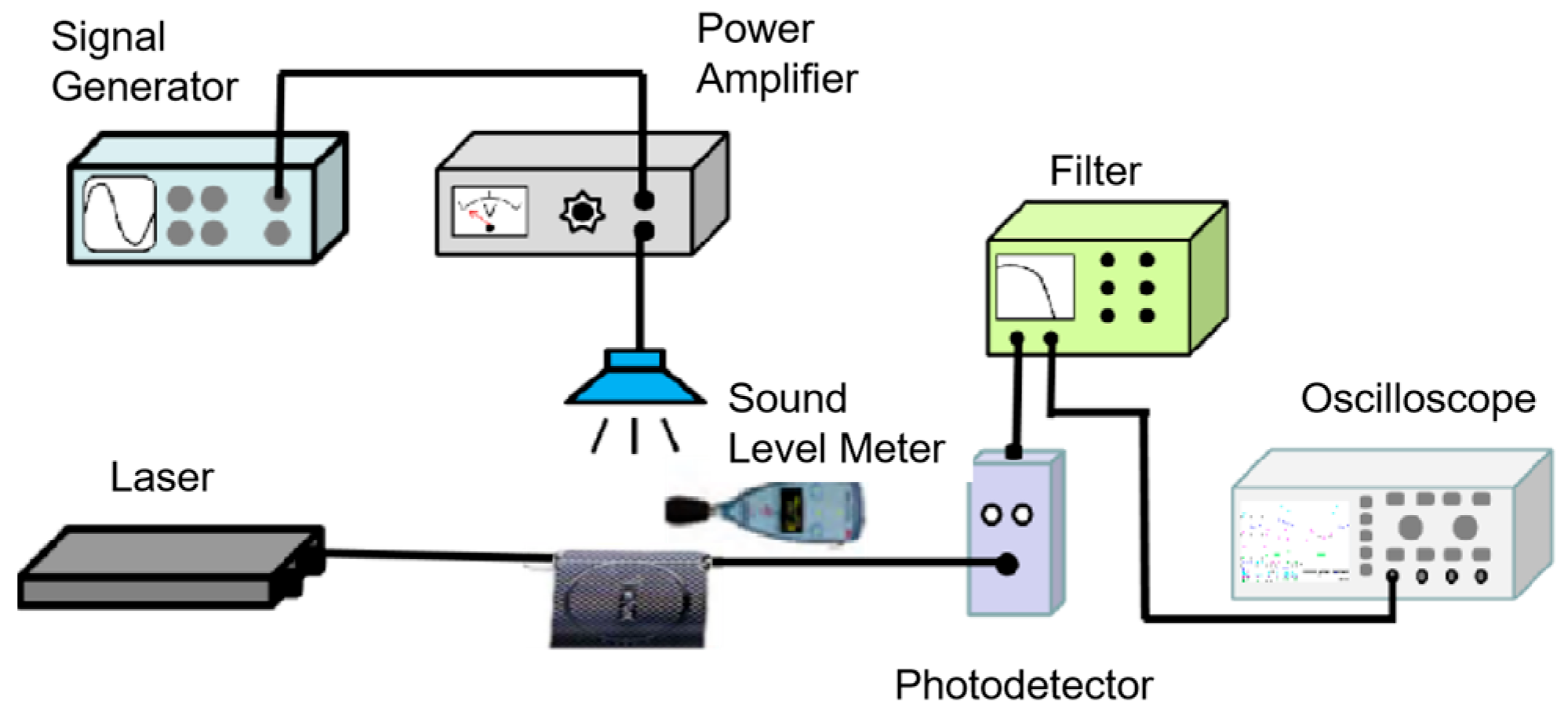
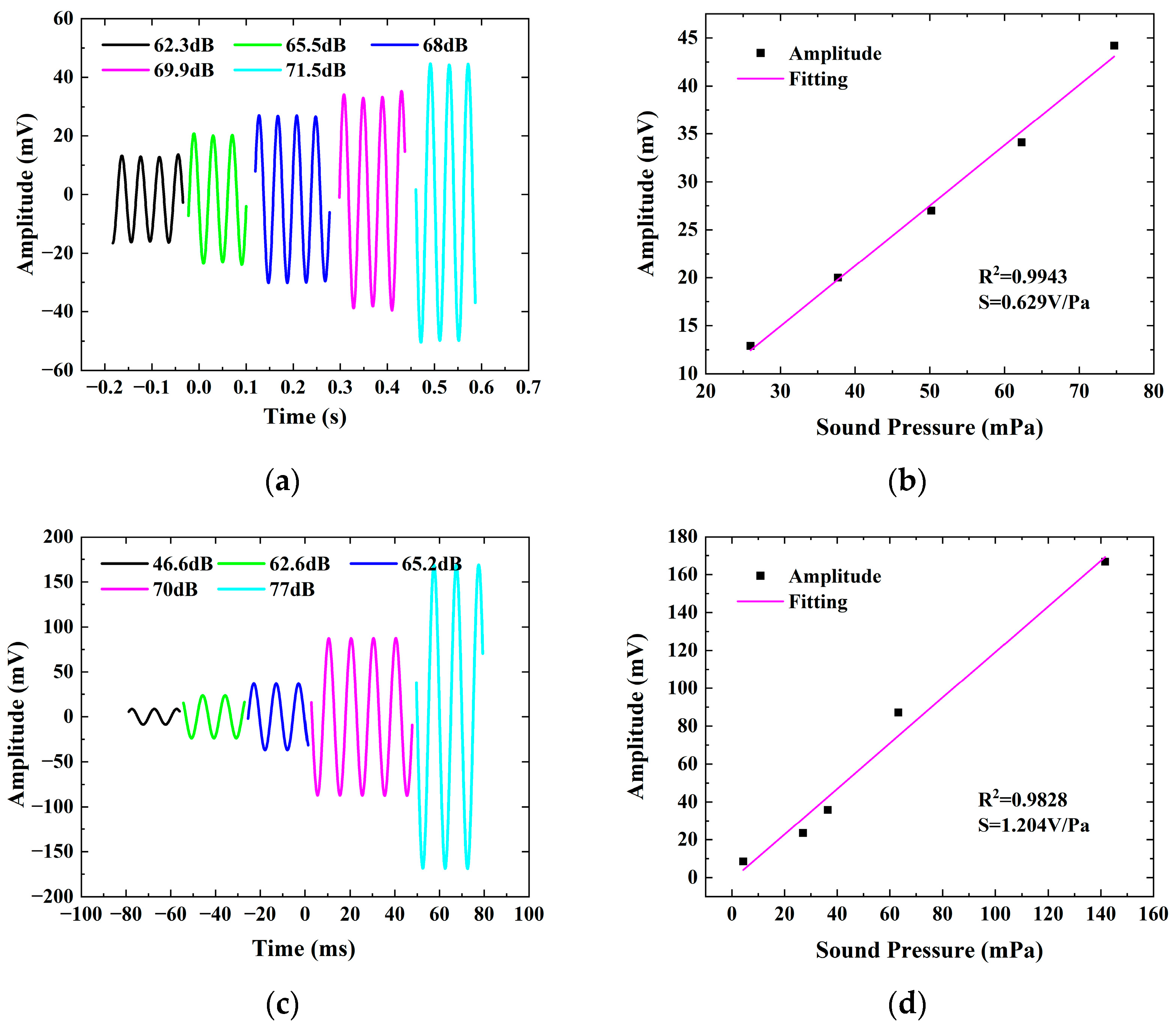
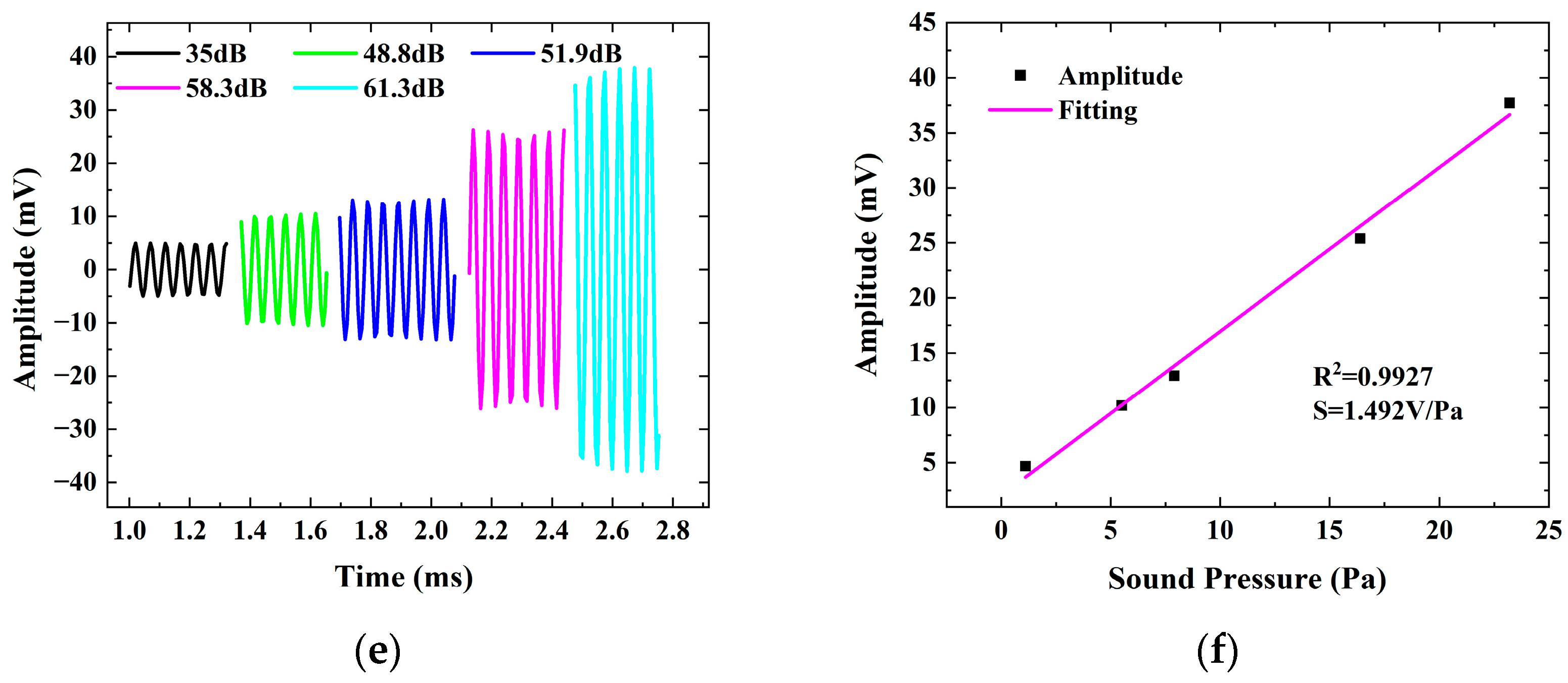
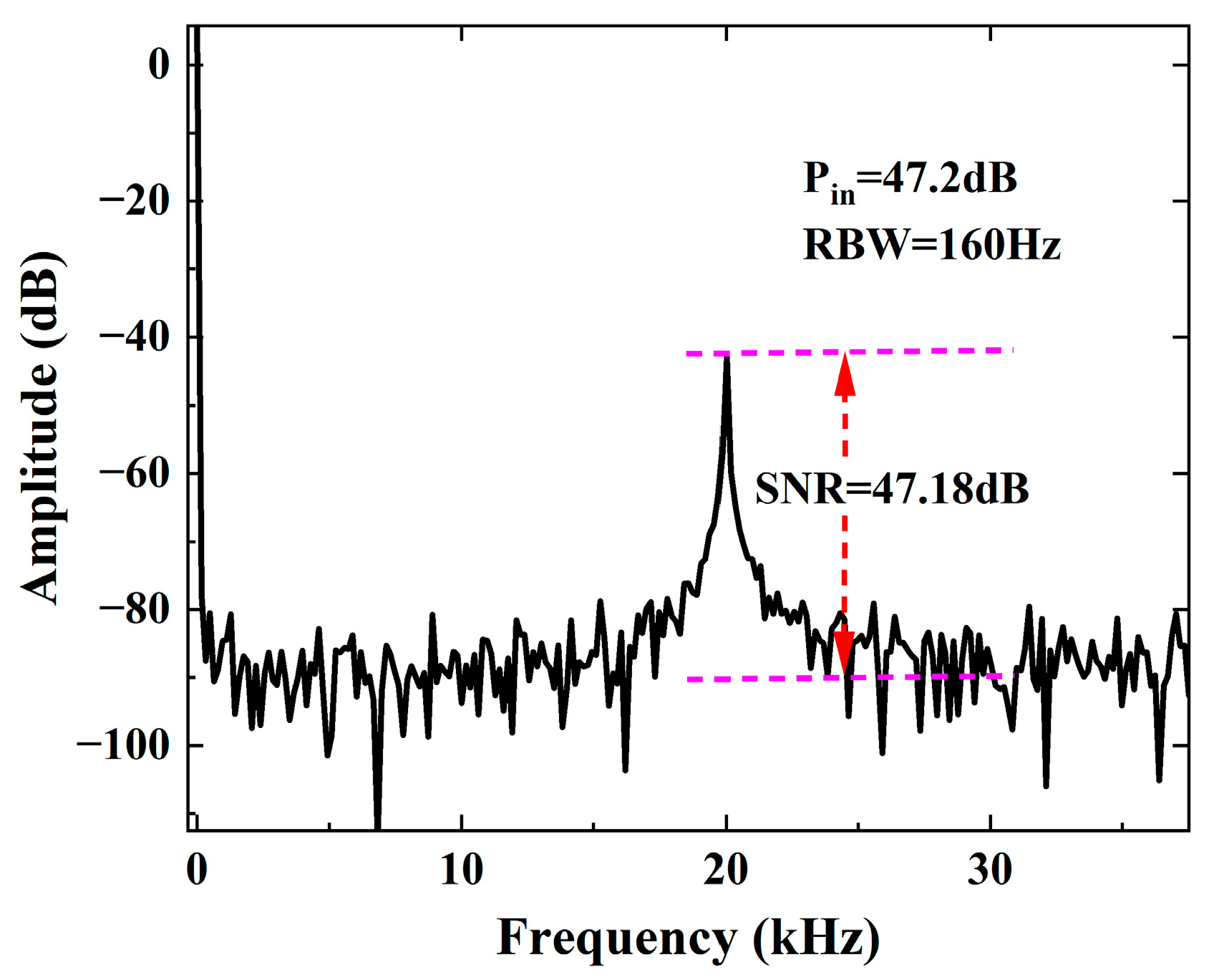
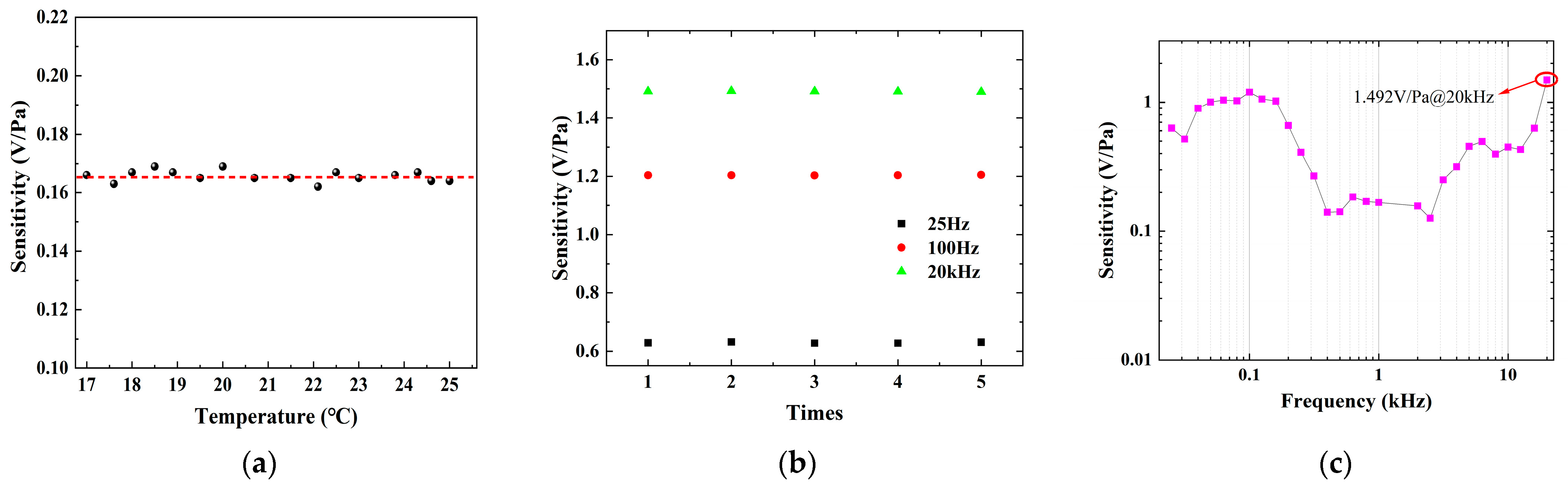
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, M.; Wu, X.; Liu, L.Y.; Xu, L. Self-referencing optofluidic ring resonator sensor for highly sensitive biomolecular detection. Anal. Chem. 2013, 85, 9328–9332. [Google Scholar] [CrossRef]
- Yao, B.C.; Yu, C.B.; Wu, Y.; Huang, S.-W.; Wu, H.; Gong, Y.; Chen, Y.; Li, Y.; Wong, C.W.; Fan, X.; et al. Graphene-enhanced Brillouin optomechanical microresonator for ultrasensitive gas detection. Nano Lett. 2017, 17, 4996–5002. [Google Scholar] [CrossRef]
- Lim, J.; Liang, W.; Savchenkov, A.A.; Matsko, A.B.; Maleki, L.; Wong, C.W. Probing 10 µK stability and residual drifts in the cross-polarized dual-mode stabilization of single-crystal ultrahigh-Q optical resonators. Light-Sci. Appl. 2019, 8, 1. [Google Scholar] [CrossRef] [PubMed]
- Xing, T.; Xing, E.B.; Jia, T.; Li, J.; Rong, J.; Li, L.; Tian, S.; Zhou, Y.; Liu, W.; Tang, J.; et al. An ultrahigh sensitivity acoustic sensor system for weak signal detection based on ultrahigh-Q CaF2 resonator. Microsyst. Nanoeng. 2023, 9, 65. [Google Scholar] [CrossRef]
- Chen, J.M.; Xue, C.Y.; Zheng, Y.Q.; Wu, L.; Chen, C.; Han, Y. Micro-fiber-optic acoustic sensor based on high-Q resonance effect using Fabry-Pérot etalon. Opt. Express 2021, 29, 16447–16454. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Mishra, R.D.; Babu, P.; Pandey, S.K.; Pal, M.K.; Kumar, M. Nanophotonic Ring Resonator Based on Slotted Hybrid Plasmonic Waveguide for Biochemical Sensing. IEEE Sens. J. 2023, 23, 5695–5702. [Google Scholar] [CrossRef]
- Zhang, P.; Ding, Y.L.; Wang, Y.F. Asymmetrical microring resonator based on whispering gallery modes for the detection of glucosecon centration. Optik 2018, 171, 642–647. [Google Scholar] [CrossRef]
- Song, J.; Pan, J.; Wan, L.; Chen, Z.S.; Zhu, Y.; Yang, Z.; Chen, Y.; Zhang, M.; Yi, X.; Li, Z. Ultrasound Measurement Using On-Chip Optical Micro-Resonators and Digital Optical Frequency Comb. J. Light. Technol. 2020, 38, 5293–5301. [Google Scholar] [CrossRef]
- Li, H.; Dong, B.Q.; Zhang, Z.; Zhang, H.F.; Sun, C. A transparent broad-band ultrasonic detector based on an optical micro-ring resonator for photoacoustic microscopy. Sci. Rep. 2016, 4, 44961–44968. [Google Scholar]
- Chen, H.; Shao, Z.H.; Hao, Y.X.; Rong, Q. A high-frequency hydrophone using an optical fiber microknot resonator. Opt. Commun. 2019, 446, 77–83. [Google Scholar] [CrossRef]
- De Freitas, J.M.; Birks, T.A.; Rollings, M.D. Optical micro-knot resonator hydrophone. Opt. Express 2015, 23, 5850–5860. [Google Scholar] [CrossRef]
- Zhai, X.P.; Zhang, W.D.; Cui, J.G.; Huang, H.; Wang, Y.; Zhang, G.; Wang, R.; Yang, Y.; Wang, Y. Underwater acoustic sensor based on microfiber knot resonator. Opt. Fiber Technol. 2024, 84, 103711. [Google Scholar] [CrossRef]
- Wang, K.; Wang, H.; Wu, X.-Y.; Zhang, Y.; Yang, D.; Jiao, R.; Wang, C. Ultrasound Sensing Using Packaged Microsphere Cavity in the Underwater Environment. Sensors 2022, 22, 4190. [Google Scholar] [CrossRef] [PubMed]
- Tu, X.; Wang, W.X.; Guo, Z.H.; Chen, Z.; Huang, T.; Wu, X.; Luo, W. Underwater Acoustic Wave Detection Based on Packaged Optical Microbubble Resonator. J. Light. Technol. 2022, 40, 6272–6279. [Google Scholar] [CrossRef]
- Wang, Y.S.; Rong, J.M.; Xing, E.B.; Li, J.; Ji, R.; Tang, J.; Liu, J. A Lever-Type PDMS Flexible Cavity for Acoustic Vector Sensor With High Sensitivity. IEEE Sens. J. 2023, 23, 5637–5642. [Google Scholar] [CrossRef]
- Xi, Q.; Ma, B.H.; Tian, Z.Y.; Li, R.; Wang, Y.; Ma, Z. Micro-Fabricated Compact Extrinsic Fabry-Perot Sensor for In-Situ Harsh Environment Acoustic Measurement. IEEE Photonics J. 2025, 17, 6800807. [Google Scholar] [CrossRef]
- Cao, Z.W.; Zhang, H.J.; Li, X.; Sun, J.; Zhang, Z. High-resolution optical fiber underwater acoustic sensor enhanced by PDMS coating. Opt. Fiber Technol. 2024, 87, 103953. [Google Scholar] [CrossRef]
- Wei, H.M.; Wei, Y.; Zhang, C.Q.; He, G.; Yang, T.; Zhang, X.; Pang, F.; Wang, T.; Krishnaswamy, S.; Caucheteur, C.; et al. Sensitivity-Enhanced Fiber-Optic FabryPerot Ultrasonic Sensor Based on Direct Laser Writing of Dual-Resonant Cavity. IEEE Trans. Instrum. Meas. 2025, 74, 7000706. [Google Scholar]
- Leinders, S.M.; Westerveld, W.J.; Pozo, J.; van Neer, P.; Snyder, B.; O’bRien, P.; Urbach, H.; de Jong, N.; Verweij, M.D. A sensitive optical micro-machined ultrasound sensor (OMUS) based on a silicon photonic ring resonator on an acoustical membrane. Sci. Rep. 2015, 5, 14328. [Google Scholar] [CrossRef]
- Chu, X.X.; Cui, J.G.; Zhu, M.; Wu, B.; Zhang, G.; Wang, R.; Zhang, W.; Yang, Y.; Ren, Y. Study on Acoustic Sensing Characteristics of a Novel Grooved SiO2 Waveguide Resonator. IEEE Sens. J. 2023, 23, 8206–8213. [Google Scholar] [CrossRef]
- Bhola, B.; Steier, W.H. A Novel Optical Microring Resonator Accelerometer. IEEE Sens. J. 2007, 7, 1759–1766. [Google Scholar] [CrossRef]
- Martin, P.; Pavel, C.; Daniel, B.; Jens, H.S.; James, P.; Robert, H.; Alejandro, O.-M.; Gonzalo, W.-P.; Winnie, N.Y.; Dan-Xia, X.; et al. Fiber-chip edge coupler with large mode size for silicon photonic wire waveguides. Opt. Express 2016, 24, 5026–5038. [Google Scholar] [CrossRef]
- Brunetti, G.; Heuvink, R.; Schreuder, E.; Armenise, M.N.; Ciminelli, C. Silicon nitride spot size converter with very low-loss over the C-band. IEEE Photonics Technol. Lett. 2023, 35, 1215–1218. [Google Scholar] [CrossRef]
- Rao, N.; Jing, Z.G.; Zhang, S.; Liu, Y.; Cheung, Y.; Peng, W. All-Fiber Acoustic Sensor Based on Anti-Resonant Refective Optical Waveguide. IEEE Sens. J. 2024, 24, 17709–17717. [Google Scholar] [CrossRef]
- Hong, G.Q.; Chen, B.Q.; Liu, S.; Chen, P.; Liu, B.; Xiao, H.; Ding, W.; Yan, W.; Wang, Y. Optical fiber acoustic sensor with gold diaphragm based Fabry-Perot interferometer. Sens. Actuators A Phys. 2024, 366, 114930. [Google Scholar] [CrossRef]


| Sensor | Sensor Medium | Q | Size (Diameter) | Sensitivity | Range of Frequency | |
|---|---|---|---|---|---|---|
| Paper [15] | Spherical | PDMS | 2.0 × 105 | 2.44 mm | 23.58 mV/Pa@4 kHz | 0.2–10 kHz |
| Paper [16] | FP | Si | - | 5 mm | 95.73 mV/Pa@18 kHz | 0.1–20 kHz |
| Paper [20] | OWR | SiO2 | 1.82 × 106 | 20 mm | 1.143 V/Pa@8 kHz | 0.4–15 kHz |
| Paper [24] | Fiber | Fiber | - | 80 μm | 1.189 V/Pa@290 Hz | 0.1–14.2 kHz |
| Paper [25] | FP | Gold Diaphragm | - | 75 μm | 147.5 mV/Pa@1 kHz | 0.07–20 kHz |
| This work | OWR | SiO2 | 2.75 × 106 | 10 mm | 1.492 V/Pa@20 kHz | 0.025–20 kHz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chu, X.; Zhao, Z.; Cui, J.; Zang, J. High-Sensitivity Broadband Acoustic Wave Detection Using High-Q, Undercoupled Optical Waveguide Resonators. Photonics 2025, 12, 1128. https://doi.org/10.3390/photonics12111128
Chu X, Zhao Z, Cui J, Zang J. High-Sensitivity Broadband Acoustic Wave Detection Using High-Q, Undercoupled Optical Waveguide Resonators. Photonics. 2025; 12(11):1128. https://doi.org/10.3390/photonics12111128
Chicago/Turabian StyleChu, Xiaoxia, Zhongqiang Zhao, Jiangong Cui, and Junbin Zang. 2025. "High-Sensitivity Broadband Acoustic Wave Detection Using High-Q, Undercoupled Optical Waveguide Resonators" Photonics 12, no. 11: 1128. https://doi.org/10.3390/photonics12111128
APA StyleChu, X., Zhao, Z., Cui, J., & Zang, J. (2025). High-Sensitivity Broadband Acoustic Wave Detection Using High-Q, Undercoupled Optical Waveguide Resonators. Photonics, 12(11), 1128. https://doi.org/10.3390/photonics12111128





