High-Efficiency Terahertz Generation Using a Photoconductive Antenna with Vertically Distributed Ring-Disc Electrodes
Abstract
1. Introduction
2. Optical Simulation
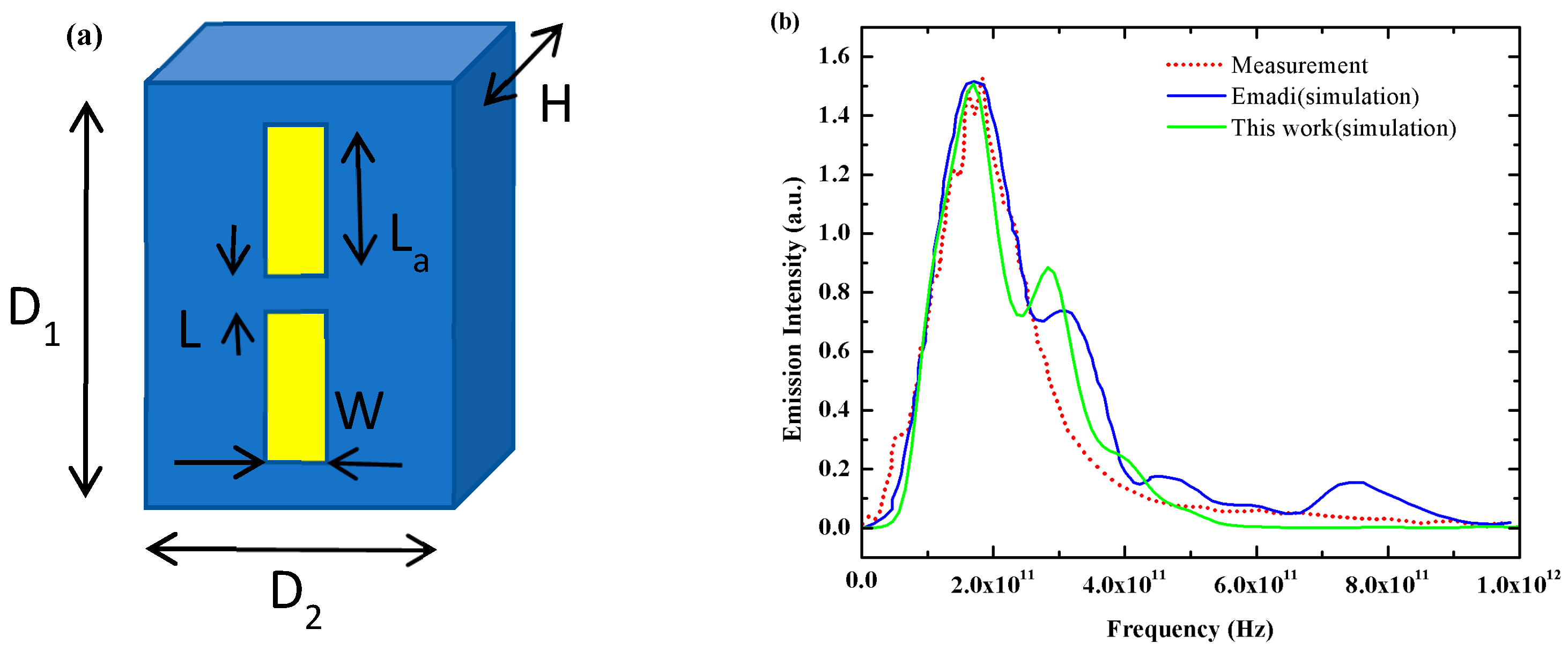
2.1. Optical Response
2.2. Electrical Response
3. Simulation Models and THz-PCA Performance Comparison
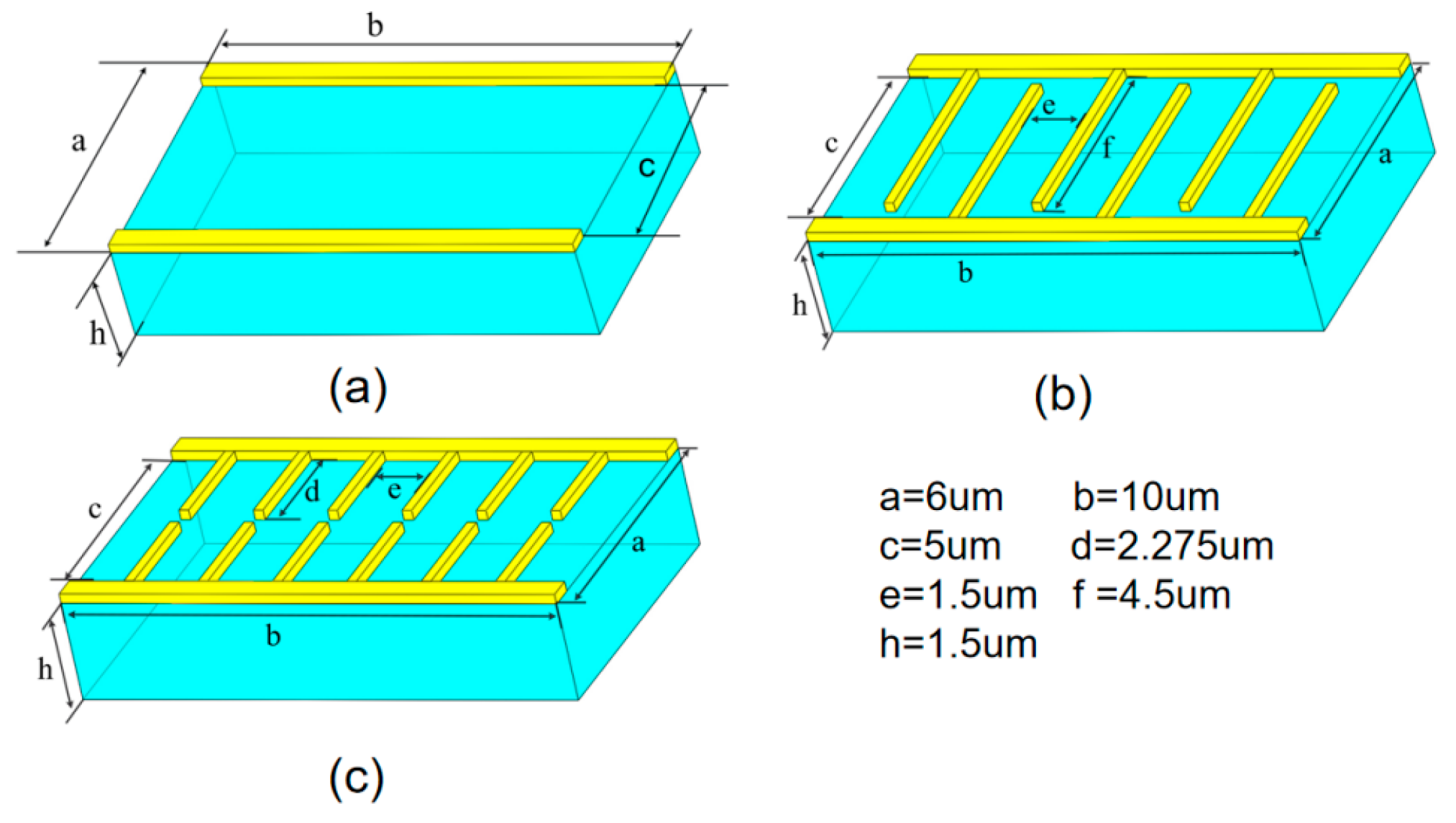
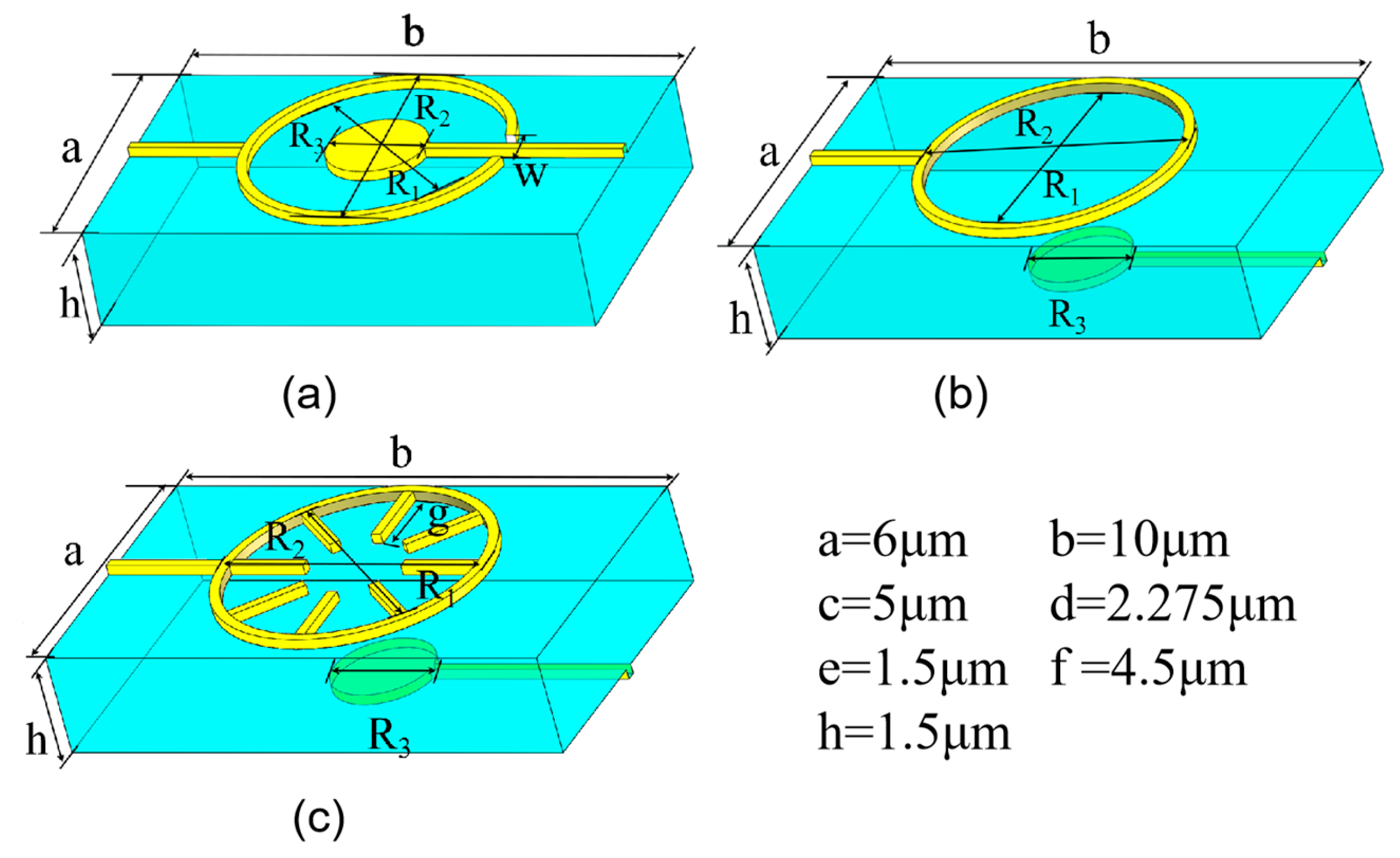
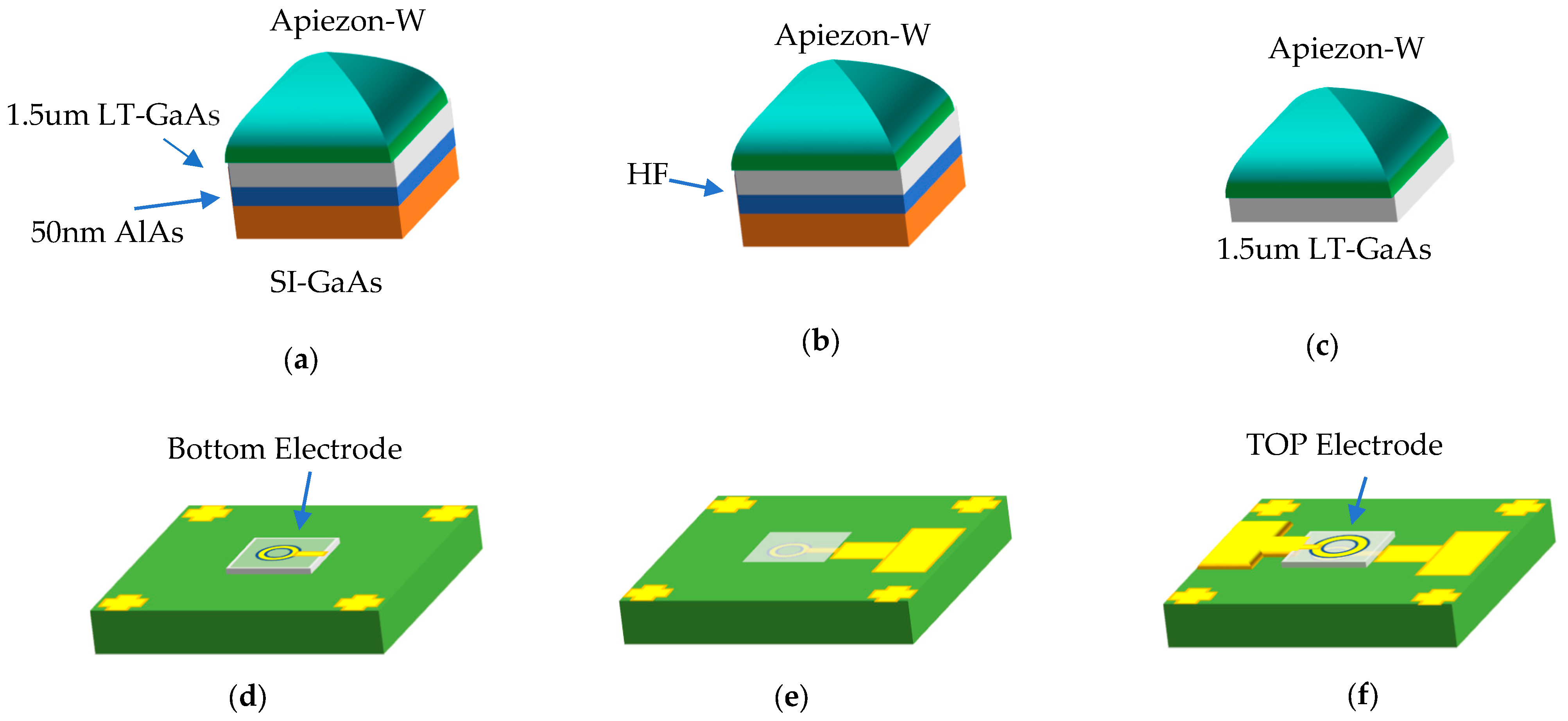
3.1. Simulation Models
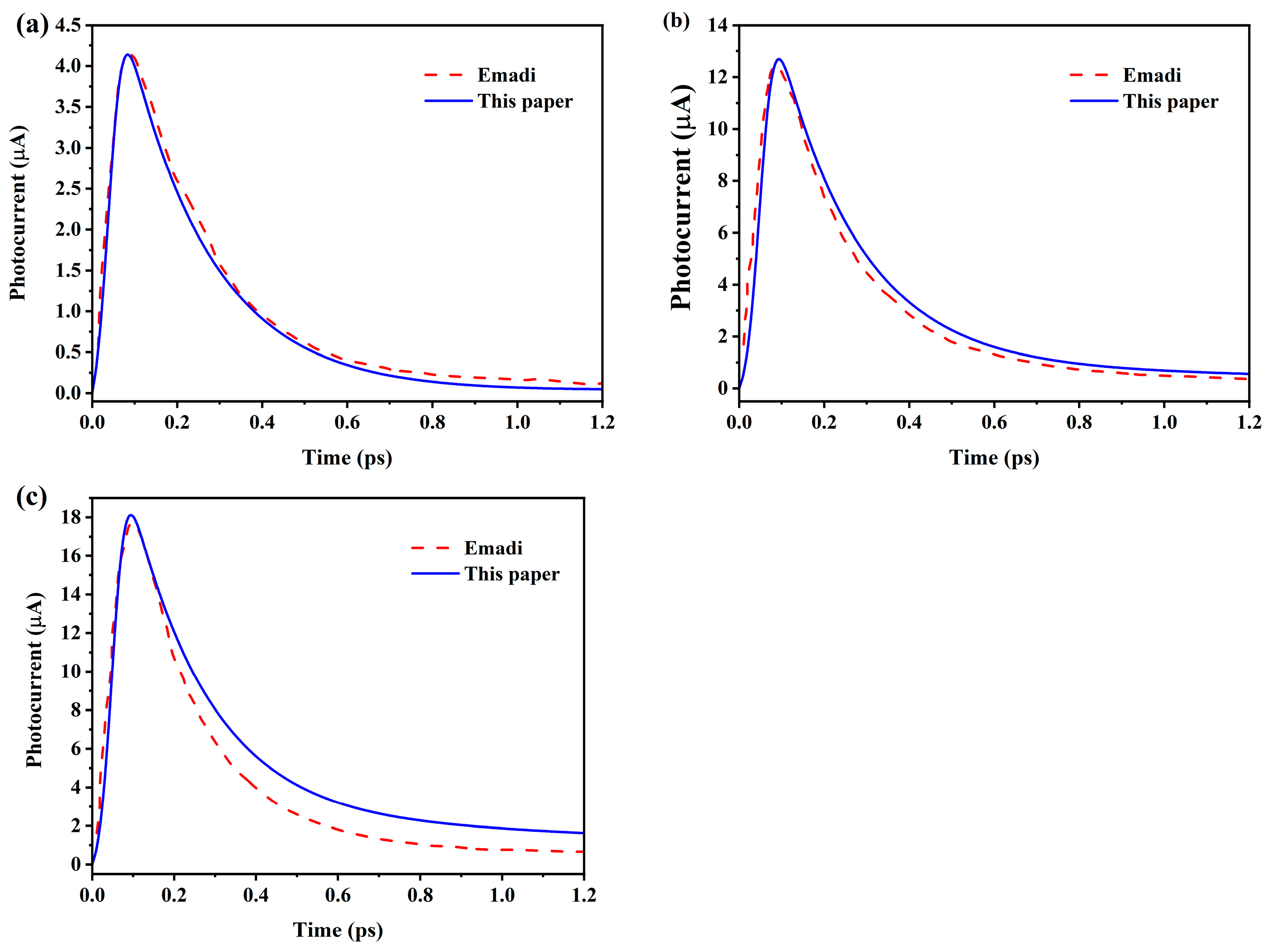
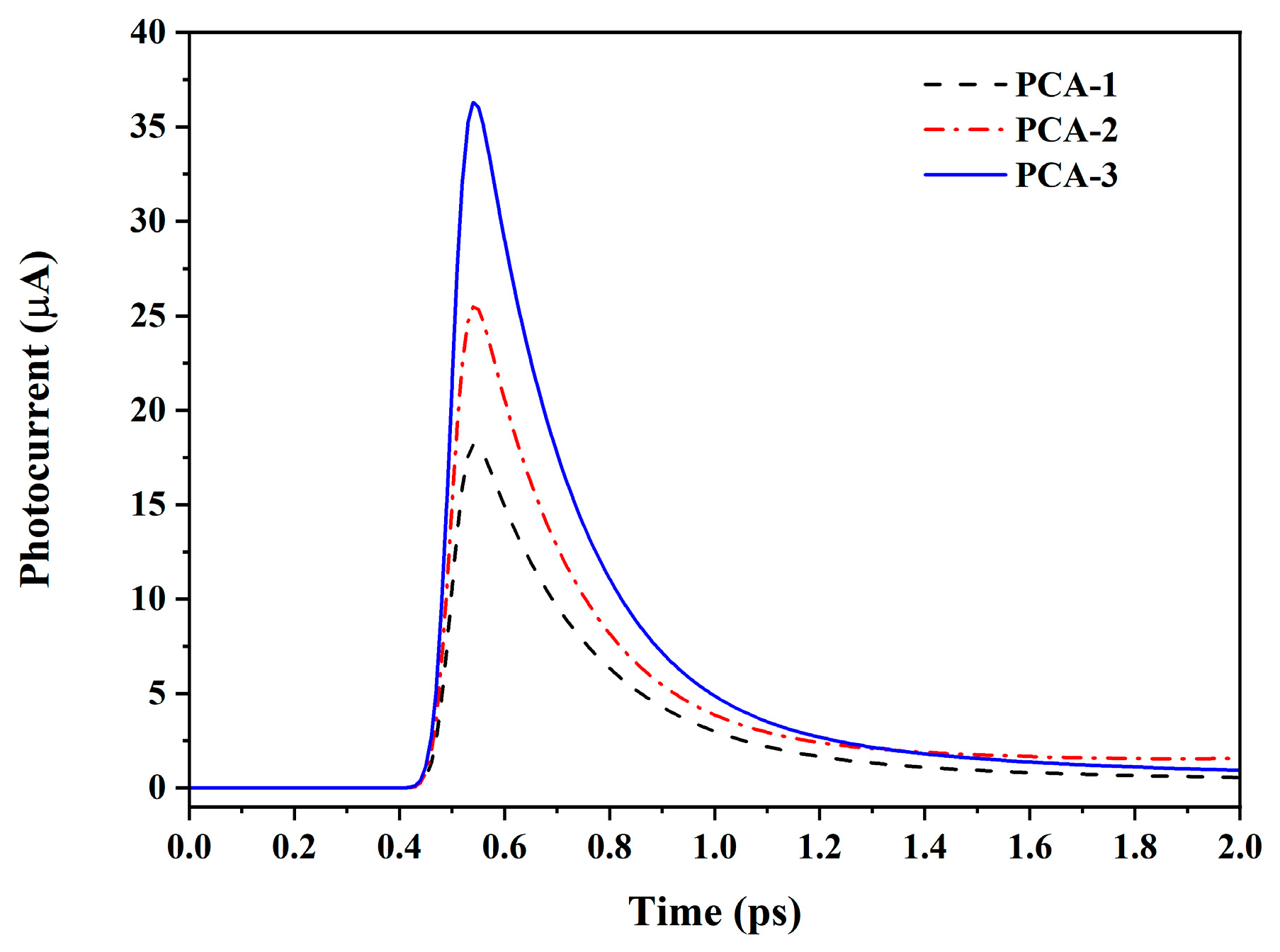
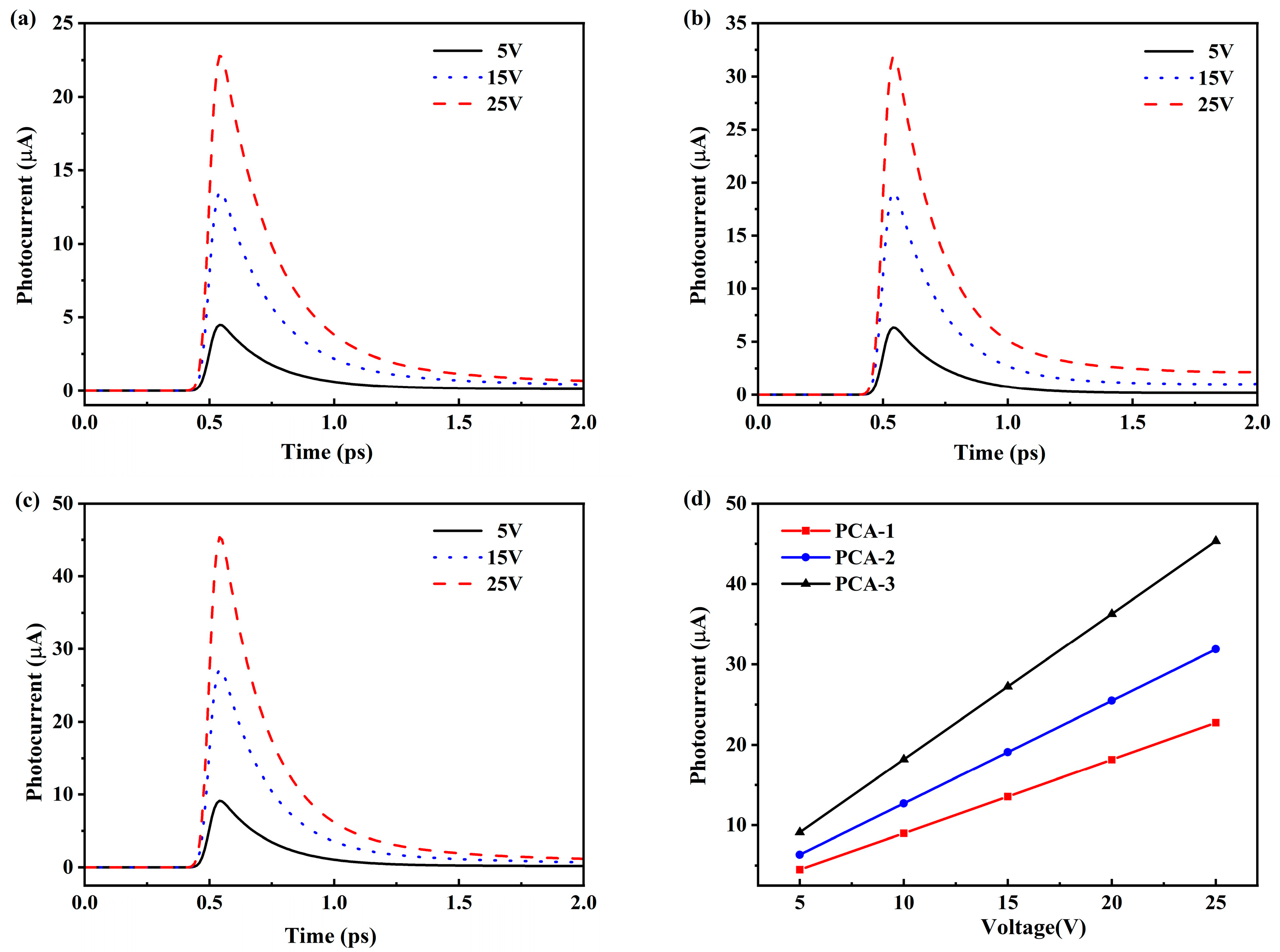
3.2. The Performance Comparison
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Ferguson, B.; Zhang, X.-C. Materials for Terahertz Science and Technology. Nat. Mater. 2002, 1, 26–33. [Google Scholar] [CrossRef]
- Mittleman, D.M. Perspective: Terahertz Science and Technology. J. Appl. Phys. 2017, 122, 230901. [Google Scholar] [CrossRef]
- Meng, D.; Liu, J.; Chen, W.; Cheng, Y.-Y.; You, K.-W.; Fan, Z.-C.; Ye, Q.; Huang, P.-H.; Chen, Y.-S. Study on the Enhancement Mechanism of Terahertz Molecular Fingerprint Sensing. Results Phys. 2022, 39, 105766. [Google Scholar] [CrossRef]
- Redo-Sanchez, A.; Heshmat, B.; Aghasi, A.; Naqvi, S.; Zhang, M.; Romberg, J.; Raskar, R. Terahertz Time-Gated Spectral Imaging for Content Extraction through Layered Structures. Nat. Commun. 2016, 7, 12665. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.; Zheng, Z.; Zhang, M.; Zhang, T.; Zhang, Z.; Huang, H. The Application of THz-TDS in the Characterization of Bayan Obo Magnetite Ore Composition. Sci. Rep. 2024, 14, 15033. [Google Scholar] [CrossRef] [PubMed]
- Bao, R.; Qin, F.; Chen, R.; Chen, S.; Zhan, H.; Zhao, K.; Yue, W. Optical Detection of Oil Bearing in Reservoir Rock: Terahertz Spectroscopy Investigation. IEEE Access 2019, 7, 121755–121759. [Google Scholar] [CrossRef]
- Zhu, J.; Li, C.; Fang, B.; Lu, J.; Hong, Z.; Jing, X. Advancements in Biosensing Detection Based on Terahertz Metasurfaces. Opt. Laser Technol. 2024, 176, 110978. [Google Scholar] [CrossRef]
- Shao, Y.; Zhou, Y.; Wan, J.; Zhu, Z.; Peng, Y.; Zhao, C.; Zhu, Y.; Tang, W. Using Terahertz Spectroscopy to Quantify Bioactive Flavonoids in Moxa Wool as Predictor of Rheumatoid Arthritis Treatment Outcomes. Phytomedicine 2024, 133, 155927. [Google Scholar] [CrossRef]
- Ahmadivand, A.; Gerislioglu, B.; Ramezani, Z.; Kaushik, A.; Manickam, P.; Ghoreishi, S.A. Functionalized Terahertz Plasmonic Metasensors: Femtomolar-Level Detection of SARS-CoV-2 Spike Proteins. Biosens. Bioelectron. 2021, 177, 112971. [Google Scholar] [CrossRef]
- Li, J.; Li, X.; Yardimci, N.T.; Hu, J.; Li, Y.; Chen, J.; Hung, Y.-C.; Jarrahi, M.; Ozcan, A. Rapid Sensing of Hidden Objects and Defects Using a Single-Pixel Diffractive Terahertz Sensor. Nat. Commun. 2023, 14, 6791. [Google Scholar] [CrossRef]
- Akyildiz, I.F.; Han, C.; Hu, Z.; Nie, S.; Jornet, J.M. Terahertz Band Communication: An Old Problem Revisited and Research Directions for the Next Decade. IEEE Trans. Commun. 2022, 70, 4250–4285. [Google Scholar] [CrossRef]
- Kumar, A.; Gupta, M.; Pitchappa, P.; Wang, N.; Szriftgiser, P.; Ducournau, G.; Singh, R. Phototunable Chip-Scale Topological Photonics: 160 Gbps Waveguide and Demultiplexer for THz 6G Communication. Nat. Commun. 2022, 13, 5404. [Google Scholar] [CrossRef]
- Li, X.; Li, J.; Li, Y.; Ozcan, A.; Jarrahi, M. High-Throughput Terahertz Imaging: Progress and Challenges. Light Sci. Appl. 2023, 12, 233. [Google Scholar] [CrossRef] [PubMed]
- Yu, Q.; Cai, H.; Zhu, X.; Liu, Z.; Yin, H.; Li, L. Terahertz Bistatic Three-Dimensional Computational Imaging of Hidden Objects through Random Media. Sci. Rep. 2024, 14, 6147. [Google Scholar] [CrossRef] [PubMed]
- He, Y.; Chen, Y.; Zhang, L.; Wong, S.-W.; Chen, Z.N. An Overview of Terahertz Antennas. China Commun. 2020, 17, 124–165. [Google Scholar] [CrossRef]
- Lepeshov, S.; Gorodetsky, A.; Krasnok, A.; Rafailov, E.; Belov, P. Enhancement of Terahertz Photoconductive Antenna Operation by Optical Nanoantennas. Laser Photonics Rev. 2017, 11, 1600199. [Google Scholar] [CrossRef]
- Loata, G.C.; Thomson, M.D.; Löffler, T.; Roskos, H.G. Radiation Field Screening in Photoconductive Antennae Studied via Pulsed Terahertz Emission Spectroscopy. Appl. Phys. Lett. 2007, 91, 232506. [Google Scholar] [CrossRef]
- Burford, N.M.; El-Shenawee, M.O. Review of Terahertz Photoconductive Antenna Technology. Opt. Eng. 2017, 56, 010901. [Google Scholar] [CrossRef]
- Wang, D.; Yang, L.; Hu, Z.; Wang, F.; Yang, Y.; Pan, X.; Dong, Z.; Tian, S.; Zhang, L.; Han, L.; et al. Antiferromagnetic Semimetal Terahertz Photodetectors Enhanced through Weak Localization. Nat. Commun. 2025, 16, 25. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Z.; Yang, Q.; Sun, S.; Liu, F.; Xu, H.; Wang, X.; Zhao, Y.; Zhou, N.; Dong, G.; et al. Strong Anisotropy and Giant Photothermoelectricity of 1D Alloy Nb3 Se12 I-Based Photodetector for Ultrabroadband Light-Detection and Encryption Imaging Application. Adv. Mater. 2025, 37, 2410275. [Google Scholar] [CrossRef]
- Auston, D.H.; Cheung, K.P.; Smith, P.R. Picosecond Photoconducting Hertzian Dipoles. Appl. Phys. Lett. 1984, 45, 284–286. [Google Scholar] [CrossRef]
- Park, S.-G.; Jin, K.H.; Yi, M.; Ye, J.C.; Ahn, J.; Jeong, K.-H. Enhancement of Terahertz Pulse Emission by Optical Nanoantenna. ACS Nano 2012, 6, 2026–2031. [Google Scholar] [CrossRef] [PubMed]
- Park, S.-G.; Choi, Y.; Oh, Y.-J.; Jeong, K.-H. Terahertz Photoconductive Antenna with Metal Nanoislands. Opt. Express 2012, 20, 25530. [Google Scholar] [CrossRef] [PubMed]
- Cox Iii, C.H.; Diadiuk, V.; Yao, I.; Leonberger, F.J.; Williamson, R.C. InP Optoelectronic Switches And Their High-Speed Signal-Processiny Applications. In Proceedings of the 27th Annual Technical Symposium, San Diego, CA, USA, 28 November 1983; pp. 164–168. [Google Scholar]
- Emadi, R.; Barani, N.; Safian, R.; Nezhad, A.Z. Hybrid Computational Simulation and Study of Terahertz Pulsed Photoconductive Antennas. J. Infrared Millim. Terahertz Waves 2016, 37, 1069–1085. [Google Scholar] [CrossRef]
- Maussang, K.; Palomo, J.; Mangeney, J.; Dhillon, S.S.; Tignon, J. Large-Area Photoconductive Switches as Emitters of Terahertz Pulses with Fully Electrically Controlled Linear Polarization. Opt. Express 2019, 27, 14784. [Google Scholar] [CrossRef]
- Sotoodeh, M.; Khalid, A.H.; Rezazadeh, A.A. Empirical Low-Field Mobility Model for III–V Compounds Applicable in Device Simulation Codes. J. Appl. Phys. 2000, 87, 2890–2900. [Google Scholar] [CrossRef]
- Jiang, X.-Q.; Fan, W.-H.; Song, C.; Chen, X.; Wu, Q. Terahertz Photoconductive Antenna Based on Antireflection Dielectric Metasurfaces with Embedded Plasmonic Nanodisks. Appl. Opt. 2021, 60, 7921. [Google Scholar] [CrossRef]
- Burford, N.; El-Shenawee, M. Computational Modeling of Plasmonic Thin-Film Terahertz Photoconductive Antennas. J. Opt. Soc. Am. B 2016, 33, 748. [Google Scholar] [CrossRef]
- Bashirpour, M.; Poursafar, J.; Kolahdouz, M.; Hajari, M.; Forouzmehr, M.; Neshat, M.; Hajihoseini, H.; Fathipour, M.; Kolahdouz, Z.; Zhang, G. Terahertz Radiation Enhancement in Dipole Photoconductive Antenna on LT-GaAs Using a Gold Plasmonic Nanodisk Array. Opt. Laser Technol. 2019, 120, 105726. [Google Scholar] [CrossRef]
- Amirjani, A.; Sadrnezhaad, S.K. Computational Electromagnetics in Plasmonic Nanostructures. J. Mater. Chem. C 2021, 9, 9791–9819. [Google Scholar] [CrossRef]
- Lesina, A.C.; Vaccari, A.; Berini, P.; Ramunno, L. On the Convergence and Accuracy of the FDTD Method for Nanoplasmonics. Opt. Express 2015, 23, 10481. [Google Scholar] [CrossRef]
- Miyamaru, F.; Saito, Y.; Yamamoto, K.; Furuya, T.; Nishizawa, S.; Tani, M. Dependence of Emission of Terahertz Radiation on Geometrical Parameters of Dipole Photoconductive Antennas. Appl. Phys. Lett. 2010, 96, 211104. [Google Scholar] [CrossRef]
- Jepsen, P.U.; Jacobsen, R.H.; Keiding, S.R. Generation and Detection of Terahertz Pulses from Biased Semiconductor Antennas. J. Opt. Soc. Am. B 1996, 13, 2424. [Google Scholar] [CrossRef]
- Rodriguez, G.; Taylor, A.J. Screening of the Bias Field in Terahertz Generation from Photoconductors. Opt. Lett. 1996, 21, 1046. [Google Scholar] [CrossRef] [PubMed]
- Tong-Yi, Z.; Jun-Cheng, C. Study of the Surface and Far Fields of Terahertz Radiation Generated by Large-Aperture Photoconductive Antennas. Chin. Phys. 2004, 13, 1742–1746. [Google Scholar] [CrossRef]
- Atalla, M.R.M.; Jiang, Z.; Liu, J.; Wang, L.; Ashok, S.; Xu, J. Modeling the Spectral Responsivity of Ultraviolet GaN Schottky Barrier Photodetectors under Reverse Bias. J. Appl. Phys. 2015, 117, 134503. [Google Scholar] [CrossRef]
- Long, J.W.; Dunn, B.; Rolison, D.R.; White, H.S. Three-Dimensional Battery Architectures. Chem. Rev. 2004, 104, 4463–4492. [Google Scholar] [CrossRef]
- Yablonovitch, E.; Gmitter, T.; Harbison, J.P.; Bhat, R. Extreme Selectivity in the Lift-off of Epitaxial GaAs Films. Appl. Phys. Lett. 1987, 51, 2222–2224. [Google Scholar] [CrossRef]
- Yang, Z.; Albrow-Owen, T.; Cui, H.; Alexander-Webber, J.; Gu, F.; Wang, X.; Wu, T.-C.; Zhuge, M.; Williams, C.; Wang, P.; et al. Single-Nanowire Spectrometers. Science 2019, 365, 1017–1020. [Google Scholar] [CrossRef]
- Patkar, M.P.; Chin, T.P.; Woodall, J.M.; Lundstrom, M.S.; Melloch, M.R. Very Low Resistance Nonalloyed Ohmic Contacts Using Low-Temperature Molecular Beam Epitaxy of GaAs. Appl. Phys. Lett. 1995, 66, 1412–1414. [Google Scholar] [CrossRef]
- Ríos, R.D.V.; Bikorimana, S.; Ummy, M.A.; Dorsinville, R.; Seo, S.-W. A Bow-Tie Photoconductive Antenna Using a Low-Temperature-Grown GaAs Thin-Film on a Silicon Substrate for Terahertz Wave Generation and Detection. J. Opt. 2015, 17, 125802. [Google Scholar] [CrossRef]
- Yardimci, N.T.; Lu, H.; Jarrahi, M. High Power Telecommunication-Compatible Photoconductive Terahertz Emitters Based on Plasmonic Nano-Antenna Arrays. Appl. Phys. Lett. 2016, 109, 191103. [Google Scholar] [CrossRef]
- Yardimci, N.T.; Jarrahi, M. High Sensitivity Terahertz Detection through Large-Area Plasmonic Nano-Antenna Arrays. Sci. Rep. 2017, 7, 42667. [Google Scholar] [CrossRef]
- Berry, C.W.; Wang, N.; Hashemi, M.R.; Unlu, M.; Jarrahi, M. Significant Performance Enhancement in Photoconductive Terahertz Optoelectronics by Incorporating Plasmonic Contact Electrodes. Nat. Commun. 2013, 4, 1622. [Google Scholar] [CrossRef]



| Symbol | Description | Value |
|---|---|---|
| λ | Free-space wavelength | 800 [nm] |
| Pave | Average laser power | 10 [mW] |
| fp | Laser repetition rate | 80 [MHz] |
| x0 | Pulse x-axis center location | 3 [µm] |
| t0 | Pulse center location (time) | 60 [fs] |
| Dx = Dy | Pulse half-power beam width (x = y direction) | 2.5 [µm] |
| Dt | Laser pulse duration | 50 [fs] |
| n1 + ik1 | LT-GaAs at 800 nm | 3.68 + 0.06i |
| n2 + ik2 | Au at 800 nm | 0.15 + 4.91i |
| µr | Magnetic permeability (all) | 1 |
| âe | Polarization vector | âx |
| εr | LT-GaAs Relative permittivity | 13.18 |
| Nc | Conduction band density of states | 9 × 1018 [1/cm3] |
| Nv | Valence band density of states | 4.7 × 1017 [1/cm3] |
| µn | Electron mobility | 0.04 [m2/V/s] |
| µp | Hole mobility | 0.01 [m2/V/s] |
| Cn | Auger electron coefficient | 7 × 10−30 |
| Cp | Auger hole coefficient | 7 × 10−30 |
| Eg | Bandgap | 1.424 [V] |
| χ | Electron affinity | 4.07 [V] |
| γp | Hole degeneracy factor | 4 |
| γn | Electron degeneracy factor | 2 |
| ni,eff | Effective intrinsic carrier concentration | 1.23 × 10−12 [1/m3] |
| σ | LT-GaAs electrical conductivity | 1.1 × 103 [S/m] |
| T | Room temperature | 300 [K] |
| τn = τp | Electron/hole lifetime | 0.1 [ps]/0.1 [ps] |
| Vbias | DC bias voltage | 20 [V] |
| kpc | Photoconductor extinction coefficient | 0.0625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Du, H.; Liu, G.; Liu, X.; Li, Z.; Song, S.; Liu, L. High-Efficiency Terahertz Generation Using a Photoconductive Antenna with Vertically Distributed Ring-Disc Electrodes. Photonics 2025, 12, 1116. https://doi.org/10.3390/photonics12111116
Du H, Liu G, Liu X, Li Z, Song S, Liu L. High-Efficiency Terahertz Generation Using a Photoconductive Antenna with Vertically Distributed Ring-Disc Electrodes. Photonics. 2025; 12(11):1116. https://doi.org/10.3390/photonics12111116
Chicago/Turabian StyleDu, Hao, Guipeng Liu, Xingpeng Liu, Zhuofeng Li, Shuxiang Song, and Linsheng Liu. 2025. "High-Efficiency Terahertz Generation Using a Photoconductive Antenna with Vertically Distributed Ring-Disc Electrodes" Photonics 12, no. 11: 1116. https://doi.org/10.3390/photonics12111116
APA StyleDu, H., Liu, G., Liu, X., Li, Z., Song, S., & Liu, L. (2025). High-Efficiency Terahertz Generation Using a Photoconductive Antenna with Vertically Distributed Ring-Disc Electrodes. Photonics, 12(11), 1116. https://doi.org/10.3390/photonics12111116





