Compact Six-Degree-of-Freedom Displacement Sensing Based on Laser Reflection and Position-Sensitive Detectors

Abstract

To meet pose-control and vibration-suppression requirements in confined spaces, a compact, noncontact six-degree-of-freedom (6-DoF) displacement-sensing method is proposed. The method is based on laser reflection and a position-sensitive detector (PSD) and features an adjustable incidence angle. An adjustable-incidence-angle PSD–corner-cube retro-reflector (CCR) configuration is devised, which reduces the PSD’s spatial footprint to 10.4% of that of a conventional layout. Building on this configuration, an analytical model is derived that maps the target’s 6-DoF displacement to the PSD spot motion as a function of the fixed relative pose between the PSD and the CCR mounted on the target. The model is linearized under the small-angle assumption. Experiments show an accuracy of 5.89 μm for translation within ±1.5 mm and 0.0027° for rotation within ±0.5°. The method couples a compact architecture with high precision and provides both a theoretical basis and an engineering-ready pathway for high-bandwidth pose sensing in confined spaces.

1. Introduction

6-DoF displacement metrology underpins numerous critical domains, including active microgravity vibration isolation, precision attitude and position control, astronomical observation, precision manufacturing, and large-scale equipment assembly [1,2,3,4,5,6,7,8]. Its core objective is to localize a target in 2D or 3D by measuring multi-axis displacements and angles. In practice, multiple displacement and/or angular sensors are arranged to estimate the target’s pose relative to a reference frame [9,10,11,12]. For planar and three-dimensional positioning, an orthogonal array of linear displacement sensors provides the most direct solution.

Mainstream linear displacement sensors include PSDs, laser interferometers, grating (linear) encoders, capacitive displacement sensors, high-precision strain gauges, and fiber-optic sensors. Laser interferometers measure displacement by referencing the optical wavelength. A key advantage is the ease of building multi-axis systems [13,14,15]: by aligning each orthogonal laser beam with the corresponding motion axis, cross-axis error can be effectively suppressed. However, they are susceptible to refractive index fluctuations in air induced by environmental perturbations. Under harsh conditions, refractive index errors pose a major challenge for multi-axis measurements, necessitating further performance optimization [16,17,18,19]. For grating encoders, accuracy depends chiefly on the precision and uniformity of the grating pitch. The stability of this physical scale enables accurate measurements even under harsh environmental conditions. With appropriate optical path design, these encoders can also perform angular measurement [20,21,22,23]. However, high-quality encoders are often bulky, complicating motion–control integration in practice. Although configurations using prisms [24] or convex lenses [25] have been proposed, complex assembly and tight focal length matching still constrain miniaturization. Capacitive displacement sensors [26,27,28], high-precision strain gauges [29,30], and fiber-optic sensors [31] can achieve submicrometer or even nanometer accuracy. However, their typical ranges—on the order of a few hundred micrometers—restrict their use to narrowly defined conditions. In recent years, integrating deep learning with optical metrology has markedly improved robustness and real-time performance across key tasks, including fringe processing, structured-light 3D imaging, and digital image correlation [32]. A recent review organizes the hierarchy of image-formation models and algorithms and argues that data-driven and physics-based approaches will coexist and evolve synergistically over the long term, rather than replace one another [33].

In spaceborne microgravity missions requiring active vibration isolation and precision attitude control, the harsh, variable environment and strict compactness constraints severely constrain the use of laser interferometers and grating encoders. In parallel, optical-field metrology based on vortex beams (carrying orbital angular momentum, OAM) has been used for highly sensitive detection of angular velocity and three-dimensional motion, showing promise for sensing in complex media and for long-range, noncontact measurement [34]. However, these approaches typically require complex optical field modulation and free-space optical paths, posing substantial engineering challenges for highly integrated implementations in confined spaces. Accordingly, this study focuses on PSD–CCR measurement configurations [35,36,37], which are more amenable to compact deployment. By contrast, PSDs offer clear advantages in such scenarios owing to their simple construction, environmental robustness, and reliable accuracy under severe conditions [38,39,40,41]. For example, Gao et al. realized 6-DoF pose measurement for the Tianzhou-1 microgravity active vibration isolation system by coordinating three PSD–laser pairs to satisfy relative-motion sensing requirements [42]. However, as isolation targets tighten, cabling between lasers/PSDs mounted on the target and external electronics adds stiffness and transmits vibration, forming a key bottleneck to further isolation improvements. To mitigate this, researchers proposed mounting a CCR on the target as a passive reflector to eliminate these issues. Building on this concept, Yu et al. proposed a 6-DoF displacement-sensing configuration integrating a CCR with a PSD. Under the small-angle approximation, the measurement equations decouple and linearize, enabling noncontact displacement sensing [43]. Subsequent studies by Chen et al. systematically analyzed the error characteristics of this configuration, providing theoretical support for precision measurements using CCRs [44,45].

Notably, prior studies adopted a layout with normal incidence on both the CCR and the PSD. Although this configuration avoids refraction-induced errors from oblique incidence, it results in a bulky PSD–CCR assembly. For spaceborne microgravity isolation, where stringent volume constraints are paramount, there is a pressing need for a more compact 6-DoF measurement system. To address this need, a compact 6-DoF displacement-sensing method employing three PSD–CCR pairs is proposed. On this basis, a decoupled analytical model is derived that maps 6-DoF displacement to PSD spot motion. Experiments first validate the displacement mapping with a single PSD–CCR pair and then demonstrate the feasibility and accuracy of full 6-DoF reconstruction using three PSD–CCR pairs.

2. Detection Methods and Theoretical Modeling

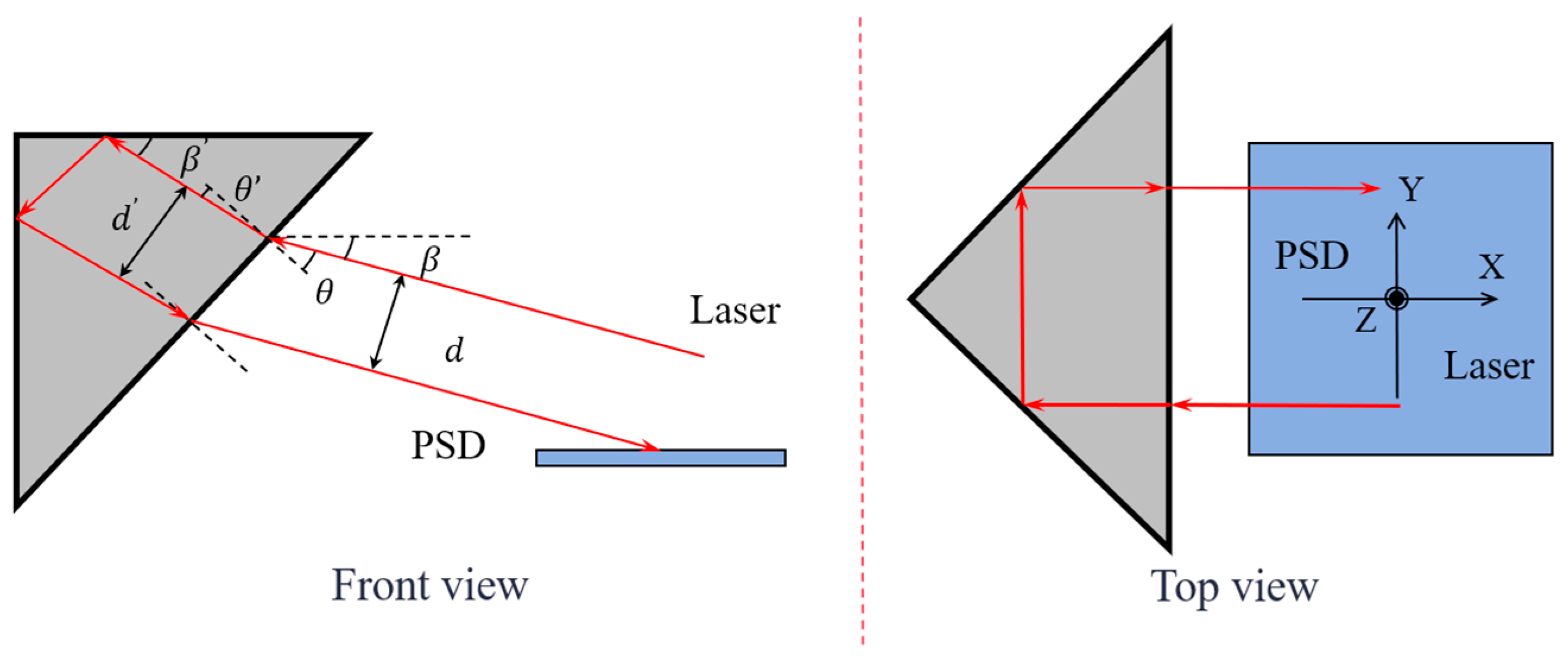
2.1. Operating Principle of the CCR

An ideal CCR retro-reflects the incident ray such that the emerging ray is antiparallel to the incident ray, as shown in Figure 1. An incident ray A₁ undergoes three successive reflections from the mutually orthogonal faces and emerges as A₄. Define a coordinate system with the apex as the origin and the three mutually perpendicular edges aligned with the X, Y, and Z axes. The unit normal vectors to the reflecting planes XOY, YOZ, and XOZ are, respectively, as follows:

$$\overrightarrow{{\mathit{n}}_1}={\left[0 0 1\right]}^{\mathrm{T}}, \overrightarrow{{\mathit{n}}_2}={\left[1 0 0\right]}^{\mathrm{T}}, \overrightarrow{{\mathit{n}}_3}={\left[0 1 0\right]}^{\mathrm{T}}$$

(1)

The unit direction vector of incident ray A₁ in the CCR-fixed coordinate frame is as follows:

$$\overrightarrow{{\mathit{a}}_1}={\left[x_1 y_1 z_1\right]}^{\mathrm{T}}$$

(2)

Let A₁ and A₂ denote the incident and reflect rays at the YOZ plane, respectively, by the law of specular reflection, as follows:

$$\overrightarrow{{\mathit{a}}_2}=\overrightarrow{{\mathit{a}}_1}-2\left(\overrightarrow{{\mathit{a}}_1}·\overrightarrow{{\mathit{n}}_2}\right)·\overrightarrow{{\mathit{n}}_2}={\left[{-x}_1 y_1 z_1\right]}^{\mathrm{T}}$$

(3)

Similarly, the rays reflected from the XOY and XOZ planes are, respectively, as follows:

$$\begin{gathered} \overrightarrow{{\mathit{a}}_3}=\overrightarrow{{\mathit{a}}_2}-2\left(\overrightarrow{{\mathit{a}}_2}·\overrightarrow{{\mathit{n}}_1}\right)·\overrightarrow{{\mathit{n}}_1}={\left[{-x}_1 -y_1 z_1\right]}^{\mathrm{T}}, \\ \overrightarrow{{\mathit{a}}_4}=\overrightarrow{{\mathit{a}}_3}-2\left(\overrightarrow{{\mathit{a}}_3}·\overrightarrow{{\mathit{n}}_3}\right)·\overrightarrow{{\mathit{n}}_3}={\left[{-x}_1 {-y}_1 {-z}_1\right]}^{\mathrm{T}} \end{gathered}$$

(4)

Consequently, $\overrightarrow{{\mathit{a}}_4}$ is the negative of $\overrightarrow{{\mathit{a}}_1}$; the emergent and incident rays are antiparallel. In matrix form, this relationship reads as follows:

$$\overrightarrow{{\mathit{a}}_4}=\left[\begin{array}{ccc}-1& 0& 0\\ 0& -1& 0\\ 0& 0& -1\end{array}\right]\overrightarrow{{\mathit{a}}_1}$$

(5)

Assuming the CCR undergoes translations Δx, Δy, and Δz along the X, Y, and Z axes, respectively, the incident ray in the CCR-fixed coordinate frame is shifted accordingly:

$$\overrightarrow{{\mathit{a}}_1}={\left[x_1-\Delta x y_1-\Delta y z_1-\Delta z\right]}^{\mathrm{T}}$$

(6)

Then:

$$\overrightarrow{{\mathit{a}}_4}={\left[-x_1+\Delta x -y_1+\Delta y {-z}_1+\Delta z\right]}^{\mathrm{T}}$$

(7)

The emergent rays are shifted by 2Δx, 2Δy, and 2Δz along the X, Y, and Z axes, respectively. In other words, a displacement of the CCR produces an emergent-ray displacement twice as large.

2.2. Theoretical Model for the Single PSD–CCR

In prior layouts, normal incidence was typically used as follows: the PSD active area was parallel to the incident face of the CCR, and the beam entered the CCR at normal incidence. This configuration eliminates refraction at both entry and exit. Normal incidence on the PSD active area simplifies the analysis. However, this approach offers limited layout flexibility. In compact assemblies, a tilted PSD consumes excessive vertical clearance, complicating the overall design. To address this limitation, a new layout is proposed (Figure 2).

In this layout, the PSD active area is parallel to the CCR mounting plane; the angle between the incident beam and the mounting planes of both the PSD and the CCR is denoted by β. In the conventional 45° layout, the PSD was tilted by 45°, and the vertical clearance depended on its width, with d₁ scaling as $\sqrt{2}$d. In the proposed layout, the out-of-plane envelope depends solely on the PSD thickness. Define the spatial–occupancy ratio r_SO, where h₁ is the vertical clearance in the proposed layout and d₁ is that in the 45° layout:

$$r_{SO}={\displaystyle \frac{h_1}{d_1}}$$

(8)

The current PSD dimensions are a width (d) of 54 mm and a thickness (h₁) of 4 mm. Substituting these values into Equation (8) yields r_SO of 10.4%, indicating that the PSD occupies only 10.4% of the vertical clearance relative to the 45° layout, thereby markedly reducing the detector footprint. Under this layout, because the beam is not normally incident on the PSD, refraction occurs at both entry and exit. Consequently, the mapping from the CCR pose to the PSD spot position must be analyzed.

Within the CCR, the emergent ray remains antiparallel to the incident ray; refraction at entry and exit preserves this relationship between the emitted beam and the light received by the PSD. Define a PSD-fixed coordinate frame with the X and Y axes aligned to the active-area axes and the origin at the active-area center. Assume the beam projection on the PSD plane is aligned with the PSD X axis (Figure 3).

In the top view, one reflection is omitted because it has no component in the projection plane. In the PSD coordinate frame, the entry and exit faces of the CCR are parallel to the Y axis; accordingly, the normal surface has no Y-component. When the incident ray direction also has zero Y-component, the plane spanned by the incident ray direction and the face normal is perpendicular to the PSD’s Y axis. The refracted ray remains in this plane, so refraction at entry does not change the PSD Y-direction. Because a CCR returns the ray parallel to its incident direction, refraction at exit likewise leaves the PSD Y-direction unchanged. Therefore, when the CCR translates along the PSD-frame Y axis by Δy_PSD, the PSD spot translates along Y by 2Δy_PSD.

$$\overrightarrow{\mathit{n}}={\left[x 0 z\right]}^{\mathrm{T}}$$

(9)

In the front view, the two in-plane reflections are represented by a single effective reflection (Figure 3). Let the separation of the two parallel beams outside the CCR be d, the separation inside the CCR be d′, and the projected in-plane separation between the incident and emergent beams be l; the geometry then yields the following:

$$\left\{\begin{array}{c}d=l\cos \theta \\ d^{\prime }=l\cos {\theta }^{\prime }\end{array}\right.$$

(10)

Therefore, the following relation holds:

$${\displaystyle \frac{d}{d^{\prime }}}={\displaystyle \frac{\cos \theta }{\cos {\theta }^{\prime }}}$$

(11)

In the PSD-fixed frame, when the CCR translates along the X and Z axes by Δx_PSD and Δz_PSD, respectively, the separation d′ of the parallel beams inside the CCR varies by Δd_x′ and Δd_z′; the resulting relations are as follows:

$$\Delta {d_{\mathrm{x}}}^{\prime } = 2\sin {\beta }^{\prime }{\Delta x}_{\mathrm{P}\mathrm{S}\mathrm{D}}, \Delta {d_{\mathrm{z}}}^{\prime } = 2\cos {\beta }^{\prime }{\Delta z}_{\mathrm{PSD}}$$

(12)

where β′ is defined as β + θ − θ′. The variations Δd_x′ and Δd_z′ induce changes Δd_x and Δd_z in the parallel beam separation d outside the CCR, which in turn produce X axis spot shifts Δx_x and Δx_z on the PSD. From geometry, the following relations hold:

$$\Delta X_{\mathrm{PSD}-\mathrm{x}} = {\displaystyle \frac{{\Delta d}_{\mathrm{x}}}{\sin \beta }}, \Delta X_{\mathrm{PSD}-\mathrm{z}} = {\displaystyle \frac{{\Delta d}_{\mathrm{z}}}{\sin \beta }}$$

(13)

Combining Equations (11)–(13) yields the following relation:

$$\begin{gathered} \Delta X_{\mathrm{PSD}-\mathrm{x}} = 2{\displaystyle \frac{\cos \theta \sin \left(\beta +\theta -{\theta }^{\prime }\right)}{\cos {\theta }^{\prime } \sin \beta }}{\Delta x}_{\mathrm{P}\mathrm{S}\mathrm{D}}, \Delta X_{\mathrm{PSD}-\mathrm{z} }= 2{\displaystyle \frac{\cos \theta \cos \left(\beta +\theta -{\theta }^{\prime }\right)}{\cos {\theta }^{\prime } \sin \beta }}{\Delta z}_{\mathrm{P}\mathrm{S}\mathrm{D}}, \\ \Delta X_{\mathrm{PSD}}=\Delta X_{\mathrm{PSD}-\mathrm{x}}+\Delta X_{\mathrm{PSD}-\mathrm{z}} \end{gathered}$$

(14)

In matrix form, this relation can be written as follows:

$$\left[\begin{array}{c}\Delta X_{\mathrm{PSD}}\\ \Delta Y_{\mathrm{PSD}}\end{array}\right]=2\mathbf{T}\left[\begin{array}{c}{\Delta x}_{\mathrm{P}\mathrm{S}\mathrm{D}}\\ {\Delta y}_{\mathrm{P}\mathrm{S}\mathrm{D}}\\ {\Delta z}_{\mathrm{P}\mathrm{S}\mathrm{D}}\end{array}\right]=2\left[\begin{array}{ccc}{\displaystyle \frac{\cos \theta \sin (\beta +\theta -\theta \prime )}{\cos {\theta }^{\prime } \sin \beta }}& 0& {\displaystyle \frac{\cos \theta \cos (\beta +\theta -\theta \prime )}{\cos {\theta }^{\prime } \sin \beta }}\\ 0& 1& 0\end{array}\right]\left[\begin{array}{c}{\Delta x}_{\mathrm{P}\mathrm{S}\mathrm{D}}\\ {\Delta y}_{\mathrm{P}\mathrm{S}\mathrm{D}}\\ {\Delta z}_{\mathrm{P}\mathrm{S}\mathrm{D}}\end{array}\right]$$

(15)

where T denotes the transformation matrix that maps CCR pose increments, expressed in a single PSD coordinate frame, to the corresponding PSD spot position. In this configuration, target motion is amplified by >2× along X and Z and by 2× along Y. Theoretically, the estimation error is reduced by the corresponding factors.

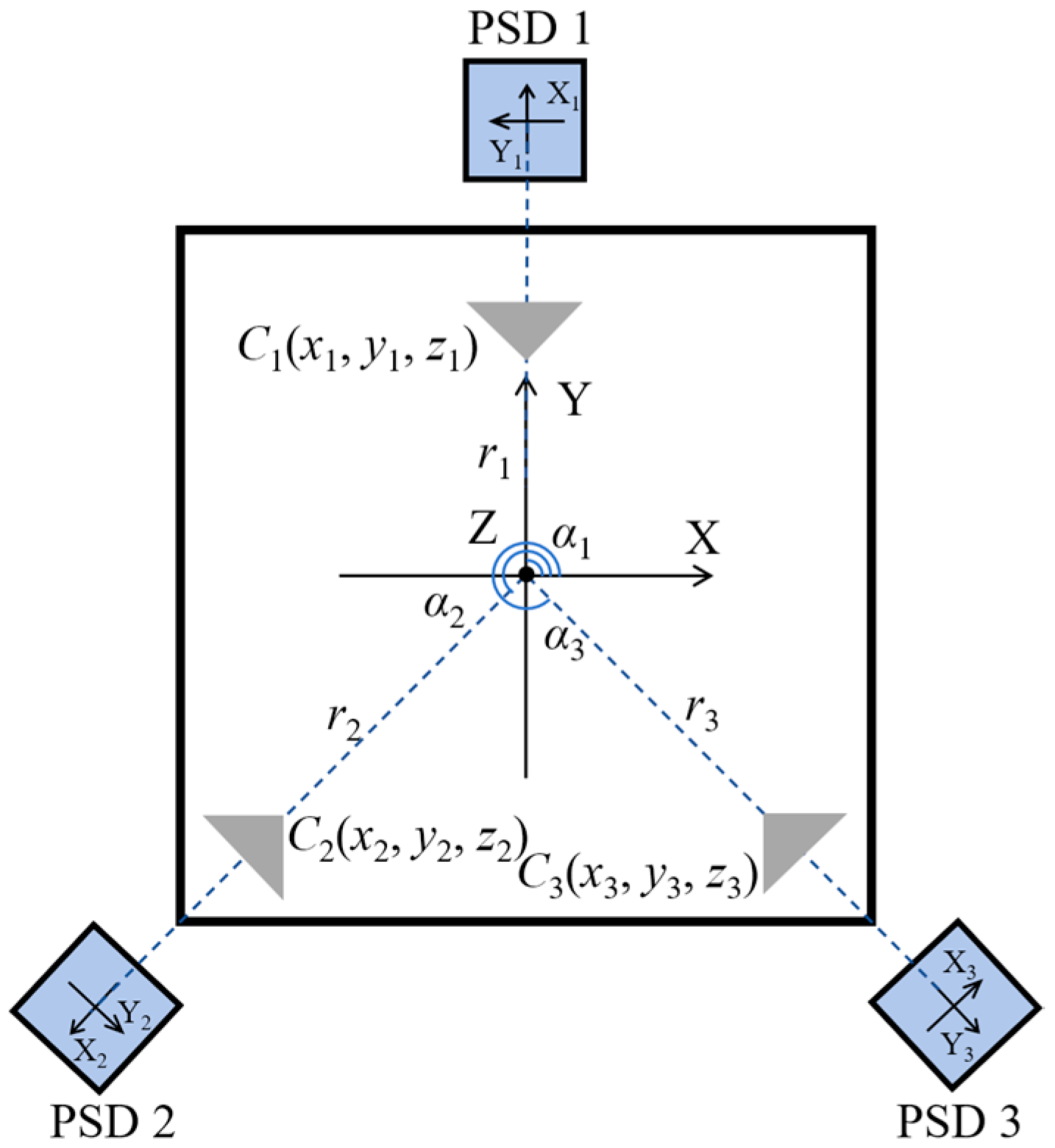
2.3. Overall Theoretical Model

Achieving 6-DoF displacement requires at least three 2D PSD units. For compactness, these sensors are preferably arranged coplanarly. Accordingly, a layout using three PSD–CCR pairs is adopted. The overall system layout is shown in Figure 4. The target may assume an arbitrary shape. Define a right-handed Cartesian frame O–XYZ with the target’s center of mass at the origin. The mounting surface is taken as a plane parallel to XOY. Three CCR blocks are mounted on the target’s base surface, with the centers of their entrance faces located at C₁(x₁, y₁, z₁), C₂(x₂, y₂, z₂), and C₃(x₃, y₃, z₃). Their projections onto XOY are C₁′(x₁, y₁, z₁), C₂′(x₂, y₂, z₂), and C₃′(x₃, y₃, z₃). Let α₁, α₂, and α₃ denote the angles between the X axis and the lines OC₁′, OC₂′, and OC₃′, respectively. Each CCR is paired with a PSD located on a plane parallel to XOY. For each PSD, the projection X_i of its X axis onto XOY coincides with the line OC_i′ that connects the corresponding projected CCR center to the origin.

Since only relative pose changes are considered, the CCR motion is represented by the following rotation matrix:

$$\left[\begin{array}{c}{\Delta x}_{i-\mathrm{P}\mathrm{S}\mathrm{D}}\\ {\Delta y}_{i-\mathrm{P}\mathrm{S}\mathrm{D}}\\ {\Delta z}_{i-\mathrm{P}\mathrm{S}\mathrm{D}}\end{array}\right]= {\mathbf{R}}_i\left[\begin{array}{c}{\Delta x}_{i-\mathrm{O}}\\ {\Delta y}_{i-\mathrm{O}}\\ {\Delta z}_{i-\mathrm{O}}\end{array}\right]=\left[\begin{array}{ccc}\cos {\alpha }_i& \sin {\alpha }_i& 0\\ -\sin {\alpha }_i& \cos {\alpha }_i& 0\\ 0& 0& 1\end{array}\right]\left[\begin{array}{c}{\Delta x}_{i-\mathrm{O}}\\ {\Delta y}_{i-\mathrm{O}}\\ {\Delta z}_{i-\mathrm{O}}\end{array}\right]$$

(16)

When the target-fixed frame translates by Δx, Δy, and Δz along the X, Y, and Z axes, respectively, the coordinates of CCR C_i update to (x_i + Δx, y_i + Δy, and z_i + Δz). When the target-fixed frame rotates about the X, Y, and Z axes by ΔRx, ΔRy, and ΔRz, the coordinates of CCR C_i transform to (x_i, y_icosΔRx − z_isinΔRx, y_isinΔRx + z_icosΔRx), (x_icosΔRy + z_isinΔRy, y_i, −x_isinΔRy + z_icosΔRy), and (x_icosΔRz − y_isinΔRz, y_icosΔRz + x_isinΔRz, z_i), respectively. Stacking these variations, the updates can be written in matrix form as follows:

$$\left[\begin{array}{c}{\Delta x}_{i-\mathrm{O}}\\ {\Delta y}_{i-\mathrm{O}}\\ {\Delta z}_{i-\mathrm{O}}\end{array}\right]={ \mathbf{P}}_i\left[\begin{array}{c}\begin{array}{c}\Delta x\\ \Delta y\\ \Delta z\end{array}\\ \begin{array}{c}\sin \Delta Rx\\ \sin \Delta Ry\\ \sin \Delta Rz\end{array}\\ \begin{array}{c}1-\cos \Delta Rx\\ 1-\cos \Delta Ry\\ 1-\cos \Delta Rz\end{array}\end{array}\right]=\left[\begin{array}{ccccccccc}1& 0& 0& 0& z_i& {-y}_i& 0& x_i& x_i\\ 0& 1& 0& {-z}_i& 0& x_i& y_i& 0& y_i\\ 0& 0& 1& y_i& {-x}_i& 0& z_i& z_i& 0\end{array}\right]\left[\begin{array}{c}\begin{array}{c}\Delta x\\ \Delta y\\ \Delta z\end{array}\\ \begin{array}{c}\sin \Delta Rx\\ \sin \Delta Ry\\ \sin \Delta Rz\end{array}\\ \begin{array}{c}1-\cos \Delta Rx\\ 1-\cos \Delta Ry\\ 1-\cos \Delta Rz\end{array}\end{array}\right]$$

(17)

Combining Equations (15)–(17) yields the following relation:

$$\left[\begin{array}{c}\Delta X_{1-\mathrm{PSD}}\\ \Delta Y_{1-\mathrm{PSD}}\\ \Delta X_{2-\mathrm{PSD}}\\ \Delta Y_{2-\mathrm{PSD}}\\ \Delta X_{3-\mathrm{PSD}}\\ \Delta Y_{3-\mathrm{PSD}}\end{array}\right]=2·{\mathbf{M}}_{6\times 9}·{\mathbf{N}}_{9\times 9}·{\mathbf{O}}_{9\times 9}·\left[\begin{array}{c}\begin{array}{c}\Delta x\\ \Delta y\\ \Delta z\end{array}\\ \begin{array}{c}\sin \Delta Rx\\ \sin \Delta Ry\\ \sin \Delta Rz\end{array}\\ \begin{array}{c}1-\cos \Delta Rx\\ 1-\cos \Delta Ry\\ 1-\cos \Delta Rz\end{array}\end{array}\right]$$

(18)

Here, M denotes the transformation matrix that maps CCR coordinates expressed in a PSD frame to the corresponding PSD spot position; N maps the object frame to each PSD frame; and O maps object 6-DoF increments to CCR displacements expressed in the object frame, specifically as follows:

$$\mathbf{M}={\left[\begin{array}{ccc}{\mathbf{T}}_{2\times 3}& 0& 0\\ 0& {\mathbf{T}}_{2\times 3}& 0\\ 0& 0& {\mathbf{T}}_{2\times 3}\end{array}\right]}_{6\times 9}, \mathbf{N}={\left[\begin{array}{ccc}{\mathbf{R}}_{1 3\times 3}& 0& 0\\ 0& {\mathbf{R}}_{2 3\times 3}& 0\\ 0& 0& {\mathbf{R}}_{3 3\times 3}\end{array}\right]}_{9\times 9}, \mathbf{O}={\left[\begin{array}{c}{\mathbf{P}}_{1 3\times 9}\\ {\mathbf{P}}_{2 3\times 9}\\ {\mathbf{P}}_{3 3\times 9}\end{array}\right]}_{9\times 9}$$

(19)

A theoretical correspondence has been established between the PSD spot pattern and the displacement induced by the target’s 6-DoF motion. For fixed CCR placement on the target and a fixed incidence angle, the transformation matrices M, N, and O are determined. Consequently, the PSD spot displacement follows directly from the target’s 6-DoF motion. In practice, the inverse problem must be solved by infering the target’s 6-DoF motion from the PSD spot displacement. The composite mapping 2·M·N·O has a dimension of 6 × 9, so the system is underdetermined (not of full column rank), and the unknowns are nonlinearly coupled, which precludes a direct solution. The terms sinΔRx, sinΔRy, and sinΔRz and 1 − cosΔRx, 1 − cosΔRy, and 1 − cosΔRz are correlated; dimensionality reduction can be used to decouple them [46,47].

In practice, small rotations permit the small-angle approximation [48,49], with sinΔRx ≈ ΔRx, sinΔRy ≈ ΔRy, and sinΔRz ≈ ΔRz, and cosΔRx ≈ 1, cosΔRy ≈ 1, and cosΔRz ≈ 1. Substituting these approximations into the unknowns yields are as follows:

$$\left[\begin{array}{c}\begin{array}{c}\Delta x\\ \Delta y\\ \Delta z\end{array}\\ \begin{array}{c}\sin \Delta Rx\\ \sin \Delta Ry\\ \sin \Delta Rz\end{array}\\ \begin{array}{c}1-\cos \Delta Rx\\ 1-\cos \Delta Ry\\ 1-\cos \Delta Rz\end{array}\end{array}\right]~\left[\begin{array}{c}\begin{array}{c}\Delta x\\ \Delta y\\ \Delta z\end{array}\\ \Delta Rx\\ \Delta Ry\\ \Delta Rz\\ \begin{array}{c}0\\ 0\\ 0\end{array}\end{array}\right]$$

(20)

After eliminating the zero entries, the 3 × 9 P_i reduces to a 3 × 6 matrix Q_i; the resulting relation is as follows:

$${\mathbf{Q}}_{\mathrm{i}}=\left[\begin{array}{cccccc}1& 0& 0& 0& z_i& {-y}_i\\ 0& 1& 0& {-z}_i& 0& x_i\\ 0& 0& 1& y_i& {-x}_i& 0\end{array}\right]$$

(21)

Accordingly, the transformation matrix 9 × 9 O reduces to 9 × 6 O₁ as follows:

$${\mathbf{O}}_{1 9\times 6}={\left[\begin{array}{c}{\mathbf{Q}}_1\\ {\mathbf{Q}}_2\\ {\mathbf{Q}}_3\end{array}\right]}_{9\times 6}$$

(22)

At this stage, Equation (18) takes the following form:

$$\left[\begin{array}{c}\Delta X_{1-\mathrm{PSD}}\\ \Delta Y_{1-\mathrm{PSD}}\\ \Delta X_{2-\mathrm{PSD}}\\ \Delta Y_{2-\mathrm{PSD}}\\ \Delta X_{3-\mathrm{PSD}}\\ \Delta Y_{3-\mathrm{PSD}}\end{array}\right]=2·\mathbf{M}·\mathbf{N}·{\mathbf{O}}_1·\left[\begin{array}{c}\begin{array}{c}\Delta x\\ \Delta y\\ \Delta z\end{array}\\ \Delta Rx\\ \Delta Ry\\ \Delta Rz\end{array}\right]$$

(23)

Therefore, the following relation holds:

$$\left[\begin{array}{c}\begin{array}{c}\Delta x\\ \Delta y\\ \Delta z\end{array}\\ \Delta Rx\\ \Delta Ry\\ \Delta Rz\end{array}\right]={\displaystyle \frac{1}{2}}·{\left(\mathbf{M}·\mathbf{N}·{\mathbf{O}}_1\right)}^{-1}\left[\begin{array}{c}\Delta X_{1-\mathrm{PSD}}\\ \Delta Y_{1-\mathrm{PSD}}\\ \Delta X_{2-\mathrm{PSD}}\\ \Delta Y_{2-\mathrm{PSD}}\\ \Delta X_{3-\mathrm{PSD}}\\ \Delta Y_{3-\mathrm{PSD}}\end{array}\right]$$

(24)

Therefore, the following relation holds. Substituting the PSD spot displacement vector into the preceding relation enables estimation of the 6-DoF displacement components.

3. Results

3.1. Single PSD–CCR Experiment

The positioning accuracy of the proposed single-configuration PSD–CCR setup was first validated. The ground-test setup is shown in Figure 5a. In the experiments, a W204 two-dimensional (2D) PSD and a WG200 signal processor (Lightsensing, Inc., Beijing, China) were used. The laser source was a 650 nm, 5 mW diode module (Lianxing Electronic Technology, Inc., Shanghai, China). The reflective element was a silver-coated prism with a 25.4 mm diameter (Choujiang Optoelectronic Instrument Technology, Inc., Jiaxing, China). Motion was provided by a five-degree-of-freedom (5-DoF) stage (Beijing Optical Century Instrument, Inc., Beijing, China) with a linear repeatability of 0.1 µm and rotational repeatability of 0.0003°. In this test, the CCR was fixed to a 5-DoF displacement stage. The PSD and laser were mounted on an optical plane parallel to the stage; the laser was set at 30° relative to the horizontal. The stage was adjusted to center the retro-reflected spot on the PSD. A faint secondary spot, caused by reflections from the PSD protective window, was observed near the main spot. Nevertheless, the spot morphology remained stable throughout stage motion, and the secondary spot had no significant effect on position–measurement accuracy [50].

Because oblique incidence yields higher magnification along the Z axis, the usable Z-range is smaller than that along X/Y. The 5-DoF stage was translated by ±3 mm (X), ±3 mm (Y), and ±1.5 mm (Z). Positions were sampled every 0.5 mm, and 100 readings were collected per point. Results for the CCR-based (retro-reflection) solution and the direct (non-retro-reflective) solution are shown in Figure 5b. Blue markers denote the mean of 100 measurements for the CCR-based solution, while orange markers denote the mean for the direct solution. Error bars are scaled by 100× to visualize the standard deviation distribution.

For both methods, the mean deviation at each position remained within 3 μm of the theoretical value. Because the CCR magnifies object displacement, error suppression was observed along all three axes (X, Y, Z). The standard deviation of repeatability decreased by 45.65% (X), 43.42% (Y), and 65.87% (Z).

To assess the influence of CCR rotation on overall accuracy, a rotation-sensitivity test was performed. The CCR was rotated by 1° about the X, Y, and Z axes (Z axis rotation implemented using a 90° adapter fixture). Errors were compared with the no-rotation case over ±3 mm (X), ±3 mm (Y), and ±1.5 mm (Z). Over the entire motion range, the maximum errors with rotation were 4.62 μm (X), 4.51 μm (Y), and 3.16 μm (Z). These correspond to 0.154%, 0.150%, and 0.211% of full scale. The pre- and post-rotation mean position estimates differ by no more than 2.835 µm on the X/Y axes and 2.158 µm on the Z axis—below the full-range repeatability threshold. Therefore, within ±1°, CCR rotation has a negligible effect on refraction.

3.2. Overall Experiment

The overall experiment using the 3×PSD–CCR configuration is shown in Figure 6a. The CCRs were mounted to a 5-DoF displacement stage via an optical plate, and the PSDs were mounted on a second optical plate parallel to the first. In the object frame, the three CCRs were located at C₁(72.5, 72.5, −18.3), C₂(−72.5, 72.5, −18.3), and C₃(0, −105, −18.3). The stage position was adjusted until each retro-reflected spot was centered on its corresponding PSD. Subsequently, the stage was commanded to move by ±1.5 mm along X/Y/Z and ±0.5° about RX/RY/RZ. During angular measurements, because the stage pivot does not coincide with the object’s center, the motion induced by the stage can be decomposed into a rotation about the object’s center plus a translation. As rotation and translation are measured independently, the translational component does not, in principle, bias the rotational results. In practice, a compensating translation is applied during rotation to correct the offset between the rotation center and the object’s center of mass. Experimental procedures are as follows:

(1) Sweep the stage back and forth along the X, Y, and Z axes over ±1.5 mm with 0.3 mm steps.

(2) Sweep about the X, Y, and Z axes over ±0.5° with 0.1° steps. Because the stage provides rotation of only two axes, after completing the RY test, rotate the relative orientation of the stage and the object by 90° to measure the RX axis.

The results are shown in Figure 6b. For translation along X/Y/Z, the repeatability errors are 5.28 μm, 5.89 μm, and 4.39 μm, respectively. For rotation about RX/RY/RZ, the repeatability errors are 0.0027°, 0.0024°, and 0.0020°, respectively. These results validate that the proposed compact method achieves high positioning accuracy, enabling effective implementation of compact noncontact 6-DoF displacement measurement. The approach meets the stringent requirements of applications such as space microgravity vibration isolation.

4. Discussion

Much of the existing work on PSD-based 6-DoF displacement measurement uses direct-reflection configurations, which require a large spatial footprint. The refractive configuration proposed here markedly reduces the spatial footprint. Because PSD dimensions vary across studies, a universal quantitative spatial–occupancy ratio for all configurations is not meaningful. For a given PSD size, the spatial–occupancy ratio of a refractive configuration can be obtained from Equation (8).

It is also essential that the refractive configuration retain competitive measurement accuracy while achieving a superior spatial–occupancy ratio.

Table 1. Performance comparison of different configuration measurement systems.

Configuration Type		Unit Position Accuracy (×10−3)	Unit Angular Accuracy (×10−3)
Fu et al. [51]	Normal incidence	3.02	5.67
Chang et al. [52]	Normal incidence	30.00	5.00
Wang et al. [53]	Normal incidence	4.15	14.25
Kim et al. [48]	Normal incidence	10.00	22.22
Zhao et al. [54]	Normal incidence	7.73	4.45
Ours	Refraction	3.93	5.40

compares representative PSD-based 6-DoF results from the literature. Because accuracy and range are typically correlated (larger ranges entail larger errors), measurement error is normalized by the range to yield a dimensionless precision metric (error/range). Under this normalization, refractive configurations rank among the best in reported precision.

Systematic errors in this configuration are classified by subsystem into those originating from the light source, the CCR, and the PSD with its signal-processing electronics.

Light source errors include optical power fluctuations, beam drift, and mounting-tilt misalignment. For power fluctuations alone—assuming all other characteristics are ideal—the PSD spot position remains constant and the measurement is unaffected. Beam drift is negligible over short durations; over long durations it becomes non-negligible and must be compensated. Mounting-tilt error has the same qualitative effect as the rotation analyzed in Section 3.1. When the tilt is below ~1°, refraction-induced effects are small and, per Section 3.1, can be neglected. As the tilt approaches or exceeds ~1°, measurement precision degrades appreciably.

Errors associated with the CCR include alignment errors and refractive index variations. For alignment errors, pure translation preserves ray parallelism and is therefore benign for the measurement. In contrast, rotational misalignment behaves as analyzed in Section 3.1. When the misalignment angle approaches or exceeds ~1°, it can couple with other angular terms and modify the refraction geometry, producing non-negligible measurement error. The CCR’s refractive index varies with temperature. Consequently, temperature sensation and compensation are required in environments with appreciable temperature swings.

PSD-side errors primarily include measurement noise and alignment errors. Measurement noise is the dominant uncertainty rather than a systematic error; it includes dark current noise and ambient light noise. Dark current offset can be removed by acquisition settings or post-processing, and ambient light noise can be suppressed with wavelength-matched band-pass filters. PSD tilt introduces scale and offsets errors in the inferred spot displacement, degrading accuracy and thus requiring tight alignment control.

To further suppress errors, we proceeded as follows: (1) improve mechanical alignment to minimize angular errors in the laser source, CCR, and PSD; (2) implement temperature monitoring and compensation for thermal expansion and refractive index drift; (3) select PSDs with lower dark current and higher intrinsic accuracy; and (4) add wavelength-appropriate optical filters to reject ambient light.

Future work will use the 6-DoF displacement–measurement system and the accelerometers described herein as sensing elements for active vibration control of the test article. These sensors will be integrated with actuators to enable active vibration suppression. In parallel, temperature effects on the measurement system will be characterized and compensated to further improve measurement accuracy.

5. Conclusions

To meet pose-control and vibration-suppression requirements in confined spaces, a compact, noncontact 6-DoF displacement-sensing method based on laser reflection and a PSD with an adjustable incidence angle is proposed and experimentally validated. A novel layout—in which the PSD active area is parallel to the mounting plane of a CCR—replaces the conventional 45° oblique configuration. This layout converts the vertical space constraint from width-limited to thickness-limited, reducing the overall volume to 10.4% of that of a conventional layout. It achieves >2× geometric magnification along the X and Z axes and ≈2× along the Y axis, which theoretically reduces estimation error by the same factors. Based on geometric constraints and optical path relations, an analytical one-to-one mapping is derived between the target’s 6-DoF displacement and the PSD spot displacement. The model is linearized under the small-angle approximation to yield a stable closed-form solution.

Experiments show that, in the single-configuration setup, when the displacement stage scans ±3/±3/±1.5 mm along X/Y/Z, the mean repeatability error is ≤3 μm for both the retro-reflection-based solution and the direct (non-retro-reflective) solution. Geometric amplification by the CCR significantly suppresses error, reducing the repeatability standard deviation by 45.65% (X), 43.42% (Y), and 65.87% (Z). Because of oblique incidence, the Z axis exhibits higher amplification and a reduced measurement range. A rotational-sensitivity test further shows that, after rotating the CCRs by 1° about the X/Y/Z axes, the maximum error over the full linear motion range is 4.62/4.51/3.16 μm (0.154%/0.150%/0.211% of full scale), indicating negligible rotational effects. In integrated pose-reconstruction experiments using CCRs, repeatability errors reach 5.28/5.89/4.39 μm for X/Y/Z and 0.0027°/0.0024°/0.0020° for RX/RY/RZ over ±1.5 mm translation and ±0.5° rotation, quantitatively validating 6-DoF capability with micrometer-level translation and millidegree-level rotation. These results provide an engineering-ready pathway for high-bandwidth pose sensing in compact spaces.

Current limitations arise primarily from the Z axis range and from long-term calibration and thermal stability. Future work may include multi-scale variable magnification via optimizing β and folded optical paths; incorporation of self-calibration, thermal drift compensation, and uncertainty propagation analysis; and the use of anti-reflective coatings and digital filtering to further improve the signal-to-noise ratio and robustness.