Abstract
The control of mechanical effects, such as shock waves, induced by ultrashort laser pulses in water is crucial for applications in biomedicine and material processing. However, optimizing these effects requires a detailed understanding of how laser parameters, particularly pulse duration, influence the underlying energy deposition mechanisms. This study systematically investigates the dependence of shock wave amplitude on fluence (up to 10 J/cm2) and pulse duration (200 fs to 10 ps) of near-infrared laser pulses under tight focusing conditions (Numerical aperture NA = 0.42), using a combined experimental and numerical approach based on the dynamical rate equation model. Our key finding is that the shock wave amplitude is governed by the total kinetic energy of the electrons in the laser-induced plasma, leading to a distinct maximum at approximately 5 ps (confidence interval: 4.5–5.5 ps) and saturation at fluences ~7 J/cm2. This optimum arises from a balance between the increasing effectiveness of avalanche ionization for longer pulses and the competing effects of electron recombination and reduced photoionization efficiency. Consequently, these results identify a practical parameter window—pulse durations of 4–6 ps at moderate fluences—for optimizing laser-induced mechanical effects in applications such as laser surgery in aqueous media.
1. Introduction
Advances in laser technology have made short and ultrashort pulse lasers practical tools for diverse fields like material processing, medicine, and chemistry, moving them far beyond their origins as purely scientific instruments [1,2,3,4,5]. The interaction of ultrashort laser pulses (USLP) with water is particularly significant from an applied perspective, especially for studying the mechanisms of USLP effects on biological tissues (due to the high water content in biological tissues) [6,7], as well as for chemical reactions initiated by laser-induced plasma (such as the formation of oxygen, hydrogen, and hydrogen peroxide) [8,9,10,11].
In the absence of absorption, the dynamics of ultrashort laser pulse (USLP) interaction with water is multi-stage [12,13,14]. Initially, seed electrons are generated through photoionization processes (multiphoton and tunneling ionization). For sufficiently long pulses (over 100 fs), avalanche ionization becomes significant, ultimately leading to the formation of an electronic plasma with a concentration on the order of 1020–1022 cm−3 and energies up to 10 eV [15,16], for example, numerical simulations demonstrate that in SiO2, the threshold for a Ti:Sapphire laser would be twice as high for a 100 fs pulse, and an order of magnitude higher for a 1 ps pulse, if avalanche ionization were not present [17]. These calculations also demonstrate that the threshold fluence increases from ~1 J/cm2 for a 30 fs pulse to ~5 J/cm2 for a 1 ps pulse. The optical breakdown threshold, which signifies the onset of plasma formation, can be determined experimentally by observing the transition from linear to nonlinear transmission due to absorption in the laser-induced plasma [18]. Due to the high pressures and temperatures within the electronic plasma, it begins to expand rapidly and concurrently heats the water up to temperatures of approximately 105 K [19,20]. This process leads to the generation of shock waves (with pressures ~GPa) and the formation of cavitation bubbles [21,22,23,24]. The shock waves propagate quickly—within microseconds—away from the laser-irradiated region, while the cavitation bubbles undergo a prolonged cycle of growth, collapse, and re-growth, as thoroughly described in reviews [12,23,25]. All experimental investigations of shock waves presented here were performed at fluences significantly above the breakdown threshold to ensure robust plasma formation.
Nevertheless, the dynamics of shock waves and cavitation are determined by the parameters of the electronic plasma, which in turn are influenced by the characteristics of the laser pulses, such as energy, duration, wavelength, focusing conditions, and so on. Previous experimental and numerical studies have explored the dependence of mechanical post-effects (shock waves and cavitation bubbles) and laser-induced plasma on laser pulse duration [26], wavelength [16], and aberrations arising during the focusing of the laser pulse in the medium [27].
Modern ultrashort laser pulse generation systems are based on chirped pulse amplification (CPA) techniques, which allow relatively straightforward adjustment of the pulse duration by shifting the diffraction grating in the compressor. This provides the ability to modify the ratio between multiphoton and avalanche ionization processes [28]. Under the tight focusing conditions relevant to this study (NA ~0.42, NIR wavelength range, non-chirped pulses, fluences lower than 200× Fth), the shortest laser pulses provide the highest spatial precision for interaction, albeit with reduced energy transfer to mechanical post-effects like shock waves. Conversely, longer pulses exhibit diminished spatial confinement but achieve significantly higher energy coupling into these mechanical phenomena. [29,30]. Therefore, the capability to smoothly vary the pulse duration enables the identification of an optimal balance between controllability and energy efficiency. However, to better understand the underlying reasons for these observed dependencies, numerical modeling is necessary.
In numerical simulation, the interaction of femtosecond laser pulses with dielectrics, including water, two primary approaches are actively employed: the single rate equation (SRE) model and the multiple rate equation (MRE) model [31]. The SRE model describes the dynamics of free charge carriers (e.g., electrons in the conduction band) with a single equation, where the evolution of the carrier density under laser irradiation is limited by average parameters. This approach is simple and requires relatively low computational resources; however, it is insufficient for accurately capturing the gradual heating of electrons and the initiation of avalanche ionization for laser pulses shorter than 100 fs [17].
Unlike the SRE model, the MRE model employs multiple coupled differential equations to track the dynamics of electron distribution across energy levels [29,32]. This allows for the simulation of energy accumulation processes within the electron cloud, as well as ionization mechanisms such as multiphoton and avalanche ionization. Additionally, the model accounts for rapid recombination of charge carriers, which is particularly important for dielectrics with wide band gaps. The MRE approach generally provides more realistic results for ultrashort laser pulses, as the primary contribution to free carrier generation arises not only from instantaneous ionization but also from the evolution of the electrons’ energy distribution over time.
For modeling the interaction of ultrashort laser pulses with water (either in liquid form or as ice), both SRE and MRE models have been employed [29,33]. When femtosecond pulses are applied, optical breakdown occurs after reaching a threshold intensity. In this process, electron heating followed by avalanche ionization plays a crucial role in the generation of dense plasma. Recent studies utilize various versions of rate equations to reconcile theoretical calculations with experimental threshold values—applicable to both solid dielectrics and water in different phases [29,32,34].
The DRE (Dynamical Rate Equations) model was proposed to simplify and enhance computational efficiency in simulating plasma formation dynamics under ultrashort laser pulses. It maintains physical correctness by accounting for the delay associated with avalanche (breakdown) ionization. Unlike the SRE model, where ionization occurs instantaneously, and the MRE model, which considers electron heating through a multi-level system of differential equations, the DRE introduces an effective delay—a phase during which electrons are heated to the critical energy required to initiate avalanche ionization. This delay is implemented via a parameterized function that determines the fraction of electrons capable of triggering further ionization processes. This approach allows accurate reproduction of the experimental breakdown threshold and the plasma formation dynamics across various pulse durations and intensities, with nearly the same accuracy as the MRE model but with reduced computational cost and greater ease of calibration based on experimental data. Therefore, in this work, we employed the DRE model for numerical simulations [17].
In total, we employed shadow photography to assess the pressure at the shock wave front, a laser pulse transmission technique to determine the femtosecond laser breakdown threshold, and a hydrophone to measure the amplitude of the shock wave in the far field. We systematically varied the laser pulse energy and duration, which revealed that, with increasing pulse energy, the shock wave amplitude saturates, and the maximum amplitude is observed for pulses approximately 4–6 ps in duration. Numerical simulation demonstrated that the shock wave amplitude directly depends on the total kinetic energy of the electron plasma. The peak dependence on time is governed by the increasing efficiency of shock ionization at longer pulse durations (at fixed energy), as well as by the finite electron recombination time combined with a reduction in the number of seed electrons generated via photoionization.
The aim of the study was to experimentally and numerically investigate the influence of ultrashort laser pulse durations ranging from 200 fs to 10 ps on shock wave generation in water under tight focusing conditions, as well as to identify the conditions that maximize formation efficiency using the DRE model.
2. Materials and Methods
In the experiments, a femtosecond laser system (TETA-20) was used to generate laser-induced plasma. The full experimental setup is presented in Figure 1. The system operates at a wavelength of 1030 nm, with a laser pulse energy of up to 1 mJ, a repetition rate of up to 200 kHz, and a minimum pulse duration of 200 fs. To avoid the influence of preceding pulses, the experiments were performed at a repetition rate of 10 Hz (since the effects of previous pulses become significant at frequencies above 20 Hz). An increase in the repetition rate led to increased fluctuations in both the transmission and hydrophone signals (from ~3% at 10 Hz to ~7% at 20 Hz), as shown in Supplementary Materials, Figure S1. Furthermore, quasi-periodic patterns were observed in these signals. Time-resolved shadowgraphy revealed that at frequencies above ~20 Hz, residual bubbles from the collapse of previous cavitation events persist in the focal volume. The subsequent laser pulse interacts with these residual bubbles, which is the likely cause of the increased signal fluctuations.
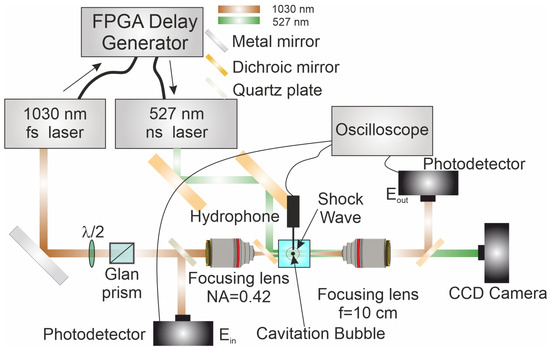
Figure 1.
Experimental Setup. Experimental setup and diagnostics. A 1030 nm femtosecond pump laser impulse (brown) is polarization-attenuated (λ/2 + Glan prism) and tightly focused into a water cell by a high-NA objective (OptoSigma PAL-20, NA = 0.42). A 527 nm nanosecond probe (green) is combined/separated with a dichroic mirror and imaged with an f = 10 cm lens onto a CCD camera for shadowgraphy of the cavitation bubble and shock wave. An FPGA delay generator sets the pump–probe time delay; a quartz plate provides fine path-length/dispersion compensation. Photodetectors record incidents and transmitted energies Ein and Eout. A needle hydrophone is positioned orthogonally near the focus to capture the pressure waveform.
For smooth variation in the laser pulse energy, a half-wave plate and a Glan prism were placed in the optical path. The pulse duration was varied by adjusting the position of a diffraction grating mounted on a motorized linear translator. Depending on the direction of the grating movement, the laser pulses acquired a chirp; positive chirp pulses are denoted with a plus sign (+), and negatively chirped pulses with a minus sign (−).
The focusing of the laser pulse into a water cuvette (length 1 cm) was achieved using a microobjective OptoSigma Pal-20 with a numerical aperture (NA) of 0.42 and a focal length of 15 mm. The laser beam had an M2 value of 1.2 and a focal spot diameter of 3.2 ± 0.5 μm, as estimated by re-imaging the focal plane onto a CCD array within a confocal microscope setup. Collimation was performed with an identical objective. The laser pulse energy before entering the cuvette and the energy of the pulse transmitted through the cuvette were monitored using germanium photodiodes (OD-1B, Avesta, Moscow, Russia). A small portion (<4%) of the beam was sampled using thin wedge-shaped quartz plates installed in the optical path and directed onto the photodiodes. The system was calibrated as follows: the photodiodes were first characterized to ensure operation in their linear response regime. A calibrated power meter (QE8SP, Gentec-EO, Quebec, QC, Canada) was then placed sequentially at the sample and detector positions to establish a precise correlation between the recorded oscilloscope voltage and the actual pulse energy (in µJ). This calibration was performed across the entire range of pulse energies and durations used in the experiment. The voltage signals from the photodetectors were recorded with a GDS 72304 four-channel digital storage oscilloscope (GW-Instek, New Taipei City, Taiwan) and transmitted to a personal computer (PC) via a COM port for further analysis.
We calculated the total optical losses in the system to be approximately 25%, attributable to the finite transmission of the objective lenses and the quartz windows of the optical cell, as well as aberrations from refractive index mismatch [35]. These aberrations also lead to a longitudinal elongation of the focal volume, which was accounted for in our analysis. The method for calculating optical aberrations is briefly outlined in the Supplementary Materials.
Since the photodetectors operated in the linear response regime, they were calibrated using a power meter QE8SP (Gentec-EO, Quebec, QC, Canada). The amplitude of the shock wave in the far field was measured using a needle hydrophone (Precision Acoustics, Dorchester, UK) with a 1 mm diameter, equipped with a preamplifier. The hydrophone had a bandwidth of 10 kHz to 50 MHz and a sensitivity of −241 dB re 1 V/μPa. It was positioned at a distance of 2.5 mm from the laser interaction point, with its axis oriented at a 90-degree angle to the optical axis to minimize the influence of direct reflections onto the active element.
The voltage signal from the hydrophone was captured by a GDS 72304 oscilloscope (GW-Instek, New Taipei City, Taiwan). To obtain the absolute pressure, we calibrate the values on the pressure retrieved from the shadowgrams. Absolute pressure was obtained by anchoring the hydrophone voltage to the shadowgraph-derived pressure (method uncertainty ~10%); since no transfer-function deconvolution was applied, the hydrophone bandwidth primarily limits the retrieved peak. Shadow images were captured using a HuatengVision CCD camera, with a spatial resolution of approximately 3 μm per pixel. The velocity and pressure at the shock wave front were determined using the shadow photography method. For this, the nanosecond LaserTech-527 laser system (Laser Components, Moscow, Russia) was synchronized with the femtosecond laser system using the FPGA (field programmed gate array), as described in [36]. By varying the delay between the main (pump) and probe pulses, the diameter of the shock wave front was recorded (see Figure 2b), which allowed for the calculation of its velocity. Subsequently, using the equations of state, the pressure at the shock wave front was reconstructed—this procedure is described in detail in [37]. The uncertainty of the method is about 10%.
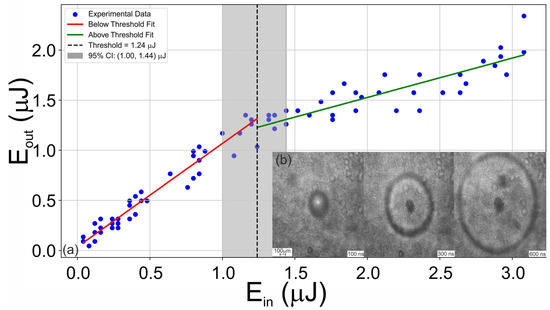
Figure 2.
Transmission threshold and shock visualization. (a) Dependence of the laser pulse energy transmitted through the water cuvette on the input energy for a pulse duration of 2 ps. The optical breakdown threshold (vertical dashed line) was determined using a segmented linear regression, with the 95% confidence interval derived from bootstrap analysis (n = 1000). (b) Shadow images of the shock wave during laser irradiation (10 J/cm2, 2 ps) of water at various time intervals.
To determine the plasma formation threshold, an Transmittance method was employed, which involves recording the dependence of the energy of the laser pulse transmitted through the cuvette (Eout) on its input energy (Ein) [18]. Below the plasma formation threshold, this dependence is linear, as shown in Figure 2a. When plasma is generated, it begins to absorb the laser radiation energy, leading to a change in transmission that allows for the threshold to be identified. These dependencies were recorded for all investigated laser pulse durations. The optical breakdown threshold was determined using segmented linear regression analysis. This method identifies the optimal breakpoint in the absorbed energy versus incident energy data by fitting two linear regimes—one below and one above threshold—and selecting the transition point that minimizes the combined residual error. The threshold value is reported to have a 95% confidence interval derived from bootstrap resampling (n = 1000 iterations).
For numerical modeling, the DRE (Dynamical Rate Equations) model was employed. Within the DRE framework, the plasma density concentration ρ can be described following Equations (1) and (2) as follows [17]:
where γu is the photon absorption rate by electrons at level u, γr is the recombination rate, υfi is the photoionization rate, ρu is density at level u and ξ can be considered as
where erfc(r) is the error function, Ec is the critical energy, and Ekin is the average kinetic energy of electrons at temperature T, given by Ekin = 3kbT/2, kb being Boltzmann’s constant. For more detailed information, this model is discussed in [17]. The parameters used in the model are presented in Table 1.

Table 1.
Parameters used in simulation and mean sensitivity of Fth. The full sensitivity report is presented in Supplementary Materials.
3. Results and Discussion
First, we examine how the amplitude of the shock wave depends on the laser pulse energy and duration. It is evident that higher pulse energies transfer more energy to the medium (though not in a proportional percentage); however, experiments show that at a fixed duration, the shock wave amplitude Asw saturates at certain energy levels, meaning further increases in energy do not lead to a corresponding increase in amplitude. This saturation is clearly illustrated in the 2D heat map of Asw(F, τ), where F is the laser fluence and τ is the pulse duration, as shown in Figure 3a. The saturation fluence is defined as the value at which the shock wave amplitude reaches 90% of its maximum plateau level.
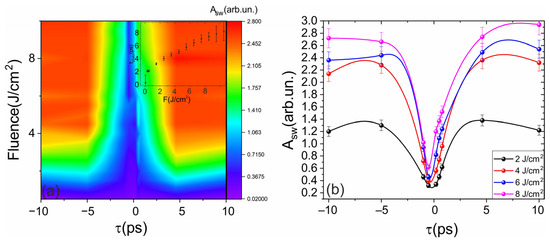
Figure 3.
Shock-wave amplitude as a function of pulse duration and fluence. (a) 2D heat map illustrating the dependence of the laser-induced shock wave amplitude Asw on pulse duration (τ) and fluence (F). The inset marks the τ where Asw reaches 90% of its plateau. The saturation fluence is defined as the value at which the shock wave amplitude reaches 90% of its maximum plateau level. The negative time durations denotes negative chirp. (b) Sections of (a) at fixed F highlight the ∼5 ps maximum and its evolution with F; shaded bands show confidence intervals where applicable. The sign of τ encodes chirp (“+”, positive; “–”, negative).
Conversely, the dependence of the shock wave amplitude on laser pulse duration at a fixed fluence exhibits a pronounced maximum at approximately 4–6 ps for fluences less than 7 J/cm2 (see Figure 3b). Increasing the laser pulse energy shifts this maximum toward longer durations, as it is presented in the inset in Figure 3a. It is also important to note that the sign of the chirp of the laser pulse has little effect on the observed phenomena, which is likely related to the relatively low group velocity dispersion at the used wavelength. The observed increase in shock wave amplitude with increasing pulse duration can be explained by changes in the role of avalanche ionization [42]. However, in this case, a distinct extremum is not clearly evident, so explaining this effect requires referring to the results of numerical modeling.
First, it was necessary to verify the employed model. This was achieved by comparing the experimentally obtained and numerically simulated optical breakdown thresholds. The methodology for measuring the optical breakdown threshold is described in Section 2. The dependence of the breakdown thresholds on pulse duration is presented in Figure 4.
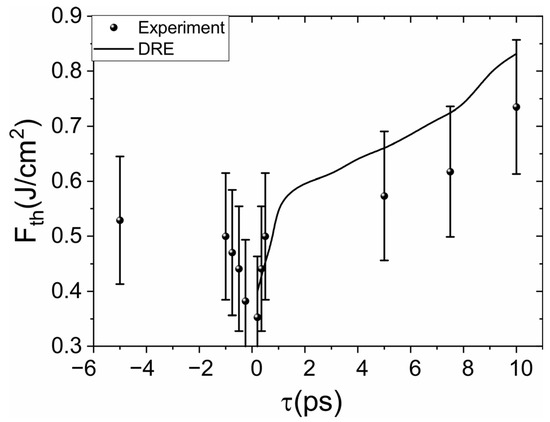
Figure 4.
Dependence of the optical breakdown threshold (Fth) on laser pulse duration (τ). Points are experimental estimates with 95% CI from the segmented-fit procedure; the solid line is the DRE prediction. The sign of τ encodes chirp (“+”, positive; “–”, negative).
Figure 4 shows that the lowest breakdown threshold is achieved at the minimal pulse duration. This is because, in this case, the intensity at the focus is maximized, and in the absence of free electrons in the dielectric, photoionization plays the dominant role, which reaches its maximum (at fixed fluence) precisely for the shortest pulse duration.
Let us examine in detail the dynamics of electron plasma generation by ultrashort laser pulses, as illustrated in Figure 5. As shown in the figure, for a relatively short pulse (200 fs), photoionization plays the primary role at the leading edge of the laser pulse; subsequently, a sufficient number of photoelectrons are generated to initiate avalanche ionization. However, for relatively “long” pulses (5 ps), the efficiency of photoionization is significantly lower, and avalanche ionization dominates. It is also important to note that at times exceeding 1 ps, recombination begins to play a substantial role. As a result, the electron concentration starts to decrease after the peak of the laser pulse, which is clearly visible in Figure 5b.
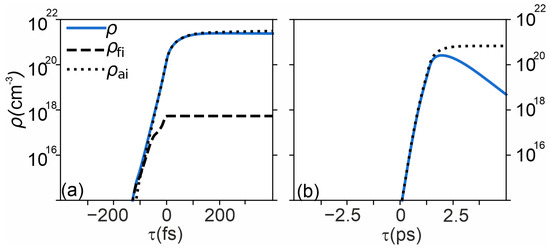
Figure 5.
Electron-plasma dynamics from the DRE model. Temporal evolution of electron density in water at F = 5 J cm−2 for (a) 200 fs and (b) 5 ps. Dashed: photoionization; dotted: avalanche ionization; solid: total (with recombination). For longer pulses, avalanche dominates; beyond ∼1 ps, recombination reduces the total electron density after the pulse peak.
Since numerical modeling provides information on the dynamics of electron plasma generation, as well as its temperature and concentration, it is possible to calculate the kinetic energy of the plasma , which is subsequently transferred to the atomic subsystem. Therefore, we assumed that the amplitude of the shock wave would be higher the greater the energy stored in the electronic subsystem. The dependence of the estimated kinetic energy and the shock wave amplitude on fluence is presented in Figure 6a. This figure demonstrates direct correlation between the total kinetic energy and the amplitude of the shock wave, the correlation analysis shows R2 = 0.837 and 95% CI is: 0.634 to 0.983.
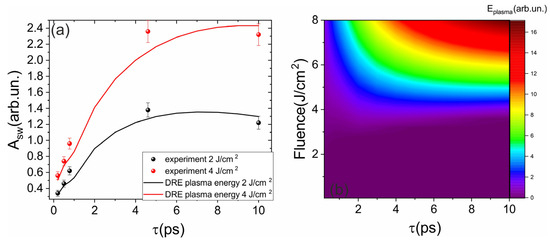
Figure 6.
(a) Dependence of the shock wave amplitude (points) and the modeled total kinetic energy of the electron plasma (line) on the laser pulse duration. (b) 2D heat maps of Ekin (F, τ), showing a maximum near ∼5 ps and saturation at higher F, mirroring Asw.
At first glance, it appears counterintuitive that a decrease in intensity with increasing pulse duration would lead to a higher shock wave amplitude. However, by examining the mechanism of shock wave generation during ultrashort laser pulse interaction with dielectrics and the plasma dynamics discussed previously, this dependence can be explained. First, the drop in electron plasma concentration with an order-of-magnitude increase in pulse duration is relatively modest (approximately a factor of 2.5). At the same time, the longer pulse duration allows for a greater interaction time between the laser pulse and the electron plasma. This enhances the plasma temperature via avalanche ionization, enabling a larger fraction of the laser pulse energy to be absorbed. Consequently, more energy is ultimately transferred to the medium. Shock wave generation occurs during the transfer of energy from the electronic to the atomic subsystem, a process that takes place on a timescale longer than 1 ps. Therefore, the pulse duration itself should not be the primary limiting factor for the shock amplitude within the studied range. It is also crucial to emphasize that for mechanical post-effects, fluence becomes a comparable, or even more relevant, metric than intensity for predicting the shock wave pressure. Therefore, the greater the energy accumulated in the electronic subsystem, the higher the shock wave amplitude. Additionally, Figure 6b shows that at a fixed fluence, there exists an “optimal” pulse duration at which the maximum total kinetic energy of the plasma electrons is achieved.
Additionally, it should be noted that at a fixed pulse duration, increasing the fluence leads to saturation of the total kinetic energy, and consequently, the amplitude of the shock wave. Further increases in pulse duration primarily result in an expansion of the plasma along the optical axis and the formation of a superfilament [43]. In this case, the shape of the shock wave transitions from spherical to cylindrical, and its amplitude saturates as the laser pulse energy continues to grow.
For processes aiming to maximize mechanical effects, such as histogenesis in laser surgery or nanoparticle synthesis via laser ablation in liquids, we identify an optimal parameter window of 4–6 ps pulse duration and 5–8 J/cm2 fluence under our experimental conditions (1030 nm, NA = 0.42). Operating within this window ensures efficient energy coupling into a shock wave while maintaining a confined plasma volume. It is crucial to delineate the boundaries of these trends. The observed saturation of shock wave amplitude and its peak versus duration are expected to break down in two key scenarios: (1) very close to the breakdown threshold, where plasma formation could be stochastic and inefficient, and (2) at very high fluences where the plasma becomes elongated into a superfilament or plume, transitioning the shock wave front from a spherical to a cylindrical geometry, which fundamentally alters its propagation and decay.
The finite bandwidth of the hydrophone, while compensated for, sets a limit on the temporal resolution of the measured pressure profile. Furthermore, potential aberration-driven changes in the focal volume, inherent to focusing through a water-glass interface with an objective, could influence the absolute energy density and thus the amplitude plateaus. We have accounted for this in our loss budget, but it remains a source of systematic uncertainty. The direct correlation between shock wave amplitude and total electron kinetic energy is strongly supported by our combined experimental and numerical data. However, we posit as a hypothesis that the peak at ~4–6 ps is due to a balance between the increasing efficiency of avalanche ionization and the growing influence of recombination. While this is the most plausible explanation given our model, future time-resolved studies of the plasma emission could provide direct validation.
Finally, we specify that our conclusions are valid within the boundary conditions of this study: near-infrared radiation (1030 nm) and tight focusing in water. Generalization to other wavelengths (e.g., in the visible or mid-IR) or different focusing geometries (e.g., loose focusing or water-immersion objectives) would require verification, as the relative roles of photoionization and avalanche ionization are wavelength-dependent, and the focal energy density is strongly NA-dependent.
4. Conclusions
In summary, we have systematically investigated the dependence of laser-induced shock wave amplitude on fluence (up to 10 J/cm2) and pulse duration (200 fs to 10 ps) for near-infrared pulses under tight focusing (NA = 0.42) using shadow photography, optoacoustic methods, and numerical modeling with dynamical rate equations. We demonstrated that the shock wave amplitude is governed by the total kinetic energy of the electrons in the laser-induced plasma. The observed maximum at approximately 5 ps (confidence interval: 4.5–5.5 ps) and 5–8 J/cm2 fluence under our experimental conditions (1030 nm, NA = 0.42) is a direct consequence of the competition between ionization mechanisms: longer pulses favor more efficient avalanche ionization, but this is ultimately limited by the finite electron recombination time and the reduced yield of seed electrons from photoionization at lower intensities. A sensitivity analysis confirmed that the position of this peak is robust against small variations in key parameters like the recombination time.
While the DRE model successfully reproduced the experimental trends after accounting for measured optical losses, its current limitation lies in the zero-dimensional treatment that neglects the spatial evolution of the plasma. A critical next step to create a fully predictive model without empirical adjustments is to couple the DRE framework with a propagation code to explicitly calculate the plasma volume and the resulting energy density. Overall, these findings identify an optimal parameter window for controlling shock waves in water and provide a mechanistic framework for optimizing laser-induced mechanical effects in liquids.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/photonics12111067/s1, Figure S1: Dependence of signals from hydrophone at frequencies 20 Hz and 10 Hz, supporting the observation that frequencies above 10 Hz lead to increased instability in transmission and hydrophone measurements due to interaction of laser pulse with residual cavitation bubbles. Figure S2. Intensity profile arising from refractive index mismatch for experimental conditions. Figure S3. Parameter Sensitivity Analysis for the Optical Breakdown Threshold. The parameter sensitivity was evaluated using a one-at-a-time (OAT) method. Each key parameter in the model (e.g., recombination time, collision time) was increased by 10% from its baseline value, and the corresponding relative change in the predicted optical breakdown threshold was calculated.
Author Contributions
Conceptualization, E.M. and V.Y.; methodology, E.M.; software, E.M.; validation, E.M. and V.Y.; formal analysis, E.M.; investigation, E.M. and N.R.; resources, E.M.; data curation, N.A. and N.R.; writing—original draft preparation, E.M.; writing—review and editing, all authors; visualization, E.M.; supervision, E.M.; project administration, E.M.; funding acquisition, E.M. All authors have read and agreed to the published version of the manuscript.
Funding
The study was supported by the grant of the Russian Science Foundation, no. 25-79-20057 as part of an experiment on the study of chemical processes under laser impact. Numerical simulation was performed with partial support within the framework of the state assignment of the Kurchatov Institute Research Center in terms of using equipment of the center for collective use “Structural diagnostics of materials”.
Data Availability Statement
The data presented in this study are available on request from the corresponding author. The data are not publicly available due to privacy.
Acknowledgments
During the preparation of this manuscript/study, the authors used DeepSeek for the purposes of fixing grammar and style after translation to English. The authors have reviewed and edited the output and take full responsibility for the content of this publication.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SRE | Single Rate Equation |
| MRE | Multiple Rate Equations |
| DRE | Dynamical Rate Equations |
| IR | Infra-Red |
| FPGA | Field Programmed Gate Array |
| PC | Personal Computer |
| COM | Common |
References
- Manshina, A.A.; Tumkin, I.I.; Khairullina, E.M.; Mizoshiri, M.; Ostendorf, A.; Kulinich, S.A.; Makarov, S.; Kuchmizhak, A.A.; Gurevich, E.L. The Second Laser Revolution in Chemistry: Emerging Laser Technologies for Precise Fabrication of Multifunctional Nanomaterials and Nanostructures. Adv. Funct. Mater. 2024, 34, 2405457. [Google Scholar] [CrossRef]
- Cios, A.; Cieplak, M.; Szymański, Ł.; Lewicka, A.; Cierniak, S.; Stankiewicz, W.; Mendrycka, M.; Lewicki, S. Effect of Different Wavelengths of Laser Irradiation on the Skin Cells. Int. J. Mol. Sci. 2021, 22, 2437. [Google Scholar] [CrossRef]
- Minaev, V.P.; Minaev, N.V.; Bogachev, V.Y.; Kaperiz, K.A.; Yusupov, V.I. Endovenous Laser Coagulation: Asymmetrical Heat Transfer (Modeling in Water). Lasers Med. Sci. 2021, 36, 1599–1608. [Google Scholar] [CrossRef]
- Stuart, B.; Feit, M.; Herman, S.; Rubenchik, A.; Shore, B.; Perry, M. Nanosecond-to-Femtosecond Laser-Induced Breakdown in Dielectrics. Phys. Rev. B Condens. Matter 1996, 53, 1749–1761. [Google Scholar] [CrossRef] [PubMed]
- Chichkov, B.N.; Momma, C.; Nolte, S.; von Alvensleben, F.; Tünnermann, A. Femtosecond, Picosecond and Nanosecond Laser Ablation of Solids. Appl. Phys. A Mater. Sci. Process. 1996, 63, 109–115. [Google Scholar] [CrossRef]
- Vogel, A.; Venugopalan, V. Mechanisms of Pulsed Laser Ablation of Biological Tissues. Chem. Rev. 2003, 103, 577–644. [Google Scholar] [CrossRef]
- Schmidt, M.; Kahlert, U.; Wessolleck, J.; Maciaczyk, D.; Merkt, B.; Maciaczyk, J.; Osterholz, J.; Nikkhah, G.; Steinhauser, M.O. Characterization of a Setup to Test the Impact of High-Amplitude Pressure Waves on Living Cells. Sci. Rep. 2014, 4, 3849. [Google Scholar] [CrossRef]
- Yan, B.; Li, Y.; Cao, W.; Zeng, Z.; Liu, P.; Ke, Z.; Yang, G. Efficient and Rapid Hydrogen Extraction from Ammonia-Water via Laser Under Ambient Conditions without Catalyst. J. Am. Chem. Soc. 2024, 146, 4864–4871. [Google Scholar] [CrossRef] [PubMed]
- Windhorn, L.; Witte, T.; Yeston, J.S.; Proch, D.; Motzkus, M.; Kompa, K.L.; Fuß, W. Molecular Dissociation by Mid-IR Femtosecond Pulses. Chem. Phys. Lett. 2002, 357, 85–90. [Google Scholar] [CrossRef]
- Thomsen, C.L.; Madsen, D.; Keiding, S.R.; Tho, J.; Christiansen, O.; Thomsen, C.L.; Madsen, D.; Keiding, S.R.; Tho, J. Two-Photon Dissociation and Ionization of Liquid Water Studied by Femtosecond Transient Absorption. Spectroscopy 2014, 110, 3453–3462. [Google Scholar] [CrossRef]
- Kraus, P.M.; Zürch, M.; Cushing, S.K.; Neumark, D.M.; Leone, S.R. The Ultrafast X-Ray Spectroscopic Revolution in Chemical Dynamics. Nat. Rev. Chem. 2018, 2, 82–94. [Google Scholar] [CrossRef]
- Lauterborn, W.; Vogel, A. Bubble Dynamics and Shock Waves; Delale, C.F., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 978-3-642-34296-7. [Google Scholar]
- Ohl, C.-D.; Kurz, T.; Geisler, R.; Lindau, O.; Lauterborn, W. Bubble Dynamics, Shock Waves and Sonoluminescence. Philos. Trans. R. Soc. A Math. Phys. Eng. Sci. 1999, 357, 269–294. [Google Scholar] [CrossRef]
- Tsibidis, G.D.; Stratakis, E. Ionization Dynamics and Damage Conditions for Transparent Materials Irradiated with Mid-Infrared Femtosecond Pulses. arXiv 2022, arXiv:2210.07790. [Google Scholar]
- Mao, S.S.; Quere, F.; Guizard, S.; Mao, X.; Russo, R.E.; Petite, G.; Martin, P. Dynamics of Femtosecond Laser Interactions with Dielectrics. Appl. Phys. A 2004, 79, 1695–1709. [Google Scholar] [CrossRef]
- Linz, N.; Freidank, S.; Liang, X.-X.; Vogel, A. Wavelength Dependence of Femtosecond Laser-Induced Breakdown in Water and Implications for Laser Surgery. Phys. Rev. B—Condens. Matter Mater. Phys. 2016, 94, 024113. [Google Scholar] [CrossRef]
- Déziel, J.L.; Dubé, L.J.; Varin, C. Dynamical Rate Equation Model for Femtosecond Laser-Induced Breakdown in Dielectrics. Phys. Rev. B 2021, 104, 045201. [Google Scholar] [CrossRef]
- Mareev, E.I.; Rumiantsev, B.V.; Migal, E.; Bychkov, A.S.; Karabutov, A.A.; Cherepetskaya, E.B.; Makarov, V.A.; Potemkin, F.V. A Comprehensive Approach for Characterisation of the Deposited Energy Density during Laser-Matter Interaction in Liquids and Solids. Meas. Sci. Technol. 2020, 31, 085204. [Google Scholar] [CrossRef]
- Mareev, E.I.; Asharchuk, N.M.; Rovenko, V.V.; Yusupov, V.I. Dynamics of Water Transition to the Supercritical State under Ultrafast Heating with Ultrashort Laser Pulses. Russ. J. Phys. Chem. B 2024, 18, 1905–1915. [Google Scholar] [CrossRef]
- Chen, X.; Munjiza, A.; Zhang, K.; Wen, D. Molecular Dynamics Simulation of Heat Transfer from a Gold Nanoparticle to a Water Pool. J. Phys. Chem. C 2014, 118, 1285–1293. [Google Scholar] [CrossRef]
- Ding, W.; Shen, Z.; Lu, J.; Ni, X. Study on the Oscillation Property of Laser-Produced Cavitation Bubbles in Water. Chin. Opt. Lett. 2005, 3, S369–S371. [Google Scholar]
- Abraham, E.; Minoshima, K.; Matsumoto, H. Femtosecond Laser-Induced Breakdown in Water: Time-Resolved Shadow Imaging and Two-Color Interferometric Imaging. Opt. Spectrosc. 2000, 176, 441–452. [Google Scholar]
- Liang, X.X.; Linz, N.; Freidank, S.; Paltauf, G.; Vogel, A. Comprehensive Analysis of Spherical Bubble Oscillations and Shock Wave Emission in Laser-Induced Cavitation. J. Fluid Mech. 2022, 940, A5. [Google Scholar] [CrossRef]
- Faccio, D.; Tamošauskas, G.; Rubino, E.; Darginavičius, J.; Papazoglou, D.G.; Tzortzakis, S.; Couairon, A.; Dubietis, A. Cavitation Dynamics and Directional Microbubble Ejection Induced by Intense Femtosecond Laser Pulses in Liquids. Phys. Rev. E 2012, 86, 036304. [Google Scholar] [CrossRef]
- Linz, N.; Freidank, S.; Liang, X.; Vogel, A. Laser-Induced Plasma Formation and Cavitation in Water: From Nanoeffects to Extreme States of Matter. arXiv 2025, arXiv:2501.11029. [Google Scholar] [CrossRef] [PubMed]
- Vogel, A.; Noack, J. Shock Wave Energy and Acoustic Energy Dissipation after Laser-Induced Breakdown. Proc. SPIE 1998, 3254, 180–189. [Google Scholar]
- Vogel, A.; Nahen, K.; Theisen, D.; Birngruber, R.; Thomas, R.J.; Rockwell, B.A. Influence of Optical Aberrations on Laser-Induced Plasma Formation in Water and Their Consequences for Intraocular Photodisruption. Appl. Opt. 1999, 38, 3636–3643. [Google Scholar] [CrossRef]
- Zhou, C. Chirped Pulse Amplification: Review and Prospective from Diffractive Optics. Chin. Opt. Lett. 2020, 18, 110502. [Google Scholar] [CrossRef]
- Liang, X.-X.; Zhang, Z.; Vogel, A. Multi-Rate-Equation Modeling of the Energy Spectrum of Laser-Induced Conduction Band Electrons in Water. Opt. Express 2019, 27, 4672. [Google Scholar] [CrossRef] [PubMed]
- Li, X.; Guan, Y. Theoretical Fundamentals of Short Pulse Laser-Metal Interaction: A Review. Nanotechnol. Precis. Eng. 2020, 3, 105–125. [Google Scholar] [CrossRef]
- Jia, X.; Zhao, X. Numerical Investigation of Ultrashort Laser Interaction with Dielectric Materials Based on a Plasma-Temperature Combined Model. J. Manuf. Process. 2017, 28, 508–514. [Google Scholar] [CrossRef]
- Rethfeld, B.; Brenk, O.; Medvedev, N.; Krutsch, H.; Hoffmann, D.H.H. Interaction of Dielectrics with Femtosecond Laser Pulses: Application of Kinetic Approach and Multiple Rate Equation. Appl. Phys. A Mater. Sci. Process. 2010, 101, 19–25. [Google Scholar] [CrossRef]
- Vogel, A.; Noack, J. Numerical Simulation of Optical Breakdown for Cellular Surgery at Nanosecond to Femtosecond Time Scales. Proc. SPIE 2001, 4260, 83–93. [Google Scholar] [CrossRef]
- Zhi, Y.; Chong, Z.; Hongchao, Z.; Jian, L. Transient Electron Temperature and Density Changes in Water Breakdown Induced by Femtosecond Laser Pulses. Opt. Commun. 2023, 546, 129803. [Google Scholar] [CrossRef]
- Marcinkevičius, A.; Mizeikis, V.; Juodkazis, S.; Matsuo, S.; Misawa, H. Effect of Refractive Index-Mismatch on Laser Microfabrication in Silica Glass. Appl. Phys. A Mater. Sci. Process. 2003, 76, 257–260. [Google Scholar] [CrossRef]
- Marchenkov, N.; Mareev, E.; Potemkin, F.; Kulikov, A.; Pilyak, F.; Ibragimov, E.; Scholar, G. Hybrid Approach for Multiscale and Multimodal Time-Resolved Diagnosis of Ultrafast Processes in Materials via Tailored Sychronization of Laser and X-Ray Sources at MHz Repetition Rates. Optics 2023, 5, 1–10. [Google Scholar] [CrossRef]
- Potemkin, F.V.; Mareev, E.I.; Podshivalov, A.A.; Gordienko, V.M. Laser Control of Filament-Induced Shock Wave in Water. Laser Phys. Lett. 2014, 11, 106001. [Google Scholar] [CrossRef]
- Lamoureux, G.; MacKerell, A.D.; Roux, B. A Simple Polarizable Model of Water Based on Classical Drude Oscillators. J. Chem. Phys. 2003, 119, 5185–5197. [Google Scholar] [CrossRef]
- Delibasic, H.; Petrovic, V.; Petrovic, I. Laser Breakdown in Water Induced by λ = 532 Nm Nanosecond Pulses: Analytical Calculation of the Number Density of Free Electrons. J. Phys. Soc. Japan 2020, 89, 114501. [Google Scholar] [CrossRef]
- Liu, W.; Kosareva, O.; Golubtsov, I.S.; Iwasaki, A.; Becker, A.; Kandidov, V.P.; Chin, S.L. Femtosecond Laser Pulse Filamentation versus Optical Breakdown in H2O. Appl. Phys. B Lasers Opt. 2003, 76, 215–229. [Google Scholar] [CrossRef]
- Gauduel, Y.; Pommeret, S.; Migus, A.; Antonetti, A. Some Evidence of Ultrafast H2O+-Water Molecule Reaction in Femtosecond Photoionization of Pure Liquid Water: Influence on Geminate Pair Recombination Dynamics. Chem. Phys. 1990, 149, 1–10. [Google Scholar] [CrossRef]
- Vogel, A.; Noack, J.; Nahen, K.; Theisen, D.; Busch, S.; Parlitz, U.; Hammer, D.X.; Noojin, G.D.; Rockwell, B.A. Energy Balance of Optical Breakdown in Water at Nanosecond to Femtosecond Time Scales. Appl. Phys. B 1999, 68, 271–280. [Google Scholar] [CrossRef]
- Potemkin, F.V.; Mareev, E.I.; Podshivalov, A.A.; Gordienko, V.M. Highly Extended High Density Filaments in Tight Focusing Geometry in Water: From Femtoseconds to Microseconds. New J. Phys. 2015, 17, 053010. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).