Optimization of Tungsten Anode Target Design for High-Energy Microfocus X-Ray Sources via Geant4 Monte Carlo Simulation
Abstract
1. Introduction
2. Materials and Methods
2.1. Simulation Framework
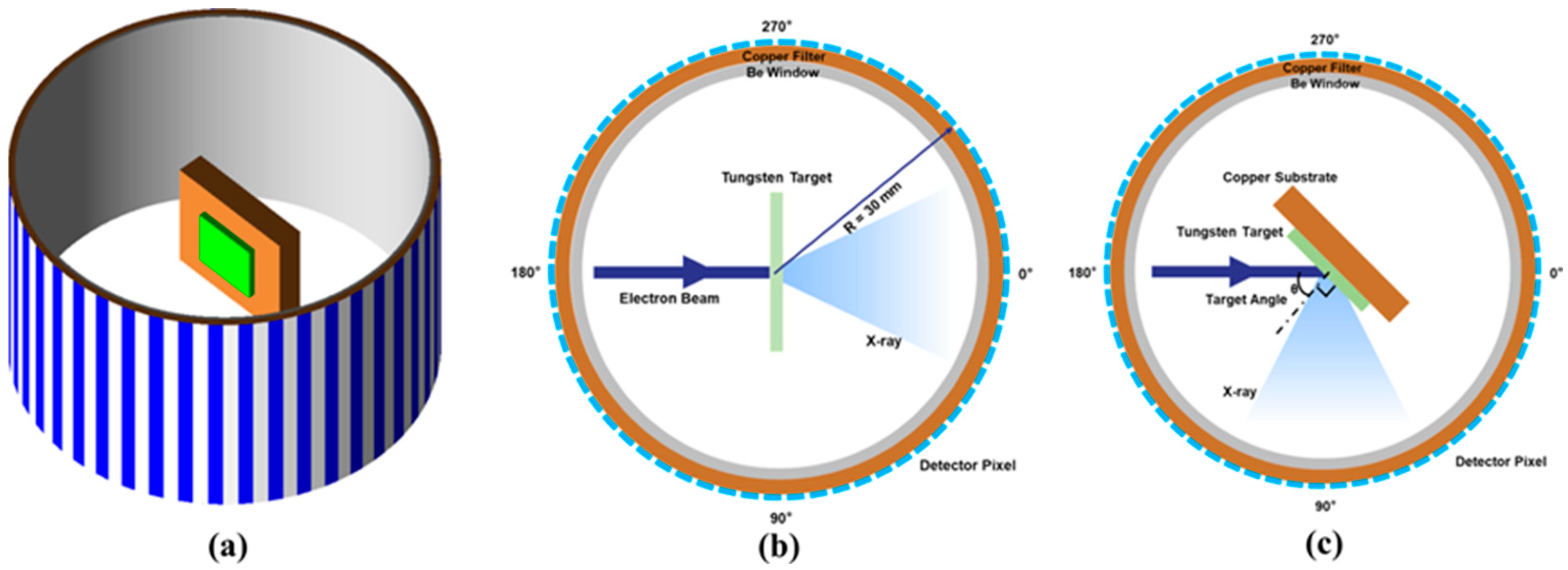
2.2. Target Geometry and Materials
2.3. Beryllium Window and Filters
2.4. Scoring and Data Collection
3. Results and Discussion
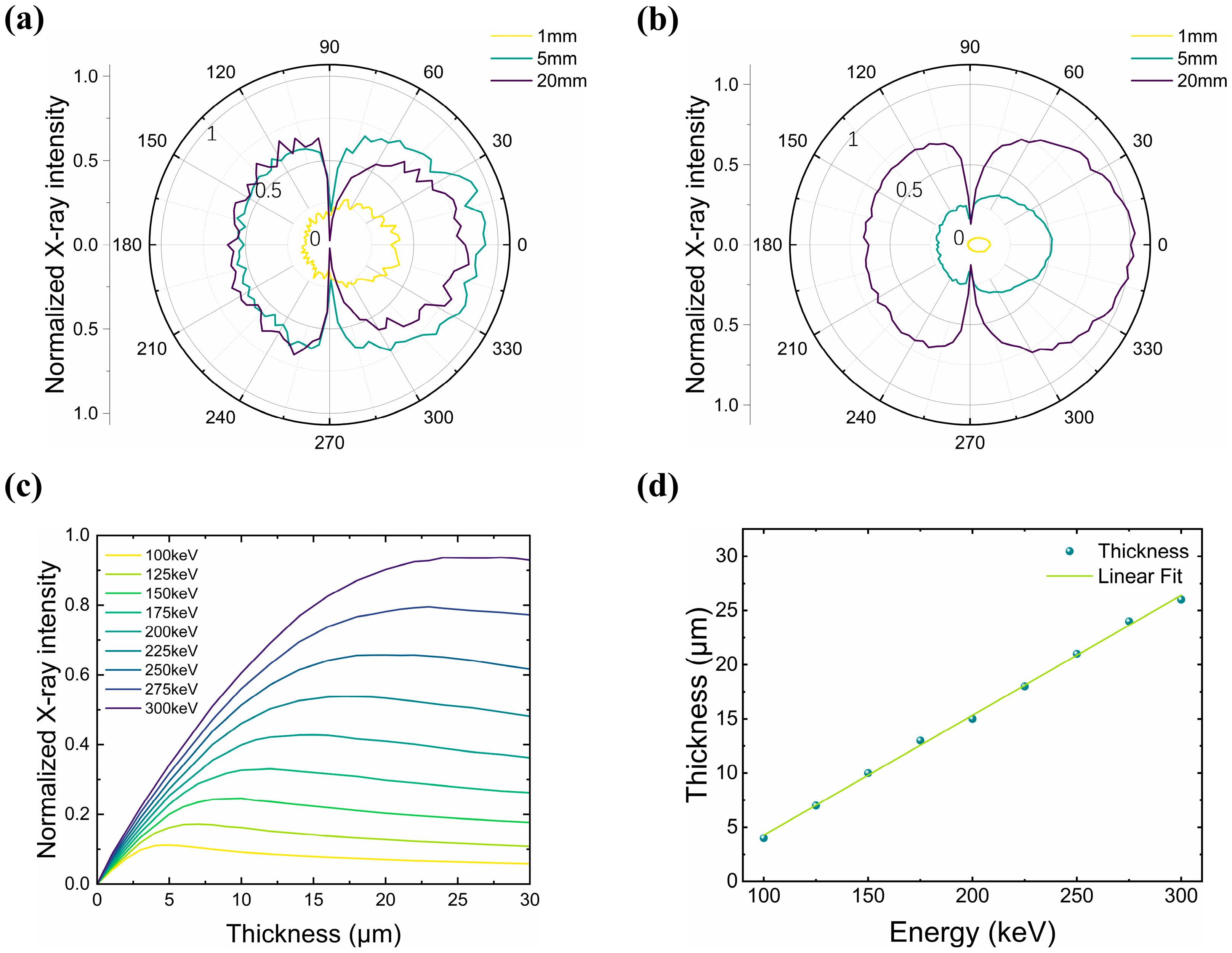
3.1. Transmission-Anode Tungsten Target
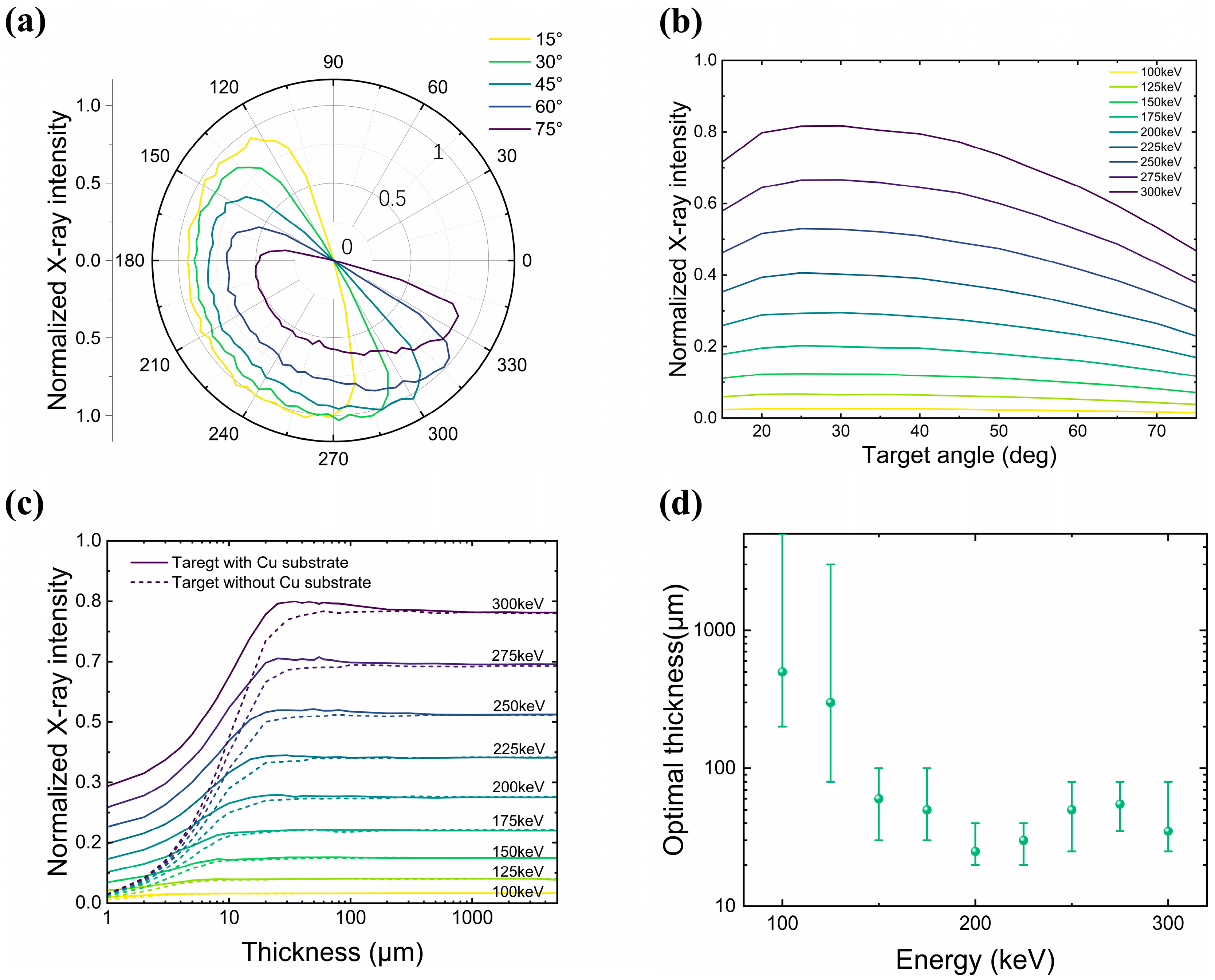
3.2. Reflection-Anode Tungsten Target
3.3. Influence of Beryllium Window Thickness and Filter
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- De Chiffre, L.; Carmignato, S.; Kruth, J.-P.; Schmitt, R.; Weckenmann, A. Industrial applications of computed tomography. CIRP Ann. 2014, 63, 655–677. [Google Scholar] [CrossRef]
- Kak, A.C.; Slaney, M.; Wang, G. Principles of Computerized Tomographic Imaging. Phys. Med. 2002, 29, 107. [Google Scholar] [CrossRef]
- Carmignato, S.; Dewulf, W.; Leach, R. Industrial X-Ray Computed Tomography; Springer: Cham, Switzerland, 2018; Volume 10. [Google Scholar]
- Withers, P.J.; Bouman, C.; Carmignato, S.; Cnudde, V.; Grimaldi, D.; Hagen, C.K.; Maire, E.; Manley, M.; Plessis, A.D.; Stock, S.R. X-ray computed tomography. Nat. Rev. Methods Primers 2021, 1, 18. [Google Scholar] [CrossRef]
- Hendee, W.R.; Ritenour, E.R. Medical Imaging Physics; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Cierniak, R. X-Ray Computed Tomography in Biomedical Engineering; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Lassner, E.; Schubert, W.-D. Tungsten: Properties; Chemistry, Technology of the Element, Alloys, and Chemical Compounds; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Poludniowski, G.G.; Evans, P.M. Calculation of X-ray spectra emerging from an X-ray tube. Part I. Electron penetration characteristics in X-ray targets. Med. Phys. 2007, 34, 2164–2174. [Google Scholar] [CrossRef]
- Goorley, T.; James, M.; Booth, T.; Brown, F.; Bull, J.; Cox, L.J.; Durkee, J.; Elson, J.; Fensin, M.; Forster, R.A.; et al. Initial MCNP6 Release Overview. Nucl. Technol. 2012, 180, 298–315. [Google Scholar] [CrossRef]
- Baró, J.; Sempau, J.; Fernández-Varea, J.M.; Salvat, F. PENELOPE: An algorithm for Monte Carlo simulation of the penetration and energy loss of electrons and positrons in matter. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. At. 1995, 100, 31–46. [Google Scholar] [CrossRef]
- Böhlen, T.; Cerutti, F.; Chin, M.; Fassò, A.; Ferrari, A.; Ortega, P.; Mairani, A.; Sala, P.; Smirnov, G.; Vlachoudis, V. The FLUKA Code: Developments and Challenges for High Energy and Medical Applications. Nucl. Data Sheets 2014, 120, 211–214. [Google Scholar] [CrossRef]
- Kawrakow, I. Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version. Med. Phys. 2000, 27, 485–498. [Google Scholar] [CrossRef]
- Agostinelli, S.; Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce, P.; Asai, M.; Axen, D.; Barrand, G.; Behner, F.; et al. Geant4—A simulation toolkit. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2003, 506, 250–303. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Araujo, H.; Arce Dubois, P.; Asai, M.; Barrand, G.; Capra, R.; Chauvie, S.; Chytracek, R.; et al. Geant4 developments and applications. IEEE Trans. Nucl. Sci. 2006, 53, 270–278. [Google Scholar] [CrossRef]
- Allison, J.; Amako, K.; Apostolakis, J.; Arce, P.; Asai, M.; Aso, T.; Bagli, E.; Bagulya, A.; Banerjee, S.; Barrand, G.; et al. Recent developments in Geant4. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2016, 835, 186–225. [Google Scholar] [CrossRef]
- Nasseri, M.M. Determination of Tungsten Target Parameters for Transmission X-ray Tube: A Simulation Study Using Geant4. Nucl. Eng. Technol. 2016, 48, 795–798. [Google Scholar] [CrossRef]
- Nasseri, M.M. Determination of molybdenum target parameters for transmission X-ray tube: A Geant4 simulation study. Pramana 2019, 92, 54. [Google Scholar] [CrossRef]
- Kandlakunta, P.; Thomas, A.; Tan, Y.; Khan, R.; Zhang, T. Design and numerical simulations of W-diamond transmission target for distributed x-ray sources. Biomed. Phys. Eng. Express 2019, 5, 025030. [Google Scholar] [CrossRef]
- Geng, N.; Wei-xia, Z.; Jun-biao, L.; Li, H.; Yu-tian, M. Optimization and design of target of low energy X-ray microscopy. J. Chin. Electron Microsc. Soc. 2019, 38, 384–388. [Google Scholar]
- Niu, G.; Liu, J.; Zhao, W.; Han, L.; Ma, Y. Effect of Focused Bombarding Electron Beam on Transmission Microfocus X-Ray Source. Acta Opt. Sin. 2019, 39, 0634001. [Google Scholar] [CrossRef]
- Lei, Z.; Huarong, L.; Buliang, S.; Junting, W.; Tingting, L.; Yijing, L. Optimization of Transmission-Type Anode Target in Microfocus X-Ray Tube. Chin. J. Vaccum Sci. Technol. 2015, 35, 1443–1448. [Google Scholar]
- Carrier, J.F.; Archambault, L.; Beaulieu, L.; Roy, R. Validation of GEANT4, an object-oriented Monte Carlo toolkit, for simulations in medical physics. Med. Phys. 2004, 31, 484–492. [Google Scholar] [CrossRef]
- Seco, J.; Verhaegen, F. Monte Carlo Techniques in Radiation Therapy; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Keall, P.J.; Siebers, J.V.; Libby, B.; Mohan, R. Determining the incident electron fluence for Monte Carlo-based photon treatment planning using a standard measured data set. Med. Phys. 2003, 30, 574–582. [Google Scholar] [CrossRef]
- Kanaya, K.; Okayama, S. Penetration and energy-loss theory of electrons in solid targets. J. Phys. D Appl. Phys. 1972, 5, 43. [Google Scholar] [CrossRef]
- Bakri, F.; Gareso, P.L.; Tahir, D. Advancing radiation shielding: A review the role of Bismuth in X-ray protection. Radiat. Phys. Chem. 2024, 217, 111510. [Google Scholar] [CrossRef]
- National Institute of Standards and Technology(NIST). XCOM: Photon Cross Sections Database. Available online: https://physics.nist.gov/PhysRefData/Xcom/html/xcom1.html (accessed on 1 October 2025).
- X-Ray Worx [EB/OL]. Available online: https://www.x-ray-worx.com/ (accessed on 20 October 2025).
- Behling, R. Modern Diagnostic X-Ray Sources: Technology, Manufacturing, Reliability; CRC Press: Boca Raton, FL, USA, 2021. [Google Scholar]
- Oostveen, L.J.; Tunissen, S.; Sechopoulos, I. Comparing organ and effective dose of various CT localizer acquisition strategies: A Monte Carlo study. Med. Phys. 2025, 52, 576–584. [Google Scholar] [CrossRef]
- Behling, R. X-ray sources: 125 years of developments of this intriguing technology. Phys. Medica 2020, 79, 162–187. [Google Scholar] [CrossRef]
- Paul, S. Biomedical Engineering and Its Applications in Healthcare; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Doane, D.P. Aesthetic frequency classifications. Am. Stat. 1976, 30, 181–183. [Google Scholar] [CrossRef]
- Hsieh, J. Computed Tomography: Principles; Design; Artifacts; Recent Advances; SPIE: Washington, DC, USA, 2003. [Google Scholar]
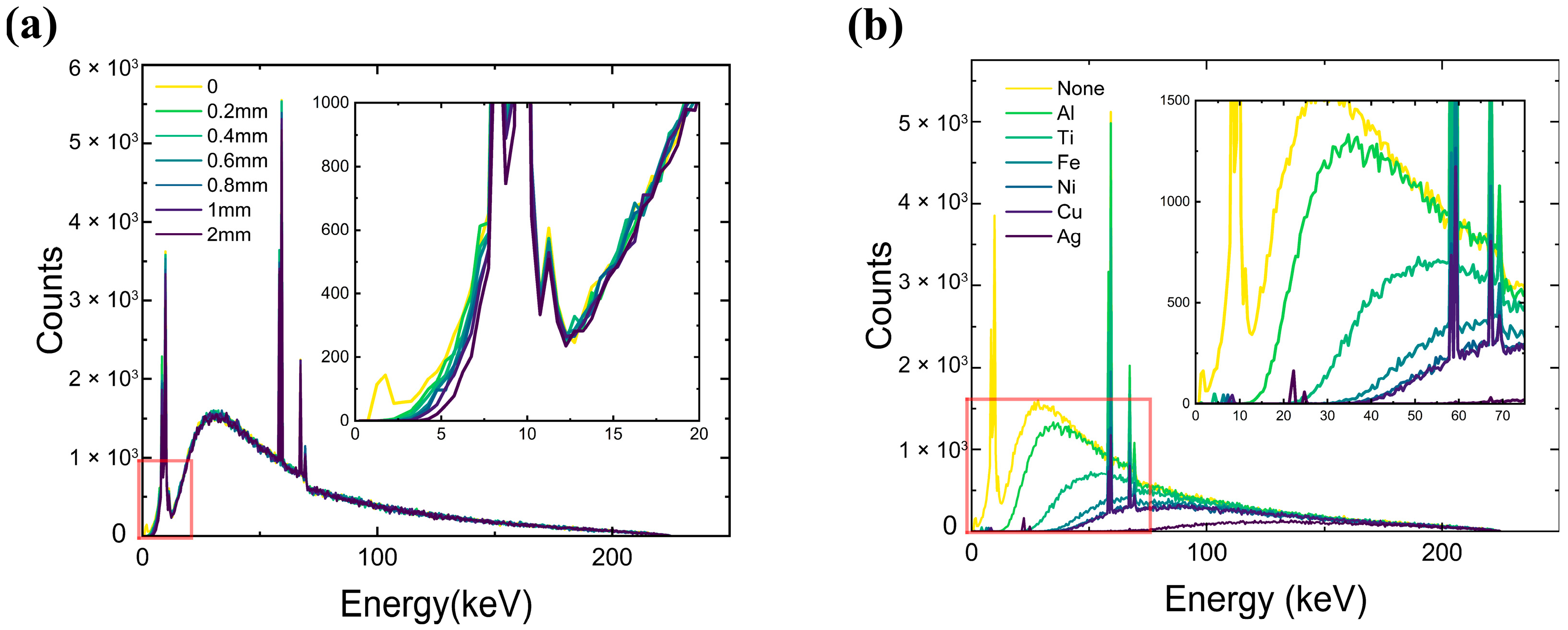
| Material (Z) | No Filter | Al(13) | Ti(22) | Fe(26) | Ni(28) | Cu(29) | Ag(47) |
|---|---|---|---|---|---|---|---|
| transmittance | 1.00 | 0.82 | 0.53 | 0.35 | 0.29 | 0.29 | 0.11 |
| Mean Energy/keV | 62.6 | 71.8 | 88.4 | 102.5 | 108.6 | 109.8 | 140.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Li, L.; Liu, Y.; Zhang, X.; Xin, L.; Fu, Z.; Tian, J.; Zhao, W.; Luo, D. Optimization of Tungsten Anode Target Design for High-Energy Microfocus X-Ray Sources via Geant4 Monte Carlo Simulation. Photonics 2025, 12, 1062. https://doi.org/10.3390/photonics12111062
Liu Y, Li L, Liu Y, Zhang X, Xin L, Fu Z, Tian J, Zhao W, Luo D. Optimization of Tungsten Anode Target Design for High-Energy Microfocus X-Ray Sources via Geant4 Monte Carlo Simulation. Photonics. 2025; 12(11):1062. https://doi.org/10.3390/photonics12111062
Chicago/Turabian StyleLiu, Yuetian, Lili Li, Yiheng Liu, Xue Zhang, Liwei Xin, Zhengkun Fu, Jinshou Tian, Wei Zhao, and Duan Luo. 2025. "Optimization of Tungsten Anode Target Design for High-Energy Microfocus X-Ray Sources via Geant4 Monte Carlo Simulation" Photonics 12, no. 11: 1062. https://doi.org/10.3390/photonics12111062
APA StyleLiu, Y., Li, L., Liu, Y., Zhang, X., Xin, L., Fu, Z., Tian, J., Zhao, W., & Luo, D. (2025). Optimization of Tungsten Anode Target Design for High-Energy Microfocus X-Ray Sources via Geant4 Monte Carlo Simulation. Photonics, 12(11), 1062. https://doi.org/10.3390/photonics12111062






