Solitons in a One-Dimensional Rhombic Waveguide Array

Abstract

We present an analytical and numerical study of nonlinear wave localization in a one-dimensional rhombic (diamond) waveguide array that combines forward- and backward-propagating channels. This mixed-index configuration, realizable through Bragg-type couplers or corrugated waveguides, produces a tunable spectral gap and supports nonlinear self-localized states in both transmission and forbidden-band regimes. Starting from the full set of coupled-mode equations, we derive the effective evolution model, identify the role of coupling asymmetry and nonlinear coefficients, and obtain explicit soliton solutions using the method of multiple scales. The resulting envelopes satisfy a nonlinear Schrödinger equation with an effective nonlinear parameter $\theta$, which determines the conditions for soliton existence ($\theta >0$) for various combinations of focusing and defocusing nonlinearities. We distinguish solitons formed outside and inside the bandgap and analyze their dependence on the dispersion curvature and nonlinear response. Direct numerical simulations confirm the analytical predictions and reveal robust propagation and interactions of counter-propagating soliton modes. Order-of-magnitude estimates show that the predicted effects are accessible in realistic integrated photonic platforms. These results provide a unified theoretical framework for soliton formation in mixed-index lattices and suggest feasible routes for realizing controllable nonlinear localization in Bragg-type photonic structures.

1. Introduction

Nonlinear waveguide arrays provide a versatile platform for exploring the interplay between discreteness, nonlinearity, and dispersion in optical systems [1,2]. By tailoring their geometry and material composition, such arrays can support a wide variety of localized states, including discrete solitons, flat-band modes, and topological edge states [3,4,5,6,7,8,9]. Among different geometries, the rhombic (diamond) lattice is often associated with flat-band phenomena in purely transverse band diagrams [10,11,12,13,14].

An additional degree of freedom arises when combining waveguides with positive and negative refractive indices [15,16,17]. This mixed-index configuration modifies the coupling between sublattices and produces a band structure with a spectral gap and a flat band, thus creating favorable conditions for nonlinear localization [18,19]. While linear propagation in such systems has been investigated extensively, systematic analytical results for soliton formation remain scarce. Previous studies have reported soliton solutions only in reduced models, for instance, when nonlinearities were absent in two of the sublattices [14].

Moreover, it is worth emphasising that the realization of effectively negative refractive index channels in photonic structures need not rely solely on canonical metamaterials. In practice, backward-wave guidance, resonant coupling, and periodic waveguide or photonic crystal architectures can yield effective opposite-sign phase and energy velocities (and thus mimic “negative index” behaviour) in frequency windows of interest [20,21,22].

In this work, we present a comprehensive analytical derivation of soliton solutions in a one-dimensional rhombic waveguide array with both positive and negative refractive indices. Using the method of multiple scales, we construct longitudinal solitons in the form of envelope states propagating outside the gap, at the gap edge, and within the gap. Explicit conditions for soliton existence are obtained, revealing the role of nonlinearities and coupling asymmetry. Direct numerical simulations confirm the analytical predictions and demonstrate the robustness of the solutions.

The results presented here broaden the understanding of nonlinear localization in flat-band lattices with alternating refractive indices. Beyond their fundamental significance, they provide new opportunities for engineering robust localized states in complex photonic structures, with potential applications in light-guiding, switching, and integrated signal processing. To place our contribution in context, we next review the most relevant prior work in this area.

2. Related Work

The modeling of nonlinear discrete optical phenomena has a long history. In particular, coupled waveguide arrays have been widely used as optical analog simulators for diverse physical processes, ranging from analogue gravity to quantum lattice dynamics [23,24,25,26]. Such structures provide a convenient platform where discreteness, nonlinearity, and inter-site coupling can be explored under well-controlled conditions [3,4,6,27]. For example, phenomena such as flat-band localization [7,28,29], non-Hermitian transport in photonic lattices [30,31,32], and exotic lattice geometries including Lieb, sawtooth, kagome, or dice lattices [29,33,34,35] have all been demonstrated.

Inspired by topological insulators in condensed matter [36,37], there has been a surge of interest in topological photonics—the study of photonic lattices that support topologically protected modes. Optical waveguide arrays are an ideal platform for realizing such topological phases [37], especially when combined with optical nonlinearity and gain. Various topologically nontrivial states have been realized experimentally, including robust one-way edge modes and disorder-immune transport [4,38]. On the flat-band side, the realization of all-band-flat photonic lattices [39] provides powerful routes toward controlled localization. Theoretically, recent studies have explored nonlinearity-induced bandgap transmission in dispersive versus flat-band systems [40], and beam dynamics in chirped waveguide arrays exhibiting robust discrete soliton motion [41]. Nonlinearity unlocks additional functionalities such as topological solitons [42,43] and topological lasers [31]. Several reviews highlight these developments in both linear and nonlinear regimes [4,37]. As a practical application, topologically engineered waveguide lattices enable robust and broadband mode couplers insensitive to fabrication imperfections [44].

Early studies of discrete nonlinear optics focused on uniform one-dimensional chains, which served as prototypical models for discrete diffraction and soliton formation [45,46]. It was established that optical beams in periodic arrays can form discrete solitons under self-focusing nonlinearity [45]. Moving beyond uniform lattices, researchers explored more elaborate coupling schemes to engineer bandgaps and localized states. The dimerized waveguide array realizes the celebrated Su–Schrieffer–Heeger (SSH) model [5,47], where alternating couplings produce topologically distinct phases supporting edge states in the linear regime and nonlinear gap solitons [42,43]. Other engineered geometries include binary superlattices with alternating positive and negative index sites [19], or twisted multicore fibers emulating synthetic magnetic fluxes [48]. Two-dimensional lattices with non-Bravais geometries (e.g., honeycomb, kagome, Lieb) further enrich discrete soliton physics [30,49,50]. Even non-uniform ring and quasicrystal geometries have been explored for state transfer and localization [50].

Within this broad landscape, the rhombic (diamond) waveguide array stands out as a quasi-one-dimensional geometry with a strictly flat band in its linear spectrum [10,11,12,13,14]. This flat band supports compact localized modes or Aharonov–Bohm cages [10,51,52]. Experimental observations confirmed the existence of flat-band modes in laser-written diamond lattices [11]. When combined with nonlinearity, the rhombic array supports new families of localized states [14], continuing the tradition of nonlinear localization studied in earlier works on polariton and transparency solitons [53,54]. Recent analyses revealed how disorder and interactions lift degeneracies and stabilize localized modes in flat-band systems [12,13], while fine-tuning of couplings enables control over flat-band solitons [7]. Despite these advances, systematic analytical results for soliton formation in rhombic lattices remain scarce. Our work addresses this gap by developing a theoretical framework for nonlinear wave propagation in mixed-index rhombic arrays, deriving explicit soliton solutions, and bridging the continuum theory of nonlinear pulse propagation [54] with discrete flat-band physics.

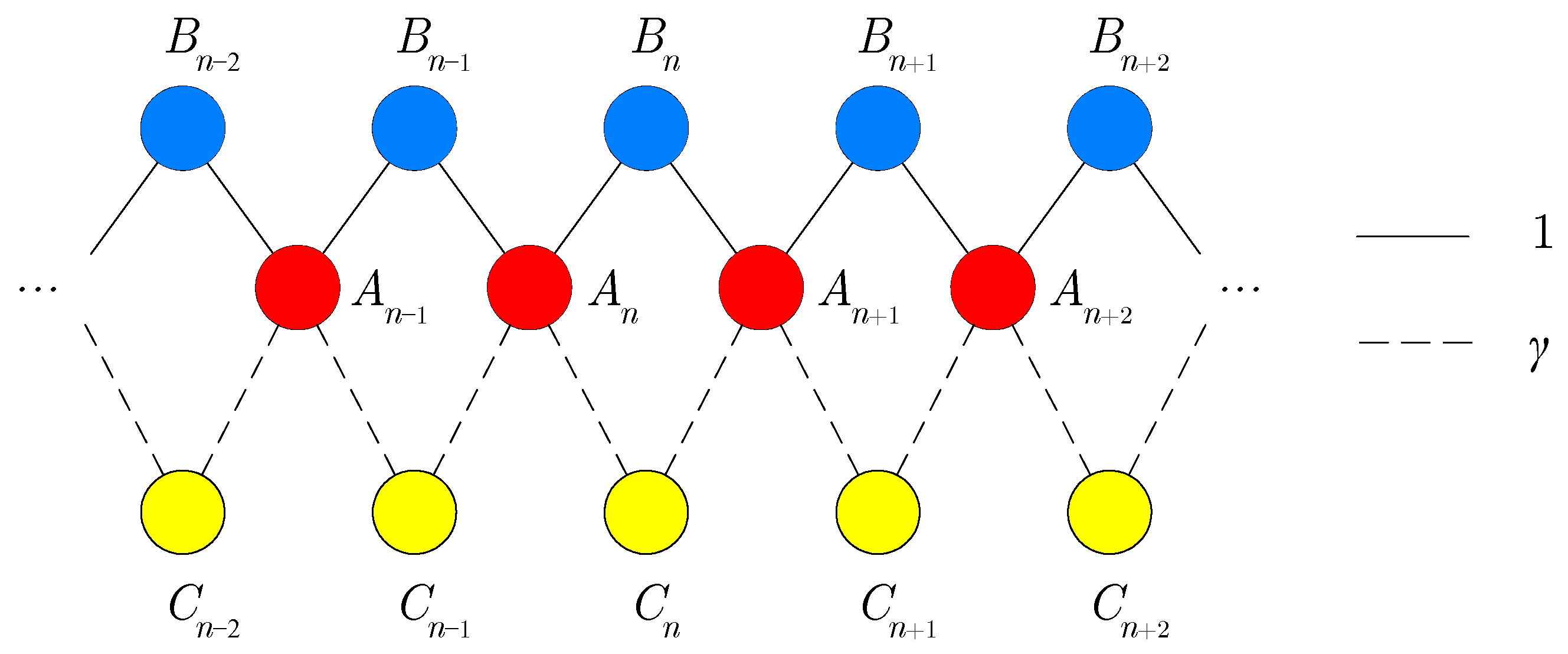
3. Theoretical Model

We consider wave propagation in a rhombic lattice of coupled nonlinear waveguides, schematically shown in Figure 1. To describe the system dynamics, we begin with the standard coupled-mode approach [16,55,56], which accounts for the mutual interaction of the electric field envelopes in the neighboring channels:

$$\begin{array}{cc}\hfill & i\left({\displaystyle \frac{1}{v_a}}{\displaystyle \frac{\partial \mathcal{A}}{\partial t}}+{\sigma }_a{\displaystyle \frac{\partial \mathcal{A}}{\partial x}}\right)+k_{ab}\mathcal{B}{e}^{+i{\omega }_{1}z}+k_{ac}\mathcal{C}{e}^{+i{\omega }_{2}z}+{\mu }_a{\left|\mathcal{A}\right|}^2\mathcal{A}=0,\hfill \\ \hfill & i\left({\displaystyle \frac{1}{v_b}}{\displaystyle \frac{\partial \mathcal{B}}{\partial t}}+{\sigma }_b{\displaystyle \frac{\partial \mathcal{B}}{\partial x}}\right)+k_{ba}\mathcal{A}{e}^{-i{\omega }_{1}z}+{\mu }_b{\left|\mathcal{B}\right|}^2\mathcal{B}=0,\hfill \\ \hfill & i\left({\displaystyle \frac{1}{v_c}}{\displaystyle \frac{\partial \mathcal{C}}{\partial t}}+{\sigma }_c{\displaystyle \frac{\partial \mathcal{C}}{\partial x}}\right)+k_{ca}\mathcal{A}{e}^{-i{\omega }_{2}z}+{\mu }_c{\left|\mathcal{C}\right|}^2\mathcal{C}=0.\hfill \end{array}$$

(1)

Here, $\mathcal{A},\mathcal{B},\mathcal{C}$ are the slowly varying complex field amplitudes in the respective waveguides, $v_{a,b,c}$ are the group velocities, and ${\sigma }_{a,b,c}=\pm 1$ determine the propagation direction (forward or backward) of each channel. The coupling coefficients $k_{ij}$ describe the influence of the field in waveguide j on the field in waveguide i, ${\mu }_{a,b,c}=n_2{\omega }_0/\left(c{A}_{\mathrm{eff}}\right)$ are the nonlinear coefficients related to the Kerr response $n_2$, and the effective mode area is $A_{\mathrm{eff}}$. Here, c is the speed of light in vacuum, and ${\omega }_0$ is the carrier angular frequency. The terms with ${\omega }_{1,2}$ represent small mismatches between propagation constants. If ${\omega }_1={\omega }_2$, the exponential factors can be eliminated by redefining the envelopes, whereas for ${\omega }_1\ne {\omega }_2$, the corresponding beating terms can be neglected under the assumption of synchronism (${\omega }_1={\omega }_2=0$) or for sufficiently short interaction lengths. We further restrict our consideration to slowly varying, quasi-continuous pulses, for which higher-order dispersion and Raman effects can be neglected [57].

For simplicity, we assume symmetric coupling $k_{ab}=k_{ba}$ and $k_{ac}=k_{ca}$. By introducing dimensionless variables and normalizing all coefficients, the system for the discrete array of waveguides, including the nearest-neighbor interactions, takes the form

$$\begin{array}{cc}\hfill & i\left({\displaystyle \frac{\partial }{\partial t}}+{\sigma }_a{\displaystyle \frac{\partial }{\partial x}}\right)A_n+\left(B_n+B_{n-1}\right)+\gamma \left(C_n+C_{n-1}\right)+{\mu }_a{\left|A_n\right|}^2{A}_n=0,\hfill \\ \hfill & i\left({\displaystyle \frac{\partial }{\partial t}}+{\sigma }_b{\displaystyle \frac{\partial }{\partial x}}\right)B_n+\left(A_n+A_{n+1}\right)+{\mu }_b{\left|B_n\right|}^2{B}_n=0,\hfill \\ \hfill & i\left({\displaystyle \frac{\partial }{\partial t}}+{\sigma }_c{\displaystyle \frac{\partial }{\partial x}}\right)C_n+\gamma \left(A_n+A_{n+1}\right)+{\mu }_c{\left|C_n\right|}^2{C}_n=0,\hfill \end{array}$$

(2)

where all quantities have been renormalized, and $\gamma$ denotes the relative coupling strength between sublattices A and C.

In our equations, the parameters ${\sigma }_{a,b,c}=\pm 1$ encode the sign of the group velocity in each channel (forward vs. backward propagation) rather than the sign of the material refractive index. Hence, a true negative-index medium is not required. A practical and widely used route is to realize a backward-propagating Bloch mode via Bragg reflection: integrated waveguides with shallow surface corrugations (distributed Bragg reflectors) or fiber/planar Bragg gratings. Near the Bragg condition, a forward wave couples to a counter-propagating wave; the coupled-mode equations are contra-directional and map directly onto Equation (2) with opposite signs of the $\partial /\partial x$ terms [56,57,58]. In the rhombic geometry, this is achieved by designing one arm to support a backward Bragg mode while the central arm supports a forward mode, thus realizing the mixed-index (mixed-$\sigma$) unit cell without invoking metamaterials.

In the linear regime (${\mu }_a={\mu }_b={\mu }_c=0$), plane-wave solutions of the form

$$A_n,B_n,C_n\propto e^{i(kx-\omega t+qn)},$$

lead to the dispersion relation

$${\omega }^2=k^2+2(1+{\gamma }^2)(1+cosq),$$

(3)

in addition to a trivial branch $\omega =k$. Here, $\omega$ is the temporal frequency, k is the longitudinal propagation constant along the array (continuous coordinate x), and q is the Bloch quasi-momentum associated with the discrete transverse index n.

Equation (3) reveals the presence of a forbidden bandgap

$${\delta }^2=2(1+{\gamma }^2)(1+cosq),$$

(4)

and a flat band (a q–independent branch that is flat with respect to the transverse Bloch wavenumber q) in the spectrum. These features are responsible for the existence of localized nonlinear excitations such as solitons. Previously, a soliton solution was obtained only in the reduced case of ${\mu }_b={\mu }_c=0$ [14], where system (2) simplifies to a two-waveguide model.

Analytical expressions for the field amplitudes in the linear regime of a rhombic waveguide array can be found in [59], where exact solutions of the coupled-mode equations were derived using the generating function method.

To facilitate the analysis of soliton formation in the system (2), the subsequent sections are organized as follows. In Section 4, we perform a linear analysis and highlight the key distinctions between arrays containing negative-index channels and conventional all-positive-index lattices [60,61,62]. For this purpose, we also consider an auxiliary configuration consisting of two coupled waveguides, whose properties are later inherited by the three-waveguide rhombic cell that constitutes our main object of study. In Section 5, we analyze modulated wave packets and identify the characteristic features that precede the formation of localized nonlinear states. Section 6 is devoted to constructing stable soliton configurations in different spectral regions and discussing their parameter dependence. Finally, in Section 7, we provide a physical interpretation of the obtained results and discuss the mechanisms responsible for soliton formation in mixed-index lattices.

4. Linear Problems

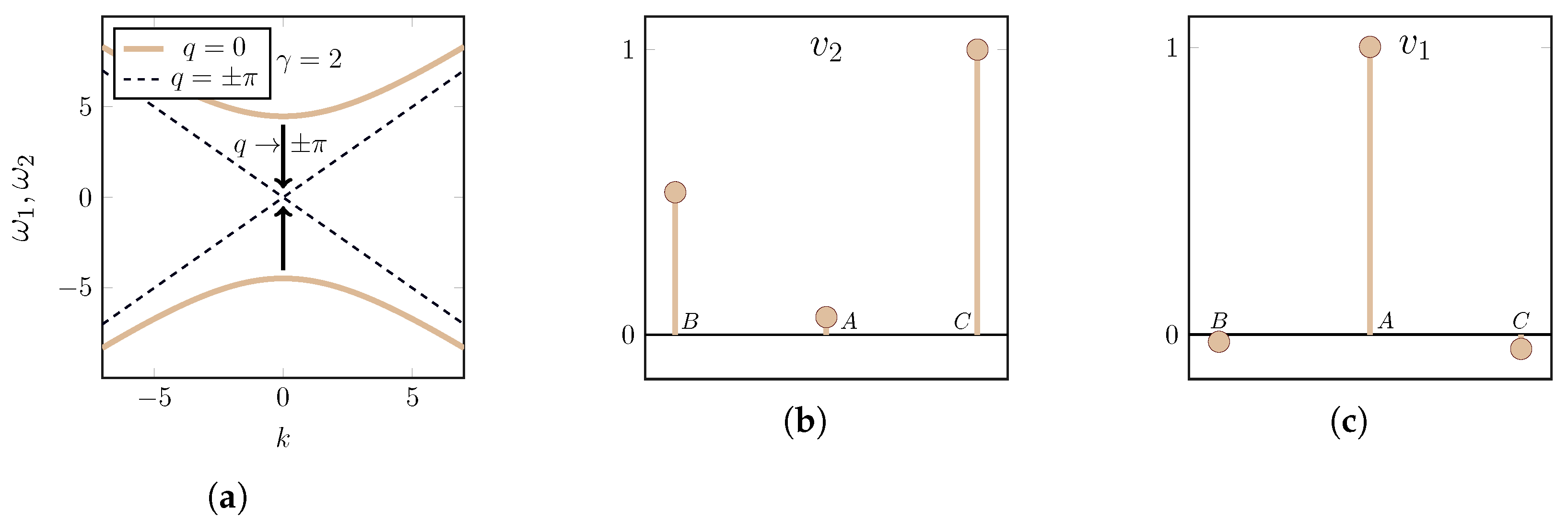
4.1. Three Waveguides with Positive Refractive Indices

We begin by recalling the properties of a homogeneous rhombic system consisting of three waveguides with ${\sigma }_a={\sigma }_b={\sigma }_c=+1$. By substituting plane-wave solutions of the form $\propto e^{i(kx+qn-\omega t)}$ into the governing Equation (2), we obtain the following linear algebraic system:

$$\begin{array}{cc}\hfill & (\omega -k)A+(1+e^{-iq})B+\gamma (1+e^{-iq})C=0,\hfill \\ \hfill & (\omega -k)B+(1+e^{iq})A=0,\hfill \\ \hfill & (\omega -k)C+\gamma (1+e^{iq})A=0,\hfill \end{array}$$

(5)

which can be regarded as an eigenvalue problem for $\omega$ (dispersion relation) with corresponding eigenvectors $v=\{A,B,C\}$.

This yields three branches of solutions:

$$\begin{array}{cc}{\omega }_I=\sqrt{2(1+{\gamma }^2)(1+cosq)}+k,\hfill & \hfill v_I(q=0)=\left\{\sqrt{1+{\gamma }^2},1,\gamma \right\},\\ {\omega }_{II}=-\sqrt{2(1+{\gamma }^2)(1+cosq)}+k,\hfill & \hfill v_{II}(q=0)=\left\{-\sqrt{1+{\gamma }^2},1,\gamma \right\},\\ {\omega }_{III}=k,\hfill & \hfill v_{III}(q=0)=\{0,\gamma ,-1\}.\end{array}$$

(6)

Here, only the amplitude ratios $\{A,B,C\}$ are essential, so we set $q=0$ for convenience. Figure 2 illustrates the dispersion curves and the corresponding eigenvectors. Note that degeneracy occurs as $q\to \pm \pi$. Importantly, the eigenvectors are constant in this case.

4.2. A Pair of Waveguides

The two-waveguide system with ${\sigma }_a=+1$ and ${\sigma }_b=-1$ is well known from Bragg scattering problems, and also appears in the context of waveguide arrays. Its governing equations are

$$\begin{array}{cc}\hfill & i\left({\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{\partial }{\partial x}}\right)A_n+\gamma (B_n+B_{n+1})=0,\hfill \\ \hfill & i\left({\displaystyle \frac{\partial }{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\right)B_n+\gamma (A_n+A_{n-1})=0.\hfill \end{array}$$

(7)

The dispersion relations and eigenvectors are given by

$$\begin{array}{cc}{\omega }_{+}=\sqrt{2{\gamma }^2(1+cosq)+k^2},\hfill & \hfill v_{+}(q=0)=\{k+\sqrt{k^2+4{\gamma }^2},-2\gamma \},\\ {\omega }_{-}=-\sqrt{2{\gamma }^2(1+cosq)+k^2},\hfill & \hfill v_{-}(q=0)=\{-k+\sqrt{k^2+4{\gamma }^2},2\gamma \}.\end{array}$$

(8)

Unlike the previous case, the eigenvectors $v_{\pm }$, i.e., the amplitudes in A and B, now depend explicitly on the wave number k. For $k\gg \gamma$, suppression occurs in one of the channels (Figure 3):

$$\{k+\sqrt{k^2+4{\gamma }^2},-2\gamma \}\to \{1,0\},\{-k+\sqrt{k^2+4{\gamma }^2},2\gamma \}\to \{0,1\}.$$

(9)

This feature is characteristic of arrays with alternating positive and negative refractive indices.

4.3. Three Waveguides with Alternating Refractive Indices

Finally, we focus on the system of principal interest in this study, namely the array characterized by ${\sigma }_a=+1$ and ${\sigma }_b={\sigma }_c=-1$:

$$\begin{array}{cc}\hfill & i\left({\displaystyle \frac{\partial }{\partial t}}+{\displaystyle \frac{\partial }{\partial x}}\right)A_n+(B_n+B_{n-1})+\gamma (C_n+C_{n-1})=0,\hfill \\ \hfill & i\left({\displaystyle \frac{\partial }{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\right)B_n+(A_n+A_{n+1})=0,\hfill \\ \hfill & i\left({\displaystyle \frac{\partial }{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\right)C_n+\gamma (A_n+A_{n+1})=0.\hfill \end{array}$$

(10)

Its dispersion relations and eigenvectors are

$$\begin{array}{cc}{\omega }_1=\sqrt{2(1+{\gamma }^2)(1+cosq)+k^2},\hfill & \hfill v_1(q=0)=\left\{k+\sqrt{4(1+{\gamma }^2)+k^2},-2,-2\gamma \right\},\\ {\omega }_2=-\sqrt{2(1+{\gamma }^2)(1+cosq)+k^2},\hfill & \hfill v_2(q=0)=\left\{-k+\sqrt{4(1+{\gamma }^2)+k^2},2,2\gamma \right\},\\ {\omega }_3=k,\hfill & \hfill v_3(q=0)=\{\gamma ,0,-1\}.\end{array}$$

(11)

Equations (10) can be rearranged to highlight the effective pair interaction between A and $B+\gamma C$:

$$i\left({\displaystyle \frac{\partial }{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\right)(B_n+\gamma C_n)+(1+{\gamma }^2)(A_n+A_{n+1})=0,$$

(12)

$$i\left({\displaystyle \frac{\partial }{\partial t}}-{\displaystyle \frac{\partial }{\partial x}}\right)(B_n-\gamma C_n)+(1-{\gamma }^2)(A_n+A_{n+1})=0.$$

(13)

This representation clarifies that the system supports suppression of light in two different modes. For $k\gg \gamma ,1$, one finds

$$\begin{array}{c}\hfill \{k-\sqrt{4(1+{\gamma }^2)+k^2},2,2\gamma \}\to \{1,0,0\},\\ \hfill \{k+\sqrt{4(1+{\gamma }^2)+k^2},2,2\gamma \}\to \{0,1,\gamma \}.\end{array}$$

(14)

Thus, one can control light distribution among the waveguides using high-frequency wave packets. The corresponding mode profiles are shown in Figure 4.

Interestingly, these modes propagate with different group velocities $\partial \omega /\partial k$, similar to the case of the two-waveguide system. From an application perspective, this suggests the possibility of transmitting signals in opposite directions along different channels (A versus $B,C$). Interactions between such counter-propagating packets would occur at their crossing points, a phenomenon that merits further investigation beyond the scope of this work.

Note that ${\omega }_3=k$ is independent of q, which suppresses transverse diffraction for that branch, yet the longitudinal dispersion persists through k–dependence. The soliton families constructed below do not require compact-localized eigenstates; their parameters are set by the longitudinal curvature ${\omega }_{kk}$ and the nonlinear coefficient $\theta$ (see below).

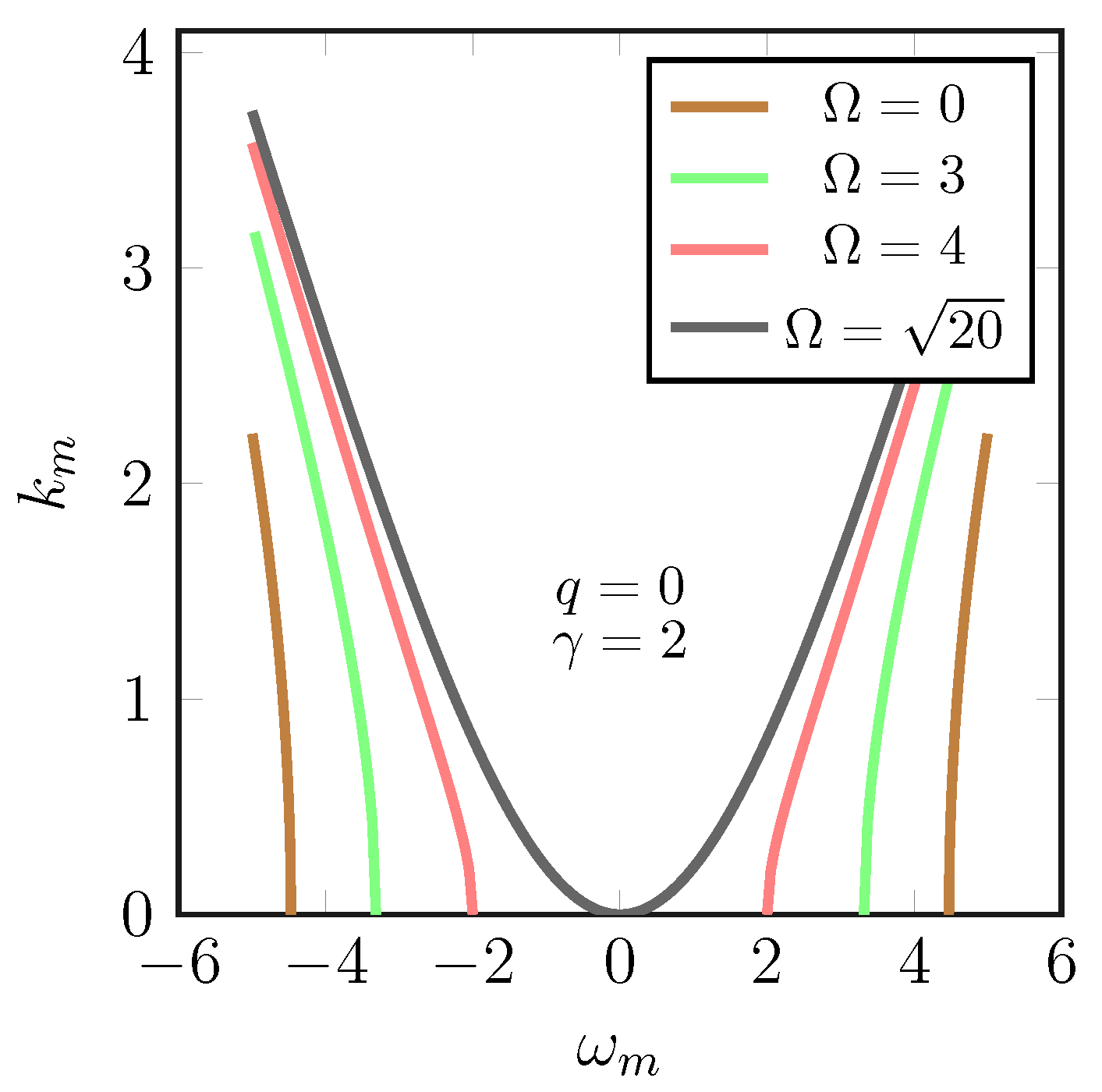
5. Modulated Linear Waves

The study of ordinary linear waves is an important but not sufficient part of the study of wave packet propagation. Here, we will touch upon the topic of modulated packets and their characteristics for the case ${\sigma }_a=+1$ and ${\sigma }_b={\sigma }_c=-1$.

We now proceed from the full array of waveguides (Equation (2)) to a single elementary cell by setting

$$A_n=A{e}^{iqn},B_n=B{e}^{iqn},C_n=C{e}^{iqn}.$$

(15)

This reduction yields three coupled equations. Their solutions are sought in the form of slowly modulated wave packets [53,54]:

$$\begin{array}{cc}\hfill & A(x,t)=\tilde{A}\left(\xi \right)e^{i(kx-\omega t+\phi (\xi \left)\right)},\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & B(x,t)=\left[\tilde{B}\left(\xi \right)+i\tilde{b}\left(\xi \right)\right]e^{i(kx-\omega t+\phi (\xi \left)\right)},\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill & C(x,t)=\left[\tilde{C}\left(\xi \right)+i\tilde{c}\left(\xi \right)\right]e^{i(kx-\omega t+\phi (\xi \left)\right)},\hfill \end{array}$$

(18)

where $\xi =x-Vt$ is the comoving coordinate moving with velocity V, which physically corresponds to the group velocity of the envelope, $\tilde{A},\tilde{B},\tilde{C}$ are real-valued slowly varying amplitudes of the three sublattice fields, $\tilde{b},\tilde{c}$ denote small quadrature components accounting for phase shifts between the B and C sublattice waves and the reference phase, and $\phi \left(\xi \right)$ is the slowly varying envelope phase. Here, $\omega$ is the carrier frequency of the wave packet and k is the longitudinal wave number along the array.

Substitution into Equation (2) yields the following system:

$$\begin{array}{cc}\hfill i(1-V)\dot{\tilde{A}}-\left[k-\omega +(1-V)\dot{\phi }\right]\tilde{A}+(1+e^{iq})\left[\tilde{B}+i\tilde{b}+\gamma (\tilde{C}+i\tilde{c})\right]+{\mu }_a{\tilde{A}}^3& =0,\hfill \\ \hfill -i(1+V)\left(\dot{\tilde{B}}+i\dot{\tilde{b}}\right)+(k+\omega +(1+V)\dot{\phi })\left(\tilde{B}+i\tilde{b}\right)+\tilde{A}(1+e^{iq})+{\mu }_b\left({\tilde{B}}^2+{\tilde{b}}^2\right)(\tilde{B}+i\tilde{b})& =0,\hfill \\ \hfill -i(1+V)\left(\dot{\tilde{C}}+i\dot{\tilde{c}}\right)+(k+\omega +(1+V)\dot{\phi })\left(\tilde{C}+i\tilde{c}\right)+\tilde{A}(1+e^{iq})+{\mu }_c\left({\tilde{C}}^2+{\tilde{c}}^2\right)(\tilde{C}+i\tilde{c})& =0.\hfill \end{array}$$

(19)

Here, dots denote derivatives with respect to $\xi$. By separating the real and imaginary parts, one obtains a closed system of six equations, which will be analyzed below.

By setting $A,B,C=\mathrm{const}$ and linearizing these equations, we obtain dispersion law (3).

Now let us consider an exponentially modulated packet, which we will need to find soliton solutions. To carry this out, we assume the amplitude functions are $\propto exp(\Omega \xi )$ and linearize the system of six equations obtained from Equation (19). This linear system does not contain $\phi$, since it was included in the form of multiplication by amplitude functions. Thus, we have five unknowns and six equations in a system whose compatibility is possible only under the fulfillment of two conditions:

$$k_m^2={\displaystyle \frac{{\Omega }^2+{\omega }_m^2-2(1+{\gamma }^2)(1+cosq)}{1+{\Omega }^2/{\omega }_m^2}},$$

(20)

$$V_m=k_m/{\omega }_m,$$

(21)

where we use the index m to emphasize that $\omega$ and k belong to the dispersion law of modulated waves. Their meaning is easily revealed in the limit of $\Omega \to 0$: the first is the dispersion law (3) written in an inverted form, and the second is the group velocity. Relation (20) implies that when $|\Omega |\ne 0$, the gap in the spectrum narrows (it closes at $|\Omega |\ge 2(1+{\gamma }^2)(1+cosq)$), and we have the opportunity to utilize previously inaccessible harmonics. Generally speaking, at $q\to \pi$, the gap in the spectrum closes, as can be seen in Figure 4, but we note that at $q=\pm \pi$, the spectrum becomes degenerate. Formula (20) states that for exponentially modulated packets, the gap closes even at a fixed q, without spectral degradation (Figure 5). Based on this fact, in the next section, we will obtain gap solitons at a fixed q.

Let us show what the eigenvectors $\{\tilde{A},\tilde{B},\tilde{b},\tilde{C},\tilde{c}\}$ look like in the presence of modulation $\Omega$, using the decomposition ${\omega }_m\to \pm \infty$:

$$\begin{array}{cc}\hfill & \mathrm{for}{\omega }_m\to +\infty v_{1m}(q=0)=\{-2{\omega }_m^2,{\omega }_m,\Omega ,{\omega }_m\gamma ,\Omega \gamma \}\hfill \\ \hfill & \mathrm{for}{\omega }_m\to -\infty v_{2m}(q=0)=\{(1+{\gamma }^2),2|{\omega }_m|,-2\Omega ,2|{\omega }_m|\gamma ,-2\Omega \gamma \}.\hfill \end{array}$$

(22)

As we can see, modulation does not have a significant impact. Assuming weak modulation $\Omega \ll {\omega }_m$, we again arrive at the vectors (14).

6. Solitons

We will assume $\Omega =\epsilon \omega$ with $\epsilon \ll 1$, since we want to consider wave packets containing a large number of oscillations. To analyze the soliton envelope, we then switch to the slow variable $\Omega \xi$.

6.1. Outside the Gap (${\omega }_m>\delta$)

Since a small parameter $\epsilon$ is present in our problem, we expand the solution as a power series:

$$\{\tilde{A},\tilde{B},\tilde{b},\tilde{C},\tilde{c},\phi \}=\sum _{n=1}^{\infty }{\epsilon }^n\{{\tilde{A}}_n,{\tilde{B}}_n,{\tilde{b}}_n,{\tilde{C}}_n,{\tilde{c}}_n,{\phi }_n\}.$$

(23)

We also expand the dispersion relation:

$$k=k_0+k_2{\epsilon }^2+o\left({\epsilon }^2\right),$$

(24)

where for brevity we introduce

$$k_0=\sqrt{{\omega }_m^2-{\delta }^2},k_2={\displaystyle \frac{{\delta }^2}{2\sqrt{{\omega }_m^2-{\delta }^2}}}.$$

Here, $\delta$ denotes the gap width (see Equation (4)).

Substituting these expansions into system (19), separating real and imaginary parts, and analyzing terms of each order in $\epsilon$, we obtain the following results.

At order $\epsilon$:

$${\tilde{B}}_1={\displaystyle \frac{{\tilde{C}}_1}{\gamma }}=-{\displaystyle \frac{\alpha }{{\omega }_m+k_0}}{\tilde{A}}_1,\{{\tilde{b}}_1,{\tilde{c}}_1\}={\displaystyle \frac{\beta }{\alpha }}\{{\tilde{B}}_1,{\tilde{C}}_1\}.$$

(25)

At order ${\epsilon }^3$:

$${\ddot{\tilde{A}}}_1={\tilde{A}}_1-2\theta {\left({\tilde{A}}_1\right)}^3,$$

(26)

which is the standard nonlinear oscillator equation admitting a soliton solution, where

$$\theta ={\displaystyle \frac{{\delta }^2}{2{(1+{\gamma }^2)}^2{({\omega }_m+k_0)}^3}}\left({\mu }_b+{\gamma }^4{\mu }_c+{\mu }_a{\displaystyle \frac{{({\omega }_m+k_0)}^2(1+{\gamma }^2)}{{\delta }^2}}\right).$$

(27)

Thus, to lead the order in $\epsilon$, the soliton solution takes the form

$$\tilde{A}\left(\xi \right)={\displaystyle \frac{\epsilon e^{i(k_{m}x-{\omega }_{m}t)}}{\sqrt{\theta }cosh(\Omega \xi /2)}}.$$

(28)

Equation (25) then determines the corresponding soliton profiles in the B and C waveguides. From Equation (25), it is clear that the ratio of amplitudes approximately satisfies Equation (22). The number of internal oscillations within the soliton is controlled by the scaling $\Omega \sim 1/\epsilon$, while the peak amplitude scales as ∼$\epsilon$.

In Figure 6, we illustrate the collision of solitons corresponding to the eigenvectors given in Equation (14), where the fields are nearly suppressed in certain channels. The trajectories of solitons are shown for different values of q. It can be verified that both branches ${\omega }_{1,2}$ allow for $\theta >0$. In particular, a simple asymptotic analysis in the limit $\omega \gg 1$ demonstrates that for ${\mu }_a=-{\mu }_{b,c}=1$, both modes can simultaneously support soliton formation.

Solitons obtained outside the spectral gap correspond to nonlinear envelope states that can propagate across the array without distortion. In this regime, the carrier frequency lies well within the transmission band, and localization arises primarily from the balance between dispersion and nonlinearity. As a result, these solitons resemble conventional envelope solitons in continuous media, yet are strongly modified by the underlying lattice geometry and the alternating refractive indices of the waveguides.

6.2. On the Gap and Inside the Gap ($\omega \le \delta$)

The expansion of the dispersion relation (24) at the band edge ($\omega =\delta$) is

$$k=\epsilon \delta +o\left({\epsilon }^2\right)=\epsilon k_1+o\left({\epsilon }^2\right),$$

(29)

with $k_1=\omega =\delta$.

Inside the gap, we set $\omega =\delta -d·{\epsilon }^2$, which yields

$$k=\epsilon \sqrt{{\delta }^2-2d\delta }+o\left({\epsilon }^2\right)=\epsilon k_1+o\left({\epsilon }^2\right),$$

(30)

where $k_1=\sqrt{{\delta }^2-2d\delta }$ and hence $d\lesssim \delta /2$. Since the two expansions are identical up to notation, the resulting system of equations derived from Equation (19) must coincide in both cases.

At order $\epsilon$ we obtain

$${\tilde{B}}_1={\displaystyle \frac{{\tilde{C}}_1}{\gamma }}=-{\displaystyle \frac{\alpha }{\delta }}{\tilde{A}}_1,\{{\tilde{b}}_1,{\tilde{c}}_1\}={\displaystyle \frac{\beta }{\alpha }}\{{\tilde{B}}_1,{\tilde{C}}_1\}.$$

(31)

At order ${\epsilon }^3$ we arrive at

$${\ddot{\tilde{A}}}_1={\tilde{A}}_1-2\theta {\left({\tilde{A}}_1\right)}^3,$$

(32)

with

$$\theta ={\displaystyle \frac{1}{\delta {(1+{\gamma }^2)}^2}}\left[{(1+{\gamma }^2)}^2{\mu }_a+{\mu }_b+{\gamma }^4{\mu }_c\right].$$

(33)

The form of the soliton solution is the same as in Equation (28). The difference is that the characteristic number of oscillations supported by this soliton is of order $k/\Omega \sim 1$. For example, if we set $d=\delta /m$, then according to Equation (21), the soliton velocity is approximately

$$V\approx \epsilon \sqrt{1-2/m}.$$

In Figure 7, the analytical trajectories are compared with direct numerical simulations. The agreement confirms that solitons can propagate both outside and inside the forbidden gap.

The type of solution is the same as that described in Equation (32). The difference is that the characteristic number of oscillations carried by this soliton is on the order of $k/\Omega \sim 1$. If we put $d=\delta /m$ for simplicity, then the velocity of the soliton is approximately equal to $\epsilon \sqrt{1-2/m}$ according to Equation (21). Figure 7b shows the soliton trajectories for different values of the d.

The situation inside the forbidden gap differs qualitatively from that outside the gap. Here, linear modes cannot propagate, but nonlinearity enables the formation of localized states that effectively “self-create” a propagation channel. These gap solitons owe their existence to the delicate compensation between the bandgap-induced evanescence and the nonlinear phase shift. Consequently, they are more strongly localized than their outside-the-gap counterparts and exhibit only a small number of oscillations within their envelope, as confirmed by the analytical estimates of their velocity and structure.

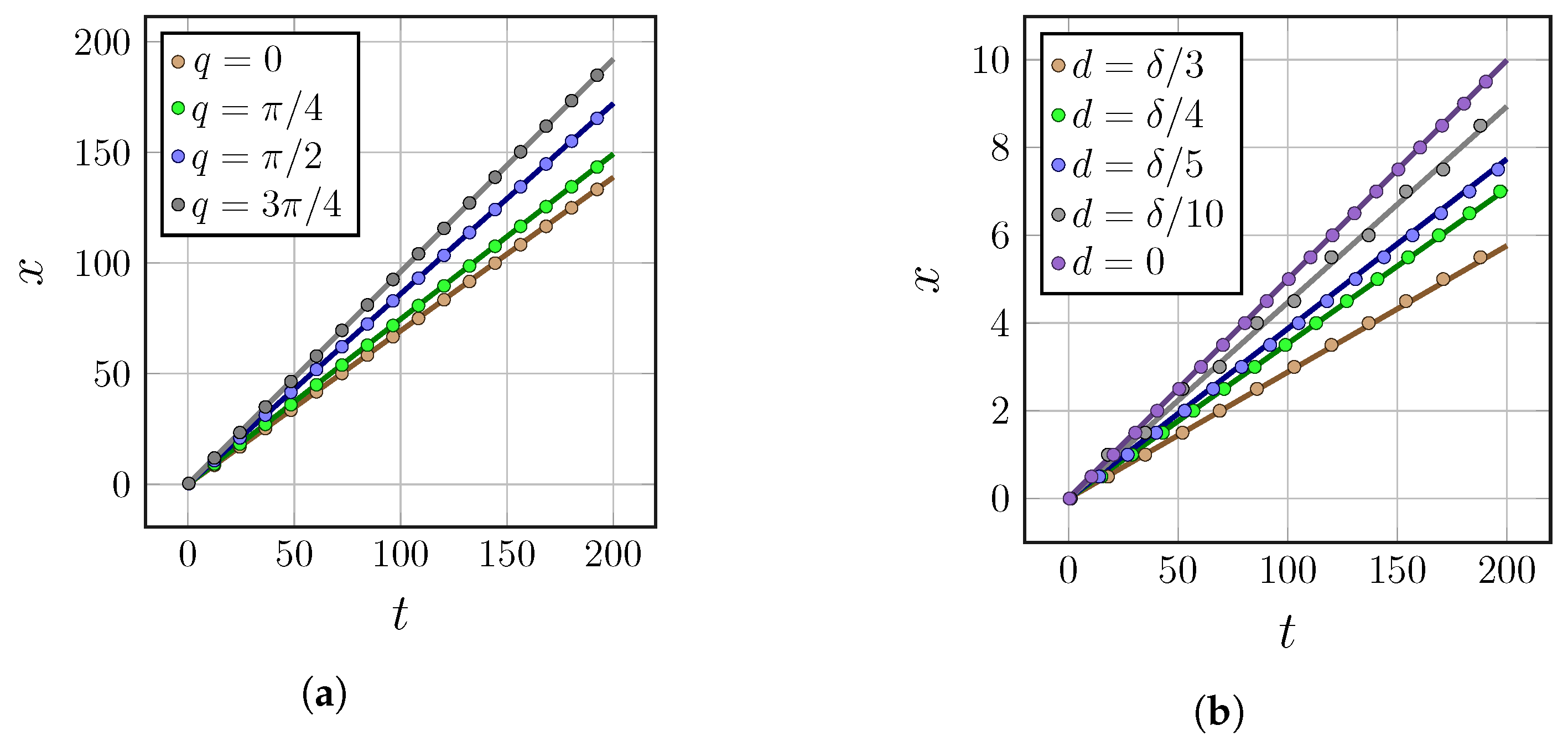
7. Formation of Solitons

7.1. Benchmark Against Bragg-Type Couplers and Standard Metrics

To connect our model to well-established results, consider the reduction of Equation (2) at $q=0$ with $\gamma =1$ and ${\mu }_c=0$, which suppresses one arm of the rhombic cell. In this limit, the system reduces to a contra-directional (Bragg-type) two-mode coupler for $\{A,B\}$ with forward–backward coupling and a bandgap centered at $\omega =\pm k$, recovering the classical coupled-mode description of gap solitons [56,57,58]. The dispersion curves (8) and the group velocity $v_g=\partial \omega /\partial k$ coincide with the textbook Bragg model, while our mixed-index rhombic array generalizes it by (i) an additional arm C and (ii) the tunable asymmetry parameter $\gamma$.

For later use, we also record the standard soliton metrics in the nonlinear Schrödinger (NLS) equation reduction (42). Writing the envelope equation in the canonical form

$$i{\displaystyle \frac{\partial U}{\partial \tau }}+{\displaystyle \frac{1}{2}}{\beta }_2^{\mathrm{eff}}{\displaystyle \frac{{\partial }^{2}U}{\partial {\xi }^2}}+{\gamma }_{\mathrm{eff}}{\left|U\right|}^{2}U=0,$$

(34)

we identify ${\beta }_2^{\mathrm{eff}}=2{\omega }_{kk}$ and ${\gamma }_{\mathrm{eff}}=\theta$. The soliton number (a commonly used metric) for an initial pulse of duration $T_0$ and peak envelope $U_0$ is

$$N^2={\displaystyle \frac{L_D}{L_{NL}}}={\displaystyle \frac{T_0^2}{|{\beta }_2^{\mathrm{eff}}|}}{\gamma }_{\mathrm{eff}}{U}_0^2={\displaystyle \frac{T_0^2}{2|{\omega }_{kk}|}}\theta U_0^2.$$

(35)

Fundamental solitons correspond to $N\simeq 1$; higher N predicts fission into multi-soliton trains. Equation (35) will be used below to estimate experimental power levels.

7.2. Formation of the Soliton Profile

When considering an extended array of coupled waveguides, it is not sufficient to launch identical single–waveguide soliton profiles into each channel to obtain a collective soliton inside the structure. As follows from the dispersion analysis, each individual channel supports waves with a normalized group velocity $v=1$, whereas the collective modes of the array propagate with a reduced effective velocity $V=k/\omega$ (see Equation (21) and Figure 4), which is always smaller than unity. Consequently, the temporal envelopes of simultaneously injected pulses become progressively desynchronized along the propagation direction. If the initial pulse duration is $T_0$, its spatial length $v{T}_0$ contracts to $V{T}_0$, implying that the peak power of the coupled pulse increases approximately as $P\approx P_{\mathrm{in}}v/V$.

Physically, the reduced velocity of the composite wave arises from the interference between counter-propagating components, analogous to the mechanism observed in Bragg reflection waveguides [56]. In our system, two eigenmodes ${\omega }_{1,2}$ with eigenvectors $v_{1,2}$ correspond to forward- and backward-propagating waves. Any excitation inside the array inevitably contains both components, and their interference leads to a net slowdown of the resulting envelope.

To analyze how an input pulse evolves into localized nonlinear states, we consider, following [58], the case $q=0$ in Equations (2) and (11). We represent the total field vector as a superposition of the two eigenmodes ${\omega }_{\pm }$:

$$\mathcal{V}=\left(\begin{array}{c}B\\ A\\ C\end{array}\right)=\left(\epsilon U{v}_{+}+{\epsilon }^{2}W{v}_{-}\right)e^{i(k{x}_0-{\omega }_{+}{t}_0)},$$

(36)

where U and W are the slowly varying modal amplitudes (Bloch envelopes). Introducing the multiple-scale expansion

$$t=t_0+\epsilon t_1+\dots ,x=x_0+\epsilon x_1+\dots ,$$

(37)

and substituting Equation (36) into the evolution system, we obtain

$$\left(iE{\displaystyle \frac{\partial }{\partial t}}+i{E}^{\prime }{\displaystyle \frac{\partial }{\partial x}}+L+N\right)\mathcal{V}=0,$$

(38)

where E is the identity matrix

$$E^{\prime }=\left(\begin{array}{ccc}-1& 0& 0\\ 0& 1& 0\\ 0& 0& -1\end{array}\right),L=\left(\begin{array}{ccc}0& 2& 0\\ 2& 0& \gamma \\ 0& 2\gamma & 0\end{array}\right),N=E\left(\begin{array}{c}{\mu }_b{\left|B\right|}^2\\ {\mu }_a{\left|A\right|}^2\\ {\mu }_c{\left|C\right|}^2\end{array}\right).$$

(39)

At order ${\epsilon }^2$, one obtains

$$i\left({\displaystyle \frac{\partial }{\partial t_1}}+E^{\prime }{\displaystyle \frac{\partial }{\partial x_1}}\right)v_{+}U=({\omega }_{-}-{\omega }_{+})v_{-}W.$$

(40)

Multiplying from the left by $v_{+}^T$ and $v_{-}^T$ gives

$$\left({\displaystyle \frac{\partial }{\partial t_1}}+v_g{\displaystyle \frac{\partial }{\partial x_1}}\right)U=0,W={\displaystyle \frac{v_{-}^T{E}^{\prime }{v}_{+}}{({\omega }_{-}-{\omega }_{+})v_{-}^T{v}_{-}}}{\displaystyle \frac{\partial U}{\partial x_1}},$$

(41)

where $v_g=\left(v_{+}^T{E}^{\prime }{v}_{+}\right)/\left(v_{+}^T{v}_{+}\right)=\partial {\omega }_{+}/\partial k$ is the group velocity. Hence, U and W depend on $x_1$ and $t_1$ only through ${\xi }_1=x_1-v_g{t}_1$.

Proceeding to order ${\epsilon }^3$, we obtain the nonlinear Schrödinger equation for the envelope U:

$$i\left({\displaystyle \frac{\partial U}{\partial t_2}}+v_g{\displaystyle \frac{\partial U}{\partial x_2}}\right)+{\omega }_{kk}{\displaystyle \frac{{\partial }^{2}U}{\partial {\xi }_1^2}}-\theta {\left|U\right|}^{2}U=0,$$

(42)

where ${\omega }_{kk}={\partial }^2\omega /\partial k^2$ and $\theta =-v_{-}^{T}N{v}_{+}$ defines the effective nonlinear coefficient. Equation (42) coincides with the standard nonlinear Schrödinger equation, implying that the system supports stable solitons provided $\theta >0$. This condition links the nonlinear coefficients ${\mu }_{a,b,c}$ in the same manner as derived in the previous section.

If $\theta >0$, the evolution of a sufficiently strong initial pulse leads to the formation of a dispersive shock wave, which subsequently breaks into a soliton train [63,64]. The number of emerging solitons can be estimated using the well-known Bohr–Sommerfeld quantization rule for the integrable NLS equation [65,66]. In the dimensionless variables $t\to \theta t$ and $x\to x\sqrt{\theta /{\omega }_{kk}}$, and for

$$U(x,t)=\sqrt{\rho (x,t)}exp\left(i\underset{0}{\overset{x}{\int }}v(x^{\prime },t)d{x}^{\prime }\right),$$

the approximate number of solitons N generated from an initial smooth pulse is

$$N\simeq {\displaystyle \frac{1}{2\pi }}\underset{-\infty }{\overset{+\infty }{\int }}p(\rho \left(x\right),v\left(x\right),0)dx,$$

(43)

where $p^2(\rho ,v,q)={(q-v\left(x\right))}^2-4\rho \left(x\right)$. The discrete soliton parameters correspond to quantized values $q_n$ satisfying

$$\underset{x_1\left(q_n\right)}{\overset{x_2\left(q_n\right)}{\int }}p(\rho \left(x\right),v\left(x\right),q_n)dx=2\pi n,$$

(44)

with $x_{1,2}$ being the turning points defined by $p=0$. This approach provides a natural physical picture for the transformation of an incoming nonlinear pulse into a sequence of solitons within the rhombic lattice.

In practice, the expected number of emerging solitons and the corresponding power thresholds follow from (35) and (45) for the chosen operating point $(k,q)$.

7.3. Order-of-Magnitude Power Levels

To provide an intuitive scale, we translate the NLS envelope (42) to physical units. Let $A_{\mathrm{phys}}$ denote the optical field envelope in one arm, with nonlinear coefficient ${\gamma }_{\mathrm{NL}}=n_2{\omega }_0/\left(c{A}_{\mathrm{eff}}\right)$ (SI units) and effective second-order dispersion ${\beta }_2^{\mathrm{eff}}=2{\omega }_{kk}$ extracted from the linear spectrum at the operating point. For a transform-limited input pulse of duration $T_0$ and peak power $P_0$, the fundamental-soliton condition ($N\simeq 1$) in the canonical NLS form is [57]:

$$P_0\approx {\displaystyle \frac{|{\beta }_2^{\mathrm{eff}}|}{{\gamma }_{\mathrm{NL}}{T}_0^2}}.$$

(45)

Typical parameters for integrated platforms in the telecom band are as follows:

• Si₃N₄ waveguidesat ${\lambda }_0\simeq 1550$ nm: $n_2\sim 2.4\times {10}^{-19}$ m²/W, $A_{\mathrm{eff}}\sim 0.5$–$1.0\mu$m²⇒ ${\gamma }_{\mathrm{NL}}\sim 0.6$–$1.2$ W⁻¹m⁻¹ [67,68].
• Effective dispersion near a Bragg point can reach $|{\beta }_2^{\mathrm{eff}}|\sim {10}^{-25}$ s²/m, depending on design [69].

Inserting $T_0=1$ ps and these values into Equation (45) gives $P_0\sim 0.05$–$0.2$ W, while for $T_0=100$ fs the estimate increases to several watts, consistent with the $1/T_0^2$ scaling. Such levels are routinely achieved in pulsed on-chip experiments. In our mixed-index lattice, the effective coefficients ${\beta }_2^{\mathrm{eff}}$ and ${\gamma }_{\mathrm{eff}}=\theta$ are tunable through the operating point $(k,q)$ and coupling ratio $\gamma$, allowing a reduction of $P_0$ by approaching steeper portions of the dispersion (larger $|{\omega }_{kk}|$) while maintaining $\theta >0$.

7.4. Concrete Device Sketches

Two practical realizations compatible with the present theory are as follows:

• Corrugated (Bragg) rhombic cell. The A-arm is a straight waveguide (forward mode), while the B/C arms incorporate weak Bragg corrugations tuned to contra-directionally couple forward/backward Bloch modes at the operating wavelength. The lattice constant is set by the horizontal pitch of the rhombi; the grating period obeys $\Lambda \simeq {\lambda }_0/\left(2n_{\mathrm{eff}}\right)$.
• FBG-assisted coupler chain. A 1D array in which every second arm carries a shallow Bragg grating (backward mode), interleaved with unmodulated arms (forward mode). The nearest-neighbour couplings implement the rhombic connectivity; the coupling asymmetry is adjusted to set $\gamma$.

Both designs map directly onto Equation (2) with ${\sigma }_a=+1$, ${\sigma }_{b,c}=-1$ and support the soliton families constructed in Section 3, Section 4, Section 5, Section 6 and Section 7.

8. Conclusions

We have investigated nonlinear wave localization in a rhombic waveguide array composed of three types of waveguides, including channels with opposite signs of the refractive index. Within this framework, longitudinal soliton solutions were derived in the form of exponentially modulated envelope states that propagate robustly across all three sublattices. Their analytical description was obtained using the method of multiple scales.

In contrast to conventional rhombic lattices with only positive refractive indices, the inclusion of a negative-index channel enables selective control of the field intensity within individual cells of the structure, offering enhanced tunability for potential applications. Numerical simulations demonstrate that pulses propagating through such mixed-index arrays can exhibit asymmetric suppression of individual field components and mutual interactions between counter-propagating waves, consistent with the analytical predictions.

The existence of soliton solutions is governed by the effective nonlinear parameter $\theta$, defined by Equations (27) and (33). Solitons arise whenever $\theta >0$, which imposes explicit constraints on the nonlinear coefficients ${\mu }_{a,b,c}$ and allows for various combinations of focusing and defocusing nonlinearities. Direct numerical simulations confirm the analytical results and illustrate the robustness of the obtained soliton families across a broad range of parameters.

Furthermore, by reducing the initial system to a nonlinear Schrödinger equation for the Bloch envelope describing the superposition of forward- and backward-propagating fields, we have outlined a mechanism for soliton formation from an intense smooth input pulse. Within this approach, the number and parameters of emergent solitons can be evaluated using standard methods of the integrable NLS theory, linking the present model to the broader framework of dispersive shock waves and soliton trains in nonlinear optics.

Our results highlight several important aspects of nonlinear localization in rhombic lattices with positive- and negative-index waveguides. First, the interplay between the spectral gap and the coupling asymmetry between forward- and backward-propagating channels strongly affects the conditions for localization, enabling both outside-the-gap and gap solitons. Second, the explicit dependence of the soliton parameter on the nonlinear coefficients provides a route to engineer and control the stability of localized states. From a broader perspective, these findings are conceptually related to recent studies of solitons in lattices with suppressed diffraction or engineered dispersion [28,29,70,71], and open possibilities for applications in robust light guiding, nonlinear filtering, and compact photonic devices.

In this study, we neglected linear losses, higher-order dispersion, self-steepening, Raman scattering, and structural disorder. These effects can, in principle, be included perturbatively and are not expected to alter the fundamental soliton existence condition $\theta >0$, although they may impose practical limitations on the achievable soliton length and interaction distance. The nonlinear Schrödinger reduction used here assumes slowly varying envelopes and operation away from strong avoided crossings, except near the targeted Bragg resonance.

Beyond their fundamental interest, the presented analytical framework can be extended to higher-dimensional and topological lattices, offering new insights into nonlinear effects in structured photonic media and paving the way for controllable soliton-based light transport in integrated photonic circuits.