Novel High-Contrast Photoacoustic Imaging Method for Cancer Cell Monitoring Based on Dual-Wavelength Confocal Metalenses
Abstract
1. Introduction
2. Methods
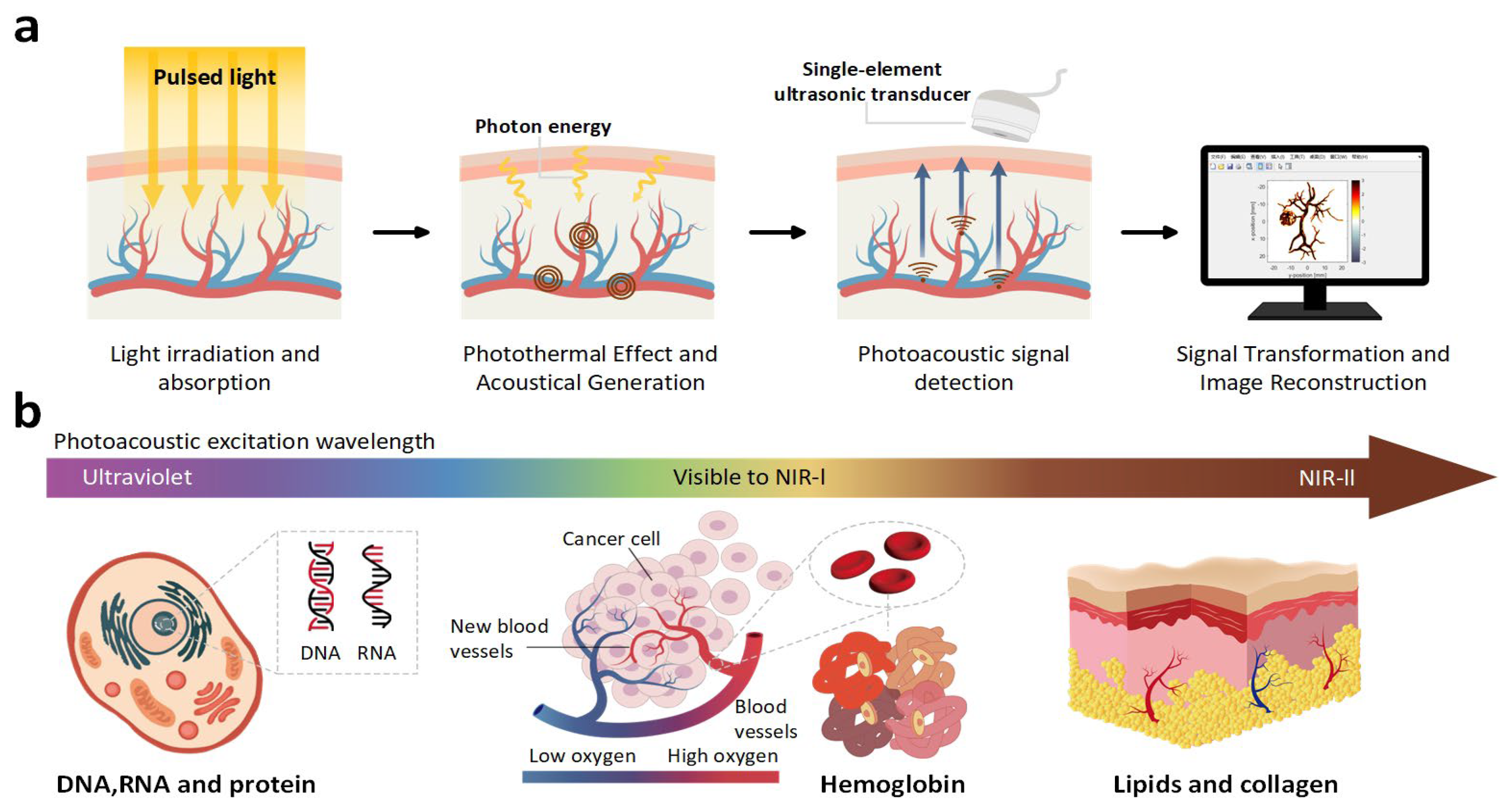
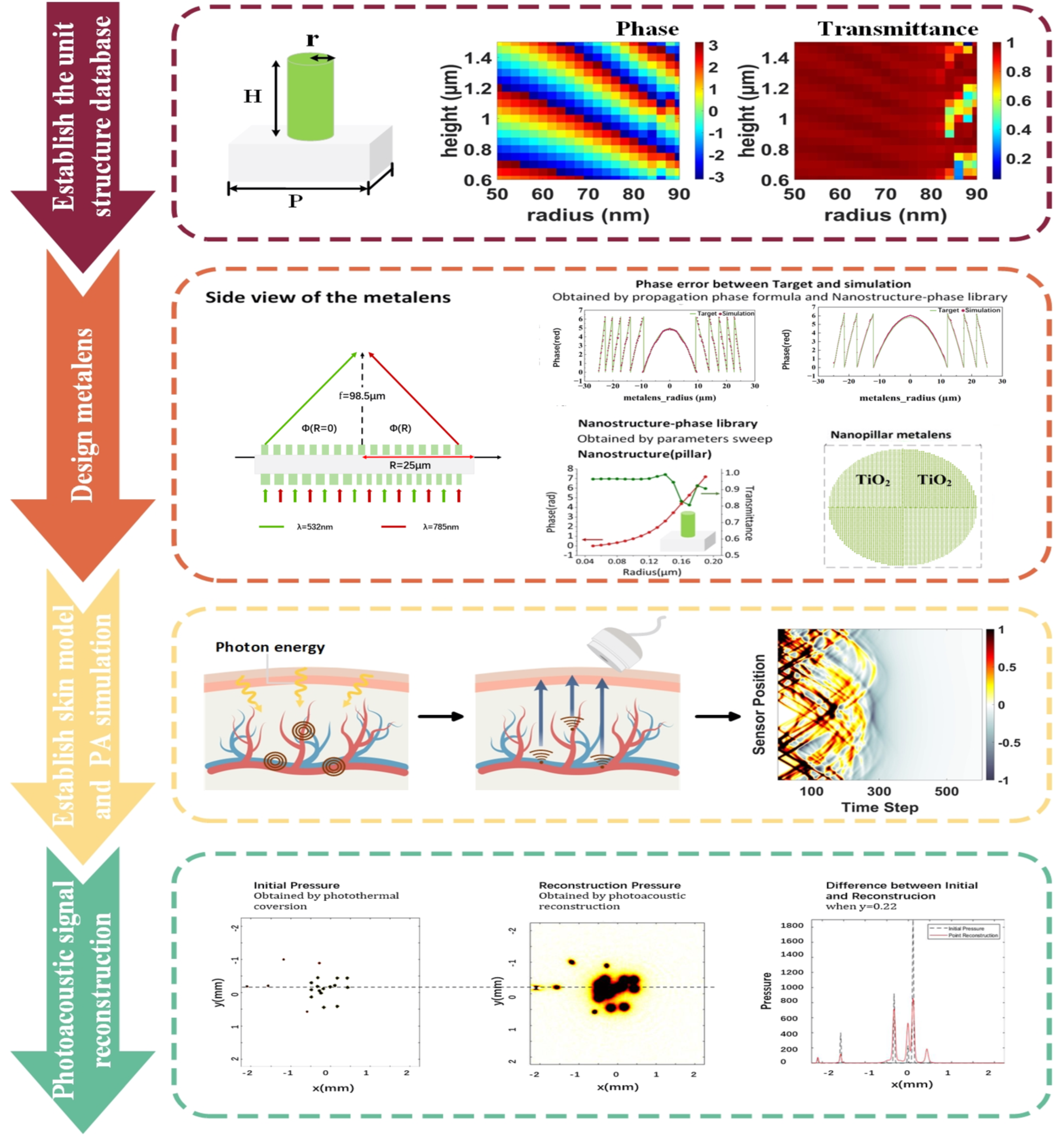
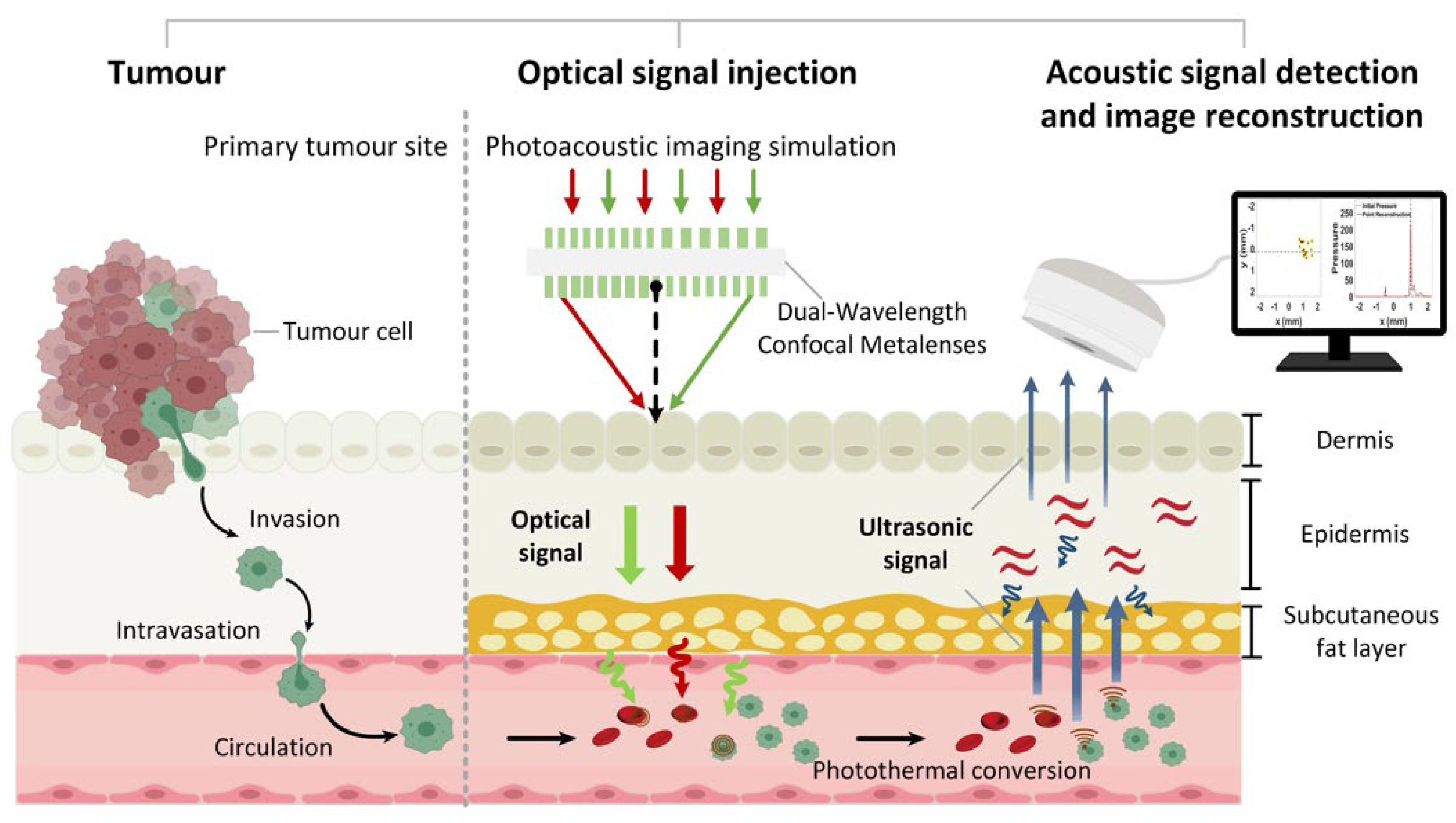
2.1. Overall Strategy
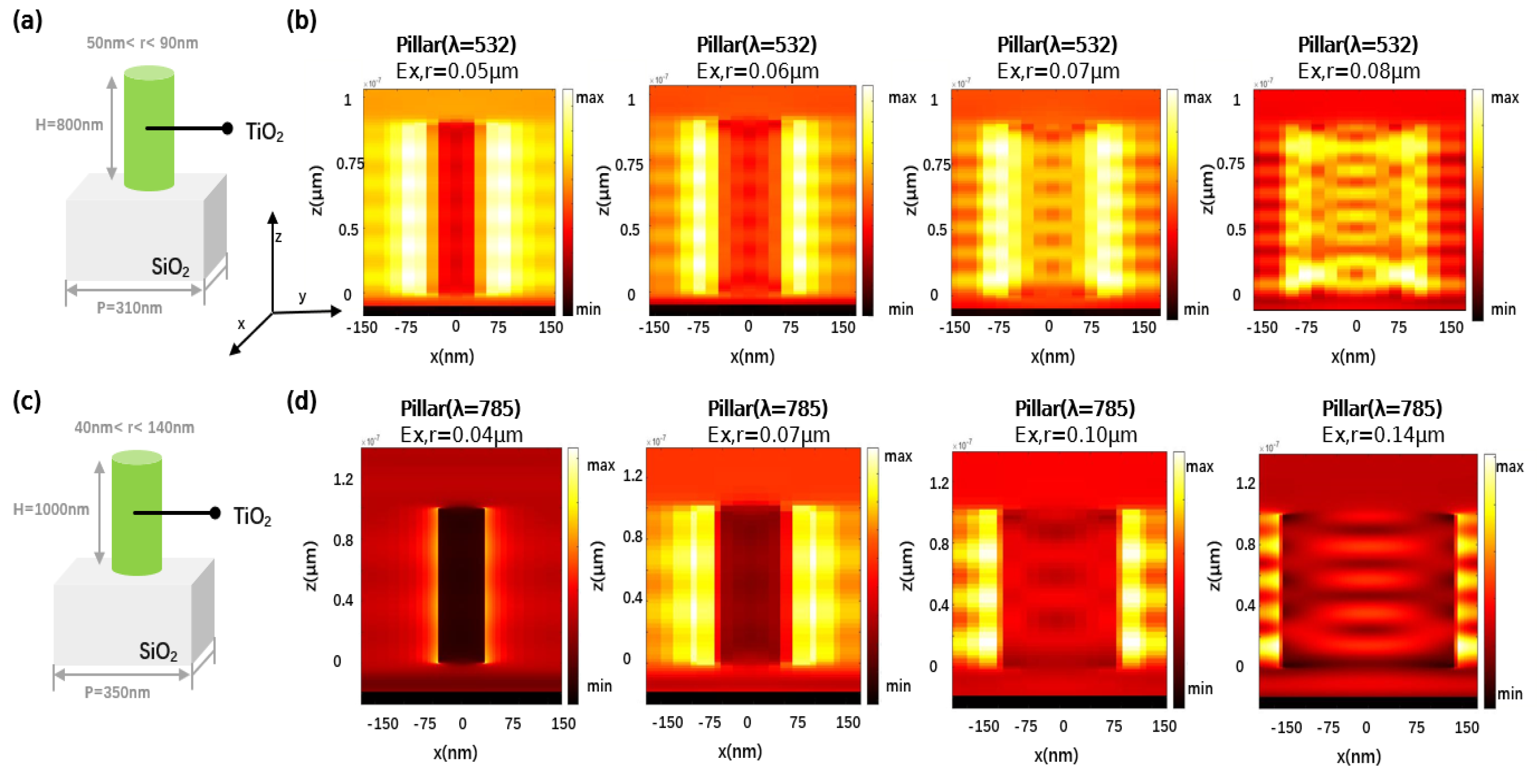
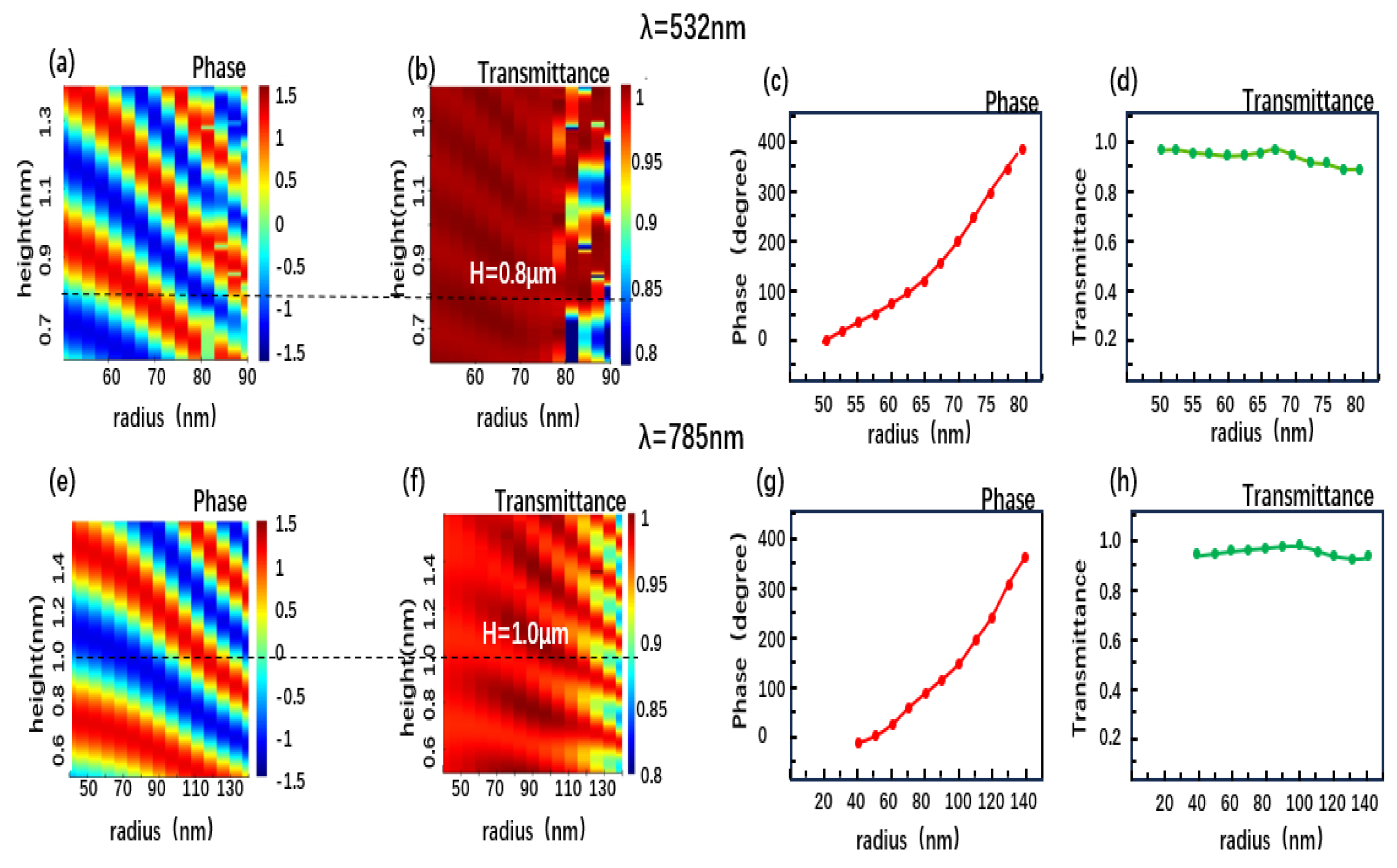
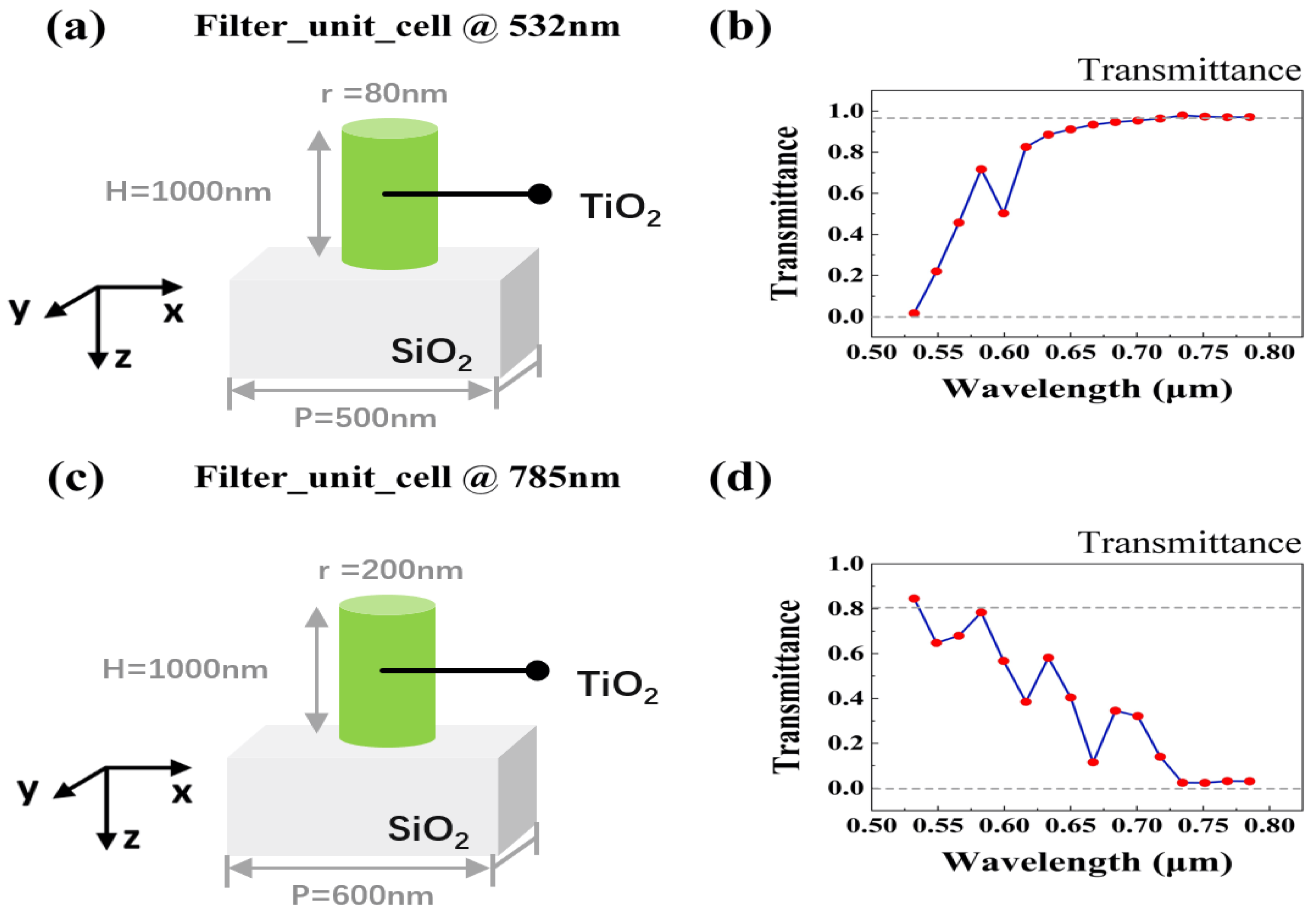
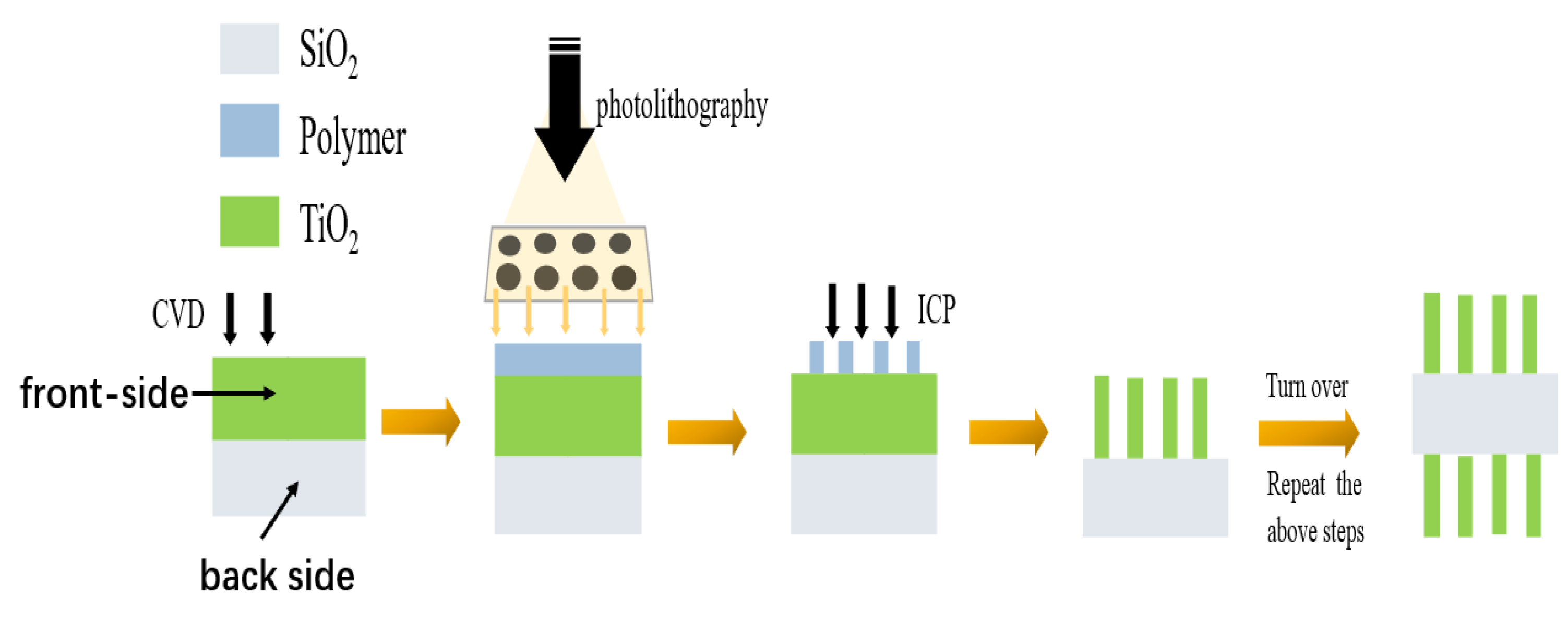
2.2. The Design of Metalens
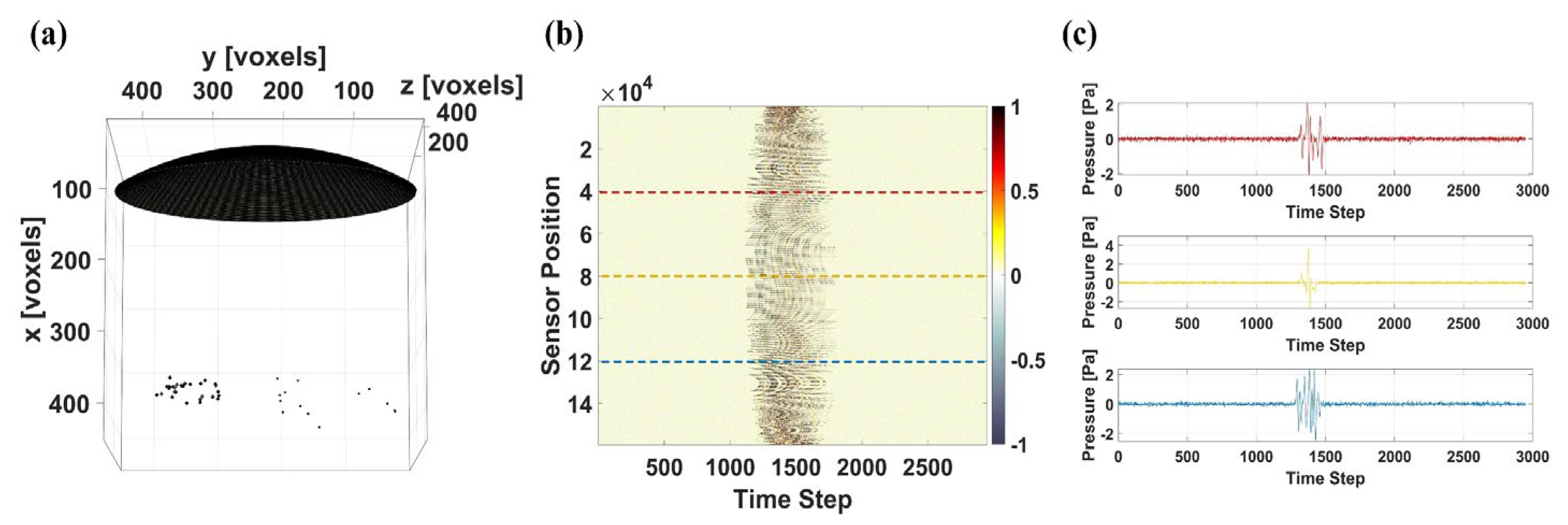
2.3. Three-Dimensional Photoacoustic Simulation
3. Results
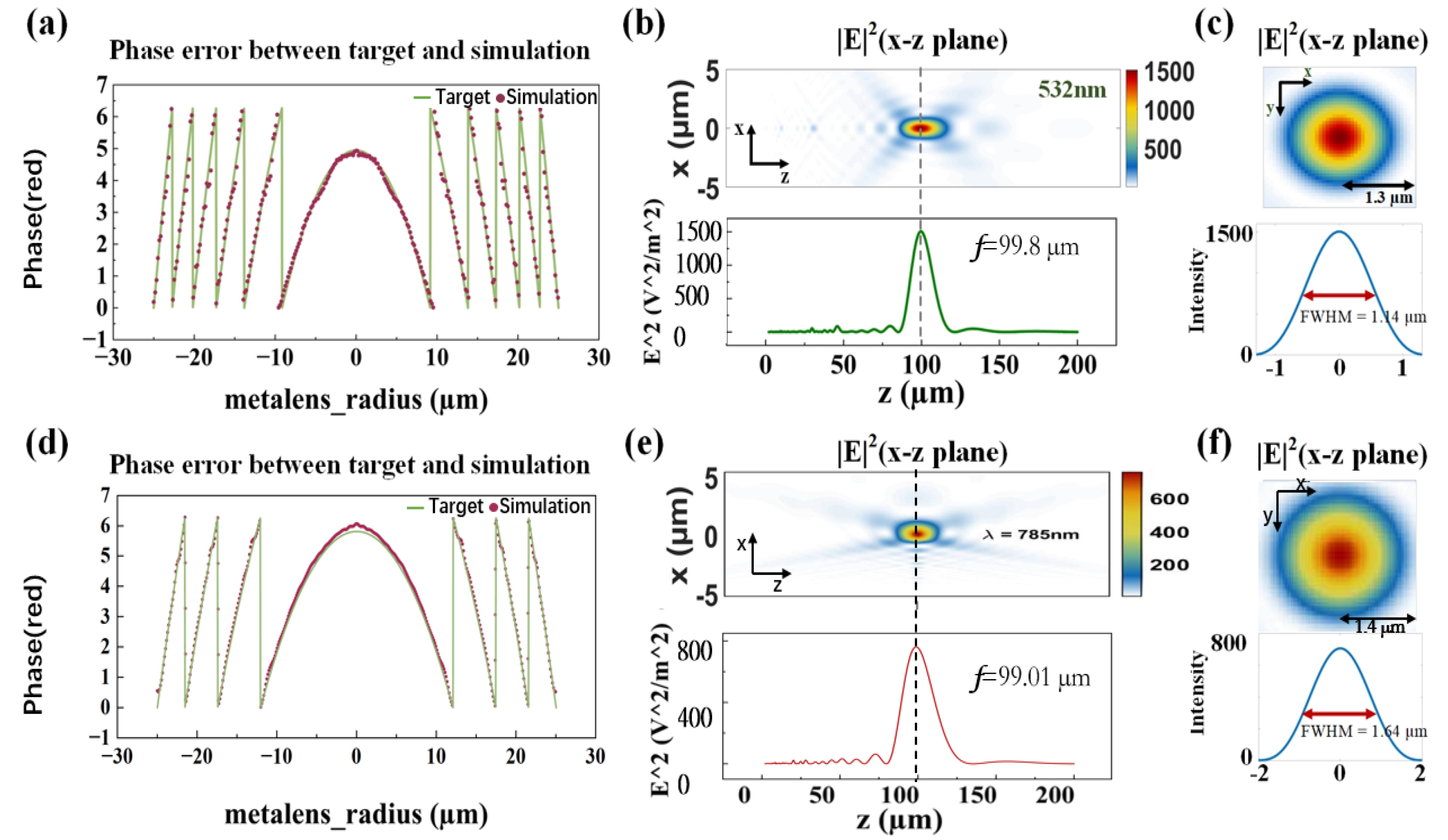
3.1. Focusing Properties of Single-Wavelength Metalens
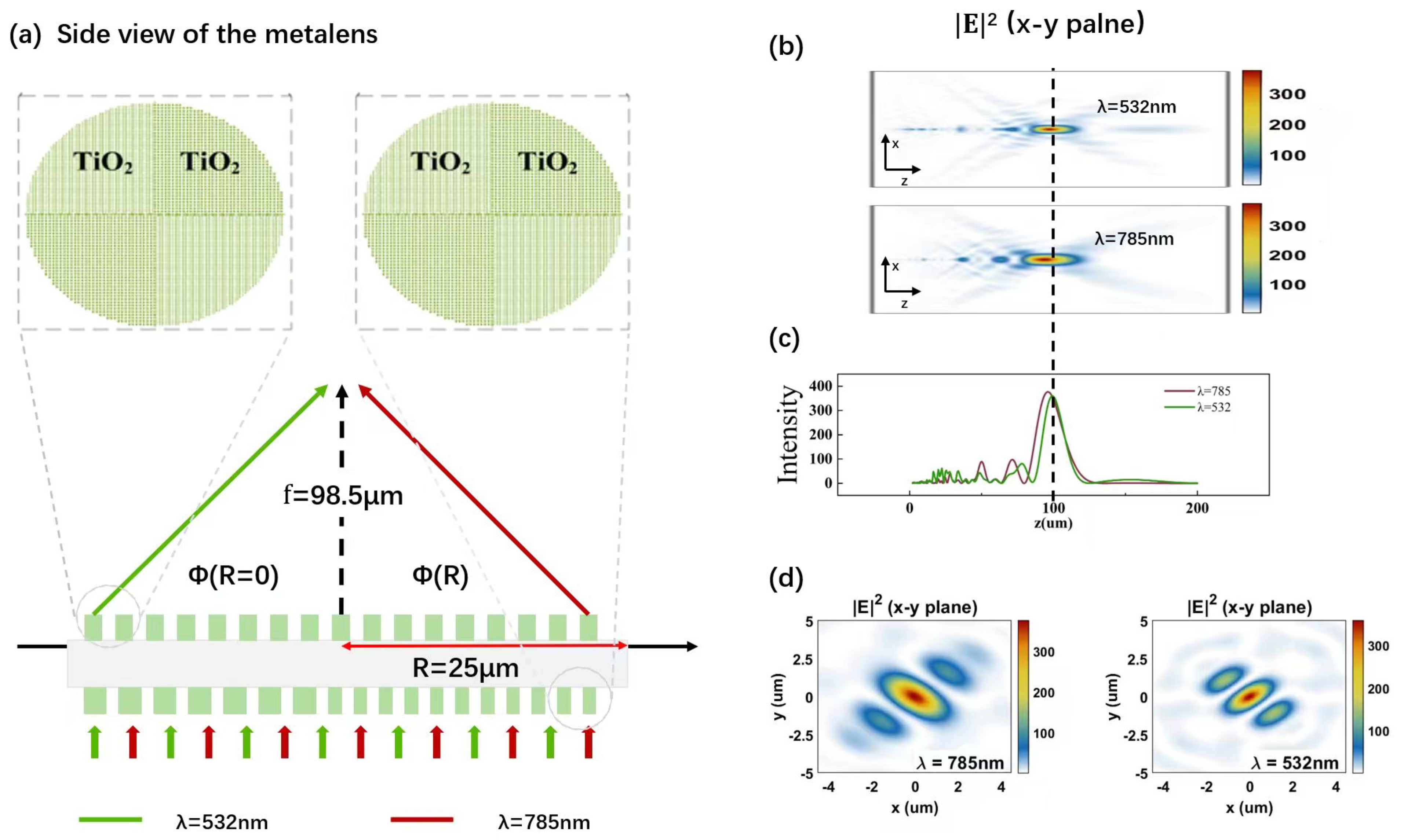
3.2. Simulation Results of the Visible-IR Metalens
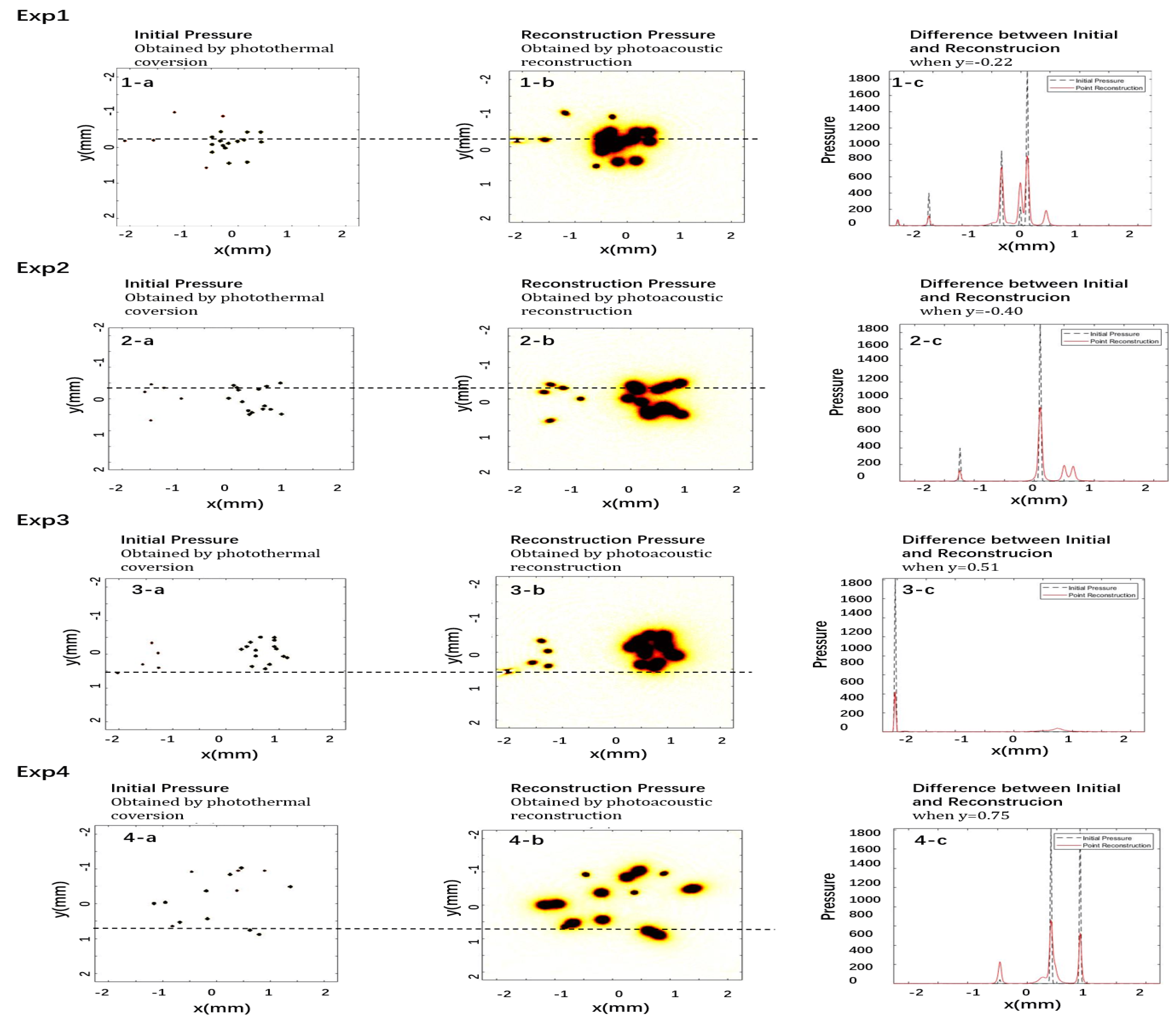
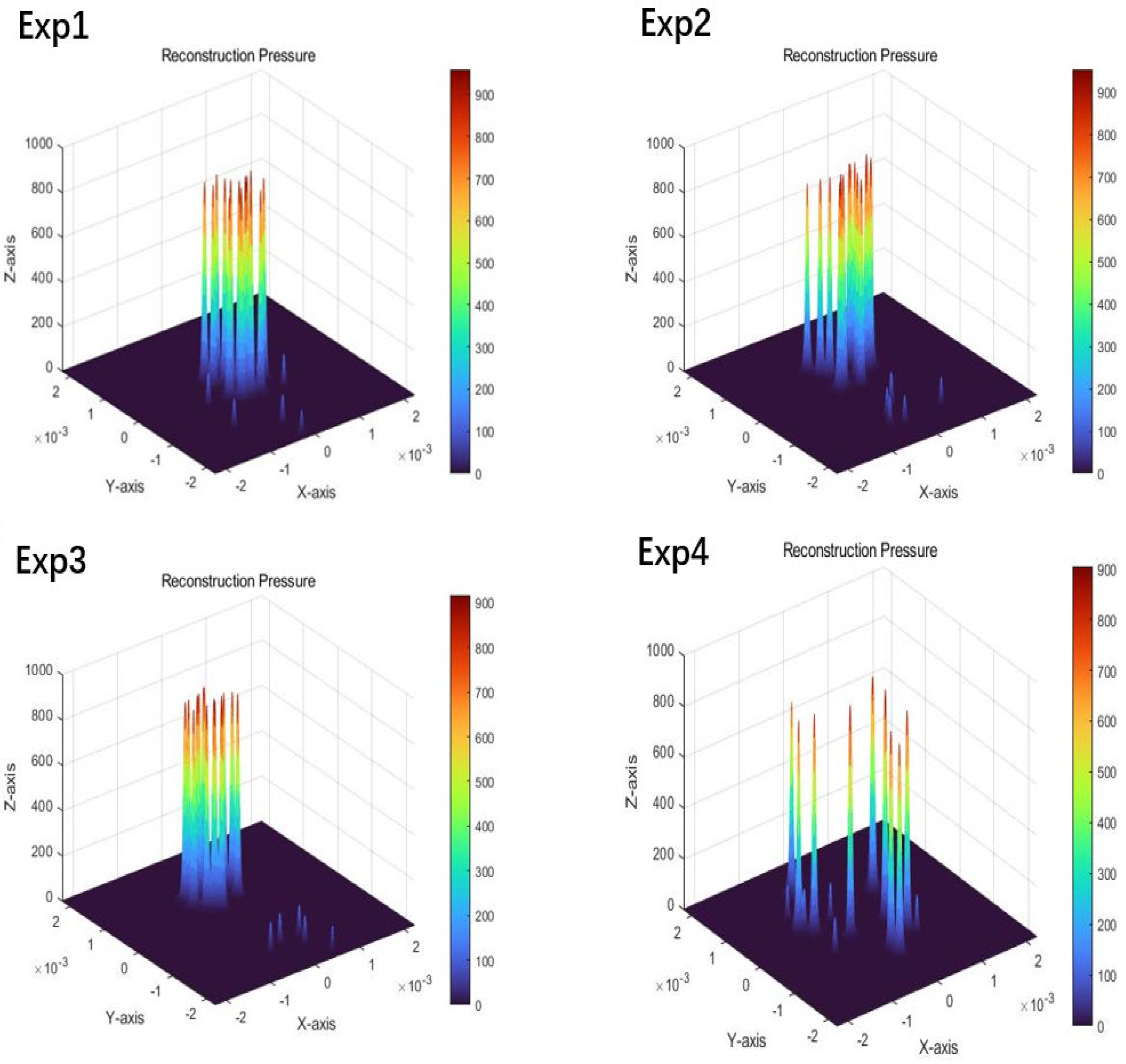
3.3. Results of 3D PA
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bray, F.; Laversanne, M.; Sung, H.; Ferlay, J.; Siegel, R.L.; Soerjomataram, I.; Jemal, A. Global cancer statistics 2022: GLOBOCAN estimates of incidence and mortality worldwide for 36 cancers in 185 countries. CA A Cancer J. Clin. 2024, 74, 229–263. [Google Scholar] [CrossRef] [PubMed]
- Momose, A. Phase-sensitive imaging and phase tomography using X-ray interferometers. Opt. Express 2003, 11, 2303–2314. [Google Scholar] [CrossRef]
- Wang, Y.; Ge, X.; Ma, H.; Qi, S.; Zhang, G.; Yao, Y. Deep Learning in Medical Ultrasound Image Analysis: A Review. IEEE Access 2021, 9, 54310–54324. [Google Scholar] [CrossRef]
- Yao, J.; Wang, L.V. Perspective on fast-evolving photoacoustic tomography. J. Biomed. Opt. 2021, 26, 060602. [Google Scholar] [CrossRef]
- Wang, L.V.; Yao, J. A practical guide to photoacoustic tomography in the life sciences. Nat. Methods 2016, 13, 627–638. [Google Scholar] [CrossRef]
- Yao, J.; Wang, L.V. Photoacoustic tomography: Fundamentals, advances and prospects. Contrast Media Mol. Imaging 2011, 6, 332–345. [Google Scholar] [CrossRef]
- Bell, A.G. On the production and reproduction of sound by light. Am. J. Sci. 1880, 20, 305–324. [Google Scholar] [CrossRef]
- Xu, M.; Wang, L.V. Photoacoustic imaging in biomedicine. Rev. Sci. Instrum. 2006, 77, 041101. [Google Scholar] [CrossRef]
- Razansky, D. Volumetric multi-spectral optoacoustic tomography for high performance structural, functional, and molecular imaging. J. Acoust. Soc. Am. 2016, 140 (Suppl. 4), 2978–2979. [Google Scholar] [CrossRef]
- Tang, J.; Coleman, J.E.; Dai, X.; Jiang, H. Wearable 3-D Photoacoustic Tomography for Functional Brain Imaging in Behaving Rats. Sci. Rep. 2016, 6, 25470. [Google Scholar] [CrossRef]
- Gottschalk, S.; Fehm, T.F.; Deán-Ben, X.L.; Razansky, D. Noninvasive real-time visualization of multiple cerebral hemodynamic parameters in whole mouse brains using five-dimensional optoacoustic tomography. J. Cereb. Blood Flow Metab. Off. J. Int. Soc. Cereb. Blood Flow Metab. 2015, 35, 531–535. [Google Scholar] [CrossRef]
- Wang, L.; Maslov, K.; Xing, W.; Garcia-Uribe, A.; Wang, L.V. Video-rate functional photoacoustic microscopy at depths. J. Biomed. Opt. 2012, 17, 106007. [Google Scholar] [CrossRef]
- Ahmed, R.; Butt, H. Metalens sensors: Strain-Multiplex Metalens Array for Tunable Focusing and Imaging (Adv. Sci. 4/2021). Adv. Sci. 2021, 8, 2170019. [Google Scholar] [CrossRef]
- Cui, T.J. Microwave metamaterials. Natl. Sci. Rev. 2018, 5, 134–136. [Google Scholar] [CrossRef]
- Jahani, S.; Jacob, Z. All-dielectric metamaterials. Nat. Nanotechnol. 2016, 11, 23–36. [Google Scholar] [CrossRef]
- Jang, M.; Horie, Y.; Shibukawa, A.; Brake, J.; Liu, Y.; Kamali, S.M.; Arbabi, A.; Ruan, H.; Faraon, A.; Yang, C. Wavefront shaping with disorder-engineered metasurfaces. Nat. Photonics 2018, 12, 84–90. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, W.; Moitra, P.; Kravchenko, I.I.; Briggs, D.P.; Valentine, J. Dielectric Meta-Reflectarray for Broadband Linear Polarization Conversion and Optical Vortex Generation. Nano Lett. 2014, 14, 1394–1399. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Genevet, P.; Yu, N.; Kats, M.A.; Gaburro, Z.; Capasso, F. Out-of-Plane Reflection and Refraction of Light by Anisotropic Optical Antenna Metasurfaces with Phase Discontinuities. Nano Lett. 2012, 12, 1702–1706. [Google Scholar] [CrossRef]
- Huang, L.; Chen, X.; Mühlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Zentgraf, T.; Zhang, S. Dispersionless Phase Discontinuities for Controlling Light Propagation. Nano Lett. 2012, 12, 5750–5755. [Google Scholar] [CrossRef]
- Wang, S.; Wu, P.C.; Su, V.-C.; Lai, Y.-C.; Hung Chu, C.; Chen, J.-W.; Lu, S.-H.; Chen, J.; Xu, B.; Kuan, C.-H.; et al. Broadband achromatic optical metasurface devices. Nat. Commun. 2017, 8, 187. [Google Scholar] [CrossRef] [PubMed]
- Aieta, F.; Kats, M.A.; Genevet, P.; Capasso, F. Multiwavelength achromatic metasurfaces by dispersive phase compensation. Science 2015, 347, 1342–1345. [Google Scholar] [CrossRef]
- Khorasaninejad, R.; Shi, Z.; Zhu, A.; Chen, W.T.; Sanjeev, V.; Capasso, F. Achromatic Metalens over 60 nm Bandwidth in the Visible and Metalens with Reverse Chromatic Dispersion. Nano Lett. 2017, 17, 1819–1824. [Google Scholar] [CrossRef]
- Ou, X.; Zeng, T.; Zhang, Y.; Jiang, Y.; Gong, Z.; Fan, F.; Jia, H.; Duan, H.; Hu, Y. Tunable Polarization-Multiplexed Achromatic Dielectric Metalens. Nano Lett. 2022, 22, 10049–10056. [Google Scholar] [CrossRef]
- Cao, R.; Kilroy, J.P.; Ning, B.; Wang, T.; Hossack, J.A.; Hu, S. Multispectral photoacoustic microscopy based on an optical–acoustic objective. Photoacoustics 2015, 3, 55–59. [Google Scholar] [CrossRef]
- Chao, L.; Jiangbo, C.; Yachao, Z.; Jingyi, Z.; Lidai, W. Five-wavelength optical-resolution photoacoustic microscopy of blood and lymphatic vessels. Adv. Photonics 2021, 3, 016002. [Google Scholar] [CrossRef]
- Barulin, A.; Park, H.; Park, B.; Kim, I. Dual-wavelength UV-visible metalens for multispectral photoacoustic microscopy: A simulation study. Photoacoustics 2023, 32, 100545. [Google Scholar] [CrossRef] [PubMed]
- Kesharwani, P.; Ma, R.; Sang, L.; Fatima, M.; Sheikh, A.; Abourehab, M.A.S.; Gupta, N.; Chen, Z.-S.; Zhou, Y. Gold nanoparticles and gold nanorods in the landscape of cancer therapy. Mol. Cancer 2023, 22, 98. [Google Scholar] [CrossRef] [PubMed]
- Goddard, Z.R.; Marín, M.J.; Russell, D.A.; Searcey, M. Active targeting of gold nanoparticles as cancer therapeutics. Chem. Soc. Rev. 2020, 49, 8774–8789. [Google Scholar] [CrossRef]
- Vines, J.B.; Yoon, J.-H.; Ryu, N.-E.; Lim, D.-J.; Park, H. Gold Nanoparticles for Photothermal Cancer Therapy. Front. Chem. 2019, 7, 167. [Google Scholar] [CrossRef]
- Chen, X.; Huang, L.; Mühlenbernd, H.; Li, G.; Bai, B.; Tan, Q.; Jin, G.; Qiu, C.-W.; Zhang, S.; Zentgraf, T. Dual-polarity plasmonic metalens for visible light. Nat. Commun. 2012, 3, 1198. [Google Scholar] [CrossRef]
- Arbabi, E.; Arbabi, A.; Kamali, S.M.; Horie, Y.; Faraon, A. Controlling the sign of chromatic dispersion in diffractive optics with dielectric metasurfaces. Optica 2017, 4, 625–632. [Google Scholar] [CrossRef]
- Yu, N.; Genevet, P.; Kats, M.A.; Aieta, F.; Tetienne, J.-P.; Capasso, F.; Gaburro, Z. Light Propagation with Phase Discontinuities: Generalized Laws of Reflection and Refraction. Science 2011, 334, 333–337. [Google Scholar] [CrossRef]
- Treeby, B.; Zhang, E.; Cox, B. Photoacoustic tomography in absorbing acoustic media using time reversal. Inverse Probl. Inverse Probl. 2010, 26157, 115003–115020. [Google Scholar] [CrossRef]
- Sim, J.Y.; Ahn, C.-G.; Jeong, E.-J.; Kim, B.K. In vivo Microscopic Photoacoustic Spectroscopy for Non-Invasive Glucose Monitoring Invulnerable to Skin Secretion Products. Sci. Rep. 2018, 8, 1059. [Google Scholar] [CrossRef]
- Andrieux, A.; Mennemanteuil, M.-M.; Geoffroy, N.; Emo, M.; Markey, L.; Hammani, K. Optimized ICPCVD-Based TiO2 for Photonics. Materials 2022, 15, 2578. [Google Scholar] [CrossRef]
- Hassaan, M.; Saleem, U.; Singh, A.; Haque, A.J.; Wang, K. Recent Advances in Positive Photoresists: Mechanisms and Fabrication. Materials 2024, 17, 2552. [Google Scholar] [CrossRef]
- Fan, Z.; Xu, L.; Zhou, B.; Chen, T. Fabrication of Anti-Reflective Composite Structures on Inverted Pyramids Using Inductively Coupled Plasma Etching. Micromachines 2025, 16, 503. [Google Scholar] [CrossRef]
- Barulin, A.; Barulina, E.; Oh, D.K.; Jo, Y.; Park, H.; Park, S.; Kye, H.; Kim, J.; Yoo, J.; Kim, J.; et al. Axially multifocal metalens for 3D volumetric photoacoustic imaging of neuromelanin in live brain organoid. Science advances 2025, 11, eadr0654. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Jiang, X.; Qu, G.; Han, J.; Li, C.; Bo, B.; Ruan, Q.; Liu, Z.; Song, Q.; Xiao, S. On-chip integration of achromatic metalens arrays. Nat. Commun. 2025, 16, 7485. [Google Scholar] [CrossRef]

| Physical Layer | Acoustic Properties | |||
|---|---|---|---|---|
| Ρ (kg·m−3) | Vc (m·s−1) | Zc (kg·m−2s−1) | L (mm) | |
| Dermis | 1200 | 1645 | 1.7 × 10−6 | 0.1 |
| Epidermis | 1200 | 1595 | 1.7 × 10−6 | 1.4 |
| Subcutaneous fat layer | 1000 | 1450 | 1.7 × 10−6 | 2 |
| Blood | 100 | 1500 | 1.7 × 10−6 | 1 |
| Physical Layer | Optical Properties (532 nm) | ||||
|---|---|---|---|---|---|
| (mm−1) | (mm−1) | g | n | L (mm) | |
| Dermis | 1.44 ± 0.69 | 7.04 ± 1.48 | 0.9 | 1.34 | 0.1 |
| Epidermis | 0.10 ± 0.03 | 3.96 ± 0.89 | 0.9 | 1.39 | 1.4 |
| Subcutaneous fat layer | 0.15 ± 0.07 | 1.89 ± 0.45 | 0.9 | 1.44 | 2 |
| Physical Layer | Optical Properties (785 nm) | ||||
|---|---|---|---|---|---|
| (mm−1) | (mm−1) | g | n | L (mm) | |
| Dermis | 0.17 ± 0.09 | 3.17 ± 0.85 | 0.9 | 1.33 | 0.1 |
| Epidermis | 0.07 ± 0.01 | 1.45 ± 0.29 | 0.9 | 1.40 | 1.4 |
| Subcutaneous fat layer | 0.04 ± 0.02 | 1.18 ± 0.17 | 0.9 | 1.44 | 2 |
| Cell Type | 532 nm | 785 nm | ||
|---|---|---|---|---|
| Red blood cell | 0.2 | 0.15 | 0.1 | 0.01 |
| Cancer cells (with AuNPs) | 0.3 | 0.2 | 0.2 | 0.2 |
| Exp Code | Initial | Reconstruction | ||||
|---|---|---|---|---|---|---|
| Number | Number | Pressure (Pa) | ||||
| Normal | Cancer | Normal | Cancer | Normal | Cancer | |
| Exp1 | 5 | 15 | 5 | 15 | 123.75 | 861.78 |
| Exp2 | 5 | 15 | 5 | 15 | 132.61 | 897.67 |
| Exp3 | 7 | 18 | 5 | 15 | 117.12 | 904.5 |
| Exp4 | 14 | 11 | 5 | 10 | 132.31 | 818.82 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Zhang, R.; Zhang, H.; Zhang, B.; Qin, L.; Du, J.; Zhao, T.; Wang, B. Novel High-Contrast Photoacoustic Imaging Method for Cancer Cell Monitoring Based on Dual-Wavelength Confocal Metalenses. Photonics 2025, 12, 1053. https://doi.org/10.3390/photonics12111053
Chen Z, Zhang R, Zhang H, Zhang B, Qin L, Du J, Zhao T, Wang B. Novel High-Contrast Photoacoustic Imaging Method for Cancer Cell Monitoring Based on Dual-Wavelength Confocal Metalenses. Photonics. 2025; 12(11):1053. https://doi.org/10.3390/photonics12111053
Chicago/Turabian StyleChen, Zixue, Ruihao Zhang, Hongbin Zhang, Bingqiang Zhang, Lei Qin, Jiansen Du, Tao Zhao, and Bin Wang. 2025. "Novel High-Contrast Photoacoustic Imaging Method for Cancer Cell Monitoring Based on Dual-Wavelength Confocal Metalenses" Photonics 12, no. 11: 1053. https://doi.org/10.3390/photonics12111053
APA StyleChen, Z., Zhang, R., Zhang, H., Zhang, B., Qin, L., Du, J., Zhao, T., & Wang, B. (2025). Novel High-Contrast Photoacoustic Imaging Method for Cancer Cell Monitoring Based on Dual-Wavelength Confocal Metalenses. Photonics, 12(11), 1053. https://doi.org/10.3390/photonics12111053





