Investigation of Debris Mitigation in Droplet-Based Terbium Plasma Sources Produced by Laser Ablation Under Varying Buffer Gas Pressures

Abstract

The fragment suppression ability of terbium plasma generated by laser at different environmental pressures is investigated, with a focus on exploring the slowing effect of buffer gas on high-energy particles. Using two-dimensional radiation hydrodynamic simulations with the FLASH code, this study evaluates the debris mitigation efficiency of terbium plasma across a range of buffer gas pressures (50–1000 Pa). Key findings reveal that helium buffer gas exhibits a nonlinear pressure-dependent response in plasma dynamics and debris suppression. Specifically, at 1000 Pa helium, the plasma shockwave stops within stopping distance $x_{st}$ = 12.13 mm with an attenuation coefficient of b = 0.0013 ns⁻¹, reducing radial expansion by 40% compared to 50 Pa ($x_{st}$ = 23.15 mm, b = 0.0010). This pressure scaling arises from enhanced collisional dissipation, confining over 80% of debris kinetic energy below 200 eV under 1000 Pa conditions. In contrast, argon exhibits superior stopping power within ion energy domains (≤1300 eV), attaining a maximum stopping power of 2000 eV·mm⁻¹ at 1300 eV–a value associated with a 6.4-times-larger scattering cross-section compared to helium under equivalent conditions. The study uncovers a nonlinear relationship between kinetic energy and gas pressure, where the deceleration capability of buffer gases intensifies with increasing kinetic energy. This work demonstrates that by leveraging argon’s broadband stopping efficiency and helium’s confinement capacity, debris and high energy ions can be effectively suppressed, thereby securing mirror integrity and source efficiency at high repetition rates.

1. Introduction

Laser-produced plasma (LPP) has been extensively studied in various applications, such as inertial confinement fusion, pulsed laser deposition in materials science, and lithography techniques [1]. Beyond extreme ultraviolet (BEUV) lithography is regarded as a promising technology for manufacturing next-generation semiconductor devices with resolutions below 5 nm [2]. LPP has been developed as a BEUV light source due to its high efficiency, power scalability, and spatial flexibility around the plasma. In industrial applications, EUV radiation is generated by focusing pre-laser pulses onto micron-sized tin droplets to induce deformation [3]. A higher intensity main pulse laser then heats the deformed droplets, generating plasma that emits sufficient radiation at a wavelength of 13.5 nm, which can be effectively captured by Mo/Si multilayer mirrors (MLM) [4]. To achieve higher resolution, production process parameters can generally be advanced, and the optical numerical aperture can be increased; however, the simplest and most effective method is to shorten the wavelength of the exposure source [5]. Recent studies suggest that La/B₄C multilayer mirrors could achieve theoretical reflectivity approaching 70% at 6.7 nm [6]. At this wavelength, terbium plasma is considered an ideal emitter, primarily due to the formation of unresolved transition arrays (UTA) during the n = 4 to n = 4 transitions, which can emit strong BEUV radiation near 6.7 nm [7]. This radiative characteristic endows terbium plasma with significant potential in BEUV light source applications, particularly in next-generation semiconductor manufacturing technologies. The complex electronic structure of terbium, especially the energy level distribution of its 4f electrons, allows for multiple transitions in the excited state, leading to overlapping transitions that result in high-intensity radiation output [8]. The high temperature and density of terbium plasma lead to enhanced radiation efficiency, which in turn fulfills the critical requirements for high brightness and resolution in modern lithography.

The interaction of the laser beam with solid or liquid terbium droplets leads to the generation of vapor, plasma, and the formation of nano and micro-sized debris [9]. In the high-temperature, high-density plasma environment, the laser energy not only produces high-energy ions and neutral fragments, but these particles also move in all directions as the plasma expands, significantly interfering with the collection mirrors for BEUV radiation [10]. Low-energy atoms from sputtered materials or condensable fuels may deposit on the mirror surface, forming thin films that affect its optical performance; meanwhile, high-energy ions and charge-exchanged neutral atoms may cause sputtering, implantation, and roughening of the mirror surface [11]. These effects can reduce the reflectivity of the mirrors, thereby impacting the overall efficiency and performance of the BEUV light source. Therefore, effective measures must be taken to suppress the emission of particles and ions from the source to prevent these particles from striking the collection mirrors, thus prolonging the lifespan of the mirrors and enhancing the reliability and efficiency of the light source [12]. Currently, various methods exist to mitigate debris and ion emission, such as using buffer gases, magnetic field capture techniques, and optimizing laser parameters. The use of buffer gases is a simple and effective approach for suppressing plasma debris [13]. According to the study by S. S. Harilal et al., argon gas effectively thermalizes and decelerates tin particles through collisional interactions, with this effect being particularly significant beyond a distance of 6 mm [14]. Furthermore, experimental work by Davide Bleiner et al. demonstrate that the axial stopping power of argon for tin fragments reaches 425 eV/mm, which is approximately four times that of helium, indicating higher efficiency of argon in dissipating kinetic energy [15].

There has been limited research on the behavior of terbium plasma debris after the laser pulse under different ambient pressures. Terbium and tin differ fundamentally in their physical properties, such as atomic mass, electronic energy-level structures, and ionization energies. This suggests that Tb may exhibit different laser energy coupling efficiency due to different charge-to mass ratio. This study primarily investigates the debris suppression capabilities of laser-produced BEUV sources from terbium plasma under varying pressures. The FLASH 4.8 program was utilized to simulate the interactions between the laser, terbium, and the ambient gas. This software package includes models for the interaction of laser photons with the target/vapor/plasma, gas dynamics, as well as radiation and thermal processes. 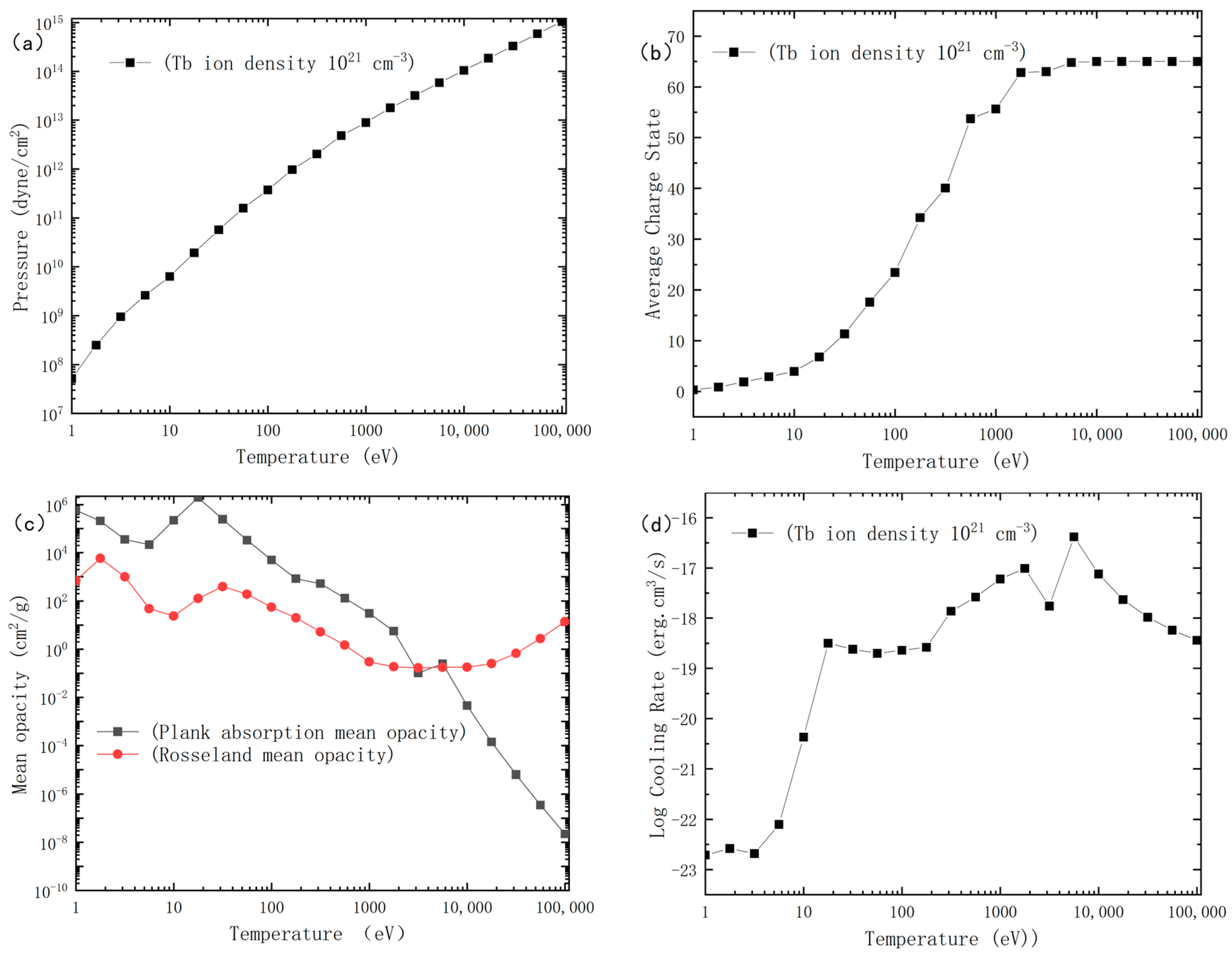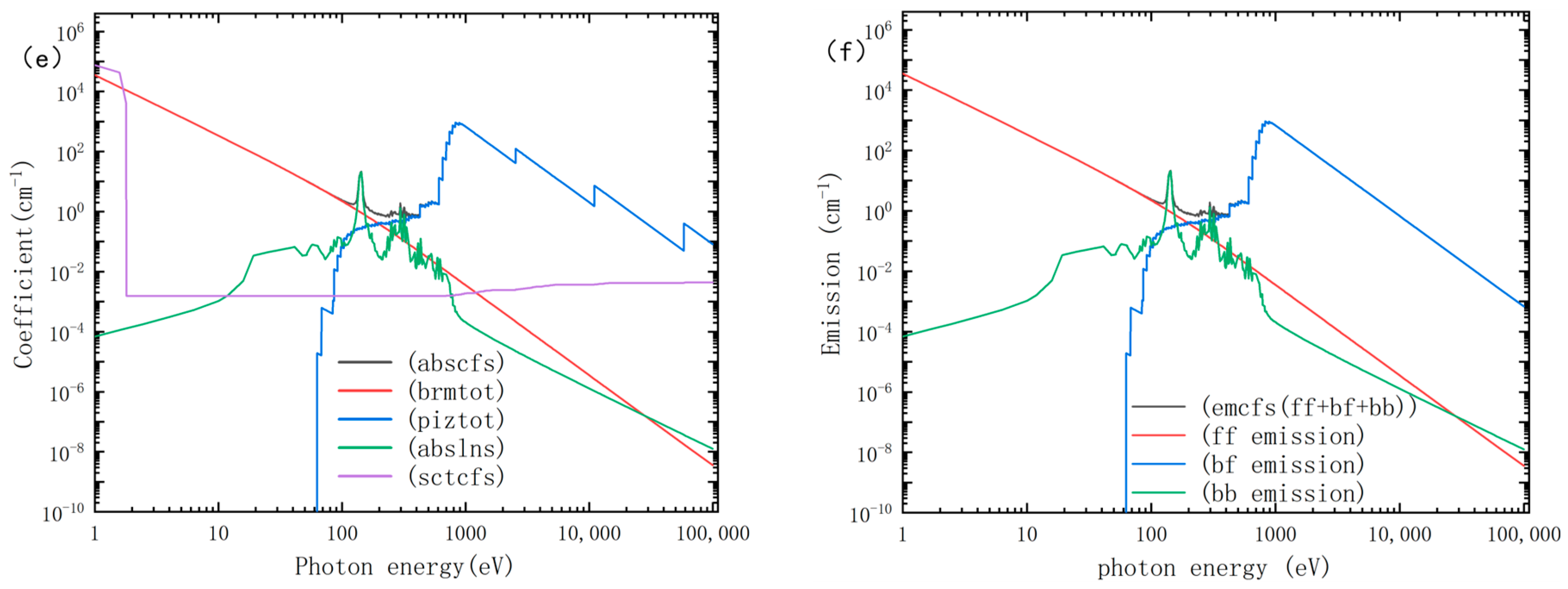The organizational structure of this paper is as follows: In Section 2, we introduce the FLASH 4.8 fluid dynamics code, the equation of state for terbium plasma, and computational methods for radiative opacity. Section 3 presents an analysis of background gas effects on plasma debris stopping power at varying pressure levels, including the suppression efficiency of different background gases for mitigating plasma debris generation. Finally, Section 4 summarizes the key findings of our study and suggests potential directions for future research.

2. Simulation Methods

2.1. RHD Simulation Program of Laser Ablation Plasma of Terbium Targets Based on FLASH Code

In this study, we employ the FLASH 4.8 computational framework to conduct radiation hydrodynamics simulations of laser-generated plasmas in terbium liquid droplet targets, with the aim of advancing the development of beyond extreme ultraviolet lithography sources [16]. FLASH 4.8 is a cutting-edge code for astrophysical and high-energy-density physics simulations, particularly well-suited for investigating laser-driven plasma dynamics within the context of radiation hydrodynamics (RHD). The code employs an adaptive mesh refinement (AMR) strategy to handle multiscale spatial resolution requirements and complex physical phenomena with high computational efficiency. Although FLASH 4.8 supports one-to-three-dimensional modeling, our analysis focuses on two-dimensional simulations of pulsed laser ablation processes in terbium liquid droplet targets. Liquid droplet targets offer distinct advantages over solid counterparts by enabling uniform and stable plasma generation through self-regulating surface dynamics, continuous mass replenishment via microfluidic delivery systems, and precise parameter control over energy deposition [17]. These characteristics collectively enhance experimental controllability and expand the applicability of such targets in extreme environments. Our simulations systematically investigate the fundamental plasma formation mechanisms, including laser-target interaction kinetics, energy absorption profiles, and radiative transport processes in terbium plasmas. By tracking temporal evolution of key plasma parameters—such as electron temperature, mass density distributions, velocity fields, and average charge-state populations, this methodology not only elucidates the underlying physical processes but also establishes a predictive framework for optimizing BEUV source performance through liquid droplet target technology.

FLASH is used to solve the hydrodynamic equations for the evolution of plasma in the absence of magnetic fields as follows:

$${\displaystyle \frac{𝜕\rho }{𝜕t}}+\nabla ·\left(\rho \overrightarrow{v}\right)=0$$

(1)

$${\displaystyle \frac{𝜕\rho \overrightarrow{v}}{𝜕t}}+\nabla ·\left(\rho \overrightarrow{v}\overrightarrow{v}\right)+\nabla ·P_{tot}=0$$

(2)

$${\displaystyle \frac{𝜕\left(\rho E_{tot}\right)}{𝜕t}}+\nabla ·\left[\left(\rho E_{tot}+P_{tot}\right)\overrightarrow{v}\right]=Q_{las}-\nabla ·\overrightarrow{q}$$

(3)

where $\rho$ is the mass density of the fluid, $\overrightarrow{v}$ is the average velocity of the fluid, $P_{\mathrm{t}\mathrm{o}\mathrm{t}}$ is the total pressure of the fluid, $E_{tot}$ is the specific kinetic energy, and $Q_{\mathrm{l}\mathrm{a}\mathrm{s}}$ is the energy deposition of the incident laser, total heat flux is denoted by $\overrightarrow{q}$, which is calculated by the energy deposition module in FLASH 4.8.

2.2. Equation of State and Radiation Opacity

FLASH does not provide relevant data on the radiation opacity of terbium plasma. To perform the calculations, it is necessary for the user to provide values for the radiation opacity, pressure, density, and charge state of the plasma at different electron and ion temperatures. We utilized and extended the program IONMIX [18], developed by the Computer Physics Communications Program Library at Queen’s University Belfast, to obtain the equation of state and radiation opacity for terbium ions. The equation used in IONMIX to calculate the plasma energy is as follows:

$$\begin{array}{c}E={\displaystyle \frac{n_{tot}}{\rho }}\left\{{\displaystyle \frac{3}{2}}\left(1+〈Z〉\right)T\right.\hfill \\ \left.\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+{\displaystyle \sum _k}{f}_k{\displaystyle \sum _{j=1}^{Z_k}}{f}_{jk}\left[\left({\displaystyle \sum _{I=0}^{j-1}}{\Phi }_{lk}\right)+\left({\displaystyle \sum _{i=n_0+1}}{f}_{ijk}{\left(∆E_{i{n}_0}\right)}_{jk}\right)\right]\right\}\hfill \end{array}$$

(4)

where $\rho$ is the mass density of the plasma, $n_{tot}$ is the total atomic nucleus density of a specific element in the plasma, and the proportions of the element in specific ionization and excitation states are defined as follows: $f_k={\displaystyle \frac{n_k}{n_{tot}}}$, $f_{jk}={\displaystyle \frac{n_{jk}}{n_k}}$, and $f_{ijk}={\displaystyle \frac{n_{ijk}}{n_{jk}}}$, where $n_k$, $n_{jk}$, and $n_{ijk}$ represent the atomic nucleus density of the element, the atomic nucleus density of the element in the j-th ionization state, and the atomic nucleus density of the element in the j-th ionization state and i-th excitation state, respectively. ${\Phi }_{lk}$ is the ionization energy of the k-th atom in the L-th ionization state, and $∆E_{i{n}_0}$ is the excitation energy of the atom in the i-th excited state relative to the ground state atom. The average charge state of the ions is defined as follows:

$$〈Z〉=\sum _k{f}_k\sum _{j=1}^{Z_k}{f}_{jk}j$$

(5)

The pressure of the plasma is defined as:

$$P=\left(1+〈Z〉\right)n_{tot}{k}_{B}T$$

(6)

where T is the temperature of the plasma. In IONMIX, the calculation of radiation opacity for the plasma is divided into two parts: Rosseland radiation opacity and Planck radiation opacity. The Rosseland radiation opacity is typically used to define the transport properties of radiation in a medium, while the Planck average opacity is used to calculate the energy exchange rate between the plasma and the radiation field. Since the plasma is generally not in thermal equilibrium, the Planck average opacity is further divided into Planck absorption average opacity and Planck emission average opacity, which are defined for photon energies in the range from $x_g=h{v}_g/T_B$ to $x_{g+1}=h{v}_{g+1}/T_B$ as follows:

$${\sigma }_{P,g}^A={\displaystyle \frac{1}{\rho }}{\displaystyle \frac{{\int }_{x_g}^{x_{g+1}}{B}_{\nu }\left(T_R\right){\kappa }_{\nu }dx}{{\int }_{x_g}^{x_{g+1}}{B}_{\nu }\left(T_R\right)dx}}$$

(7)

$${\sigma }_{P,g}^E={\displaystyle \frac{1}{\rho }}{\displaystyle \frac{{\int }_{x_g}^{x_{g+1}}{n}_{\nu }dx}{{\int }_{x_g}^{x_{g+1}}{B}_{\nu }\left(T_R\right)dx}}$$

(8)

where $\rho$ is the mass density, ${\kappa }_{\nu }$ and $n_{\nu }$ are the absorption coefficient and radiation coefficient, respectively, and $B_{\nu }\left(T_R\right)$ is the Planck distribution function as a function of the radiation temperature $T_R$.

The Rosseland average opacity is related to the weighted average of ${\kappa }_V$ and $S_v$:

$${\sigma }_{R,g}={\displaystyle \frac{1}{\rho }}{\displaystyle \frac{{\int }_{x_g}^{x_{g+1}}\left(\frac{𝜕B_{\nu }}{𝜕T_R}\right)dx}{{\int }_{x_g}^{x_{g+1}}\left(\frac{𝜕B_{\nu }}{𝜕T_R}\right)\frac{1}{{\kappa }_{\nu }+S_v}dx}}$$

(9)

where $S_v$ is the light scattering coefficient, and $S_v=6.66\times {10}^{-25}{n}_e$ and $n_e$ are the electron densities. Figure 1 shows the pressure, average charge state, Planck and Rosseland average radiation opacities, radiation cooling rate, and the emission and absorption coefficients for the terbium plasma at an electron density of $1.0\times {10}^{21} {\mathrm{c}\mathrm{m}}^{-3}$ as a function of electron temperature.

Figure 1 systematically presents and analyzes the key thermodynamic and radiative properties of Terbium (Tb) plasma under a fixed electron density condition ($N_e = 1.0\times {10}^{21} {\mathrm{c}\mathrm{m}}^{-3}$), providing crucial physical data for subsequent hydrodynamic simulations. Comprising six subplots (a–f), the figure offers a comprehensive description of the plasma’s equation of state, ionization degree, radiation opacity, and spectral characteristics. Subplot (b) of the mean ionization degree demonstrates the production of highly charged ions (e.g., Tb²⁵⁺/Tb²⁶⁺) at elevated temperatures, which is essential for the 6.7 nm emission. Subplot (c) reveals the radiation transport properties within the plasma through the Planck and Rosseland mean opacity, while subplot (d) quantifies its cooling efficiency via the volumetric radiative energy loss rate. Subplots (e) and (f), respectively, depict the absorption and emission spectral properties of the plasma at an isothermal temperature of 100 eV. The sharp emission peak observed around 185 eV photon energy (corresponding to ~6.7 nm) directly confirms the superior performance of terbium plasma as an efficient source for BEUV radiation.

3. Results and Discussion

This study investigates the dynamic response characteristics of terbium (Tb) plasmas under dual-pulse laser irradiation through parametric radiation hydrodynamics simulations using the FLASH 4.8 multiphysics code. The computational domain, defined in a cylindrical coordinate system (30 mm × 60 mm), encompasses a Tb target with an initial density of 8.2 g/cm³ and three helium gas environments with varying initial densities and pressures (8.0 × 10⁻⁸ g/cm³/50 Pa, 3.2 × 10⁻⁷ g/cm³/200 Pa, and 1.6 × 10⁻⁶ g/cm³/1000 Pa). A dual-pulse fiber laser (wavelength: 1.064 μm) was modeled with total energy of 75 mJ (pre-pulse: 5 mJ, main pulse: 70 mJ) and pulse duration of 10 ns for both pulses. Computational optimization strategies were implemented to balance numerical accuracy and resource efficiency. Notably, the fiber laser configuration exhibits significantly enhanced photoelectric conversion efficiency (~40% improvement) and compact thermal management advantages compared to CO₂ lasers [19]. 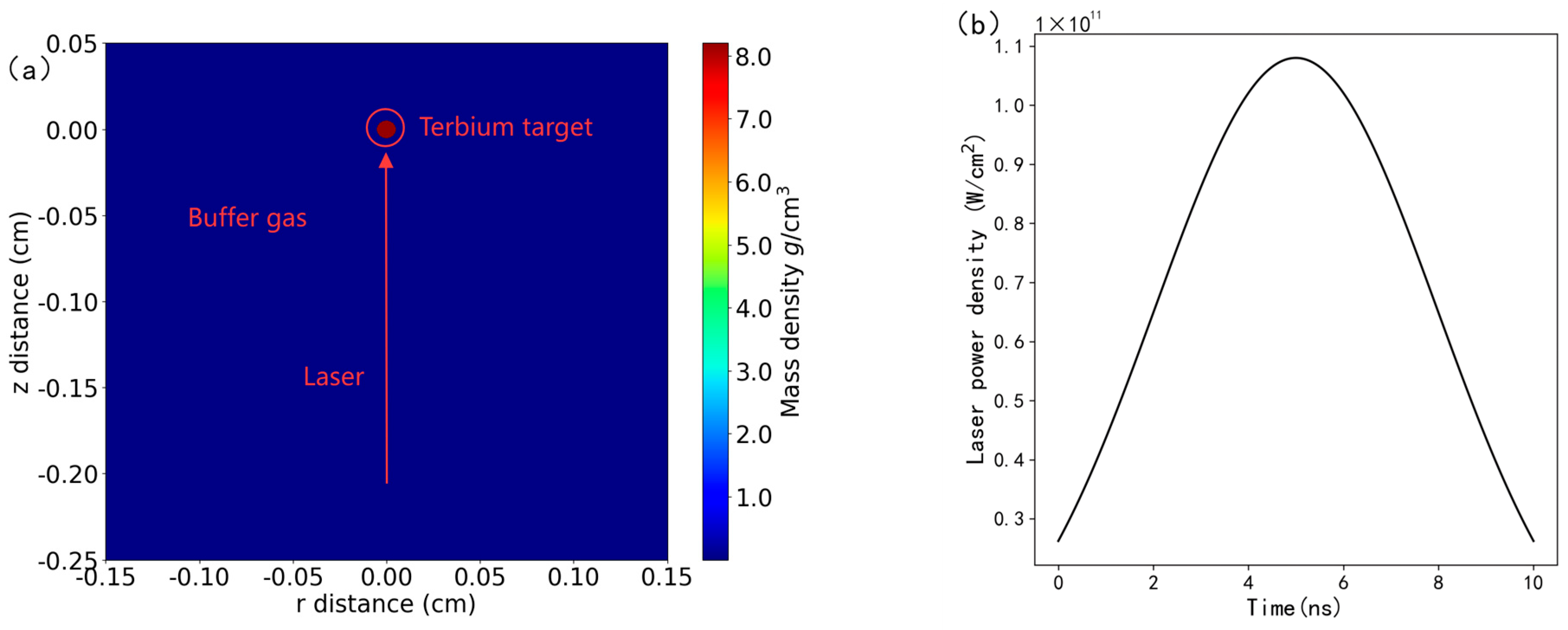Figure 2 illustrates the initial state of the plasma (a) and the temporal evolution of the laser power density (b). A liquid droplet terbium target with a density of 8.2 g/cm³ is positioned at the origin of the coordinates, surrounded by helium gas at a specific pressure. The laser is incident normally onto the target surface from the negative direction of the r-axis. The instantaneous power density of the laser pulses is defined as:

$$I\left(r\right)=I_{0}exp\left\{-{\left[{\left({\displaystyle \frac{x}{R_x}}\right)}^2+{\left({\displaystyle \frac{y}{R_y}}\right)}^2\right]}^{{\displaystyle \frac{\gamma }{2}}}\right\}$$

(10)

where $R_x$ and $R_y$ are the radii of the beam on the x and y axes, respectively. They are set to be equal, resulting in a circular beam, with $\gamma$ representing the Gaussian exponent.

The formula for calculating the instantaneous power of the laser is:

$$P=2\pi {\int }_0^{R}I\left(r\right)r dr$$

(11)

where r is the radius of the beam. Based on the pulse energy, the beam radius, and the pulse duration, we can obtain the required power density distribution.

Equation (10) describes the spatial intensity distribution of the laser beam across its cross-sectional plane, characterizing the non-uniform energy distribution within the spot. Equation (11) calculates the instantaneous total power carried by the laser by integrating this intensity distribution over the beam radius.

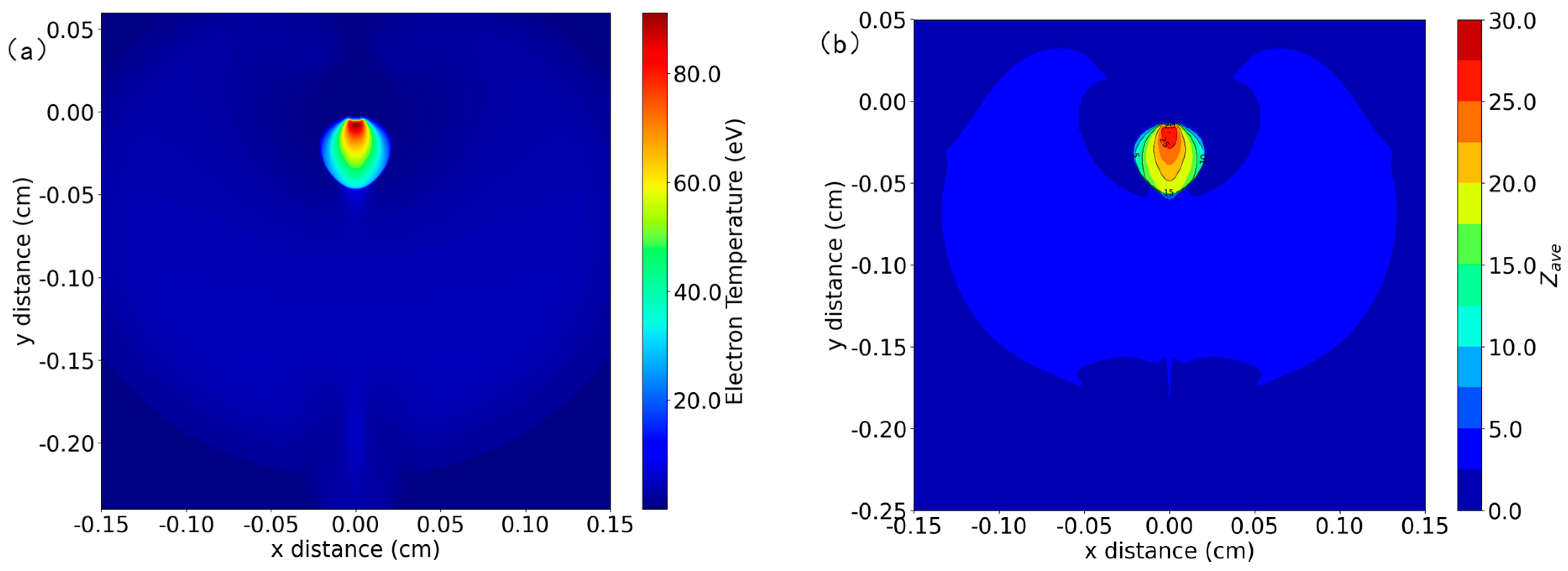
To resolve the plasma characteristics at peak laser intensity, we maintained fixed laser parameters (wavelength: 1.064 μm, total energy: 75 mJ) and target configuration (Tb density: 8.2 g/cm³). The computational domain was refined to a 1.5 mm × 3 mm region with laser focus radius 50 μm, simulating three background He gas pressures (50 Pa, 200 Pa, 1000 Pa). Experimental spectral diagnostics reveal that the 6.x nm beyond extreme ultraviolet (BEUV) emission from Tb plasma predominantly arises from transitions in Tb²⁵⁺ (4d–4f) and Tb²⁶⁺ (4p–4d) ions. As shown in Figure 3, the electron temperature and mean charge state distributions at 1000 Pa background pressure demonstrate that laser-induced T_e ≈ 100 eV sufficiently ionizes Tb to charge states 25+ and 26+, satisfying the ionization potential thresholds (Tb²⁵⁺: ~93 eV; Tb²⁶⁺: ~105 eV) required for BEUV photon generation. This confirms the self-consistency between the simulated plasma conditions and experimentally observed spectral features.

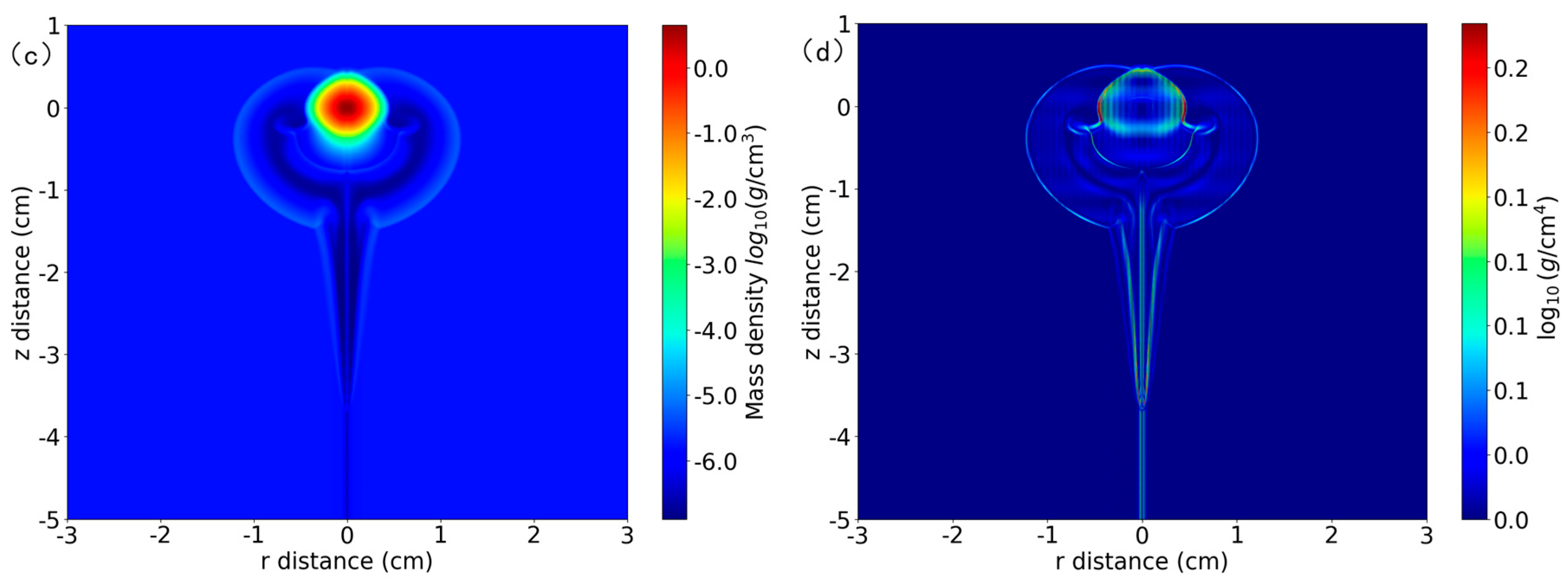
This study investigates the spatiotemporal evolution of terbium plasmas under varying background pressures (50 Pa, 200 Pa, 1000 Pa) through radiation hydrodynamics simulations in a planar domain of 30 mm × 60 mm. The dual-pulse temporal sequence was configured with a 4 μs total simulation duration: the pre-pulse laser initiated at 10 ns, followed by the main pulse 50 ns after the pre-pulse. Figure 4 displays the plasma mass density distributions at 2 μs for each pressure condition. At elevated pressures (1000 Pa), the shockwave exhibits a compact spatial profile with steep density gradients, attributed to enhanced collisional energy transfer and faster thermalization rates under high-density plasma conditions [20]. Conversely, reduced background pressure (50 Pa) results in diffuse shockwave expansion due to decreased particle collision frequency and prolonged energy dissipation timescales. Intermediate pressure conditions (200 Pa) demonstrate transitional behavior between these regimes, illustrating the pressure-dependent modulation of plasma confinement dynamics.

A laser-induced density depression is universally observed within the irradiation channel across all background pressure conditions (50–1000 Pa). This rarefaction phenomenon originates from localized energy deposition through inverse bremsstrahlung absorption, which thermally excites gas molecules and triggers hydrodynamic expansion. The resultant transient pressure gradient drives radial particle flux, forming a low-density channel aligned with the laser propagation axis.

At elevated pressures (e.g., 1000 Pa), collisional energy transfer dominates over free expansion dynamics, as evidenced by the constrained rarefaction zone dimensions in Figure 4c. The enhanced collision frequency under high-pressure conditions effectively dissipates directed kinetic energy into thermal motion, thereby suppressing large-scale density depletion. Conversely, reduced background pressures permit extended mean free paths, enabling sustained directional expansion that amplifies the rarefaction volume. Figure 4d displays the spatial gradient distribution of plasma mass density, where the plasma-background interface (plume expansion front) is identified through detection of regions exhibiting significant gradient magnitudes. This methodology leverages sharp density gradients at the expansion front to demarcate the boundary between the laser-ablated plasma and the ambient medium. Analysis of sharp density gradients accurately determines the contact interface position, providing a robust diagnostic for tracking plume dynamics under varying background pressures.

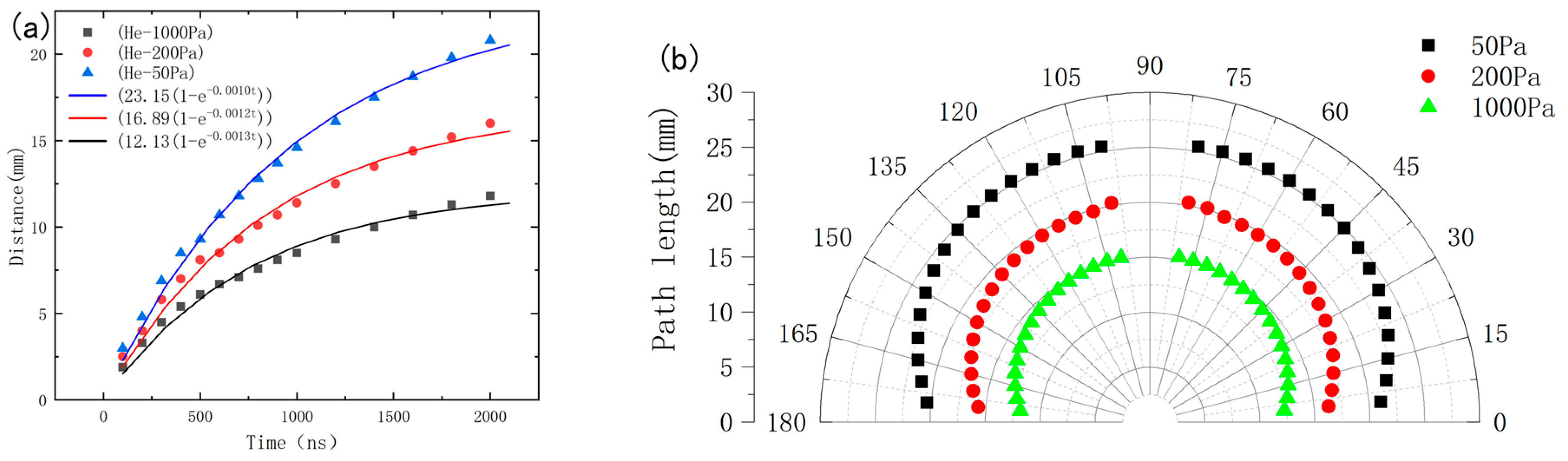
Figure 5a illustrates the variation of the plasma shock wave expansion distance over time at different helium pressure levels (1000 Pa, 200 Pa, and 50 Pa). Simulation data for each pressure is represented by different symbols, while the fitted curves are shown with lines of different colors. When a certain background gas pressure is applied to the chamber, the expansion behavior of the plasma can typically be described using a resistance model, expressed as $x\left(t\right)=x_{st}(1-e^{-bt})$, where $x_{st}$ is the stopping distance and $b$ is the attenuation coefficient [21]. According to this model, the expansion of the plume will eventually stop due to collisions with gas atoms. However, beyond 4 μs, the model predicts a shorter expansion distance than experimentally observed, suggesting that it fails to fully capture the gas dynamics and the complex shock wave-gas interactions during prolonged expansion. As time increases, the expansion distance of the plasma shock wave shows an upward trend at all pressures. The shockwave propagation range exhibits a pronounced pressure dependence, with the 1000 Pa case demonstrating a constrained spatial extent. This confinement arises from enhanced collisional energy dissipation in the high-density ambient medium, which rapidly attenuates the shockwave’s kinetic energy. Conversely, reduced background pressures (200 Pa and 50 Pa) permit extended propagation distances, attributed to diminished gas-phase collisionality that facilitates sustained energy transfer through directional hydrodynamic expansion. The observed pressure-modulated attenuation mechanism aligns with classical blast wave theory, where ambient density inversely governs shockfront deceleration rates [22]. Figure 5b presents the contact front obtained during the simulation at 2 μs under different helium pressure levels. The droplet terbium target is positioned at the center of the polar coordinates, with the plume front expanding relative to the target surface. The non-uniform radial expansion can be clearly observed through the polar coordinate grid.

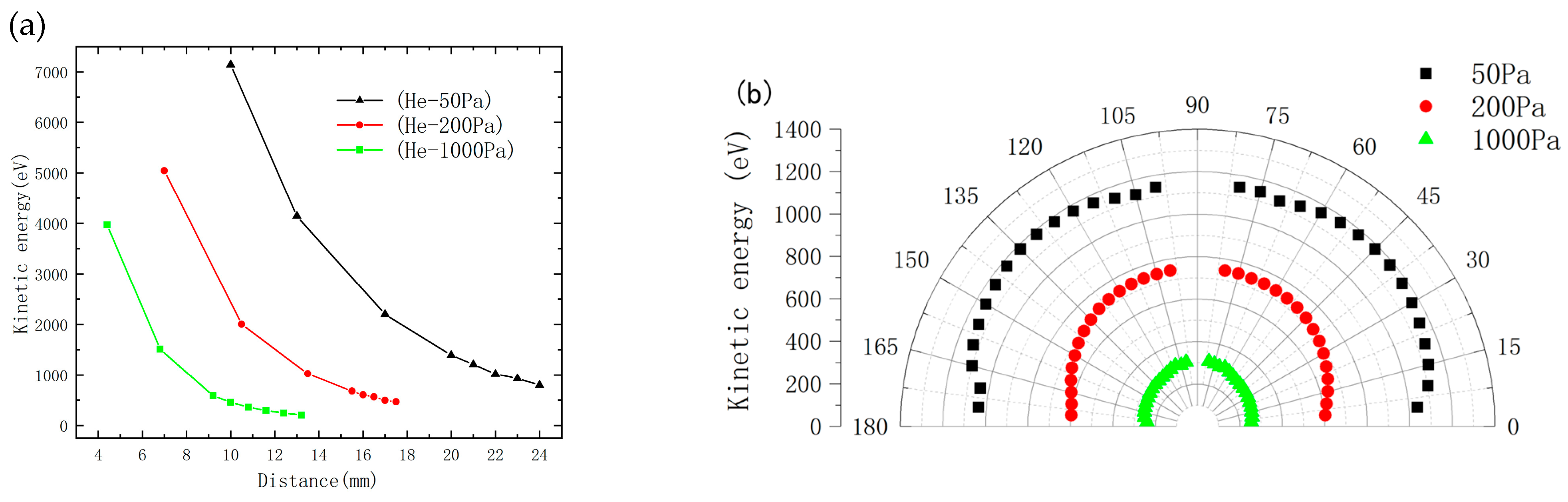
Figure 6a shows the distribution of plasma kinetic energy obtained during the simulation at 2 μs under different helium pressure levels (1000 Pa, 200 Pa, and 50 Pa). The kinetic energy $\epsilon$ is determined by the expression $\epsilon =1/2 \mathrm{m}{\mathrm{v}}^2$, where the mass of the terbium ion is taken as the standard atomic mass of terbium, and the velocity is the average speed within the range of the plasma shock wave. Regardless of pressure, the kinetic energy distribution decreases radially from the target surface during expansion, with the most significant reduction occurring along the normal direction. As helium pressure increases, the kinetic energy declines and the distribution becomes more concentrated, indicating altered shockwave energy transfer. The plume kinetic energy shows a clear inverse dependence on pressure, decreasing from about 1200 eV at 50 Pa to 300 eV at 1000 Pa. Under high-pressure conditions, increased gas density enhances collision frequency, leading to rapid thermalization of shockwave energy, reduced propagation efficiency, and strengthened confinement from the ambient medium, which collectively cause an earlier deceleration of the plume. In contrast, lower pressure reduces collisional interactions, facilitating sustained directional energy transport and prolonged plume expansion. Figure 6b depicts the relationship between kinetic energy and distance along the normal direction of the target surface at different helium pressures (1000, 200, and 50 Pa). The results reveal a consistent deceleration of kinetic energy at comparable time delays after the laser pulse, indicating considerable influence of the background gas on shockwave propagation. Specifically, at a given path length, the kinetic energy decreases progressively with rising pressure, consistent with prior studies. Moreover, the kinetic energy exhibits a nonlinear decline with increasing plume path length or delay time, suggesting that the damping effect of the buffer gas intensifies with variation in kinetic energy, reflecting complex gas–shockwave interaction mechanisms.

Figure 7 shows the relationship between stopping power (defined as kinetic energy loss per unit distance, $d\epsilon /dx$) and the normal component of thermal kinetic energy at different helium pressures [23]. Stopping power exhibits strong energy dependence, which is more pronounced at higher energies and diminishes at lower energies. This trend results from the interplay between gas dynamics and collision frequency under varying pressures. As pressure increases, the gas front flattens, altering energy dissipation mechanisms through increased collision rates and modified energy transfer efficiency. Simulations show that at 200 Pa, the stopping power is 350 eV/mm for 3000 eV particles, while at 1000 Pa, it decreases to 200 eV/mm for 1500 eV particles. This inverse correlation indicates that higher pressures enhance dissipation efficiency within specific energy ranges but reduce effectiveness outside these ranges.

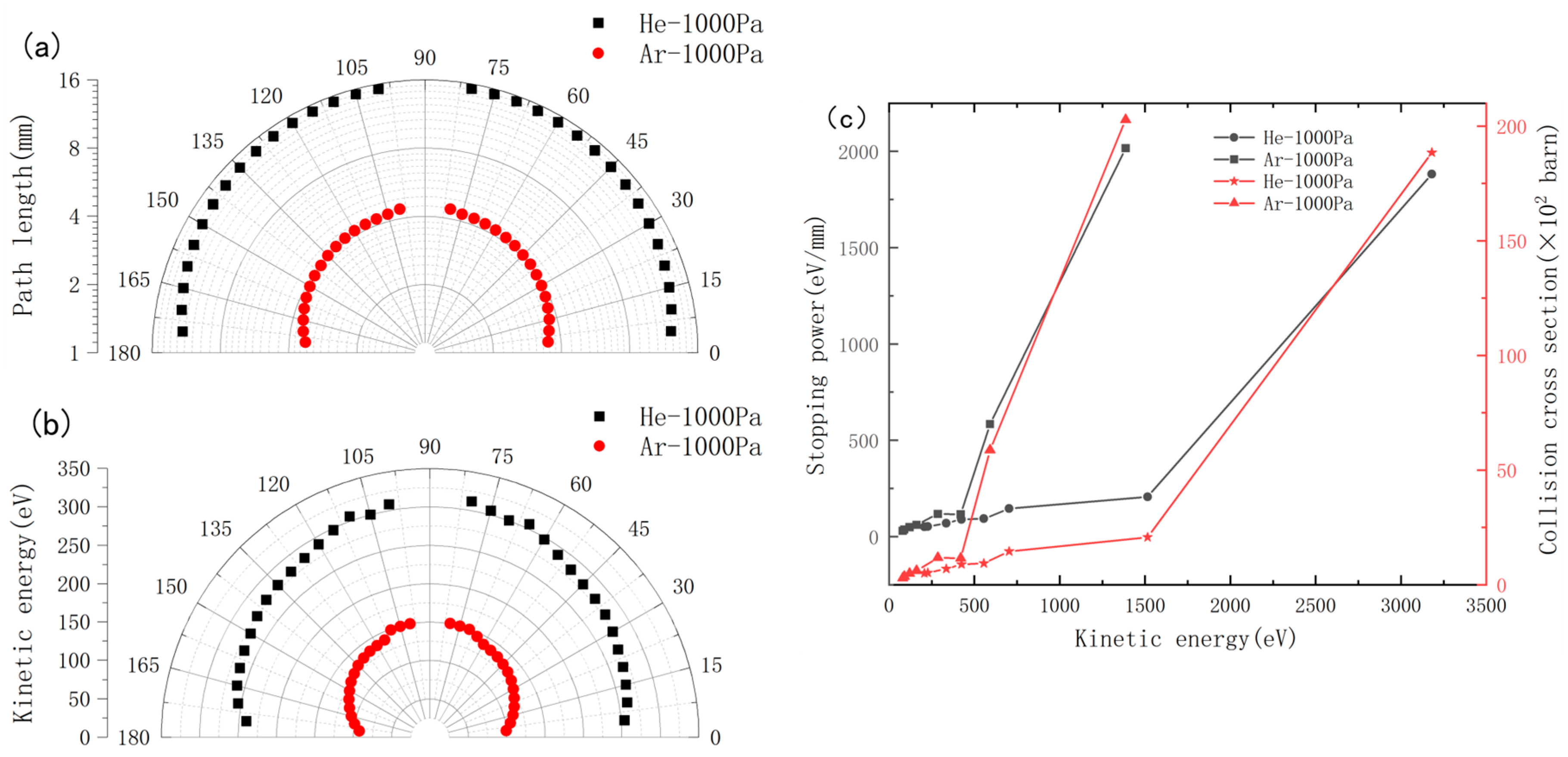
Figure 8 Comparative analysis of plasma plume expansion in helium and argon background gases: (a) Plume front morphology at a simulation time of 2 μs under identical pressure conditions; (b) Kinetic energy distribution contrast between helium- and argon-buffer gas plasmas. The results reveal anisotropic expansion characteristics common to both gas environments, with preferential energy dissipation along the target normal direction compared to radial propagation. Notably, helium demonstrates superior plasma confinement capability relative to argon, as evidenced by systematically reduced kinetic energy magnitudes across all spatial domains. This enhanced suppression effect arises from helium’s lower atomic mass and higher ionization potential, which amplify collisional energy transfer efficiency between the plasma and background medium. Figure 8c presents the stopping power and scattering cross-sections for helium and argon at equivalent pressure levels. The black curves (left axis) represent the stopping power of helium and argon, while the red curves (right axis) denote their scattering cross-sections, defined as $\sigma =(dx/d\epsilon )/\epsilon n$, where $n$ is the number density of the buffer gas [24]. Argon demonstrates superior performance in the low-energy regime (<1300 eV), achieving a peak stopping power of 2000 eV/mm at 1300 eV kinetic energy, significantly exceeding helium’s 1800 eV/mm at 3000 eV. Additionally, argon’s collision cross-section at 600 eV is approximately 6.4 times larger than helium’s (58 × 10² vs. 9 × 10² barn). This enhancement arises from argon’s higher atomic mass (40 amu), which improves momentum matching with debris particles and increases collision energy transfer efficiency. According to the Bohr nuclear stopping model, argon’s nuclear stopping contribution dominates in this regime, while electronic stopping is negligible, further amplifying its cross-sectional advantage [24].

The nonlinear deceleration mechanism of terbium plasma fragments is a complex physical process resulting from the interplay between microscopic particle collisions and macroscopic hydrodynamic behavior. At the microscopic level, the nonlinearity originates from the functional dependence of the stopping power ($d\epsilon /dx$) on the kinetic energy of the particles. High-kinetic-energy fragments dissipate energy more effectively via nuclear stopping mechanisms—which dominate in heavy gases such as argon—or electronic stopping mechanisms, which become significant in light gases like helium. Moreover, the scattering cross-section exhibits notable kinetic energy dependence, further contributing to the dynamic nonlinear enhancement of deceleration efficiency. For instance, at 600 eV, the scattering cross-section of argon is 6.4 times that of helium, underscoring the profound influence of medium properties on stopping capability. At the macroscopic scale, the nonlinear deceleration behavior is primarily governed by collective interaction effects under high-pressure conditions: the expanding plasma plume compresses the ambient gas through a “snowplow effect,” forming a shock-wave structure. The kinetic energy dissipated in this process increases nonlinearly with rising gas pressure (or density). Simultaneously, high collision frequencies facilitate the rapid conversion of the directed kinetic energy of fragments into random thermal motion of the system. This form of energy transfer and dissipation is highly efficient in high-pressure environments, thereby resulting in strongly nonlinear characteristics where deceleration efficiency increases sharply with pressure [25,26].

4. Conclusions

Terbium plasma, featuring intense BEUV radiation around 6.7 nm through 4f unresolved transition array (UTA) transitions, emerges as a core candidate material for next-generation lithography light sources. However, accompanying high-energy ions and neutral fragments (with energies reaching keV-level) induce collector mirror reflectivity degradation, severely limiting source longevity. This study investigates the suppression capability of plasma debris generated by laser ablation of terbium droplets under varying ambient gas pressures (50–1000 Pa), focusing on the damage mechanisms of high-energy particles to optical components in 6.x nm band BEUV light sources and the mitigation effects of buffer gases. Two-dimensional simulations using the FLASH code reveal significant regulatory effects of buffer gas type and pressure on plasma dynamic characteristics and debris kinetic energy distribution. The research demonstrates that argon exhibits superior debris deceleration performance in the low-energy regime (<1300 eV), achieving a peak stopping power of 2000 eV/mm (corresponding to 1300 eV kinetic energy). Its scattering cross-section at 600 eV approximates 6.4 times that of helium (58 × 10² vs. 9 × 10² barn), attributed to favorable momentum matching between argon atoms (40 amu) and debris through nuclear stopping-dominated energy transfer mechanisms. In contrast, helium at high pressure (1000 Pa) restricts plasma plume radial expansion via enhanced collision frequency, reducing debris kinetic energy below 150 eV. Its stopping power shows nonlinear growth with increasing pressure across 50–1000 Pa, concentrating kinetic energy distribution in the low-energy regime.

Based on the analysis of the nonlinear attenuation characteristics of buffer gases in suppressing plasma debris kinetic energy, this study reveals that the stopping power of argon at 1300 eV exceeds that of helium at 3000 eV by a factor of 1.1, indicating that the deceleration efficiency of buffer gases increases with kinetic energy. High-pressure helium rapidly dissipates plasma energy through frequent collisions, thereby sharpening the plume boundary and restricting debris diffusion space, while argon at equivalent pressure further reduces mirror sputtering risks due to its superior momentum matching capability. These findings demonstrate the clear energy-range limitations of single-gas configurations in kinetic energy suppression. Therefore, the use of mixed buffer gases or the development of dynamic gas control technology holds significant potential. By enabling real-time coordination of gas composition and pressure, such approaches could achieve improved kinetic energy suppression across a broad energy range while maintaining extreme ultraviolet (EUV) output efficiency. This offers a promising technical pathway for synergistically optimizing debris suppression and radiation performance in high-repetition-rate BEUV sources. This work is subject to certain limitations. It should be noted that this study employs a two-dimensional axisymmetric model, which does not account for three-dimensional effects or self-generated magnetic fields. While this simplification aligns with our primary focus on hydrodynamic dissipation as the dominant mechanism, we acknowledge that it may lead to an underestimation of certain anisotropic transport effects or electron-driven micro-instabilities. Furthermore, the opacity data used in the simulations were sourced from the IONMIX database. We recognize that the inherent computational uncertainties associated with this database may affect the absolute quantitative values of the kinetic energy distribution and stopping power. However, it must be emphasized that the relative comparisons and the main physical conclusions of this study remain robust. Future research should explore multi-component gas dynamic models and inelastic collision processes affecting 6.x nm radiation spectra to advance semiconductor lithography technology toward practical implementation.