Inverse-Designed Narrow-Band and Flat-Top Bragg Grating Filter

Abstract

Integrated optical filters are fundamental and indispensable components of silicon photonics, which enhance the data throughput of high-demand communication networks. Grating-assisted filters have been widely used due to the merits they offer: flat top, low crosstalk, and no FSR. In this paper, we report an inverse-designed narrow-band silicon Bragg grating filter that unites lateral-misalignment apodization with cooperative particle swarm optimization (CPSO). The initial coupling-coefficient profile of the filter is first yielded by a layer-peeling algorithm (LPA). Subsequently, the final structure is designed by CPSO to approach the desired spectral response. The filter is fabricated on a 220 nm silicon-on-insulator platform. The measured results exhibit 3.39 nm bandwidth, 19.34 dB side lobe suppression ratio (SLSR), and 1.75 dB insertion loss. The proposed design method effectively solves the problem of excessively high side lobes in uniform gratings and LPA-designed gratings when designing narrow-bandwidth filters.

1. Introduction

Integrated photonic filters have become a key building block in silicon photonics, enabling compact, low-loss, and CMOS-compatible wavelength management for WDM, microwave-photonic, and quantum systems [1,2]. In recent years, the explosive growth of network traffic has intensified the demand for bandwidth in communication systems [3]. Bandwidth, as a finite and increasingly valuable resource, makes narrow-band, flat-top filters indispensable in wavelength-division-multiplexing (WDM) systems [4]. Box-like filters, combining a steep roll-off with a flat passband, simultaneously enable narrower channel spacing and higher signal fidelity, making them key enablers for dense-WDM and next-generation ROADM systems [5,6,7]. Silicon photonic filters are indispensable in optical networks, where their primary role is to provide cost-efficient channel separation and signal routing in WDM systems [8]. With the rapid advancement of optical communication technologies, continuously increasing demands are imposed on silicon photonic filters, encompassing superior filtering characteristics, more compact footprints, lower insertion loss, and highly flexible tunability. At present, on-chip silicon-based filters mainly fall into four architectures: microring resonators (MRRs) [9,10], Mach–Zehnder interferometers (MZIs) [11,12,13], arrayed waveguide gratings (AWGs) [14,15], and Bragg gratings [16,17,18,19,20,21,22].

MRR filters feature a simple and compact geometry, offering narrow bandwidths. However, the wavelength range is bound by the free-spectral range (FSR), making wideband coverage difficult. Moreover, the box-like responses need to use multiple cascaded rings, making fine joint tuning necessary. MZI filters provide larger bandwidths, well suited for CWDM with wide channel spacing, and allow flexible wavelength tuning. Additionally, their Lorentzian lineshapes require multi-stage cascading to achieve flat-top profiles. Like MRR, they are also FSR-limited, restricting their applicability in scenarios demanding ultra-broad bandwidths. AWG filters can process tens of wavelength channels and simultaneously offer excellent wavelength stability, but their tunability is limited and their large footprint hinders large-scale on-chip integration. Bragg gratings provide a flat spectral response and flexible wavelength selection with a tuning range that is not constrained by the FSR. Using conventional fiber, achieving narrow-band filtering usually requires a long grating length. Silicon-on-insulator (SOI), a silicon photonics platform with large refractive index contrast, significantly shrinks the footprint of Bragg gratings, making silicon-based Bragg gratings an ideal solution for realizing narrow-band, flat-top filtering. However, conventional uniform Bragg gratings typically exhibit large passbands, ranging from a few nanometers to several hundred nanometers. The abrupt refractive index transitions at the grating ends give rise to pronounced spectral side lobes. In designing silicon Bragg gratings, the narrower the targeted spectral bandwidth, the higher the side lobes flanking the resonance peak [16,17].

A key challenge in Bragg grating design is achieving both narrow-band filtering and a high side lobe suppression ratio (SLSR). The grating bandwidth is primarily controlled by the coupling coefficient. Due to the high refractive index contrast of the silicon photonics platform, the performance of silicon Bragg gratings is highly sensitive to corrugation amplitude, and achieving a narrow bandwidth requires extremely small corrugation amplitudes, posing significant challenges to the manufacturing process [23]. The high SLSR can be achieved through apodization [24]. Common apodization techniques for waveguide Bragg gratings include corrugation-amplitude modulation, duty-cycle modulation, and phase modulation. These approaches can reduce side lobe levels, but the suppression capability is ultimately limited due to the reliance on fixed functional forms, such as Gaussian or sinusoidal profiles, to tailor the grating structure. These fixed-profile curves cannot fully optimize the performance of Bragg gratings.

To further optimize performance and realize narrow-band Bragg grating filters with high side lobe suppression, this paper innovatively combines lateral-misalignment apodization with inverse design. A hybrid optimization algorithm is employed to optimize the lateral-misalignment offsets, thereby tailoring the coupling coefficient. Meanwhile, the grating parameters are iteratively refined in reverse to meet the targeted spectral response. The measured filtering bandwidth is 3.39 nm with an SLSR of 19.34 dB, outperforming the uniform grating (11.53 nm, 0.837 dB) and the LPA-designed grating (3.39 nm, 7.675 dB). The experimental results demonstrate that our design method can further effectively optimize the coupling coefficient of the grating compared to uniform gratings and LPA, thereby enhancing the performance of the grating. This approach offers a fresh paradigm for the design of high-performance, narrow-band silicon filters.

2. Device Structure

As schematically illustrated in Figure 1a, the designed Bragg grating structures are placed in the two arms of a Michelson interferometer based on a balanced MZI, with interference regions at both ends formed by a pair of MMIs. This design addresses the limitations of conventional Bragg gratings in efficiently separating and collecting reflected signals, thereby enhancing the gratings’ integration into WDM systems [21,22]. In this design, 220 nm thick silicon strip waveguides are sandwiched between a 2 μm thick buried oxide (BOX) layer and a 2.2 μm thick SiO₂ cladding layer.

The operational mechanism can be described as follows. An optical signal injected into the input port is first equally split by a 2 × 2 MMI coupler, yielding two output beams with a 90° phase difference. These beams propagate along the two arms of a Michelson interferometer, where each arm is embedded with an identical Bragg grating. Light satisfying the phase-matching condition of the grating is reflected toward the coupler. Upon recombining in the MMI, the two reflected beams accumulate an additional 90° phase shift, resulting in a total 180° phase difference at the input port, where they interfere destructively. Conversely, at the drop port, the beams arrive in 0° phase, interfering constructively to efficiently extract the resonant wavelength, thereby realizing a bandpass functionality. Non-resonant light transmits through the gratings and constructively recombines at the through port, functioning as a band-stop filter. The peak of the reflected light T_peak is determined by the grating length $L$ and the coupling coefficient $\kappa$, as denoted in Equation (1):

$$T_{\mathrm{peak}}={\tanh }^2\left(\kappa L\right)$$

(1)

As shown in Figure 1b, the uniform Bragg grating waveguide features corrugations with an amplitude of $\Delta W$, which creates a periodic refractive index perturbation. This results in a periodic modulation of the effective refractive index along the direction of light propagation, thereby generating distributed reflection. Optical signals at the Bragg wavelength undergo constructive interference and are reflected, while signals at other wavelengths pass through the grating and are transmitted. In a single-mode grating waveguide, both the incident and reflected light propagate in the TE₀ mode. Here, the phase-matching condition is given as

$${\lambda }_B=\left[\left(1-\rho \right)n_{eff1}+\rho n_{eff2}\right]\Lambda$$

(2)

where $n_{eff1}$ and $n_{eff2}$ denote the effective refractive indices of the $\mathrm{TE}0$ mode in the narrow waveguide $W_{g1}$ and wide waveguide $W_{g2}$ in Figure 1b. $\rho$ is the duty cycle (ratio of corrugation width to Λ). We set $W_1=500\mathrm{nm}$ to be the width of a standard single-mode waveguide at 1550 nm. Considering fabrication constraints, we set $W_2=640\mathrm{nm}$, resulting in a $\Delta W$ of 70 nm. Figure 1c illustrates the wavelength-dependent effective index evolution of the grating waveguide mode. With the parameters above, and from Figure 1c and Equation (2), we obtain $\Lambda =304\mathrm{nm}$ to achieve a Bragg resonance near 1550 nm.

In uniform silicon Bragg gratings, the abrupt refractive index transitions at the termination interfaces give rise to high side lobes adjacent to the resonance peak. The suppression of these parasitic features is most effectively achieved through apodization techniques. The essence of apodization is to adjust the coupling coefficient, which is mainly achieved physically by adjusting the structural parameters of the device to change the distribution of the refractive index [25]. Established apodization methodologies encompass corrugation width modulation [26], duty-cycle modulation [27], periodic phase modulation [28,29], and complementary lateral-misalignment modulation (CLMM) [25]. Notably, CLMM has been demonstrated to be particularly promising among contemporary approaches. This technique operates through complementary symmetric adjustment of corrugation center positions along both waveguide sidewalls, to tune the grating coupling coefficient. Because this lateral-misalignment approach lowers the sensitivity of coupling-coefficient tuning, it overcomes fabrication-resolution limits and enables finer adjustment of κ and enables precise phase front engineering without introducing deleterious grating phase errors, thereby affecting substantial suppression of spectral side lobes. A significant advancement over conventional amplitude-modulated grating schemes, CLMM affords an order-of-magnitude improvement in both apodization resolution and modulation fidelity [30].

This work employs CLMM as an apodization strategy to engineer the spatial refractive index profile of the grating. Through this approach, the grating coupling coefficient is precisely tailored, leading to significant suppression of side lobes in the optical spectral response. As illustrated in Figure 1d, CLMM simultaneously alters the phase of corrugations on both waveguide sidewalls and the expression for the coupling coefficient, as expressed in Equation (3):

$$\kappa =\left|{\kappa }_0{e}^{j\Delta \varphi }+{\kappa }_0\right|=2{\kappa }_0\cos ({\displaystyle \frac{\Delta \varphi }{2}})$$

(3)

Here, the phase difference within a single period is expressed as $\Delta \varphi =2\pi \Delta L/\Lambda$. The phase shift $\Delta \varphi$ is induced by lateral-misalignment $\Delta L$ ranges from 0 to $\pi$, as the maximum misalignment $\Delta L$ is constrained to half the grating period. Equation (3) demonstrates that the lateral-misalignment phase shift $\Delta \varphi$ is cosine-related to the coupling coefficient $\kappa$.

3. Device Design Method

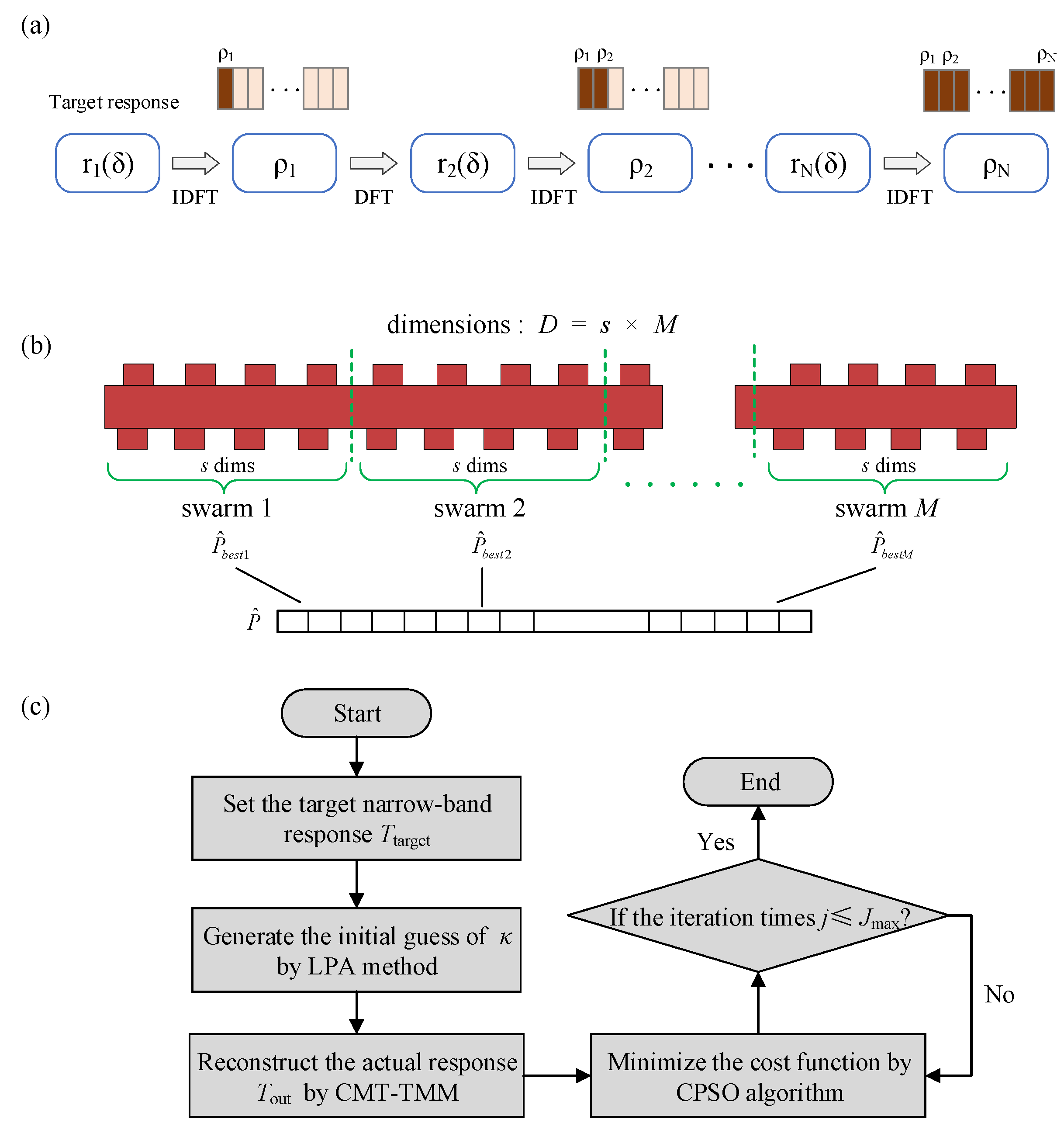
The layer-peeling algorithm (LPA) is a widely adopted inverse-scattering approach for Bragg grating synthesis. The principle of the LPA is illustrated in Figure 2a. By segmenting the grating into cascaded uniform periods, LPA reconstructs the coupling and reflection coefficients of each period in reverse order, starting from the prescribed target spectrum, thereby retrieving the physical parameters of the grating [31,32]. Although computationally efficient and straightforward to implement, LPA exhibits intrinsic limitations under realistic conditions. Specifically, for gratings of high reflectivity or extended length, the majority of the optical power is reflected before reaching the terminal sections, engendering progressively erroneous coupling coefficients toward the grating’s far end. These inaccuracies accumulate layer by layer, ultimately producing a reconstructed profile that deviates from the desired spectral response [33,34].

To overcome these deficiencies, this work presents a hybrid optimization framework that synergistically integrates LPA with cooperative particle swarm optimization (CPSO). CPSO is a more efficient optimization method for designing grating. It decomposes the search space into multiple lower-dimensional subcomponents (swarms), each optimized separately by a standard PSO. Figure 2b illustrates the basic principle of the CPSO algorithm for optimizing grating structural parameters. To reduce the search complexity of a single population, the CPSO algorithm decomposes a D-dimensional optimization problem into M subspaces, i.e., the number of populations in the PSO algorithm is M, and the search space of each population is s-dimensional. Each population evolves independently within its assigned parameter subspace. After optimization, the populations collaborate and share information by concatenating their current best solutions ${\widehat{P}}_{best-j}$ into a global candidate solution $\widehat{P}$. The fitness of this global candidate is evaluated and then fed back to all subpopulations to guide the next movement of the particles. In this work, the number of populations is set to 60, so the search space of each population is 40-dimensional, i.e., $s=40$. Compared with the LPA, CPSO can tune the coupling coefficient more finely, thereby better approximating the target response.

The overall flowchart of the inverse design method is shown in Figure 2c. First, the target response is set at $T_{\mathrm{target}}$. Next, the grating’s $\kappa$ is obtained from $T_{\mathrm{target}}$ via the LPA; this $\kappa$ will serve as the initial value for the CPSO. Then, the grating $\kappa$ is further optimized using CPSO. To evaluate the spectrum of the grating after each CPSO iteration, the transfer-matrix method is employed for grating modeling. The formulation of the coupled-mode-theory-based transfer-matrix method (CMT-TMM) is given by

$$T_j=\left[\begin{array}{cc}\cosh (\gamma \Delta z)+i{\displaystyle \frac{\delta }{\gamma }}\sinh (\gamma \Delta z)& {\displaystyle \frac{q}{\gamma }}\sinh (\gamma \Delta z)\\ {\displaystyle \frac{q^{*}}{\gamma }}\sinh (\gamma \Delta z)& \cosh (\gamma \Delta z)-i{\displaystyle \frac{\delta }{\gamma }}\sinh (\gamma \Delta z)\end{array}\right]$$

(4)

where $\gamma ={\left|q\right|}^2-{\delta }^2$. Each segment is modeled via the CMT-TMM approach, and the transmission characteristics of the entire grating are obtained by cascading the transfer matrices of all segments and obtaining the $T_{out}$. Subsequently, we minimize the cost function using the CPSO algorithm. The cost function is defined as the mean square error (MSE) function between the target response $T_{\mathrm{target}}$ and the actual spectral response $T_{out}$, as expressed in Equation (5)

$$MSE={\displaystyle \frac{1}{N}}{\displaystyle \sum _{k=1}^N{\left|T_{\mathrm{target}}\left(k\right)-T_{out}\left(k\right)\right|}^2}$$

(5)

where N is the number of sampling wavelength points. This function quantifies the discrepancy between $T_{\mathrm{target}}$ and $T_{out}$. When the maximum iteration count is reached, the optimization terminates, and we obtain an optimized set of grating coupling coefficients $\kappa$. These k-values can be mapped to the actual physical structure apodized by the CLMM method through Equation (3), yielding our final optimized grating design.

4. Simulation

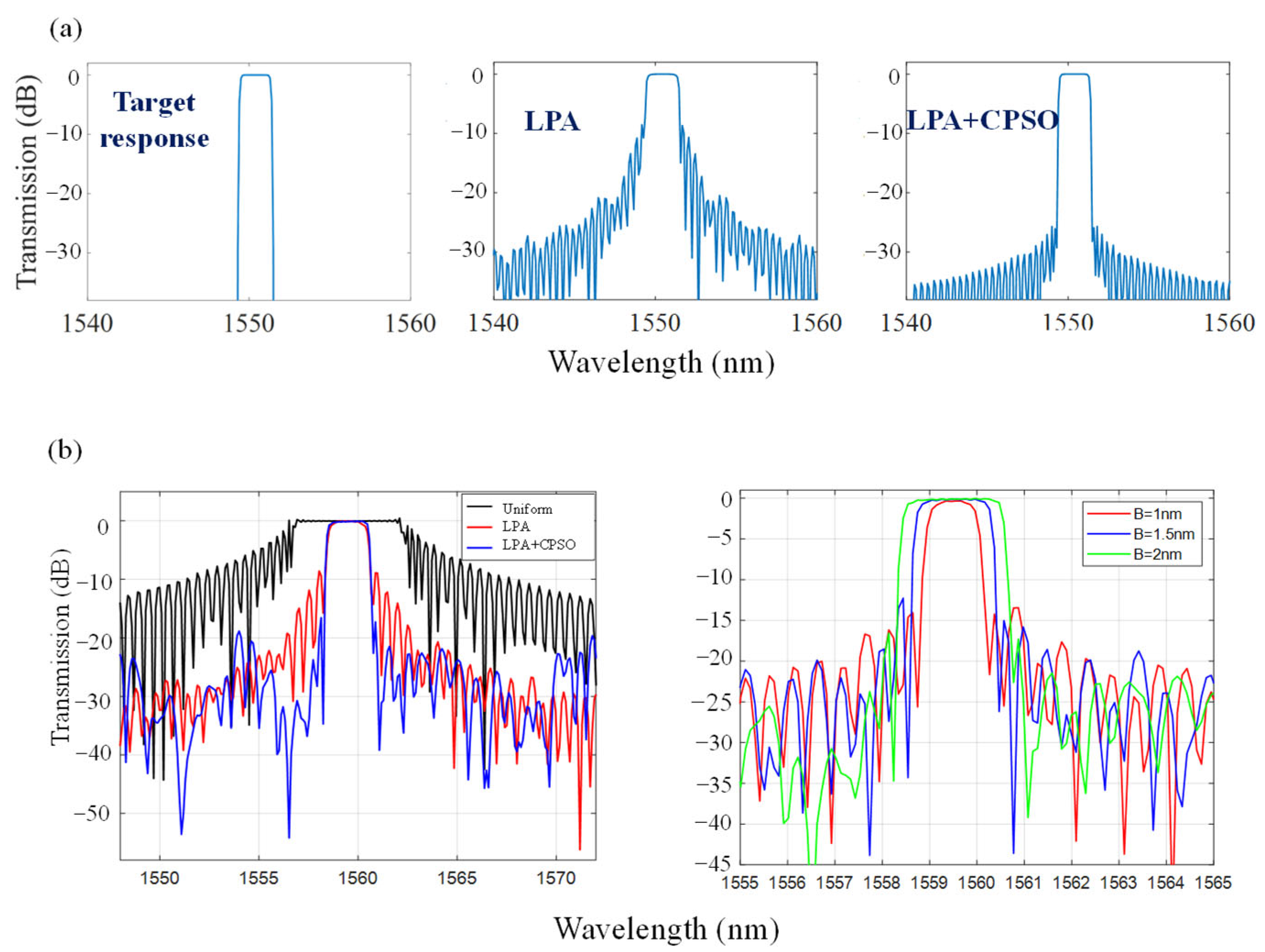
To validate the proposed design method, a narrow-band filter with a target bandwidth of 2 nm is specified, and its ideal spectral response is illustrated in Figure 3a (left plot). Consistent with Section 2, the Bragg grating, designed to resonate at 1550 nm, is implemented on a 500 nm wide single-mode waveguide with a corrugation width of 70 nm. To reduce the in-band insertion loss, and to suit the CPSO algorithm, we set the grating period to 2400 nm, each with a periodicity of 304 nm. In the traditional forward design of gratings, FDTD is typically employed to sweep through a range of grating parameters in search of the optimal device configuration. This process often necessitates dozens to hundreds of simulation iterations, consuming substantial computational resources and time. It is worth emphasizing that in this study, the FDTD method is used only to validate the final optimized structure, rather than to perform exhaustive parametric searches, thus minimizing the computational burden while reliably verifying target performance. Thus, after numerical optimization, a finite-difference time-domain (FDTD) tool is used to validate the performance of Bragg grating filters. To ensure an accurate evaluation of the optimized grating’s performance, a mesh convergence level of six was maintained throughout all simulations.

Figure 3a (middle plot) presents the spectral response optimized via the LPA, showing that while the bandwidth of the resulting grating filter meets the target specifications, its side lobe suppression capability remains limited (smaller than 10 dB), which can be attributed to insufficiently accurate coupling coefficients derived from the algorithm. To achieve enhanced side lobe suppression, the CPSO algorithm was applied to refine the initial solution generated by the LPA. This approach allows flexible optimization of the grating coupling coefficients, enabling closer convergence toward the target spectral response. The optimized spectrum is shown in Figure 3a (right plot). In the CPSO algorithm, we employ 60 particle swarms to optimize the coupling coefficient $\kappa$. Compared to the LPA, the hybrid optimization approach achieved a significantly improved side lobe suppression ratio of 25 dB in the spectral response.

Table 1. Simulation results of performance analysis for the three Bragg gratings.

Bragg Grating	IL (dB)	3dB Bandwidth (nm)	SLSR (dB)	SF
Uniform	0.13	5.1	0.54	/
LPA	0.21	1.92	8.77	0.86
LPA + CPSO	0.34	1.98	18.8	0.91

summarizes the spectral performance metrics, and Figure 3b (left plot) compares the corresponding spectral responses of the uniform Bragg grating, the grating designed using the LPA, and the grating optimized via the hybrid algorithm. By superimposing the spectral responses of the three Bragg gratings, the superiority of the structure further optimized by CPSO is clearly demonstrated. The shape factor (SF) [35], defined as the ratio of the 3 dB to the 10 dB bandwidth, is a key metric for passband steepness, with a value approaching unity indicating a more rectangular filter response. From the simulation results, the uniform Bragg grating has a fairly wide bandwidth of 5.1 nm, an insertion loss (IL) of 0.13 dB, and an SLSR of only 0.54 dB. The grating optimized using the LPA has an IL of 0.21 dB, a 3 dB bandwidth of 1.92 nm, and an SF of 0.86. However, the spectral response still exhibits significant side lobes, with an SLSR of only 8.77 dB, indicating that there is still room for improvement in spectral quality. By applying the CPSO algorithm to optimize the grating coupling coefficient, we obtained a grating design that displays significantly improved filtering performance, with a 3 dB bandwidth of 1.98 nm, an IL of 0.34 dB, a significantly improved SLSR of 18.8 dB, and an SF of 0.91, which is closer to the ideal value of 1. This demonstrates excellent roll-off characteristics, making it suitable for optical communication applications with high filter performance requirements, such as WDM systems.

To validate the algorithm’s adaptability, Bragg gratings targeting 1.2 nm, 1.6 nm, and 2 nm bandwidths were inversely designed using the hybrid optimization approach. The optimized grating structures were then simulated in FDTD, with resultant spectra presented in Figure 3b (right plot). The actual bandwidth of the optimized gratings is close to the target bandwidth, and the SLSR is greater than 14 dB, demonstrating the hybrid algorithm’s capability to precisely control coupling coefficients while suppressing side lobes under varying design requirements. The algorithm maintains consistent performance across target bandwidths spanning 1.2–2 nm (variation < 5%), demonstrating its scalability for designing narrow-band filters with >14 dB SLSR and <0.5 dB insertion loss.

5. Fabrication and Measurement

To validate our design, we fabricate the Bragg grating on a standard SOI wafer. The thickness of the top silicon and the BOX layer are 220 nm and 2 μm, respectively. Figure 4a presents an optical micrograph of the complete fabricated device. The MMI structure employed for the Michelson interferometer and the grating structure employed for fiber coupling are detailed in Figure 4a.

The spectral response of the fabricated device was characterized using a tunable laser source (Agilent 81642A; Keysight Technologies, Santa Rosa, CA, USA) and an optical power meter (Agilent 81636B; Keysight Technologies, Santa Rosa, CA, USA). The wavelength sweep was configured from 1528 nm to 1565 nm. The wavelength step was set to 10 pm. The spectral responses of the fabricated uniform grating, the laterally misalignment-apodized grating designed by the LPA, and the laterally misalignment-apodized grating optimized by the CPSO algorithm are presented in Figure 4b.

As observed, the uniform grating exhibits a bandwidth of 11.53 nm, far exceeding the 2 nm target, and is accompanied by high side lobes, while its insertion loss remains low at 0.15 dB. The laterally misalignment-apodized grating realized with the LPA exhibits a 3 dB bandwidth of 3.4 nm, an insertion loss of 1.38 dB, and an out-of-band side lobe level of 7.675 dB. The laterally misalignment-apodized grating optimized by the CPSO algorithm achieves a 3 dB bandwidth of 3.39 nm, an insertion loss of 1.75 dB, and an out-of-band side lobe suppression of 19.34 dB. Steep roll-off can reduce inter-channel crosstalk and increase channel capacity, while a high SLSR mitigates the impact of channel noise on communication quality. These advantages enable our designed grating filter to meet the application requirements of WDM systems. The performance analysis of the experimental results for the three gratings is presented in

Table 2. Experimental results of performance analysis for the three Bragg gratings.

Bragg Grating	IL (dB)	3dB-Bandwidth (nm)	SLSR (dB)	SF
Uniform	0.15	11.53	0.837	/
LPA	1.38	3.4	7.675	0.8
LPA + CPSO	1.75	3.39	19.34	0.82

.

The experimental results are in good agreement with the simulations and demonstrate the superior performance of our proposed design method: further optimization of the grating coupling coefficients with the CPSO algorithm on the basis of the LPA solution yields an additional, noticeable improvement in grating performance. The insertion losses of the LPA and LPA+CPSO gratings are higher than expected, likely because the CLMM introduces greater loss in fabrication than predicted. All three gratings exhibit bandwidths exceeding the target value, presumably due to the fabricated ridge height being larger than designed. Iterative optimization can narrow down the bandwidth to the desired value. The SF matches the simulated result closely.

6. Conclusions

We present a design methodology for narrow-band, flat-top silicon Bragg gratings that synergistically combines LPA with the CPSO algorithm. After the coupling coefficient is optimized, we leverage complementary lateral-misalignment apodization to directly encode the Bragg grating’s physical structure. The proposed design algorithm first employs the LPA to generate an iterative initial guess and then refines the grating coupling coefficient with the CPSO, progressively converging toward the target response. To validate the proposed design method, we set the Bragg wavelength to 1550 nm and targeted a 2 nm bandwidth response, yielding simulated performances of 1.98 nm bandwidth, 18.8 dB side lobe suppression, 0.34 dB insertion loss, and a 0.91 shape factor—substantially outperforming both uniform and LPA-only designs. To further validate the manufacturability of the proposed design methodology, we fabricated devices on a 220 nm SOI platform, which exhibit 3.39 nm bandwidth, 19.34 dB side lobe suppression, and 1.75 dB insertion loss, confirming the validity of the design methodology. Introducing the CPSO algorithm can reduce the cumulative error of the LPA, enabling a closer approximation to the target response. The proposed hybrid optimization framework provides a practical route to high-performance, narrow-band silicon filters for dense wavelength-division multiplexing systems.