Development of a Large-Range FBG Strain Sensor Based on the NSGA-II Algorithm
Abstract
1. Introduction
2. Working Principle of Large-Range FBG Strain Sensor
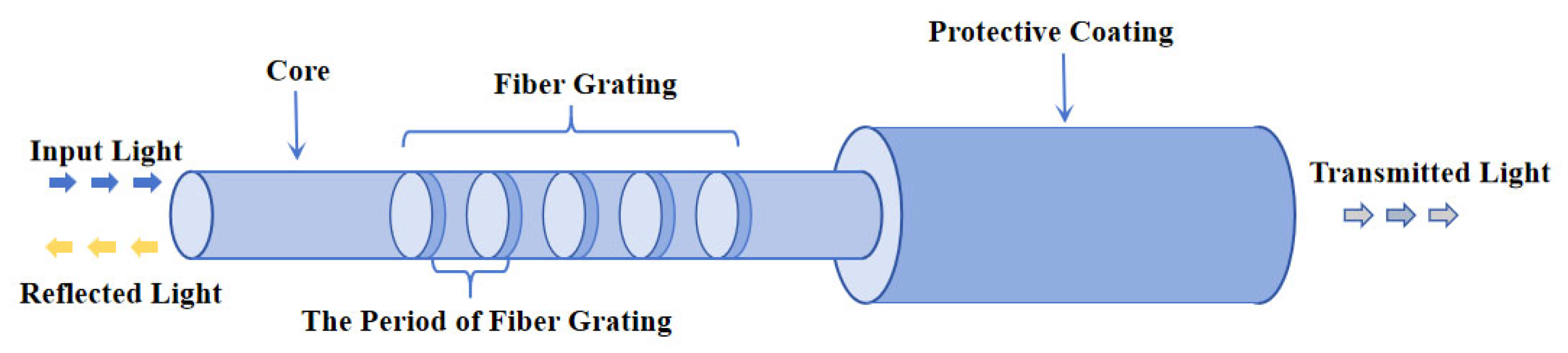
2.1. FBG Sensing Principle
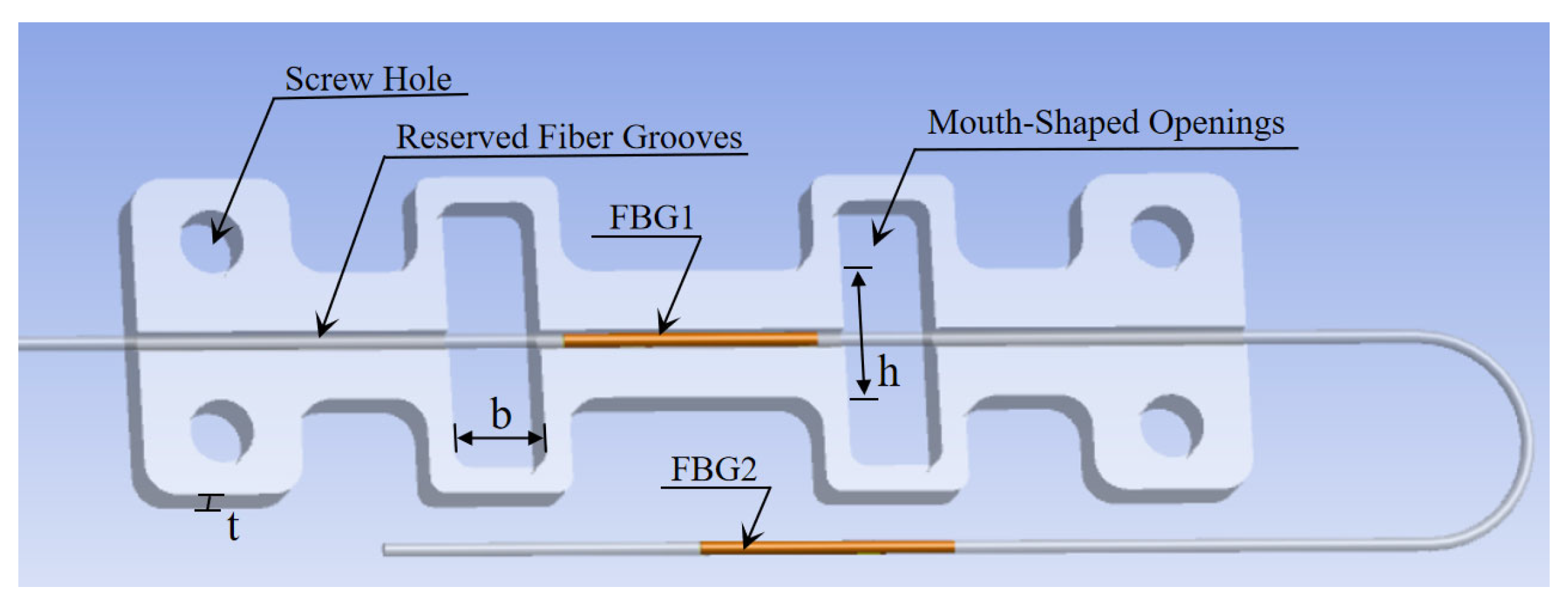
2.2. Structural Form of Large-Range FBG Strain Sensor
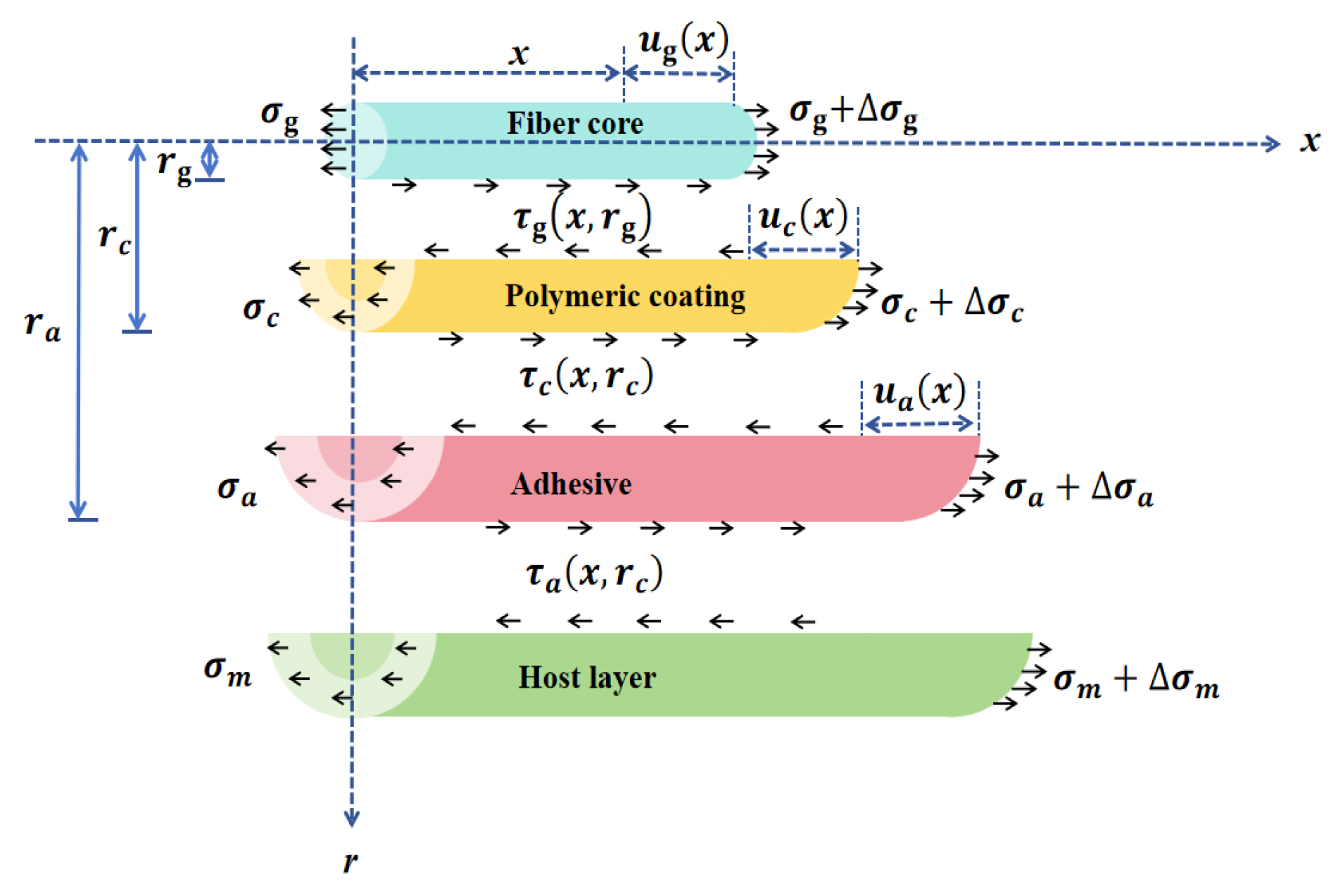
2.3. Transmission Principle
3. Structural Optimization Method for Large-Range FBG Strain Sensor
3.1. Subgroup Analysis of Structural Optimization for Large-Range FBG Strain Sensor
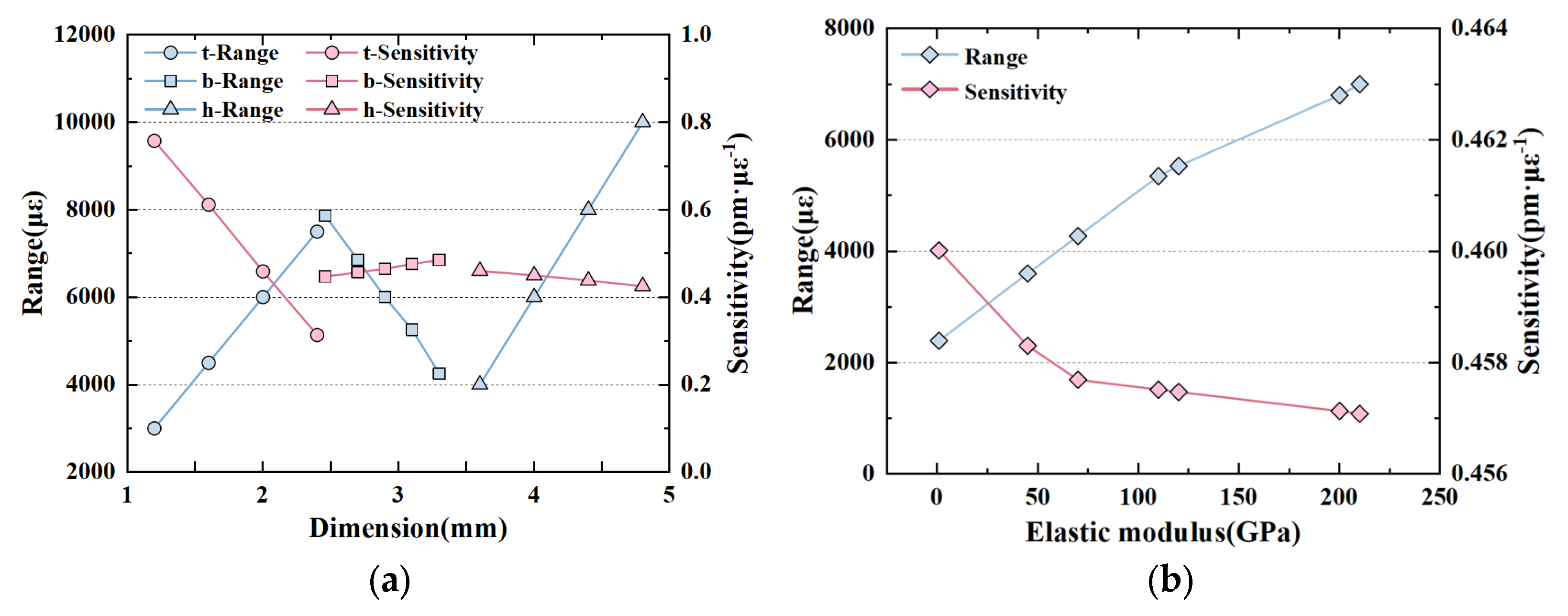
3.2. Structural Dimension Optimization of Large-Range FBG Strain Sensor
4. Linearity Test
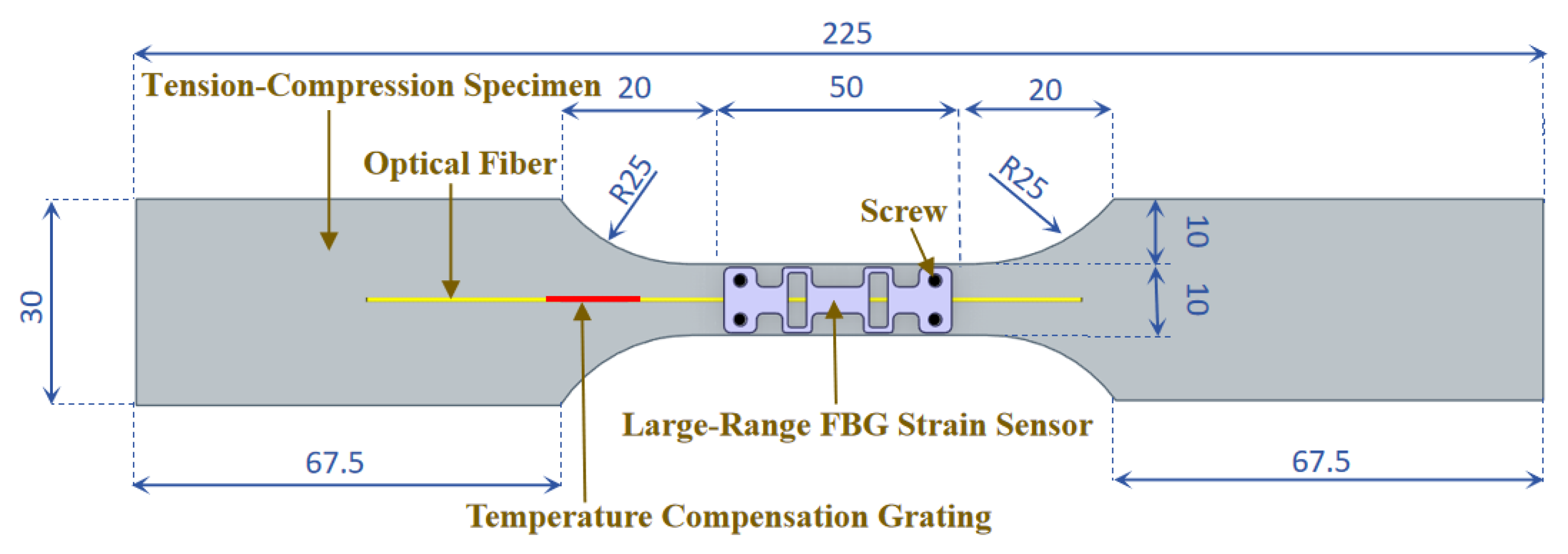
4.1. Test Design
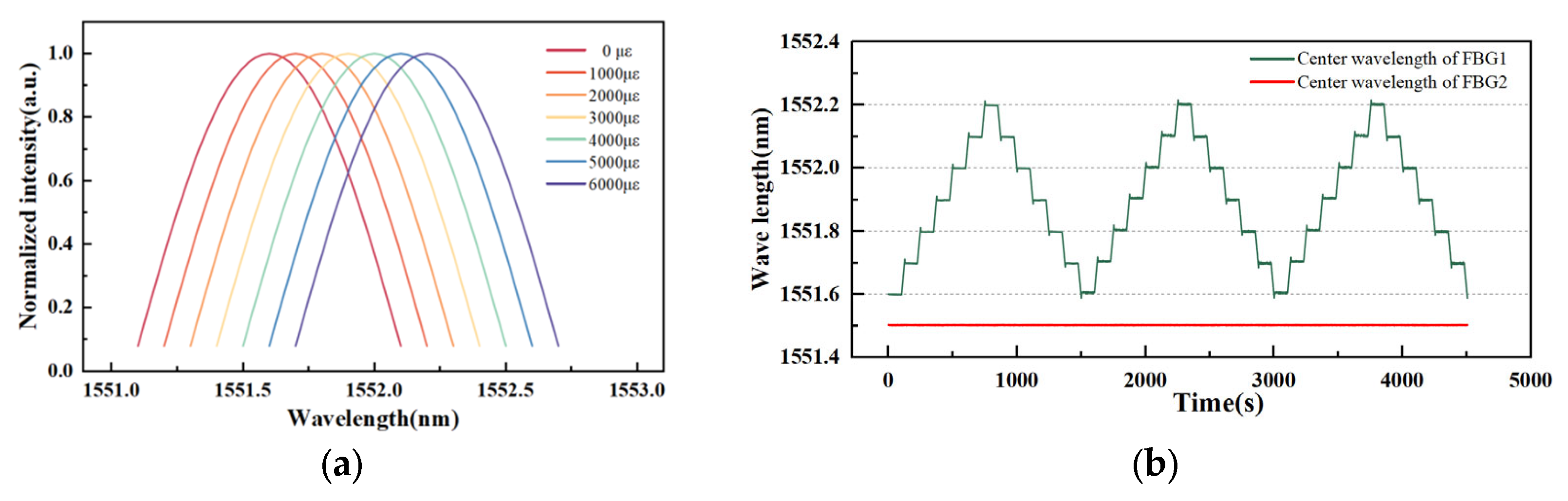
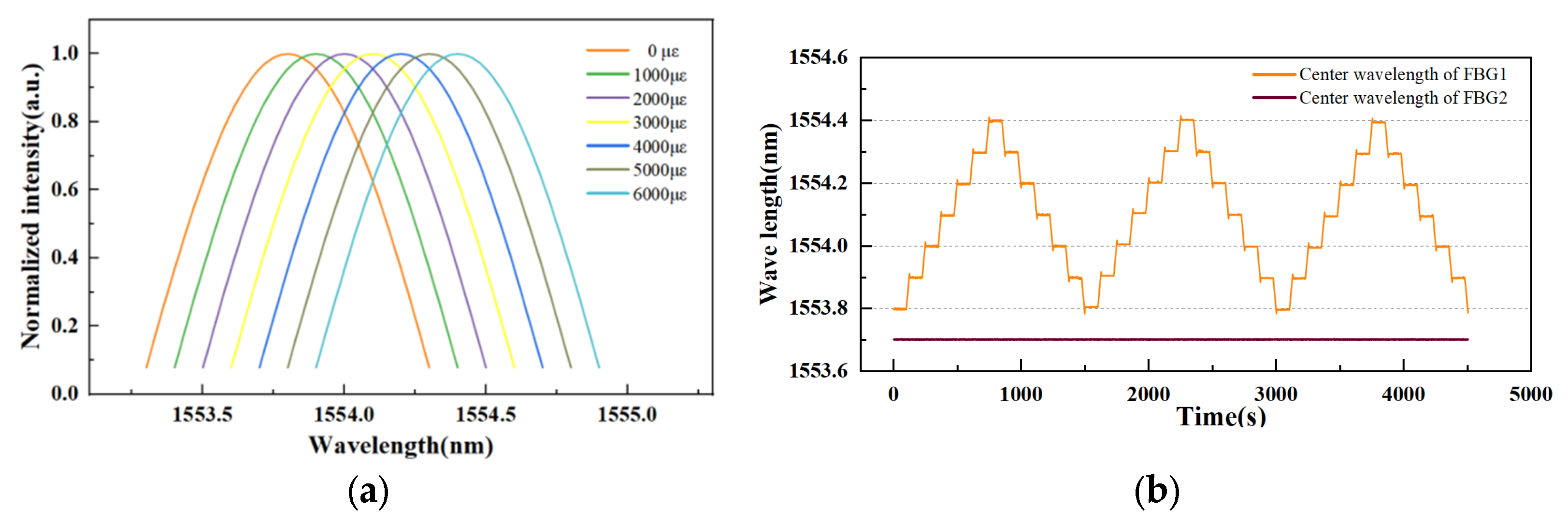
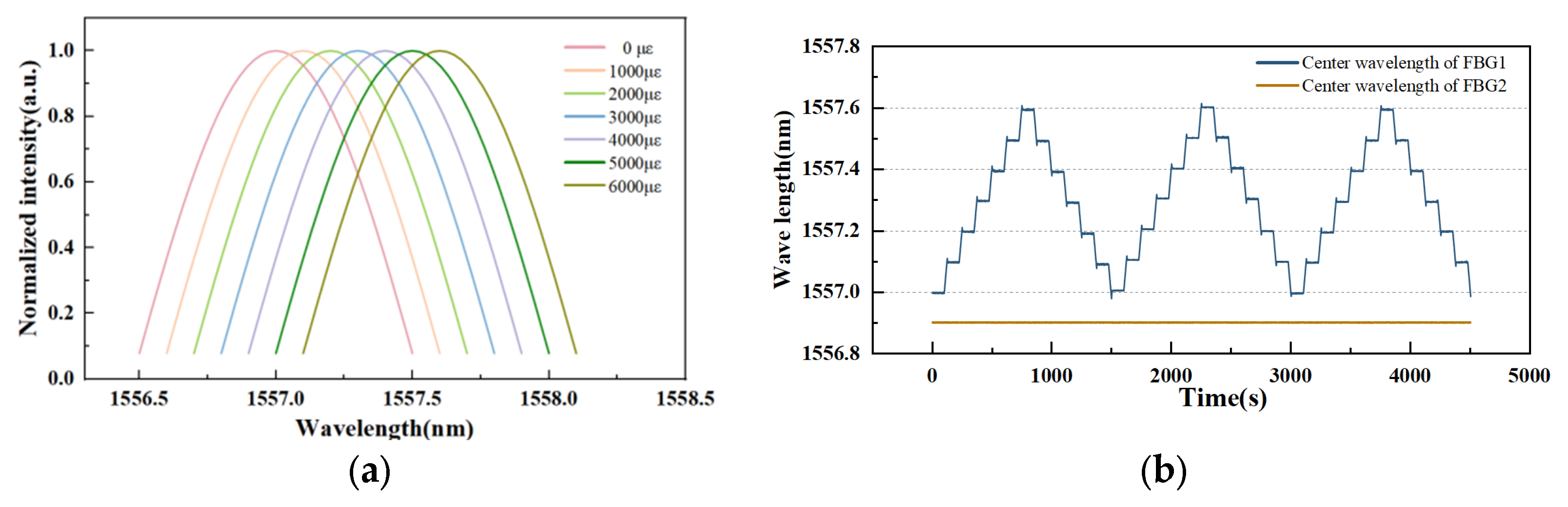
4.2. Tensile Experiment
5. Monitoring Experiment on Mortise—Tenon Joints of Dong Drum Tower
5.1. Experimental Design
5.2. Experimental Results
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.L.; Yao, K.; Lin, Q.J.; Zhao, Y.L. Application of Structural Health Monitoring System in Ancient Timber Buildings. J. Sens. Technol. 2024, 37, 1295–1306. [Google Scholar]
- Roberto, M.; Gianluca, R.; Emanuela, S. Fibre Bragg Gratings for the Monitoring of Wooden Structures. Materials 2018, 11, 7. [Google Scholar]
- Wu, W.J.; Sun, B.; Chen, S.Y.; Gong, W.M.; Wei, H.M. Membrane-Based Optical Fiber Bragg Grating Pressure Sensor for Health Monitoring of Pile Foundations. Appl. Opt. 2024, 63, 3039–3045. [Google Scholar] [CrossRef]
- Kim, J.M.; Kim, C.M.; Choi, S.Y.; Lee, B.Y. Enhanced Strain Measurement Range of an FBG Sensor Embedded in Seven-Wire Steel Strands. Sensors 2017, 17, 1654. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Zhu, X.; Ni, Y. Temperature Compensated Three-Directional Fiber Bragg Grating Strain Sensor with Big Measurement Range and High ·Accuracy. Opt. Eng. 2018, 57, 117113. [Google Scholar] [CrossRef]
- Sun, L.; Li, C.; Zhang, C.; Liang, T.Q.; Zhao, Z.H. The Strain Transfer Mechanism of Fiber Bragg Grating Sensor for Extra Large Strain Monitoring. Sensors 2019, 19, 1851. [Google Scholar] [CrossRef]
- Liu, C.Y.; Wang, X.; Chang, X.Q.; Wu, Z.S.; Huang, H.; Norri, M.; Altabey, W.A. Innovative Design and Sensing Performance of a Novel Large-Strain Sensor for Prestressed FRP Plates. Dev. Built Environ. 2024, 20, 100567. [Google Scholar] [CrossRef]
- Delyová, I.; Frankovský, P.; Bocko, J.; Trebuňa, P.; Živčák, J.; Schürger, B.; Janigová, S. Sizing and Topology Optimization of Trusses Using Genetic Algorithm. Materials 2021, 14, 715. [Google Scholar] [CrossRef]
- Wang, Z.C.; Cao, Z.G.; Fan, F.; Sun, Y. Shape Optimization of Free-Form Grid Structures Based on the Sensitivity Hybrid Multi-Objective Evolutionary Algorithm. J. Build. Eng. 2021, 44, 102538. [Google Scholar] [CrossRef]
- Kociecki, M.; Adeli, H. Two-Phase Genetic Algorithm for Topology Optimization of Free-Form Steel Space-Frame Roof Structures with Complex Curvatures. Eng. Appl. Artif. Intell. 2014, 32, 218–227. [Google Scholar] [CrossRef]
- Kociecki, M.; Adeli, H. Shape Optimization of Free-Form Steel Space-Frame Roof Structures with Complex Geometries Using Evolutionary Computing. Eng. Appl. Artif. Intell. 2015, 38, 168–182. [Google Scholar] [CrossRef]
- Kookalani, S.; Cheng, B.; Xiang, S. Shape Optimization of GFRP Elastic Gridshells by the Weighted Lagrange ε-Twin Support Vector Machine and Multi-Objective Particle Swarm Optimization Algorithm Considering Structural Weight. Structures 2021, 33, 2066–2084. [Google Scholar] [CrossRef]
- Sardone, L.; Fiore, A.; Manuello, A.; Greco, R. Performative Structural Design Optimization: Generative Algorithm for a Preliminary Study of a Voided Beam. Appl. Sci. 2022, 12, 8663. [Google Scholar] [CrossRef]
- Carbas, S.; Artar, M. Optimum Design of Cold-Formed Steel Frames via Five Novel Nature-Inspired Metaheuristic Algorithms under Consideration of Seismic Loading. Structures 2021, 33, 4011–4030. [Google Scholar] [CrossRef]
- Shan, W.; Liu, J.; Zhou, J. Integrated Method for Intelligent Structural Design of Steel Frames Based on Optimization and Machine Learning Algorithm. Eng. Struct. 2023, 284, 115980. [Google Scholar] [CrossRef]
- Stankovic, T.; Storga, M.; Marjanovic, D. Synthesis of Truss Structure Designs by NSGA-II and NodeSort Algorithm. J. Mech. Eng. 2012, 58, 204–212. [Google Scholar] [CrossRef][Green Version]
- Hill, K.O.; Malo, B.; Bilodeau, F.; Johnson, D.C.; Albert, J. Bragg gratings fabricated in monomode photosensitive optical fiber by UV exposure through a phase mask. Appl. Phys. Lett. 1993, 62, 1035–1037. [Google Scholar] [CrossRef]
- Wei, H.; Tao, C.; Zhu, Y.; Krishnaswamy, S. Fiber Bragg grating dynamic strain sensor using an adaptive reflective semiconductor optical amplifier source. Appl. Opt. 2016, 55, 2752–2759. [Google Scholar] [CrossRef]
- Zhang, G.H.; Chai, J.; Mi, X.F.; Li, Y.; Li, X.J.; Hao, L. Strain Sensitivity of Fiber Gratings on Different Substrates. Opt. Commun. Technol. 2013, 37, 30–32. [Google Scholar]
- Feng, X.; Zhou, J.; Sun, C.; Zhang, X.T. Theoretical and Experimental Investigations into Crack Detection with BOTDR Distributed Fiber Optic Sensors. J. Eng. Mech. 2013, 139, 1797–1807. [Google Scholar] [CrossRef]
- Zhang, R.L.; Wu, X.; Hong, L.; Jin, J.H.; Li, G.L. High-sensitivity fiber Bragg grating strain sensor of the substrate type. Appl. Opt. 2022, 61, 10567–10573. [Google Scholar] [CrossRef]
- Yan, J.H.; Zou, J.; Xue, T.; Lv, R.L.; Zhao, K.Z.; Wang, B. Fiber Bragg Grating Strain Sensor With Extended Measurement Range via Strain Relief Ring. Sens. J. IEEE 2025, 25, 2675–2681. [Google Scholar] [CrossRef]
- Liu, M.; Wang, W.; Song, H.; Zhou, S.; Zhou, W. A High Sensitivity FBG Strain Sensor Based on Flexible Hinge. Sensors 2019, 19, 1931. [Google Scholar] [CrossRef]
- Li, X.; Zheng, M.; Hou, D.; Wen, Q. Advantageous Strain Sensing Performances of FBG Strain Sensors Equipped with Planar UV-Curable Resin. Sensors 2023, 23, 2811. [Google Scholar] [CrossRef]
- Hong, Y.; Zhang, Y.F.; Su, D.; Yin, Z.Y. Development of a FBG Based Hoop-Strain Sensor Using 3D Printing Method. IEEE Access 2019, 7, 107154–107160. [Google Scholar] [CrossRef]



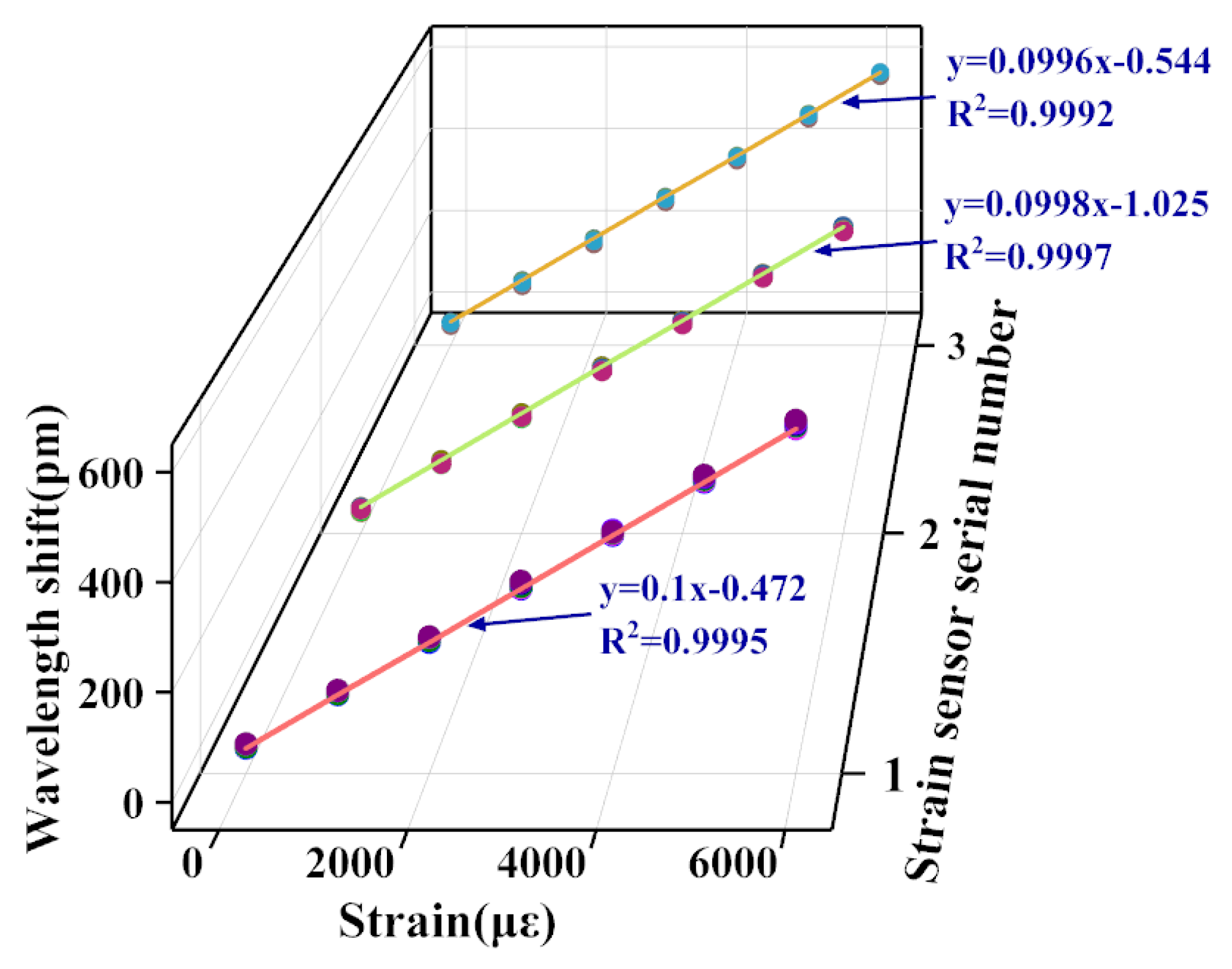

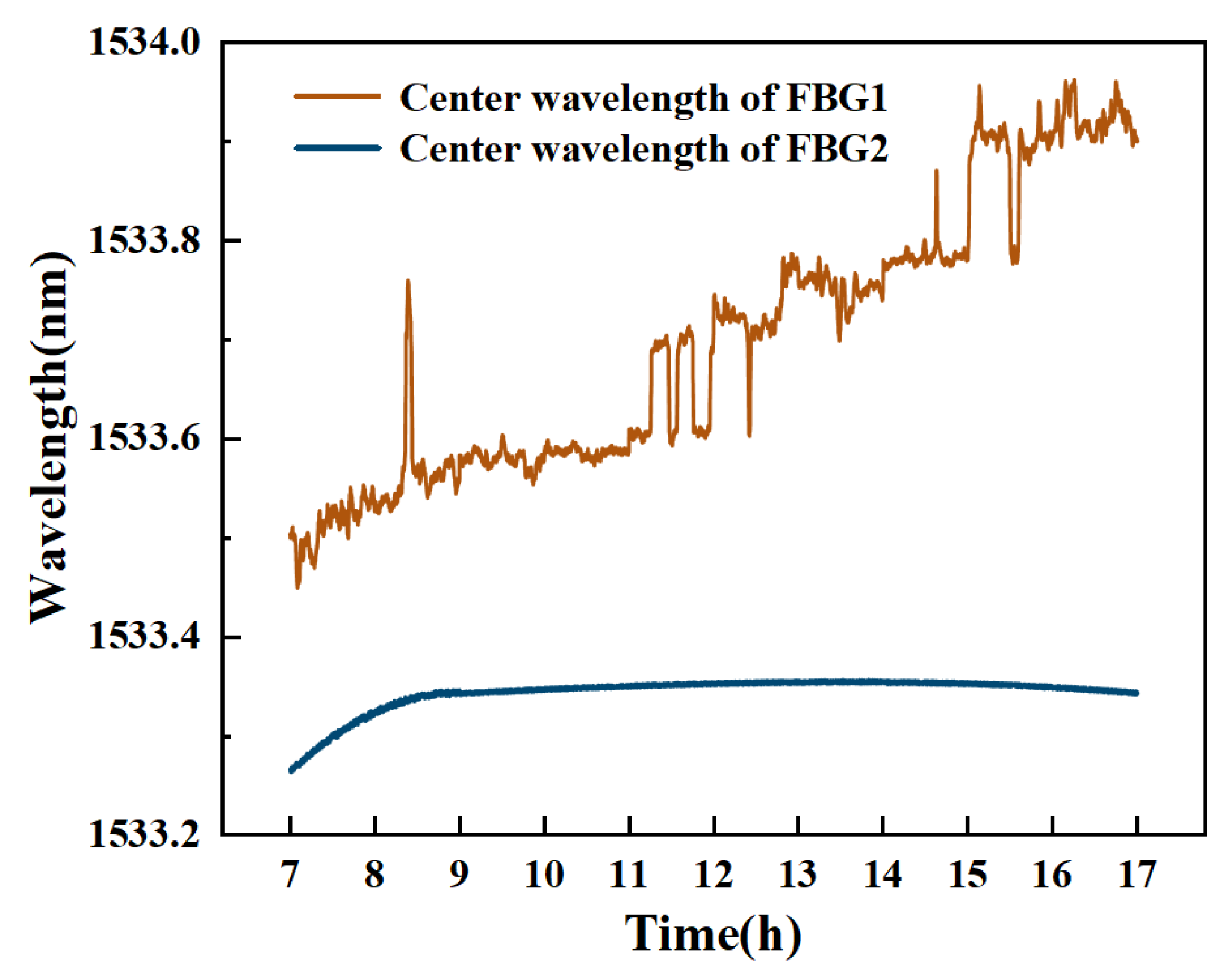
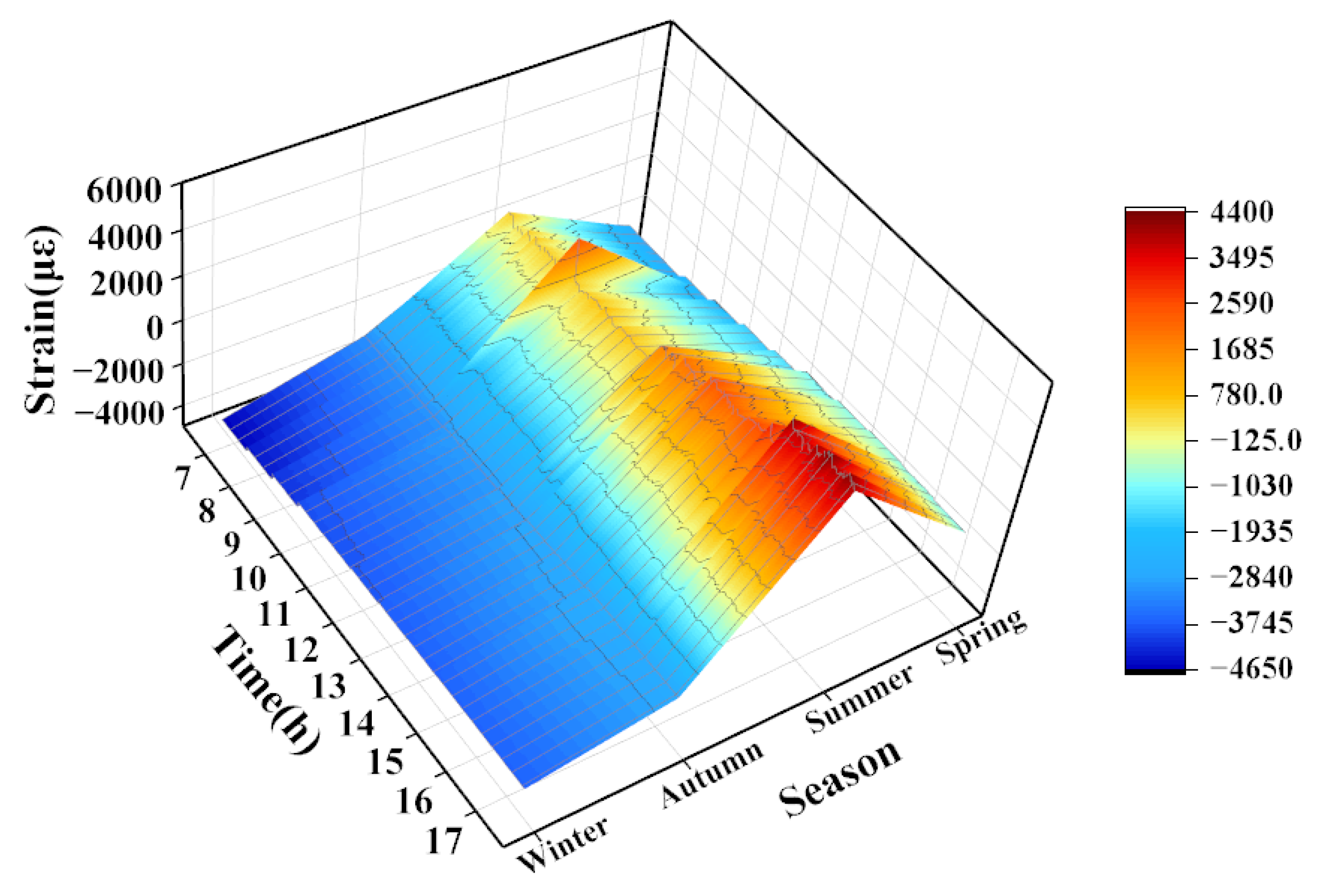
| t/mm | b/mm | h/mm | E/Gpa | |
|---|---|---|---|---|
| 1# | 1.85 | 2.98 | 4.25 | 70 |
| 2# | 1.89 | 3.04 | 3.78 | 70 |
| 3# | 1.9 | 2.85 | 3.90 | 70 |
| Sensor Type | Research Group | Sensitivity (pm/με) | Measurement Range (με) |
|---|---|---|---|
| Metal Substrate | Zhang et al. [21] | 3.21 | - |
| Metal Substrate | Yan et al. [22] | 0.151 | 0–12,148 |
| Metal Substrate | Liu et al. [23] | 10.84 | 0–200 |
| Composite Substrate | Li et al. [24] | 1.5 | −2000–2000 |
| Composite Substrate | Hong et al. [25] | 2.48 | 0–1000 |
| Metal Substrate | This work | 0.1 | −4650–6000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, W.; Yang, Z.; Chen, X.; Wei, H.; Wu, X.; Zhang, D. Development of a Large-Range FBG Strain Sensor Based on the NSGA-II Algorithm. Photonics 2025, 12, 985. https://doi.org/10.3390/photonics12100985
Wu W, Yang Z, Chen X, Wei H, Wu X, Zhang D. Development of a Large-Range FBG Strain Sensor Based on the NSGA-II Algorithm. Photonics. 2025; 12(10):985. https://doi.org/10.3390/photonics12100985
Chicago/Turabian StyleWu, Wenjing, Zhenpeng Yang, Xinxing Chen, Heming Wei, Xiao Wu, and Dengwei Zhang. 2025. "Development of a Large-Range FBG Strain Sensor Based on the NSGA-II Algorithm" Photonics 12, no. 10: 985. https://doi.org/10.3390/photonics12100985
APA StyleWu, W., Yang, Z., Chen, X., Wei, H., Wu, X., & Zhang, D. (2025). Development of a Large-Range FBG Strain Sensor Based on the NSGA-II Algorithm. Photonics, 12(10), 985. https://doi.org/10.3390/photonics12100985







