Dual-Frequency Soliton Generation of a Fiber Laser with a Dual-Branch Cavity

Abstract

We report the simultaneous generation of conventional solitons (CSs) and dissipative solitons (DSs) in an erbium-doped mode-locked fiber laser with a dual-branch cavity configuration based on the nonlinear polarization rotation (NPR) technique. By incorporating fibers with different dispersion properties in two propagation branches, the laser can establish simultaneous operation in the normal and anomalous dispersion regimes within the respective loops, enabling the generation of two distinct soliton types. The CSs exhibit a 3 dB spectral bandwidth of 9.7750 nm and a pulse duration of 273 fs, while the DSs have a quasi-rectangular spectrum spanning 18.7074 nm and a pulse duration of 2.2 ps, which can be externally compressed to 384 fs. The fundamental repetition rate is approximately 21 MHz, with a repetition rate difference of 216 Hz for the two pulse trains. Stable second-order, third-order, and fourth-order harmonic mode-locking (HML) can be achieved through optimization of pump power and intracavity polarization states. The laser we build in this work has significant potential for applications in high-precision spectroscopy and asynchronous optical sampling.

1. Introduction

Passive mode-locked fiber lasers exhibit inherent advantages of high beam quality, efficient heat dissipation, and free alignment, which have attracted considerable attention and have become an essential platform in various applications [1,2,3]. Particularly, a dual-repetition-rate mode-locked fiber laser can produce a pair of different-repetition-rate pulse trains from a single-cavity system without complex active phase-locking [4,5,6]. Because of the common-mode noise cancelation, the pulses with two repetition rates have excellent stability and high mutual coherence [7,8]. These simple and cost-effective lasers show great potential for applications in spectroscopy [9], optical sensing [10], and absolute-distance ranging [11].

The generation of various types of solitons in fiber lasers is determined by the setting of net cavity dispersion. Variations in dispersion conditions alter the intracavity nonlinear pulse dynamics, producing solitons featuring distinctive temporal and spectral properties. The formation of CSs operating in the anomalous dispersion regime results from the balance between fiber nonlinearity and anomalous dispersion [12,13,14]. Particularly, DSs operating in net normal dispersion regimes are distinguished by their wave-breaking-free dynamics, which enables the generation of ultrafast pulses with exceptionally high peak powers [15]. The formation of DSs stems from the intricate interplay among normal dispersion, fiber nonlinearity, gain, and loss [16,17]. Research has primarily focused on single-soliton regimes, while achieving multiple-soliton-type emissions in a single laser cavity typically requires adjusting the net cavity dispersion to induce distinct soliton types—for instance, by varying the length of fibers with specific dispersion values to modify the intracavity dispersion [18]. However, little exploration has been devoted to achieving simultaneous emission of multiple soliton types in a single fiber laser while maintaining a fixed cavity configuration.

Of particular interest is the development of a laser capable of simultaneously generating CSs and DSs without structural modifications to the cavity [19]. The realization of dual-solitons would enhance the multi-scenario adaptability of dual-comb spectroscopy: CSs, with their femtosecond pulse durations, meet the precise temporal resolution requirements of ultrafast transient absorption spectroscopy, while DSs, owing to their broad spectral bandwidth and high pulse energy, exhibit unique advantages in weak-signal detection and broadband spectroscopic measurements. In 2013, Liu et al. first reported the simultaneous generation of CSs and DSs in a mode-locked fiber laser by exploiting two CFBGs and a four-port circulator [20]. In 2015, Han et al. proposed a nanotube mode-locked fiber laser using two CFBGs consisting of a linear and ring oscillator, delivering CSs and DSs simultaneously [21]. In 2019, Dong et al. first achieved a bidirectional mode-locked fiber with a CFBG to generate CSs and DSs [22]. Because of the narrow reflection bandwidth of the CFBG, these studies show the output performances of CSs have a narrow 3 dB spectral bandwidth (<1.02 nm) that results in a wider pulse duration, with a duration on the picosecond scale. The cavity space-multiplexing technique typically incorporates a shared path alongside dedicated sub-paths for dual-repetition-rate pulse generation [23]. Flexible control over the output characteristics of the dual-repetition-rate mode-locked pulses is achieved by employing a specific design in the non-common paths [24,25]. This architecture also serves as an effective method for generating CSs and DSs by applying different dispersion management in each separate branch. In 2013, Liu et al. achieved the realization of CSs and DSs in an erbium-doped fiber laser through a mixture of graphene and a single-walled carbon nanotube saturable absorber [26]. In 2018, Sun et al. described a multiplexed laser outputting CSs and DSs based on the NPR technique. Particularly, the CS can realize wavelength-tunable and multi-wavelength mode-locked output [27]. In 2018, Zhao et al. presented a nanotube mode-locked fiber laser with a tunable wavelength of ~15 nm in CSs and ~25 nm in DSs [28]. However, these aforementioned investigations with dual-branch configurations can only generate CSs or DSs individually, with no demonstrated capability for simultaneous operation. The need to repeatedly readjust cavity parameters such as the pump power, the loss through attenuators, or the intracavity polarization state through PCs for switching between soliton states may increase system complexity. Moreover, due to the long cavity lengths, previous studies were predominantly confined to fiber lasers with repetition rates below 11 MHz, and their output exhibited significant repetition rate differences. This limitation has hindered their deployment in high-speed asynchronous sampling applications.

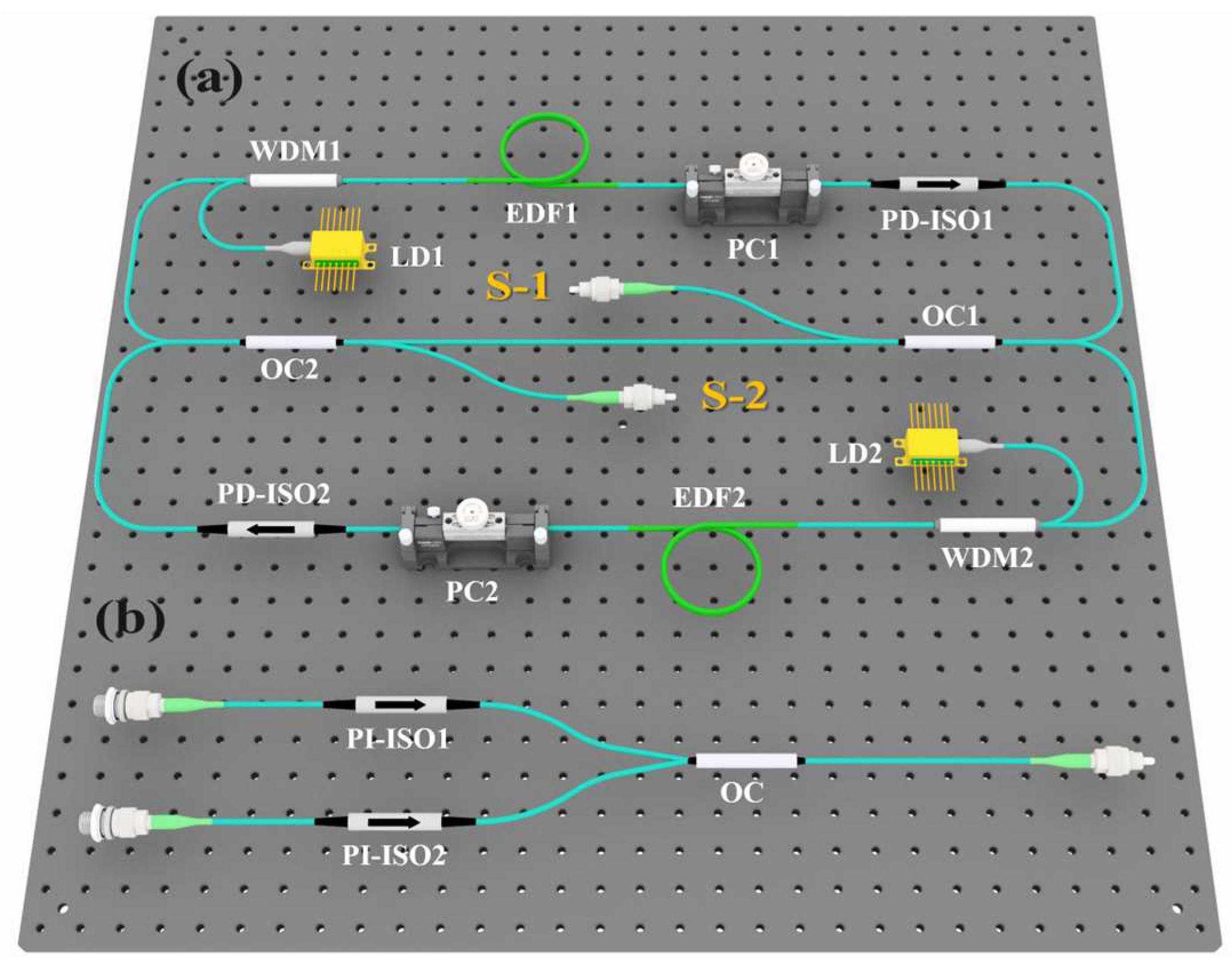
Here, we present an erbium-doped mode-locked fiber laser with a dual-branch structure to achieve simultaneous generation of CSs and DSs. Each subring exhibits an opposing dispersion distribution, enabling the propagation and generation of distinct soliton types in their respective loops. In addition, benefiting from the high damage threshold and polarization tunability offered by the artificial saturable absorber based on the NPR technique, stable HML operations can be achieved by appropriately increasing the pump power and adjusting the intracavity polarization state. To the best of our knowledge, this work demonstrates the first realization of HML operation with simultaneous output of multiple soliton types. Thus, the proposed cavity space-multiplexing fiber laser, capable of tuning both repetition rates and the repetition rate difference via the HML technique, can not only serve as a versatile platform for practical applications in asynchronous optical sampling, optical spectroscopy, and high-speed communication, but also provide a new path to explore the nonlinear dynamics between different types of solitons.

2. Fiber Laser Setup

A schematic diagram of the dual-repetition-rate mode-locked fiber laser is illustrated in Figure 1a, which consists of a shared path and two sub-paths. Each sub-path, in conjunction with the shared path, forms an independent subring laser cavity. Two 2 × 2 optical couplers (OCs) with a coupling ratio of 50/50 are not only employed to form two independent resonant cavities, but also provide two 50% outputs for the respective cavities. CSs and DSs are generated separately in two subring lasers with distinct dispersion values. Mode-locking operation is implemented through the NPR technique, with each sub-path containing a PC and a polarization-dependent isolator (PD-ISO) to ensure unidirectional operation. Each subring cavity is pumped via a 980/1550 nm wavelength division multiplexer (WDM) using a 980 nm laser diode (LD) of 400 mW maximum output power. Two independent gain fibers are used to alleviate the strong gain competition between two subrings. Two segments of erbium-doped fiber (EDF, Coherent EDFL-980-HP), with lengths of 2.5 m and 5.5 m and a group velocity dispersion (GVD) of 0.023 ps²/m, are employed in subrings S−1 and S−2, respectively. The remaining fibers in the cavity are standard single-mode fibers (SMFs, Corning SMF-28e), having a GVD of −0.022 ps²/m. The entire laser system is constructed on an optical breadboard, such that all components experience the same environmental disturbances. The cavity lengths in S−1 and S−2 are each measured around 9.5 m, resulting in net cavity dispersions of about −0.097 ps² and 0.039 ps² at 1550 nm, respectively. Therefore, different mode-locking states in S−1 and S−2 can be controlled independently via adjustment of two pump powers and PCs, enabling the CSs and DSs to be output separately or simultaneously.

The optical spectrum is measured with an optical spectrum analyzer (YOKOGAWA, AQ6370C). A high-speed photodetector (Thorlabs, DET08CFC) is used with a digital oscilloscope (RIGOL, DS4054) and a radio frequency (RF) spectrum analyzer (RIGOL, DSA815) to capture the time-domain trace and acquire the RF spectrum, respectively. An autocorrelator (APE, PulseCheck) characterizes the autocorrelation trace, and an optical power meter (Thorlabs, PM20) records the average output power.

3. Experimental Results and Discussion

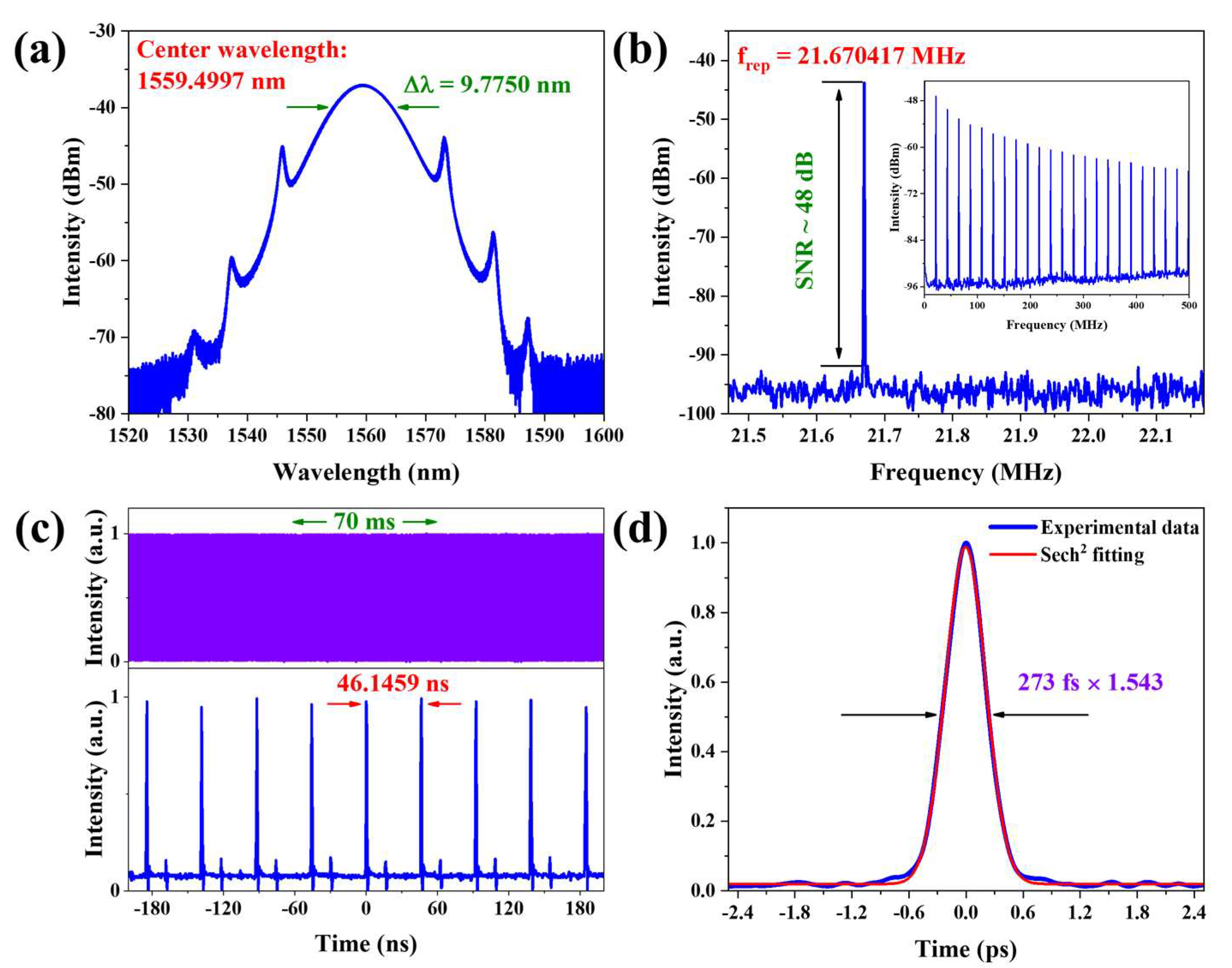
By suitably tuning the pump powers and intracavity polarization states, synchronous mode-locking can be established in both subrings. The thresholds of S−1 and S−2 are around 15 mW and 70 mW, respectively. The fundamental mode-locking characteristics of the dual-branch fiber laser are presented in Figure 2 and Figure 3. In S−1, a CS is achieved at a pump power of 18.2 mW. As presented in Figure 2a, the spectrum exhibits a 3 dB bandwidth of 9.7750 nm, centered at 1559.4997 nm. Characteristically, the spectrum exhibits symmetrically distributed Kelly sidebands around the center wavelength, originating from constructive interference between the soliton pulse and dispersive waves [29]. Figure 2b presents the RF spectrum with 100 Hz resolution bandwidth (RBW). The fundamental repetition rate is 21.670417 MHz, which corresponds to the cavity length. The 48 dB high signal-to-noise ratio (SNR) demonstrates the good stability of the CS mode-locked operation. Figure 2b, inset, displays the broadband RF spectrum over 0–500 MHz using an RBW of 3 kHz, suggesting single-pulse operation. Moreover, the pulse train shown in Figure 2c has an interval of ~46.1459 ns. The upper panel of Figure 2c shows the pulse train over a 70 ms time span, where the flat-top profile demonstrates excellent pulse stability. Additionally, Figure 2d presents the autocorrelation trace, yielding a pulse duration of 273 fs under a sech²-shaped pulse assumption. Compared with previously reported pulse durations of 1.1 ps [28], 1.64 ps [26], 3.96 ps [22], 5.47 ps [21], and 15.1 ps [20], our study demonstrates a significant improvement in pulse duration, which originates from precise dispersion management within S−1. The time–bandwidth product (TBP) is approximately 0.3289, nearing the theoretical minimum of 0.315 for a hyperbolic secant pulse and confirming near-transform-limited operation of the CS pulse. The average output power is measured to be 3.668 mW, corresponding to a single pulse energy of ~169 pJ.

In S−2, a DS is achieved at a pump power of 78.3 mW. The spectrum in Figure 3a exhibits a near-rectangular profile featuring steep edges. Notably, the NPR-induced spectral filtering attenuates the broadened edges of the pulse spectrum to form steep spectral edges, a characteristic feature of DSs [30]. Centered at 1572.3542 nm, the spectrum has a 3 dB bandwidth of 18.7074 nm. Figure 3b,c present the fundamental repetition rate of 21.670201 MHz and a pulse train with an interval of ~46.1463 ns, respectively. The long-time scale pulse train and the high SNR over 57 dB show the high stability of DS pulses. Figure 3d shows that Gaussian profile fitting of the autocorrelation trace yields a pulse duration of 2.2 ps. The TBP is calculated as 4.9906, which significantly exceeds the theoretical minimum of 0.441 for a Gaussian pulse, indicating strong chirping characteristics. The output average power is 5.857 mW, corresponding to a single pulse energy of 0.27 nJ.

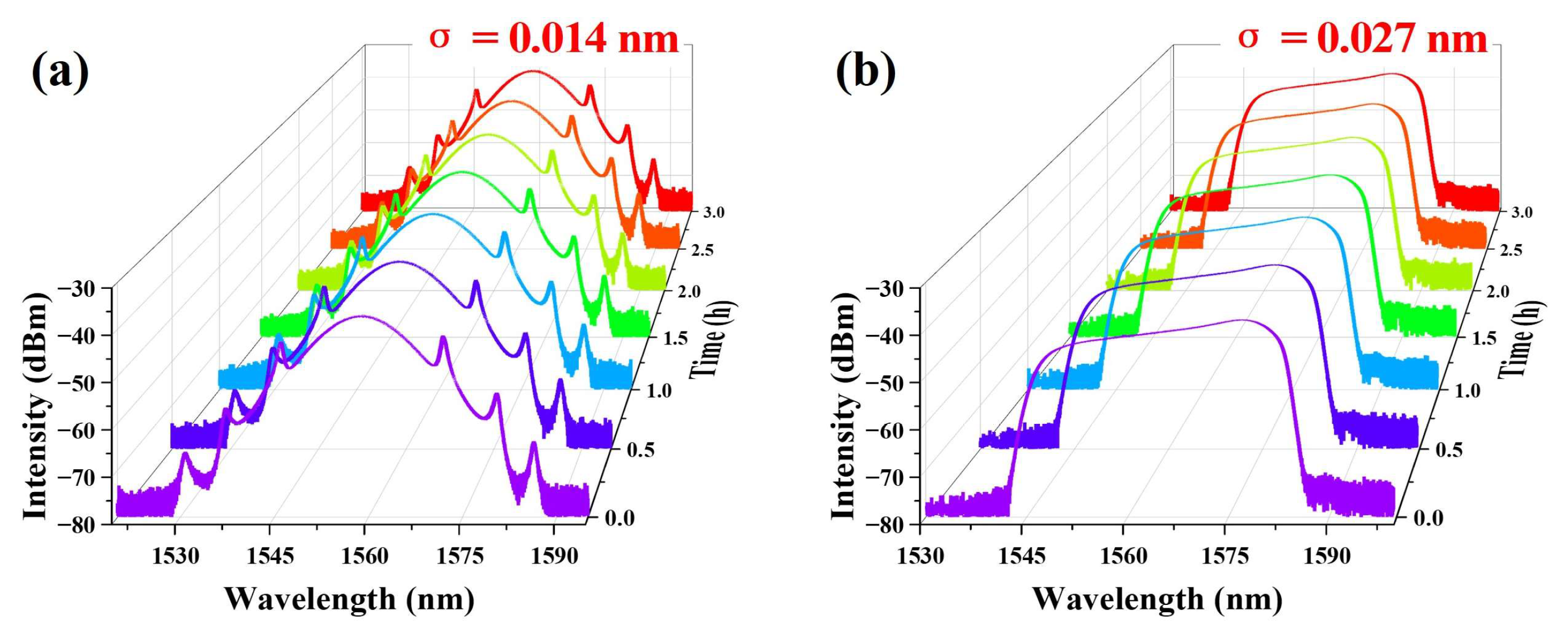
Through ingenious cavity design, our work overcomes the limitation of mutual gain competition between CSs and DSs in dual-branch configurations reported in prior studies [22,26,27], achieving their simultaneous output. Once obtained, mode-locking operation is capable of being maintained for extended periods. The output spectra of CSs and DSs have been investigated at room temperature with 30 min intervals over 3 h, as shown in Figure 4. No obvious changes are observed in the shapes of spectra during the whole period of time in Figure 4a,b. At the same time, recordings are also made of the center wavelength variations. For the CS and DS spectra, only slight shifts are detected, with respective standard deviations $\sigma$ of 0.014 nm and 0.027 nm. Therefore, the proposed cavity design demonstrates good stability by suppressing thermal and mechanical perturbations. This is achieved through the compact placement of all optical components, ensuring uniform exposure to environmental disturbances.

The configuration in Figure 1b combines the CS and DS pulse trains for precise measurement of their repetition rate difference, utilizing two mating sleeves and a 50/50 1 × 2 OC. Two polarization-independent isolators (PI-ISOs) serve to prevent the recoupling of reflected light into the ring cavity, thereby ensuring mode-locking stability. Figure 5a depicts two dominant peaks at 21.670201 MHz and 21.670417 MHz, which signify that the two pulse trains have different pulse repetition rates. The fundamental pulse repetition rates achieved in this study are twofold higher than the previously reported maximum (10.05 MHz [22]) and eight times the lowest recorded frequency (2.57 MHz [26]). Correspondingly, the two RF tones exhibit a frequency spacing of 216 Hz with a SNR of ~50 dB at a RBW of 10 Hz. Furthermore, equally spaced peaks with lower SNR (~20 dB) appear on both sides of the main signals, maintaining the 216 Hz interval. These sidebands originate from interference between the two main RF signals. For our proposed fiber laser with a two-subring structure, the repetition rate difference $∆f$ is mainly caused by cavity length difference between the two subrings. This is determined by $∆f={\displaystyle \frac{c}{n_{eff}}}\left({\displaystyle \frac{L_1-L_2}{L_1{L}_2}}\right)$, where $c$ is the speed of light, $n_{eff}$ is the effective refractive index of fiber, and $L_1$ and $L_2$ represent the cavity lengths of S−1 and S−2, respectively. The different fiber lengths of the non-common branches will directly affect the optical path in both subrings, which in turn affects $∆f$. To evaluate the relative stability of $∆f$, we conduct continuous measurement of the RF spectrum over 3 h at 30 min intervals. Owing to the RF spectrum analyzer’s 10 Hz resolution limit, no detectable drift is observed in either the individual repetition rates or their difference during the measurement period. The results indicate that both CS and DS pulse repetition rates fluctuate within a 10 Hz range, confirming the good stability of our mode-locked fiber laser design.

Additionally, due to the fixed group velocity difference between the two soliton pulse trains, periodic collisions occur. Oscilloscope measurements also confirm the repetition rate difference. Figure 5b depicts the interferogram of the pulse trains with a time range of 32 ms. Equally spaced interference peaks are observed, with an interval of ~4.61 ms between adjacent beat-note signal peaks. This result is consistent with the repetition rate difference of 216 Hz observed in the RF spectrum in Figure 5a. Figure 5c displays an expanded oscilloscope trace with a 280 ns time window, revealing two pulse trains with distinct relative intensities. Through a joint analysis of temporal periodicity and relative RF signal intensities, we conclusively identify the higher-intensity pulse train as DSs and the lower-intensity one as CSs. The upper and lower panels in Figure 5c display the oscilloscope traces of the combined pulse trains at different moments. The observed temporal variation in the interval between the two pulse trains, particularly the continuous phase shift of the CS pulses relative to the DS pulses, provides direct evidence of their asynchronous nature resulting from the slight repetition rate difference. Figure 5d displays an optical spectrum centered at 1561.8820 nm, revealing a broad spectral overlap between the long-wavelength components of CSs and the short-wavelength components of DSs.

Furthermore, HML operation can be achieved for both CSs and DSs in the two subrings. The fundamental repetition rate of a mode-locked ring laser is determined by the formula $f_0=c/(n_{eff}·L)$, where $L$ is the cavity length. Shortening the cavity length is a straightforward method for obtaining a high repetition rate pulse output. Nevertheless, this approach has an inherent limitation: indefinitely reducing the cavity length is impractical for significantly increasing the repetition rate. In other words, the minimum achievable fiber length of the laser resonator fundamentally constrains further improvement of the repetition rate. HML presents a practical solution for significantly increasing the repetition rate with its intrinsic advantage of repetition rate self-stabilization [31]. As the pump power exceeds a specific threshold value, multiple pulses emerge in the laser cavity during a single round-trip. These pulses initially exhibit non-uniform temporal distribution due to complex interactions between gain dynamics and nonlinear effects. By carefully optimizing the PC state, we can precisely manipulate the intracavity dynamics to achieve temporally equidistant pulse spacing, creating stable HML operation. HML produces pulse trains at repetition rates that are integer multiples ($N$ times) of the fundamental mode-locking frequency. This method can achieve repetition rates ranging from hundreds of MHz to several GHz while maintaining excellent pulse-to-pulse uniformity [32,33].

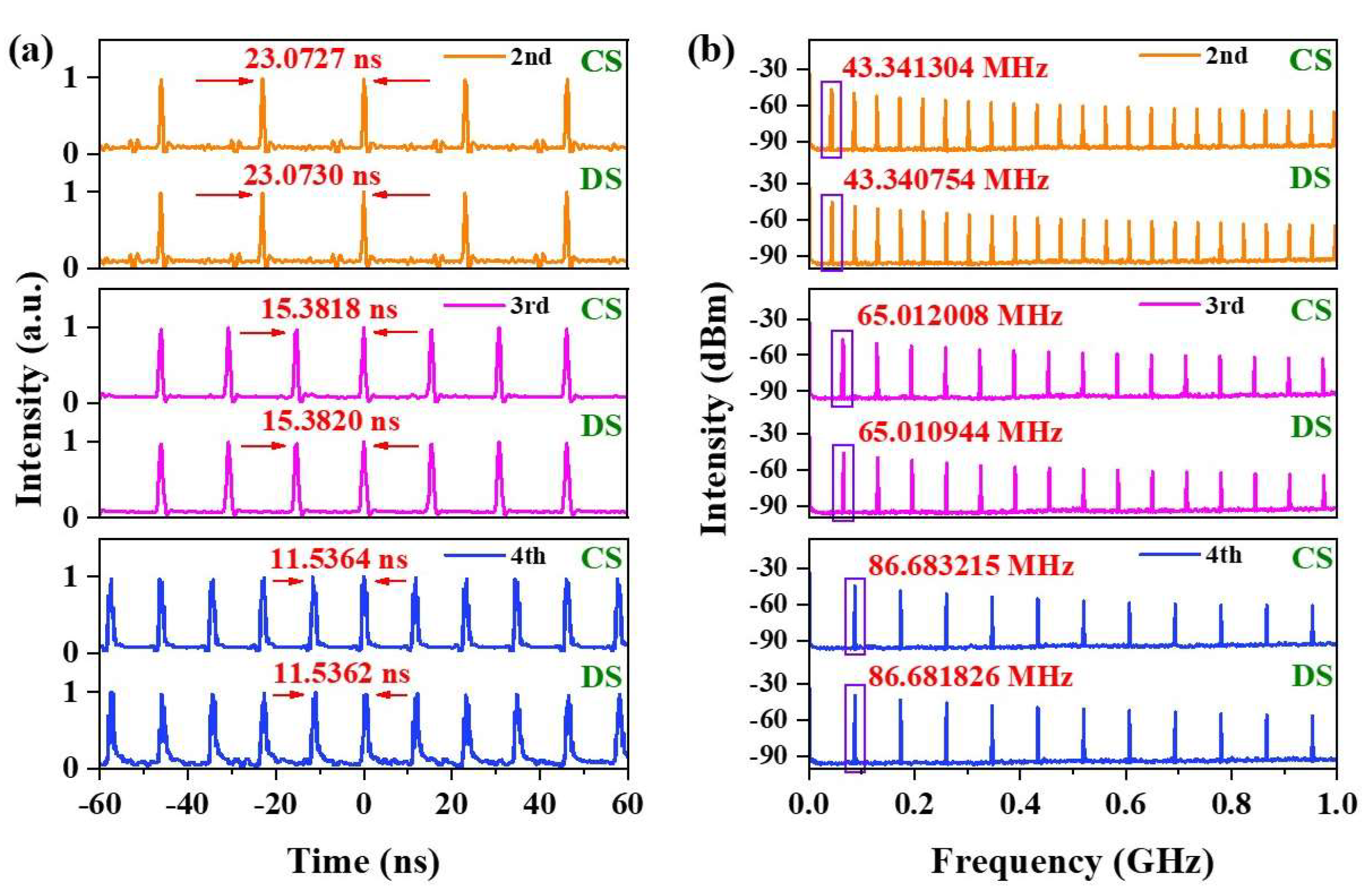
Stable HML of CSs and DSs becomes achievable when pump powers are gradually raised and the PCs are adjusted with precision. Figure 6 illustrates the characteristic features of HML from the second to the fourth order as the pump powers increase. Figure 6a displays the temporal pulse trains of CSs and DSs under different harmonic states within the same time observation range. When the powers of LD1 in S−1 and LD2 in S−2 reach 36.9 mW and 123.8 mW, respectively, second-order HML is achieved, with a pulse interval of ~23 ns. At LD1/LD2 powers of 49.4 mW and 193.1 mW, third-order HML reduces the pulse interval to ~15 ns. When the pump power is further increased to 61.4 mW (LD1) and 305.7 mW (LD2), fourth-order HML is attained, with a pulse interval of ~11 ns. The experimental results demonstrate that under Nth-order HML states, the pulse trains exhibit equally spaced distributions, with intervals equal to 1/N of the fundamental mode-locking pulse interval. Because of the constraints in the available pump power, DSs in our laser achieve stable HML only up to the fourth order, while CSs can form higher-order HML states within the available power range. Our study specifically focuses on achieving nearly identical repetition rates between two solitons, which require synchronized harmonic orders. Thus, we only demonstrate HML up to the fourth order for consistency. Nevertheless, we note that employing higher-power pump sources would enable the realization of higher-order HML states in DSs.

Figure 6b displays the corresponding RF spectra of CSs and DSs over a 1 GHz span at a 3 kHz RBW. The first peaks enclosed by purple solid rectangles correspond to the repetition rates of the HML CS and DS pulses. The repetition rates increase from ~43.34 MHz at the second harmonic to ~86.68 MHz at the fourth harmonic. In HML operation, the RF spectrum typically consists of main peaks accompanied by spurious supermode peaks, a characteristic feature of HML fiber lasers [34]. The main peaks correspond to multiples of the HML frequency, while the spurious supermode peaks appear at multiples of the fundamental mode-locking frequency. Notably, for both CSs and DSs at all harmonic orders, the clean RF spectra demonstrate no detectable supermode noise. Even when employing higher RBW scanning, no supermode peaks are observed. The supermode suppression ratio (SMSR), a critical metric for evaluating the quality of HML lasers, is defined as the intensity ratio of the main peak to the strongest supermode. In our system, the achieved SMSR can be regarded as the SNR of >48 dB, confirming the outstanding supermode suppression performance of the developed laser.

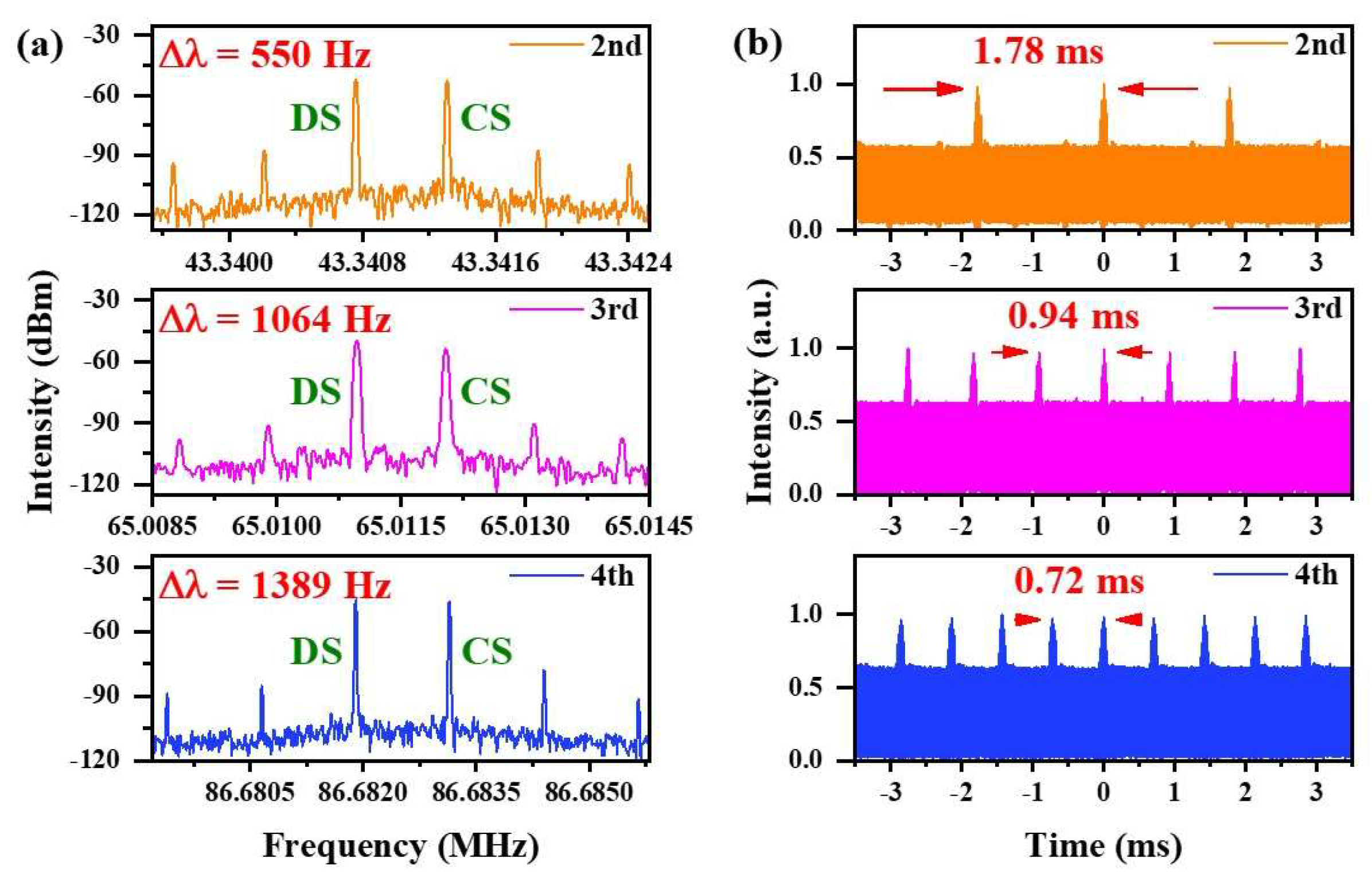
We also measured the repetition rate difference between the two solitons under different HML states, as shown in Figure 7. As harmonic order N increases, the repetition rate difference between the two subring outputs grows from 550 Hz to 1389 Hz in Figure 7a. The corresponding interference peak intervals in the oscilloscope trace of Figure 7b decrease from 1.78 ms to 0.72 ms, consistent with the frequency-domain results. This occurs because in the Nth HML state, the repetition rate of each subring becomes $N\times f_0$, leading to a corresponding increase in the repetition rate difference ($N\times f_{01}-N\times f_{02}$). The NPR technique can induce a wavelength-dependent spectral filtering effect, manifesting as a comb-like filtering profile with a sinusoidal spectral transmission function and multiple transmission peaks [35]. Adjusting the PC alters the wavelength of these transmission peaks, which selectively modulates the gain and loss of longitudinal modes. In our study, higher-order HML is achieved by increasing the pump power and tuning the PCs. Therefore, adjustments to the PC result in changes in the center wavelength of pulses with different longitudinal modes, as shown in

Table 1. Summary of output characteristics recorded at different HML states.

Harmonic Order (N)	Soliton Type	${\mathit{P}}_{\mathit{o}\mathit{u}\mathit{t}}$ (mW)	${\mathit{E}}_{\mathit{p}}$ (nJ)	${\mathit{f}}_{\mathit{r}\mathit{e}\mathit{p}}$ (MHz)	$∆\mathit{f}$ (Hz)	${\mathit{\lambda }}_{\mathit{c}}$ (nm)	$∆\mathit{\lambda }$ (nm)	$\mathit{\tau }$ (ps)	TBP
1	CS	3.668	0.169	21.670417	216	1559.4997	9.7750	0.273	0.3289
	DS	5.857	0.270	21.670201		1572.3542	18.7074	2.2	4.9906
2	CS	5.759	0.133	43.341304	550	1558.8085	9.8105	0.264	0.3195
	DS	9.848	0.227	43.340754		1570.5095	15.9471	4.0	7.7532
3	CS	8.277	0.127	65.012008	1064	1557.0870	9.8857	0.289	0.3533
	DS	18.841	0.290	65.010944		1571.4082	22.0388	2.0	5.3513
4	CS	10.782	0.124	86.683215	1389	1558.4360	10.6520	0.347	0.4563
	DS	24.865	0.287	86.681826		1569.6424	14.8135	3.6	6.4890

$P_{out}$: average output power; $E_p$: single pulse energy; $f_{rep}$: pulse repetition rate; $∆f$: repetition rate difference; ${\lambda }_c$: center wavelength; $∆\lambda$: 3 dB spectral bandwidth; $\tau$: pulse duration; TBP: time–bandwidth product.

. Due to the GVD in the fiber, the group refractive index varies with the optical wavelengths, causing pulse envelopes with different center wavelengths to propagate at different group velocities. As a result, the time required for them to complete a cavity round-trip differs, which is directly reflected in a slight change in the repetition rate. Consequently, the repetition rate difference in different HML states does not scale exactly as an integer multiple of the fundamental frequency difference. Although the repetition rate difference $∆f$ increases when the harmonic order increases, for application in asynchronous optical sampling, the sampling time step is determined by $∆f/(f_1·f_2)$. When the repetition rates increase, the corresponding time step decreases, thereby enabling higher measurement precision.

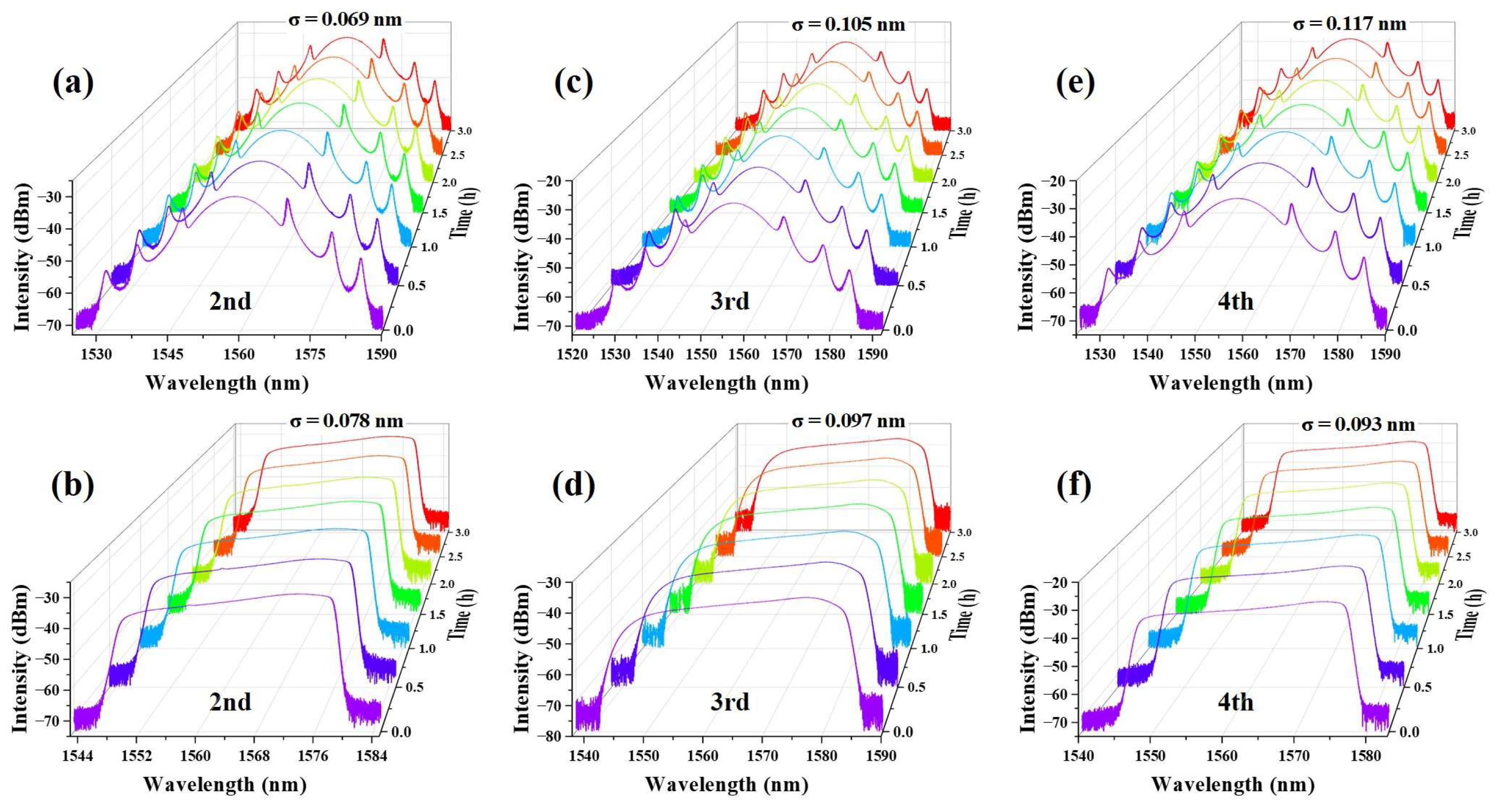
The output spectra are recorded every 30 min over a continuous 3 h monitoring period. As shown in Figure 8, no significant observable changes occurred in the overall spectral profiles, center wavelengths, or intensities throughout the entire observation period. This strongly demonstrates the good steady-state performance of our laser during HML operations and its effective resistance to environmental disturbances. To further evaluate stability, the drifts of the center wavelengths across all recorded spectra are tracked, and the standard deviations $\sigma$ are calculated, which are all small values. These low standard deviations confirm a high concentration of the output laser’s center wavelengths, with no significant drift. Overall, these results indicate that the HML state achieved in this dual-branch laser is not only attainable but can also be maintained with high stability over extended periods.

To further explore the behavior of the laser, Table 1 summarizes the laser output parameters measured at different HML states through continuous increases in pump powers. The average output powers of CSs and DSs are observed to increase with the harmonic order. Experimental results demonstrate that the DSs can support relatively higher single pulse energy $E_p$ compared to the CSs. This observation further confirms the advantage of DS formation mechanisms in accommodating larger pulse energy. Wider pulse duration reduces peak power and avoids pulse splitting due to accumulation of excessive nonlinear phase shifts, thereby supporting higher $E_p$. The TBPs of CSs at each HML operation are all close to the theoretical minimum TBP for a hyperbolic secant pulse, indicating that the output pulse has excellent characteristics and is nearly chirp-free. Notably, DSs typically possess highly linear chirp characteristics, with pulse durations of 2.0–4.0 ps, which can be dechirped to sub-picosecond durations through extra-cavity compression using SMF [36].

Furthermore, a notable spectral difference is observed in the 3 dB bandwidth of DSs operating at nearly identical center wavelengths across different HML states. The NPR-induced intracavity filtering effect is the underlying cause of this phenomenon. The free spectral range (FSR) of the filtering function is given by the equation $\mathsf{\Delta }\lambda ={\lambda }_c^2/(\mathsf{\Delta }n·L)$, where ${\lambda }_c^2$ is the center wavelength, $L$ is the length of SMF, and $∆n=n_s-n_f$ is the birefringence, defined as the difference between the refractive indices of the fast and slow axes. This equation demonstrates that dynamically tuning the intracavity birefringence precisely adjusts the spectral filtering period. In our dual-branch laser architecture, the spectral properties of the soliton pulses are actively tuned by adjusting the stress applied to the fiber through the fiber-squeezer PC, inducing controlled variations in the birefringence characteristics, thereby altering the spectral filtering period within the cavity. This enables the realization of distinct mode-locked states, each exhibiting unique spectral bandwidth characteristics. The obtained 3 dB bandwidth of the DS spectra at different HML varies from 14.8135 nm to 22.0388 nm.

4. Conclusions

In summary, we propose a dual-repetition-rate erbium-doped mode-locked fiber laser with a dual-branch structure to simultaneously generate CSs and DSs. The fundamental mode-locked pulses exhibit a repetition rate difference of 216 Hz at a repetition rate of about 21 MHz. CSs in S−1 and DSs in S−2 have a spectrum with a 3 dB bandwidth of 9.7750 nm and 18.7074 nm, respectively. By increasing the pump powers and adjusting the PCs, we demonstrate simultaneous second- and third- and fourth-order HML operation in both subrings. This novel fiber laser featuring tunable HML will play a significant role in the applications of spectroscopy, ranging, and high-speed asynchronous sampling.