Hybrid Reflection/Transmission Diffraction Grating Solar Sail

Abstract

Diffractive sail components may be used in part or whole for in-space propulsion and attitude control. A sun-facing hybrid diffractive solar sail having reflective front facets and transmissive side facets is described. This hybrid design seeks to minimize the undesirable scattering from side facets. Predictions of radiation pressure are compared for analytical geometrical optics and numerical finite difference time domain approaches. Our calculations across a spectral irradiance band from 0.5 to 3 μm suggest the transverse force in a sun facing configuration reaches 48% when the refractive index of the sail material is 1.5. Diffraction measurements at a representative optical wavelength of 633 nm support our predictions.

1. Introduction

In the 1920s, Tsander and Tsiolkvosy proposed using radiation pressure from the sun to propel objects in space [1,2]. Over the past half century, numerous studies [3,4,5,6] and several in-space demonstrations by JAXA [7], NASA [8,9], and the Planetary Society [10] have advanced the technical readiness level of solar sails. Such sails are based on a thin metalized film. Perhaps the most promising class of such missions achieves inward (outward) spiral trajectories by decreasing (increasing) the orbital velocity, i.e., by producing a force perpendicular to the sun line. This force is attributed to the change in optical momentum that occurs owing to directional light scattering. A reflective solar sail tilted by roughly ${35}^{\circ }$ from the sun line was originally proposed for this mission type. At that angle, an ideal reflective sail converts up to $77\%$ of the available optical momentum into the component of force perpendicular to the sun line. In practice, the efficiency will be smaller than this value owing to a combination of absorption in the metallic layer, wrinkling and bowing, diffuse scattering, and re-radiated heat [11]. Additionally, the ${35}^{\circ }$ cant angle of a reflective sail may introduce a misalignment between science instruments and the sail axis, posing engineering challenges, such as camera alignment, momentum management, and thermal control.

Recent focus has turned to a different optical phenomenon for solar sailing—the physical optics property of diffraction [12,13,14,15,16,17,18,19,20,21,22,23]. Diffraction occurs when light undergoes selective constructive and destructive interference after scattering from an optically periodic body. In principle, a well-designed diffraction grating may asymmetrically diffract sunlight, with the change in optical momentum producing an equal and opposite change on the grating, resulting in radiation pressure force.

Perhaps the most consequential use of solar sails in the coming decades will be the placement of a constellation of them at the Earth-Sun $L_1$ Lagrange point to function as sun shades. Originally proposed in 1989 by Early [24] and 2006 by Angel [25], solar sail type structures at $L_1$ provide a geo-engineering method of cooling the entire Earth in the event runaway global warming becomes a widespread existential threat to life (see, for example, [26,27]). Lacking sufficient urgency to stem greenhouse gases, scientific and engineering studies of sun shades has attracted growing interest in recent years [28,29,30,31,32,33,34,35]. More technically difficult solar sailing missions seeking large accelerations along the sun line to, for example, place an observatory at the gravitational lensing point of the sun [36,37] are not discussed here.

The law of conservation of linear momentum suggests that the transverse momentum transfer efficiency may reach $100\%$ if two ideal conditions are satisfied: the sail is sun-facing (i.e., not tilted), and all available sunlight scatters in a single ${90}^{\circ }$ direction. There is no known optical phenomenon that satisfies these conditions for wavelengths spanning the entire solar spectrum. Diffractive sails have been proposed as a means to address sun-facing conditions [12] and to explore whether large momentum transfer efficiencies can be reached. Radiation pressure has been directly measured on commercially available diffraction gratings [13], as well as geometric phase gratings [14]. Measurements have also been recently reported on a microscopic metasurface [23].

In the ideal case, long period gratings were found to be more favorable for achieving large values of the net transverse momentum transfer efficiency (MTE) compared to short period gratings [16]. In practice, light does not exhibit ideal scattering. For example, surface relief gratings impose obstructions from the facets, scattering light in undesirable directions. 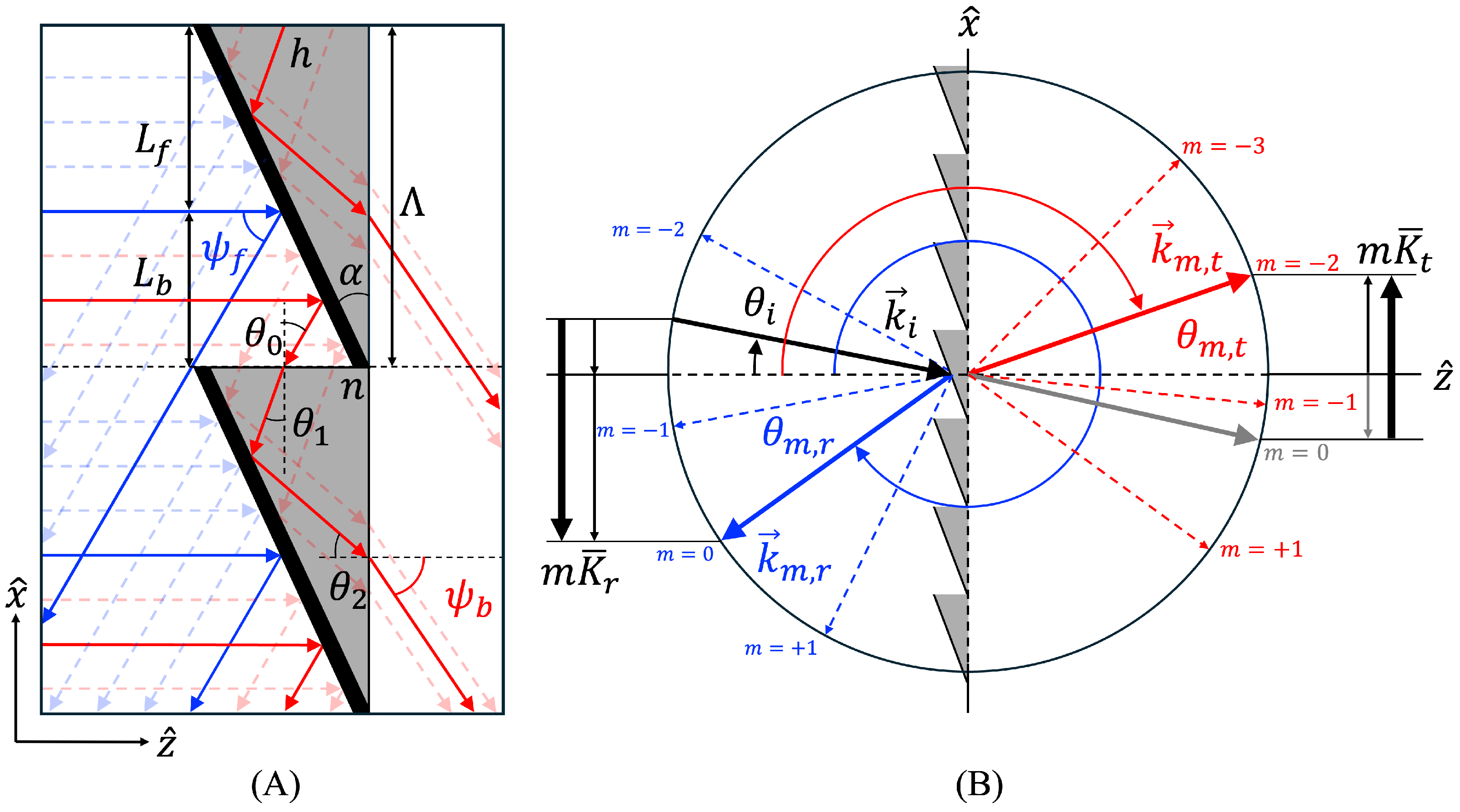Here, we propose a potential solution to this problem by designing a partially reflective hybrid grating that reflects light from the front facets and transmits light through the side facets, as depicted in Figure 1. If a significant fraction of sunlight can be cast at a large average angle, then a hybrid diffractive sail may have advantages that differ from those of a flat, canted reflective sail.

This report is organized into the following sections. The principle of momentum transfer is used to describe radiation pressure in Section 2. Ray tracing using geometric optics principles is used to estimate radiation pressure on a right prism in Section 3. The reflected and refracted ray directions may be used to describe the optical field near a grating composed of a periodic array of such prisms. Wavelength dispersion and polarization are ignored in Section 3. Far from the grating, the optical field is described with wave theory, which is reviewed in Section 4. In this section, the MTE is wavelength-dependent owing to diffraction; thus, the net MTE is found by integration over the spectral irradiance distribution of the light source. Both Section 2 and Section 3 provide tractable equations that aid in the design of diffractive light sails. These two approaches do not account for physical phenomena such as polarization-dependent Fresnel reflection and transmission coefficients, as well as for internal reflections within the structure. More accurate modeling requires the use of a numerical Maxwell solver. Using such solvers, we calculate the MTE using two methods: The Maxwell stress tensor in Section 6, and a rigorous modal analysis that is closely aligned with Section 4 is detailed in Section 7. Results from the latter two approaches are discussed in Section 8. Preliminary experimental results are presented in Section 9 for a long period grating ($\mathrm{\Lambda }=30$ μm) [17]. The concluding section includes a comparison between the MTE values obtained using both the geometric optics approximation and the Maxwell solver solutions. For example, at a refractive index of $n=1.5$, a prism angle of $\alpha =22.5^{\circ }$, and a grating period of $\mathrm{\Lambda }=3$ μm, the geometric optics approximation $({\eta }_x=0.63)$ greatly overestimates the Maxwell solver value $({\eta }_x=0.48)$. We attribute this discrepancy to the fact that the wavelength of light is on the same order of magnitude as the grating period, resulting in strong diffraction effects that are not accounted for by the geometric model. On the other hand, when the grating period is much greater than the illuminating wavelengths, geometric optics are expected to provide a better agreement. In fact, the experimentally measured MTE values using a grating period of $\mathrm{\Lambda }=30$ μm are in good agreement with the geometric optics value: ${\eta }_x=0.47$ vs. $0.40$, respectively.

2. Radiation Pressure Review

The force that comes with radiation pressure may be understood by combining Newton’s second law (which asserts that the force on a body is equal to the change in momentum per unit time) and Newton’s third law (stating that, for every action, there is an equal and opposite reaction [38]). Let us describe light of wavelength $\lambda$ as a collection of rays or photons having momentum $\hslash \overrightarrow{k}$, where ℏ is the Planck constant and $k=|\overrightarrow{k}|=2\pi /\lambda$ is the magnitude of the wave vector. If incident and elastically scattered wave vectors, ${\overrightarrow{k}}_i$ and ${\overrightarrow{k}}_f$, subtend the optical axis with angles ${\theta }_i$ and ${\theta }_f$, respectively, then the relative change in the momentum provided to the scatter may may be expressed:

$$\overrightarrow{\eta }={\displaystyle \frac{{\overrightarrow{k}}_i-{\overrightarrow{k}}_f}{k}}=(cos{\theta }_i-cos{\theta }_f) \widehat{z}+(sin{\theta }_i-sin{\theta }_f) \widehat{x}$$

(1)

In the case ${\theta }_f={\theta }_i$, there is no scattering, and Equation (1) provides $\overrightarrow{\eta }=0$ as expected. Further, if light is back scattered (e.g., a light normal incident upon an ideal mirror) such that ${\theta }_f={\theta }_i+\pi$, then $\overrightarrow{\eta }=2cos{\theta }_i \widehat{z}+2sin{\theta }_i \widehat{x}$, providing a magnitude $\eta =2$, which is the direction of the incident beam. As another example, consider light scattered at right angles to the incident beam, such that ${\theta }_f={\theta }_i+\pi /2$ so that $\overrightarrow{\eta }=(cos{\theta }_i+sin{\theta }_i) \widehat{z}+(sin{\theta }_i-cos{\theta }_i) \widehat{x}$. Projecting $\overrightarrow{\eta }$ onto the incident direction provides a relative momentum change of $100\%$ in that direction. Furthermore, projecting $\overrightarrow{\eta }$ onto the scattering direction provides $-100\%$ in that direction. The latter represents the optimal transverse MTE; the ability to attain it is desirable for solar sailing missions, where a large radiation pressure component of force perpendicular to the sun line allows a light sail to spiral toward or away from the sun [11]. If a bundle of rays of combined power $P_0$ all participate identically in the scattering process, then the radiation pressure on the scatterer is given by ${\overrightarrow{F}}_0=(2P_0/c)\overrightarrow{\eta }$. On the other hand, a correction factor is required if for any reason all the rays do not participate, e.g., when a flat solar sail is not sun-facing, reducing its effective cross-section by $cos{\theta }_{\mathrm{si}}$, where ${\theta }_{\mathrm{si}}$ is the sun incidence angle.

3. Geometric Optics Approximation

Our proposed hybrid diffractive sail, as illustrated in Figure 1A, shows a light incident from the left at a normal incident to the plane of the sail. The sail is composed of a series of right triangular prisms of base length $\mathrm{\Lambda }$ and apex angle $0<\alpha <\pi /4$. A portion of the beam is reflected from the front facet (blue colored rays in the diagram), and the remainder of the beam is transmitted through the side facet and then out the back face. The fraction of reflected and transmitted beam power is given by the respective ratios $P_f/P_0=L_f/\mathrm{\Lambda }$ and $P_b/P_0=L_b/\mathrm{\Lambda }$, where $P_0$ is the incident beam power. Expressions for the characteristic front and back “window” widths $L_f$ and $L_b$ may be found by defining an effective threshold height $h_f$, delineating which rays are reflected and which are transmitted:

$$\begin{array}{cc}\hfill h_f/L_f& =tan\alpha \hfill \end{array}$$

(2a)

$$\begin{array}{cc}\hfill L_b/h_f& =tan\left({\psi }_f\right)=tan\left(2\alpha \right)\hfill \end{array}$$

(2b)

$$\begin{array}{cc}\hfill L_f+L_b& =\mathrm{\Lambda }\hfill \end{array}$$

(2c)

from which we obtain

$$\begin{array}{cc}\hfill h_f& =\mathrm{\Lambda }tan\alpha cos\left(2\alpha \right)=hcos\left(2\alpha \right)\hfill \end{array}$$

(3a)

$$\begin{array}{cc}\hfill P_f/P_0& =L_f/\mathrm{\Lambda }=cos\left(2\alpha \right)\hfill \end{array}$$

(3b)

$$\begin{array}{cc}\hfill P_b/P_0& =L_b/\mathrm{\Lambda }=1-cos\left(2\alpha \right)\hfill \end{array}$$

(3c)

Note that the powers and lengths must all be positive; thus, $\left|\alpha \right|<\pi /4$. Also note that equal amounts of power are transmitted and reflected when $\alpha ={30}^{\circ }$.

Radiation pressure on the hybrid sail has two sources—the reflected beam and the transmitted beam. At a normal incidence $({\theta }_i=0)$, the weighted radiation pressure force may be expressed as ${\overrightarrow{F}}_{\mathrm{hybrid}}=(2P_0/c){\overrightarrow{\eta }}_{\mathrm{hybrid}}$:

$$\begin{array}{cc}\hfill {\overrightarrow{\eta }}_{\mathrm{hybrid}}& ={\displaystyle \frac{P_f}{P_0}}{\overrightarrow{\eta }}_f+{\displaystyle \frac{P_b}{P_0}}{\overrightarrow{\eta }}_b=cos\left(2\alpha \right){\overrightarrow{\eta }}_f+(1-cos\left(2\alpha \right)){\overrightarrow{\eta }}_b\equiv {\eta }_x \widehat{x}+{\eta }_z \widehat{z}\hfill \end{array}$$

(4a)

$$\begin{array}{cc}\hfill {\overrightarrow{\eta }}_f& =(1-cos{\theta }_f) \widehat{z}-sin{\theta }_f \widehat{x}=(1+cos\left(2\alpha \right)) \widehat{z}+sin\left(2\alpha \right) \widehat{x}\hfill \end{array}$$

(4b)

$$\begin{array}{cc}\hfill {\overrightarrow{\eta }}_b& =(1-cos{\theta }_b) \widehat{z}-sin{\theta }_b \widehat{x}\hfill \end{array}$$

(4c)

where use has been made of the following front and back surface angles. Front surface scattering angle ${\theta }_f=\pi +{\psi }_f$, where the law of reflection provides ${\psi }_f=2\alpha$; back surface scattering angle ${\theta }_b=-{\psi }_b$. The transmitted deviation angle ${\psi }_b$ is governed by Snell’s law at the back face:

$$sin{\psi }_b=nsin{\theta }_2$$

(5)

The internal angle ${\theta }_2$ is governed by refraction through the side facet and internal reflection from the front facet:

$$sin{\theta }_0=nsin{\theta }_1$$

(6)

$${\theta }_2={90}^{\circ }-(2\alpha +{\theta }_1)$$

(7)

where ${\theta }_0=90-2\alpha$. A critical condition may exist at the output face where light undergoes total internal reflection, i.e., if $nsin{\theta }_2\ge 1$. Solving for the value of n at the critical condition when $\alpha =0$ provides $n=\sqrt{2}$. Calculated values of the back deviation angle ${\psi }_b$ are plotted in Figure 2, along with the front deviation angle $2\alpha$ for comparison.

The net transverse and longitudinal components of the momentum transfer efficiencies are, therefore,

$$\begin{array}{cc}\hfill {\eta }_x& =cos\left(2\alpha \right)sin\left(2\alpha \right)+(1-cos\left(2\alpha \right))sin{\psi }_b\hfill \end{array}$$

(8a)

$$\begin{array}{cc}\hfill {\eta }_z& =cos\left(2\alpha \right)(1+cos\left(2\alpha \right))+(1-cos\left(2\alpha \right))(1-cos{\psi }_b)\hfill \end{array}$$

(8b)

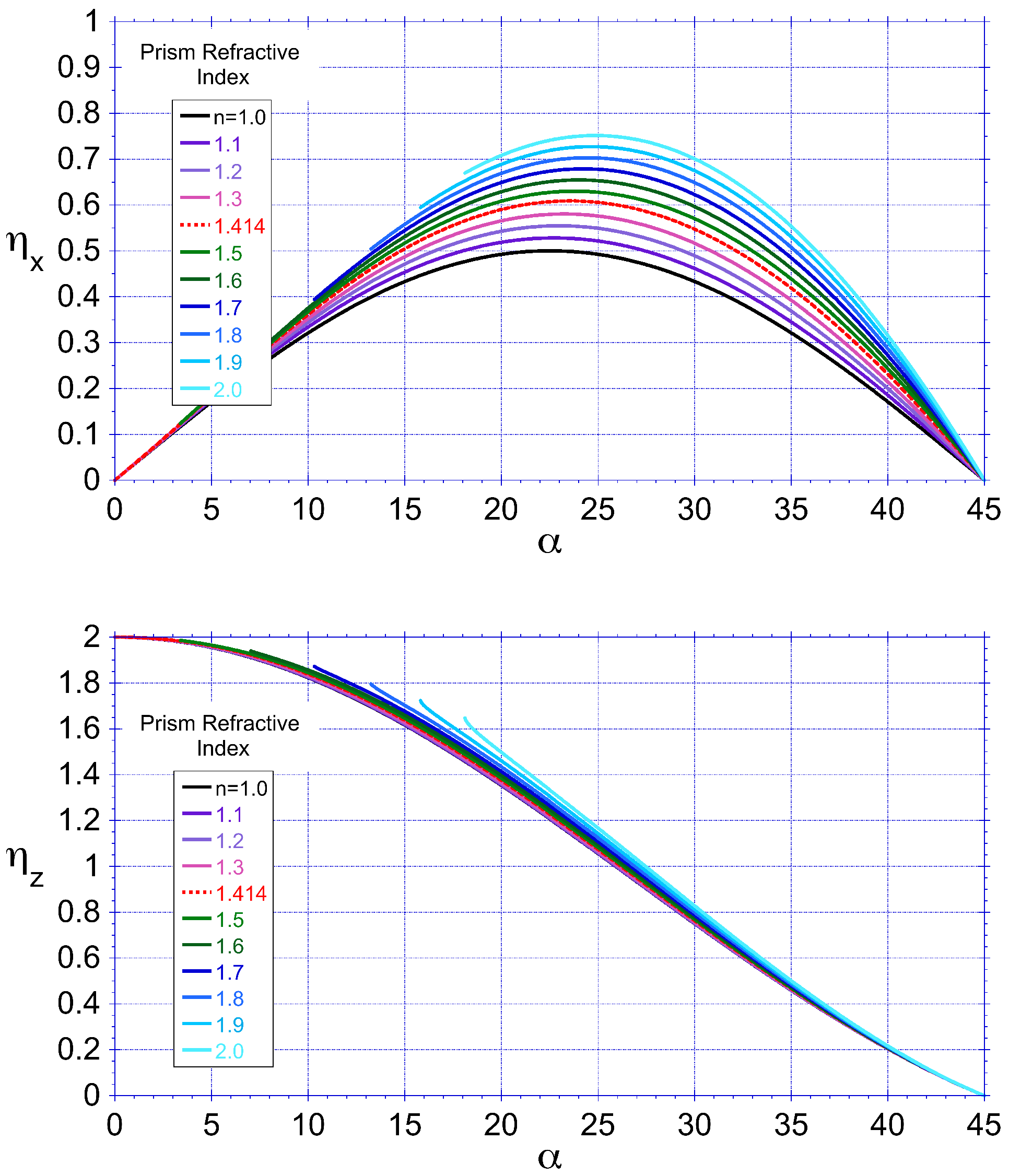
Values of ${\eta }_x$ and ${\eta }_z$ are plotted in Figure 3 as a function of the apex angle $\alpha$ for different refractive index values. Larger values of refractive index provide larger values of ${\eta }_x$. For example, when $n=1.5$, the values ${\eta }_x=0.63$ and ${\eta }_z=1.16$ at $\alpha =23.8^{\circ }$.

4. Wave Optics Approach

Whereas the foregoing geometric optics analysis describes the direction of light at the front and back faces of the structure, a diffractive wave analysis is required to describe the distribution of light in the far field. First, we make use of the Floquet–Bloch theory for a function having period $\mathrm{\Lambda }$ and wave vector magnitude $K=2\pi /\mathrm{\Lambda }$:

$$\begin{array}{cc}\hfill T\left(x\right)& =T(x+\mathrm{\Lambda })=\sum _{m=-\infty }^{\infty }{t}_{m}exp\left(imKx\right)\hfill \end{array}$$

(9a)

$$\begin{array}{cc}\hfill t_m& ={\displaystyle \frac{1}{\mathrm{\Lambda }}}{\int }_0^{\mathrm{\Lambda }}T\left(x\right)exp(-imK)dx\hfill \end{array}$$

(9b)

If $T\left(x\right)$ describes a transmission function and $E_{0}exp\left(i{k}_{x,i}x\right)$ describes an incident planar electric field at $z=0$, then the propagating transmitted field in the half space $z>0$ for the wavelength $\lambda$ may be expressed as

$$E(x,z)=E_{0}exp\left(i{k}_{x,i}x\right)\sum _{m_{\min }}^{m_{\max }}{t}_{m}exp\left(imKx\right)exp\left(i{k}_{z,m}z\right)$$

(10)

where $k_{x,i}=(2\pi /\lambda )sin{\theta }_i$ is the transverse component of the incident wave vector, ${\theta }_i$ is the angle the incident wave subtends the optical axis, and $k_{z,m}$ is the longitudinal component of the propagating field (described below).

The transmission function of the prism grating described above may be approximated by $T\left(x\right)=exp\left(i{k}_{x,b}x\right)$ over a range of length $L_b$ and zero valued otherwise, where $k_{x,b}=(2\pi /\lambda )sin{\theta }_b$, and ${\theta }_b$ is the refraction angle found from the geometrical optics. Setting the dummy variable ${\tilde{k}}_x=k_{x,b}-mK$, we write

$$\begin{array}{cc}\hfill t_m& ={\displaystyle \frac{E_0}{\mathrm{\Lambda }}}{\int }_0^{L_b}exp\left(i{\tilde{k}}_{x}x\right)dx=E_0{\displaystyle \frac{L_b}{\mathrm{\Lambda }}}exp(i{\tilde{k}}_x{L}_b/2){\displaystyle \frac{sin({\tilde{k}}_x{L}_b/2)}{{\tilde{k}}_x{L}_b/2}}\hfill \end{array}$$

(11)

Hence, the total propagating field is given by

$$E(x,z)={\displaystyle \frac{E_0{L}_b}{\mathrm{\Lambda }}}exp\left(i{k}_{x,i}x\right)\sum _{m_{\min }}^{m_{\max }}exp(i{\tilde{k}}_x{L}_b/2){\displaystyle \frac{sin({\tilde{k}}_x{L}_b/2)}{{\tilde{k}}_x{L}_b/2}}exp\left(imKx\right)exp\left(i{k}_{z,m}z\right)$$

(12)

Hence, the field is a superposition of $m^{\mathrm{th}}$ order components having the phase ${\overrightarrow{k}}_m·\overrightarrow{r}$, where ${\overrightarrow{k}}_m=(k_{x,i}+imK) \widehat{x}+k_{z,m} \widehat{z}$. Since the wavelength cannot change, the wave vectors magnitudes must all be equal $k_m^2={(k_{x,i}+mK)}^2+k_{z,m}^2={(2\pi /\lambda )}^2=k^2$ and thus

$$k_{z,m}=\sqrt{k^2-{(k_{x,i}+mK)}^2}={\displaystyle \frac{2\pi }{\lambda }}\sqrt{1-{(sin{\theta }_i+m\lambda /\mathrm{\Lambda })}^2}$$

(13)

The value of $k_{z,m}$ must be real for the field to propagate to infinity; thus, m can only assume the values satisfying ${(sin{\theta }_i+m\lambda /\mathrm{\Lambda })}^2\le 1$.

If we equate the $x$−component of ${\overrightarrow{k}}_m$ to a single term, we have the following: $k_{x,m}=(2\pi /\lambda )sin{\theta }_m\equiv k_{x,i}+mK$. Then, we obtain the so-called grating equation:

$$sin{\theta }_m=sin{\theta }_i+m\lambda /\mathrm{\Lambda }$$

(14)

The irradiance of the $m\mathrm{th}$ order plane wave described by Equation (12) is given by

$$I_m={\left|E(x,z)\right|}^2={\left({\displaystyle \frac{E_0{L}_b}{\mathrm{\Lambda }}}\right)}^2{\displaystyle \frac{{sin}^2({\tilde{k}}_x{L}_b/2)}{{\left({\tilde{k}}_x{L}_b/2\right)}^2}}$$

(15)

The intensity is a maximum for the value of m that best satisfies ${\tilde{k}}_x{L}_b/2=0$, i.e.,

$${\tilde{k}}_x=k_{x,b}-mK\approx 0\to m=\mathrm{INT}[k_{x,b}/K]=\mathrm{INT}[\mathrm{\Lambda }sin{\theta }_b/\lambda ]$$

(16)

The same formalism can be applied to the optical field reflected from the front facet by replacing ${\theta }_b$ with the front deviation angle ${\theta }_f$, $L_b$ with $L_f$, and by changing the sign of $k_{z,m}$.

Although a simple closed-form expression for $\overrightarrow{\eta }$ does not generally exist, one may expect stronger scattering at angles that satisfy either the law of reflection for reflected light or Snell’s law for the transmitted light, especially in the geometric optic limit $\lambda <<\mathrm{\Lambda }$ (see Section 5).

For a light source having the spectral irradiance distribution $I\left(\nu \right)$, the momentum transfer efficiency of the transmitted light can be estimated from diffraction theory. Integration over frequency $\nu =c/\lambda$, where c is the speed of light, is adopted instead of integration over wavelength because the former provides equal sampling intervals across the diffraction orders.

$${\overrightarrow{\eta }}_b={\displaystyle \frac{1}{I_0}}{\left({\displaystyle \frac{L_b}{\mathrm{\Lambda }}}\right)}^2\int I\left(\nu \right)\sum _{M_{\min ,\nu }}^{M_{\max ,\nu }} {\displaystyle \frac{{sin}^2((k_{x,b}-mK)L_b/2)}{{((k_{x,b}-mK)L_b/2)}^2}} {\displaystyle \frac{{\overrightarrow{k}}_i-{\overrightarrow{k}}_m}{k}} d\nu$$

(17)

where ${\overrightarrow{k}}_i=k(cos{\theta }_i \widehat{z}+sin{\theta }_i \widehat{x})$; ${\overrightarrow{k}}_b=k(cos{\theta }_b \widehat{z}+sin{\theta }_b \widehat{x})$; ${\overrightarrow{k}}_m=k(cos{\theta }_m \widehat{z}+sin{\theta }_m \widehat{x})$; $sin{\theta }_m=sin{\theta }_i+m\lambda /\mathrm{\Lambda }$; $cos{\theta }_m=+\sqrt{1-{sin}^2{\theta }_m}$; $I_0=\int I\left(\nu \right) d\nu$. The extremum mode values are given by $M_{\max ,\nu }=\mathrm{INT}\left[(\mathrm{\Lambda }/\lambda )(1-sin{\theta }_i)\right]$ and $M_{\min ,\nu }=\mathrm{INT}\left[(\mathrm{\Lambda }/\lambda )(-1-sin{\theta }_i)\right]$, where INT is the operation that returns the integer value of the argument, rounded toward zero.

For front surface reflections at the deviation angle ${\theta }_f$, we have

$${\overrightarrow{\eta }}_f={\displaystyle \frac{1}{I_0}}{\left({\displaystyle \frac{L_f}{\mathrm{\Lambda }}}\right)}^2\int I\left(\nu \right)\sum _{M_{\min ,\nu }}^{M_{\max ,\nu }} {\displaystyle \frac{{sin}^2((k_{x,f}-mK)L_f/2)}{{((k_{x,f}-mK)L_f/2)}^2}} {\displaystyle \frac{{\overrightarrow{k}}_i-{\overrightarrow{k}}_m}{k}} d\nu$$

(18)

where ${\overrightarrow{k}}_i=k(cos{\theta }_i \widehat{z}+sin{\theta }_i \widehat{x})$; ${\overrightarrow{k}}_f=k(-cos{\theta }_f \widehat{z}+sin{\theta }_f \widehat{x})$; ${\overrightarrow{k}}_m=k(cos{\theta }_m \widehat{z}+sin{\theta }_m \widehat{x})$; $sin{\theta }_m=sin{\theta }_i+m\lambda /\mathrm{\Lambda }$; $cos{\theta }_m=-\sqrt{1-{sin}^2{\theta }_m}$; $I_0=A\int I_{\nu } d\nu$.

A factor of $cos{\theta }_i$ must be in included in Equations (17) and (18) in the event the light source overfills the sail, as occurs in space. In the laboratory, the light source may be a small pencil of light that underfills the sail and thus does not acquire the $cos{\theta }_i$ projection factor. At normal sun incidence ${\theta }_i=0$, Equations (17) and (18) may be expressed as

$${\overrightarrow{\eta }}_b={\displaystyle \frac{1}{I_0}}{\left({\displaystyle \frac{L_b}{\mathrm{\Lambda }}}\right)}^2\int \sum _{M_{\min ,\nu }}^{M_{\max ,\nu }} {\tilde{I}}_{m,b}\left(\nu \right)\left(-sin{\theta }_m \widehat{x}+(1-\sqrt{1-{sin}^2{\theta }_m} ) \widehat{z}\right) d\nu$$

(19)

$${\overrightarrow{\eta }}_f={\displaystyle \frac{1}{I_0}}{\left({\displaystyle \frac{L_f}{\mathrm{\Lambda }}}\right)}^2\int \sum _{M_{\min ,\nu }}^{M_{\max ,\nu }} {\tilde{I}}_{m,f}\left(\nu \right)\left(-sin{\theta }_m \widehat{x}+(1+\sqrt{1-{sin}^2{\theta }_m} ) \widehat{z}\right) d\nu$$

(20)

$${\tilde{I}}_{m,b}\left(\nu \right)={\displaystyle \frac{{sin}^2((k_{x,b}-mK)L_b/2)}{{((k_{x,b}-mK)L_b/2)}^2}} I\left(\nu \right)$$

(21)

$${\tilde{I}}_{m,f}\left(\nu \right)={\displaystyle \frac{{sin}^2((k_{x,f}-mK)L_f/2)}{{((k_{x,f}-mK)L_f/2)}^2}} I\left(\nu \right)$$

(22)

where $M_{\min ,\nu }=M_{\max ,\nu }=\mathrm{INT}\left[(\mathrm{\Lambda }/\lambda )\right]=\mathrm{INT}\left[(\mathrm{\Lambda }\nu /c)\right]$. Note that these equations do not account for effects such as polarization and internal reflections. Section 6 will address such issues.

5. Wave-Ray Comparison

Let us briefly compare the ray and wave optics predictions for ${\eta }_x$, which allows a solar sail to propel toward or away from the sun via a spiral trajectory. We expect the two approaches to agree in the small wavelength limit, $\lambda <<\mathrm{\Lambda }$. A more complete description is provided in the next section. In the case of normal sun incidence $({\theta }_i=0)$ and refractive index $n=1$, the transmitted rays are undeviated $({\theta }_b={\psi }_b=0)$. Therefore, the MTE is solely attributed to front surface reflections. To make use of the above diffractive analysis, we simply replaced $L_b$ with $L_f$. For example, the ray optic analysis predicted a peak value of ${\eta }_x$ at $\alpha =22.5^{\circ }$, resulting from the product of $P_f/P_0=L_f/\mathrm{\Lambda }=cos\left(2\alpha \right)=0.707$ and the sine of the deviation angle $2\alpha$; thus, ${\eta }_x=cos\left(2\alpha \right)sin\left(2\alpha \right)=0.5$. For the purpose of comparison, a scatter plot of the angular distribution of diffracted modal intensities for a grating of period $\mathrm{\Lambda }=3.0 \left[\mathsf{\mu }\mathrm{m}\right]$ and wavelengths ranging from $\lambda$: 0.40–3.0 $\left[\mathsf{\mu }\mathrm{m}\right]$ is shown in Figure 4. As expected from diffraction theory, the peak modal intensity agrees with ${(L_f/\mathrm{\Lambda })}^2=0.5$. Although this peak appears at ${\theta }_m={45}^{\circ }$, the mean centroid is slightly lower $<{\theta }_m>=41.2^{\circ }$ owing to the diffractive cut-off at ${90}^{\circ }$. The net transverse MTE is $<{\eta }_x>=(P_f/P_0)sin<{\theta }_m>=0.466$, which is a loss of efficiency compared to the geometric optics value of $0.034$. The inset in Figure 4 depicts the narrowing of the angular distribution when the period greatly exceeds the wavelengths of the light source (e.g., when $\mathrm{\Lambda }=20 \left[\mathsf{\mu }\mathrm{m}\right]$), in which case the two models agree.

We expect the deviation angle of the transmitted rays to be greater than zero when $n>1$; thus, the net transverse MTE is predicted to increase.

6. Maxwell Stress Tensor Numerical Analysis

To account for the effects of polarization-dependent Fresnel reflections and multiple internal reflections within the hybrid structure, a model that satisfies Maxwell’s equations is required. Although this approach does not provide tractable closed-form solutions, numerical open-source and commercial software packages are readily available [39,40,41]. Another approach involves a rigorously coupled wave analysis [42]. These packages typically compute radiation pressure from the Maxwell stress tensor (MST), which represents the momentum flux density of the electromagnetic field:

$${\overline{\overline{T}}}_{i,j}^{s,p}={ϵ}_0(E_i^{s,p}{E}_j^{s,p}-{\displaystyle \frac{1}{2}}|E^{s,p}{|}^2{\delta }_{ij})+{\mu }_0(H_i^{s,p}{H}_j^{s,p}-{\displaystyle \frac{1}{2}}|H^{s,p}{|}^2{\delta }_{ij})$$

(23)

where ${ϵ}_0$ and ${\mu }_0$ are the permittivity and permeability of free space, respectively; ${\delta }_{ij}$ is the Kronecker delta function; and $E_i^{s,p}\left(\nu \right)$ and $B_i^{s,p}\left(\nu \right)$ are the electric and magnetic field amplitudes, respectively, for the s and p polarized component of light at the optical frequency $\nu$, with indexes corresponding to Cartesian coordinates $i:(x,y,z)$ and $j:(x,y,z)$. The components of force in the x and z directions may be found by integrating over a close surface S. For an infinite periodic grating, the net momentum flux into a unit cell of length $\mathrm{\Lambda }$ from the two adjacent unit cells must cancel. Thus, it suffices to integrate over a front surface in the $-\widehat{z}$ direction and back surface in the $+\widehat{z}$ direction over one unit cell of area $A_0={\mathrm{\Lambda }}^2$. The total area of the sail may be expressed as $A_{\mathrm{sail}}=L_x{L}_y=N_x{N}_y{\mathrm{\Lambda }}^2$, where $L_x$ and $L_y$ are the side lengths of a rectangular sail, and $N_x=L_x/\mathrm{\Lambda }$ and $N_y=L_y/\mathrm{\Lambda }$. At a given optical frequency $\nu$, the components of force on a single cell of area $A_0$ may be expressed as

$$\begin{array}{cc}\hfill F_x^{s,p}\left(\nu \right)& ={\oint }_S{\overline{\overline{T}}}_{x,j}^{ s,p}\left(\nu \right)·d{\overrightarrow{S}}_j=\int \left({\overline{\overline{T}}}_{x,z}^{ s,p}\left(\nu \right){|}_{\mathrm{back}}-{\overline{\overline{T}}}_{x,z}^{ s,p}\left(\nu \right){|}_{\mathrm{front}}\right)·\widehat{z} d{A}_0\hfill \end{array}$$

(24a)

$$\begin{array}{cc}\hfill F_z^{s,p}\left(\nu \right)& ={\oint }_S{\overline{\overline{T}}}_{z,j}^{ s,p}\left(\nu \right)·d{\overrightarrow{S}}_j=\int \left({\overline{\overline{T}}}_{z,z}^{ s,p}\left(\nu \right){|}_{\mathrm{back}}-{\overline{\overline{T}}}_{z,z}^{ s,p}\left(\nu \right){|}_{\mathrm{front}}\right)·\widehat{z} d{A}_0\hfill \end{array}$$

(24b)

These expressions can be calculated by Maxwell solvers, such as MEEP. For example, Srivastava [18] showed that, using MEEP, a low-refractive-index metasurface grating produces a larger transverse radiation pressure force compared to gratings composed of silicon nitride. For s-polarized light (TE), the electric field is perpendicular to the plane of incidence: ${\overrightarrow{E}}^s=E^s \widehat{y}$. Whereas, for p-polarized light (TM), the magnetic field is perpendicular to the plane of incidence: ${\overrightarrow{H}}^s=H^s \widehat{y}$. Thus, the stress tensors needed for the radiation pressure on the grating may be expressed as

$${\overline{\overline{T}}}_{x,z}^{ s}={\displaystyle \frac{{\mu }_0}{2}}\mathrm{Re}\left(H_x{H}_z^{*}\right)$$

(25)

$${\overline{\overline{T}}}_{z,z}^{ s}=-{\displaystyle \frac{{ϵ}_0}{4}}\mathrm{Re}\left(E_y{E}_y^{*}\right)+{\displaystyle \frac{{\mu }_0}{4}}(\mathrm{Re}\left(H_z{H}_z^{*}\right)-\mathrm{Re}\left(H_x{H}_x^{*}\right))$$

(26)

$${\overline{\overline{T}}}_{x,z}^{ p}={\displaystyle \frac{{ϵ}_0}{2}}\mathrm{Re}\left(E_x{E}_z^{*}\right)$$

(27)

$${\overline{\overline{T}}}_{z,z}^{ p}=-{\displaystyle \frac{{\mu }_0}{4}}\mathrm{Re}\left(H_y{H}_y^{*}\right)+{\displaystyle \frac{{ϵ}_0}{4}}(\mathrm{Re}\left(E_z{E}_z^{*}\right)-\mathrm{Re}\left(E_x{E}_x^{*}\right))$$

(28)

It is important to note that MEEP calculates the MST at a given frequency for a unit irradiance (i.e., not for an arbitrary value consistent with the spectral irradiance of the light source). Thus, for given spectral irradiance distributions $I^{s,p}\left(\nu \right)$, the net components of force are found by integration over all frequencies:

$$\begin{array}{cc}\hfill F_x& =F_x^s+F_x^p=\int I^s\left(\nu \right)F_x^s\left(\nu \right) d\nu +\int I^p\left(\nu \right)F_x^p\left(\nu \right) d\nu \hfill \end{array}$$

(29a)

$$\begin{array}{cc}\hfill F_z& =F_z^s+F_z^p=\int I^s\left(\nu \right)F_z^s\left(\nu \right) d\nu +\int I^p\left(\nu \right)F_z^p\left(\nu \right) d\nu \hfill \end{array}$$

(29b)

For unpolarized light, $I^s\left(\nu \right)=I^p\left(\nu \right)\equiv (1/2)\tilde{I}\left(\nu \right)$. For example, the solar irradiance incident on the Earth may be approximated by the blackbody frequency spectral irradiance distribution:

$$\tilde{I}\left(\nu \right)={\displaystyle \frac{R_{\mathrm{S}}^2}{r_{\mathrm{E}}^2}}{\displaystyle \frac{2\pi h}{c^2}}{\displaystyle \frac{{\nu }^{3}d\nu }{exp(h\nu /k_{B}T)-1}}$$

(30)

where $R_{\mathrm{S}}=6.96\times {10}^8$ [m] is the solar radius, $r_{\mathrm{E}}=1.5\times {10}^{11}$ [m], $h=6.63\times {10}^{-34}$ [J· s] is the Planck constant, c is the speed of light, and $k_B=1.38\times {10}^{-23}$ [J/K] is the Boltzmann constant. We let $T=5770$ [K] as the effective surface temperature of the sun, whereupon integrating over all frequencies provides the so-called solar constant $I_{sun}=1360$ [W/m²]. Thus, for a light sail orbiting at the semi-major axis of the Earth, the force on each element of area $A_0$ at normal sun incidence is given by

$$\begin{array}{cc}\hfill F_x& ={\displaystyle \frac{1}{2}}\left(\int \tilde{I}\left(\nu \right)F_x^s\left(\nu \right) d\nu +\int \tilde{I}\left(\nu \right)F_x^p\left(\nu \right) d\nu \right)\hfill \end{array}$$

(31a)

$$\begin{array}{cc}\hfill F_z& ={\displaystyle \frac{1}{2}}\left(\int \tilde{I}\left(\nu \right)F_z^s\left(\nu \right) d\nu +\int \tilde{I}\left(\nu \right)F_z^p\left(\nu \right) d\nu \right)\hfill \end{array}$$

(31b)

The components of the MTE are then found by dividing by the characteristic force magnitude $F_0=A_0{I}_{\mathrm{sun}}/c$:

$$\begin{array}{cc}\hfill {\eta }_x& ={\eta }_x^s+{\eta }_x^p={\displaystyle \frac{1}{2}}\left(\int \tilde{I}\left(\nu \right)F_x^s\left(\nu \right) d\nu +\int \tilde{I}\left(\nu \right)F_x^p\left(\nu \right) d\nu \right){\displaystyle \frac{1}{A_0{I}_{\mathrm{sun}}/c}}\hfill \end{array}$$

(32a)

$$\begin{array}{cc}\hfill {\eta }_z& ={\eta }_z^s+{\eta }_z^p={\displaystyle \frac{1}{2}}\left(\int \tilde{I}\left(\nu \right)F_z^s\left(\nu \right) d\nu +\int \tilde{I}\left(\nu \right)F_z^p\left(\nu \right) d\nu \right){\displaystyle \frac{1}{A_0{I}_{\mathrm{sun}}/c}}\hfill \end{array}$$

(32b)

Note that MEEP is unable to account for the illumination projection factor $cos{\theta }_i$ in the event the illumination source overfills the sail area, in which case ${\eta }_{x,z}$ must be replaced by ${\eta }_{x,z}cos{\theta }_i$.

It is not practical to determine the MST across all frequencies in MEEP as computational resource demands and computing times become unwieldy when $\lambda /\mathrm{\Lambda }<<1$. For this reason, we limited the integration from an arbitrary minimum frequency somewhat below the diffractive cut-off condition, ${\nu }_0=c/\mathrm{\Lambda }$, to an arbitrary upper value ${\nu }_{\max }=c/{\lambda }_{\min }$. Unless stated otherwise, a normal sun incidence angle $({\theta }_i=0)$ was assumed, as well as a grating period of $\mathrm{\Lambda }=3 \left[\mathsf{\mu }\mathrm{m}\right]$ $({\nu }_0=100 \left[\mathrm{THz}\right])$, a minimum frequency of ${\nu }_{\min }=50 \left[\mathrm{THz}\right]$, and a maximum frequency of ${\nu }_{\max }=600 \left[\mathrm{THz}\right]$, corresponding to ${\lambda }_{\min }=0.5 \left[\mathsf{\mu }\mathrm{m}\right]$. 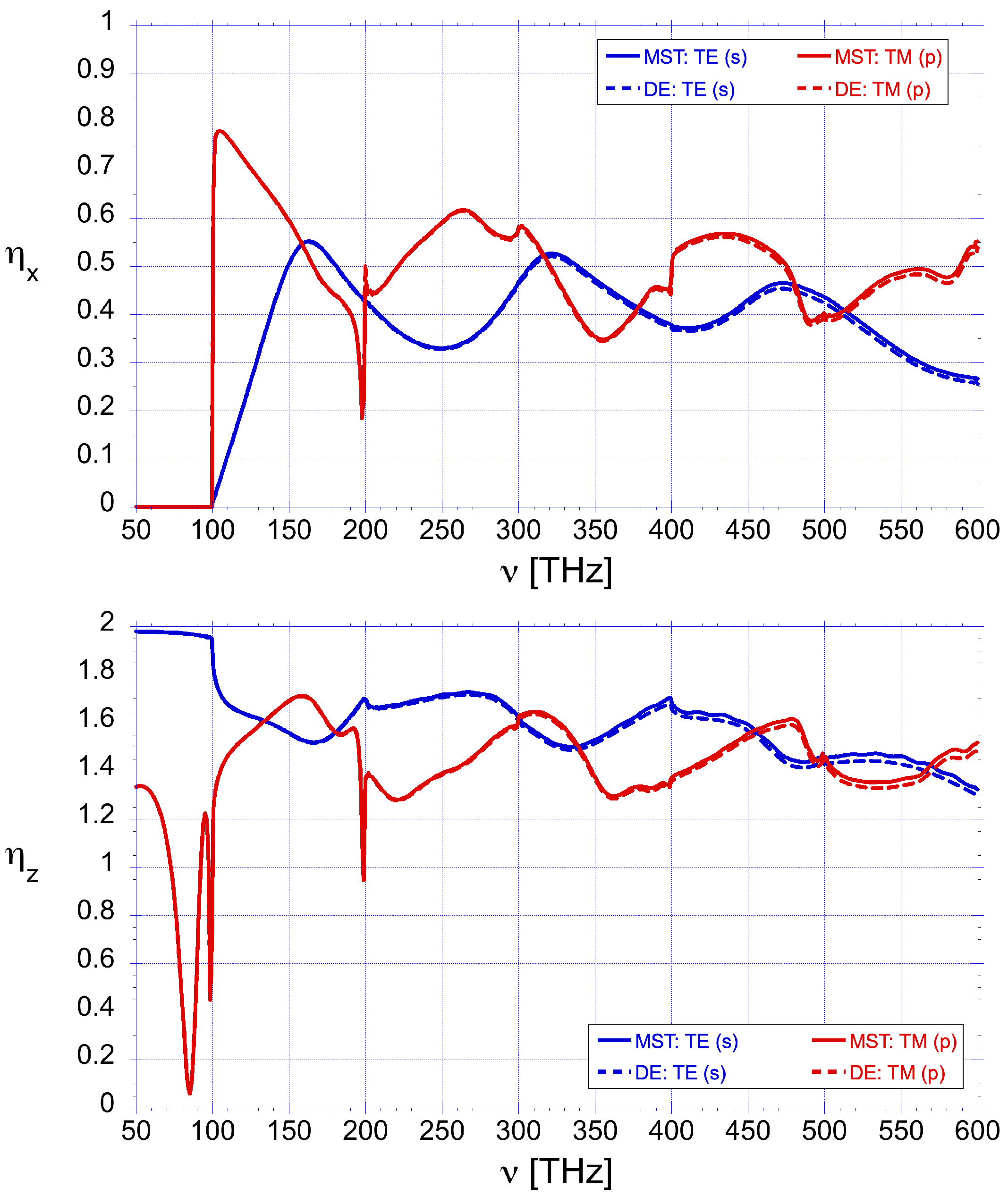This range of frequencies encompasses 75% of the solar frequency spectrum, as illustrated in Figure 5 (bottom).

In the geometric optics model described in Section 3, for the case where the prism refractive index was unity, the peak value of ${\eta }_x=0.5$ was found at the prism angle $\alpha =22.5^{\circ }$ (see Figure 3). Larger peak values of ${\eta }_x$ were predicted for larger value of n, in which case the value of $\alpha$ was marginally larger. Using MEEP to calculate ${\eta }_x$ across the frequency range 50–600 THz, and making use of the complex refractive index values of gold and aluminum, we found similar results for a prism index of $n=1$. The front facet was metallized with a $0.1 \left[\mathsf{\mu }\mathrm{m}\right]$ thick coating. The calculated variation of ${\eta }_x$ vs. $\alpha$ is plotted in Figure 5 (top). The spectral reflectance curves plotted in Figure 5 (bottom) illustrate the general trend for metals, e.g., the s-polarized field (which is tangential to the interface) was more strongly reflected than the p-polarized field (which had a component normal to the interface). The higher reflection values were expected to provide larger values of ${\eta }_x$. The average (unpolarized) value peaks were ${\eta }_x=0.46$ at $\alpha =22.5^{\circ }$.

The polarization-averaged differences between aluminum and gold were negligible, and the choice of material depended on other concerns such as mass density, spectral bandwidth, and space weathering. The low reflectance of gold at wavelengths shorter than $0.5 \left[\mathsf{\mu }\mathrm{m}\right]$ (above 600 THz) is also a concern. A comparison of the values of ${\eta }_x$ for the numerical MST analysis and the geometric optics analysis shows a smaller value in the former case, which we attribute to p-polarized light.

The geometric optics model also predicted that, for a given value of $\alpha$, the value of ${\eta }_x$ increases with an increasing refractive index (see Figure 3). Let us compare this prediction with the MEEP model. The polarization-averaged spectral distributions for aluminum are plotted in Figure 6 for three different prism refractive index values, $n=1, 1.5, 2$, resulting in the corresponding frequency-integrated values ${\eta }_x$: $0.46$, $0.48$, $0.44$ and ${\eta }_z$: $1.53$, $1.49$, $1.51$. The grating period $\mathrm{\Lambda }=3 \left[\mathsf{\mu }\mathrm{m}\right]$ corresponds to a fundamental frequency ${\nu }_0=c/\mathrm{\Lambda }=100$ THz, which corresponds to the diffractive cut-off frequency. Evidence of strong diffractive effects at multiples of ${\nu }_0$ is evident in Figure 6.

7. Modal Numerical Analysis

In Section 3 and Section 6, we calculated the momentum transfer efficiency with respective geometric optics and Maxwell stress tensor models. A third method based on modal analysis was described in Section 4. In the later case, closed-form analytical expressions for the frequency-dependent modal intensities were determined (see Equation (19)). That model was unable to physically account for the scattering of light in the diffractive frequency cut-off zone ($|m\lambda /\mathrm{\Lambda }|>1$). Maxwell solver software packages, such as MEEP, overcome this shortcoming, albeit over a limited frequency band.

$${{\overrightarrow{\eta }}_b}^{\mathrm{s},\mathrm{p}}={\int }_{{\nu }_{\min }}^{{\nu }_{\max }} {\displaystyle \frac{1}{2}}{I}_{\mathrm{sun}}^{\prime }\left(\nu \right)\sum _{M_{\min ,\nu }}^{M_{\max ,\nu }} {\tilde{I}}_{m,b}^{ \prime s,p}\left(\nu \right)\left(-sin{\theta }_{m,b} \widehat{x}+(1-\sqrt{1-{sin}^2{\theta }_{m,b}} ) \widehat{z}\right) d\nu$$

(33)

$${{\overrightarrow{\eta }}_f}^{\mathrm{s},\mathrm{p}}={\int }_{{\nu }_{\min }}^{{\nu }_{\max }} {\displaystyle \frac{1}{2}}{I}_{\mathrm{sun}}^{\prime }\left(\nu \right)\sum _{M_{\min ,\nu }}^{M_{\max ,\nu }} {\tilde{I}}_{m,f}^{ \prime s,p}\left(\nu \right)\left(-sin{\theta }_{m,f} \widehat{x}+(1+\sqrt{1-{sin}^2{\theta }_{m,f}} ) \widehat{z}\right) d\nu$$

(34)

$${\eta }_x=\left({\overrightarrow{\eta }}_f^{ s}+{\overrightarrow{\eta }}_f^{ p}+{\overrightarrow{\eta }}_b^{ s}+{\overrightarrow{\eta }}_b^{ p}\right)·\widehat{x}$$

(35)

$${\eta }_z=\left({\overrightarrow{\eta }}_f^{ s}+{\overrightarrow{\eta }}_f^{ p}+{\overrightarrow{\eta }}_b^{ s}+{\overrightarrow{\eta }}_b^{ p}\right)·\widehat{z}$$

(36)

where the MEEP program determines the normalized front and back modal intensities, ${\tilde{I}}_{m,f}^{\prime }\left(\nu \right)$ and ${\tilde{I}}_{m,b}^{\prime }\left(\nu \right)$, where ${\tilde{I}}_{m,f}^{\prime }\left(\nu \right)+{\tilde{I}}_{m,b}^{\prime }\left(\nu \right)=1$, and the wave vectors scattered are out the front ${\overrightarrow{k}}_{m,f}=k(-cos{\theta }_{m,f} \widehat{z}+sin{\theta }_{m,f} \widehat{x})$ and back ${\overrightarrow{k}}_{m,b}=k(cos{\theta }_{m,b} \widehat{z}+sin{\theta }_{m,b} \widehat{x})$. In practice, ${\theta }_{m,f}$ and ${\theta }_{m,b}$ may different. The factor $I_{\mathrm{sun}}^{\prime }$ is the normalized spectral irradiance of the light source. As stated previously for the normal sun incident, we have $M_{\min ,\nu }=M_{\max ,\nu }=\mathrm{INT}[\mathrm{\Lambda }c/\nu ]$. For cases where the bandwidth of the source is restricted, we opted to normalize not with the full solar constant, but instead with the band-limited factor:

$$I_{\mathrm{sun}}^{\prime }\left(\nu \right)=I_{\mathrm{sun}}\left(\nu \right)/{\int }_{{\nu }_{\min }}^{{\nu }_{\max }} I_{\mathrm{sun}}\left(\nu \right) d\nu$$

(37)

The factor $1/2$ preceding $I_{\mathrm{sun}}^{\prime }\left(\nu \right)$ accounts for the equal distribution of unpolarized sunlight into the two polarization states. In our case, where ${\nu }_{\min }=$ 50 THz and ${\nu }_{\max }=$ 600 THz, the normalization constant in the denominator was ∼75% of the solar constant (see Figure 5).

8. Comparison of Diffractive and Maxwell Stress Tensor Models

Let us compare the transverse momentum transfer efficiency discussed in Section 6 with the diffracted modal analysis presented in Section 7. Values of the calculated spectral MTE for a grating with $\mathrm{\Lambda }=3$ μm, $\alpha =22.5^{\circ }$, and $n=1$ are plotted in Figure 7, with Maxwell stress tensor and modal analysis results depicted by solid and dashed lines, respectively. The two methods agreed well (<5% difference) across most of the spectrum but began to diverge at higher frequencies. This deviation may be attributed to the limited number of diffractive modes considered in the modal analysis.

The longitudinal values of ${\eta }_z$ do not display the cut-off signature characteristic of ${\eta }_x$ at ${\nu }_0=c/\mathrm{\Lambda }=100$ THz. This is attributed to the fact that no modes other than the zero order mode propagates when $\nu <{\nu }_0$. We note that both polarization components for ${\eta }_x$ and ${\eta }_z$ depicted transitions at integer multiples of ${\nu }_0$. These were attributed to the diffraction cut-off conditions at higher diffraction orders.

9. Hybrid Grating Fabrication and Verification

To help assess the veracity of the above calculations, direct-write grayscale lithography (DWL) was used to fabricated a hybrid grating composed of a low index polymer via a polymer replication process. This technique is suitable for long period structures (compared to visible wavelengths) and may, therefore, be expected to agree with the high optical frequency results from our MEEP simulations. To provide structural stiffness, the polymer grating ($n_{\mathrm{poly}}$ = 1.56) was applied to a 2 mm thick boro-float substrate ($n_{\mathrm{sub}}$ = 1.47). The long slanted facet of the grating was coated with 70 nm of aluminum using physical vapor deposition, leaving the shorter side facet uncoated. A scanning electron microscope (SEM) image of a replicated hybrid grating, as depicted in Figure 8, indicated rounded features owing to the fabrication process. To lessen the degree of non-ideal scattering from the rounded regions, we elected to produce a grating of period $\mathrm{\Lambda }=30 \mathsf{\mu }\mathrm{m}$, a height $h=17.3 \mathsf{\mu }\mathrm{m}$, and a prism angle $\alpha \sim {36}^{\circ }$. The angular scattering distribution shown in Figure 9 was measured with a purpose-built in-house scatterometer at the HeNe laser wavelength $\lambda =633$ [nm]. As many as $\mathrm{INT}[\mathrm{\Lambda }/\lambda ]=47$ diffraction orders are expected on each side of the optical axis.

The scattering data was used to calculate the theoretically expected momentum transfer efficiencies as follows:

$${\eta }_x={\displaystyle \frac{1}{P_0}}\left(\int I_T\left({\theta }_T\right)sin{\theta }_T d{\theta }_T+\int I_R\left({\theta }_R\right)sin{\theta }_R d{\theta }_R\right)=0.53$$

(38a)

$${\eta }_z={\displaystyle \frac{1}{P_0}}\left(\int I_T\left({\theta }_T\right)(1-cos{\theta }_T) d{\theta }_T+\int I_R\left({\theta }_R\right)(1+cos{\theta }_R) d{\theta }_R\right)=0.91$$

(38b)

where $P_0=\int I_T\left({\theta }_T\right) d{\theta }_T+\int I_R\left({\theta }_R\right) d{\theta }_R$ is the scattered HeNe beam power and the irradiance values have been adjusted for bias and gain:

$$\begin{array}{cc}\hfill I_R\left({\theta }_R\right)& =\mathrm{STEP}[I_{\mathrm{R},\mathrm{raw}}-{\widehat{I}}_{\mathrm{R},\mathrm{raw}}]\hfill \end{array}$$

(39a)

$$\begin{array}{cc}\hfill I_T\left({\theta }_T\right)& =\mathrm{STEP}[I_{\mathrm{T},\mathrm{raw}}\ast G_T-{\widehat{I}}_{\mathrm{T},\mathrm{G}}]\hfill \end{array}$$

(39b)

where ${\widehat{I}}_{\mathrm{R},\mathrm{raw}}=25$ is the sum of the average value of $I_{\mathrm{R},\mathrm{raw}}$ in the range ${\theta }_R$: $({60}^{\circ },{90}^{\circ })$ and one standard deviation; ${\widehat{I}}_{\mathrm{T},\mathrm{raw}}=22$ is the sum of the average value of $G_T{I}_{\mathrm{T},\mathrm{raw}}$ in the range ${\theta }_T$: $({60}^{\circ },{90}^{\circ })$ and one standard deviation; $G_T=18/40.4$ is the estimated relative gain factor of the two measurements; and the STEP function sets negative values to zero. The corresponding high optical frequency MEEP values are ${\eta }_x$∼ 0.50 and ${\eta }_z$∼ 1.5. The measured and calculated values of ${\eta }_x$ are in good agreement. The discrepancy between the values of ${\eta }_z$ may be attributed to less back-reflection from the fabricated structure.

10. Conclusions

We examined a hybrid reflection/transmission grating composed of metallized front facing facets and transmissive side facing facets, as shown in Figure 1, for solar sailing missions requiring spiral trajectories toward (or away from) the sun. The hybrid grating is designed to reduce the effects of undesired scattering from the side facets while maintaining a sun-facing orientation. We compared the radiation pressure force efficiency on the grating using geometric optics approximations and numerical finite difference time domain methods. Additionally, a prototype hybrid grating was fabricated to verify the momentum transfer efficiency predicted in the geometric and numerical studies.

Making use of the Maxwell solver MEEP, we computed the momentum transfer efficiency of a hybrid grating of period $\mathrm{\Lambda }=3 \mathsf{\mu }\mathrm{m}$ and apex angle $\alpha =22.5^{\circ }$, finding the net transverse MTE in a sun facing configuration reaches ${\eta }_x=48\%$ when the refractive index of the sail material is 1.5. At optical frequencies beyond our upper computational range of 600 THz (i.e., shorter than $\lambda =0.5 \mathsf{\mu }\mathrm{m}$), a geometrical optics limit (where diffraction effects become increasingly negligible) is expected, whereupon the MTE becomes weakly independent of wavelength (owing, for example, to material dispersion). However, the geometrical optics model presented in Section 3 is insufficient for computing this limit as it does not account for the Fresnel reflection and transmission coefficients at the interface between vacuums and the substrate. Nevertheless, the geometrical optics value of ${\eta }_x=0.50$, when $n=1$ (i.e., no dielectric boundary), is in remarkably good agreement with the Maxwell solver value of $0.46$. What is more, a hybrid grating designed for the geometrical optics range (with period $\mathrm{\Lambda }=30 \mathsf{\mu }\mathrm{m}$ being much greater than the wavelength $\lambda =633$ nm) was found to have an angular scattering distribution in excellent agreement with our predicted value of ${\eta }_x$ 47% vs. 48%. Finally, our numerical model found no significant difference between the use of gold and aluminum for the reflective coating. Aluminum may be preferable, however, owing to the absorption in gold being beyond 600 THz.