Fiber Laser Model Considering Excited-State Absorption and Cooperative Upconversion

Abstract

In this paper, we present the results of a comprehensive study on how excited-state absorption and concentration effects influence fiber laser efficiency and the optimization of the laser cavity’s output coupler reflection. The concentration effects discussed include the cooperative interaction between two closely spaced active ions and the pair-induced quenching typically observed in heavily doped gain fibers. The laser is simulated using a model based on the laser, pump, and spontaneous emission waves propagating along the gain fiber, where the intensities of these waves determine their absorption or amplification. The model considers the radial distributions of optical fields and populations of the energy levels of the active ions, which is crucial to comply with the law of conservation of energy. The results discussed in this paper are essential for applications related to the optimization of heavily doped fiber lasers. The physics behind the reported results is discussed.

1. Introduction

Fiber lasers (FLs) are versatile light sources widely used in many applications such as material processing, including laser cutting [1,2], welding [3], marking [4,5], cleaning [6], additive manufacturing [7], biomedicine [8,9,10], military [11], as a pump source for frequency doubling [12], sensing [13,14,15], etc. Usually, silica-based FLs operate in the near-infrared optical band, covering the optical ranges of 0.98 to 1.2 microns (ytterbium window), 1.53 to 1.6 microns (erbium window), and 1.9 to 2.2 microns (thulium and holmium windows) [16,17], the latter limited from the longer wavelengths by the strong infrared absorption in silica glass above 2 microns [18].

Typically, rare-earth ions used as active dopants in gain fibers (GFs) have multilevel energy schemes (erbium, neodymium, thulium, and holmium; see [15,16,19]), which lead to excited state absorption (ESA) at the pump and laser wavelengths. ESA significantly limits laser efficiency because it causes a large portion of pump and laser photons to be used in ESA transitions, creating thermal issues [20,21]. Since ESA depends on both the pump and laser wavelengths [22,23,24], the thermal loss induced by this phenomenon also is wavelength-dependent. ESA’s influence on laser operation is discussed in a number of papers; see, for example, refs. [24,25].

In the case of double-clad GFs where the absorption coefficient at the pump wavelength is small due to an extremely low overlap factor of the pump wave with the fiber core (around a few decimal percent), or when a short-length laser cavity is required, high-doped GFs are used [26,27]. In this type of fiber, additional thermal (phonon) loss occurs due to cooperative upconversion resulting from the interaction between two closely spaced active ions, both excited to the laser level: when one of them rapidly de-excites, significantly reducing the laser level effective lifetime [28,29,30,31], and the other ion jumps to the upper excited level with the subsequent phonon decay to the laser level [32,33,34]; see Figure 1. These processes lead to a deterioration of laser efficiency, as ESA discussed above. The influence of cooperative upconversion on the efficiency of fiber lasers and amplifiers has been reported in a number of papers, some of which include references [32,33,34,35,36].

In this paper, we discuss the results of a detailed numerical study on how the combination of ESA and the cooperative interaction (CI) between two nearby active ions (a pair) affects the efficiency of a fiber laser operating in continuous wave (CW) mode. Our study is aimed at optimizing the laser in the sense of finding such a laser cavity output reflector at which the laser output power reaches its maximum. This kind of optimization is important because it permits one to optimize the laser with a given length of the gain fiber (GF). We selected a silica fiber heavily doped with erbium (EDF) as the gain medium, since its ESA parameters are well known [22,37].

We show how CI, which includes homogeneous upconversion (HUC) and pair-induced quenching (PIQ) between neighboring active ions [29,30,31], along with ESA, impacts the fiber laser optimization. In this study, we consider that the laser operates at 1550 nm, the common wavelength of erbium-doped fiber lasers (EDFLs). The results of our work demonstrate that the optimal reflection of the output mirror depends on the ESA presence and the HUC constant that characterizes the cooperative upconversion strength.

The method proposed for laser optimization is based on the frequently used Traveling Waves’ Model (TWM) [25,38]. In this model, the fiber gain and pump absorption vary along the GF due to changes in the populations of active ions’ energy levels, which depend on the powers of counter-propagating waves at the laser, amplified spontaneous emission (ASE), and pump wavelengths. We also accounted for the radial distributions of the intensities of these waves, allowing one to determine the radial distribution of the populations of energy levels. This step is crucial for calculating the key characteristics of the GF, such as gain at the laser and spontaneous emission (SE) wavelengths and pump absorption. These results differ from those obtained by considering only the wave intensities at the fiber core axis and overlap factors at the respective wavelengths [36], which are commonly used in fiber laser simulations. Note that including the radial distributions of counter-propagating waves and the energy levels’ populations of the active ions in a model is essential to comply with the law of conservation of energy, an important detail related to the accuracy of modeling [38].

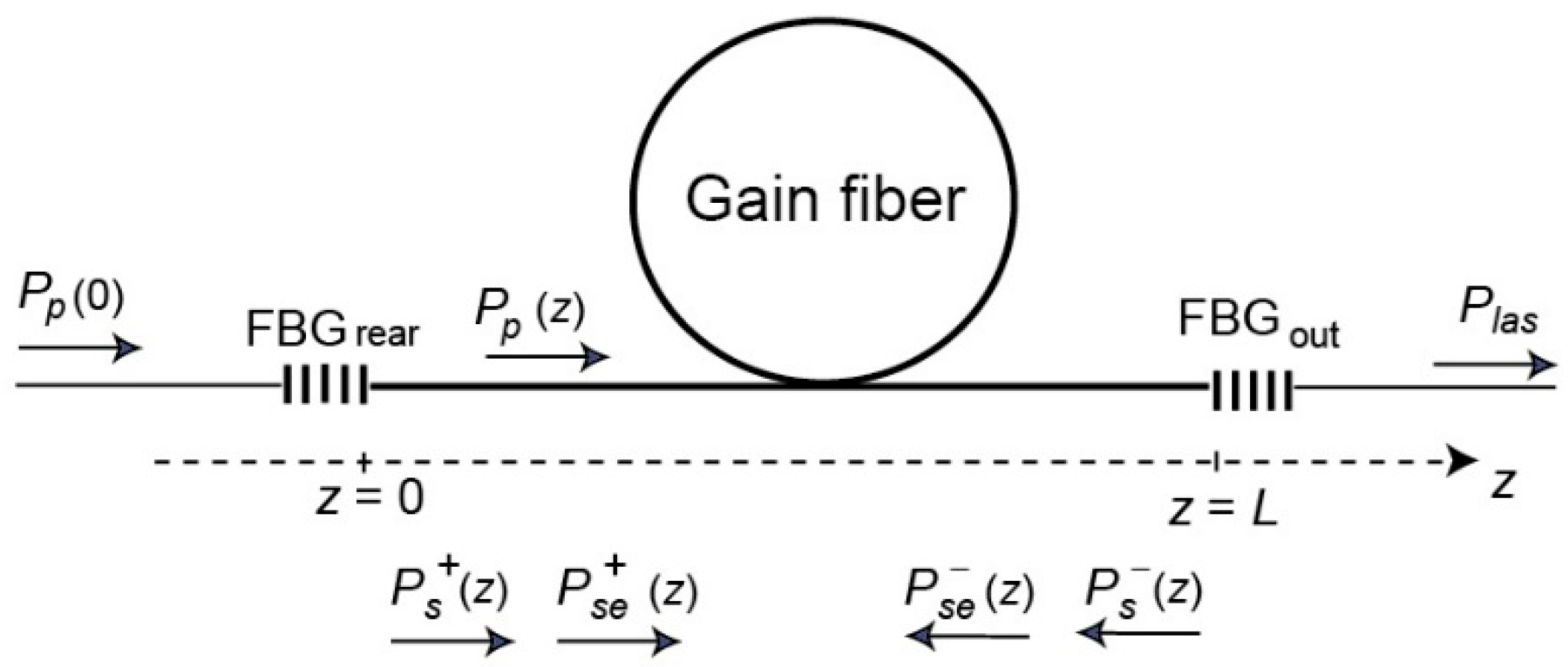
2. Arrangement of the Fiber Laser and the Boundary Conditions

The laser arrangement used in the discussion is shown in Figure 1. The single-mode gain fiber, with length L, is placed between two fiber Bragg gratings (FBGs) that act as the selective reflectors forming the Fabry–Perot laser cavity. The low-signal absorption of the GF at 1530 nm is chosen to be relatively high, 40 dB/m at 1530 nm, which is about an order higher than that of the commercial fiber low-doped with erbium (for example, M5-980-125), in which CI are negligible [39]. The reflection of the rear grating, FBG_rear, is R_rear = 100%, and that of the output grating, FBG_out, is R_out = R < 100%. The latter is the subject for optimization. Both gratings reflect at the laser wavelength λ_s. The GF is optically pumped through FBG_rear at the pump wavelength λ_p at which FBGs are transparent. The pump photon energy hν_p = hc/λ_p (h is the Planck constant and c is the free-space light velocity) corresponds to the transition of the active ions from the ground level to the pump level. The pump power at the GF input is P_p(0), and the laser power, P_las, is measured from the right side of FBG_out. The GF is enlarged along the z-axis.

Five waves propagating along the GF are considered in the laser simulation: P_p(z) represents the power of the pump wave (with P_p(0) being the input pump power), P_s⁺(z) and P_s(z) denote the powers of the counter-propagating laser (signal) waves, and P_se⁺(z) and P_se⁻ (z) are the powers of the counter-propagating waves of spontaneous emission (SE) centered at 1530 nm, including amplified spontaneous emission (ASE). All waves propagate along the z-axis, with the directions indicated in Figure 1.

From this figure, the boundary conditions for powers of the laser and SE/ASE waves are as follows:

$$P_s^{+}\left(0\right)=P_s^{-}\left(0\right)$$

(1a)

$$P_s^{-}\left(L\right)=P_s^{+}\left(L\right)R_{out}$$

(1b)

$$P_{se}^{+}\left(0\right)=P_{se}^{-}\left(L\right)=0$$

(1c)

The laser output power is found as

$$P_{las}=P_s^{+}\left(L\right)T_{out}$$

(1d)

where T_out = (1 − R_out) is the output grating transmission at the Bragg wavelength.

3. The Energy Levels of the Active Ions and the Balance Equations

The energy levels of a neighboring pair of erbium ions are shown in Figure 2. The levels are labeled with sequential numbers from below and also with the conventional designations related to the corresponding electron–electron and electron–host interactions [19]. The transitions marked with λ_p, λ_s, and λ_se illustrate absorption at the pump, laser, and SE wavelengths from the ground (⁴I_15/2) and excited (⁴I_13/2 and ⁴I_11/2) states, respectively. τ₂ to τ₅ indicate the lifetimes of the excited levels. Dash arrows represent fast phonon transitions, and the dotted arrow indicates photon transitions related to spontaneous emission (SE). The solid blue arrow from the laser level to the ground state shows the laser transition (stimulated emission). We limit the energy level scheme to five levels since these levels participate in the laser operation under study. For this reason the short-living levels, including ⁴F_9/2, situated between the levels ⁴I_9/2 and ⁴S_3/2, and also all above ⁴F_7/2, are omitted. Since populations of the levels 4 and 5 are very low, the possible ESA transitions from them are negligible.

The ions interact with each other non-radiatively when they are spaced closely enough; see the red arrows: when both ions are excited to the laser level (⁴I_13/2), one of them (donor) transfers energy to another one (acceptor), which results in de-exciting the donor and an energy jump of the acceptor ion to the ⁴I_9/2 excited state. The non-radiative interaction between ions when both are excited to the pump level is not considered because its population is relatively small.

Since the simplified energy diagram of the erbium ions includes five levels, a set of equations describing populations of the energy levels is also five. The steady-state balance equations for active ions are written as [32,34], in which the rate coefficients W_ij describing transitions between the levels i and j [40] are expressed in terms of microscopic parameters of active ions, light intensities at corresponding wavelengths, and the fiber waveguide characteristics [41]. The first four equations describe populations of the second, third, fourth, and fifth levels, while the last is used for calculating the ground-level population:

$$\left({\displaystyle \frac{{\sigma }_{12}^s{I}_s}{h{\nu }_s}}+{\displaystyle \frac{{\sigma }_{12}^{se}{I}_{se}}{h{\nu }_{se}}}\right)N_1-\left({\displaystyle \frac{{\sigma }_{21}^s{I}_s}{h{\nu }_s}}+{\displaystyle \frac{{\sigma }_{21}^{se}{I}_{se}}{h{\nu }_{se}}}\right)N_2-\left({\displaystyle \frac{{\sigma }_{24}^s{I}_s}{h{\nu }_s}}+{\displaystyle \frac{{\sigma }_{24}^{se}{I}_{se}}{h{\nu }_{se}}}\right)N_2+{\displaystyle \frac{N_3}{{\tau }_3}}-{\displaystyle \frac{N_2}{{\tau }_2}}-2C{\left(N_2\right)}^2=0$$

(2a)

$${\displaystyle \frac{{\sigma }_{13}^p{I}_p}{h{\nu }_p}}{N}_1-{\displaystyle \frac{{\sigma }_{31}^p{I}_p}{h{\nu }_p}}{N}_3-{\displaystyle \frac{{\sigma }_{35}^p{I}_p}{h{\nu }_p}}{N}_3-{\displaystyle \frac{N_3}{{\tau }_3}}+{\displaystyle \frac{N_4}{{\tau }_4}}=0$$

(2b)

$$\left({\displaystyle \frac{{\sigma }_{24}^s{I}_s}{h{\nu }_s}}+{\displaystyle \frac{{\sigma }_{24}^{se}{I}_{se}}{h{\nu }_{se}}}\right)N_2+C{\left(N_2\right)}^2-{\displaystyle \frac{N_4}{{\tau }_4}}+{\displaystyle \frac{N_5}{{\tau }_5}}=0$$

(2c)

$${\displaystyle \frac{{\sigma }_{35}^p{I}_p}{h{\nu }_p}}{N}_3-{\displaystyle \frac{N_5}{{\tau }_5}}=0$$

(2d)

$$N_1+N_2+N_3+N_4+N_5=N_0$$

(2e)

In these equations, N₀ is the active ions’ concentration in the uniformly doped fiber core; N₁ to N₅ are the radially and longitudinally dependent populations of the corresponding energy levels shown in Figure 2; σ_ij^las, σ_ij^se, and σ_ij^p are the cross-sections of the energy transitions of the active ions from i-level to j-level observed at the pump (p), the laser (s), and SE (se) wavelengths. I_p, I_s, and I_se are the radially and longitudinally dependent intensities of the pump, laser, and SE waves, respectively. hν_p, hν_s, and hν_se are the energies of the pump, laser, and SE photons (h is the Planck constant and ν_p, ν_s, and ν_se are the waves’ frequencies), and τ_i is the i-level’s lifetime.

Equation (2a) describes the population of the second (laser) level: the first term corresponds to the transition from the ground state to the laser one due to absorption at the laser and SE wavelengths, the second term corresponds to the stimulated emission from the laser level at these wavelengths, the third term describes the ESA transitions from the laser level, the fourth term demonstrates the populating rate of the laser level due to the phonon relaxation with the characteristic time τ₃, and the fifth term corresponds to the photon relaxation of the laser level, which actually describes SE irradiated to all directions. The last term corresponds to the PIQ-assisted decay of the laser level population, in which the proportionality constant C, known as the HUC coefficient, characterizes the decay of the laser level due to the non-radiative interactions of the closely spaced active ions [30,33]. The multiplier “2” shows the double decay of population N₂ compared to the increase in the population of the fourth level due to the energy transfer described by the second term in Equation (2c), which shows the fast de-excitation of the one interacting ion to the ground state and transition of the other to the ⁴I_9/2 excited state.

Equation (2b) includes the terms that describe transitions from the ground level (ground state absorption, GSA) and the pump level (ESA) at the pump wavelength, the stimulated transition at the pump wavelength to the ground level (see ref. [37]), phonon decay to the laser level, and phonon decay from the fourth level. Equation (2c) contains the terms corresponding to the ESA at the laser and SE wavelengths, and the transition from the laser to the fourth level due to CI. Equation 2(d) describes populating of the fifth level due to ESA at the pump wavelength and its fast non-radiative decay. The last equation represents the balance of the populations of all levels considered in the model.

As shown in Equation (2d), the population of the fifth level is expressed in terms of the population of the third level, so the last term in Equation (2c) can be replaced with the first term in Equation (2d). The population of the fourth level (Equation (2c)) is expressed, after consideration of Equation (2d), in terms of the populations of the second and third levels. Therefore, Equation (2c) is eliminated after substituting the term N₄/τ₄ in Equation (2b) with its value obtained from Equation (2c). Since τ₄ is very short (see

Table 1. The gain fiber parameters used in modeling.

Parameter	Formula or Comment	Value	Ref.
α0	GF small-signal absorption at 1530 nm	40 dB/m (9.2 m−1)
αp0	GF small-signal absorption at 976 nm	20 dB/m (4.7 m−1)
αBG	Passive loss for commercial EDF	20 dB/km
${\sigma }_{13}^p$	Absorption cross-section of Er ion at 976 nm	1.5 × 10−25 m2	[42]
${\sigma }_{12}^{se}$	Absorption cross-section of Er ion at 1530 nm	5.1 × 10−25 m2	[19,42]
${\sigma }_{12}^s$	Absorption cross-section of Er ion at 1550 nm	2.4 × 10−25 m2	[19,42]
${\tau }_2$	Lifetime of the laser level	10 ms	[42]
${\tau }_3$	Lifetime of the pump level	5 μs	[42]
${\tau }_4$	Lifetime of the 4I9/2 level	5 ns	[42]
${\tau }_5$	Lifetime of the fifth level	1 μs	[42]
${\xi }_p$	${\sigma }_{31}^p/{\sigma }_{13}^p$	1.08	[21]
${\xi }_{se}$	${\sigma }_{21}^{se}/{\sigma }_{12}^{se}$	1.08	[21]
${\xi }_s$	${\sigma }_{21}^s/{\sigma }_{12}^s$	1.52	[21]
${\epsilon }_p$	${\sigma }_{35}^p/{\sigma }_{13}^p$	0.95	[37]
${\epsilon }_{se}$	${\sigma }_{24}^{se}/{\sigma }_{12}^{se}$	0.17	[21]
${\epsilon }_s$	${\sigma }_{24}^s/{\sigma }_{12}^s$	0.22	[21]
${\gamma }_1$	${\tau }_2/{\tau }_3$	1.9 × 103
${\gamma }_2$	${\tau }_5/{\tau }_2$	10−4
a	GF core radius	1.7 μm
NA	GF numerical aperture	0.20
n	Cladding refractive index	1.44
$w_p$	Equation (3b)	1.76 µm
$w_{se}$	Equation (3b)	2.96 µm
$w_s$	Equation (3b)	3.04 µm
$A_p$	$\pi w_p^2/2$	4.86 µm2
$A_{se}$	$\pi w_{se}^2/2$	13.8 µm2
$A_s$	$\pi w_s^2/2$	14.5 µm2
Γp	Equation (3c)	0.77
Γse	Equation (3c)	0.49
Γs	Equation (3c)	0.47
$P_p^{sat}$	$\left[\left(h{\nu }_p\right)/\left({\sigma }_{12}^p{\tau }_2\right)\right]A_p$	0.66 mW
$P_{se}^{sat}$	$\left[\left(h{\nu }_{se}\right)/\left({\sigma }_{12}^{se}{\tau }_2\right)\right]A_{se}$	0.35 mW
$P_s^{sat}$	$\left[\left(h{\nu }_s\right)/\left({\sigma }_{12}^s{\tau }_2\right)\right]A_s$	0.63 mW
Ω	$\pi {NA}^2/n^2$	0.061

), the population of the fourth level is negligible and can be ignored. Finally, the set of Equation (2a–e) is simplified as follows:

$$\left[s_s+s_{se}\right]n_1-\left[\left({\xi }_s{s}_s+{\xi }_{se}{s}_{se}\right)+\left({\epsilon }_s{s}_s+{\epsilon }_{se}{s}_{se}\right)+1\right]n_2-C^{*}{\left(n_2\right)}^2+{\gamma }_1{n}_3=0$$

(3a)

$$s_p{n}_1+\left({\epsilon }_s{s}_s+{\epsilon }_{se}{s}_{se}\right)n_2+0.5C^{*}{\left(n_2\right)}^2-\left({\xi }_p{s}_p+{\gamma }_1\right)n_3=0$$

(3b)

$$n_5={\epsilon }_p{\gamma }_2{s}_p{n}_3$$

(3c)

$$n_1+n_2+n_3{+n}_5=1$$

(3d)

where n_i = N_i/N₀ (i = 1…5) are the normalized populations of the corresponding energy levels, C* = C_HUCN₀τ₂ is the dimensionless HUC constant, the variables $s_s=P_s/P_s^{sat}$, $s_{se}=P_{se}/P_{se}^{sat}$, and $s_p=P_p/P_p^{sat}$, are the radially and longitudinally dependent pump, laser signal, and SE powers normalized to the values of the GF saturation powers at the corresponding wavelengths. The saturation powers, in turn, are found as $P_s^{sat}=I_s^{sat}{A}_s$, $P_{se}^{sat}=I_{se}^{sat}{A}_{se}$, and $P_p^{sat}=I_p^{sat}{A}_p$, where $I_s^{sat}=\left(h{\nu }_s\right)/\left({\sigma }_{12}^s{\tau }_2\right)$, $I_{se}^{sat}=\left(h{\nu }_{se}\right)/\left({\sigma }_{12}^{se}{\tau }_2\right)$, and $I_p^{sat}=\left(h{\nu }_p\right)/\left({\sigma }_{12}^p{\tau }_2\right)$ are the GF saturation intensities, where h is the Planck constant, and ν_s, ν_se, and ν_p are the optical frequencies of the laser, SE and pump waves. A_s, A_se, and A_p are the Gaussian beams areas found using the formalism introduced by Marcuse [41], which considered the Gaussian radial distribution of the light intensities (i means s, se, or p) in single-mode fiber:

$$I_i(r)=I_{i0}\mathrm{e}\mathrm{x}\mathrm{p}\left(-2{\left({\displaystyle \frac{r}{w_i}}\right)}^2\right)$$

(4a)

where I_i0 are intensities at the fiber core axis, and the beams’ radii are found as

$$w_i=a\left(0.65+1.619{V_i}^{-3/2}+2.879{V_i}^{-6}\right)$$

(4b)

The waveguide parameters V_i = ak_iNA are the normalized frequencies [41] (k_i = 2π/λ_i are the wave vectors) and NA is the fiber numerical aperture. The values of all microscopic parameters of the active ions, the saturation powers, and the GF geometrical characteristics are introduced in Table 1.

The set of Equation (3a–d) is solved analytically. To simplify the solution, we ignore the population of the 5th level since its lifetime is short, about 1 μs (see Table 1). This simplification does not affect the simulation results since the n₅ values are of the order of 10⁻³ (see Refs. [25,38] for details). Therefore, Equation (3d) is simplified as n₁ + n₂ + n₃ = 1. Other details of the analytical solution are discussed in the Appendix A.

4. The Laser Equations

According to the model, the GF is divided into N_z short segments of length Δz = L/N_z. In turn, the core of each fiber segment is divided into N_r nested rings of width Δr = a/N_r, where a is the core radius. Both N_z and N_r should be large enough to diminish the possible errors in the laser simulation. In our case, considering that Δz = 1 cm and Δr = a/20 results in an error in compliance with the law of conservation of energy of less than 0.5%. Also, we suppose that the GF background losses are the same at the pump, laser, and ASE wavelengths, and that the losses of fiber splices are small enough to be ignored.

The evolution of powers of the waves considered in the model and propagating along the gain fiber is described as follows:

$$d{P}_p\left(z\right)=-{\alpha }_p\left(z\right)P_p\left(z\right)dz$$

(5a)

$$d{P}_s^{\pm }\left(z\right)=\pm g_s\left(z\right)P_s^{\pm }\left(z\right)dz$$

(5b)

$$d{P}_{se}^{\pm }\left(z\right)={\pm g}_{se}\left(z\right)P_{se}^{\pm }\left(z\right)dz\pm \delta P_{se}^{\pm }\left(z\right)dz$$

(5c)

where α_p is the pump absorption, g_s and g_se are the fiber gains at the laser and SE wavelengths, δP_se(z) is the power of SE generated in the fiber section dz, and captured by the core. We considered, for simplification, that the SE spectrum is centered at λ_se = 1530 nm at which the SE spectral peak is observed, and that g_se corresponds to this wavelength. After considering the Gaussian radial distributions of all waves accounted for in the model, these parameters are found as follows [37,38]

$${\alpha }_p(z)={\displaystyle \frac{{\alpha }_{p0}}{{\mathsf{\Gamma }}_p{A}_p}}{\int }_0^a\left[n_1\left(r,z\right)-{(\xi }_p-{\epsilon }_p\left)n_3\right(r,z)\right]\mathrm{e}\mathrm{x}\mathrm{p}\left[-2{\left(r/w_p\right)}^2\right]2\pi rdr+{\alpha }_{BG}$$

(6a)

$$g_s(z)={\displaystyle \frac{{\alpha }_{s0}}{{\mathsf{\Gamma }}_s{A}_s}}{\int }_0^a\left[{(\xi }_s-{\epsilon }_s)n_2\left(r,z\right)-n_1(r,z)\right]\mathrm{e}\mathrm{x}\mathrm{p}\left[-2{\left(r/w_s\right)}^2\right]2\pi rdr-{\alpha }_{BG}$$

(6b)

$$g_{se}(z)={\displaystyle \frac{{\alpha }_{se0}}{{\mathsf{\Gamma }}_{se}{A}_{se}}}{\int }_0^a\left[{(\xi }_{se}-{\epsilon }_{se})n_2\left(r,z\right)-n_1(r,z)\right]\mathrm{e}\mathrm{x}\mathrm{p}\left[-2{\left(r/w_{se}\right)}^2\right]2\pi rdr-{\alpha }_{BG}$$

(6c)

SE emitted and captured by the fiber core is given by [37,38]

$$\delta P_{se}^{\pm }\left(z\right)={\displaystyle \frac{\mathsf{\Omega }}{4\pi }}{\displaystyle \frac{N_0}{{\tau }_2}}h{\nu }_{se}{\int }_0^a{n}_2(r,z)2\pi rdr$$

(6d)

where Ω/4π is a solid angle in which SE photons are accepted by the fiber core, normalized to the solid angle of the whole sphere (4π), N₀/τ₂ is a fraction of SE photons radiated by a gain fiber during lifetime τ₂ to all directions.

In practice, the integrals shown in Equation (6a–d) must be replaced with the corresponding algebraic sums. The values of all parameters used in the simulation are shown in Table 1.

5. Results and Discussion

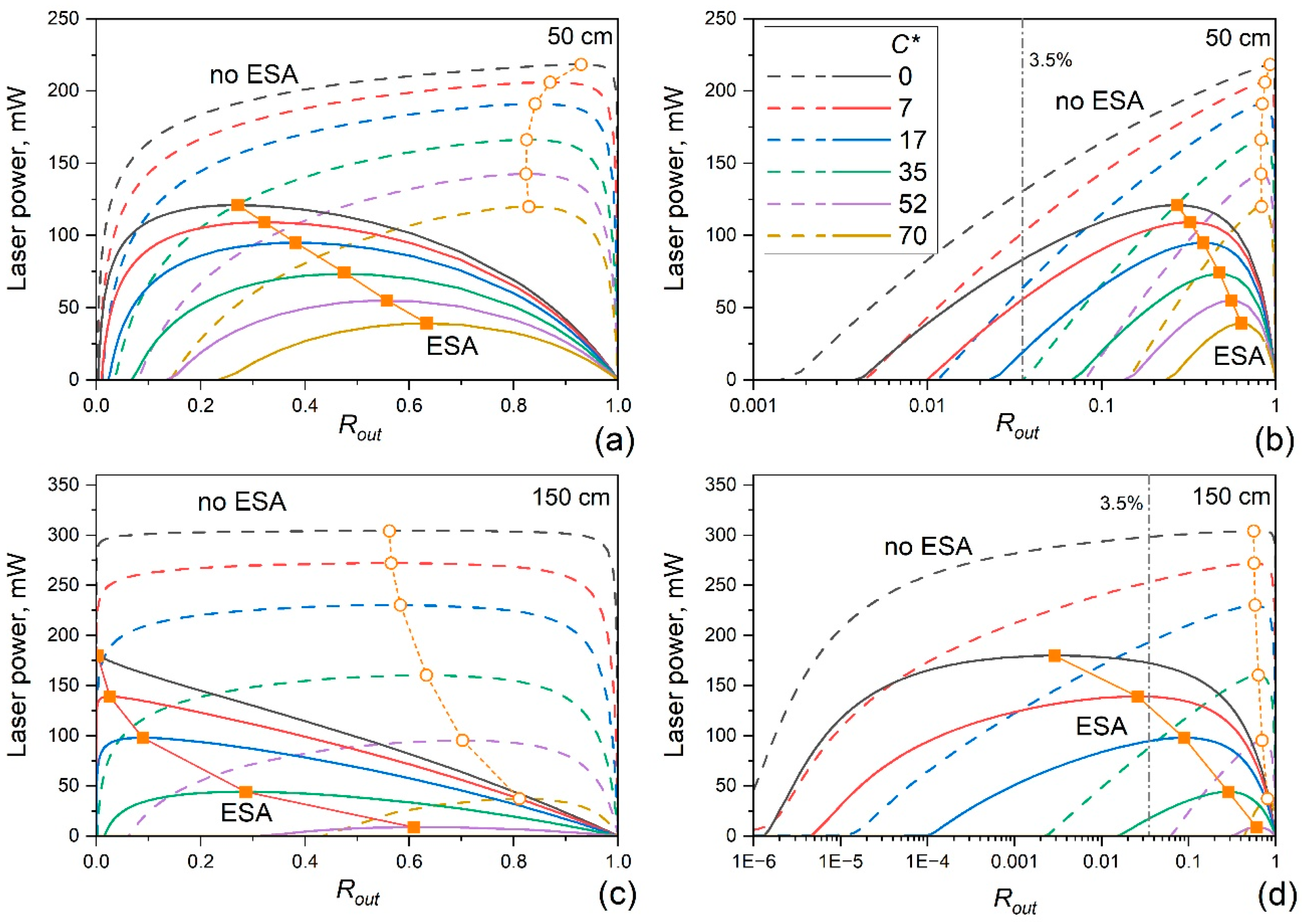
First, we simulated the laser output power as a function of the reflectivity of the output FBG for different GF lengths and the dimensionless HUC constant C*, both with and without ESA. This allowed us to compare the effects of cooperative interactions and ESA on laser efficiency. In Figure 3, these results are shown in a linear (left column) and a semi-logarithmic (right column) scale for two fiber lengths, 50 and 150 cm. The laser operates at 1550 nm, a commonly used wavelength, and the pump power is 500 mW.

Without both ESA (ε_s = ε_se = ε_p = 0) and the cooperative effects (C* = 0), the laser power and efficiency are mainly limited by losses caused by the Stokes shift, which equals the energy difference between the pump and laser photons, background (passive) fiber loss, and residual (not absorbed) pump power. If GF is not too long but absorbs most of the pump power, the laser power can be approximated as P_las = P_p(0)(λ_p/λ_s) = 315 mW, representing the upper limit set by the Stokes shift. Figure 3c,d show results for L = 150 cm, where the laser power reaches 304 mW at an optimal reflection R_out of 56%. When L = 50 cm Figure 3a,b, the laser power decreases to 218 mW, and the optimal R_out increases to 93%.

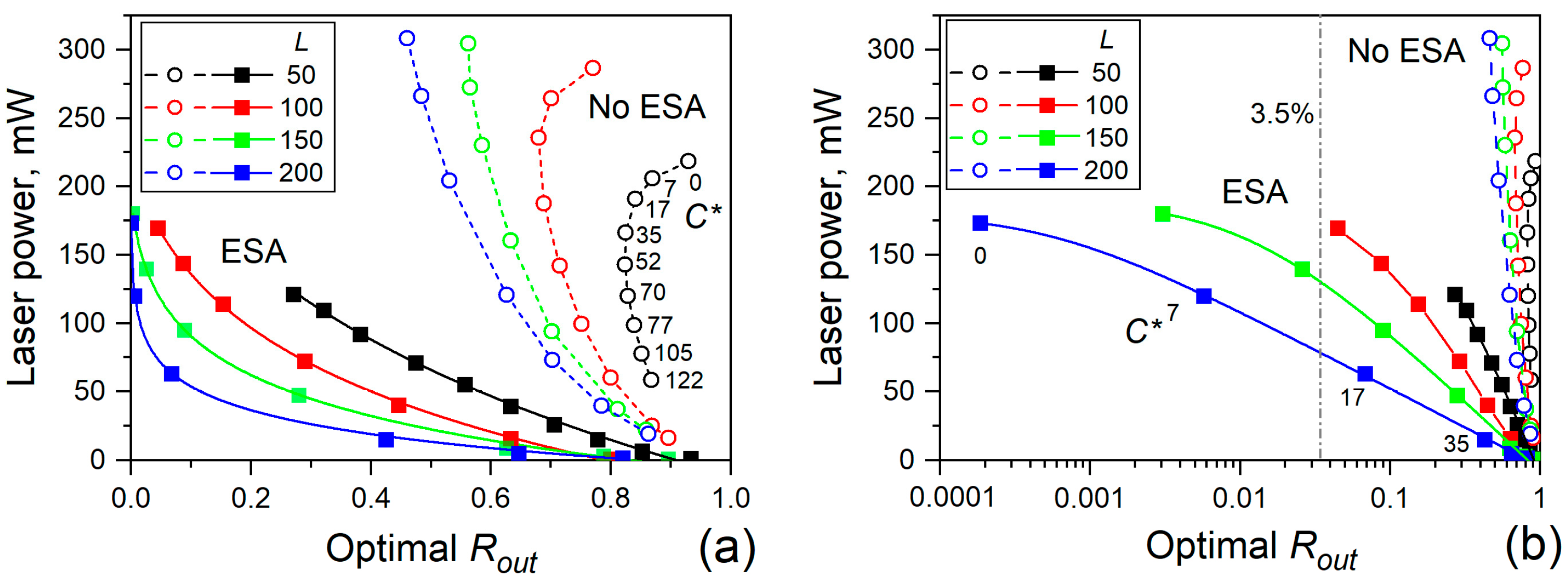
In the first case, the important part of pump power is absorbed by the GF, and the optimal value of R_out is set so that the contribution of the passive fiber loss is minimized by the relatively short photon lifetime in the cavity due to the not-so-high reflection of the output FBG, and SE, important in the longer GF, is not amplified as much. In the second case, the high R_out reduces the specific fiber gain, decreasing the laser level population and increasing the ground level population responsible for pump absorption.

At optimal R_out, the pump absorption and the influence of passive fiber loss are balanced. The longer the GF, the lower the optimal reflection of FBG_out is. Generally, the optimal reflection exceeds 45% for each considered fiber length; see Figure 4a.

In the presence of cooperative effects and the absence of ESA (as in ytterbium-doped fiber) and a relatively short GF, the optimal reflection initially decreases with increasing C* and then increases. Figure 3 and Figure 4 show this pattern by a set of dashed curves simulated for several C* values and various GF lengths. This effect can be explained by the fact that when the GF is short, the population inversion must be high enough to sustain a high specific gain to offset intra-cavity losses, which include intensity-dependent HUC and PIQ. Therefore, as C* increases, the optimal reflection decreases, reducing the influence of CI. However, it increases again due to the difficulty in lowering or maintaining a low optimal reflection of the output grating when losses from CI become too high. If the GF is long (L = 150 cm and 200 cm), the optimal reflection decreases monotonically with increasing C*, since the gain required to compensate for the cavity losses is achieved with a smaller inversion.

When only ESA is observed (see the upper solid curve in Figure 3 and the upper filled squares in Figure 4, the case of low-doped gain fibers), the optimal reflection is significantly lower compared to when both effects are absent; the larger the GF, the greater the decrease in R_out. For example, at L = 50 cm, R_out decreases by a factor of 3.4 and the laser power by a factor of 1.8, while at L = 150 cm, it drops by a factor of 185, with power decreasing by the same factor. A similar trend appears at other GF lengths. When both ESA and CI are considered, R_opt increases and the laser power decreases monotonously as C* increases (see other curves and points in Figure 3 and Figure 4). Note that in practice, the minimal reflection of the FL cavity output mirror is usually limited by Fresnel reflection from the orthogonal cut of the laser output fiber, about 3.5% (see the vertical dash-dot lines in Figure 3b,d. Therefore, the area to the left of these lines is only for understanding the physics behind FL optimization.

Decreasing R_opt as C* increases reduces the intra-cavity laser power, which lowers the probability of ESA transitions at the laser wavelength. Therefore, there is an optimal balance among three parameters: the ESA loss, the loss caused by CI—both controlled by the reflection of the laser cavity’s output mirror—and the transmission of the mirror, at which the laser produces maximum output power and/or operates at maximum efficiency.

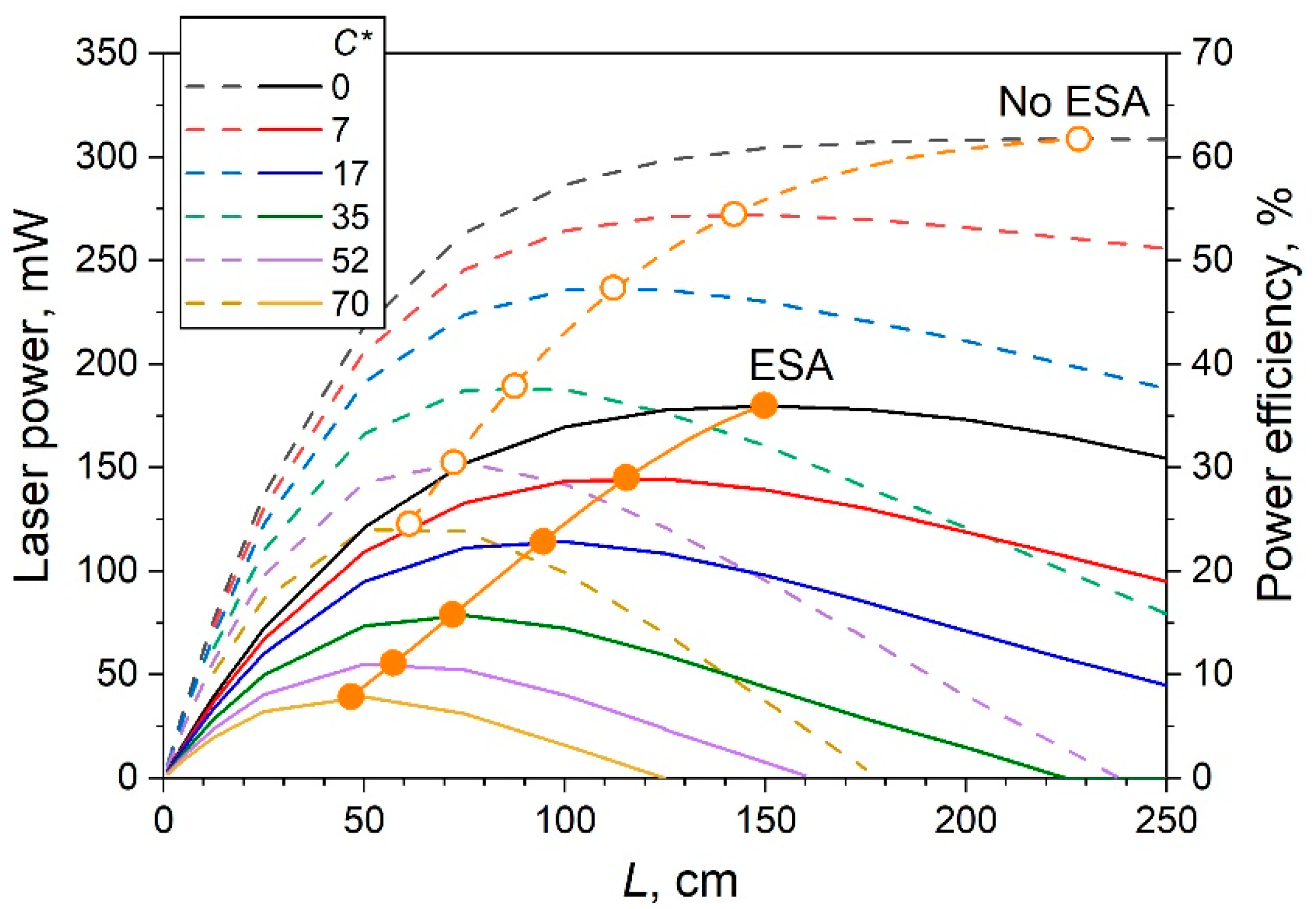
Figure 5 illustrates how ESA and CI impact laser power (left scale) and power efficiency (right scale) as a function of GF length. (Power efficiency refers to the ratio of the laser output power to the pump input power.) The curves were simulated for scenarios with and without ESA (solid and dashed lines, respectively), covering a wide range of the dimensionless HUC parameter C*.

As shown in this figure, the optimal fiber length, at which the laser power reaches the maximum, can be found for each considered GF length, regardless of whether the ESA phenomenon occurs or not, and for any value of C*. It is also apparent that, in the absence of ESA and CI, the laser power maximum (308 mW) is approximately equal to the pump power reduced by the Stokes shift, achieved at L = 230 cm, corresponding to a power efficiency of about 62%. When ASE is considered (see solid lines) but C* = 0, the maximum laser power decreases to 180 mW (36% power efficiency at L = 150 cm). When both ESA and CI are considered, the laser power gradually decreases with increasing C*, and the optimal GF length becomes shorter.

Figure 6 helps the reader better understand the physics behind the fiber laser operation. Specifically, it shows how the input pump photons are distributed among different processes, including laser generation, pump absorption, ESA at the pump, laser, and SE wavelengths, cooperative interactions (HUC and PIQ), and ASE. The output grating reflection is optimized.

This figure shows that most input pump photons are spent on residual pump when the gain fiber is short (L < 30 cm). As the fiber length increases, the contributions from photon-consuming processes depend on whether the ESA is included (see the dashed and solid lines). Figure 6a presents these contributions when C* = 0. It shows that in both cases—whether ESA is present or not—most pump photons are spent on the laser signal. When ESA is present, about 57% of pump photons are used for the laser signal, limited from above by ESA loss (around 30%). When ESA is absent, this percentage rises to about 97% or more, limited by a small contribution from ASE (a few percent). Additionally, the ESA contribution at the pump wavelength stays around 7–8% over a wide range of GF lengths (50 cm to 2 m), while at the laser wavelength, it increases from 15% to 24% as the GF length grows.

When CI are considered, a significant portion of the pump photons is spent on CI-related losses, which increase as C* grows. Additionally, the presence of ESA causes a further increase in CI losses, as illustrated by the dashed and solid green lines in Figure 6b,c, respectively, showing this effect without and with ESA. As a result, the increase in CI losses raises the relative share of ESA losses compared to the contribution from laser photons: at lower C* Figure 6b, the fraction of pump photons lost to ESA is smaller (when L < 1.7 m), whereas at higher C* Figure 6c, it becomes larger.

At an optimal GF length, a clearly defined maximum of the number of pump photons spent on lasing is observed, which decreases as C* increases. At high C* values, there is a critical GF length beyond which lasing does not occur because the gain of the active fiber becomes insufficient to compensate for the losses caused by CI and ESA. This is shown by the vertical dashed line in Figure 6c, on the right side of which the laser does not operate.

Another observation concerns the absorbed pump power. As shown in Figure 6, when ESA is not considered, pump power is absorbed by GF more strongly than when it is considered. This effect can be explained by the fact that ESA consumes an important fraction of pump photons, so to maintain the necessary gain in the active fiber—which depends on the difference between the populations of the laser and ground energy levels multiplied by the corresponding cross-sections (σ₂₁^sn₂ − σ₁₂^sn₁)—the population of the ground level must be lower than in the case when ESA is not accounted for. As a result, pump absorption is lower in the former than in the latter.

The final remark concerns ASE. As seen from Figure 6, ASE is noticeable only when GF is long (longer than 170 cm) and only when ESA is taken into account. This occurs because the optimal reflectivity of the output mirror in the latter is significantly lower than in the former (see Figure 3 and Figure 4), leading to a strong increase in fiber gain, including at the SE wavelength. Otherwise, ASE is negligible. It is a reason for its presence only in Figure 6a.

6. Conclusions

In this paper, the results of studying how excited-state absorption (ESA) and collective interactions (CI) between closely spaced active ions affect the efficiency of a fiber laser are presented. For the laser simulation, the Traveling Waves Model was used, which considers both fiber gain and pump absorption variations along the gain fiber based on the populations of the active ions’ energy levels. These populations, in turn, depend on the powers of the counter-propagating laser, amplified spontaneous emission, and pump waves. In the model, a five-level model of the active ions’ energy levels was considered, which accounts for all possible transitions between them during laser operation. The balance equations describing the energy levels’ populations were solved analytically. The model also includes the radial distributions of wave intensities, which determine the radial distributions of the energy levels’ populations of active ions. The latter is crucial for accurately calculating pump absorption and laser signal gain. Ensuring these parameters obey the law of conservation of energy—a fundamental principle of physics—is essential for obtaining reliable simulation results.

We proposed optimizing the fiber laser by adjusting the reflection of the output mirror in the laser cavity to maximize laser power. We show that the optimal reflection of this mirror depends on whether ESA and CI are considered and on the strength of CI. It is also demonstrated that when ESA is ignored but CI is included, the optimal reflection is significantly higher than when ESA is accounted for. For example, with a relatively long gain fiber, the optimal reflection in the first case is about 60% or more, increasing as the CI effect grows. Conversely, in the second case, it ranges from a fraction of a percent to a few percent as CI increases. We also show that the optimal gain fiber length is longer when ESA is ignored and shorter when it is considered, and that in both cases, it decreases as the CI effect increases.

Our detailed analysis of laser operation focuses on how pump photons are utilized in laser generation processes, especially those involving ESA and CI. We also examine the physical mechanisms behind laser functioning.

We believe the reported results are important for optimizing fiber lasers, particularly when active ions display excited-state absorption and cooperative interactions in heavily doped gain fibers.