Prediction of Shock Wave Velocity Temporal Evolution Induced by Ms-Ns Combined Pulse Laser Based on Attention-LSTM
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiment
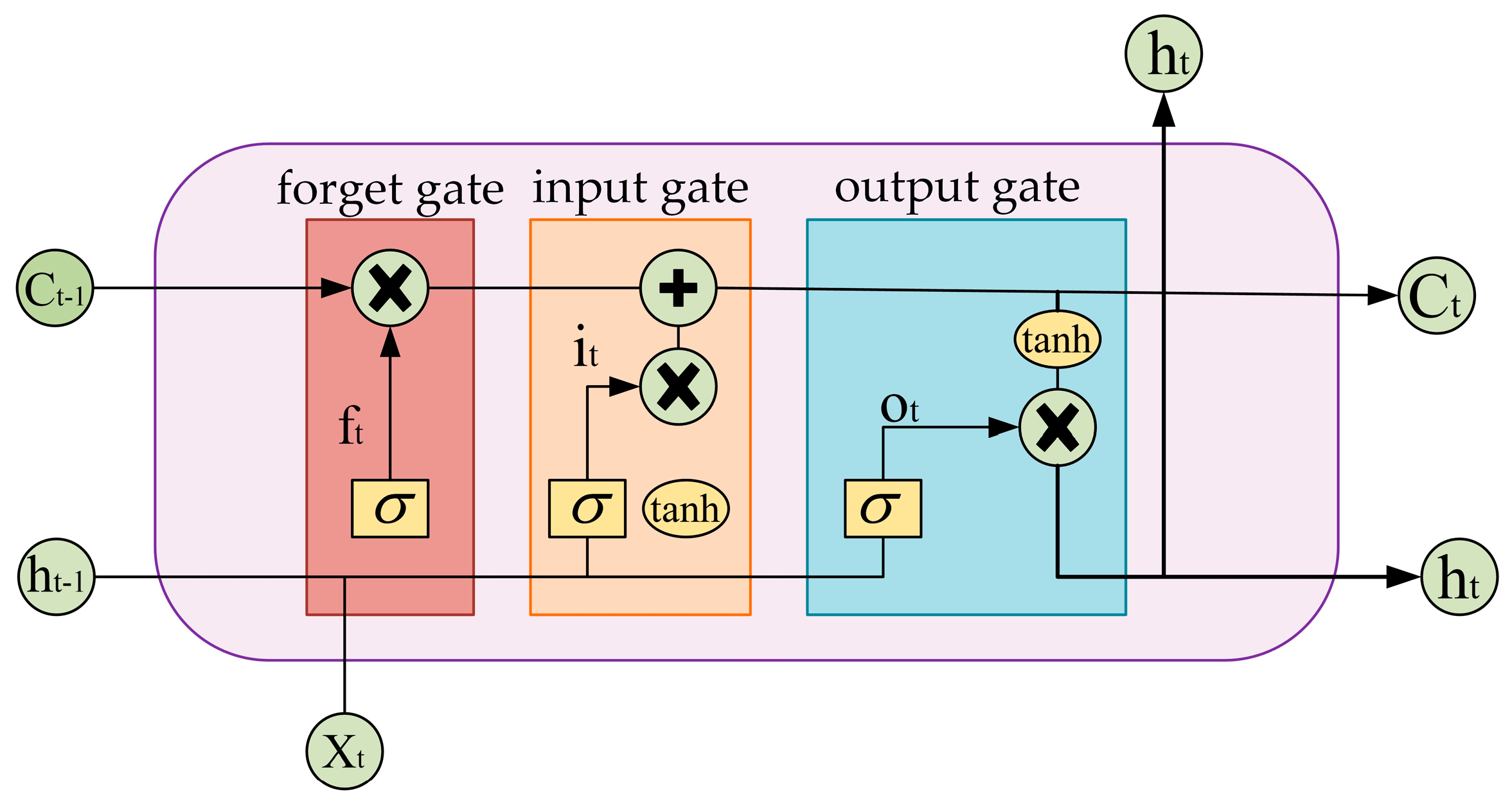
2.2. LSTM
2.3. Attention Mechanism
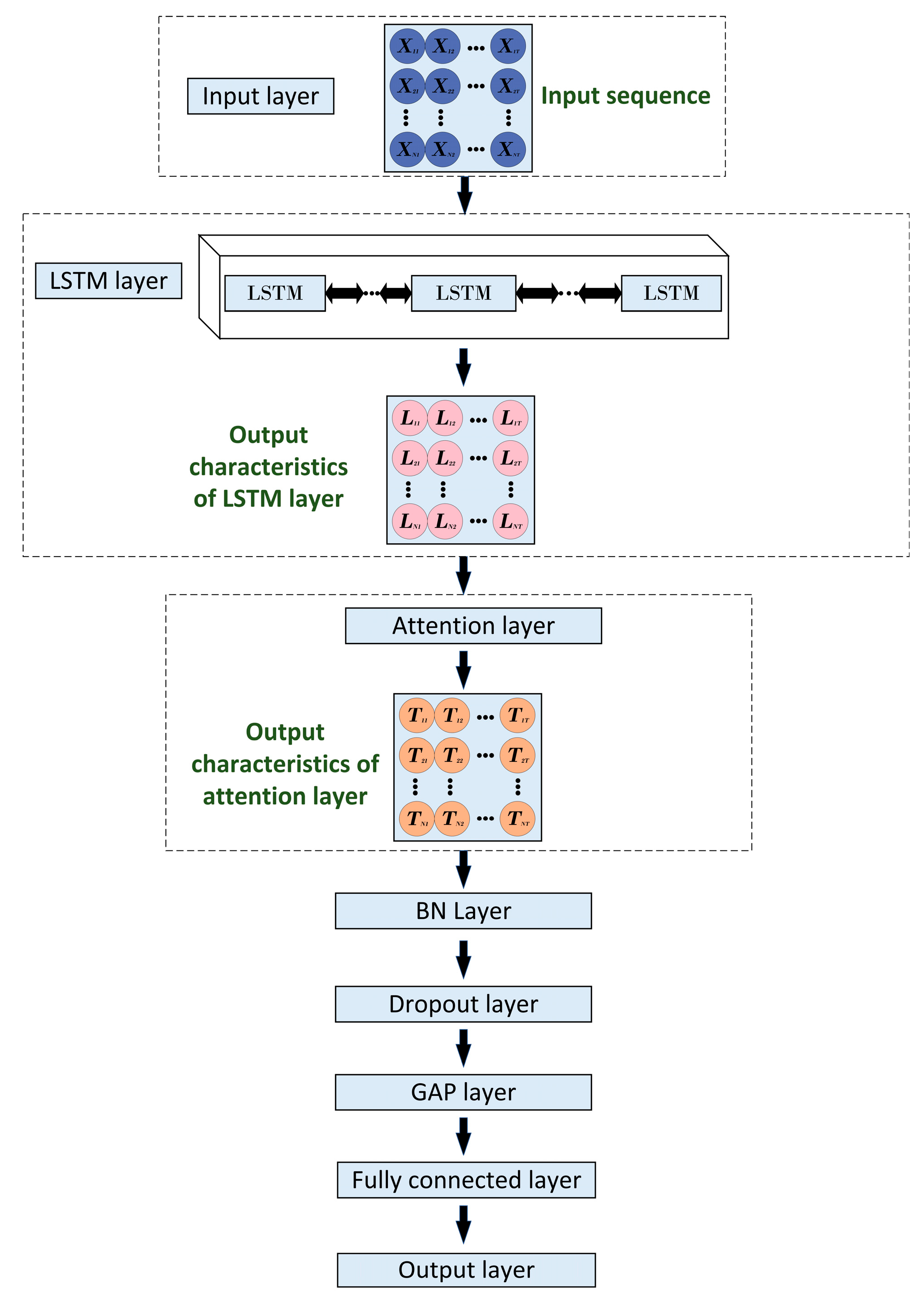
2.4. Attention-LSTM Architecture
Model Evaluation Indicators
3. Results and Discussion
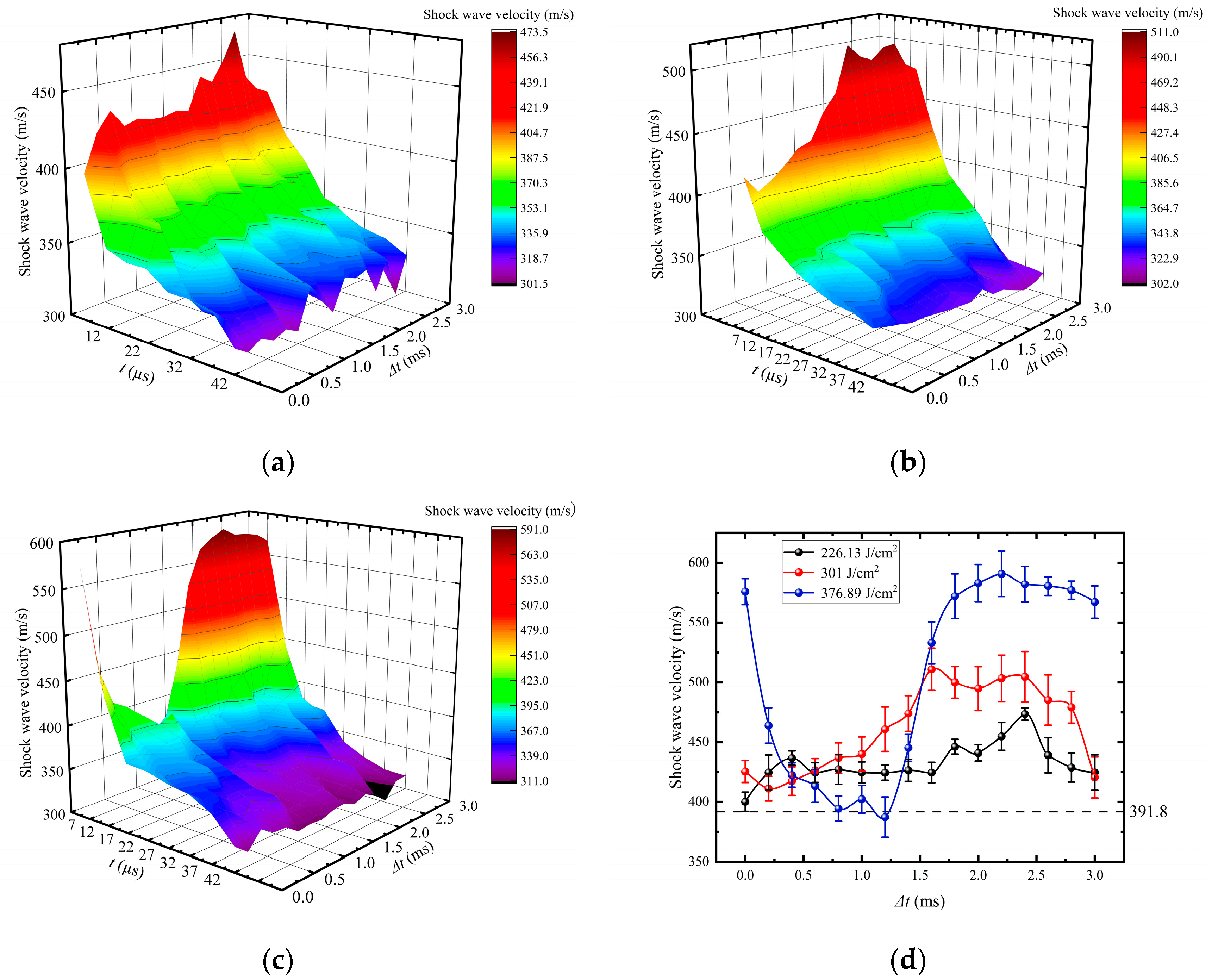
3.1. The Variation Law of Shock Wave Velocity Induced by CPL
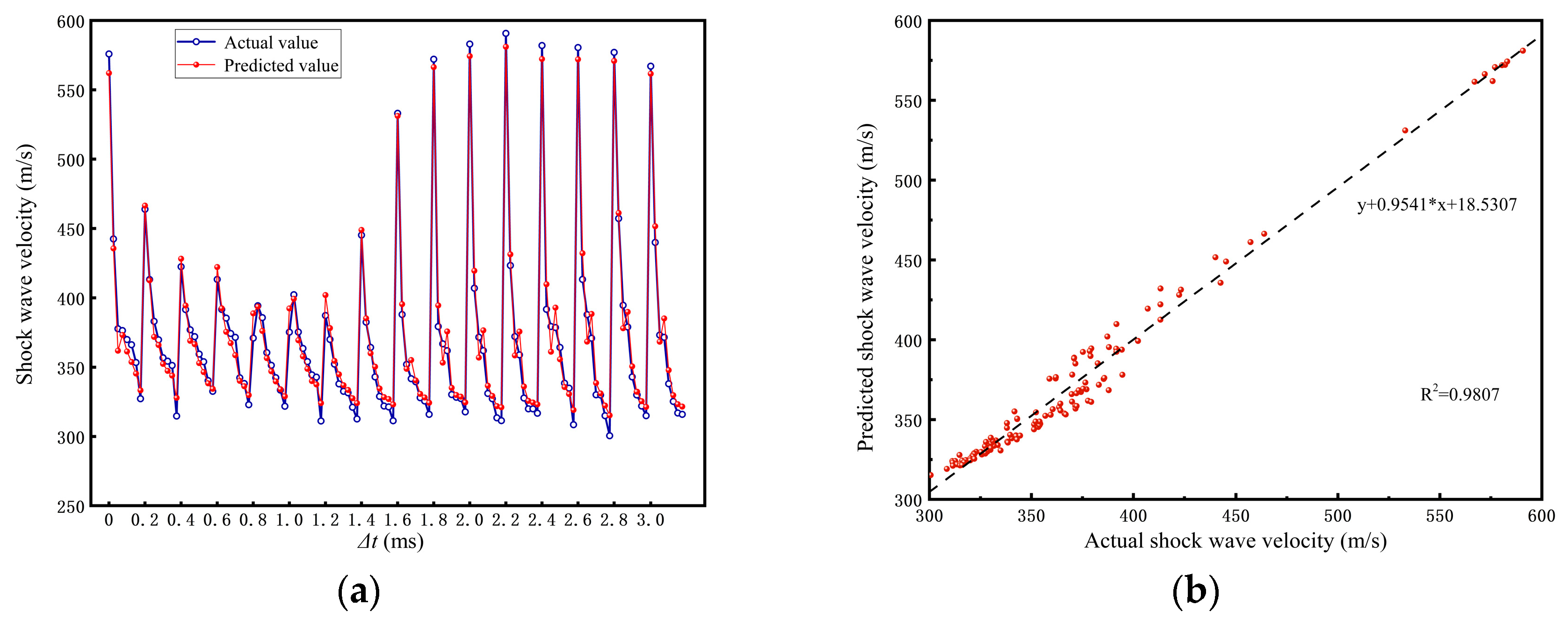
3.2. LSTM Prediction for Shock Wave Velocity
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Eliezer, S.; Martinez-Val, J.M.; Henis, Z.; Nissim, N.; Pinhasi, S.V.; Ravid, A.; Werdiger, M.; Raicher, E. Physics and applications with laser-induced relativistic shock waves. High Power Laser Sci. 2016, 4, 46–59. [Google Scholar] [CrossRef]
- Su, B.; Xu, S.; Wang, H.; Wang, J.; Cao, Y.; Hua, G. Influence of high strain rate on the transient transmission of laser shock waves. Shock Waves 2022, 32, 451–460. [Google Scholar] [CrossRef]
- Nie, X.; Tang, Y.; Zhao, F.; Li, Y.; He, W.; Wei, C.; Wang, X.; Wu, H.; Yan, L. Experimental study on the pressure characteristics of laser-induced shock waves under different energy distribution. Phys. Scr. 2023, 98, 075602. [Google Scholar] [CrossRef]
- Garbaruk, A.V.; Gritskevich, M.S.; Kalmykov, S.G.; Sasin, M.E. Computational simulation of laser plasma emission with shockwave-affected density distribution in the gas-jet target. Technol. Phys. Lett. 2016, 42, 993–996. [Google Scholar] [CrossRef]
- Ukai, T.; Kontis, K.; Yang, L. Flow structure generated by laser-induced blast wave propagation through the boundary layer of a flat plate. Aerosp. Sci. Technol. 2018, 78, 569–573. [Google Scholar] [CrossRef]
- Sakhvadze, G.Z.; Sakhvadze, G.G. Strengthening Mechanisms upon Implantation of Nanoparticles in Materials Using Laser Shock Waves. J. Mach. Manuf. Reliab. 2024, 8, 53. [Google Scholar] [CrossRef]
- Wu, L.; Dai, F.; Chen, X. Effect of Surface Roughness and Compressive Residual Stress on the Fatigue Performance of TC4 Titanium Alloy Subjected to Laser Shock Wave Planishing. Fatigue Fract. Eng. M. 2024, 48, 371–381. [Google Scholar] [CrossRef]
- Liu, H.; Yang, H.; Tong, Z.; Yang, D.; Ge, Y.; Ren, X. Effects of laser shock peening post-treatment on microstructure and corrosion resistance of phosphate conversion coatings. Opt. Laser Technol. 2023, 162, 109289. [Google Scholar] [CrossRef]
- Zhu, D.; He, X.; Zhong, L.; Wang, G.; Wei, G.; Pang, G.; Liao, W. Effect of laser shock peening on tribological properties of 55SiMoVA bearing steel. Opt. Laser Technol. 2025, 181 Pt A, 111704. [Google Scholar] [CrossRef]
- Sakhvadze, G.Z. Application of laser shock waves in additive technology. Russ. Eng. Res. 2023, 7, 43. [Google Scholar] [CrossRef]
- Ouyang, P.; Dong, Z.; Luo, X.; Zhang, S.; Liu, L.; Sun, B.; Zhou, L. Effect of combined treatment of laser shock peening and shot peening on fatigue performance of laser-powder-bed-fusioned GH4169 nickel-based alloy. Opt. Laser Technol. 2025, 182 Pt B, 112141. [Google Scholar] [CrossRef]
- Bae, J.; Byun, H.; Yoon, T.; Carter, C.D.; Do, H. Novel calibration-free seedless velocimetry using laser-induced shockwave. Exp. Therm. Fluid Sci. 2021, 126, 110384. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Dong, H.; Zhang, W.; Jin, G. Simulation and experimental study of the evolution of shock waves during laser paint removal. Jpn. J. Appl. Phys. 2024, 63, 012002. [Google Scholar] [CrossRef]
- Lapostolle, L.; Morin, L.; Derrien, K.; Berthe, L.; Castelnau, O. Modeling and simulation of laser shock waves in elasto-plastic polycrystalline microstructures. J. Mech. Phys. Solids 2023, 176, 105310. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Zhou, Y.; Yuan, B.; Cai, J.; Jin, G. The acceleration mechanism of shock wave induced by millisecond-nanosecond combined-pulse laser on silicon. Plasma Sci. Technol. 2021, 23, 055507. [Google Scholar] [CrossRef]
- Wu, H.; Cao, M.; Liu, F.; Chong, Z.; Zhang, Y. Dynamic modeling of the interfacial bonding strength of cfrp composites detected by laser shockwave. Opt. Laser Technol. 2025, 182 Pt B, 112184. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Li, Y.; Jin, G. The Acceleration Phenomenon of Shock Wave Induced by Nanosecond Laser Irradiating Silicon Assisted by Millisecond Laser. Photonics 2023, 10, 260. [Google Scholar] [CrossRef]
- Radziejewska, J.; Strzelec, M.; Ostrowski, R.; Sarzyński, A. Experimental investigation of shock wave pressure induced by a ns laser pulse under varying confined regimes. Opt. Laser. Eng. 2020, 126, 105913. [Google Scholar] [CrossRef]
- Jiang, H.; Song, H.; Koh, H.; Yoon, T.; Kwon, Y. Shock wave generation in water by nanosecond pulse laser irradiation with 1064 and 2940nm wavelengths. Opt. Laser Technol. 2023, 167, 109670. [Google Scholar] [CrossRef]
- Rehman, Z.U.; Raza, A.; Qayyum, H.; Ullah, S.; Mahmood, S.; Qayyum, A. Characterization of laser-induced shock waves generated during infrared laser ablation of copper by the optical beam deflection method. Appl. Opt. 2022, 61, 29. [Google Scholar] [CrossRef]
- Jiang, H.; Cheng, H.; He, Y.; Liu, L.; Liu, S.; Li, H. Propagation characteristics of nanosecond pulse laser-induced shock wave and the non-contact removal of particle. Appl. Phys. A Mater. Sci. Process. 2021, 127, 241. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, C.; Li, C. Evolution of ns pulsed laser induced shock wave on aluminum surface by numerical simulation. Results Phys. 2021, 22, 103920. [Google Scholar] [CrossRef]
- Jiang, X.; Yu, X.; Deng, X.; Shao, Y.; Peng, P. Investigation on laser-induced shock pressure with condensed matter model and experimental verification. Exp. Tech. 2019, 43, 161–167. [Google Scholar] [CrossRef]
- Pretorius, J.G.; Desai, D.A.; Snedden, G. Effect of Laser Shock Peening on Fatigue Life at Stress Raiser Regions of a High-Speed Micro Gas Turbine Shaft: A Simulation Based Study. Int. J. Eng. Res. Afr. 2019, 4747, 15–27. [Google Scholar] [CrossRef]
- Xiang, Y.F.; Mei, R.L.; Wang, S.P.; Azad, F.; Zhao, L.Z.; Su, S.C. Numerical investigation of the effect of laser shock peening parameters on the residual stress and deformation response of 7075 aluminum alloy. Optik 2021, 243, 167446. [Google Scholar] [CrossRef]
- Wu, J.; Li, Y.; Zhao, J.; Qiao, H.; Lu, Y.; Sun, B.; Hu, X.; Yang, Y. Prediction of residual stress induced by laser shock processing based on artificial neural networks for FGH4095 superalloy. Mater. Lett. 2021, 286, 129269. [Google Scholar] [CrossRef]
- Jose, S.S.S.; Mishra, S.K.; Upadhyay, R.K.; Muthukannan, D. Prediction of irregularities and study of mechanical properties in laser shock peened nickel alloy. Discov. Mater. 2025, 5, 31. [Google Scholar] [CrossRef]
- Wu, J.; Huang, Z.; Qiao, H.; Zhao, Y.; Li, J.; Zhao, J. Artificial neural network approach for mechanical properties prediction of TC4 titanium alloy treated by laser shock processing. Opt. Laser Technol. 2021, 143, 107385. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Li, Y.; Jin, G. Prediction of Shock Wave Velocity Induced by a Combined Millisecond and Nanosecond Laser Based on Convolution Neural Network. Photonics 2023, 10, 1034. [Google Scholar] [CrossRef]



| Sample Number | Ems/J/cm2 | Δt/ms | t/µs |
|---|---|---|---|
| 1–8 | 0 | 0 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 9–16 | 226.13 | 0 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 17–24 | 226.13 | 200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 25–32 | 226.13 | 400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 33–40 | 226.13 | 600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 41–48 | 226.13 | 800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 49–56 | 226.13 | 1000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 57–64 | 226.13 | 1200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 65–72 | 226.13 | 1400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 73–80 | 226.13 | 1600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 81–88 | 226.13 | 1800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 89–96 | 226.13 | 2000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 97–104 | 226.13 | 2200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 105–112 | 226.13 | 2400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 113–120 | 226.13 | 2600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 121–128 | 226.13 | 2800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 129–136 | 226.13 | 3000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 137–144 | 301 | 0 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 145–152 | 301 | 200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 153–160 | 301 | 400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 161–168 | 301 | 600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 169–176 | 301 | 800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 177–184 | 301 | 1000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 185–192 | 301 | 1200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 193–200 | 301 | 1400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 201–208 | 301 | 1600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 209–216 | 301 | 1800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 217–224 | 301 | 2000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 225–232 | 301 | 2200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 233–240 | 301 | 2400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 241–248 | 301 | 2600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 249–256 | 301 | 2800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 257–264 | 301 | 3000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 265–272 | 376.89 | 0 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 273–280 | 376.89 | 200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 281–288 | 376.89 | 400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 289–296 | 376.89 | 600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 297–304 | 376.89 | 800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 305–312 | 376.89 | 1000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 313–320 | 376.89 | 1200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 321–328 | 376.89 | 1400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 329–336 | 376.89 | 1600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 337–344 | 376.89 | 1800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 345–352 | 376.89 | 2000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 353–360 | 376.89 | 2200 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 361–368 | 376.89 | 2400 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 369–376 | 376.89 | 2600 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 377–384 | 376.89 | 2800 | 7, 12, 17, 22, 27, 32, 37, 42 |
| 385–392 | 376.89 | 3000 | 7, 12, 17, 22, 27, 32, 37, 42 |
| Ems/J/cm2 | Δt/ms | Shock Wave Velocity/m/s | Incremental Percentage/% | |
|---|---|---|---|---|
| case 1 | 226.13 | 2.4 | 473.4 | 20.83 |
| case 2 | 301 | 1.6 | 510.86 | 30.39 |
| case 3 | 376.89 | 0 | 575.87 | 46.98 |
| case 4 | 376.89 | 2.2 | 590.7 | 50.77 |
| Model | Training Set | Test Set | ||||||
|---|---|---|---|---|---|---|---|---|
| MAE | RMSE | MBE | R2 | MAE | RMSE | MBE | R2 | |
| Plain LSTM | 9.95 | 14.13 | 0.55 | 0.87 | 23.29 | 32.23 | 17.42 | 0.82 |
| Attention-LSTM | 4.48 | 5.83 | 0.17 | 0.98 | 7.65 | 9.01 | 1.47 | 0.98 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Liang, R.; Liu, J.; Sun, J. Prediction of Shock Wave Velocity Temporal Evolution Induced by Ms-Ns Combined Pulse Laser Based on Attention-LSTM. Photonics 2025, 12, 1040. https://doi.org/10.3390/photonics12101040
Li J, Liang R, Liu J, Sun J. Prediction of Shock Wave Velocity Temporal Evolution Induced by Ms-Ns Combined Pulse Laser Based on Attention-LSTM. Photonics. 2025; 12(10):1040. https://doi.org/10.3390/photonics12101040
Chicago/Turabian StyleLi, Jingyi, Rongfan Liang, Junjie Liu, and Jingdong Sun. 2025. "Prediction of Shock Wave Velocity Temporal Evolution Induced by Ms-Ns Combined Pulse Laser Based on Attention-LSTM" Photonics 12, no. 10: 1040. https://doi.org/10.3390/photonics12101040
APA StyleLi, J., Liang, R., Liu, J., & Sun, J. (2025). Prediction of Shock Wave Velocity Temporal Evolution Induced by Ms-Ns Combined Pulse Laser Based on Attention-LSTM. Photonics, 12(10), 1040. https://doi.org/10.3390/photonics12101040




