DMSR: Dynamic Multipath Secure Routing Against Eavesdropping in Space-Ground Integrated Optical Networks
Abstract
1. Introduction
- (1)
- Blackhole Attack
- (2)
- DoS/DDoS
- (3)
- Communication Eavesdropping
2. System Model
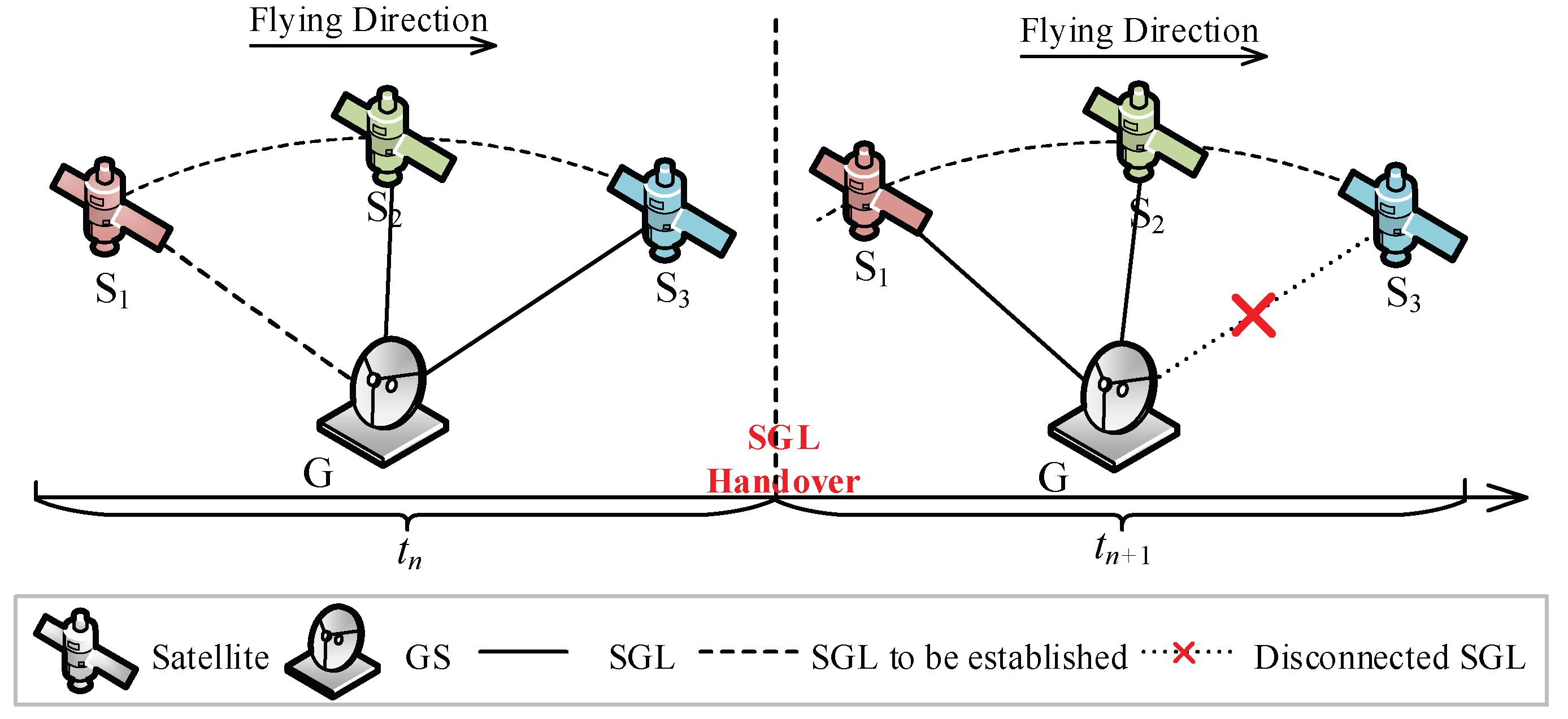
2.1. Network Architecture
2.2. Network Model
2.3. Service Model
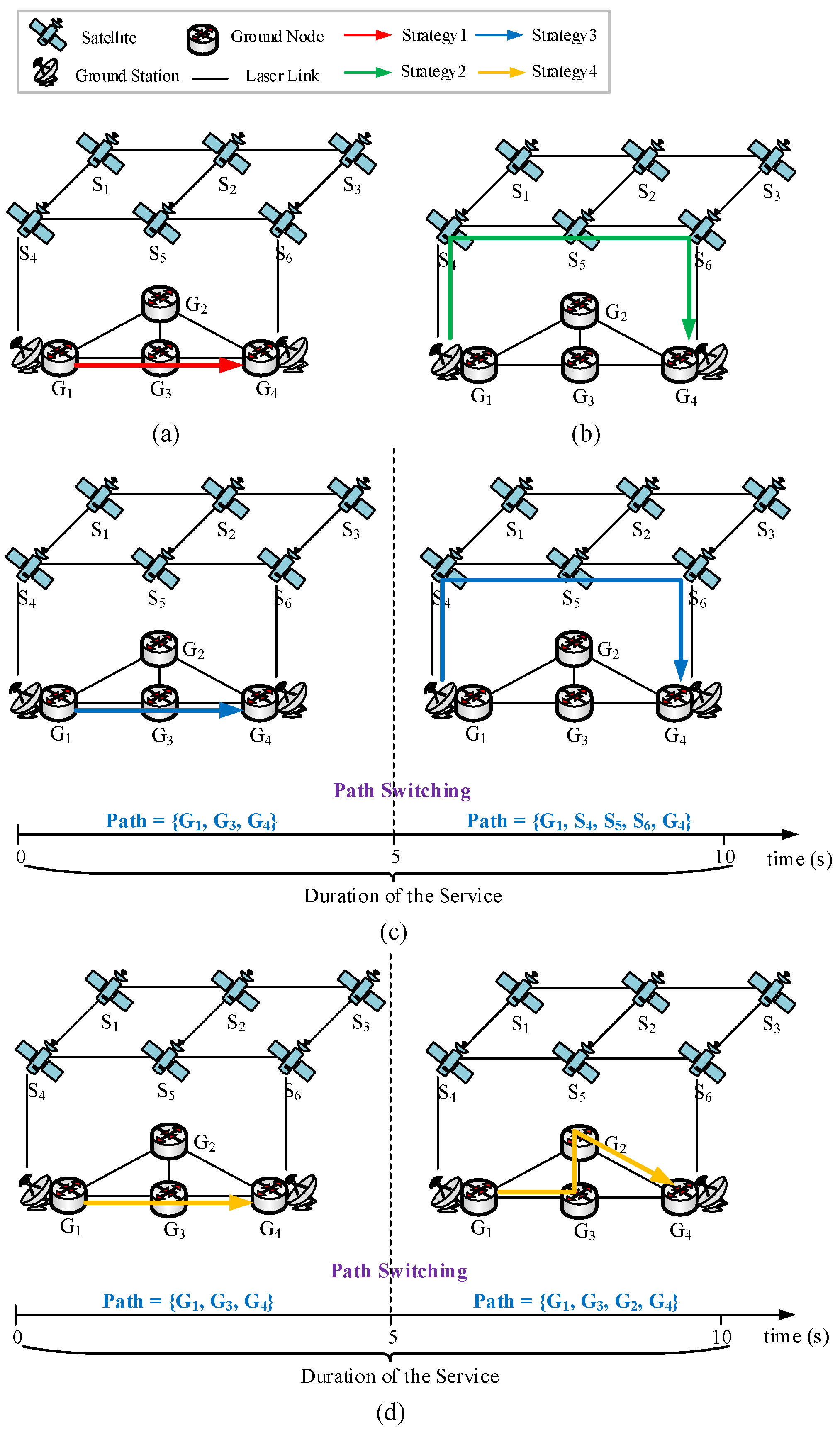
3. The DMSR Scheme
3.1. Service Eavesdropping Ratio
3.2. DMSR
4. Heuristic Algorithms
| Algorithm 1: Dynamic Multipath Secure Routing (DMSR) |
| Input: TON topology , SGION topology , service request , the number of service path switches , the number of the shortest paths ; |
| Output: the set of routing paths , the set of path switching instants ; |
| 1: Initialize: , , ; |
| 2: Calculate the path switching time interval ; |
| 3: Call Algorithm 2 to obtain the routing path at time slot in the TON; |
| 4: if then |
| 5: Add and to and , respectively; |
| 6: ; |
| 7: else |
| 8: Call Algorithm 3 to obtain the routing path and next path switching instant in the SGION; |
| 9: if then |
| 10: Add and to and , respectively; |
| 11: ; |
| 12: else |
| 13: Block service ; |
| 14: end if |
| 15: end if |
| 16: while do |
| 17: Call Algorithm 2 to obtain the routing path on the TON; |
| 18: if then |
| 19: Add and to and , respectively; |
| 20: ; |
| 21: else |
| 22: Call Algorithm 3 to obtain the routing path and next path switching instant in the SGION; |
| 23: if then |
| 24: Add and to and , respectively; |
| 25: ; |
| 26: else |
| 27: Block service ; |
| 28: end if |
| 29: end if |
| 30: end while |
| 31: return , ; |
| Algorithm 2: Routing Path Determination in the TON |
| Input: time slot , TON topology at time slot , service request , path switching time interval , the number of the shortest paths ; |
| Output: routing path at time slot ; |
| 1: Initialize: ; |
| 2: for to do |
| 3: for each link do |
| 4: if then |
| 5: Remove link from ; |
| 6: end if |
| 7: end for |
| 8: end for |
| 9: Use the KSP algorithm to search the shortest paths between and in graph ; |
| 10: for each path do |
| 11: Calculate the SER of service , assuming its remaining data is fully transmitted through path ; |
| 12: end for |
| 13: Obtain the path with the minimum SER in as ; |
| 14: return ; |
| Algorithm 3: Routing Path Determination in the SGION |
| Input: time slot , SGION topology at time slot , service request , path switching time interval , the number of the shortest paths ; |
| Output: routing path at time slot , next path switching instant ; |
| 1: Initialize: , , ; |
| 2: for to do |
| 3: for each link do |
| 4: if or then |
| 5: Remove link from ; |
| 6: end if |
| 7: end for |
| 8: if there is no path between and in graph then |
| 9: ; |
| 10: ; |
| 11: break; |
| 12: else |
| 13: ; |
| 14: end if |
| 15: end for |
| 16: Use the KSP algorithm to search the shortest paths between and in graph ; |
| 17: for each path do |
| 18: Calculate the SER of service , assuming its remaining data is fully transmitted through path ; |
| 19: end for |
| 20: Obtain the path with the minimum SER in as ; |
| 21: return , ; |
5. Performance Evaluation
5.1. Simulation Setup
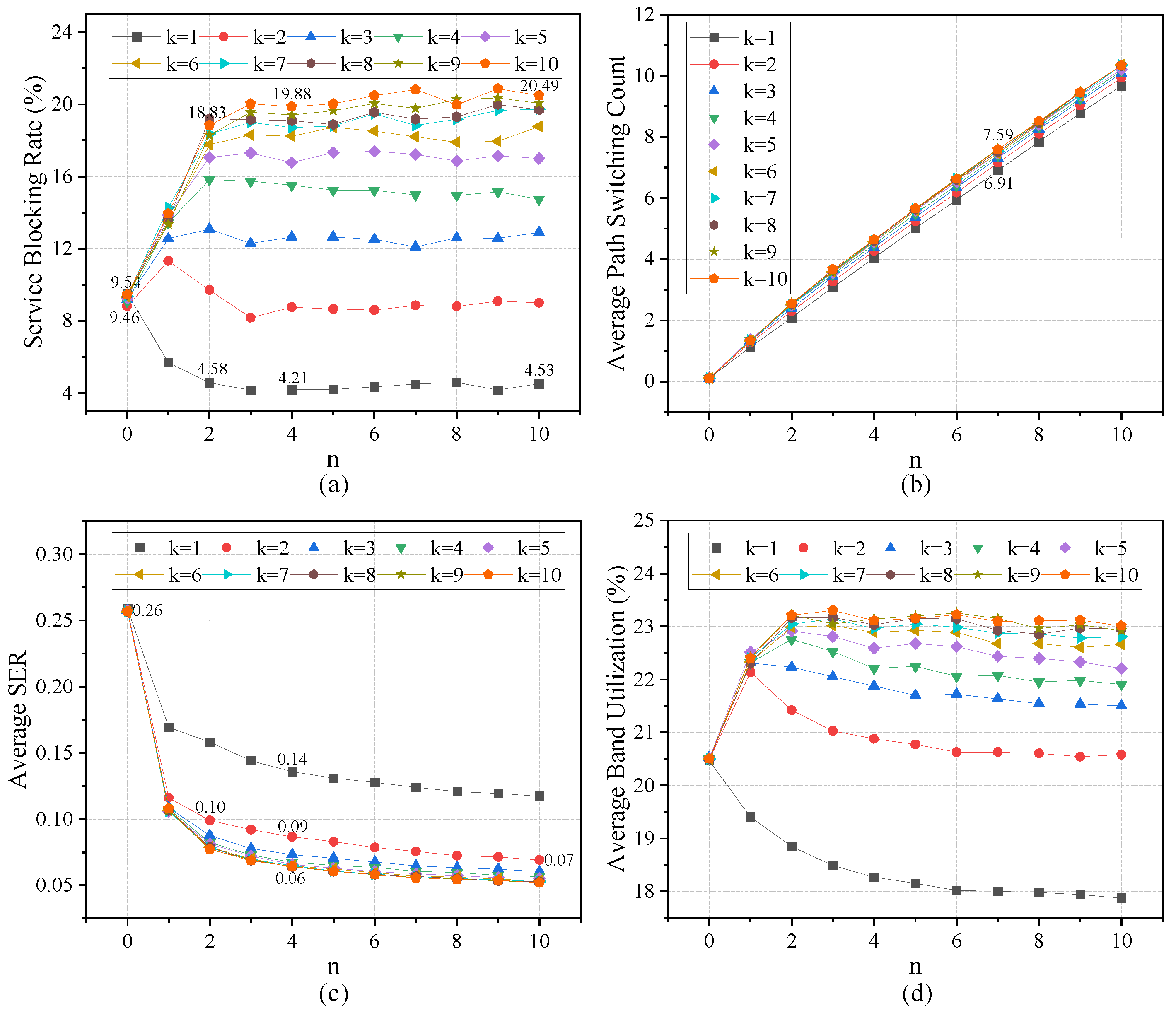
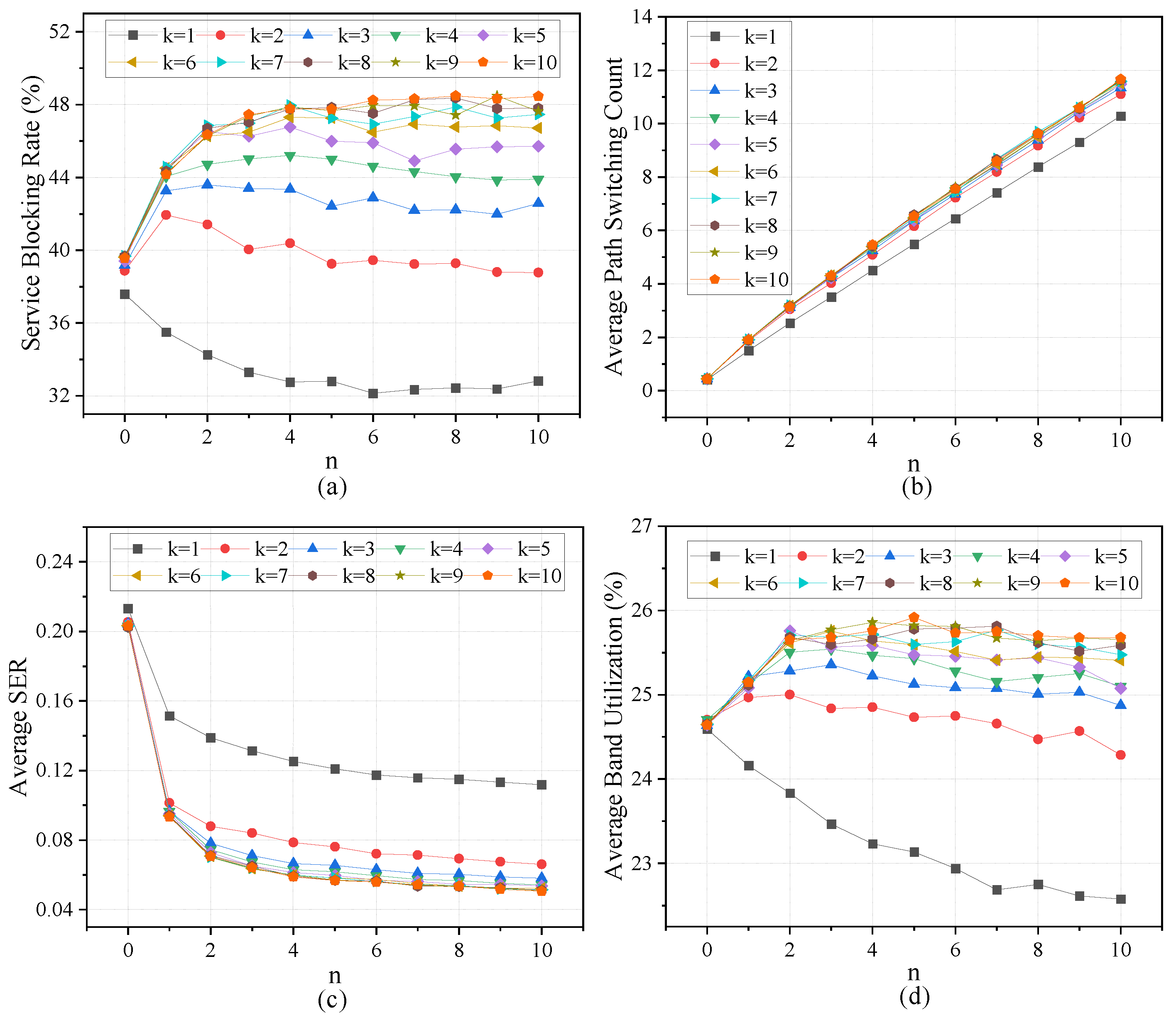
5.2. Influence of System Parameters
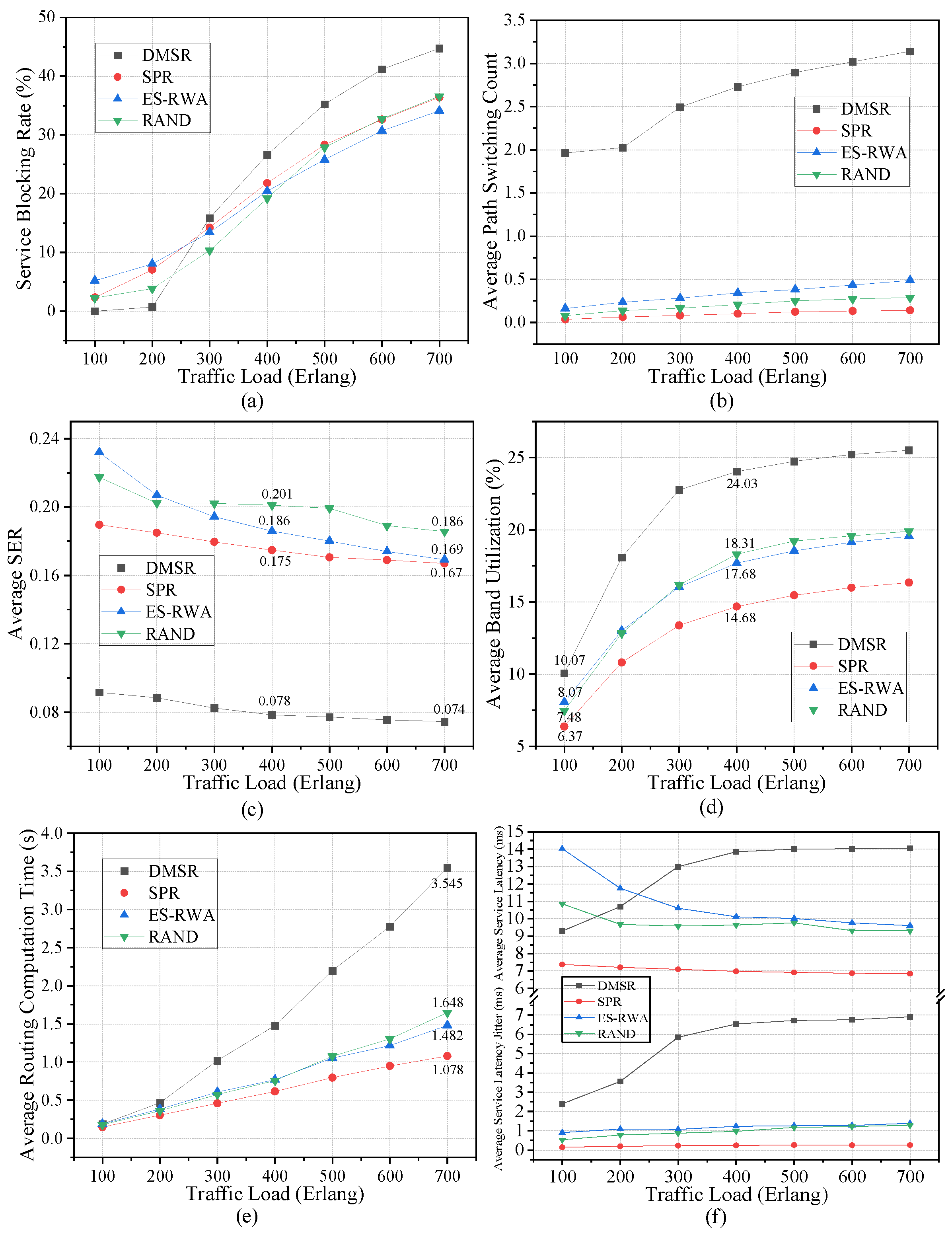
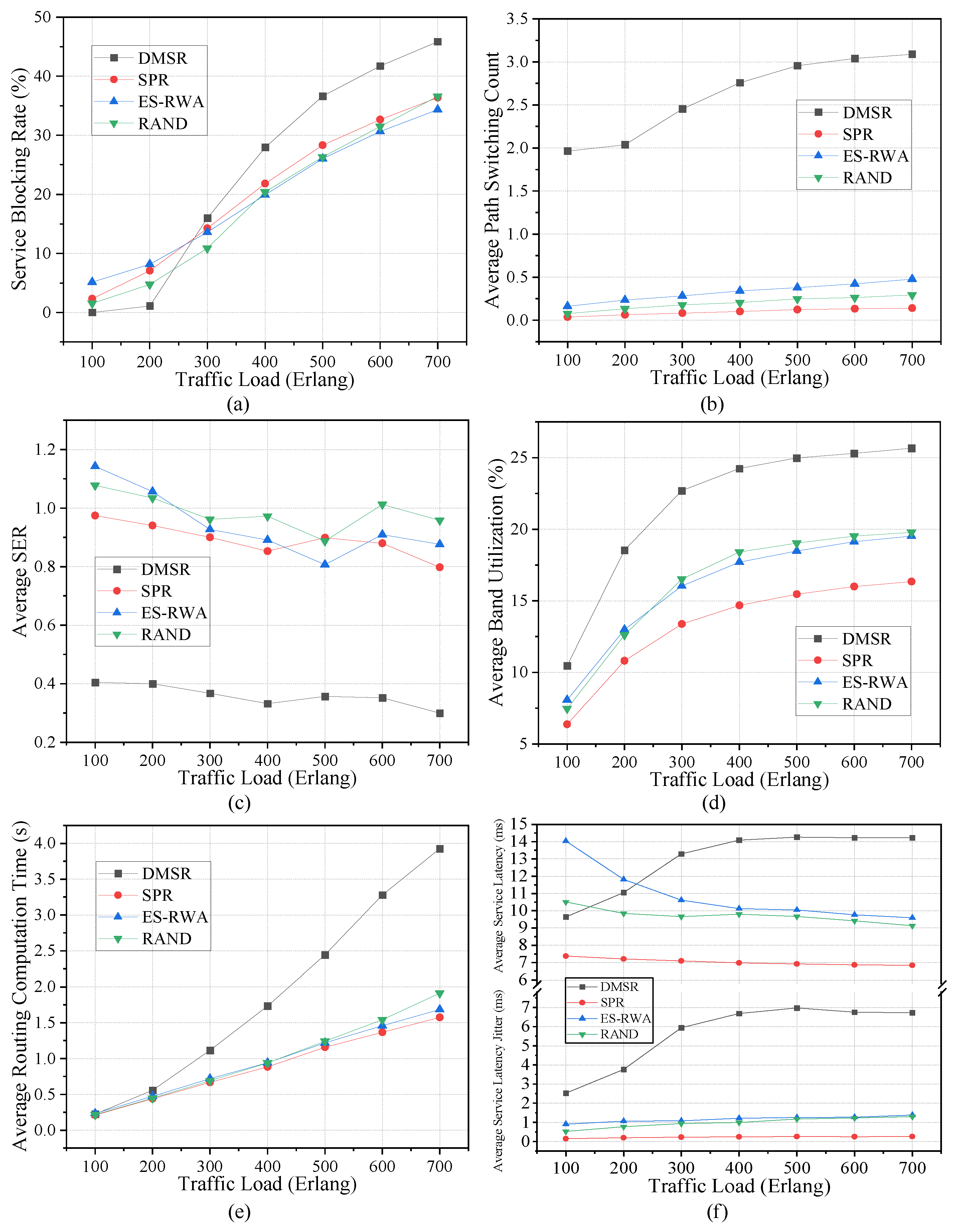
5.3. Performance Comparison
6. Discussion
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| LEO | Low earth orbit |
| QKD | Quantum key distribution |
| FCS | Frame check sequence |
| QoS | Quality of service |
| SR | Storage and relaying |
| SRT | Storage relay topology |
| GQKD | Global quantum key distribution |
| SMS | Short message service |
| SGION | Space-ground integrated optical network |
| DSMR | dynamic multipath secure routing |
| SON | Satellite optical network |
| TON | Terrestrial optical network |
| GS | Ground station |
| IoT | Internet of Things |
| SER | Service eavesdropping ratio |
| SNR | Signal-to-noise ratio |
References
- Li, J.; Li, X.; Li, C. A Review of LEO Satellite Network Security Research. In Proceedings of the 2023 2nd International Conference on Data Analytics, Computing and Artificial Intelligence (ICDACAI), Zakopane, Poland, 17–19 October 2023. [Google Scholar]
- Darwish, T.; Kurt, G.K. LEO Satellites in 5G and Beyond Networks: A Review from a Standardization Perspective. IEEE Access 2022, 10, 35040–35060. [Google Scholar] [CrossRef]
- McDowell, J.C. The Low Earth Orbit Satellite Population and Impacts of the SpaceX Starlink Constellation. Astrophys. J. Lett. 2020, 892, 36. [Google Scholar] [CrossRef]
- Radtke, J.; Kebschull, C. Interactions of the space debris environment with mega constellations—Using the example of the OneWeb constellation. Acta Astronaut. 2017, 131, 55–68. [Google Scholar] [CrossRef]
- Osoro, O.B.; Oughton, E.J. A Techno-Economic Framework for Satellite Networks Applied to Low Earth Orbit Constellations: Assessing Starlink, OneWeb and Kuiper. IEEE Access 2021, 9, 141611–141625. [Google Scholar] [CrossRef]
- Zhong, P.; Tan, T. Enlightenment for China’s LEO Internet Satellite Industry from Typical Development Model of European Commercial Satellite. In Proceedings of the 2022 International Symposium on Networks, Computers and Communications (ISNCC), Shenzhen, China, 19–21 July 2022. [Google Scholar]
- Satellites: Taking Flight. The Ecosystem, Opportunities and Hurdles. Available online: https://www.eet-china.com/mp/a384787.html (accessed on 25 February 2025).
- Wazid, M.; Katal, A. Detection and prevention mechanism for Blackhole attack in Wireless Sensor Network. In Proceedings of the 2013 International Conference on Communication and Signal Processing, Melmaruvathur, India, 3–5 April 2013. [Google Scholar]
- Yang, X.; Ma, T.; Shi, Y. Typical DoS/DDoS Threats under IPv6. In Proceedings of the 2007 International Multi-Conference on Computing in the Global Information Technology (ICCGI’07), Guadeloupe, French Caribbean, 4–9 March 2007. [Google Scholar]
- Zhong, X.; Fan, C.; Zhou, S. Eavesdropping area for evaluating the security of wireless communications. China Commun. 2022, 19, 145–157. [Google Scholar] [CrossRef]
- Masdari, M.; Ahmadzadeh, S. A survey and taxonomy of the authentication schemes in telecare medicine information systems. J. Net. Comput. Appl. 2017, 87, 1–19. [Google Scholar] [CrossRef]
- Yahia, O.B.; Erdogan, E. Optical Satellite Eavesdropping. IEEE Trans. Veh. Technol. 2022, 71, 10126–10131. [Google Scholar] [CrossRef]
- Jung, D.H.; Ryu, J.G.; Choi, J. When Satellites Work as Eavesdroppers. IEEE Trans. Inf. Forensics Secur. 2022, 17, 2784–2799. [Google Scholar] [CrossRef]
- Miller, A. Micius, the world’s first quantum communication satellite, was hackable. In Proceedings of the 2025 International Conference on Quantum Communications, Networking, and Computing (QCNC), Nara, Japan, 31 March–2 April 2025. [Google Scholar]
- Pavur, J.; Moser, D. Secrets in the sky: On privacy and infrastructure security in DVB-S satellite broadband. In Proceedings of the 12th Conference on Security and Privacy in Wireless and Mobile Networks, New York, NY, USA, 15–17 May 2019. [Google Scholar]
- Pavur, J.; Moser, D. A Tale of Sea and Sky on the Security of Maritime VSAT Communications. In Proceedings of the 2020 IEEE Symposium on Security and Privacy (SP), San Francisco, CA, USA, 18–21 May 2020. [Google Scholar]
- Yue, P.; An, J.; Zhang, J.; Pan, G.; Wang, S.; Xiao, P.; Hanzo, L. On the Security of LEO Satellite Communication Systems: Vulnerabilities, Countermeasures, and Future Trends. arXiv 2022, arXiv:2201.03063. [Google Scholar]
- Yue, P. Low Earth Orbit Satellite Security and Reliability: Issues, Solutions, and the Road Ahead. IEEE Commun. Surv. Tutor. 2023, 25, 1604–1652. [Google Scholar] [CrossRef]
- Li, H.; Shi, D. Secure routing for LEO satellite network survivability. Comput. Netw. 2022, 211, 109011. [Google Scholar] [CrossRef]
- Yu, Z.; Zhou, H.; Wu, Z. A trust-based secure routing protocol for multi-layered satellite networks. In Proceedings of the 2012 IEEE International Conference on Information Science and Technology, Wuhan, China, 23–25 March 2012. [Google Scholar]
- He, X. Routing and secret key assignment for secure multicast services in quantum satellite networks. J. Opt. Commun. Netw. 2022, 14, 190–203. [Google Scholar] [CrossRef]
- Jiang, C.; Wang, X. Security in space information networks. IEEE Commun. Mag. 2015, 53, 82–88. [Google Scholar] [CrossRef]
- Schraml, M.G.; Schwarz, R.T.; Knopp, A. Multiuser MIMO Concept for Physical Layer Security in Multibeam Satellite Systems. IEEE Trans. Inf. Forensics Secur. 2020, 16, 1670–1680. [Google Scholar] [CrossRef]
- Zheng, G.; Arapoglou, P.D.; Ottersten, B. Physical layer security in multibeam satellite systems. IEEE Trans. Wireless Commun. 2012, 11, 852–863. [Google Scholar] [CrossRef]
- Li, B.; Fei, Z. Physical-Layer Security in Space Information Networks: A Survey. IEEE Internet Things J. 2020, 7, 33–52. [Google Scholar] [CrossRef]
- An, K.; Lin, M.; Ouyang, J. Secure Transmission in Cognitive Satellite Terrestrial Networks. IEEE J. Sel. Areas Commun. 2016, 34, 3025–3037. [Google Scholar] [CrossRef]
- Ekici, E.; Akyildiz, I.F.; Bender, M.D. A distributed routing algorithm for datagram traffic in LEO satellite networks. IEEE/ACM Trans. Netw. 2001, 9, 137–147. [Google Scholar] [CrossRef]
- Liu, J.; Du, H. Satellite routing in space-air-ground integrated IoT networks. In Proceedings of the 2021 International Wireless Communications and Mobile Computing (IWCMC), Harbin, China, 28 June–2 July 2021. [Google Scholar]
- Ding, X.; Zhang, Z.; Liu, D. Low-delay Secure Handover for Space-air-ground Integrated Networks. In Proceedings of the 2020 IEEE 31st Annual International Symposium on Personal, Indoor and Mobile Radio Communications, London, UK, 31 August–3 September 2020. [Google Scholar]
- Bai, W.; Yang, H.; Yu, A.; Xiao, H.; He, L.; Feng, L.; Zhang, J. Eavesdropping-aware routing and spectrum allocation based on multi-flow virtual concatenation for confidential information service in elastic optical networks. Opt. Fiber Technol. 2018, 40, 18–27. [Google Scholar] [CrossRef]
- Fratty, R.; Saar, Y.; Kumar, R.; Arnon, S. Random routing algorithm for enhancing the cybersecurity of LEO satellite networks. Electronics 2023, 12, 518. [Google Scholar] [CrossRef]



| SON (Iridium) | |
|---|---|
| Number of orbital planes | 6 |
| Number of satellites per orbital plane | 11 |
| Orbit altitude | 780 km |
| Orbit inclination | 86.4° |
| Phase factor | 0 |
| Minimum elevation angle | 8.2° |
| ISLL capacity | 8 × 12.5 Gbps |
| TON (NSFNET) | |
| Number of nodes | 14 |
| Number of fiber links | 21 |
| Fiber link capacity | 16 × 12.5 Gbps |
| SGL capacity | 4 × 12.5 Gbps |
| Service requests | |
| Source\Destination | Ground nodes |
| Arrival rate | 1/s |
| Service rate | 1/[100, 700] |
| Other parameters | |
| Link eavesdropping probability | 0.1/[0, 1] |
| Simulation period | 1000 s |
| Time slot length | 1 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, G.; Wang, X. DMSR: Dynamic Multipath Secure Routing Against Eavesdropping in Space-Ground Integrated Optical Networks. Photonics 2025, 12, 1039. https://doi.org/10.3390/photonics12101039
Wang G, Wang X. DMSR: Dynamic Multipath Secure Routing Against Eavesdropping in Space-Ground Integrated Optical Networks. Photonics. 2025; 12(10):1039. https://doi.org/10.3390/photonics12101039
Chicago/Turabian StyleWang, Guan, and Xingmei Wang. 2025. "DMSR: Dynamic Multipath Secure Routing Against Eavesdropping in Space-Ground Integrated Optical Networks" Photonics 12, no. 10: 1039. https://doi.org/10.3390/photonics12101039
APA StyleWang, G., & Wang, X. (2025). DMSR: Dynamic Multipath Secure Routing Against Eavesdropping in Space-Ground Integrated Optical Networks. Photonics, 12(10), 1039. https://doi.org/10.3390/photonics12101039




