Design of Hollow-Core Anti-Resonant Fibers Supporting Few Weakly Coupled Polarization-Maintaining Modes
Abstract
1. Introduction
2. Fiber Structure and Design Method
3. Optimization of the Nested Semi-Tube HC-ARFs
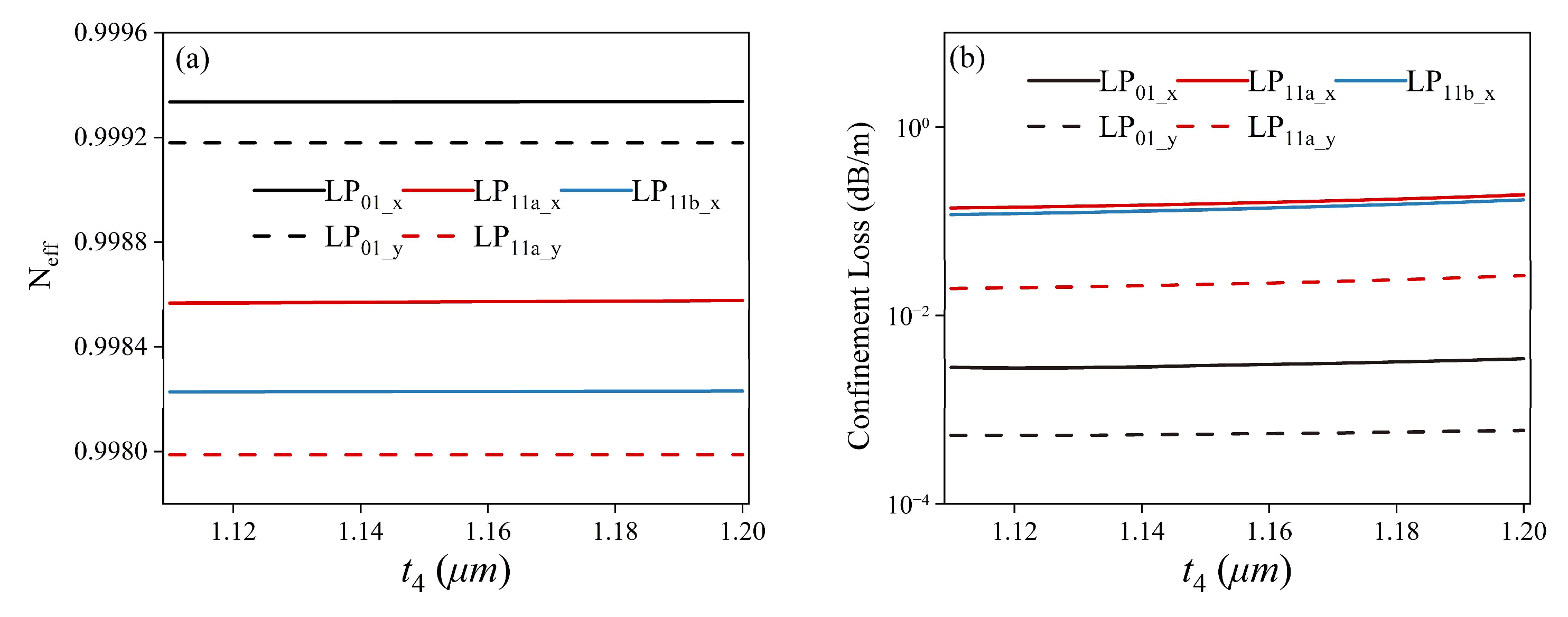
3.1. Effect of the Thickness of the Silicon Film, t3
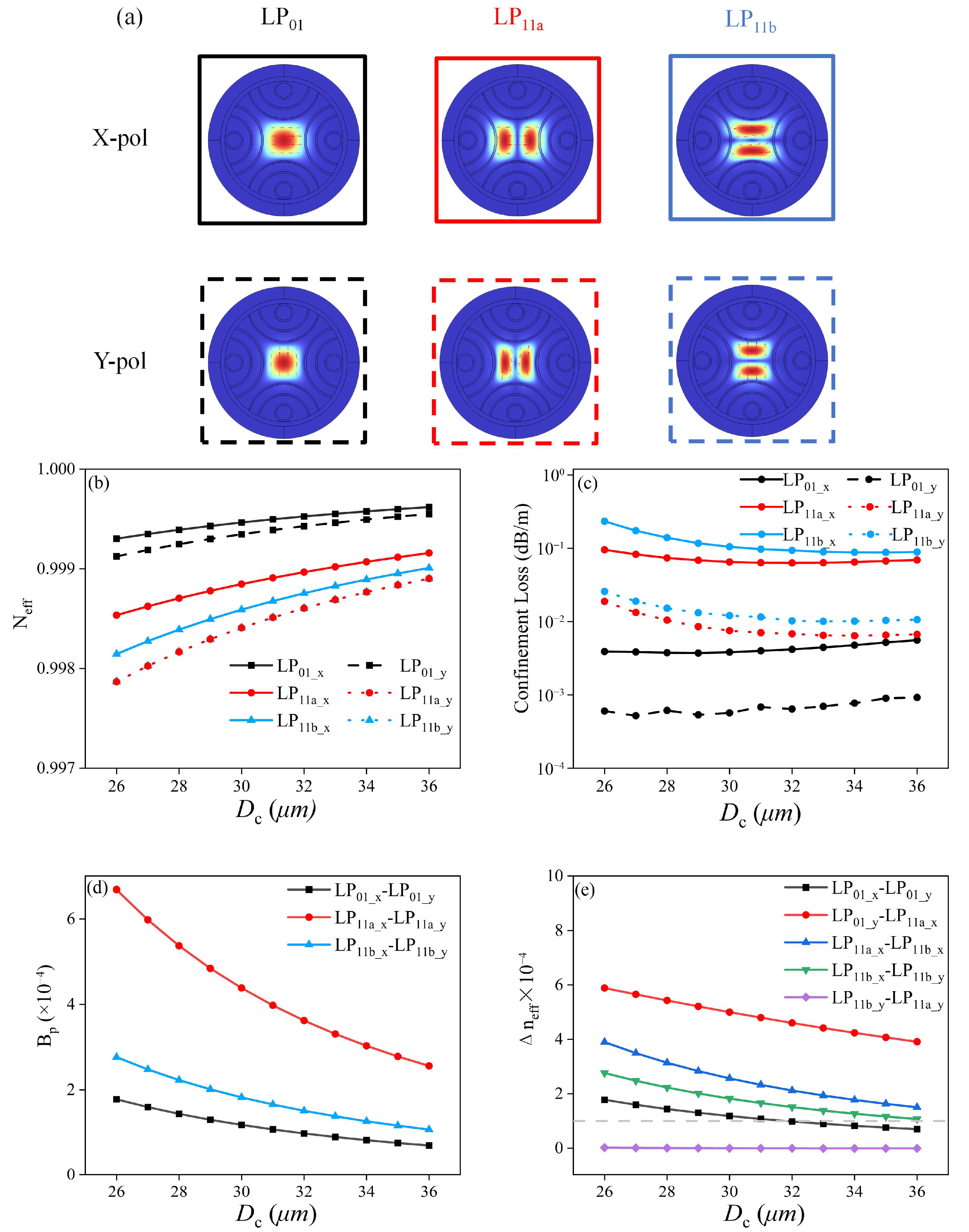
3.2. Effect of the Diameter of the Fiber Core, Dc
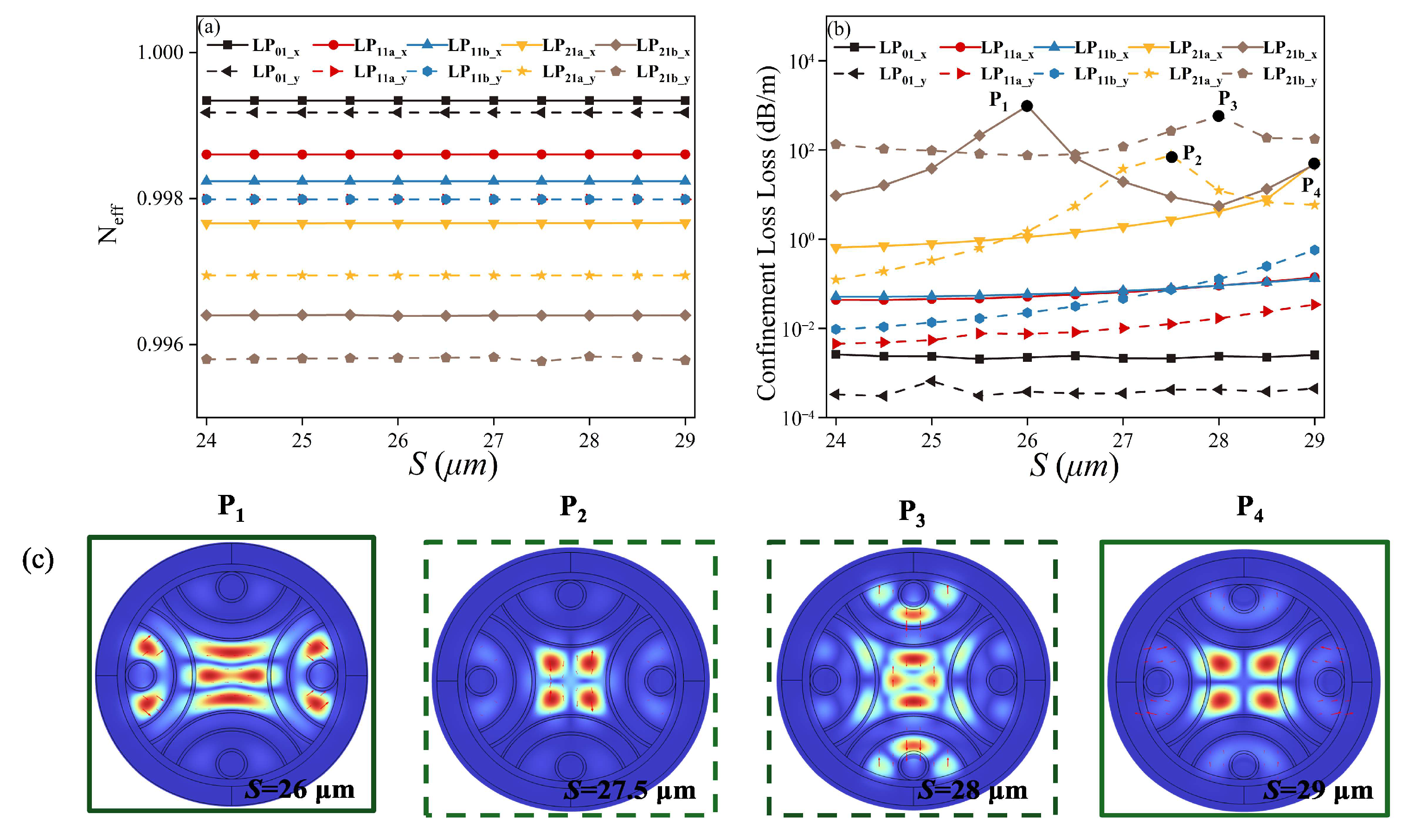
3.3. Effect of the Distance Between the First Layer of the Semi-Tube and the Thick Silica Wall, S
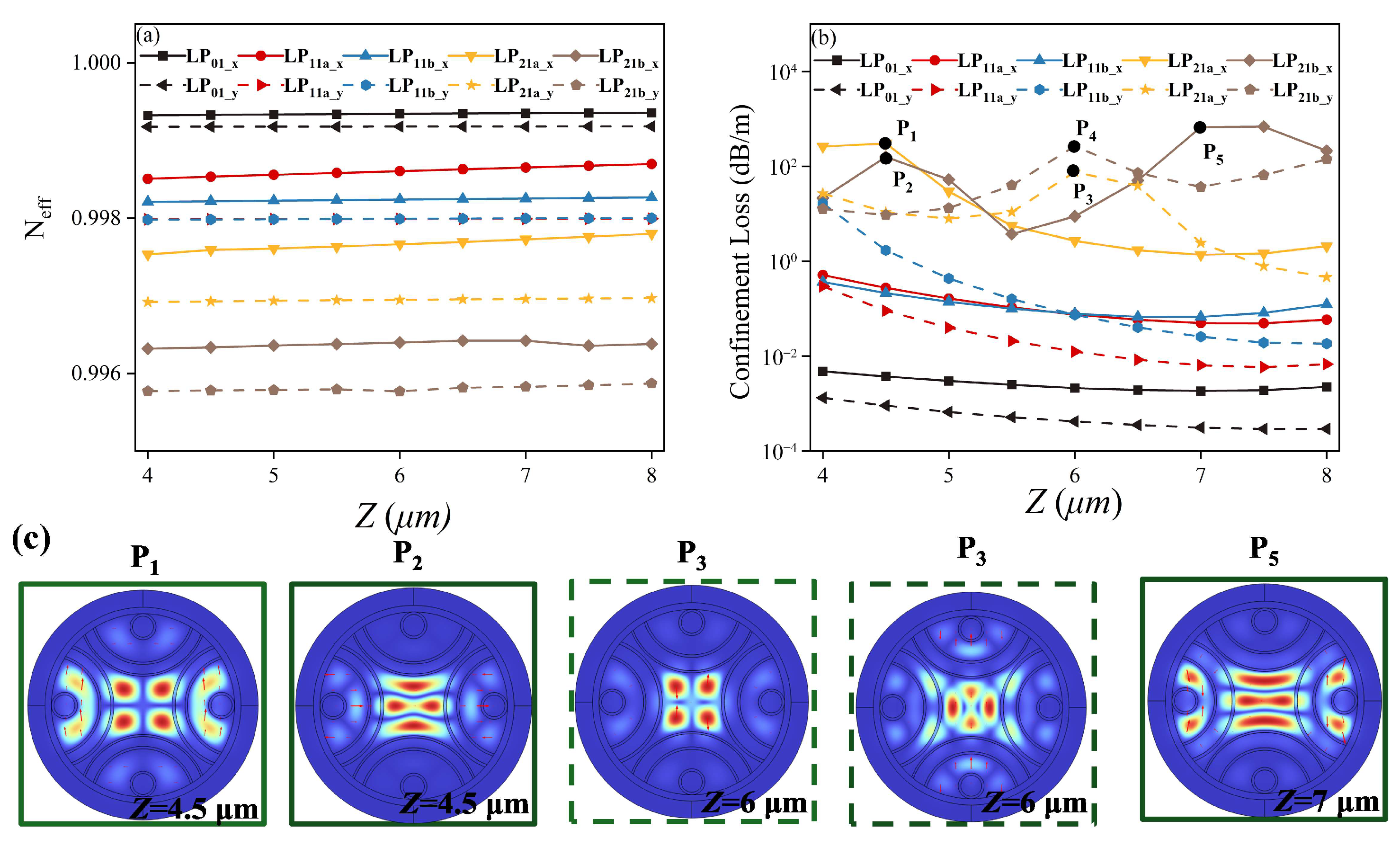
3.4. Effect of Distance Between the Two Semi-Tube Layers, Zi
4. Transmission Characteristics of the Nested Semi-Tube HC-ARFs
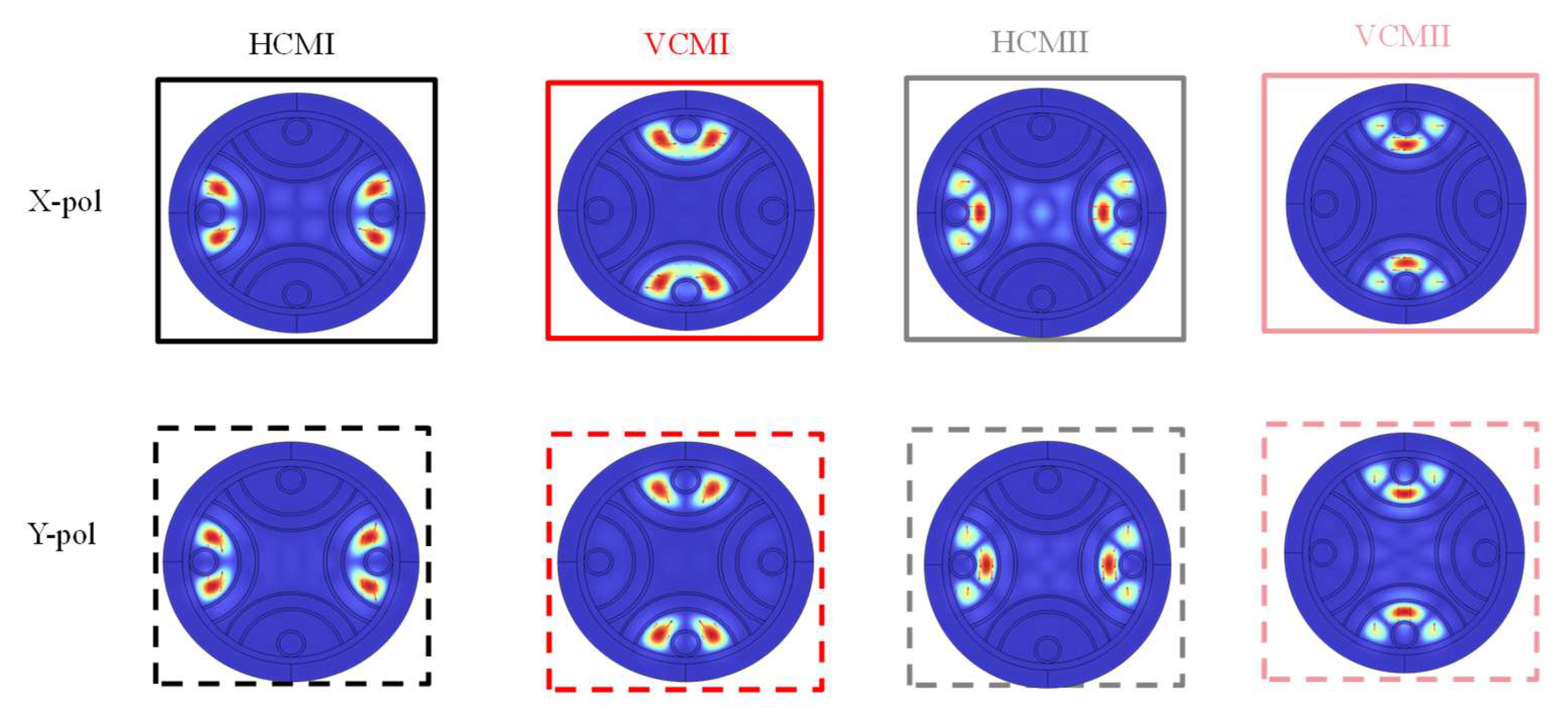
4.1. Few-Mode Division Performances
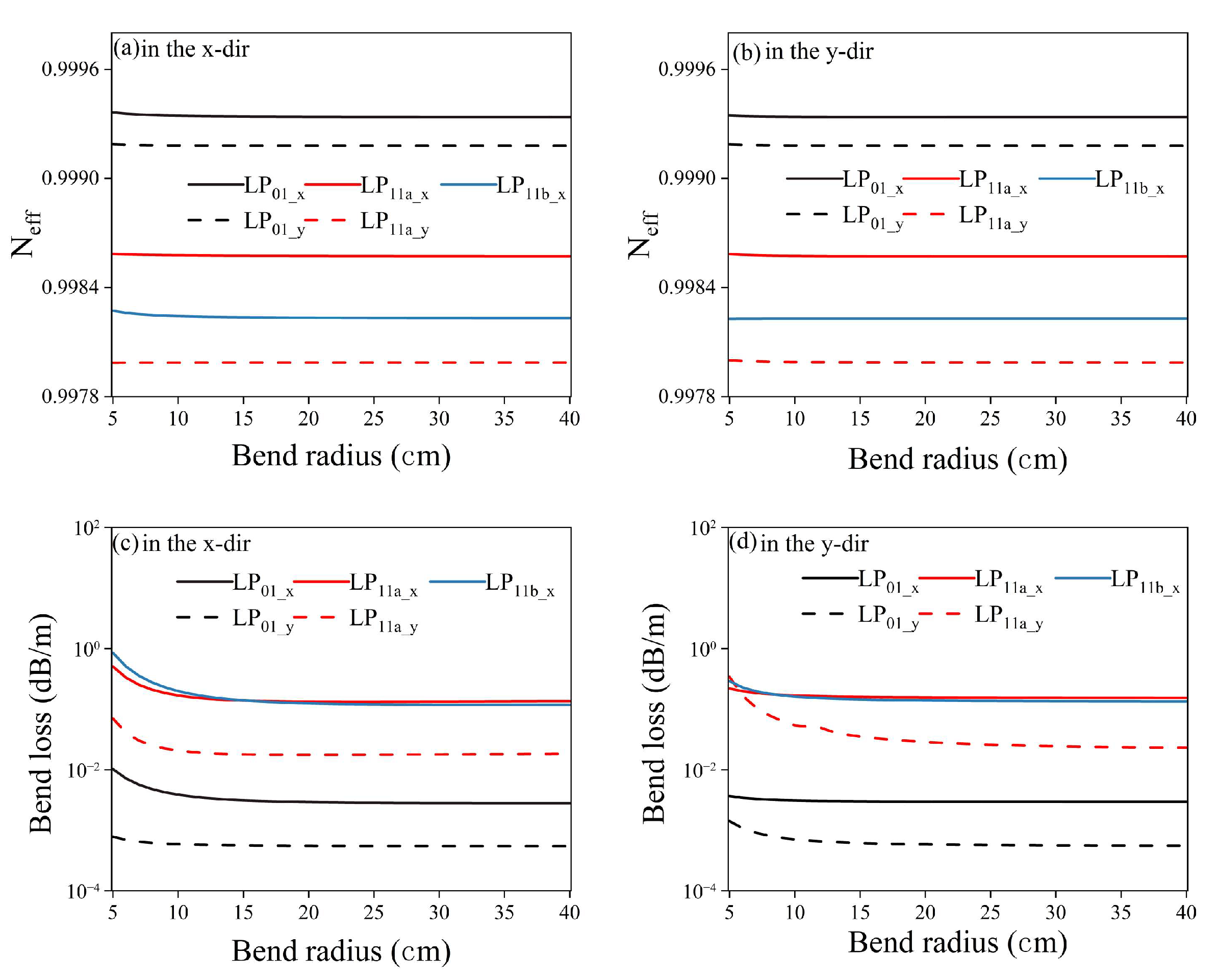
4.2. Bending Performances
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Debord, B.; Amsanpally, A.; Chafer, M.; Baz, A.; Maurel, M.; Blondy, J.M.; Hugonnot, E.; Scol, F.; Vincetti, L.; Gérôme, F.; et al. Ultralow transmission loss in inhibited-coupling guiding hollow fibers. Optica 2017, 4, 209–217. [Google Scholar] [CrossRef]
- Gao, S.F.; Wang, Y.Y.; Ding, W.; Jiang, D.-L.; Gu, S.; Zhang, X.; Wang, P. Hollow-core conjoined-tube negative-curvature fiber with ultralow loss. Nat. Commun. 2018, 9, 2828. [Google Scholar] [CrossRef]
- Zhu, Y.H.; Li, W.; Gao, F.Y.; Xu, X.; Song, N. Small-core hollow-core nested antiresonant nodeless fiber with simi-circular tubes. Opt. Express 2022, 30, 20373–20388. [Google Scholar] [CrossRef]
- Liu, Z.X.; Karanov, B.; Galdino, L.; Petrovich, M.N.; Richardson, D.J.; Poletti, F.; Slavik, R.; Bayvel, P.; Hayes, J.R.; Lavery, D.; et al. Nonlinearity-free coherent transmission in hollow-core antirenant fiber. J. Light. Technol. 2019, 37, 909–916. [Google Scholar] [CrossRef]
- Mukasa, K.; Takagi, T. Hollow core fiber cable technologies. Opt. Fiber Technol. 2023, 80, 103447. [Google Scholar] [CrossRef]
- Mesegure, A.C.; Bissessur, H.; Antona, J.C. Potential of hollow-core fibers for submarine systems. Opt. Fiber Technol. 2024, 84, 103750. [Google Scholar] [CrossRef]
- Hong, Y.; Bradley, D.; Taengnoi, N.; Bottrill, K.R.H.; Hayes, J.R.; Jasion, G.T.; Poletti, F.; Petropoulos, P.; Richardson, D.J. Hollow-core NANF for high-speed short-reach transmission in the S+C+L-bands. J. Light. Technol. 2021, 39, 6167–6174. [Google Scholar] [CrossRef]
- Zhu, X.Y.; Wu, D.K.; Wang, Y.Z.; Yu, F.; Li, Q.; Qi, Y.; Knight, J.; Chen, S.; Hu, L. Delivery of CW laser power up to 300 watts at 1080 nm by an uncooled low-loss antiresonant hollow-core fiber. Opt. Express 2021, 29, 1492–1501. [Google Scholar] [CrossRef]
- Cooper, M.A.; Wahlen, J.; Yerolatsitis, S.; Cruz-Delgado, D.; Parra, D.; Tanner, B.; Ahmadi, P.; Jones, O.; Habib, S.; Divliansky, I.; et al. 2.2 kW single-mode narrow-linewidth laser delivery through a hollow-core fiber. Optica 2023, 10, 1253–1259. [Google Scholar] [CrossRef]
- Liu, S.; Dong, X.L.; Cao, H.; Lv, J.; Zhao, L.; Xia, Y.; Wang, Y.; Lv, Z. Mid-infrared photothermal spectroscopy for breath Nitric Oxide testing with an anti-resonant fiber. Opt. Laser Technol. 2022, 152, 108158. [Google Scholar] [CrossRef]
- Hasanuzzaman, G.K.M.; Iezekiel, S.; Markos, C.; Habib, S. Hollow-core fiber with nested anti-resonant tubes for low-loss THz guidance. Opt. Commun. 2018, 426, 477–482. [Google Scholar] [CrossRef]
- Adamu, A.I.; Wang, Y.Z.; Correa, R.A.; Bang, O.; Markos, C. Low-loss micro-machining of anti-resonant hollow-core fiber with focused ion beam for optofluidic application. Opt. Mater. Express 2021, 11, 338–344. [Google Scholar] [CrossRef]
- Wang, Z.; Tu, J.J.; Liu, Z.Y.; Yu, C.; Lu, C. Design of Weakly Coupled Two-Mode Hollow-Core Antiresonant Fiber with Low Loss. J. Light. Technol. 2020, 38, 864–874. [Google Scholar] [CrossRef]
- Mahfuz, M.A.; Habib, M.S. Enhanced Inhibited Mode-Coupling: Multi-Mode Hollow-Core Anti-Resonant Fiber Designs. IEEE J. Sel. Top. Quantum Electron. 2024, 30, 1–9. [Google Scholar] [CrossRef]
- Zhao, J.J.; Tang, M.; Oh, K.; Feng, Z.; Zhao, C.; Liao, R.; Fu, S.; Shum, P.P.; Liu, D. Polarization-maintaining few mode fiber composed of a central circular-hole and an elliptical-ring core. Photonics Res. 2017, 5, 261–266. [Google Scholar] [CrossRef]
- Xiao, H.; Li, H.S.; Jian, S.S. Hole-assisted polarization-maintaining few-mode fiber. Opt. Laser Technol. 2018, 107, 162–168. [Google Scholar] [CrossRef]
- Corsi, A.; Chang, J.H.; Rusch, L.A.; LaRochelle, S. Design of Highly Elliptical Core Ten-Mode Fiber for Space Division Multiplexing With 2 × 2 MIMO. IEEE Photonics J. 2019, 11, 1–10. [Google Scholar] [CrossRef]
- Xie, Y.H.; Pei, L.; Zheng, J.J.; Zhao, Q.; Ning, T.; Li, J. Design of steering wheel-type ring depressed-core 10-mode fiber with fully improved mode spacing. Opt. Express 2021, 29, 15067–15077. [Google Scholar] [CrossRef]
- Xue, Y.B.; Li, H.S.; Liu, Y.J. Air hole-assisted polarization-maintaining few-mode fiber supporting 10 modes. Chin. J. Lasers 2022, 49, 1706001. [Google Scholar]
- Ding, W.; Wang, Y.Y. Hybrid transmission bands and large birefringence in hollow-core anti-resonant fibers. Opt. Express 2015, 23, 21165–21174. [Google Scholar] [CrossRef]
- Mousavi, S.A.; Sandoghchi, S.R.; Richardson, D.J.; Poletti, F. Broadband high birefringence and polarizing hollow core antiresonant fibers. Opt. Express 2016, 24, 22943–22958. [Google Scholar] [CrossRef] [PubMed]
- Yao, R.M.; Lai, Y.X. Design of a negative curvature hollow-core fiber for transmitting a single-mode dark hollow beam. Optik 2023, 288, 171147. [Google Scholar]
- Hong, Y.F.; Gao, S.F.; Ding, W.; Zhang, X.; Jia, A.Q.; Sheng, Y.L.; Wang, P.; Wang, Y. Highly birefringent anti-resonant hollow-core fiber with a bi-thickness fourfold semi-tube structure. Laser Photonics Rev. 2022, 16, 2100365. [Google Scholar] [CrossRef]
- Ran, J.J.; Meng, Y.C. Broadband high birefringence and single-polarization hollow-core anti-resonant fibers with an elliptical-like core. Opt. Commun. 2025, 575, 131251. [Google Scholar] [CrossRef]
- Malitson, I.H. Interspecimen comparison of the refractive index of fused silica. J. Opt. Soc. Am. 1965, 55, 1205–1209. [Google Scholar] [CrossRef]
- Xiao, Y.Y.; Cheng, J.Y. Design of a Nested Hollow-Core Anti-Resonant Fiber Sensor for Simultaneous Measurement of Temperature and Strain. Sensors 2024, 24, 7805. [Google Scholar] [CrossRef]
- Poletti, F. Nested antiresonant nodeless hollow core fiber. Opt. Express 2014, 22, 23807–23828. [Google Scholar] [CrossRef]
- Hong, Y.F.; Jia, A.Q.; Gao, S.F.; Sheng, Y.; Lu, X.; Liang, Z.; Zhang, Z.; Ding, W.; Wang, Y. Birefringent, low loss, and broadband semi-tube anti-resonant hollow-core fiber. Opt. Lett. 2023, 48, 163–166. [Google Scholar] [CrossRef]
- Stepniewski, G.; Dobrakowski, D.; Pysz, D.; Kasztelanic, R.; Buczyński, R.; Klimczak, M. Birefringent large-mode-area anti-resonant hollow core fiber in the 1.9 μm wavelength window. Opt. Lett. 2020, 45, 4280–4283. [Google Scholar] [CrossRef]
- Yaman, F.; Bai, N.; Zhu, B.Y.; Wang, T.; Li, G. Long distance transmission in few-mode fibers. Opt. Express 2010, 18, 13250–13257. [Google Scholar] [CrossRef]
- Uebel, P.; Gunendi, M.C.; Frosz, M.H.; Ahmed, G.; Edavalath, N.N.; Ménard, J.-M.; Russell, P.S. Broadband robustly single-mode hollow-core PCF by resonant filtering of higher-order modes. Opt. Lett. 2016, 41, 1961–1964. [Google Scholar] [CrossRef]
- Cai, M.Y.; Shi, W.H.; Lou, Y.; Gu, Y. Design and theoretical analysis of broadband bend-resistant low-loss anti-resonant fiber. Appl. Opt. 2024, 63, 5692–5698. [Google Scholar] [CrossRef]
- Wong, H. Recent developments in silicon optoelectronic devices. Microelectron. Reliab. 2002, 42, 317–326. [Google Scholar] [CrossRef]
- Kazanskiy, N.L.; Khonina, S.N.; Butt, M.A. Advancing frontiers: Semiconductor fibers in modern technology. Opt. Commun. 2024, 560, 130495. [Google Scholar] [CrossRef]
- Belardi, W.; Lucia, F.D.; Poletti, F.; Sazio, P.J. Composite material hollow antiresonant fibers. Opt. Lett. 2017, 42, 2535–2538. [Google Scholar] [CrossRef]
- Shaha, K.S.R.; Khaleque, A. Hollow core antiresonant fiber based polarizer and refractive index sensor. J. Light. Technol. 2024, 42, 907–913. [Google Scholar] [CrossRef]
- Hou, D.L.; Wang, X.; Lou, S.Q.; Sheng, Z. Dual-hollow-core anti-resonant fiber with silicon layers and nested resonant tubes for constructing a single-polarization 3 dB coupler. Opt. Express 2024, 32, 38780–38792. [Google Scholar] [CrossRef]
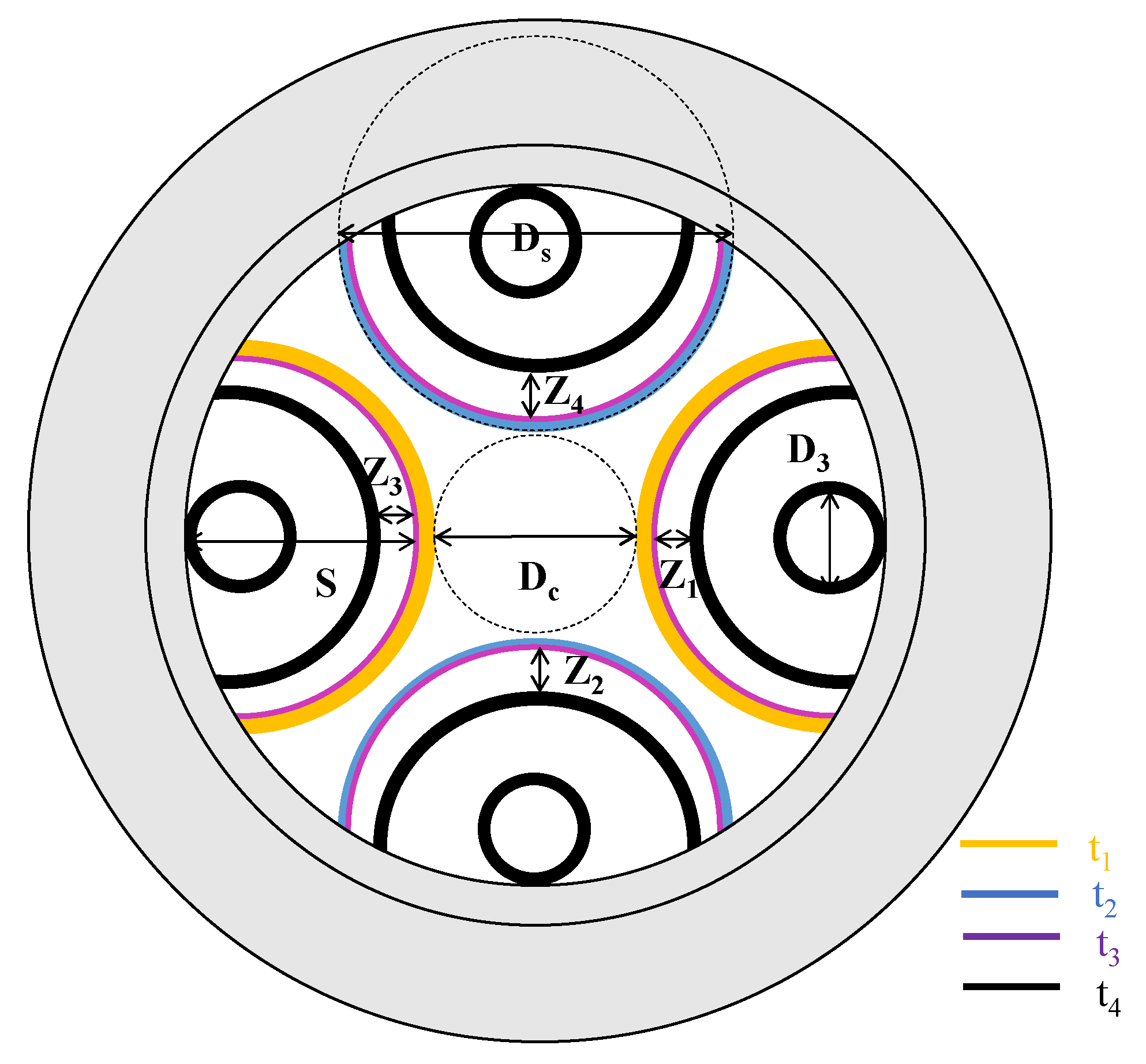



| Ds = 59.4 µm | D3 = 12 µm | t1 = 0.93 µm |
| t2 = 1.41 µm | t4 = 1.15 µm |
| Dc = 27 µm | Ds = 59.4 µm | D3 = 12 µm |
| S = 27.5 µm | Z1 = 6 µm | Z2 = 6 µm |
| Z3 = 4.5 µm | Z4 = 6 µm | t1 = 0.93 µm |
| t2 = 1.41 µm | t3 = 0.03 µm | t4 = 1.15 µm |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zong, L.; Cheng, J.; Xiao, Y. Design of Hollow-Core Anti-Resonant Fibers Supporting Few Weakly Coupled Polarization-Maintaining Modes. Photonics 2025, 12, 1018. https://doi.org/10.3390/photonics12101018
Zong L, Cheng J, Xiao Y. Design of Hollow-Core Anti-Resonant Fibers Supporting Few Weakly Coupled Polarization-Maintaining Modes. Photonics. 2025; 12(10):1018. https://doi.org/10.3390/photonics12101018
Chicago/Turabian StyleZong, Linxuan, Jiayao Cheng, and Yueyu Xiao. 2025. "Design of Hollow-Core Anti-Resonant Fibers Supporting Few Weakly Coupled Polarization-Maintaining Modes" Photonics 12, no. 10: 1018. https://doi.org/10.3390/photonics12101018
APA StyleZong, L., Cheng, J., & Xiao, Y. (2025). Design of Hollow-Core Anti-Resonant Fibers Supporting Few Weakly Coupled Polarization-Maintaining Modes. Photonics, 12(10), 1018. https://doi.org/10.3390/photonics12101018




