Designs of Time-Resolved Resonant Inelastic X-Ray Scattering Branchline at S3FEL
Abstract
1. Introduction
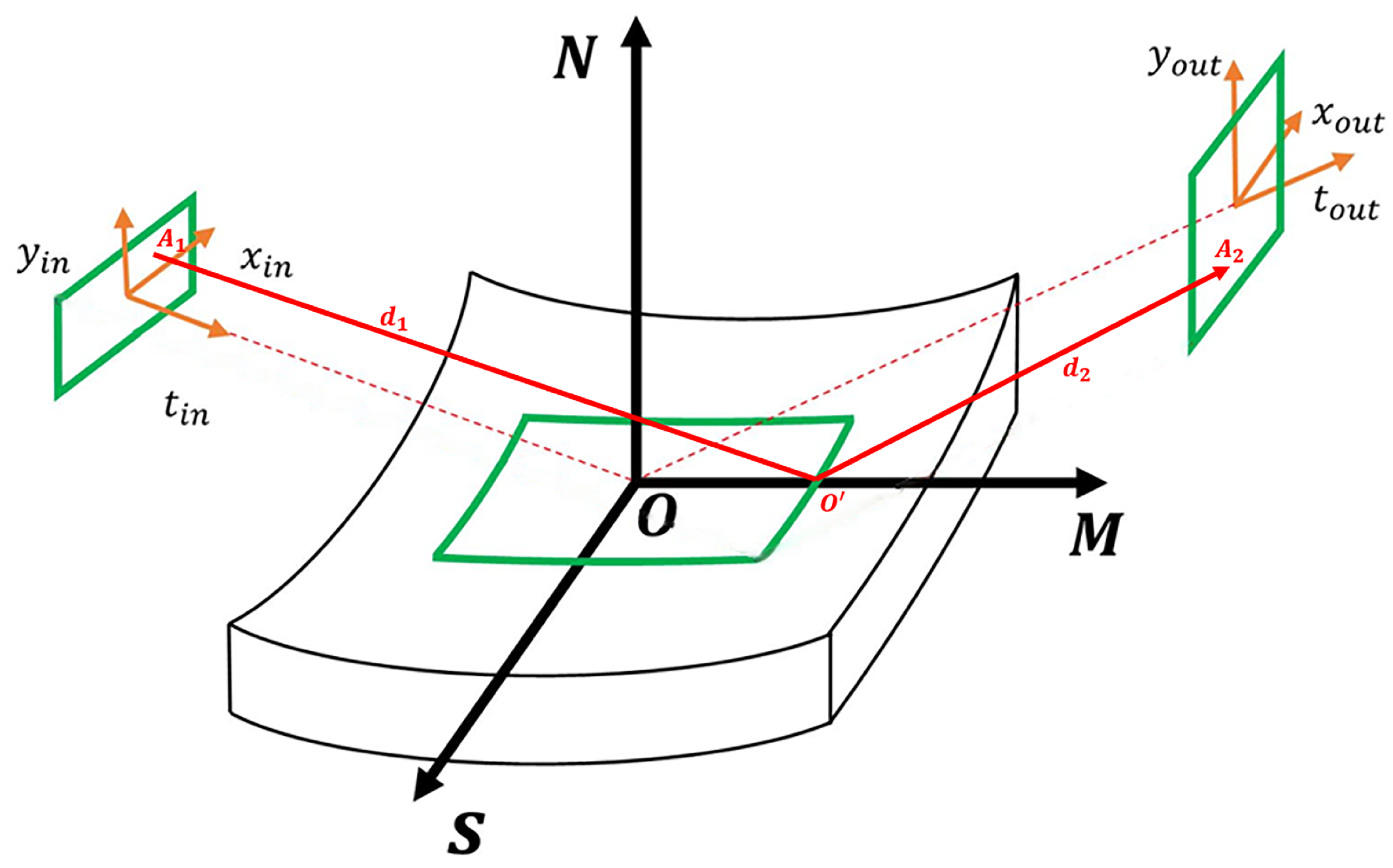
2. Simulation Method Description
3. Tr-RIXS Branchline Design
3.1. The Optical Layout
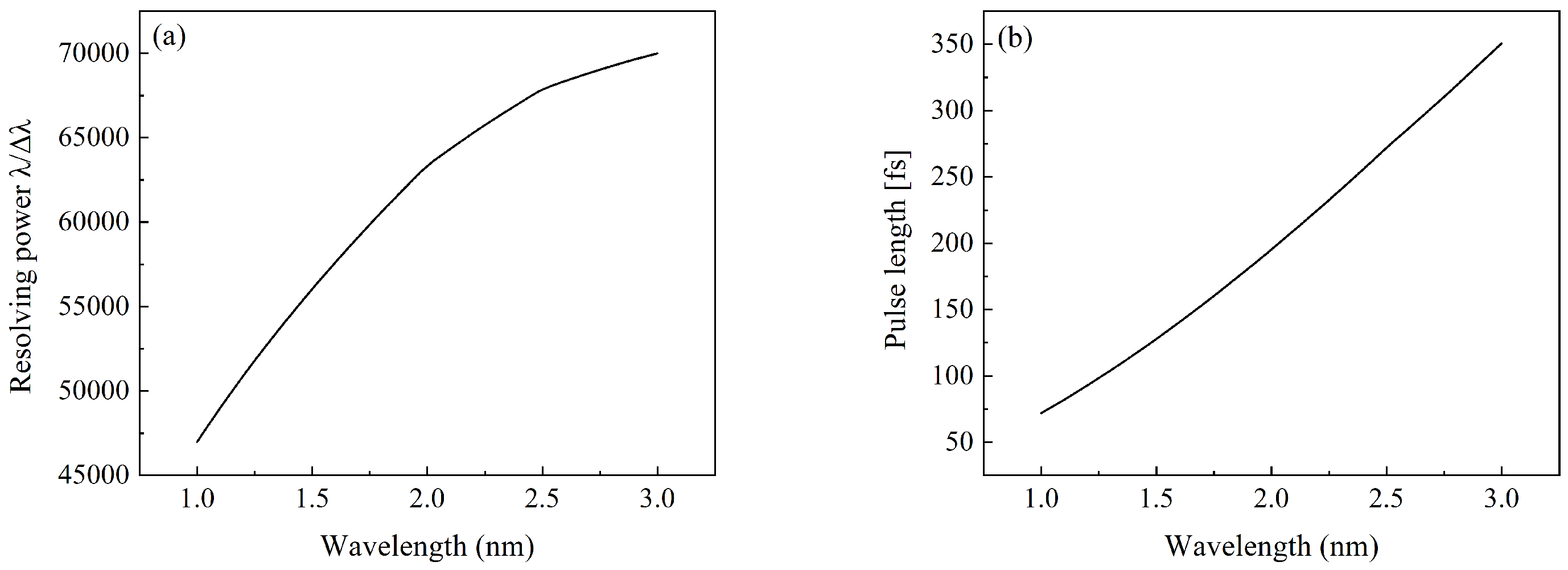
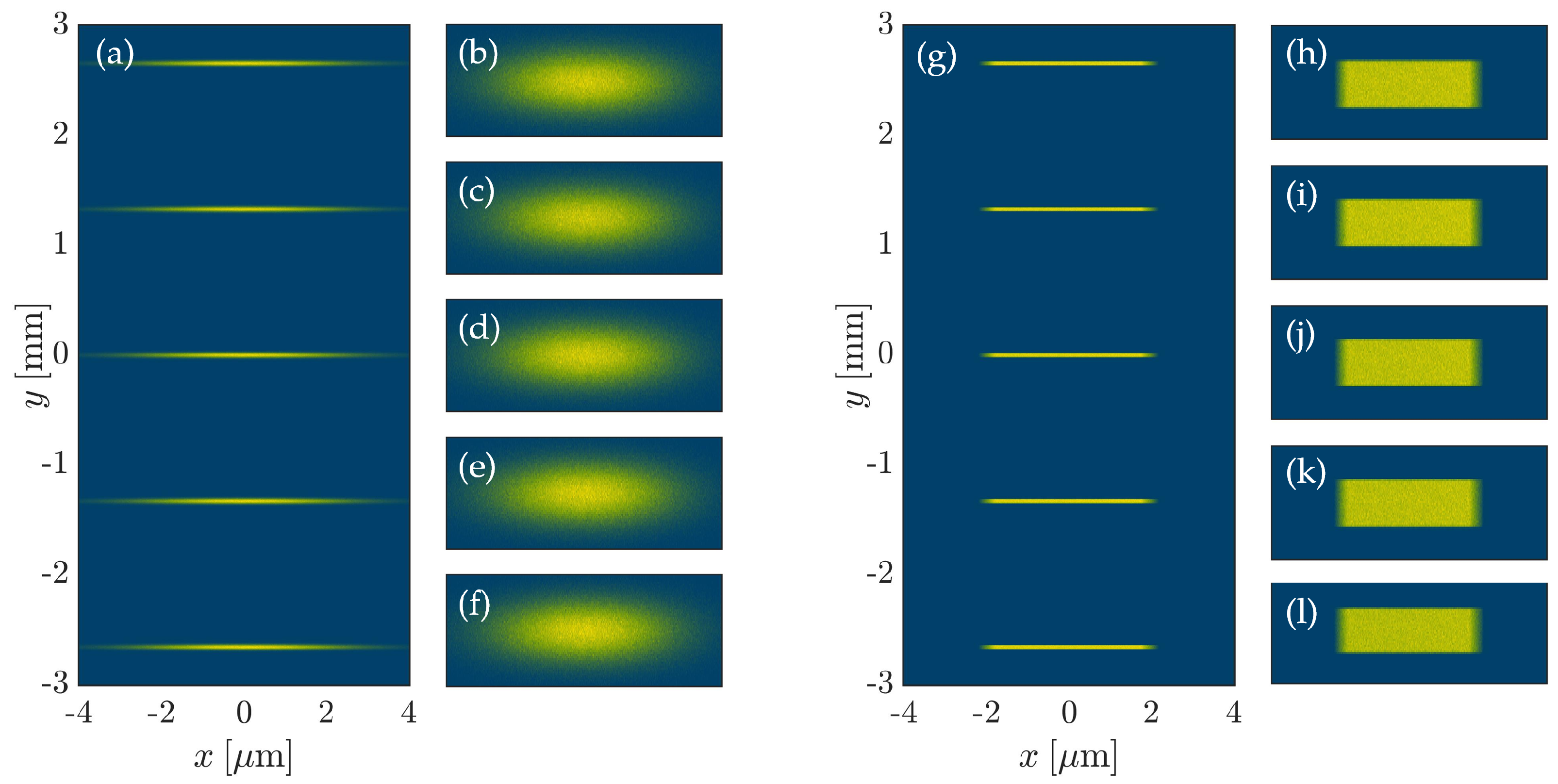
3.2. Start-to-End Simulation
4. Discussion
5. Summary
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- de Groot, F.M.; Haverkort, M.W.; Elnaggar, H.; Juhin, A.; Zhou, K.J.; Glatzel, P. Resonant inelastic X-ray scattering. Nat. Rev. Methods Prim. 2024, 4, 45. [Google Scholar] [CrossRef]
- Kotani, A.; Shin, S. Resonant inelastic x-ray scattering spectra for electrons in solids. Rev. Mod. Phys. 2001, 73, 203. [Google Scholar] [CrossRef]
- Ament, L.J.; Van Veenendaal, M.; Devereaux, T.P.; Hill, J.P.; Van Den Brink, J. Resonant inelastic x-ray scattering studies of elementary excitations. Rev. Mod. Phys. 2011, 83, 705–767. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Y.; Jia, C.; Moritz, B.; Shvaika, A.M.; Freericks, J.K.; Devereaux, T.P. Theory for time-resolved resonant inelastic x-ray scattering. Phys. Rev. B 2019, 99, 104306. [Google Scholar] [CrossRef]
- Emma, P.; Akre, R.; Arthur, J.; Bionta, R.; Bostedt, C.; Bozek, J.; Brachmann, A.; Bucksbaum, P.; Coffee, R.; Decker, F.J.; et al. First lasing and operation of an ångstrom-wavelength free-electron laser. Nat. Photonics 2010, 4, 641–647. [Google Scholar] [CrossRef]
- Ishikawa, T.; Aoyagi, H.; Asaka, T.; Asano, Y.; Azumi, N.; Bizen, T.; Ego, H.; Fukami, K.; Fukui, T.; Furukawa, Y.; et al. A compact X-ray free-electron laser emitting in the sub-ångström region. Nat. Photonics 2012, 6, 540–544. [Google Scholar] [CrossRef]
- Milne, C.J.; Schietinger, T.; Aiba, M.; Alarcon, A.; Alex, J.; Anghel, A.; Arsov, V.; Beard, C.; Beaud, P.; Bettoni, S.; et al. SwissFEL: The Swiss X-ray free electron laser. Appl. Sci. 2017, 7, 720. [Google Scholar] [CrossRef]
- Zhu, Z.; Zhao, Z.; Wang, D.; Liu, Z.; Li, R.; Yin, L.; Yang, Z. SCLF: An 8-GeV CW SCRF linac-based X-ray FEL facility in Shanghai. In Proceedings of the FEL2017, Santa Fe, NM, USA, 20–25 August 2017; pp. 20–25. [Google Scholar]
- Decking, W.; Abeghyan, S.; Abramian, P.; Abramsky, A.; Aguirre, A.; Albrecht, C.; Alou, P.; Altarelli, M.; Altmann, P.; Amyan, K.; et al. A MHz-repetition-rate hard X-ray free-electron laser driven by a superconducting linear accelerator. Nat. Photonics 2020, 14, 391–397. [Google Scholar] [CrossRef]
- Bostedt, C.; Boutet, S.; Fritz, D.M.; Huang, Z.; Lee, H.J.; Lemke, H.T.; Robert, A.; Schlotter, W.F.; Turner, J.J.; Williams, G.J. Linac coherent light source: The first five years. Rev. Mod. Phys. 2016, 88, 015007. [Google Scholar] [CrossRef]
- Beye, M.; Sorgenfrei, F.; Schlotter, W.F.; Wurth, W.; Föhlisch, A. The liquid-liquid phase transition in silicon revealed by snapshots of valence electrons. Proc. Natl. Acad. Sci. USA 2010, 107, 16772–16776. [Google Scholar] [CrossRef]
- Dean, M.P.; Cao, Y.; Liu, X.; Wall, S.; Zhu, D.; Mankowsky, R.; Thampy, V.; Chen, X.; Vale, J.G.; Casa, D.; et al. Ultrafast energy-and momentum-resolved dynamics of magnetic correlations in the photo-doped Mott insulator Sr2IrO4. Nat. Mater. 2016, 15, 601–605. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Mazzone, D.; Meyers, D.; Hill, J.; Liu, X.; Wall, S.; Dean, M. Ultrafast dynamics of spin and orbital correlations in quantum materials: An energy-and momentum-resolved perspective. Philos. Trans. R. Soc. A 2019, 377, 20170480. [Google Scholar] [CrossRef] [PubMed]
- Parchenko, S.; Paris, E.; McNally, D.; Abreu, E.; Dantz, M.; Bothschafter, E.M.; Reid, A.H.; Schlotter, W.F.; Lin, M.F.; Wandel, S.F.; et al. Orbital dynamics during an ultrafast insulator to metal transition. Phys. Rev. Res. 2020, 2, 023110. [Google Scholar] [CrossRef]
- Gerasimova, N.; La Civita, D.; Samoylova, L.; Vannoni, M.; Villanueva, R.; Hickin, D.; Carley, R.; Gort, R.; Van Kuiken, B.; Miedema, P.; et al. The soft X-ray monochromator at the SASE3 beamline of the European XFEL: From design to operation. Synchrotron Radiat. 2022, 29, 1299–1308. [Google Scholar] [CrossRef]
- Tollerud, J.O.; Sparapassi, G.; Montanaro, A.; Asban, S.; Glerean, F.; Giusti, F.; Marciniak, A.; Kourousias, G.; Billè, F.; Cilento, F.; et al. Femtosecond covariance spectroscopy. Proc. Natl. Acad. Sci. USA 2019, 116, 5383–5386. [Google Scholar] [CrossRef]
- Wang, X.; Zeng, L.; Shao, J.; Liang, Y.; Yi, H.; Yu, Y.; Sun, J.; Li, X.; Feng, C.; Wang, Z.; et al. Physical design for shenzhen superconducting soft x-ray free-electron laser (s3fel). In Proceedings of the IPAC’23, Venice, Italy, 7–12 May 2023. [Google Scholar]
- Xu, Z.; Zhang, W.; Yang, C.; Zhong, Y. Shape optimization design of the offset mirror in FEL-1 beamline at S3FEL. Sci. Rep. 2023, 13, 9653. [Google Scholar]
- Zhong, Y.; Yang, X. Advances in free-electron-laser based scattering techniques and spectroscopic methods. Acta Phys. Sin. 2024, 73, 194101. [Google Scholar] [CrossRef]
- Zhu, Y.; Yang, C.; Hu, K.; Wu, C.; Luo, J.; Hao, Z.; Xing, Z.; Li, Q.; Xu, Z.; Zhang, W. FURION: Modeling of FEL pulses propagation in dispersive soft X-ray beamline systems. Opt. Express 2024, 32, 5031–5042. [Google Scholar] [CrossRef]
- Hu, K.; Xing, Z.; Yang, C.; Zhu, Y.; Wu, C.; Xu, Z.; Wang, Q.; Zhang, W. Modeling of X-ray pulse propagation in beamline systems using a 6D phase space ray-tracing method. J. Synchrotron Radiat. 2025, 32, 942–950. [Google Scholar] [CrossRef]
- Reiche, S. GENESIS 1.3: A fully 3D time-dependent FEL simulation code. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 1999, 429, 243–248. [Google Scholar] [CrossRef]
- Sanchez del Rio, M.; Canestrari, N.; Jiang, F.; Cerrina, F. SHADOW3: A new version of the synchrotron X-ray optics modelling package. Synchrotron Radiat. 2011, 18, 708–716. [Google Scholar] [CrossRef]
- Shi, X.; Reininger, R.; Sanchez del Rio, M.; Assoufid, L. A hybrid method for X-ray optics simulation: Combining geometric ray-tracing and wavefront propagation. J. Synchrotron Radiat. 2014, 21, 669–678. [Google Scholar] [CrossRef]
- Sparrow, C.M. On spectroscopic resolving power. Astrophys. J. 1916, 44, 76. [Google Scholar] [CrossRef]
- Agåker, M.; Söderström, J.; Baumann, T.M.; Englund, C.J.; Kjellsson, L.; Boll, R.; De Fanis, A.; Dold, S.; Mazza, T.; Montaño, J.; et al. A 1D imaging soft X-ray spectrometer for the small quantum systems instrument at the European XFEL. Synchrotron Radiat. 2024, 31, 1264–1275. [Google Scholar] [CrossRef]



| Optics | Figure | [mrad] | R [m] |
|---|---|---|---|
| M1 | Flat | 12 | - |
| M2 | Bendable | 12 | 9981.6 |
| M3 | Flat | Scanning | - |
| G | Flat VLS | Scanning | - |
| M4 | Flat | 14 | - |
| M5c | Cylindrical | 14 | 9476.0 |
| KB-v | Bendable | 17 | ∞ |
| KB-h | Bendable | 17 | 264.12 |
| Parameter | Value | Unit |
|---|---|---|
| Electron energy | 2.5 | GeV |
| Energy spread | 0.4 | MeV |
| Peak current | 800 | A |
| Photon energy | 1240 | eV |
| Undulator period | 3.0 | cm |
| Pulse duration | 40 | fs |
| Average beta function | 10 | m |
| Normalized emittance | 0.375 | mm-mrad |
| Undulator parameter | 1.0915 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, W.; Yang, C.; Hu, K.; Zhu, Y.; Wu, C.; Wang, Y.; Zhong, Y.; Xu, Z.; Zhang, W. Designs of Time-Resolved Resonant Inelastic X-Ray Scattering Branchline at S3FEL. Photonics 2025, 12, 1009. https://doi.org/10.3390/photonics12101009
Sun W, Yang C, Hu K, Zhu Y, Wu C, Wang Y, Zhong Y, Xu Z, Zhang W. Designs of Time-Resolved Resonant Inelastic X-Ray Scattering Branchline at S3FEL. Photonics. 2025; 12(10):1009. https://doi.org/10.3390/photonics12101009
Chicago/Turabian StyleSun, Weihong, Chuan Yang, Kai Hu, Ye Zhu, Chen Wu, Yuhang Wang, Yinpeng Zhong, Zhongmin Xu, and Weiqing Zhang. 2025. "Designs of Time-Resolved Resonant Inelastic X-Ray Scattering Branchline at S3FEL" Photonics 12, no. 10: 1009. https://doi.org/10.3390/photonics12101009
APA StyleSun, W., Yang, C., Hu, K., Zhu, Y., Wu, C., Wang, Y., Zhong, Y., Xu, Z., & Zhang, W. (2025). Designs of Time-Resolved Resonant Inelastic X-Ray Scattering Branchline at S3FEL. Photonics, 12(10), 1009. https://doi.org/10.3390/photonics12101009






