A Hybrid Simulated Annealing Approach for Loaded Phase Optimization in Digital Lasers for Structured Light Generation
Abstract
1. Introduction
2. Simulation Method
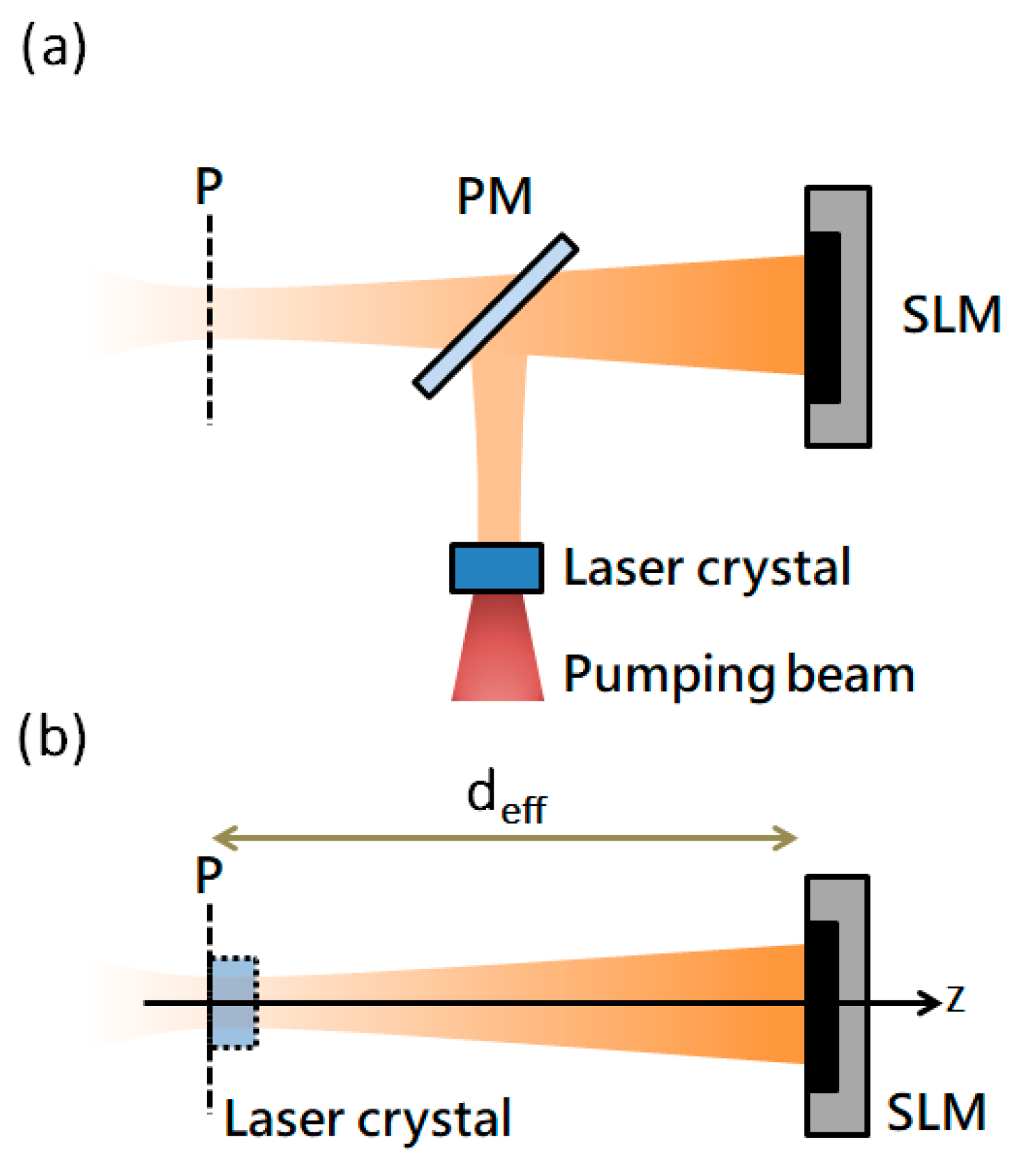
2.1. Laser Configuration in Simulation
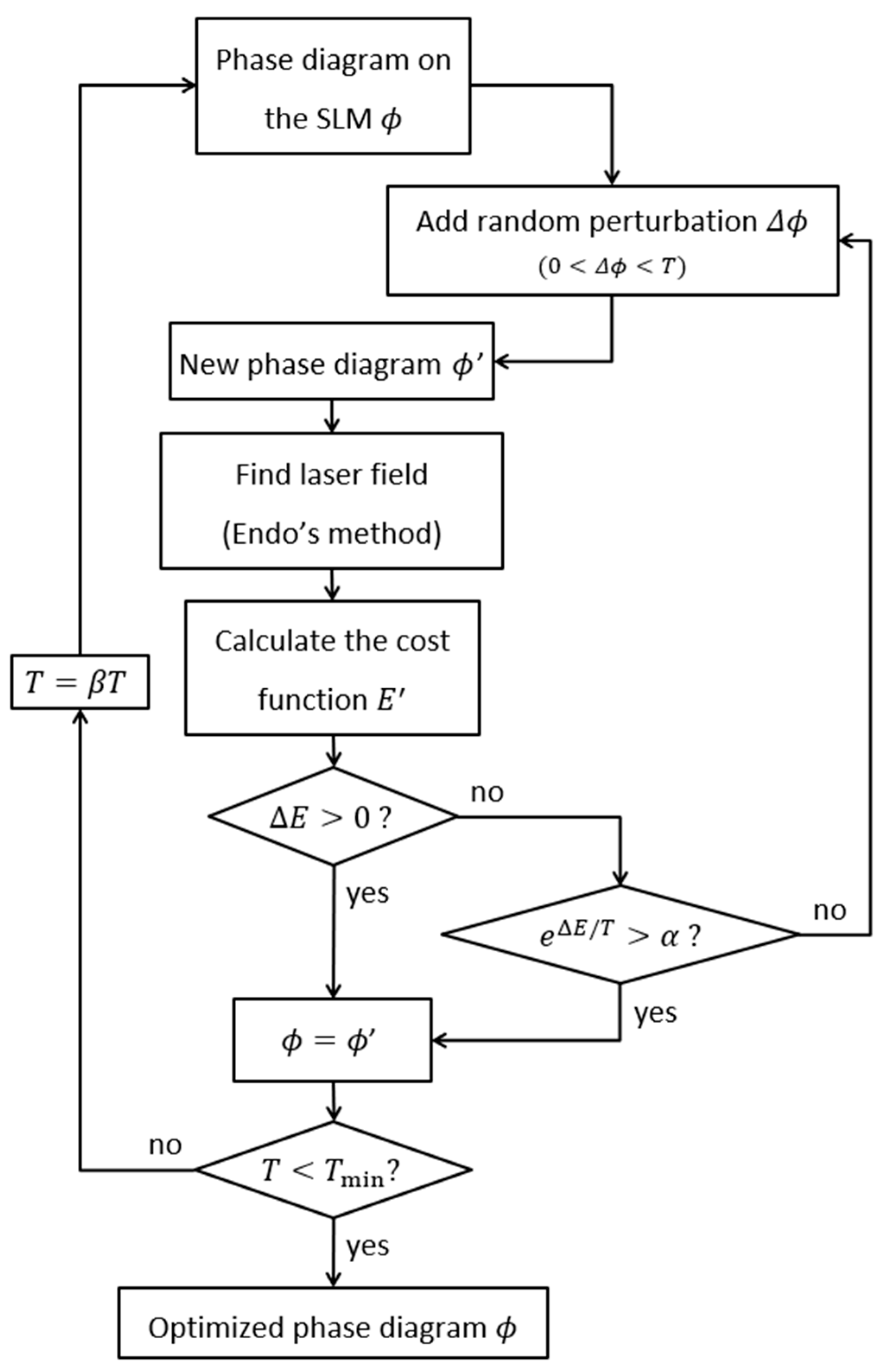
2.2. SA Method in Designing Spatial Light Modulator Projected Phase Diagram
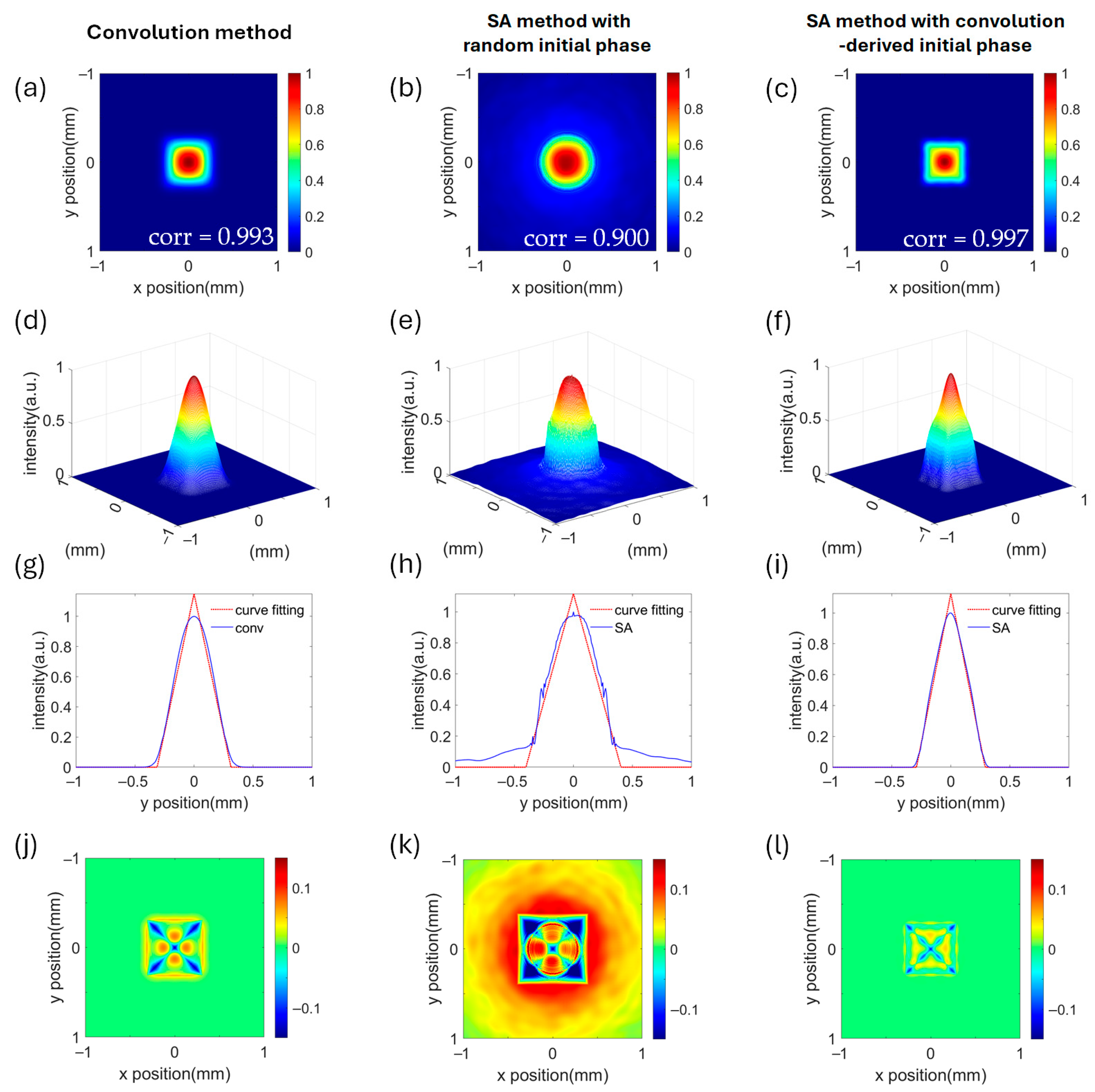
2.3. Phase Initialization
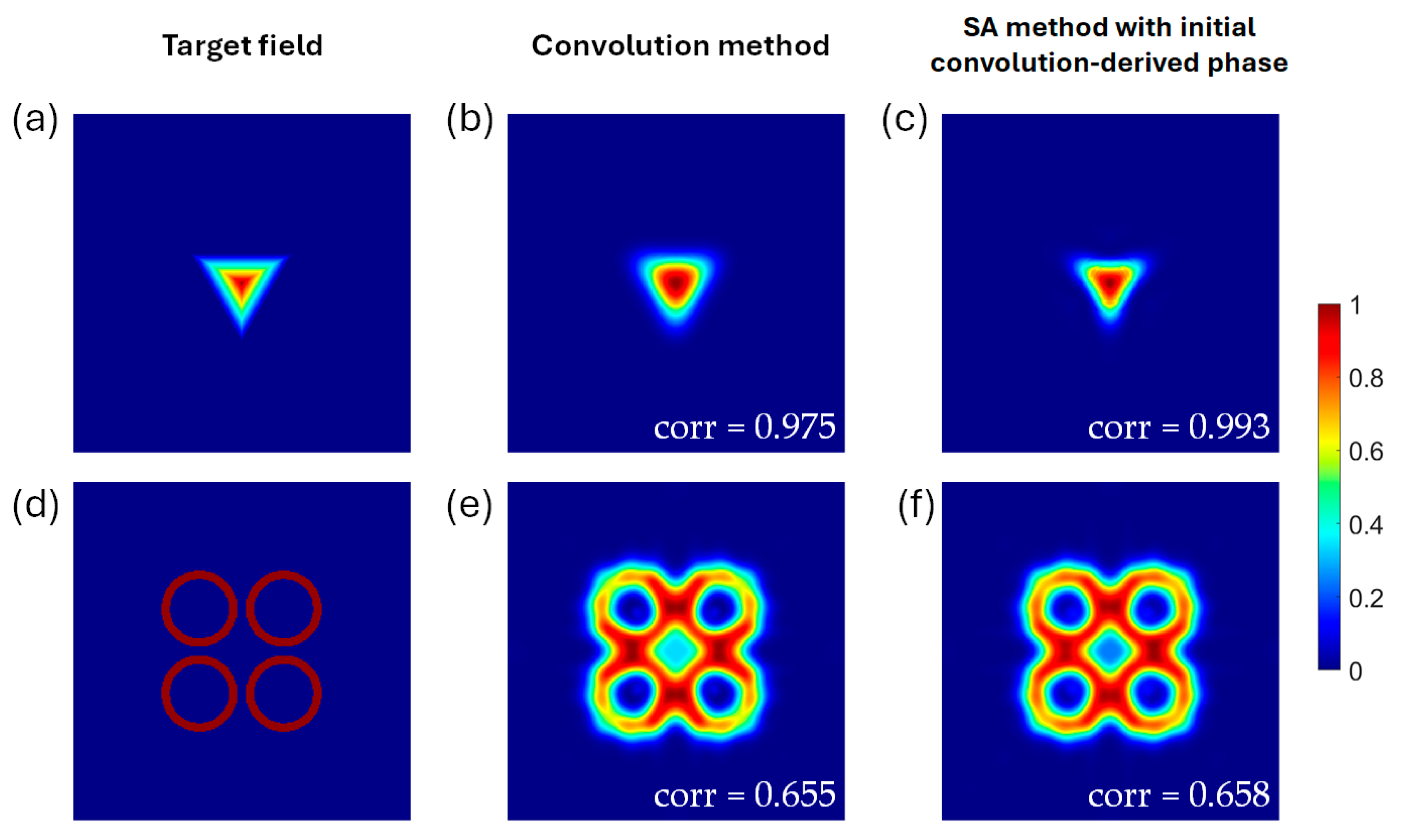
2.4. Target Field
3. Simulation Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SA | Simulated Annealing |
| SLM | Spatial Light Modulator |
| DPSSL | Diode-Pumped Solid-State Laser |
| PM | Partially reflective Mirror |
References
- Leger, J.R.; Chen, D.; Wang, Z. Diffractive optical element for mode shaping of a Nd:YAG laser. Opt. Lett. 1994, 19, 108–110. [Google Scholar] [CrossRef]
- Nakata, Y.; Osawa, K.; Miyanaga, N. Utilization of the high spatial-frequency component in adaptive beam shaping by using a virtual diagonal phase grating. Sci. Rep. 2019, 9, 4640. [Google Scholar] [CrossRef] [PubMed]
- Zhu, L.; Wang, J. Arbitrary manipulation of spatial amplitude and phase using phase-only spatial light modulators. Sci. Rep. 2014, 4, 7441. [Google Scholar] [CrossRef] [PubMed]
- Bélanger, P.A.; Lachance, R.L.; Paré, C. Super-Gaussian output from a CO2 laser by using a graded-phase mirror resonator. Opt. Lett. 1992, 17, 739–741. [Google Scholar] [CrossRef] [PubMed]
- Litvin, I.A.; Forbes, A. Intra–cavity flat–top beam generation. Opt. Express 2009, 17, 15891–15903. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Meng, J.; Chen, W. High efficiency and high-energy intra-cavity beam shaping laser. Laser Phys. 2015, 25, 095005. [Google Scholar] [CrossRef]
- Caley, A.J.; Thomson, M.J.; Liu, J.S.; Waddie, A.J.; Taghizadeh, M.R. Diffractive optical elements for high gain lasers with arbitrary output beam profiles. Opt. Express 2007, 15, 10699–10704. [Google Scholar] [CrossRef]
- Ngcobo, S.; Ait-Ameur, K.; Litvin, I.; Hasnaoui, A.; Forbes, A. Tuneable Gaussian to flat-top resonator by amplitude beam shaping. Opt. Express 2013, 21, 21113–21118. [Google Scholar] [CrossRef]
- Ngcobo, S.; Litvin, I.; Burger, L.; Forbes, A. A digital laser for on-demand laser modes. Nat. Commun. 2013, 4, 2289. [Google Scholar] [CrossRef]
- Tsai, K.-F.; Chu, S.-C. Generating laser output with arbitrary lateral shape by using multi-point beam superposition method in digital lasers. Laser Phys. 2018, 28, 075801. [Google Scholar] [CrossRef]
- Huang, C.-Y.; Chang, K.-C.; Chu, S.-C. Experimental Investigation of Generating Laser Beams of on-Demand Lateral Field Distribution from Digital Lasers. Materials 2019, 12, 2226. [Google Scholar] [CrossRef]
- Chu, S.-C.; Fu, Y.-X.; Chang, K.-C.; Huang, C.-Y. Generating a geometric structure light field from a digital laser by specifying a laser cavity phase boundary with a Gaussian-convoluted target field. Opt. Express 2021, 29, 35980–35992. [Google Scholar] [CrossRef]
- Sandile, N.; Teboho, B.; Igor, A.L.; Darryl, N.; Kamel, A.-A.; Andrew, F. Selective excitation and detection of higher-order doughnut laser modes as an incoherent superposition of two petals modes in a digital laser resonator. Proc. SPIE 2015, 2015, 95810B. [Google Scholar] [CrossRef]
- Gower, M.C. Industrial applications of laser micromachining. Opt. Express 2000, 7, 56–67. [Google Scholar] [CrossRef]
- Visconti, P.; Turco, C.; Rinaldi, R.; Cingolani, R. Nanopatterning of organic and inorganic materials by holographic lithography and plasma etching. Microelectron. Eng. 2000, 53, 391–394. [Google Scholar] [CrossRef]
- Yang, L.; El-Tamer, A.; Hinze, U.; Li, J.W.; Hu, Y.L.; Huang, W.H.; Chu, J.R.; Chichkoy, B.N. Parallel direct laser writing of micro-optical and photonic structures using spatial light modulator. Opt. Lasers Eng. 2015, 70, 26–32. [Google Scholar] [CrossRef]
- MacDonald, M.P.; Paterson, L.; Volke-Sepulveda, K.; Arlt, J.; Sibbett, W.; Dholakia, K. Creation and Manipulation of Three-Dimensional Optically Trapped Structures. Science 2002, 296, 1101–1103. [Google Scholar] [CrossRef]
- Daria, V.R.; Eriksen, R.L.; Glückstad, J. Dynamic optical manipulation of colloidal systems using a spatial light modulator. J. Mod. Opt. 2003, 50, 1601–1614. [Google Scholar] [CrossRef]
- Eriksen, R.L.; Daria, V.R.; Rodrigo, P.J.; Glückstad, J. Computer-controlled orientation of multiple optically-trapped microscopic particles. Microelectron. Eng. 2003, 67–68, 872–878. [Google Scholar] [CrossRef]
- Sanner, N.; Huot, N.; Audouard, E.; Larat, C.; Huignard, J.P. Direct ultrafast laser micro-structuring of materials using programmable beam shaping. Opt. Lasers Eng. 2007, 45, 737–741. [Google Scholar] [CrossRef]
- Jenness, N.J.; Wulff, K.D.; Johannes, M.S.; Padgett, M.J.; Cole, D.G.; Clark, R.L. Three-dimensional parallel holographic micropatterning using a spatial light modulator. Opt. Express 2008, 16, 15942–15948. [Google Scholar] [CrossRef]
- Obata, K.; Koch, J.; Hinze, U.; Chichkov, B.N. Multi-focus two-photon polymerization technique based on individually controlled phase modulation. Opt. Express 2010, 18, 17193–17200. [Google Scholar] [CrossRef]
- Gittard, S.D.; Nguyen, A.; Obata, K.; Koroleva, A.; Narayan, R.J.; Chichkov, B.N. Fabrication of microscale medical devices by two-photon polymerization with multiple foci via a spatial light modulator. Biomed. Opt. Express 2011, 2, 3167–3178. [Google Scholar] [CrossRef] [PubMed]
- Zhang, S.-J.; Li, Y.; Liu, Z.-P.; Ren, J.-L.; Xiao, Y.-F.; Yang, H.; Gong, Q. Two-photon polymerization of a three dimensional structure using beams with orbital angular momentum. Appl. Phys. Lett. 2014, 105, 061101. [Google Scholar] [CrossRef]
- Ni, J.; Wang, C.; Zhang, C.; Hu, Y.; Yang, L.; Lao, Z.; Xu, B.; Li, J.; Wu, D.; Chu, J. Three-dimensional chiral microstructures fabricated by structured optical vortices in isotropic material. Light Sci. Appl. 2017, 6, e17011. [Google Scholar] [CrossRef]
- Wang, J.; Yang, J.-Y.; Fazal, I.M.; Ahmed, N.; Yan, Y.; Huang, H.; Ren, Y.; Yue, Y.; Dolinar, S.; Tur, M.; et al. Terabit free-space data transmission employing orbital angular momentum multiplexing. Nat. Photonics 2012, 6, 488–496. [Google Scholar] [CrossRef]
- Willner, A.E.; Huang, H.; Yan, Y.; Ren, Y.; Ahmed, N.; Xie, G.; Bao, C.; Li, L.; Cao, Y.; Zhao, Z.; et al. Optical communications using orbital angular momentum beams. Adv. Opt. Photonics 2015, 7, 66–106. [Google Scholar] [CrossRef]
- Wang, J. Advances in communications using optical vortices. Photonics Res. 2016, 4, B14–B28. [Google Scholar] [CrossRef]
- Forbes, A. Structured Light from Lasers. Laser Photonics Rev. 2019, 13, 1900140. [Google Scholar] [CrossRef]
- Ren, Z.-C.; Fan, L.; Cheng, Z.-M.; Liu, Z.-F.; Lou, Y.-C.; Huang, S.-Y.; Chen, C.; Li, Y.; Tu, C.; Ding, J.; et al. On-demand orbital angular momentum comb from a digital laser. Optica 2024, 11, 951–961. [Google Scholar] [CrossRef]
- Forbes, A.; Mkhumbuza, L.; Feng, L. Orbital angular momentum lasers. Nat. Rev. Phys. 2024, 6, 352–364. [Google Scholar] [CrossRef]
- Fan, W.-Q.; Jia, S.-Q.; Fan, L.; Ding, J.; Ren, Z.-C.; Wang, X.-L.; Wang, H.-T. Cavity-enhanced nonlinear frequency conversion and manipulation of vector fields. APL Photonics 2025, 10, 036113. [Google Scholar] [CrossRef]
- Chen, X.; Liu, S.; Lin, Z.; Chen, Z.; Pu, J. Dual-cavity digital laser for intra-cavity mode shaping and polarization control. Opt. Express 2018, 26, 18182–18189. [Google Scholar] [CrossRef] [PubMed]
- Teboho, B.; Sandile, N. Intracavity second harmonic generation for higher-order laser modes. Proc. SPIE 2019, 2019, 109041P. [Google Scholar] [CrossRef]
- Matsuura, T.; Takai, T.; Iwata, F. Local electrophoresis deposition assisted by laser trapping coupled with a spatial light modulator for three-dimensional microfabrication. Jpn. J. Appl. Phys. 2017, 56, 105502. [Google Scholar] [CrossRef]
- Tradonsky, C.; Mahler, S.; Cai, G.; Pal, V.; Chriki, R.; Friesem, A.A.; Davidson, N. High-resolution digital spatial control of a highly multimode laser. Optica 2021, 8, 880–884. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Rere, L.M.R.; Fanany, M.I.; Arymurthy, A.M. Simulated Annealing Algorithm for Deep Learning. Procedia Comput. Sci. 2015, 72, 137–144. [Google Scholar] [CrossRef]
- Porth, L.; Boyd, M.; Pai, J. Reducing Risk Through Pooling and Selective Reinsurance Using Simulated Annealing: An Example from Crop Insurance. Geneva Risk Insur. Rev. 2016, 41, 163–191. [Google Scholar] [CrossRef]
- Ibn Majdoub Hassani, Z.; El Barkany, A.; Jabri, A.; El Abbassi, I.; Darcherif, A.M. A Comparative Analysis of Metaheuristic Approaches (Genetic Algorithm/Hybridization of Genetic Algorithms and Simulated Annealing) for Planning and Scheduling Problem with Energy Aspect. SAE Int. J. Mater. Manuf. 2021, 14, 363–374. [Google Scholar] [CrossRef]
- El-Agmy, R.; Bulte, H.; Greenaway, A.H.; Reid, D.T. Adaptive beam profile control using a simulated annealing algorithm. Opt. Express 2005, 13, 6085–6091. [Google Scholar] [CrossRef]
- Hao, B.; Leger, J. Polarization beam shaping. Appl. Opt. 2007, 46, 8211–8217. [Google Scholar] [CrossRef]
- Yu, Z.; Ma, H.; Du, S. Simulated annealing algorithm applied in adaptive near field beam shaping. Proc. SPIE 2010, 2010, 78480Q. [Google Scholar] [CrossRef]
- Hu, C.; Xiao, Y.; He, Y.; Liu, Y.; Song, Y.; Tang, X. Optimization of brightness in a Nd:YAG laser by maximizing the single-mode power factor with an intra-cavity spatial light modulator. Appl. Opt. 2022, 61, 1482–1491. [Google Scholar] [CrossRef] [PubMed]
- Endo, M.; Kawakami, M.; Nanri, K.; Takeda, S.; Fujioka, T. Two-dimensional simulation of an unstable resonator with a stable core. Appl. Opt. 1999, 38, 3298–3307. [Google Scholar] [CrossRef] [PubMed]
- Endo, M.; Yamaguchi, S.; Uchiyama, T.; Fujioka, T. Numerical simulation of the w-axicon type optical resonator for coaxial slab CO2 lasers. J. Phys. D Appl. Phys. 2001, 34, 68. [Google Scholar] [CrossRef]
- Endo, M. Numerical simulation of an optical resonator for generation of a doughnut-like laser beam. Opt. Express 2004, 12, 1959–1965. [Google Scholar] [CrossRef]
- Chu, S.-C.; Otsuka, K. Numerical study for selective excitation of Ince-Gaussian modes in end-pumped solid-state lasers. Opt. Express 2007, 15, 16506–16519. [Google Scholar] [CrossRef]
- Ohtomo, T.; Chu, S.-C.; Otsuka, K. Generation of vortex beams from lasers with controlled Hermite- and Ince-Gaussian modes. Opt. Express 2008, 16, 5082–5094. [Google Scholar] [CrossRef]
- Chu, S.-C.; Tsai, K.-F. Numerical study for selective excitation of Mathieu-Gauss modes in end-pumped solid-state laser systems. Opt. Express 2011, 19, 3236–3250. [Google Scholar] [CrossRef] [PubMed]
- Metropolis, N.; Rosenbluth, A.W.; Rosenbluth, M.N.; Teller, A.H.; Teller, E. Equation of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Fisher, R.A. Statistical Methods for Research Workers, 13th ed.; Hafner: New York, NY, USA, 1958. [Google Scholar]
- Kendall, M.G. The Advanced Theory of Statistics, 4th ed.; Macmillan: London, UK, 1979. [Google Scholar]
- Khonina, S.N.; Kotlyar, V.V.; Skidanov, R.V.; Soifer, V.A. Levelling the focal spot intensity of the focused gaussian beam. J. Mod. Opt. 2000, 47, 883–904. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Y.-J.; Chang, K.-C.; Yang, T.-L.; Chu, S.-C. A Hybrid Simulated Annealing Approach for Loaded Phase Optimization in Digital Lasers for Structured Light Generation. Photonics 2025, 12, 1005. https://doi.org/10.3390/photonics12101005
Chen Y-J, Chang K-C, Yang T-L, Chu S-C. A Hybrid Simulated Annealing Approach for Loaded Phase Optimization in Digital Lasers for Structured Light Generation. Photonics. 2025; 12(10):1005. https://doi.org/10.3390/photonics12101005
Chicago/Turabian StyleChen, Ying-Jung, Kuo-Chih Chang, Tzu-Le Yang, and Shu-Chun Chu. 2025. "A Hybrid Simulated Annealing Approach for Loaded Phase Optimization in Digital Lasers for Structured Light Generation" Photonics 12, no. 10: 1005. https://doi.org/10.3390/photonics12101005
APA StyleChen, Y.-J., Chang, K.-C., Yang, T.-L., & Chu, S.-C. (2025). A Hybrid Simulated Annealing Approach for Loaded Phase Optimization in Digital Lasers for Structured Light Generation. Photonics, 12(10), 1005. https://doi.org/10.3390/photonics12101005




