Implicit DFC: Blind Reference Frame Estimation in Screen-to- Camera Communication Using First-Order Statistics

Abstract

Display-field communication (DFC) is an imperceptible screen-to-camera technology that embeds and recovers data from the frequency domain of an image frame. Conventional DFC requires a reference frame for each data frame to estimate the channel, a method that, while reliable, is not bandwidth-efficient. Similarly, iterative DFC requires the transmission of pilot symbols for channel estimation. In this paper, we propose an implicit DFC (iDFC) scheme that eliminates the need for reference frames by estimating them using the first-order statistics of the received image. The system employs discrete Fourier-transform-based subcarrier mapping and adds data directly to the frequency coefficients of the host image. At the receiver, statistical estimation enables blind channel equalization without sacrificing the data rate. The simulation results show that iDFC achieves an achievable data rate (ADR) of up to $1.52\times {10}^5$ bps, a significant enhancement of approximately 97% and 11% compared to conventional and iterative DFC schemes, respectively. Furthermore, the analysis reveals a critical trade-off between communication robustness and visual imperceptibility; allocating 70% of signal power to the image maintains high visual quality but results in a symbol error rate (SER) floor of $1.5\times {10}^{-1}$, whereas allocating only 10% improves the SER to below ${10}^{-2}$ at the cost of visible artifacts. The findings also identify QPSK as the optimal modulation order that maximizes the data rate, showing that higher-order schemes can be detrimental due to system impairments such as signal clipping. The proposed iDFC scheme presents a more efficient and robust solution for high-capacity DFC applications by balancing the competing demands of data throughput and visual fidelity.

1. Introduction

With the increasing number of screens and cameras in handheld devices, display-to-camera (D2C) communication [1,2] is becoming an alternative data transfer technology that can be compared to traditional QR codes [3,4] and 2D barcodes [5,6]. It can be considered as a sub-field of visible-light communication (VLC) [7,8] and optical camera communications (OCC) [9]. VLC primarily relies on data transfer through LEDs and photodiodes and has been explored for indoor wireless communications [10], underwater data transmission [11], and vehicular communication [12]. In OCC, data are transmitted by modulating the light intensity captured by the camera sensor. D2C communication involves data exchange between a visual display and a camera. In this approach, the display acts as a transmitter, emitting visual signals that are captured by the camera’s imaging sensor. The camera then decodes these signals to extract the embedded information. By utilizing the existing display and camera hardware in devices such as smartphones, tablets, and laptops, D2C communication has gained increasing interest and found applications in different domains, including mobile device interaction, augmented/virtual reality (AR/VR), interactive installations, digital signage, advertising, and even smart TVs. Furthermore, D2C communication can operate in real time, enabling interactive and dynamic data exchange between the display and the camera. This capability supports a wide range of potential applications across different domains, such as gaming, navigation, wayfinding, remote collaboration, education, retail, and training. For example, D2C communication enables a more immersive AR/VR experience. In museums or art exhibition settings, D2C communication allows users to access detailed information about a specific art.

D2C communication encompasses all kinds of screen–camera communication, including both obtrusive [13] and unobtrusive [1,2,14] modes. However, this paper focuses on unobtrusive D2C communication, where the data are embedded such that they remain invisible to the naked eye and can only be decoded by the receiver’s camera. This type of communication enables normal human viewing of the screen and data transfer simultaneously. It becomes challenging when embedding data in image frames unobtrusively, as it must not compromise the user’s normal viewing experience. In other words, the displayed image frames must not disrupt viewers who are not interested in receiving additional information. Hence, by employing the properties of the human visual system and image frames, data must be embedded covertly so that significant visual artifacts are not introduced on the screen. Data-embedding approaches in D2C communication can be broadly categorized into spatial- and spectral-domain-based mechanisms [15,16]. Spatial-domain embedding involves modifying the pixel values or arrangement within image or video frames. For instance, in MobiScan [14], data are first encrypted using different keys and then embedded into a set of frames by the visual pattern module proposed by the authors. In [1], the authors propose modulating the display brightness with a signal function that encodes the data to be transmitted. This method is simple to implement but more vulnerable to attacks [17,18]. Spectral-domain embedding involves manipulating the frequency or transform coefficients of a signal, typically using techniques such as the discrete Fourier transform, discrete cosine transform, or wavelet transform [19,20]. Information is embedded by modifying the coefficients in the spectral domain, rather than directly modifying the pixel values. Although more complex to implement, it offers increased robustness and security and is well suited for invisible embedding.

Display-field communication (DFC) [16] is a spectral-domain data-embedding scheme that embeds data into the frequency coefficients of an image frame [21,22]. Specifically, DFC utilizes a selected frequency range, called sub-bands, in the Fourier domain to embed data such that artifacts remain imperceptible to the human eye. This is achieved through multiplicative modulation of the image’s pixel values. Although DFC supports dual-mode, full-frame, visible communication, it requires a non-embedded reference frame for every data frame to enable decoding at the receiver [21]. This reference frame serves two purposes: (1) acting as a full-pilot frame for channel estimation and decoding and (2) preserving the visual integrity of the displayed content. However, transmitting one reference frame per data frame reduces the achievable data rate (ADR) by nearly 50%.

To address this, we previously proposed pilot-pixel-assisted modulation [23,24], which removes the need for reference frames by iteratively reconstructing them at the receiver. This approach involves transmitting pilot pixels and reconstructing the spectral image through an iterative process, utilizing the pilot symbol estimates. The main idea is to multiplex known pilot symbols with the unknown data pixels. The receiver first obtains tentative pixel estimates at the positions of the pilot pixels and then computes the data pixel estimates using interpolation. In addition to known pilot symbols, the receiver utilizes auxiliary pilot symbols, which are reliable symbol estimates obtained through piecewise cubic interpolation of the information symbols. Provided that an initial channel estimate is available, iterative channel estimation utilizes data symbol estimates fed back by the channel decoder. At subsequent iterations, channel estimates are refined by utilizing fed-back symbol estimates, which serve as auxiliary pilot symbols. The efficiency of the iterative approaches, however, depends on the reliability of the data estimates. While iterative DFC nearly doubles the data rate of conventional DFC [21], the pilot pixels still consume valuable bandwidth and reduce the data rate.

In this paper, we propose a blind reference frame estimation technique for DFC, referred to as implicit DFC (iDFC). Unlike prior approaches, iDFC requires neither reference frames nor explicit pilot symbols for channel estimation. Instead, we directly add the data symbols onto the frequency-domain coefficients, and the channel (reference frame) is estimated without sacrificing the data rate. The original image, which uses a fraction of the transmission power from the information sequence, is utilized for receiver channel estimation. Because there are no pilots, the reference frame estimation is carried out using the first-order statistics of the received image. At the receiver, the reference frame is reconstructed using a maximum likelihood (ML) estimator, which relies on statistical averaging of the received signal. This blind estimation allows for subsequent channel equalization and data recovery. The simulation results show that the proposed scheme offers increased bandwidth efficiency (overall data rate) and achieves performance far better than that of conventional and iterative DFC. We also verify that the proposed scheme shows robust performance and offers comparatively low computational complexity. The main contributions of this paper can be summarized as follows:

• We propose a new iDFC framework that significantly improves bandwidth efficiency by completely eliminating the need for separate reference frames or explicit pilot symbols used in previous DFC methods.
• We introduce a robust, blind channel estimation technique. This method reconstructs the reference frame at the receiver by using the first-order statistics of the received data-embedded image, allowing for effective channel equalization without any data-rate overhead.
• We demonstrate through simulations that by removing the overhead associated with reference frames, the proposed iDFC scheme boosts the achievable data rate (ADR) by approximately 97% compared to conventional DFC and 11% compared to iterative DFC systems.
• We provide an in-depth analysis of the system, quantifying the critical trade-off between visual imperceptibility and communication robustness (SER) as a function of the power allocation factor. Our analysis also identifies an optimal modulation order (QPSK) that maximizes the data rate under practical system impairments such as perspective distortion and channel noise.

The remainder of this paper is organized as follows. Section 2 details the proposed hidden-pilot-based DFC system model and the data-embedding process and describes the hidden pilot insertion technique, including the mechanism for data and power allocation. Section 3 describes the channel impairments—particularly the perspective distortion modeling and correction. In Section 4, we describe the data detection and decoding process. Section 5 presents a performance evaluation of the proposed iDFC scheme in terms of various system design parameters. We also compare our proposed method to conventional and iterative DFC schemes. Finally, Section 6 concludes the paper.

2. Overview of the Proposed iDFC Scheme

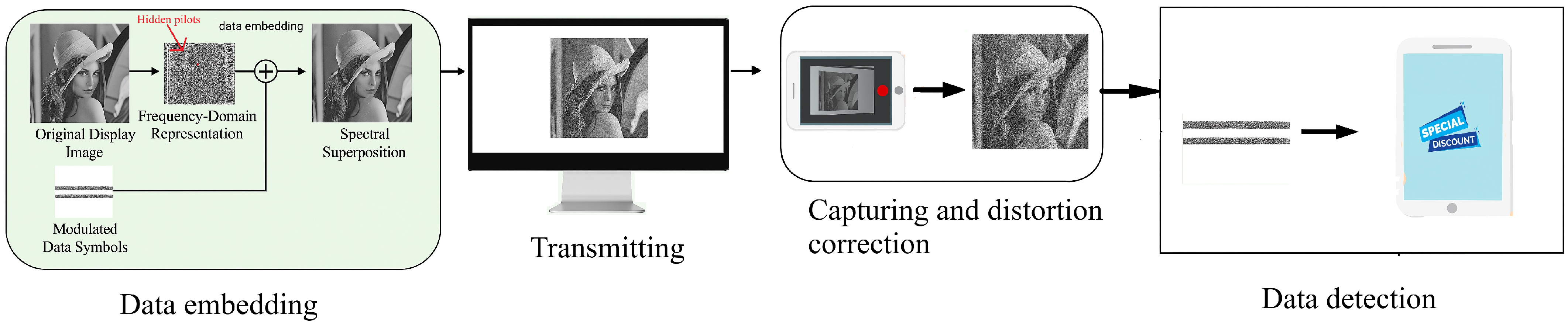
Our proposed end-to-end iDFC scheme for invisible data transmission from a display to a camera is depicted in Figure 1. The overall process can be broken down into four main stages: data embedding, transmitting, capturing and distortion correction, and data detection. The core innovation lies in eliminating the need for separate, bandwidth-consuming reference frames. Because no reference frame is required, this scheme can also be used for offline decoding—for example, extracting data from a photograph of a printed, data-embedded picture. First, the original display image is taken from its standard spatial domain and converted into the frequency domain. The result is a representation of the image in terms of its frequency coefficients. The information to be sent is converted into modulated data symbols. The key step is the additive embedding process, where the data symbols are scaled according to a power ratio and then added directly to the frequency coefficients of the original image. This process is known as spectral superposition. An inverse DFT is then performed to transform the image back into the spatial domain. The resulting data-embedded frame is visually indistinguishable from the original, making the embedded data completely unobtrusive to a human viewer. The data-embedded image is displayed on a screen, which acts as the transmitter in the communication link.

At the receiver, a camera captures the image being displayed on the screen. This process inevitably introduces noise and geometric distortions. Before the data can be read, the captured frame must be digitally processed. A crucial step is correcting for perspective distortion, which occurs when the camera is not perfectly parallel to the screen. The system models this distortion and applies a transformation to restore the image’s original rectangular geometry. Other channel effects, such as brightness and background noise, are also handled at this stage. The receiver takes the corrected image and transforms it back into the frequency domain. It then computes the first-order statistics of the received image to estimate the characteristics of the reference image—that is, how the image was distorted during transmission and capture. Using the reference frame estimate, the receiver can now accurately reverse the decoding of the data symbols. These symbols are then demodulated to reconstruct the original information.

2.1. System Model

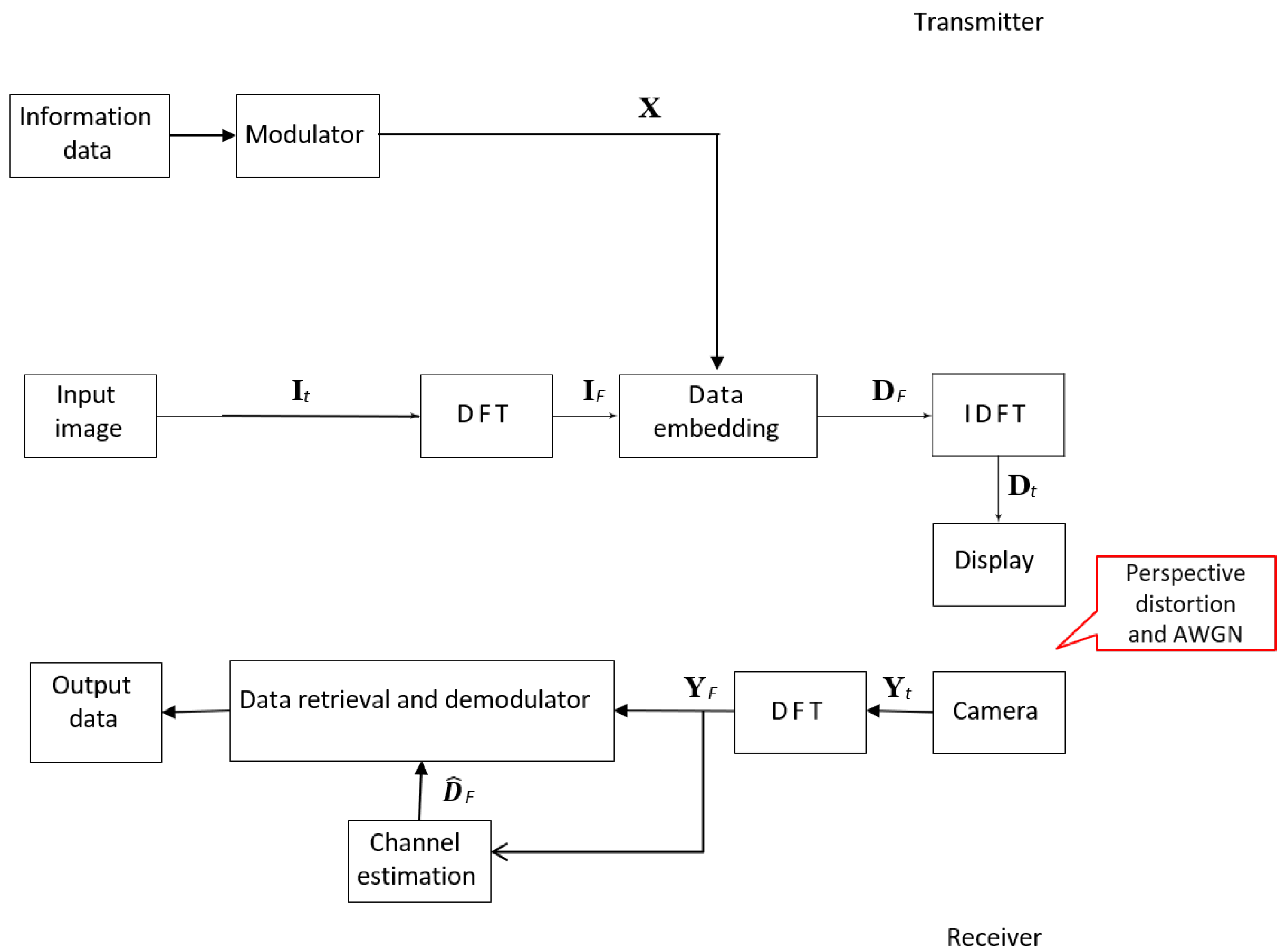
The signal flow diagram of our proposed iDFC system is illustrated in Figure 2. The process can be divided into the transmitter, the channel, and the receiver stages.

2.1.1. Transmitter

The process begins with the binary information data. These data are fed into a modulator (e.g., a QAM modulator), which maps the bits to complex symbols. The resulting matrix of modulated symbols is denoted by $\mathbf{X}$. To ensure that the final spatial-domain image is real-valued, a Hermitian symmetry constraint is applied to $\mathbf{X}$. Concurrently, the original input image, a spatial-domain signal denoted by ${\mathbf{I}}_t$, is transformed into its frequency-domain representation, ${\mathbf{I}}_F$, by applying a column-wise discrete Fourier transform (DFT). The core of the scheme lies in the data-embedding block. Here, the frequency-domain image ${\mathbf{I}}_F$ is additively combined with the scaled data matrix $\mathbf{X}$. This spectral superposition results in a new frequency-domain matrix ${\mathbf{D}}_F$, which now contains both the original image information and the hidden data. Finally, to prepare the image for display, the combined matrix ${\mathbf{D}}_F$ is converted back into the spatial domain using an inverse DFT (IDFT), yielding the final data-embedded image, ${\mathbf{D}}_t$. This image, which is visually indistinguishable from the original, is then sent to the display screen, which acts as the transmitter.

2.1.2. Channel and Receiver

The communication link between the display and the camera is subject to real-world impairments, primarily perspective distortion (due to the camera’s angle) and additive white Gaussian noise (AWGN) from ambient light and camera sensor noise. The camera at the receiver captures the distorted screen, producing the received spatial-domain image, ${\mathbf{Y}}_t$. After correcting for geometric distortions, the image ${\mathbf{Y}}_t$ is converted to the frequency domain via DFT, resulting in ${\mathbf{Y}}_F$. The key innovation occurs in the channel estimation block. The received signal ${\mathbf{Y}}_F$ is processed using our proposed statistical method to generate a blind estimate of the transmitted reference frame’s spectrum. This estimated reference is denoted by ${\widehat{\mathbf{D}}}_F$. Finally, in the data retrieval and demodulator block, the estimated reference ${\widehat{\mathbf{D}}}_F$ is subtracted from the received signal ${\mathbf{Y}}_F$ to isolate the embedded data symbols. These symbols are then demodulated to recover the original output data, completing the communication process.

2.2. Data Embedding

The first step in our data-embedding process is to convert the spatial-domain image, which consists of pixel intensity values, into its frequency-domain representation. This is achieved by applying a one-dimensional DFT to each column of the image matrix independently. The transformation for the entire image ${\mathbf{I}}_t$ is expressed as follows [21]:

$$\begin{array}{cc}\hfill {\mathbf{I}}_F& =\left[{\mathbf{i}}_{F_1},{\mathbf{i}}_{F_2},\dots ,{\mathbf{i}}_{F_Q}\right]\hfill \\ \hfill & =\left[\mathbf{F}·{\mathbf{i}}_{t_1},\mathbf{F}·{\mathbf{i}}_{t_2},\dots ,\mathbf{F}·{\mathbf{i}}_{t_Q}\right]=\mathbf{F}·{\mathbf{I}}_t,\hfill \end{array}$$

(1)

where ${\mathbf{I}}_t\in {\mathbb{R}}^{P\times Q}$ is the original spatial-domain image with P rows and Q columns. The resulting matrix, ${\mathbf{I}}_F\in {\mathbb{C}}^{P\times Q}$, is its frequency-domain representation. Here, $\mathbf{F}\in {\mathbb{C}}^{P\times P}$ represents the DFT matrix, and the vectors ${\mathbf{i}}_{t_q}$ and ${\mathbf{i}}_{F_q}$ represent the q-th columns of the spatial image ${\mathbf{I}}_t$ and frequency image ${\mathbf{I}}_F$, respectively. The elements of the DFT matrix are given by

$${\left[\mathbf{F}\right]}_{p,k}={\displaystyle \frac{1}{\sqrt{P}}}{e}^{-j{\displaystyle \frac{2\pi pk}{P}}},\mathrm{for}p,k\in \{0,1,\dots ,P-1\}.$$

(2)

In the resulting frequency-domain image ${\mathbf{I}}_F$, each point represents a particular frequency contained in the spatial-domain image. The results of the 1D-DFT exhibit low-frequency components on both sides of each column vector ${\mathbf{i}}_{F_q}$, while high-frequency components are symmetrically located in the central region. In other words, the low-frequency components, which contain most of the image’s structural information, are located at the top and bottom of each column vector, while the high-frequency components, which correspond to finer details and textures, are situated in the center.

For data embedding, we consider high-frequency sub-bands of the spectral-domain image. This choice is motivated by the fact that most of an image’s visual characteristics reside at lower frequencies, while details and noise tend to be present at higher frequencies. Since the human visual system is more sensitive to lower frequencies, the use of low-frequency components for data embedding would create visible artifacts and distract the human observer [21]. If $\mathbf{X}=\left[{\mathbf{x}}_1,{\mathbf{x}}_2,\dots ,{\mathbf{x}}_Q\right]$ represents a $P\times Q$ data matrix to be embedded, the structure for each column vector ${\mathbf{x}}_q$ is defined as follows:

$${\mathbf{x}}_q={\left[{\mathbf{0}}_{1\times (\kappa -1)}{\left({\mathbf{s}}_q\right)}^T{\mathbf{0}}_{1\times \gamma }{\left(\mathrm{flip}\left({\mathbf{s}}_q^{*}\right)\right)}^T{\mathbf{0}}_{1\times (\kappa -2)}\right]}^T,$$

(3)

where the parameters are defined as follows:

• $\kappa$: The starting row index for data embedding in the frequency domain.
• $s_q$: Column vector ${[s_q\left(1\right),\dots ,s_q\left(L\right)]}^T$ containing the L complex data symbols to be embedded in the q-th column of the image.
• L: The number of data symbols embedded per column.
• $\gamma$: The number of zero-padding elements used for spacing between the data and their conjugate, calculated as $\gamma =P-2\kappa -2L+3$.
• $flip\left(s_q^{*}\right)$: The conjugate symmetric counterpart of the data vector, given by ${[s_q^{*}\left(L\right),\dots ,s_q^{*}\left(1\right)]}^T$. This is required to ensure that the IDFT of the combined signal results in a real-valued image suitable for display.
• ${\mathbf{0}}_{1\times N}$: A row vector of N zeros used for padding to ensure that data are only placed in the designated high-frequency sub-bands.

The parameters $\kappa$ and L must satisfy $\kappa +L=P/2+2$ to properly position the data in the high-frequency region of the spectrum. In this manner, the data structure encompasses an $L\times Q$ rectangular region, as well as an additional $L\times Q$ conjugate symmetric region in the frequency-domain representation. The remaining elements are populated with $\mathbf{0}$s to ensure that only the specified high-frequency components are altered during the additive embedding process.

Figure 3a presents the original image, a grayscale Lena image, used for data embedding in our simulations. Figure 3b illustrates the location of the data-embedding region within the high-frequency sub-bands. This image is a map of the 2D frequency domain, showing exactly where the data are placed. The two horizontal white bands represent the data-embedding regions, while the black areas correspond to the frequency coefficients that are left unchanged. The bands are located in the high-frequency areas, avoiding the low-frequency information at the top and bottom of the frequency map.

In the proposed scheme, the original frequency-domain coefficients of the image itself $\left({\mathbf{I}}_F\right)$ serve as the unknown channel (reference image frame). The data embedding is performed by additively combining the modulated data symbols directly with image coefficients at high-frequency locations. The matrix of data symbols to be embedded, $\mathbf{X}$, is constructed as defined by the structure in Equation (3). To control the embedding strength, these data symbols are scaled by a power allocation factor, $\alpha$. The final data-embedded image matrix, ${\mathbf{D}}_F$, in the frequency domain is then generated by adding the scaled data matrix to the original frequency-domain image:

$${\mathbf{D}}_F=\sqrt{\alpha }{\mathbf{I}}_F+\left(\sqrt{1-\alpha }\right)\mathbf{X},$$

(4)

where $\alpha$ is the image-to-data power ratio ($0<\alpha <1$). This factor determines the power of the embedded data relative to the power of the original image content. By keeping $\alpha$ high, we ensure that the embedding remains imperceptible. Once the data-embedded frequency-domain matrix ${\mathbf{D}}_F$ is created, it is converted back to the spatial domain using the following IDFT operation:

$${\mathbf{D}}_t={\mathbf{F}}^H·{\mathbf{D}}_F,$$

(5)

where ${(·)}^H$ denotes the Hermitian transpose operator. Note that the above equation introduces a nonlinear distortion during the operations of clipping and quantization.

The primary advantage of the proposed iDFC scheme is its high spectral efficiency. By eliminating the need for separate reference frames, the ADR is more than doubled compared to conventional DFC. This creates a fundamental trade-off: to maintain visual imperceptibility, the power allocated to the data must be kept low relative to the image content, which can lead to a higher symbol error rate (SER). A key benefit of our approach is that all the pixels are now used to transmit the data, and the receiver performs estimation across all data-bearing symbols, which eliminates the need for channel interpolation and makes the scheme robust in dynamic channel conditions. In other words, there is no need to send the reference frames, as in conventional DFC [21], or to insert pilot symbols, as in iterative DFC [23].

3. Perspective Distortion

In practical DFC scenarios, perspective distortion arises when the camera is not perfectly aligned with the display. This misalignment causes geometric deformation in the captured image, which can misplace embedded data in the spectral domain and degrade symbol recovery. The geometric relationship between the original display’s coordinates and the captured image’s coordinates can be modeled using a 2D projective transformation, also known as a homography matrix $\mathbf{H}$. The general form of a homography matrix $\mathbf{H}\in {\mathbb{R}}^{3\times 3}$ is given as [25]

$$\mathbf{H}=\left[\begin{array}{ccc}{h}_{11}& h_{12}& h_{13}\\ h_{21}& h_{22}& h_{23}\\ h_{31}& h_{32}& h_{33}\end{array}\right].$$

(6)

The eight parameters of $\mathbf{H}$ are calculated by finding at least four corresponding points between the source display and the captured image (e.g., the corners of the screen). This transformation is applied to each pixel coordinate $\mathbf{p}={[x,y,1]}^T$ in the display image to obtain its corresponding coordinate ${\mathbf{p}}^{\prime }$ in the distorted image as follows:

$${\mathbf{p}}^{\prime }=\mathbf{H}·\mathbf{p}.$$

(7)

To decode the embedded information, these display boundaries must first be detected in the captured frame using computer vision techniques such as Harris corner detection. Once the corner points are found and the homography $\mathbf{H}$ is estimated, the receiver recovers the original data alignment by applying the inverse transformation ${\mathbf{H}}^{-1}$ to warp the distorted frame back to its original rectangular grid. During this rectification process, interpolation is used to estimate pixel values at non-integer coordinates. The preprocessed image can then be demodulated with improved reliability. While the proposed iDFC method exhibits partial robustness to minor distortions, significant warping can still degrade the statistical estimation used for channel correction. Therefore, accurate rectification is a crucial preprocessing step.

Figure 4 demonstrates the impact of perspective distortion on a D2C link and the effectiveness of the subsequent geometric restoration. The distortion in Figure 4a, caused by a projective transformation, skews the image’s rectangular grid into a trapezoidal shape. The restored image (cf. Figure 4b) recovers its correct alignment by compensating for this deformation. This correction is a crucial pre-processing step for a practical DFC receiver, as it ensures the integrity of the spatial data before the information is extracted.

4. Data Detection

The key advantage of the implicit pilot scheme is the ability to use all pixels for both channel estimation and data detection. However, data signals may cause interference in the channel estimation process. This interference degrades the estimation quality and can create a correlation between the channel estimates and the data. Note that realizing an ideal separation between the data and channel coefficients at the receiver is difficult [26], and the recovered reference image signal inevitably consists of data interference, which, in turn, affects the accuracy of the channel estimation. For our analysis, we assume a simplified channel model. We consider a perfect alignment between the data-transmitting screen and the camera. That is, all the light-emitting pixels from the screen are at the focus of the camera pixels, resulting in no loss of data signal energy on the pixel. Therefore, in the given scenario, we consider the AWGN channel as the loss in signal energy on a pixel; this is also attributed to the noise in that pixel. Moreover, the AWGN also captures the primary impairment from the camera sensor and background illumination, which corrupts the intensity values in the captured image. Therefore, the received spatial-domain image ${\mathbf{Y}}_t$ can be expressed as

$${\mathbf{Y}}_t={\mathbf{D}}_t+{\mathbf{N}}_t,$$

(8)

where ${\mathbf{N}}_t$ is the AWGN matrix. The received spatial-domain image is then converted to the frequency domain as

$${\mathbf{Y}}_F=\mathbf{F}·{\mathbf{D}}_t+\mathbf{F}·{\mathbf{N}}_t={\mathbf{D}}_F+{\mathbf{N}}_F.$$

(9)

All subsequent processing is performed in the frequency domain.

Since data are embedded in only L specific rows of the transmitted image, we can analyze these rows individually. Let the set of row indices be $\{l_1,l_2,\dots ,l_L\}$. The relationship for each row vector is given as

$${\mathbf{y}}_{l_k}={\mathbf{d}}_{l_k}+{\mathbf{n}}_{l_k},\mathrm{for}k=1,2,\dots ,L.$$

(10)

Assuming that the noise samples are i.i.d. Gaussian random

$$f_{{\mathbf{Y}}_{l_k}}\left({\mathbf{y}}_{l_k}\right)={\left({\displaystyle \frac{1}{2\pi {\sigma }^2}}\right)}^{Q/2}exp\left(-{\displaystyle \frac{1}{2{\sigma }^2}}{∥{\mathbf{y}}_{l_k}-{\mathbf{d}}_{l_k}∥}^2\right).$$

(11)

The joint p.d.f. of L observations is given as

$$f_{{\mathbf{Y}}_{l_1}{\mathbf{Y}}_{l_2}\dots {\mathbf{Y}}_{l_L}}({\mathbf{y}}_{l_1}{\mathbf{y}}_{l_2}\dots {\mathbf{y}}_{l_L})={\left({\displaystyle \frac{1}{2\pi {\sigma }^2}}\right)}^{LQ/2}exp\left(-{\displaystyle \frac{1}{2{\sigma }^2}}\sum _{k=1}^L{∥{\mathbf{y}}_{l_k}-{\mathbf{d}}_{l_k}∥}^2\right).$$

(12)

Note that ${\mathbf{d}}_{l_k}$ is an unknown and is the summation of data and the image frequency-domain coefficient. Now, considering the above joint p.d.f. as a function of the unknown parameter ${\mathbf{d}}_{l_k}$ gives us the likelihood function. In this paper, we use the framework of the log-likelihood estimate to find the values of the unknown parameter for which the likelihood function is at the maximum. Hence, Equation (12) is defined as the likelihood function $\mathcal{P}({\mathbf{y}}_l;{\mathbf{d}}_l)$, defined as the likelihood of observation ${\mathbf{y}}_l$ parameterized by ${\mathbf{d}}_l$, where ${\mathbf{y}}_l={\left[{\mathbf{y}}_{l_1,}{\mathbf{y}}_{l_2},\dots ,{\mathbf{y}}_{l_L}\right]}^T$. Hence, the log likelihood function is defined as

$$\mathcal{L}\left(\mathbf{y};\mathbf{d}\right)=ln\mathcal{P}(\mathbf{y};\mathbf{d})=ln\left[{\left({\displaystyle \frac{1}{2\pi {\sigma }^2}}\right)}^{LQ/2}exp\left(-{\displaystyle \frac{1}{2{\sigma }^2}}\sum _{k=1}^L{∥{\mathbf{y}}_{l_k}-\overline{\mathbf{d}}∥}^2\right)\right],$$

(13)

assuming ${\mathbf{d}}_{l_1}\approx {\mathbf{d}}_{l_2}\approx \dots \approx {\mathbf{d}}_{l_L}=\overline{\mathbf{d}}$, where $\overline{\mathbf{d}}$ is the constant row vector that we want to estimate. Now, maximizing the log-likelihood function with respect to the single unknown vector $\overline{\mathbf{d}}$ yields the maximum likelihood (ML) estimate as follows (see Appendix A):

$${\widehat{\mathbf{d}}}_{ML}={\displaystyle \frac{1}{L}}\sum _{k=1}^L{\mathbf{y}}_{l_k}.$$

(14)

This shows that the ML estimate of the transmitted signal is the sample mean of the observed row vectors. As proven in Appendix B, this estimator is unbiased, and its variance is inversely proportional to L, which mathematically confirms how averaging reduces the effect of noise. Expanding the above mathematics to the whole received image will yield an estimated reference frame spectrum ${\widehat{\mathbf{D}}}_F\in {\mathbb{C}}^{P\times Q}$, where the data-embedded rows are replaced with the estimate ${\widehat{\mathbf{d}}}_{ML}$. Then, using the subtraction receiver, we can extract the data components as follows:

$${\widehat{\mathbf{X}}}_F={\mathbf{Y}}_F-{\widehat{\mathbf{D}}}_F.$$

(15)

After the data symbols are extracted, QAM demodulation is applied to recover the transmitted bits.

5. Simulation Results

For the simulations, we assume perfect frame synchronization between the display and camera. Moreover, the camera’s frame rate is assumed to be greater than or equal to the display’s frame rate to ensure that every frame is captured successfully. We use a standard $256\times 256$ grayscale Lena image as the host content. The input information sequence is composed of i.i.d. equiprobable QAM symbols. A total of 20 frequency sub-bands are allocated for data transmission, positioned symmetrically within the high-frequency region. The power of the embedded data is controlled by the data-to-signal power ratio, $\alpha$, which is varied to analyze its impact on performance. Moreover, the DFC channel was simulated as an AWGN channel. A subtraction receiver was implemented. This receiver first estimates the reference frame from the received signal using the ML estimate. The estimation is carried out using statistical averaging of the symmetric frequency rows, under the assumption that the embedded data are zero-mean. The subtraction receiver then subtracts the estimated pilot spectrum to isolate the data components, which are subsequently demodulated. The default simulation parameters are mentioned in

Table 1. Default simulation parameters.

Parameter	Value
Host image	Grayscale ‘Lena’
Image resolution ($P\times Q$)	$256\times 256$ pixels
Channel	Perspective distortion + AWGN
Receiver type	Subtraction with ML estimation
Input data symbols	i.i.d. equiprobable QAM symbols
Modulation	BPSK (M = 2), QPSK (M = 4), 8-QAM, 16-QAM
Data sub-bands (L)	20
Image-to-data power ratio	$\alpha \in [0.1,0.9]$
Display frame rate	30 fps

.

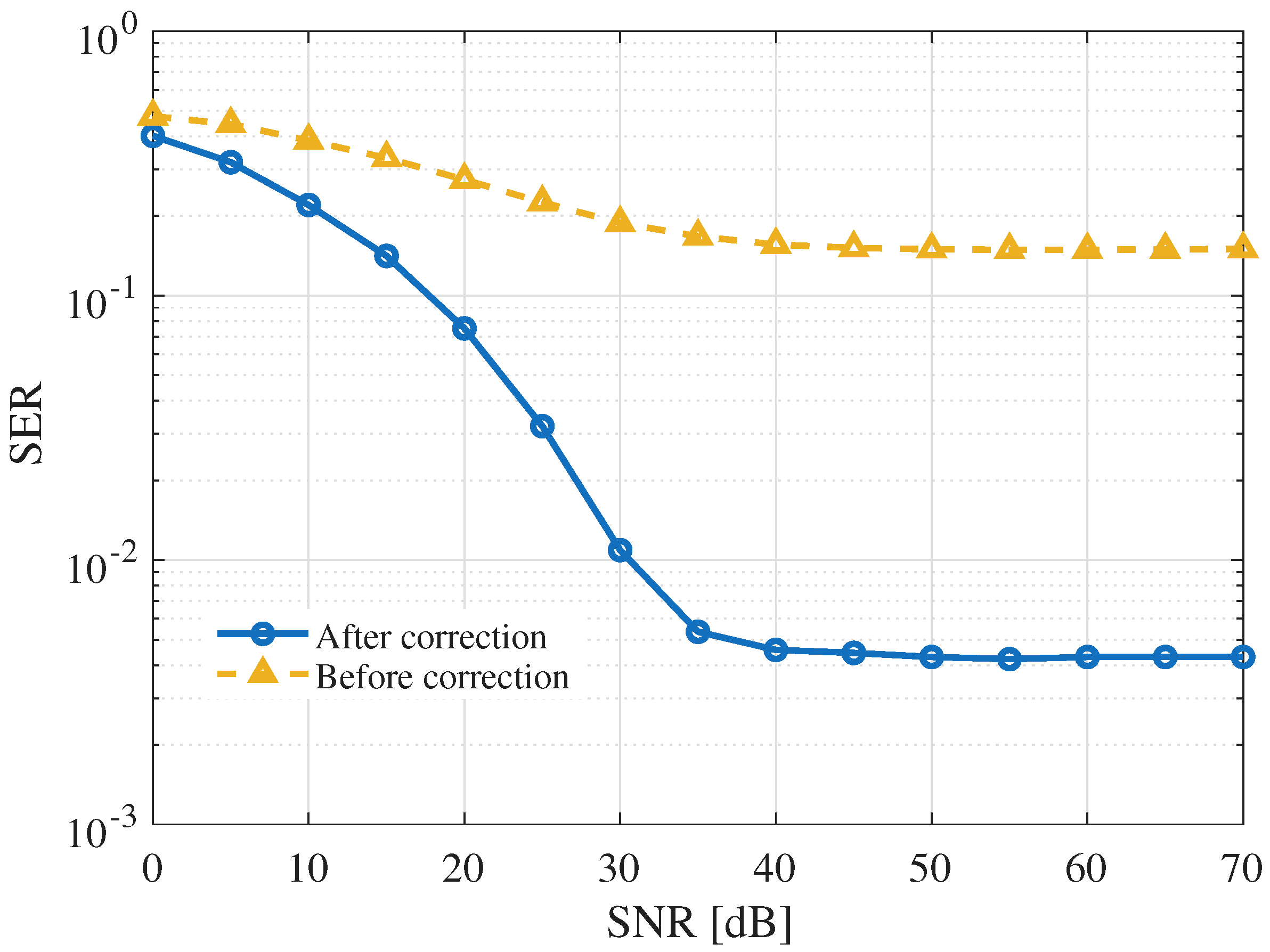
First, we look at the effect of perspective distortion. As shown in Figure 5, the ‘after correction’ curve has a waterfall shape, and the error floor is higher than the ‘before correction’ case. This performance gap is caused by the pixel interpolation that occurs during the distortion correction process. This shows that the perspective correction step is an absolutely necessary step in DFC. Without correction, the geometric distortion is so severe that the decoder cannot locate the data correctly, making its performance no better than a random guess.

Next, let us look at the visual imperceptibility of data embedding for different image-to-data power ratios, $\alpha$, depicted in Figure 6. An alpha of 0.1 means that 10% of the power is allocated to the image (and 90% to data). This visual comparison is a qualitative assessment of imperceptibility—how well the hidden data are concealed from the human eye. When the image power is low, the most visible distortion is observed in Figure 6a. In other words, since the data power is high (90%), the embedded data dominates the frequency components, resulting in visible artifacts. This confirms that very low image power compromises image quality. On the other hand, if we increase the image power, there is a significant improvement in imperceptibility. In Figure 6b,c, distortion is still visible upon close inspection, but the structure of the original image is better preserved. Finally, Figure 6d, which has 70% image power, has the least perceptible distortion. The image appears smooth and nearly identical to the original (cf. Figure 3a).

Figure 7 illustrates the SER performance of the proposed system as a function of the SNR for various image power allocation ratios, $\alpha$. The plot demonstrates a clear and direct relationship between the image power allocation and system performance. As the $\alpha$ increases from 0.1 to 0.7, the overall SER performance gets progressively worse at all SNR values. This is because as $\alpha$ is increasing, the power loaded onto the data symbols decreases simultaneously, resulting in a worse SER. In other words, when the image power is low, the data power is high. This strong data signal is robust against channel noise, resulting in a low SER. More importantly, the low overall signal amplitude causes minimal clipping, so the signal distortion is low. In addition, the results clearly demonstrate the impact of power allocation between the image signal and the data signal. First, we observe that all curves exhibit an error floor. This floor arises from inherent system errors, including clipping and quantization noise after IDFT, imperfect channel estimation using image averaging, and image-data interference in non-orthogonal embedding. The SER improves as the SNR increases up to a certain point, after which the curves flatten out. Further increases in the SNR do not improve the SER. This indicates that at high SNRs, the performance is limited by a factor other than channel noise.

The above results reveal a trade-off between visual imperceptibility and detection performance in the proposed iDFC system. As illustrated in Figure 7, reducing the image power significantly improves the SER due to the stronger data signal. However, this comes at the cost of noticeable visual artifacts (cf. Figure 6). Conversely, increasing the image power enhances visual quality by preserving the host image spectrum, but it weakens the embedded data, leading to an increased SER. This trade-off necessitates careful tuning of the power allocation factor $\alpha$ to strike a balance between communication reliability and visual transparency, depending on the target application constraints.

Next, we computed the ADR of the system, which represents the effective throughput of useful information. Mathematically, it can be related to the maximum theoretical data rate and SER as follows:

$$\mathrm{ADR}=R_{\max }(1-\mathrm{SER}),$$

(16)

where $R_{\max }$ is the maximum theoretical data rate in bits per second (bps). It can be determined by the system’s configuration as follows:

$$R_{\max }=N_{\mathrm{data}}{log}_2\left(M\right)R_f,$$

(17)

where $N_{\mathrm{data}}$ represents the total number of data-carrying pixels per frame, M denotes the modulation order, and $R_f$ stands for the frame rate of the display in frames per second.

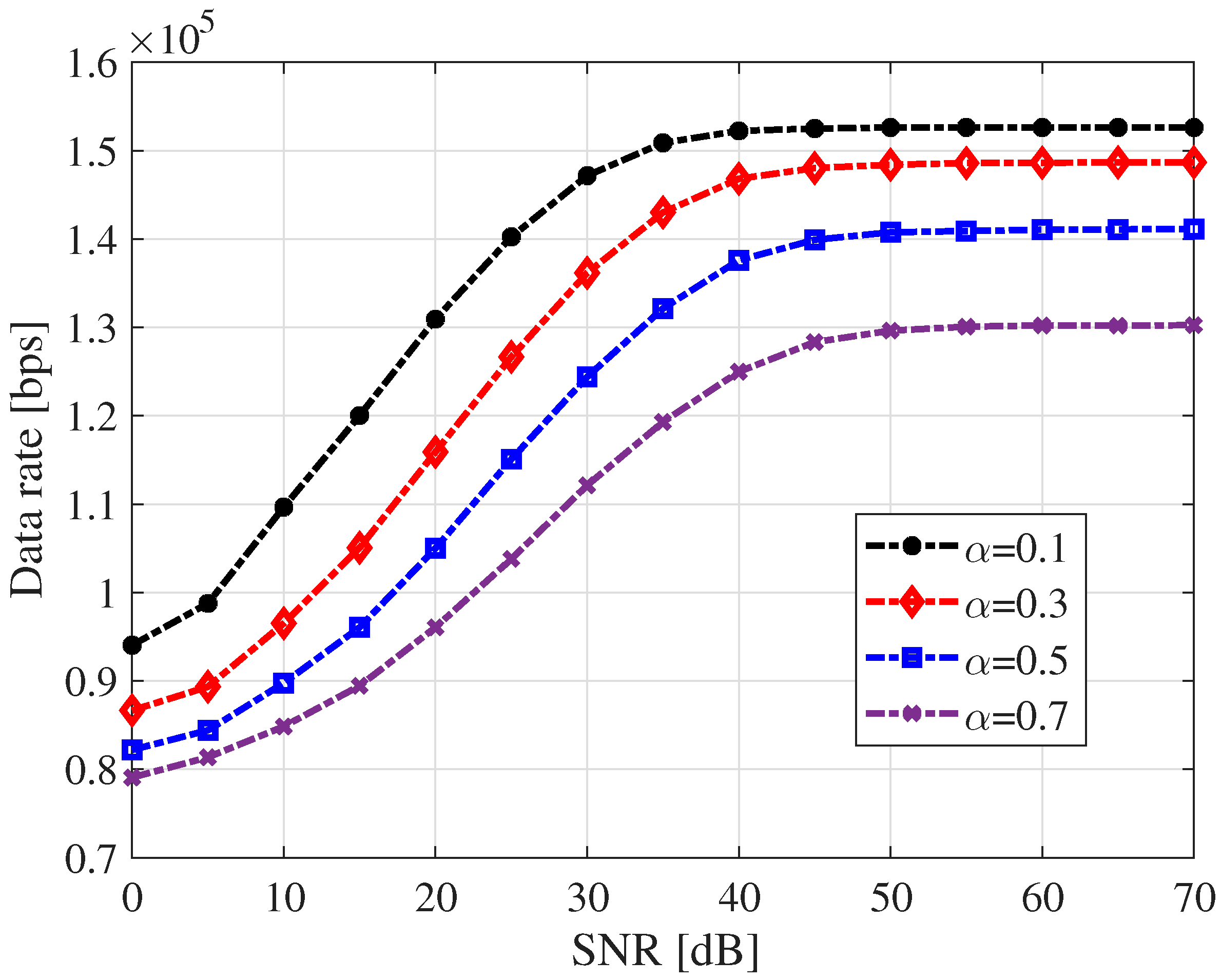
Figure 8 illustrates the ADR as a function of the SNR for different image power allocations. First, it is observed that for every power allocation, the ADR increases with the SNR until it reaches a saturation point at high SNR values. This indicates that beyond a certain point, improving the channel quality with a higher SNR yields no further increase in data throughput. This saturation occurs because the SER hits an error floor, as shown in Figure 7. At high SNRs, the performance is no longer limited by channel noise but by the various distortions caused by the system behavior. Second, the plot shows a clear inverse relationship between the image power and the maximum ADR. The configuration with the lowest image power achieves the highest ADR and vice versa. A lower image power means a higher data power. This leads to a better SER and, hence, ADR. In other words, the system successfully transmits more useful, error-free data.

5.1. Data Rate vs. Imperceptibility Trade-Off

To provide clear, quantitative guidance for selecting the power allocation factor $\alpha$, we evaluated the trade-off between the ADR and visual imperceptibility. We used the peak signal-to-noise ratio (PSNR) as the objective metric for image quality, where a higher PSNR value indicates less distortion and better imperceptibility. Figure 9 presents the Pareto frontier for our proposed iDFC system, illustrating the fundamental trade-off. The downward slope of the curve clearly demonstrates the inverse relationship between data throughput and visual fidelity. Each point on the curve represents an optimal operating point for a given image-to-data power ratio, $\alpha$. The top-left portion of the curve corresponds to low $\alpha$ values. At $\alpha$ = 0.1, the system achieves its maximum data rate, exceeding $1.5\times {10}^5$ bps. This is because a low $\alpha$ allocates most of the signal power to the data, making the transmission robust against noise and minimizing the symbol error rate. However, this high-power data signal significantly distorts the host image, resulting in the lowest image quality, with a PSNR below 30 dB. On the other hand, the bottom-right portion of the curve corresponds to high $\alpha$ values. At $\alpha$ = 0.9, the system achieves the best visual quality, with a PSNR approaching 48 dB, making the embedded data virtually invisible to the human eye. This high fidelity is achieved by allocating most of the power to the image itself. The trade-off is a significantly weaker data signal, which leads to a higher error rate and reduces the ADR to its lowest point.

This Pareto frontier serves as a valuable practical guide for system implementation. The choice of $\alpha$ depends directly on the priorities of the target application. For applications where visual quality is critical, such as digital art displays or premium advertising, we should choose a high $\alpha$ value (e.g., $\alpha \ge 0.7$) to ensure high imperceptibility. For applications where maximizing the data rate is paramount and slight visual artifacts are acceptable, a low $\alpha$ value (e.g., $\alpha$≤ 0.3) is the optimal choice. A balanced approach is represented by the “knee” of the curve (around $\alpha$ = 0.5), which offers a strong data rate of approximately $1.4\times {10}^5$ bps while maintaining a respectable PSNR of 38 dB.

5.2. Comparative Evaluation with Related Schemes

Figure 10 compares the achievable data rates of three DFC schemes: conventional DFC [21], iterative DFC [23], and the proposed iDFC. For a fair comparison, the best-case scenarios of all schemes that provide the lowest SERs are considered. In particular, the results of the seventh iteration are utilized for the iterative DFC [23], and $\alpha =0.1$ is utilized for the iDFC scheme. The results demonstrate that the iDFC method achieves the highest throughput, making it the most bandwidth-efficient DFC scheme. As mentioned above, in the conventional DFC, a separate, unaltered reference image frame is explicitly inserted between every data-embedded image frame to support data decoding, which resulted in 50% image overhead. Therefore, it uses half of its transmission time just to send reference information. In iterative DFC, we eliminate the use of reference frames by embedding images within the same frame and using auxiliary image refinement at the receiver to enhance image estimation over multiple iterations. This method is a significant improvement over the conventional DFC because every frame carries data, effectively improving the potential throughput, particularly in the high-SNR region. However, its performance is still limited by the use of dedicated pixels as image pixels, resulting in 10% image overhead. Moreover, the scheme is computationally complex due to the overhead of the iterative process, where each iteration has matrix operations. In the proposed iDFC scheme, as we are not transmitting explicit pilot symbols and the implicit frequency-domain image works as a reference image, there are no dedicated pixels working as pilot pixels. In other words, the data are multiplexed with the implicit image pixels in all sub-bands. We can observe from the figure that it significantly boosts the data rate, particularly in the low-to-mid-SNR region (10–40 dB). Even though the embedded data act as interference, through efficient power utilization, this interference can be reduced.

To contextualize the proposed iDFC, we compared it against widely referenced screen-to-camera communication schemes in

Table 2. Comparison of the proposed scheme with other screen–camera communication schemes.

Scheme	Embedding Domain	Channel Estimation/ Synchronization	Data Overhead	Imperceptibility Method	Reported Throughput
InFrame [27]/ InFrame++ [2]	Spatial/Temporal	Visible locators and alignment patterns	Low	Leverages the flicker-fusion property of human vision; requires high refresh rate displays (120 Hz).	150–360 kbps
ChromaCode [28]	Spatial/Temporal	Code borders and featured lines	Low	Outcome-based adaptive lightness changes to guarantee imperceptibility.	120 kbps (goodput); >700 kbps (raw)
MobiScan [14]	Spatial/Temporal	Locators + smartphone sensors	Low	Based on flicker-fusion principles similar to InFrame++.	190 kbps
DeepLight [29]	Spatial/Temporal	DNN-based screen extractor (no locators needed)	None	Modulates only the Blue color channel, making it highly imperceptible even on standard 60 Hz displays.	1–4.7 kbps
Proposed iDFC	Spectral (DFT)	Blind (first-order statistics)	None	Data are embedded in high-frequency bands; quality is tunable via the power ratio $\alpha$.	∼152 kbps

Notes: The reported results reflect each paper’s settings (display, camera, distance, coding).

. We observe that iDFC achieves the highest ADR in the low-to-mid-SNR region while incurring zero image overhead.

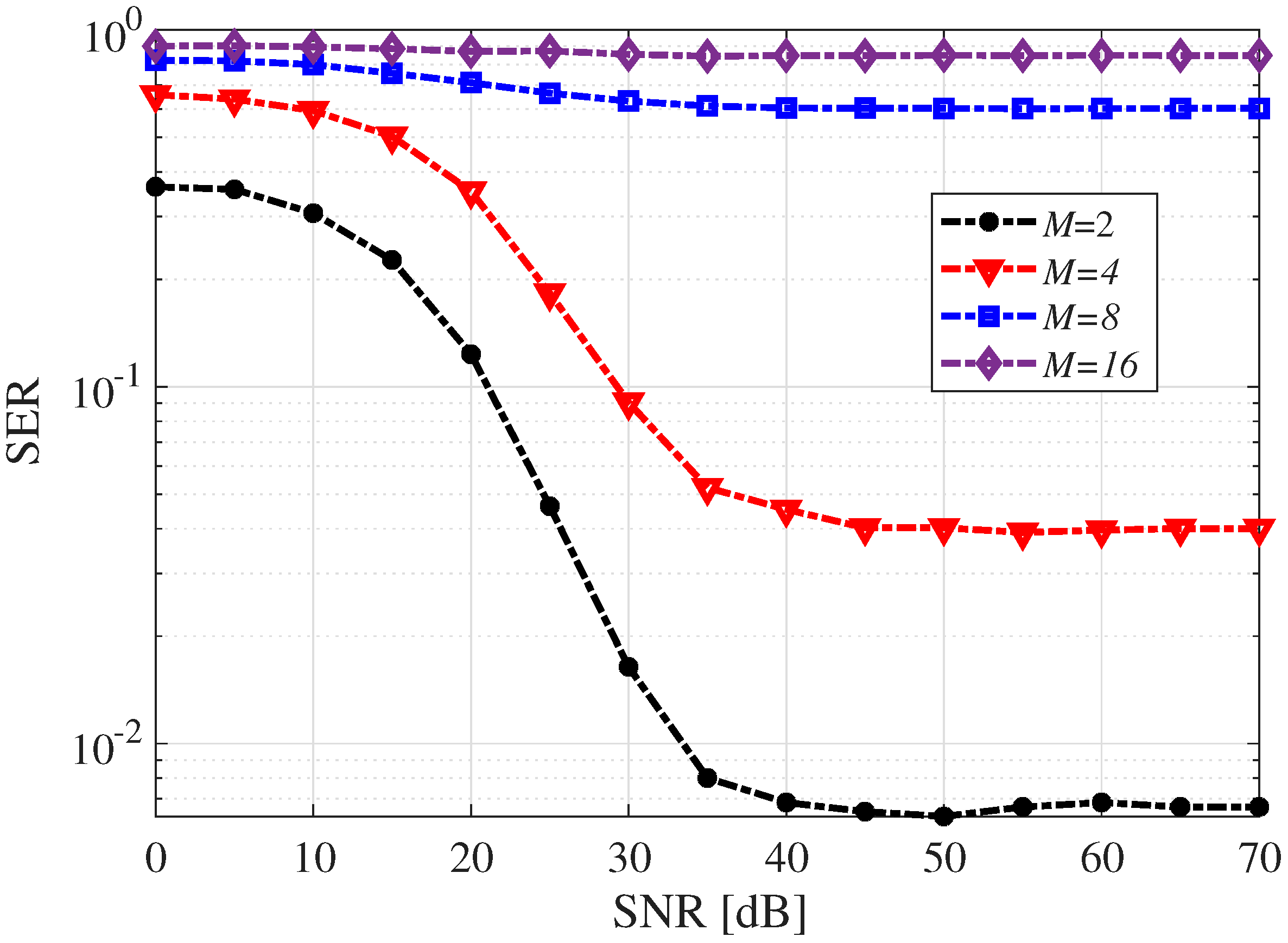
Figure 11 illustrates the SER performance of the proposed iDFC system across different modulation orders (M). It can be observed that a higher M yields a higher SER. This is due to the denser constellation points in higher-order QAM, which are more susceptible to noise and distortion. In addition, the SER saturates at high SNRs, forming an error floor due to the presence of non-Gaussian errors. Overall, lower-order modulations, such as BPSK ($M=2$) and QPSK ($M=4$), are robust and exhibit sharp SER reductions above 20 dB, making them suitable for low-SNR or high-fidelity applications. Although higher-order modulation allows more bits to be transmitted per symbol, maintaining the same average signal energy requires constellation points to be placed closer together. As a result, the Euclidean distance between adjacent symbols decreases, making the system more prone to symbol errors in the presence of noise or distortion. These effects become more pronounced as the SNR increases. The results highlight the trade-off between spectral efficiency and robustness in modulation design for DFC systems.

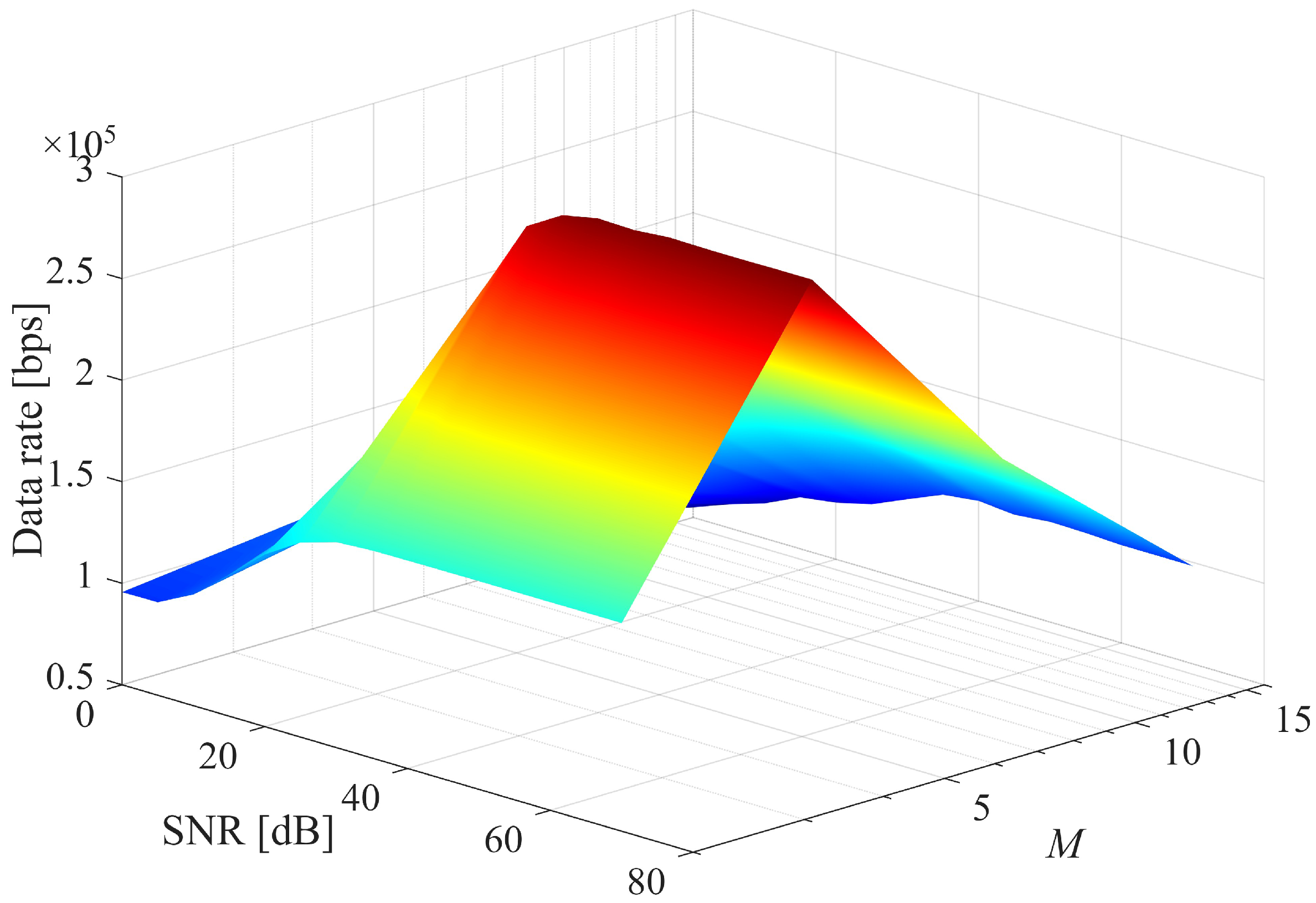
Figure 12 illustrates how the ADR varies with both the SNR and the modulation order. The data rate initially increases with both the SNR and M but then drops beyond $M=4$ at high SNRs. This results in a ridge-like peak, showing that there is an optimal M for each SNR that maximizes the data rate. For a fixed modulation order, increasing the SNR improves the data rate until it saturates. This is because the SER drops with the SNR, allowing more symbols to be decoded correctly. Regarding the effect of M, increasing M increases the spectral efficiency (more bits per symbol). However, beyond a point ($M=4$), symbol errors due to noise and tightly packed constellation points dominate, reducing the net data rate. This drop is more visible at higher M and moderate SNRs, where the decoder struggles to distinguish adjacent constellation points. This underscores the trade-off between spectral efficiency and robustness in practical iDFC systems.

5.3. Complexity Analysis

The primary computational difference between the conventional DFC [21] and our proposed iDFC lies at the receiver. The complexity is dominated by the DFT operations, which, using the fast Fourier transform algorithm, is $\mathcal{O}(NlogN)$ for an N-point transform [30,31,32]. For a $P\times Q$ image processed column-wise, the complexity becomes $\mathcal{O}(QPlogP)$.

Table 3. Comparison of the complexity of the proposed scheme with the conventional DFC scheme.

Scheme	Conventional DFC [21]	Proposed iDFC	Complexity
Frame processing	Requires processing two frames (a reference frame and a data frame).	Requires processing only one frame (the data frame).	N/A
DFT operations	Performs a full DFT on the reference frame AND the data frame.	Performs a single full DFT on the received data frame.	$\mathcal{O}(QPlogP)$ per DFT
Channel estimation	Uses the DFT of the reference frame directly.	Performs statistical averaging over L data-bearing rows	$\mathcal{O}\left(LQ\right)$
Data retrieval	Element-wise division.	Element-wise subtraction	$\mathcal{O}\left(LQ\right)$
Dominant complexity	$2\mathcal{O}(QPlogP)$	$\mathcal{O}(QPlogP)$

breaks down the key computational steps at the receiver for decoding one data frame.

As shown in Table 3, the dominant computational load for both schemes comes from the DFT operation. The subsequent estimation and data retrieval steps (e.g., averaging, division, subtraction) have a much lower complexity of $\mathcal{O}\left(LQ\right)$, where L is the number of data-bearing rows, and these are negligible compared to the DFT. The key difference is that conventional DFC requires two full DFT operations for every data frame it decodes. In contrast, our proposed iDFC scheme requires only a single DFT operation. By eliminating the need for a separate reference frame and instead performing a computationally lightweight statistical estimation, iDFC reduces the dominant computational load by approximately 50%. This makes our proposed method significantly more efficient and better suited for real-time applications on resource-constrained devices.

5.4. Practicality Considerations

The proposed iDFC scheme is designed considering several practical advantages, which can be described as follows:

• The system operates using the existing, off-the-shelf screens and cameras found in billions of consumer devices such as smartphones, monitors, and digital signage. No specialized or additional hardware is required, making the system widely deployable and cost-effective.
• A unique practical benefit of iDFC is its ability to support offline decoding. Because the system does not depend on a separate, temporally linked reference frame, data can be extracted from a single, static photograph of a data-embedded screen or even a printed picture. This is not possible with conventional DFC.
• The system design explicitly accounts for perspective distortion, a critical impairment in real-world scenarios. As demonstrated, the geometric correction step is crucial and effectively restores the signal, enabling robust communication even when the camera is not perfectly aligned with the screen.
• As detailed in the previous section, iDFC is significantly more computationally efficient than conventional methods, making it better suited for real-time processing on resource-constrained mobile devices.

6. Conclusions

This paper introduced and evaluated a novel implicit DFC scheme, which is a novel self-referenced screen-to-camera communication framework that leverages the inherent spectral characteristics of display images to enable imperceptible data embedding and blind channel estimation. This approach eliminates the need for the separate reference frames used in conventional DFC or the explicit, sparse pilots and refinement steps used in iterative DFC. The statistical properties of the host image content itself are used for the reference frame estimation. An analysis of perspective distortion effects confirmed the importance of geometric correction in practical deployment scenarios. The simulation results demonstrate that the system achieves a favorable trade-off between imperceptibility and the SER, with optimal performance occurring at moderate image power allocations. Moreover, the ADR was shown to be sensitive to both modulation order and image power, with QPSK providing the best balance between reliability and throughput. Overall, the proposed scheme is an elegant and highly efficient solution for robust, high-speed data communication in unobtrusive screen-to-camera communication.