The Dependence of Spatial Aliasing on the Amount of Defocus and Spherical Aberration in a Model Eye
Abstract
1. Introduction
2. Materials and Methods
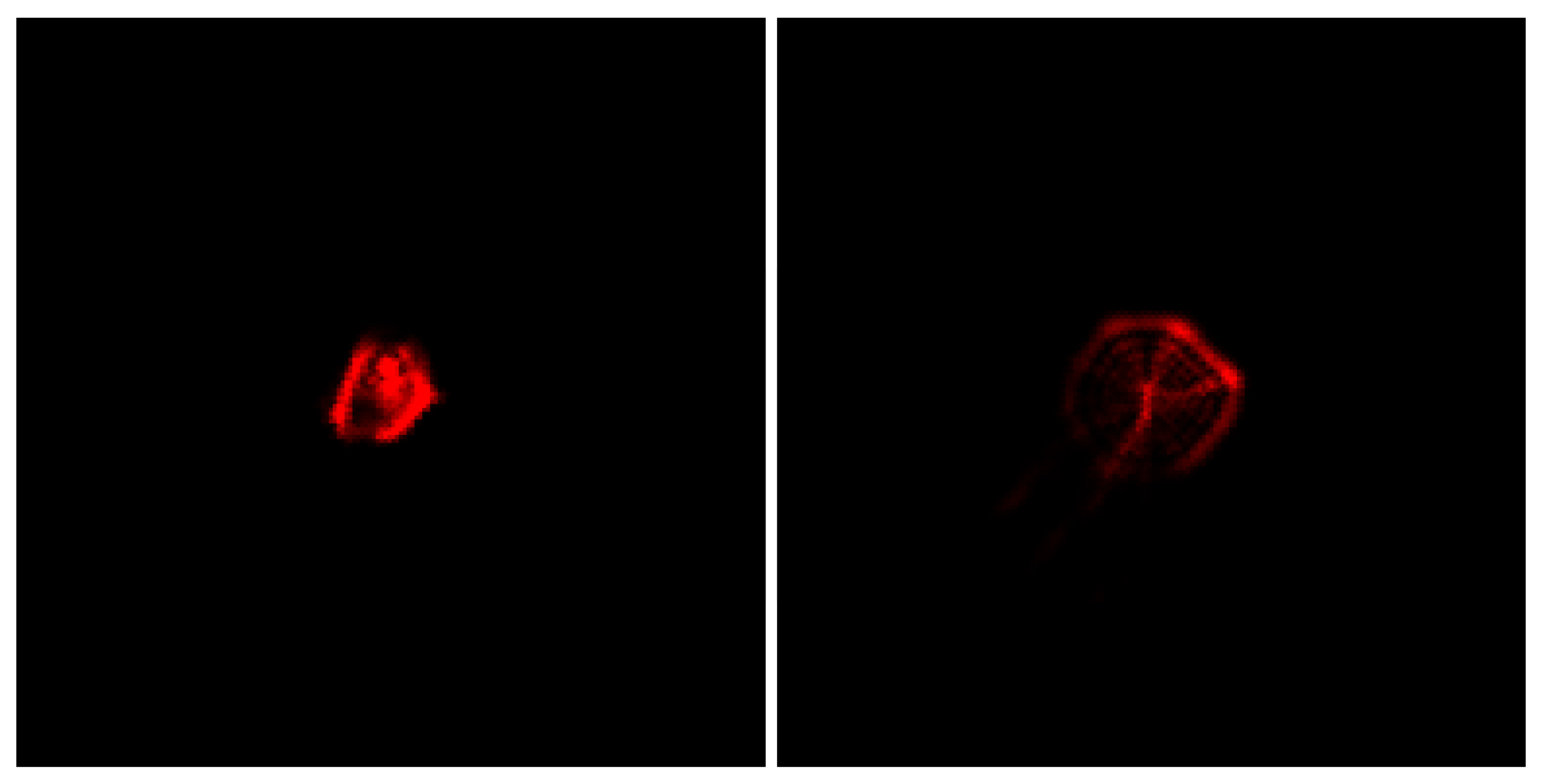
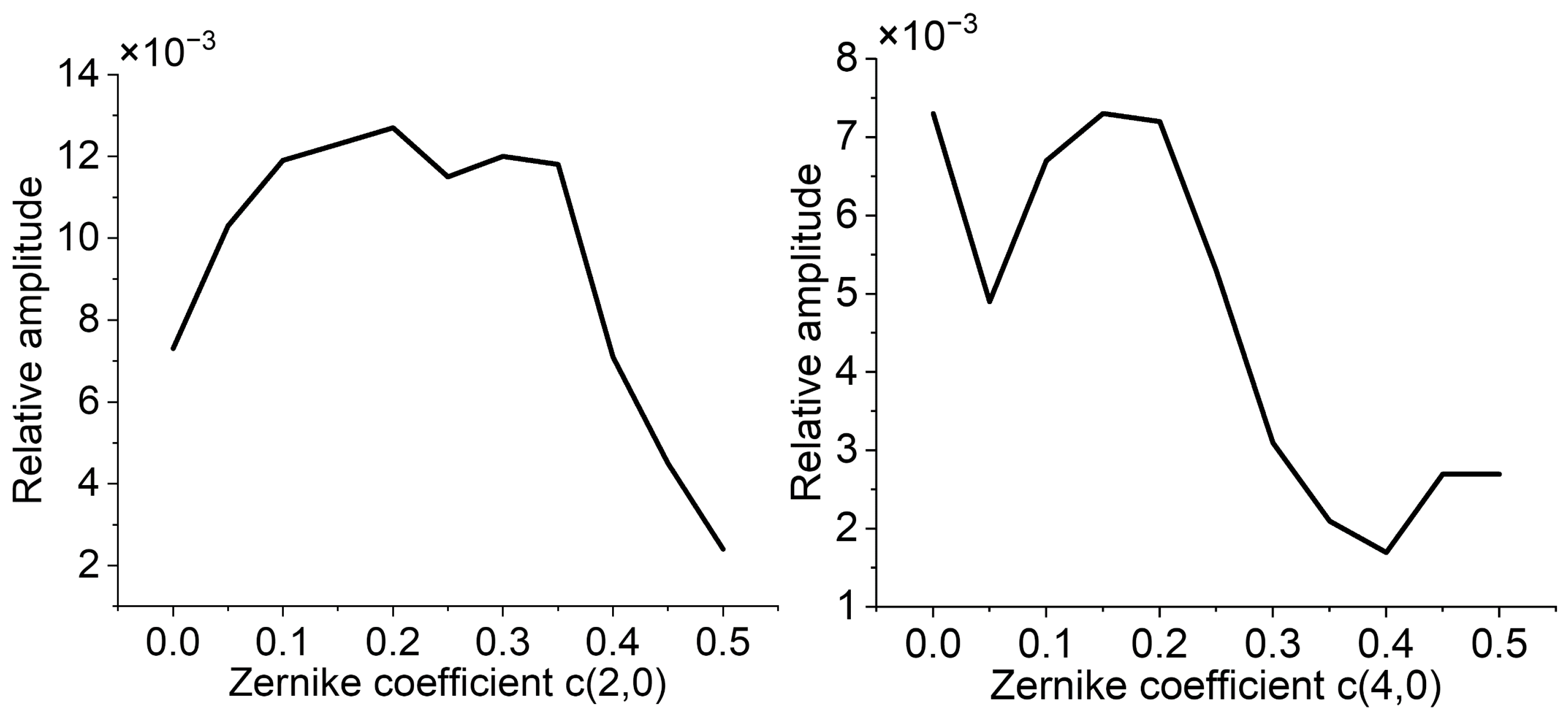
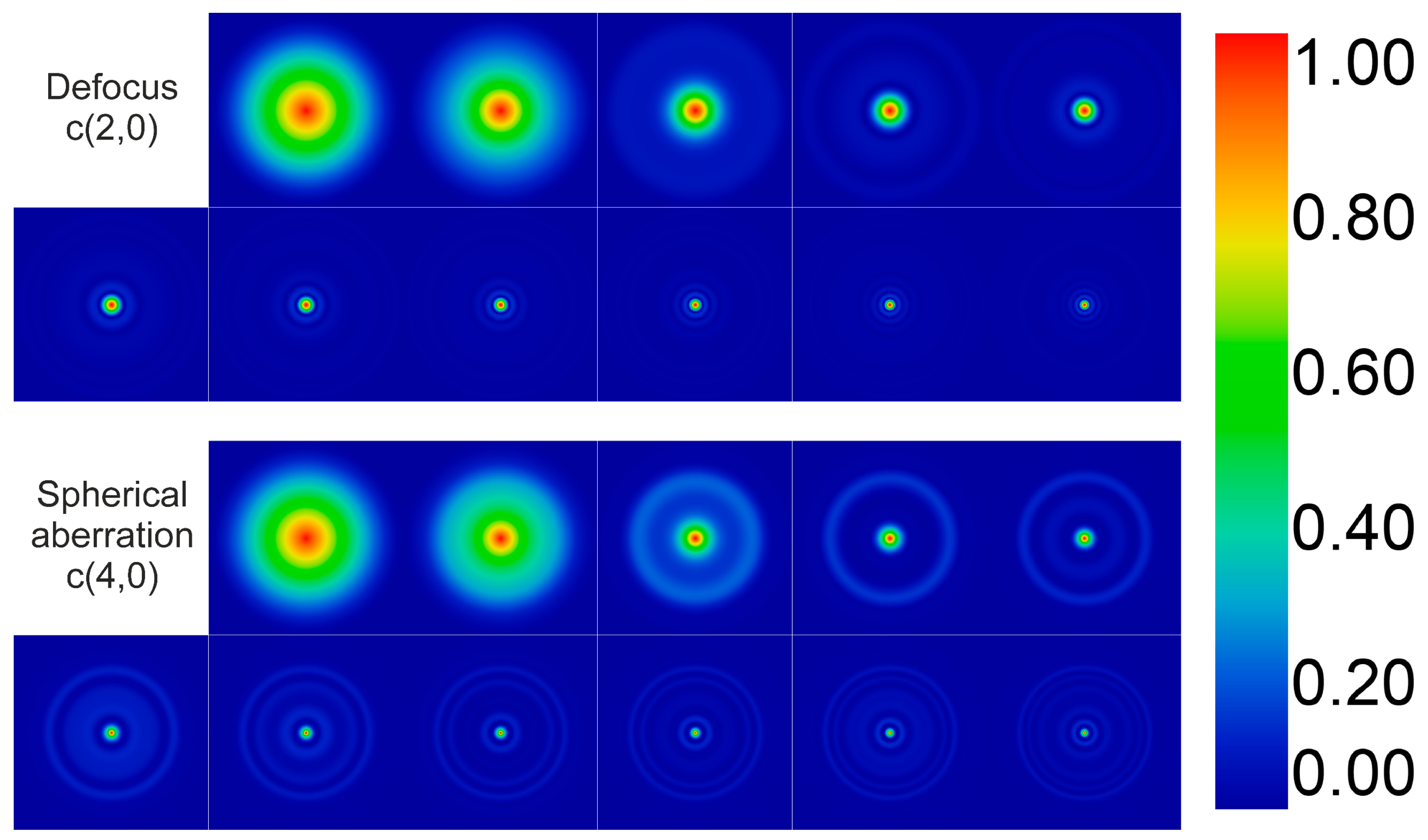
3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MTF | Modulation transfer function |
| PSF | Point spread function |
References
- Navarro, R. The Optical Design of the Human Eye: A Critical Review. J. Optom. 2009, 2, 3–18. [Google Scholar] [CrossRef]
- Atchison, D.A.; Guo, H. Subjective blur limits for higher order aberrations. Optom. Vis. Sci. 2010, 87, 890–898. [Google Scholar] [CrossRef]
- Williams, D.R.; Artal, P.; Navarro, R.; Mcmahon, M.J.; Brainard, D.H. Off-axis optical quality and retinal sampling in the human eye. Vis. Res. 1996, 36, 1103–1114. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Lundström, L.; Manzanera, S.; Prieto, P.M.; Ayala, D.B.; Gorceix, N.; Gustafsson, J.; Unsbo, P.; Artal, P. Effect of optical correction and remaining aberrations on peripheral resolution acuity in the human eye. Opt. Express 2007, 15, 12654–12661. [Google Scholar] [CrossRef]
- Williams, D.; Yoon, G.Y.; Porter, J.; Guirao, A.; Hofer, H.; Cox, I. Visual benefit of correcting higher order aberrations of the eye. J. Refract. Surg. 2000, 16, S554–S559. [Google Scholar] [CrossRef] [PubMed]
- Williams, D.R. Topography of the foveal cone mosaic in the living human eye. Vis. Res. 1988, 28, 433–454. [Google Scholar] [CrossRef] [PubMed]
- Williams, D.R. Aliasing in human foveal vision. Vis. Res. 1985, 25, 195–205. [Google Scholar] [CrossRef]
- Demirel, S.; Anderson, R.S.; Dakin, S.C.; Thibos, L.N. Detection and resolution of vanishing optotype letters in central and peripheral vision. Vis. Res. 2012, 59, 9–16. [Google Scholar] [CrossRef]
- Applegate, R.A. Limits to vision: Can we do better than nature? J. Refract. Surg. 2000, 16, S547–S551. [Google Scholar] [CrossRef]
- Artal, P.; Navarro, R. Monochromatic modulation transfer function of the human eye for different pupil diameters: An analytical expression. J. Opt. Soc. Am. A 1994, 11, 246–249. [Google Scholar] [CrossRef]
- Carkeet, A.; Leo, S.W.; Khoo, B.K.; Eong, K.G.A. Modulation transfer functions in children: Pupil size dependence and meridional anisotropy. Investig. Ophthalmol. Vis. Sci. 2003, 44, 3248–3256. [Google Scholar] [CrossRef]
- Wang, W.; Wan, Y.; Zhao, K. The aberration and the modulation transfer function in LASEK and LASIK: Pupil size dependence. Optik 2010, 121, 500–505. [Google Scholar] [CrossRef]
- Yang, Q.; Yang, Z.; Lan, Y.F.; Wu, S.T. Low-diffraction transparent micro light-emitting diode displays with optimized pixel structure. J. Soc. Inf. Disp. 2022, 30, 395–403. [Google Scholar] [CrossRef]
- Valentina, B.S.; Ramona, B.; Speranta, S.; Calin, T. The influence of optical aberrations in refractive surgery. Rom. J. Ophthalmol. 2015, 59, 217–222. [Google Scholar] [PubMed]
- De Almeida, M.S.; Carvalho, L.A. Different schematic eyes and their accuracy to the in vivo eye: A quantitative comparison study. Braz. J. Phys. 2007, 37, 378–387. [Google Scholar] [CrossRef]
- Kuts, R.I.; Korolkov, V.P.; Sametov, A.R.; Cherkashin, V.V.; Zaitseva, D.E.; Golubtsov, S.K. Thermochemical laser writing of chromium grayscale masks and their application for fabrication of multilevel diffractive optical elements. In Proceedings of the SPIE/COS Photonics Asia, Beijing, China, 27 November 2023. [Google Scholar]
- Artal, P.; Marcos, S.; Navarro, R.; Williams, D.R. Odd aberrations and double-pass measurements of retinal image quality. J. Opt. Soc. Am. A 1995, 12, 195–201. [Google Scholar] [CrossRef]
- Diaz-Santana, L.; Dainty, J.C. Effects of retinal scattering in the ocular double-pass process. J. Opt. Soc. Am. A 2001, 18, 1437–1444. [Google Scholar] [CrossRef]
- Thibos, L.N.; Hong, X.; Bradley, A.; Applegate, R.A. Accuracy and precision of objective refraction from wavefront aberrations. J. Vis. 2004, 4, 329–351. [Google Scholar] [CrossRef]
- Mustafi, D.; Engel, A.H.; Palczewski, K. Structure of cone photoreceptors. Prog. Retin. Eye Res. 2009, 28, 289–302. [Google Scholar] [CrossRef]
- Yi, A.Y.; Raasch, T.W. Design and fabrication of a freeform phase plate for high-order ocular aberration correction. Appl. Opt. 2005, 44, 6869–6876. [Google Scholar] [CrossRef]
- Maffei, L.; Morrone, C.; Pirchio, M.; Sandini, G. Responses of visual cortical cells to periodic and non-periodic stimuli. J. Physiol. 1979, 296, 27–47. [Google Scholar] [CrossRef] [PubMed]
- Allenmark, F.; Read, J.C.A. Detectability of sine- versus square-wave disparity gratings: A challenge for current models of depth perception. J. Vis. 2010, 10, 17. [Google Scholar] [CrossRef] [PubMed]
- Norcia, A.M.; Appelbaum, L.G.; Ales, J.M.; Cottereau, B.R.; Rossion, B. The steady-state visual evoked potential in vision research: A review. J. Vis. 2015, 15, 4. [Google Scholar] [CrossRef] [PubMed]
- Kirsch, W.; Kunde, W. Human perception of spatial frequency varies with stimulus orientation and location in the visual field. Sci. Rep. 2023, 13, 17656. [Google Scholar] [CrossRef] [PubMed]
- Rosa, C.; Aleci, C. Psychophysics in the ophthalmological practice—II. Contrast sensitivity. Ann. Eye Sci. 2022, 7, 35. [Google Scholar] [CrossRef]
- McTrusty, A.D.; Kennedy, G.J.; Strang, N.C.; Manahilov, V.; Gray, L.S. Foveal aliasing is orientation and luminance dependent. Investig. Ophthalmol. Vis. Sci. 2010, 51, 965. [Google Scholar]
- Kim, C.Y.; Chung, S.H.; Kim, T.I.; Cho, Y.J.; Yoon, G.; Seo, K.Y. Comparison of higher-order aberration and contrast sensitivity in monofocal and multifocal intraocular lenses. Yonsei Med. J. 2007, 20, 627–633. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karitans, V.; Jurgaite, M.; Ozolinsh, M.; Fomins, S. The Dependence of Spatial Aliasing on the Amount of Defocus and Spherical Aberration in a Model Eye. Photonics 2025, 12, 1003. https://doi.org/10.3390/photonics12101003
Karitans V, Jurgaite M, Ozolinsh M, Fomins S. The Dependence of Spatial Aliasing on the Amount of Defocus and Spherical Aberration in a Model Eye. Photonics. 2025; 12(10):1003. https://doi.org/10.3390/photonics12101003
Chicago/Turabian StyleKaritans, Varis, Megija Jurgaite, Maris Ozolinsh, and Sergejs Fomins. 2025. "The Dependence of Spatial Aliasing on the Amount of Defocus and Spherical Aberration in a Model Eye" Photonics 12, no. 10: 1003. https://doi.org/10.3390/photonics12101003
APA StyleKaritans, V., Jurgaite, M., Ozolinsh, M., & Fomins, S. (2025). The Dependence of Spatial Aliasing on the Amount of Defocus and Spherical Aberration in a Model Eye. Photonics, 12(10), 1003. https://doi.org/10.3390/photonics12101003




