A Bidirectional Mode-Locked Fiber Laser for Asynchronous Noise-like Pulse Generation

Abstract

We demonstrate a bidirectional fiber laser with an artificial saturable absorber of a step-index multimode fiber sandwiched by single-mode fibers. Two asynchronous noise-like pulse sequences with a repetition frequency difference of 3.16 kHz are obtained. The average power of the bidirectional asynchronous noise-like pulses is greater than 36 mW, and the pulse energy is greater than 3 nJ. The laser we demonstrate has potential applications in micromachining, supercontinuum spectrum generation, and signal processing.

1. Introduction

The bidirectional mode-locked fiber laser can generate two stable mode-locked pulse sequences with different repetition rates in the two opposite propagation directions. In general, the two asynchronous pulse sequences generated by the bidirectional mode-locked fiber laser are mutually coherent, and they experience the same environmental noise, so the repetition rate difference between the two pulse sequences is relatively stable and consistent [1]. As an emerging light source, bidirectional fiber lasers have shown great potential in applications such as optical sensing [2,3], dual-comb spectroscopy [4,5], and optical gyroscopes [6].

In a passive mode-locked fiber laser, a saturable absorber (SA), either a material-based SA or structure-based SA [7], is a key component in efforts to achieve mode-locking. Previous studies have demonstrated the use of carbon nanotubes [8], semiconductor saturable absorber mirrors (SESAMs) [9], and gold nanofilm [10] as SAs in bidirectional mode-locked fiber lasers. However, these material-based SAs have the disadvantages of low damage threshold and performance degradation over time. To solve these problems, an all-fiber-based SA utilizing nonlinear multimode interference (NL-MMI) has been used for mode-locking in fiber lasers [11,12]. Compared to material-based SAs, structural SAs based on the NL-MMI only require the splicing of a section of multimode fiber (MMF) between two pieces of single-mode fibers (SMFs), with the advantages of a simple manufacturing process and low manufacturing costs. In addition, structural SAs usually have high damage thresholds, long-term stability, and are suitable for various laser operating wavelengths. Their modulation depth and saturation intensity can be adjusted by stretching. In 2022, Lin et al. used the NL-MMI of graded-index multimode fiber (GIMF) as the SA in a 1.5 μm bidirectional mode-locked fiber laser [13]. Luo et al. built a two-way 1 μm mode-locked fiber laser using GIMF NL-MMI as the SA in 2023 [14].

When using an SMF-GIMF-SMF sandwich structure as SAs, the length of the GIMF must be precisely controlled to meet the interference conditions, with a precision of tens of micrometers. Achieving such high precision in practice is challenging. If the multimode fiber’s length does not match an integer multiple of the self-imaging distance, the saturable absorption effect weakens, making the structure ineffective as a mode-locking device. To address this limitation, researchers have proposed several solutions. These include adding a section of multimode fiber with a larger core diameter [15], typically several hundred micrometers long, or using hydrofluoric acid to etch the multimode fiber to form a micro-cavity [16]. Another approach is replacing GIMF with step-index multimode fiber (SIMF). Among these solutions, SIMF is easier to implement in practical applications and overcomes the length constraints of multimode fibers more effectively. In 2018, Chen et al. successfully demonstrated mode-locking with a center wavelength of 1596.6 nm using NL-MMI of 48.8 mm step-index multimode fiber (SIMF) [11]. To our knowledge, no studies have applied an SMF-SIMF-SMF structure as SAs in a bidirectional laser for achieving bidirectional mode-locking.

In addition to traditional and dissipative solitons, bidirectional fiber lasers can also generate noise-like pulses (NLPs). NLPs consist of a broad envelope containing numerous ultrashort pulses with varying widths and intensities [17]. The autocorrelation trace of an NLP typically features a sharp, narrow peak at the femtosecond scale, superimposed onto a broader pedestal that ranges from picoseconds to nanoseconds. Due to their wide temporal profile, NLPs can operate in high-pulse-energy regimes, with their energy further enhanced through fiber amplification without requiring pulse shaping [18]. This unique capability makes NLPs ideal for applications like supercontinuum generation [19], material processing [20], and low-coherence spectral interferometry [21]. Despite their potential, the generation of NLPs in bidirectional fiber lasers remains underexplored. By incorporating an SMF-SIMF-SMF sandwich-structured saturable absorber with a high damage threshold, it is possible to generate high-pulse-energy bidirectional NLPs under high pump power in fiber lasers.

In this paper, and for the first time to the best of our knowledge, we demonstrate a bidirectional mode-locked fiber laser using a structural SA based on the NL-MMI of the SIMF. The laser employs a double-loop design, allowing independent access for pulses traveling in both directions. This avoids direct and intense gain competition between bidirectional pulses and improves the stability of the laser. The sandwich structure SMF-SIMF-SMF is used as the core device of mode-locking. By adjusting the polarization controller in the laser cavity, asynchronous NLPs are obtained in the clockwise (CW) direction and counterclockwise (CCW) direction, with a repetition frequency difference of 3.16 KHz. The average output power in the CW direction is 45.1 mW, and the single-pulse energy is 4.1 nJ, while the average output power in the CCW direction is 36.2 mW, and the single-pulse energy is 3.3 nJ. Due to the SMF-SIMF-SMF structure, the damage threshold is high, and the performance is stable. During the whole experiment, at high pump powers, there is no observable performance degradation in saturable absorbers. NLPs have important applications in micromachining, supercontinuum spectrum generation, and signal processing. The study of asynchronous NLPs generated by bidirectional mode-locked lasers is extremely rare, and bidirectional operation has not been demonstrated in any mode-locked fiber lasers based on SIMF.

2. Experimental Setup

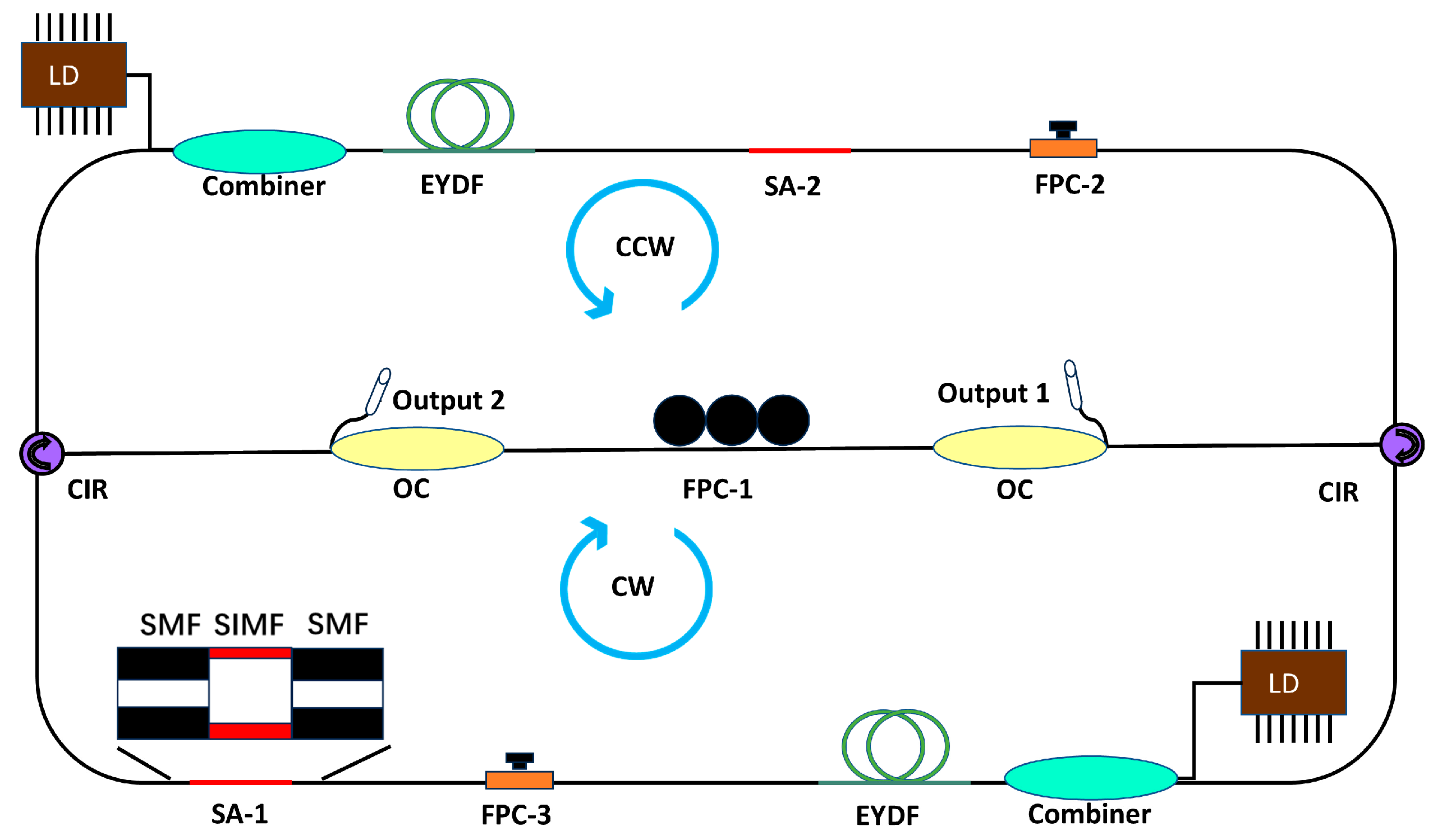
The architecture of the fiber laser in this work is depicted in Figure 1, which is a bidirectional fiber laser with a dual-ring structure, where the two counter-propagating loops are coupled together through two circulators. Due to the unidirectional transmission characteristics of the circulator (i.e., the transmission from port-1 to port-2 and port-2 to port-3), the laser propagation in both sub-loops is unidirectional. It can operate independently in CW and CCW directions. However, in the common path, the laser pulses from the two sub-loops share the same fiber and propagate in opposite directions. In this structure, two 980 nm laser diodes (LD) pump the two branches through two 980/1550 nm combiners. The gain mediums used are two pieces of erbium–ytterbium co-doped fiber (EYDF) with a length of 3 m (core/cladding diameter: 10/125 μm, manufacturer: Nufern, East Granby, CT, USA). The gains are not shared to avoid gain competition and cross-phase modulation effects. A similar structure has been used to suppress common-mode noise [22,23], which is suitable for dual-comb generation. The mode-locking operation is achieved through the saturable absorption effect, generated by the NL-MMI. A three-ring polarization controller (PC) is placed in the common cavity part, and other two squeeze-type PCs are inserted into the two branches to optimize the mode-locking characteristics. The output pulses are extracted through a 1 × 2 optical coupler (OC) with an output ratio of 10%. The pigtails of all the components are standard single-mode fibers with a dispersion parameter of −0.022 ps²/m. The total cavity lengths in the CW and CCW directions are approximately 18.26 m and 18.27 m, respectively. The laser cavity we built has anomalous dispersion of −0.528 ps² and −0.529 ps² at 1550 nm for the CW and CCW directions. The laser architecture in this work is fully fiber-based without any free-space components, which, to some extent, improves stability and robustness against environmental changes [24].

The mode-locked pulse trains are characterized with an optical spectrum analyzer (OSA, YOKOGOWA, AQ6370B, Tokyo, Japan) and a 4 GHz oscilloscope (RIGOL, DS4054, Suzhou, China) combined with a high-speed photodetector (Thorlabs DET08CFC/M, Newton, NJ, USA). The autocorrelation trace is measured using a commercial autocorrelator (FEMTOCHROME, FR-103XL, Berkeley, CA, USA). The RF spectrum is measured with a radio frequency (RF) spectrum analyzer (RIGOL, DSA 815, Suzhou, China).

The construction of the SA involves fusing an MMF between two sections of SMF. The light intensity in the SMF is coupled into many guided modes, when applied to the MMF, which can be described as follows [25]:

$$E_{SMF}\left(r,\phi ,0\right)={\sum }_1^N{C}_n{e}_n\left(r,\phi ,0\right),$$

(1)

where N represents the total number of modes in the MMF, $e_n\left(r,\phi ,0\right)$ represents the nth guided mode, and $C_n$ represents the weight of the nth mode in the total intensity. The light field distribution at a point in the MMF is equal to that at the starting position. This phenomenon is called the self-imaging effect of the fiber, and the corresponding point is called the self-imaging point. The excitation mode satisfies the following condition [11]:

$${\beta }_1{z}_s=m2\Pi +{\beta }_n{z}_s,$$

(2)

where β₁ and β_n are the propagation constants of the fundamental mode and the nth-order guided mode, m is an integer, and z_s is the one-period self-imaging distance. When the optical power is high enough, considering the self-phase modulation and cross-phase modulation effects, the self-imaging distance z_s can be changed to the following formula:

$$z_s^{\prime }={\displaystyle \frac{{\beta }_1-{\beta }_n}{({\beta }_1-{\beta }_n)+({\gamma }_1{P}_1-{\gamma }_n{P}_n)}}{z}_s,$$

(3)

where γ₁ and γ_n are the nonlinear coefficients of the fundamental mode and the nth-order guided mode, respectively, and P₁ and P_n are the equivalent optical powers of the MMF fundamental mode and the nth-order guided mode. γ₁ and P₁ are the maximum values, respectively. According to the equation, when the length of MMF is $m{z}_s^{\prime }$ or (m + 1/2)z_s, the transmission efficiency of NL-MMI for high power signals is higher than that for low power signals [11]. We fabricated SA with an SIMF (50/125 μm) length of about 5 cm (~5z_s) [26]. This length of MMF is short enough to reduce the influence of comb filtering caused by NL-MMI and is easy to operate.

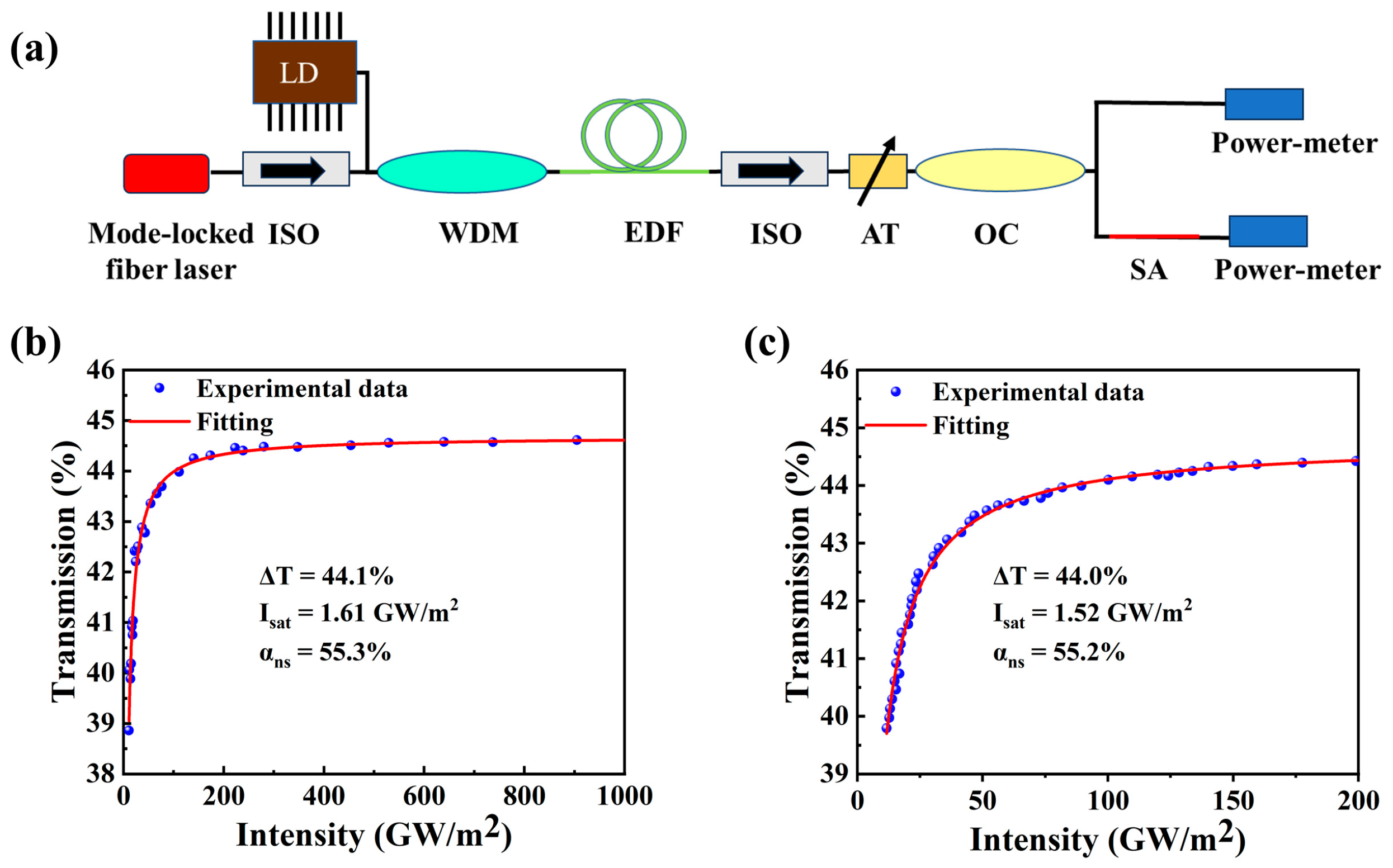
There are two methods to measure the nonlinear optical absorption characteristics of SA devices, namely Z-scan and balanced dual-detector technology. Z-scan is used to measure nonlinear absorption by changing the position of the sample on the optical axis, which involves the measurement of the absorption of the sample at different positions. The balanced dual-detector technique measures the nonlinear absorption by changing the light intensity passing through the sample, which usually involves the measurement of absorption of the sample at different light intensities at the same position. The balanced dual-detector technology device is shown in Figure 2a, which combines the amplified seed source and the attenuator (AT) as a variable intensity of ultrashort light source. The light beam is divided into test and reference channels by an OC, and the nonlinear absorption characteristics of the sample are determined by measuring the power of the two channels [27]. After amplification, the fiber laser outputs laser pulses with a center wavelength of 1557.3 nm, a pulse repetition frequency of 17.75436 MHz, and a pulse duration of 1.0 ps. By continuously adjusting the laser power, we can record the optical transmittance at different input intensities, and the experimental results are shown in Figure 2b,c. The experimental data are fitted with the following equation:

$$T=1-{\displaystyle \frac{\Delta T}{1+\frac{I}{I_{\mathit{sat}}}}}-{\alpha }_{\mathit{ns}},$$

(4)

where T is the transmittance, α_ns is the nonsaturable absorption, ΔT is the modulation depth, I is the input light intensity, and I_sat is the saturation light intensity. According to the fitting results, the saturation intensity and modulation depth of SA-1 are 1.61 GW/m² and 44.1%, respectively, while the saturation intensity and modulation depth of SA-2 are 1.52 GW/m² and 44.0%, respectively.

3. Experimental Results and Discussion

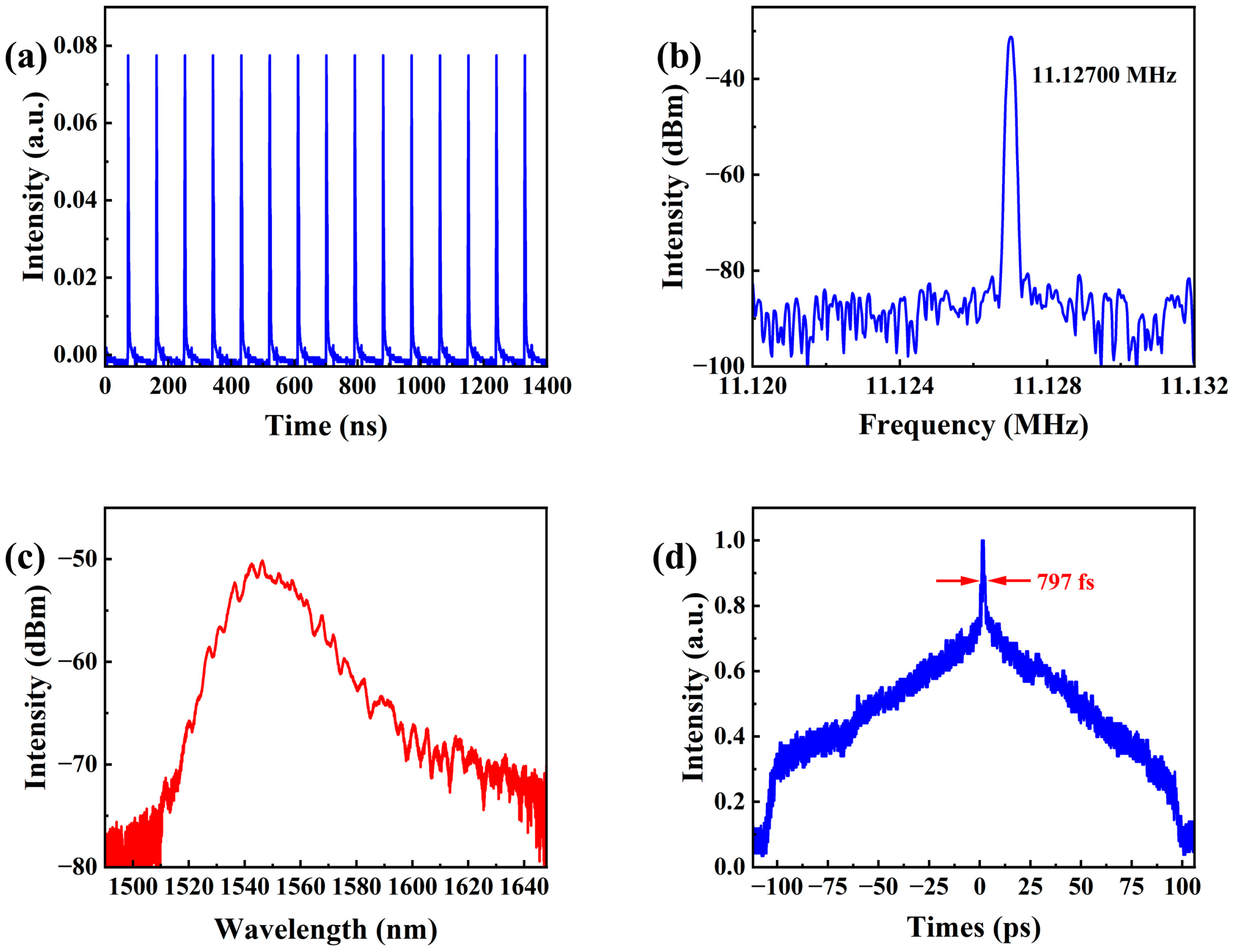
Mode-locking is supported by two branches, corresponding to the CW and CCW directions of propagation. In the CW direction, mode-locking can be achieved and maintained with a pump power of 2 W. The average output power is approximately 17.3 mW, corresponding to a single-pulse energy of about 1.6 nJ. As depicted in Figure 3a, the pulse sequence of the mode-locked operation in the CW direction exhibits a pulse interval of approximately 90 ns. The RF spectrum in Figure 3b reveals a fundamental repetition frequency of 11.12700 MHz, which correlates well with the cavity length. Despite the CW and CCW pulses being coupled within the same cavity through the circulators, the pulses in the CW direction demonstrate a broader spectral characteristic [28]. Figure 3c shows that the 3 dB bandwidth of the optical spectrum is 12.9 nm, with a central wavelength of 1548.7 nm. The autocorrelation trace in Figure 3d exhibits the typical features of NLPs, that is, a small sharp peak on a broad pedestal. The width of the broad pedestal is greater than 200 ps, and the width of the small sharp peak is 797 fs. It is noteworthy that, although the polarization controller is crucial for initiating the mode-locking through the polarization selection effect, the mode-locking operation in the present work is induced by nonlinear multimode interference rather than the nonlinear polarization selection effect, since no polarization-sensitive elements are introduced in the cavity [29].

Similarly, in the CCW direction, mode-locking is successfully realized by adjusting the pump power and polarization controller. The mode-locking threshold in the CCW direction is 700 mW. At this pump power, the average output power is about 5.4 mW, corresponding to a pulse energy of approximately 485.2 pJ. As shown in Figure 4a, the time pulse sequence of the mode-locking in the CCW direction also exhibits a pulse interval of approximately 90 ns. The RF spectrum in Figure 3b displays a fundamental repetition frequency of 11.13016 MHz, which is consistent with the cavity length. The optical spectrum of the NLPs, characterized by a smooth spectral shape, is distinctly different from those in the CW direction, with a 3 dB bandwidth of 9.6 nm and a central wavelength of 1566.2 nm, as shown in Figure 3c. The autocorrelation trace in Figure 3d also displays the typical features of noise-like pulses, i.e., a small sharp peak on a broad pedestal. The width of the broad pedestal is greater than 200 ps, and the width of the small sharp peak is 719 fs.

Under the conditions of anomalous dispersion, the formation of NLPs can be attributed to the soliton collapse effect [30], caused by the nonlinear growth of soliton pulse energy in the gain medium. Once the soliton collapses, the pulses are continuously destroyed and regenerated within the cavity. Under high-pump-power conditions, the processes of collapse and regeneration may coexist asynchronously, resulting in a series of random, narrow pulses with varying energies and widths. The envelope of these pulses constitutes the observed NLPs. The differences in the characteristics of the noise-like mode-locked pulses generated in the CW and CCW directions are due to the differences in the cavity structure. Since the counter-propagating pulses propagate through different branches, they experience different gains and losses within the cavity, leading to variations and, consequently, different breathing processes (i.e., periodic compression and stretching of the pulse width) during the counter-propagation of the CW and CCW pulses.

As the repetition frequencies of the counter-propagating pulses are slightly different, when both the CW and CCW directions are in mode-locked operation, two relatively moving pulse sequences appear on the oscilloscope, referring to the asynchronous mode-locked pulses. In this state, the output characteristics of the bidirectional dual-ring fiber laser are further investigated. In the experiment, we simultaneously initiated the pump in the two sub-cavities and increased their powers to 5 W. By properly adjusting the PCs in the two branches, we successfully achieved stable asynchronous mode-locking. In the CW direction, the average output power is approximately 45.1 mW, corresponding to a single-pulse energy of about 4.1 nJ. In the CCW direction, the average output power is about 36.2 mW, corresponding to a pulse energy of approximately 3.3 nJ.

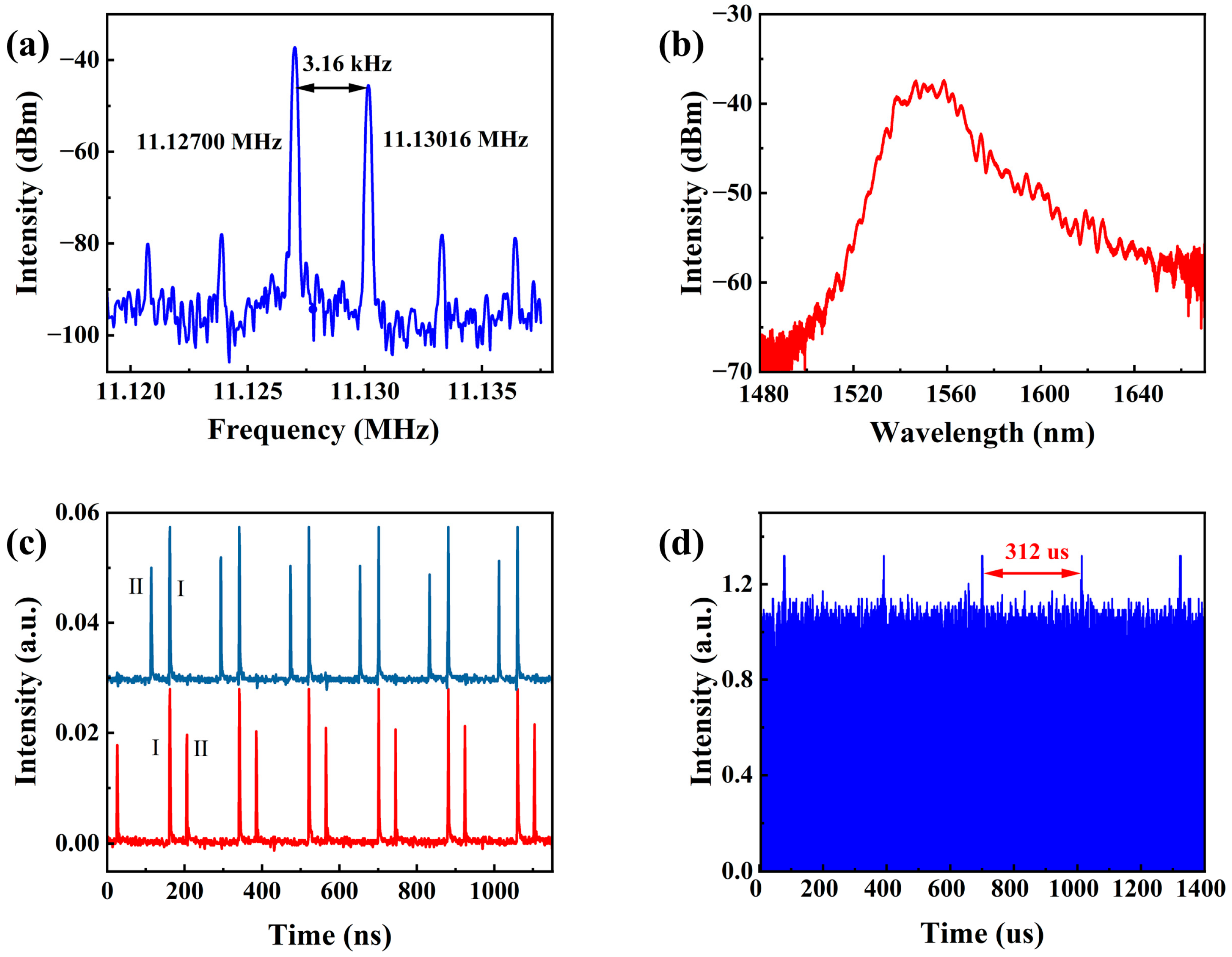
In our experimental setup, a 1 × 2 optical fiber coupler with a 50:50 coupling ratio is used to combine the mode-locked pulse sequences from the CW and CCW different output ports into a single fiber. This method can simplify the detection of the asynchronous pulse sequence and facilitate the subsequent analysis. Figure 5a shows the RF spectrum of the asynchronous pulse sequences, with two strong peaks at 11.12700 MHz and 11.13016 MHz, both with a signal-to-noise ratio (SNR) exceeding 30 dB. The repetition frequency difference between the two strong peaks is 3.16 kHz. Small, equally spaced peaks are found on both sides of the signals in Figure 5a and are attributed to additional interference between two different RF signals. Since the number of comb modes required to generate these additional interferences is much less than the modes for the repetition frequency, the SNR of these additional peaks is usually less than 20 dB [31]. Figure 5b shows the output optical spectrum with a central wavelength of 1553.1 nm and a 3 dB bandwidth of 26.8 nm. The central wavelength of the superimposed spectrum is between the two central wavelengths of the CW and CCW directions. However, it is biased towards the central wavelength of the CW pulses, since they have higher energy.

In Figure 5c, the digital oscilloscope records the temporal drift between the two pulse sequences. The red section shows two stable pulse sequences with different time intervals and optical intensities. Despite the peak amplitudes varying over time, the relative intensity between the two pulse sequences remains clear enough to distinguish them, marked as I and II, respectively. According to the time period and light intensity of the pulse, it can be determined that pulse sequence I is generated in the CW direction, and pulse sequence II is generated in the CCW direction. Comparing the red section and the dark blue section in Figure 5d, it can be seen that the time interval between pulse sequence I and pulse sequence II varies with time. In other words, the two pulse sequences are asynchronous in the time domain, and the temporal walk-off between the two pulse sequences is verified. These results are consistent with the slight differences in the repetition rates of the two pulse sequences. Figure 5d displays the interference pattern of the two pulse sequences (range of 1.4 ms). The pulse intensity is periodically enhanced since the asynchronous pulse sequences collide periodically every 312 μs [32]. The collision period can be calculated using the formula Δτ = 1/Δf, where Δf is the difference between the repetition rates of the two pulse sequences. The calculated collision period is approximately 316 μs, which matches the 312 μs shown in Figure 5d. Due to the different resolutions of the RF instrument and the oscilloscope, there are some errors in the results [33]. By controlling the intracavity loss applied to the two pulse sequences, we can activate or deactivate either of the two pulse sequences.

The mode-locking operation in two opposite propagation directions is supported simultaneously by two SAs of the SMF-SIMF-SMF structure on different branches. The general formula for calculating the repetition frequency of a ring laser is f = c/(nL); f is the repetition frequency, c is the speed of light, n is the refractive index, and L is the cavity length. It can be seen from the formula that the optical path nL directly affects the repetition frequency of the output pulse, and the adjustment of L can directly affect the optical path. For the bidirectional laser with a double-loop structure, due to the existence of non-common branches, the optical paths for the two mode-locked pulse sequences generated by the two opposite propagation directions are different, thus resulting in two mode-locked pulse sequences with different repetition rates.

The main factor affecting the stability of the bidirectional laser is the strong gain competition between the CW and CCW directions. The design of the double-loop structure allows the pulses in both directions to enjoy their own gains independently, which minimizes the instability of the pulses in the two directions. Figure 6 shows the variation in the average output power in the CW and the CCW direction of the bidirectional mode-locked state in the period of 10 h. It can be seen that the power jitter is very small, and the operation of asynchronous noise-like pulses is very stable.

The bidirectional fiber laser we designed has superior performance in terms of average output power and pulse energy.

Table 1. The comparison of the average output power and pulse energy of 1.5 μm bidirectional lasers.

SA	Average Output Power in CW (mW)	Average Output Power in CCW (mW)	Single-Pulse Energy in CW (nJ)	Single-Pulse Energy in CCW (nJ)
Carbon nanotube [34]	0.10	0.06	0.01	0.01
Carbon nanotube [8]	0.12	0.12	0.01	0.01
Graphene [35]	0.18	0.40	0.02	0.06
Gold nanofilm [10]	5.96	2.52	0.40	0.17
SMF-GIMF-SMF [13]	3.00	5.10	0.33	0.57
SMF-GIMF-SMF [36]	44.00	26.00	1.90	1.12
SMF-SIMF-SMF [This work]	45.10	36.20	4.10	3.30

summarizes the comparison between this work and previous reports of bidirectional fiber lasers at 1.5 μm in terms of average output power and pulse energy. It can be seen that our laser has a much higher average output power and pulse energy. Although the fiber lasers using graphene, carbon nanotube, and gold nanofilm as SAs can obtain bidirectional asynchronous mode-locking outputs, the average output power and pulse energy are usually low. On the one hand, compared to MMI-based SA, the damage threshold of material-based SA is low. On the other hand, solitons generated by bidirectional lasers may be unable to withstand high pulse energy, such as traditional solitons. Therefore, our bidirectional fiber laser can obtain higher average output power and pulse energy, not only because the SA based on SMF-GIMF-SMF has a higher damage threshold, but also because the bidirectional laser in this work produces noise-like pulses that can withstand high pulse energy.

By adjusting the two pump powers and the fiber PCs in the laser cavity, the gain and loss in the cavity can be adjusted, which can not only control different average output powers, but can also make the two sub-rings to work alone or simultaneously. Furthermore, the repetition rate difference can be freely adjusted by changing the lengths of the two branches.

4. Conclusions

In summary, we have successfully demonstrated a bidirectional fiber laser based on the SMF-SIMF-SMF structural SA, achieving asynchronous NLP sequences. The average output power in CW and CCW directions is greater than 36 mW, and the single-pulse energy is greater than 3 nJ. The two mode-locked pulse sequences with different repetition rates can work alone or simultaneously. Such a flexible light source has potential applications in micromachining, supercontinuum spectrum generation, and signal processing.