Abstract
Light intensity flicker is the most basic and important effect of turbulence. Fiber coupling efficiency is the primary parameter that ensures the system’s communication quality. The light intensity flicker effect caused by atmospheric turbulence significantly affects the coupling efficiency of space light in a single-mode optical fiber. Based on the principle of fiber coupling efficiency, this paper first establishes the relationship between light intensity flicker and spatial coherence radius, then analyzes the influence of light intensity flicker on fiber coupling efficiency through the spatial coherence radius. A laser communication system was built, and real-time measurement experiments on atmospheric light intensity flicker and optical fiber coupling efficiency at different transmission distances and altitudes above the ground were completed. The experimental results show that the constructed experimental system can simultaneously measure the scintillation index and fiber coupling efficiency. When the communication distance is 12,000 m and the height is 600 m above the ground, the scintillation index is measured to be 0.63, and the coupling efficiency is 0.05. The results of the study provide an experimental and theoretical basis and data support to promote the development of atmospheric laser communications.
1. Introduction
In recent years, with the changes in technology, 5G alone can no longer support the construction of future smart cities where everything is connected. A new generation of communication technology with faster speed, greater stability, and lower latency is needed [1]. The 6G mobile communication network has come into people’s view with its terahertz frequency band carrier, microsecond latency, one-in-a-million interruption probability, and ultra-high communication rate [2,3]. In order to truly realize the huge smart scene, a large number of communication satellites and terrestrial communication relay sites are needed to make up for the disadvantage of the small coverage area of the 6G single base station. Traditional satellite communication technology is far from being able to meet the needs of such high-speed data transmission scenarios. Free space optical communication (FSO) technology is undoubtedly an effective way to solve this problem [4,5,6,7]. In order to achieve an ultra-high-speed FSO communication link, it is first necessary to couple the spatial signal light into a single-mode optical fiber and then perform subsequent optoelectronic signal processing. In inter-satellite communication links, since the channel is in a near vacuum state, the space optical signal is not disturbed by the medium, and the communication quality is only affected by the performance of the satellite platform and the communication terminal. However, when the communication terminal works in the atmospheric channel, a large number of turbulent eddies of different scales, affected by diffraction and scattering effects, make the light intensity at the receiving end fluctuate randomly, resulting in the phenomenon of light intensity scintillation. This leads to random fluctuations in the signal light wavefront incident to the receiving end of the system, which makes the coupling efficiency of the space light to the single-mode fiber deviate from the theoretical optimal value and become a random variable, seriously affecting the stability and reliability of the communication link transmission. The problem of light-intensity scintillation in atmospheric channels is one of the main bottlenecks limiting the development of laser communications. Over the years, in order to accurately analyze the scintillation effect of light intensity due to atmospheric turbulence, many statistical models and experimental studies have been proposed by numerous researchers to describe the channel state of the atmosphere. Rytov et al. established a model for calculating the variance of light intensity fluctuations, and the calculated results in weak turbulence channels were consistent with experimental test results [8]. Andrews and Churnside derived a calculation model for strong turbulent light intensity fluctuations based on the asymptotic analysis method. Then, Andrews studied the light intensity fluctuation model using the assumption that small-scale turbulent fluctuations are modulated by large-scale fluctuations and obtained a general solution for the variance of weak turbulent scintillation [9]. Through experiments, Davis et al. found that the light intensity flicker variance first increases and then decreases during the light wave transmission process until it finally reaches a saturation state [10]. Habash et al. proposed a dual gamma–gamma model and proposed the use of a two-scale modulation theory to characterize the changes in the probability distribution of light intensity ups and downs during atmospheric turbulence from weak to strong [11]. When measuring the impact of atmospheric light intensity scintillation on the performance of communication systems, researchers usually use signal-to-noise ratio and bit error rate [12,13,14,15], and the coupling efficiency of spatial light to single-mode optical fiber is the primary parameter for analyzing the two. However, researchers have conducted a lot of studies on the fiber coupling efficiency problem in atmospheric laser communication systems, both theoretically and experimentally [16,17,18,19]. However, the effect of light intensity scintillation caused by atmospheric turbulence on the fiber coupling efficiency still remains to be studied.
In view of the theoretical and experimental defects in current research, this paper establishes the relationship between light intensity flicker and spatial coherence radius based on the principle of fiber coupling efficiency. The effect of light intensity scintillation on the fiber coupling efficiency is also analyzed using spatial coherence radius. A laser communication system was built. To ensure the accuracy of the experiment, the real-time measurement of was first carried out. Then, real-time measurement experiments were conducted on atmospheric light intensity flicker and optical fiber coupling efficiency at different transmission distances and altitudes above the ground.
2. Analysis of the Influence of Atmospheric Light Intensity Scintillation on Optical Fiber Coupling Efficiency
Optical signals in the transmission process will be affected by atmospheric turbulence. Turbulence-induced scintillation effects damage the phase and amplitude distortion of the optical signal to reach the receiving end of the spatial coherence, reducing the degree of matching between the focused optical field and the mode field of the single-mode fiber, reducing the coupling efficiency of the spatial light to the single-mode fiber, and affecting the quality of communication of the system. For plane wave and Kolmogorov turbulence spectra, the coupling efficiency [20] of the single-mode fiber after passing through the atmospheric turbulence channel is expressed as:
where is a zero-order first class Bessel function, is the area of the receiver aperture, is the spatial coherent area of the incident plane wave, is the spatial coherence radius of the horizontal path, and is the atmospheric refractive index structure constant. The study shows that is the optimal value to take. The coupling efficiency depends only on the spatial coherence radius.
Under the inclined path, the calculation of the spatial coherence radius is defined as:
is a parameter that measures the strength of atmospheric turbulence. Light intensity scintillation is one of the main turbulence effects affecting atmospheric laser transmission. The intensity scintillation effect can be expressed by the scintillation index, which is a statistical measure that describes the change in intensity during light propagation and is commonly used to quantify rapid fluctuations in light intensity or scintillation due to atmospheric turbulence. When Rytov is less than 1, the value is similar to the light intensity scintillation variance . For oblique range transport, the Rytov variance under the plane wave approximation is:
where is the zenith angle, H is the communication height, and is the ground station height. Then, is:
Then, we can deduce that is:
The relationship between the scintillation index and the spatial coherence radius can be obtained as follows:
Combining the above equation with Equation (1) enables the analysis of the effect of the light intensity scintillation index on the fiber coupling efficiency.
According to the above theoretical results, the receiving aperture is set to 10 cm. The variation of fiber coupling efficiency with scintillation index in the range of 0–1 is obtained by simulation, as shown in Figure 1. There is a reverse correlation between the scintillation index and the fiber coupling efficiency. When the height H above the ground is the same, the scintillation index increases with the increase in transmission distance, and the coupling efficiency decreases accordingly. When the transmission distance L is the same, as the height H from the ground decreases, the scintillation index begins to increase, and the coupling efficiency decreases accordingly. When and H < 600 m, the coupling efficiency will be less than 5%. During the experiment, in order to ensure that the scintillation index is in the range of 0–0.6, the fiber coupling efficiency is not less than 5% to control H above 600 m.
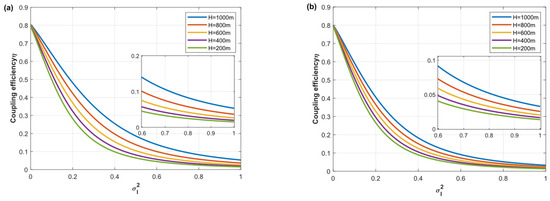
Figure 1.
Relationship of change between scintillation index and fiber coupling efficiency. (a) Link distance L = 3000 m. (b) Link distance L = 12,000 m.
3. Real-Time Measurement Scheme for Light Intensity Flicker and Fiber Coupling Efficiency
The laser communication system consists of two parts, the transmitting end and the receiving end. The real-time measurement system of atmospheric turbulence light intensity scintillation and coupling efficiency is established at the receiving end of the ground station of the laser communication system, and the received signal light is divided into two beams of light through the beam-splitting prism. A beam of light is received by the APD, and the scintillation index is measured at the same time as the optical signal is demodulated. Another beam of light passes through the lens for beam convergence, coupling spatial light into the fiber. The coupling efficiency was measured by an optical power meter. Real-time measurements of the scintillation index and coupling efficiency were accomplished. The measurement principle is shown in Figure 2.
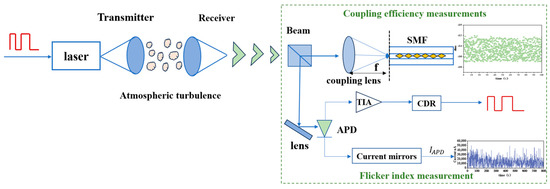
Figure 2.
Schematic diagram of real-time measurement of scintillation index and fiber coupling efficiency.
The experimental design used a self-focusing lens for beam convergence with an effective aperture of 10 mm and an equivalent focal length of 50 mm. The core diameter of the single-mode fiber used for coupling was 10 μm, and the numerical aperture NA was 0.11. An OPM-3216 optical power meter was selected to complete the received optical power measurement. The photodetector selected was an InGaAs APD high-gain-type avalanche photodiode, the bias voltage was set to 36–48 V, the current gain was up to 20 times, the detector target surface was 50 μm, the dark current was 1 nA, which can be detected at a −60 dBm weak signal.
If the phase effect of atmospheric turbulence on laser transmission is not taken into account for the time being and analyzed only from the energy point of view, the atmospheric turbulence leads to the ups and downs of the laser energy intensity. The scintillation index of the light energy received by the detector is the following:
where I is the received light intensity and denotes the long time averaging or systematic averaging. is expressed as the current signal output from the detector after photoelectric conversion. In the experiment, the background light is the main factor that generates the noise signal, which affects the change of the received photocurrent, and it is necessary to use the filter with a bandwidth of 10 nm to complete the background light filtering to ensure the received signal-to-noise ratio.
Experiments Based on Real-Time Measurement of Blimp Light Intensity Scintillation and Fiber Coupling Efficiency
During the experiment, in addition to the influence of background noise, thermal noise, quantum noise, etc., on the atmospheric turbulence scintillation index, the vibration of the platform during the descent of the airship will also affect the alignment of laser communication, causing the current value received by the APD and the coupling efficiency coupled into the single-mode optical fiber to change, affecting the communication performance of the system. When designing the communication system for airship-mounted laser communication, the coarse–fine composite tracking method is used to effectively compensate for the low-frequency signals caused by the vibration of the platform, and the median filtering method is used to remove the high-frequency signals. In order to ensure the accuracy of the experiment, the airship–airship laser communication experiment was carried out first, and was measured in real time. During the descent of the airship at an altitude of 1000 m from the ground, a set of scintillation variance values is collected every 20 m. is calculated in real time using the formula . A schematic of the airship–airship experimental link is shown in Figure 3. The communication modes and related system parameters are shown in Table 1.
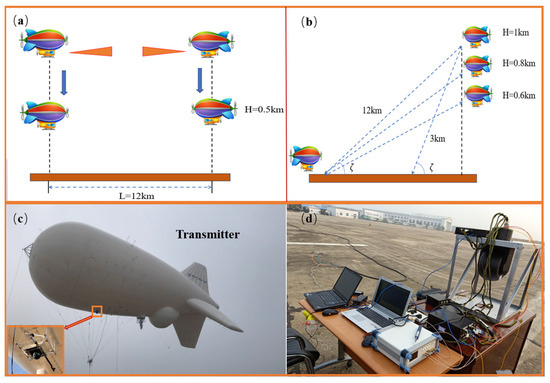
Figure 3.
(a) Schematic of atmospheric turbulence refractive index structure constant measurements. (b) Schematic of scintillation index and fiber coupling efficiency measurements (c) Airship-mounted laser communication system. (d) Ground station receiver.

Table 1.
Main parameters of laser communication system design.
The atmospheric refractive index structure constant, , varies greatly with season, day and night, altitude, geographic location, and meteorological conditions. It is an important representation parameter in laser atmosphere transmission. Hufnagel gave an empirical formula for the variation of with height, called the H-V model, which is applicable in the range of 3–24 Km, based on actual measurements, and can be expressed as follows:
where is the refractive index structure constant near the ground, and VRMS is the wind speed in the vertical transmission path.
Seasonally and diurnally varying atmospheric conditions also affect at different altitudes, and the experiments were carried out under weak and medium turbulence weather from nighttime in winter to early morning the following day. The wind speed in the H-V model is set to a typical value of 21 m/s, and is set to a typical value of at night. Figure 4 shows the results of the actual measurement and the denoising measurement compared with the H-V model [21].
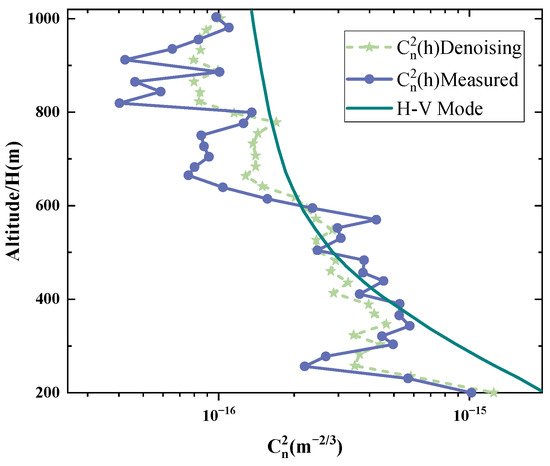
Figure 4.
Measurement results of the refractive index structure constant of atmospheric turbulence before and after denoising.
The measured value is obtained by the real-time of the laser link, which has a better real-time performance compared to the obtained by the weather forecast [22,23] model and is able to more realistically reflect the turbulence change in the channel link. The measured value after denoising is close to the theoretical value of H-V. Real-time measurements help to evaluate the effect of light intensity flicker on fiber coupling efficiency.
Since the tethered blimp is only suitable for working in the near-ground altitude range, in order to ensure the smooth progress of the on-board laser communication experiment, the blimp was lifted to a height of 1000 m. Six communication experiments between the airship and the ground were carried out under the weak and medium turbulence weather from 8:00 pm to 5:00 am the next morning in winter. The test link is shown in Figure 3, where firstly, the scintillation index and fiber coupling efficiency were measured for a link distance (L) of 3000 m, and secondly, the scintillation index and fiber coupling efficiency were measured for a link distance of 12,000 m for a blimp descending from 1000 m to 600 m. The communication mode and related system parameters are the same as in Table 1, the actual received photocurrent values measured in 800 s are shown in Figure 5, and the scintillation index measurements are shown in Table 2.
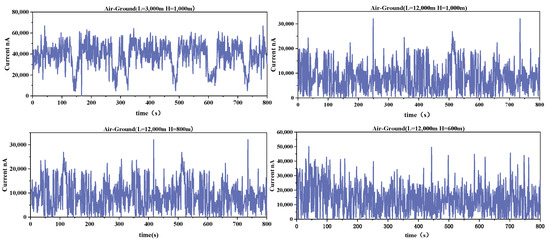
Figure 5.
Actual received optical current value of APD.

Table 2.
Test results.
The optical power meter samples and stores 3000 data points in 1 s; the core diameter of the single mode fiber is 10. In turbulent environments, the calculated instantaneous coupling efficiency is a fluctuating value due to the flickering of light intensity that causes fluctuations in the fiber coupling efficiency, so the measured coupling efficiency is recorded as the average optical power. The experimental results are shown in Table 2.
From the experimental results, it can be seen that the scintillation index has greater coupling efficiency and is lower when the airship is at 1000 m altitude, and the link distance is 12,000 m. At a communication distance of 12,000 m, the maximum current flicker index was measured to be 0.63. At this time, the airship was at an altitude of 600 m, and the coupling efficiency was 0.05.
In order to ensure the accuracy of the experiment, multiple different experimental measurements were carried out. The statistical results of the measured fiber coupling efficiency are shown in Figure 6.
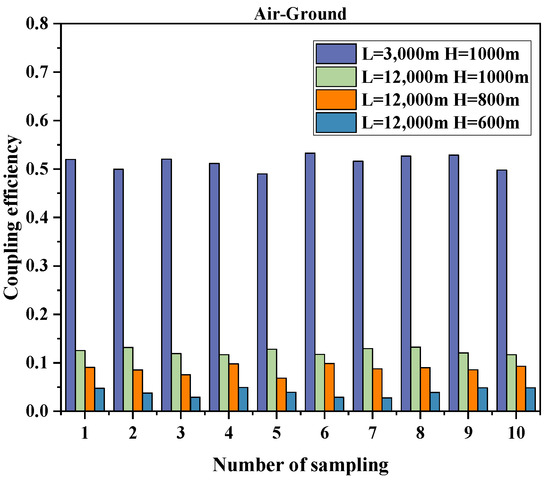
Figure 6.
Coupling efficiency measurement results.
It can be calculated from Figure 1 and Figure 6 that the maximum deviation between the experimental value and the theoretical value of the coupling efficiency does not exceed 20% as the link distance and the height above the ground change. Due to environmental restrictions, the maximum height of the airship platform in the experiment is 1000 m. The coupling efficiency can be calculated using the deviation formula , which solves the limitation that a higher platform cannot be completed due to environmental restrictions.
4. Conclusions
In space laser communication, the effect of atmospheric turbulence on the performance of laser communication systems cannot be ignored, and fiber coupling efficiency is a key factor in determining the performance of atmospheric laser communication. This paper studies the influence of the light intensity scintillation effect caused by atmospheric turbulence on the optical fiber coupling efficiency. First, the relationship between light intensity flicker and spatial coherence radius is established based on the principle of fiber coupling efficiency; then, the influence of light intensity flicker on fiber coupling efficiency is analyzed through spatial coherence radius. An experimental test system for the atmospheric turbulence scintillation index and fiber coupling efficiency has been designed based on the airship laser communication platform. Measurements were made to obtain real-time light intensity scintillation index and fiber coupling efficiency values for blimp–ground platform link distances of 3000 m and 12,000 m. The experimental results show the impact of light intensity scintillation on fiber coupling efficiency and the correspondence between them under different transmission distances and heights above ground, providing an effective method for evaluating the optical coupling efficiency through the turbulent scintillation index.
Author Contributions
X.D. and X.Z.; methodology, X.D.; software, X.D.; validation, X.D. and X.Z.; formal analysis, X.D.; investigation, X.D.; resources, X.D.; data curation, X.D.; writing—original draft preparation, X.Z.; writing—review and editing, X.Z.; visualization, X.Z.; supervision, X.Z.; project administration, X.Z.; funding acquisition, X.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Jilin Provincial Key Research and Development Program Projects, grant number No. 20180201002SF.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data in support of the findings of this paper are available within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Saad, W.; Bennis, M.; Chen, M. A vision of 6G wireless systems: Applications, trends, technologies, and open research problems. IEEE Netw. 2019, 34, 134–142. [Google Scholar] [CrossRef]
- Gui, G.; Liu, M.; Tang, F.; Kato, N.; Adachi, F. 6G: Opening new horizons for integration of comfort, security, and intelligence. IEEE WirelCommun. 2020, 27, 126–132. [Google Scholar] [CrossRef]
- You, X.; Wang, C.X.; Huang, J.; Gao, X.; Zhang, Z.; Wang, M.; Liang, Y.C. Towards 6G wireless communication networks: Vision, enabling technologies, and new paradigm shifts. Sci. China Inf. Sci. 2021, 64, 110301. [Google Scholar] [CrossRef]
- Jahid, A.; Alsharif, M.H.; Hall, T.J. A contemporary survey on free space optical communication: Potentials, technical challenges, recent advances and research direction. J. Netw. Comput. Appl. 2022, 200, 103311. [Google Scholar] [CrossRef]
- Magidi, S.; Jabeena, A. Free space optics, channel models and hybrid modulation schemes: A review. Wirel. Pers. Commun. 2021, 119, 2951–2974. [Google Scholar] [CrossRef]
- Wang, G.; Shao, L.Y.; Xiao, D.; Bandyopadhyay, S.; Jiang, J.; Liu, S.; Li, W.; Wang, C.; Yan, Z. Stable and highly efficient free-space optical wireless communication system based on polarization modulation and in-fiber diffraction. J. Light. Technol. 2021, 39, 83–90. [Google Scholar] [CrossRef]
- Luo, H.; Wang, J.; Bu, F.; Ruby, R.; Wu, K.; Guo, Z. Recent progress of air/water cross-boundary communications for underwater sensor networks: A review. IEEE. Sens. J. 2022, 22, 8360–8382. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Young, C.Y. Scintillation model for a satellite communication link at large zenith angles. Opt. Eng. 2000, 39, 3272–3280. [Google Scholar]
- Andrews, L.C.; Phillips, R.L. I–K distribution as a universal propagation model of laser beams in atmospheric turbulence. J. Opt. Soc. Am. A 1985, 2, 160–163. [Google Scholar] [CrossRef]
- Davis, C.A.; Walters, D.L. Atmospheric inner-scale effects on normalized irradiance variance. Appl. Optics. 1994, 33, 8406–8411. [Google Scholar] [CrossRef]
- Al-Habash, M.A.; Andrews, L.C.; Phillips, R.L. Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media. Opt. Eng. 2001, 40, 1554–1562. [Google Scholar] [CrossRef]
- Osborn, J.; Townson, M.J.; Farley, O.J.; Reeves, A.; Calvo, R.M. Adaptive Optics pre-compensated laser uplink to LEO and GEO. Opt. Express. 2021, 29, 6113–6132. [Google Scholar] [CrossRef] [PubMed]
- Tunick, A. Optical turbulence parameters characterized via optical measurements over a 2.33 km free-space laser path. Opt. Express. 2008, 16, 14645–14654. [Google Scholar] [CrossRef] [PubMed]
- Anguita, J.A.; Neifeld, M.A.; Vasic, B.V. Spatial correlation and irradiance statistics in a multiple-beam terrestrial free-space optical communication link. Appl. Optics. 2007, 46, 6561–6571. [Google Scholar] [CrossRef] [PubMed]
- Bayaki, E.; Schober, R.; Mallik, R.K. Performance analysis of MIMO free-space optical systems in gamma-gamma fading. IEEE Trans. Commun. 2009, 57, 3415–3424. [Google Scholar] [CrossRef]
- Takenaka, H.; Toyoshima, M. Study on the fiber coupling efficiency for ground-to-satellite laser communication links. In Proceedings of the SPIE LASE, San Francisco, CA, USA, 26 February 2010. [Google Scholar]
- Tan, L.; Li, M.; Wu, J.; Ma, J.; Yang, Q. Fiber-coupling efficiency simulation of Gaussian Schell model laser in space-to-ground optical communication link. Opt. Commun. 2015, 349, 112–119. [Google Scholar] [CrossRef]
- Ma, J.; Lu, G.; Yu, S.; Tan, L.; Fu, Y.; Li, F. Fiber coupling efficiency for satellite and space to ground downlinks with pointing errors. Optik 2020, 202, 163558. [Google Scholar] [CrossRef]
- Zhai, C. Turbulence spectrum model and fiber-coupling efficiency in the anisotropic non-Kolmogorov satellite-to-ground downlink. Results Phys. 2021, 29, 104685. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Hopen, C.Y. Aperture averaging of optical scintillations: Power fluctuations and the temporal spectrum. Wave. Random Media. 2000, 10, 53. [Google Scholar] [CrossRef]
- Wang, T.; Zhao, X.; Song, Y.; Wang, J.; Luan, Y.; Li, Y.; Chang, S. Near-surface atmospheric turbulence profile measuring technology based on an airship-mounted laser communication system. Appl. Optics. 2022, 61, 439–445. [Google Scholar] [CrossRef]
- Shikhovtsev, A.Y.; Kovadlo, P.G.; Lezhenin, A.A.; Gradov, V.S.; Zaiko, P.O.; Khitrykau, M.A.; Kirichenko, K.E.; Driga, M.B.; Kiselev, A.V.; Russkikh, I.V.; et al. Simulating atmospheric characteristics and daytime astronomical seeing using Weather Research and Forecasting Model. Appl. Sci. 2023, 13, 6354. [Google Scholar] [CrossRef]
- Frehlich, R.; Sharman, R.; Vandenberghe, F.; Yu, W.; Liu, Y.; Knievel, J.; Jumper, G. Estimates of Cn2 from numerical weather prediction model output and comparison with thermosonde data. J. Appl. Meteorol. Clim. 2010, 49, 1742–1755. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).