Abstract
The Zernike representation of wavefronts interlinks low- and high-order aberrations, which may result in imprecise clinical estimates. Recently, the Gatinel–Malet wavefront representation has been introduced to resolve this problem by deriving a new, unlinked basis originating from Zernike polynomials. This new basis preserves the classical low and high aberration subgroups’ structure, as well as the orthogonality within each subgroup, but not the orthogonality between low and high aberrations. This feature has led to conversions relying on separate wavefront reconstructions for each subgroup, which may increase the associated numerical errors. This study proposes a robust, minimised-error (lossless) analytical approach for conversion between the Zernike and Gatinel–Malet spaces. This method analytically reformulates the conversion as a nonhomogeneous system of linear equations and computationally solves it using matrix factorisation and decomposition techniques with high-level accuracy. This work fundamentally demonstrates the lossless expression of complex wavefronts in a format that is more clinically interpretable, with potential applications in various areas of ophthalmology, such as refractive surgery.
1. Introduction
Wavefront technology has become an integral part of ophthalmology, particularly in the field of refractive surgery [1,2,3]. The concept of wavefronts refers to the propagation of light waves, which can be distorted by imperfections in optical systems such as the human eye. Wavefront analysis measures these aberrations and has been adapted from its initial use in astronomy to improve our understanding of ocular optics and enhance refractive surgery techniques [4,5]. By characterising the eye’s optical aberrations, wavefront analysis has improved the accuracy and precision of refractive procedures. It enables the correction of not only lower-order aberrations like defocus and astigmatism but also higher-order aberrations, which contribute to visual disturbances otherwise not correctable by optical aids. This has led to improved visual outcomes and patient satisfaction [6]. Additionally, wavefront analysis enables the correction of higher-order aberrations, which can still lead to visual disturbances, even in patients with 20/20 visual acuity [7]. For example, addressing these aberrations, wavefront-guided refractive surgery can enhance visual performance and patient satisfaction, as well as allow for the customisation of refractive surgery procedures [8,9,10]. One challenge is the complexity of interpreting wavefront data and ensuring the accurate representation of visual quality.
Zernike polynomials have become a standard tool in ophthalmology due to their ability to effectively model corneal surfaces and analyse optical wavefronts [11,12,13]. This basis possesses useful mathematical properties, including orthogonality and normalisation on a unit circle, which facilitate their application in modelling and testing wavefronts. This wavefront basis provides a mathematical approach to determine both higher- and lower-order aberrations of the cornea and the ocular wavefront, allowing for a detailed analysis of individual components of the wavefront. Nevertheless, one of the main challenges of describing wavefronts using Zernike polynomials is the intermixing of lower- and higher-order terms, which can lead to misinterpretation of individual aberrations [14,15]. This issue is particularly relevant in ophthalmology and refractive surgery, where accurate characterisation of wavefront aberrations is crucial for clinical decision-making and surgical planning. Several alternative approaches have been proposed to circumvent this limitation, such as the Bhatia–Wolf polynomial-based method [16,17] and monomial aberrations [18]. The former results in a better modelling of the wavefront error function, with a reduction in modelling error (RMS) of 30–50% for normal subjects and a tenfold decrease in mean square error (MSE) for subjects with significant aberrations. The latter calculates individual monomial aberrations from Zernike polynomials, providing accurate knowledge of aberration nodes—essential for understanding the behaviour of an optical system such as the eye.
In a broader scope including ophthalmology and vision science, several studies have explored different mathematical functions to model wavefront aberrations. For instance, the work by [19] compared Zernike polynomials and Bessel circular functions, demonstrating that, while Zernike polynomials are widely used in ophthalmic applications due to their orthogonality on a unit circle and intuitive interpretation of low-order aberrations, they may not always provide the best fit for complex, high-order aberrations or for irregularly shaped pupils. The Bessel functions, on the other hand, offer an alternative approach that can be more flexible in fitting data across varying pupil sizes and can potentially model diffraction effects more accurately. However, they are less commonly used due to their more complex mathematical properties and lack of intuitive interpretation in a clinical context.
Similarly, other studies have explored different polynomial expansions and basis functions to represent corneal topography and ocular aberrations. The work of [20] evaluated Fourier and Taylor series expansions, finding that Fourier series could model irregular corneal shapes with high fidelity, but at the expense of computational complexity and potential overfitting with higher terms. Meanwhile, [21] discussed the use of radial basis functions, which provide excellent localisation of aberrations but require careful selection of basis parameters and can be sensitive to noise in measurement data. Furthermore, the work of [22] utilises refractive Zernike power polynomials to quantify aberrations, providing a precise and objective way to measure refractive errors like myopia, hyperopia, and astigmatism.
Recently, the Gatinel–Malet representation of wavefronts (also known as lower-degree (LD)/higher-degree (HD) polynomial decomposition) has been introduced, which segregates higher and lower aberrations in a novel way, enhancing the clinical relevance of wavefront analysis [23,24]. The new LD/HD decomposition may offer advantages in the analysis and interpretation of retinal image quality simulations [25]. However, global orthogonality across all LD/HD terms is no longer maintained; instead, orthogonality is preserved within each subspace individually. This change impairs the straightforward fitting of new polynomials to wavefronts. Indeed, this feature has led to conversions that rely on separate wavefront reconstructions for each subgroup, potentially increasing reconstruction and fit errors, as well as noise. This is particularly relevant in clinical practice due to its impact on clinical diagnosis and, for example, the planning of refractive surgery treatments.
This work proposes a direct and minimised-error analytical approach for converting Zernike to Gatinel–Malet (and vice versa) coefficients. A lossless transformation was achieved by forming an inhomogeneous system of linear equations (SLEs) and utilising computational matrix decomposition techniques (via Python) to solve the SLEs accurately and reproducibly.
2. Materials and Methods
Zernike polynomials () are used to conveniently express wavefronts in terms of optical aberrations within a circular pupil. As originally proposed, these polynomials form an orthonormal basis over a unit disk such that (in polar coordinates) as follows [26]:
where
shoud be met and the radial polynomial is defined as
Consequently, each wavefront () can be expressed as the Zernike polynomials and corresponding coefficients ,
In ophthalmology, orders below the 3rd () are considered low-order aberrations (LOA), while the remaining orders are classified as high-order aberrations (HOA), which are not correctable by spectacles. This threshold splits the aberrations; however, terms lower than parabolic () are explicitly present in both LOA and HOA polynomial spaces. This fact necessitates additional compensation for the LOA terms when addressing HOA aberrations in complex refractive surgery, a phenomenon known as the coupling of HOAs in the refractive terms. In [23], a new basis was proposed for a canonical quantification of the low- and high-degree aberrations. Hereafter, we abbreviate the new basis as and the Zernike basis as Z. The basis represents a circular wavefront W under the following definition:
where represents the azimuthal argument of Equation (1), and equates 1 for even cases and zero otherwise. Indeed, the regularisation term bypasses the possible linking of the HD to the LD polynomials. However, this mathematical revision causes a partial loss of the orthogonality between the LD and HD polynomials. Indeed, wavefronts project into 2 spaces, composed of orthogonal bases, which are mutually contravariant such that
where represents the elements of GM space.
Indeed, wavefronts project into two spaces, LD and HD, each provided with an orthonormal basis, but the two spaces are not orthogonal. Expanding a wavefront in the GM basis from its Zernike expansion can follow a two-step routine. First, the LD wavefront is obtained by adding the LD contributions from all Zernike polynomials (both LO and HO). Then, subtracting this LD component from the original wavefront provides the HD wavefront, leading to the HD coefficients through appropriate scalar products. This method was used by Gatinel and Malet [23,24].
Here, we propose a direct algebraic method using Equations (3) and (4) to convert coefficients between and bases and vice versa, which facilitate numerical handling and minimise the conversion error.
Theoretically, expanding a wavefront () in both and Z bases would equate to, i.e, from Equations (3) and (4),
Expanding both Zernike and radially when is fixed, for , the LD coefficients are found to be
where can be written as
and, for , .
There are rounds to the smallest integer. In fact, accumulates the radial coefficients of Equation (2), whereas has been kept.
Following the rationale of Equation (6), an SLE can be formed to obtain the high degree coefficients,
e.g., for , among the whole SLE, the following 5 linear equations involve for :
Equation (9) can be formulated into a matricial format:
where and are the square (M × M) matrices of and . and are the vector representation of the wavefront’s coefficients via GM and Zernike, respectively.
Since is non-singular, Equation (11) can be solved as an algebraic matrix equation given the following approach:
which results in GM (HD) coefficients obtained via existing Zernike coefficients. Equation (11) was solved using programming language applying the decomposition [27] of the matrix .
For an matrix, LU decomposition has a time complexity of O(). This is the same as the time complexity of matrix multiplication, making it suitable for large matrices compared to other methods such as Gaussian elimination performed repeatedly.
We should note that Equation (6) can identically be applied to the gradient spaces of wavefronts as
where the transverse gradient information in is primarily available, e.g., measuring the gradient of wavefronts with, e.g., a Hartmann–Shack wavefront sensor [28,29]. Indeed, Equation (13) straightforwardly forms the SLEs through measured gradients and enables a conversion to the Gatinel–Malet space without a need for wavefront reconstructions realising the lossless and noise-minimised presentation of aberrations in a new basis.
A similar methodology can be also followed to convert the Gatinel–Malet coefficients to the Zernike space by forming an SLE from the left hand of Equation (6). Thus, a lossless bijection would be achieved.
3. Results and Discussion
3.1. Centration Reference
Conventionally, ophthalmological wavefronts can be centred by either the vertex or pupil centre as a reference [30] point and affect the interpretation of wavefront data and the analysis of aberrations [31]. This section focuses on the centration, emphasising the choice of vertex, which is referred to as the wavefront’s centre, in the Zernike space and, consequently, the Gatinel–Malet space, hereafter.
For small translations, wavefronts can be expanded using a Taylor series as follows:
given that the polar translation relates to the Cartesian shifts as
Assuming that the cornea as an azimuthal symmetry optical system, the first-order perturbation is negligible until the following condition (heuristic) is met [32]:
Given the assumption that the significance of coefficients can be conventionally seen in orders less than four, the wavefront slope would be proportional to . With a relevant coefficient of few micrometers (≤10 m), the in a 6–8 mm pupil diameter should vary within the range of 30–60 m, resulting in . This estimated value practically corresponds to the limitation reported in [33]. Thus, the coefficient for the translated wavefront would not deviate from the non-translated one:
As a numerical demonstration, a lateral shift of 40 m in the relative position of the pupil centre in a close vicinity of the vertex was considered. The influence of this lateral translation on the coefficients is presented in Table 1. The limited translational shift could adequately represent the entire wavefront as well the general image of the HOAs. For instances with significantly larger shifts, such as astigmatism or hyperopic cases with 100–200 m shifts, this approximation deviates from the clinical relevance.

Table 1.
Comparison of Zernike coefficients (in m) under a lateral translation of 40 m.
Here, the point spread function (PSF) can also be intended as a qualitative measure of comparison:
where is the pupil geometry and presents the wavefront. Moreover, the PSF of HOA is of interest, particularly in refractive surgery, to characterise the correction of HOA [15].
Additionally, we define the as a measure for quantifying the reconstruction error as follows [34]:
where a fine reconstruction would result in a smaller , comparably. Here, q refers to a summation over all pixels.
The value for the translated wavefront versus the reference wavefront (Figure 1a,d) is less than , indicating a reasonable level of similarity between the two instances. The PSFs of the total and exclusively HOA terms, shown in Figure 1b,c,e,f, further illustrate the resemblance of the wavefronts without revealing any significant changes at the primary visualisation level.
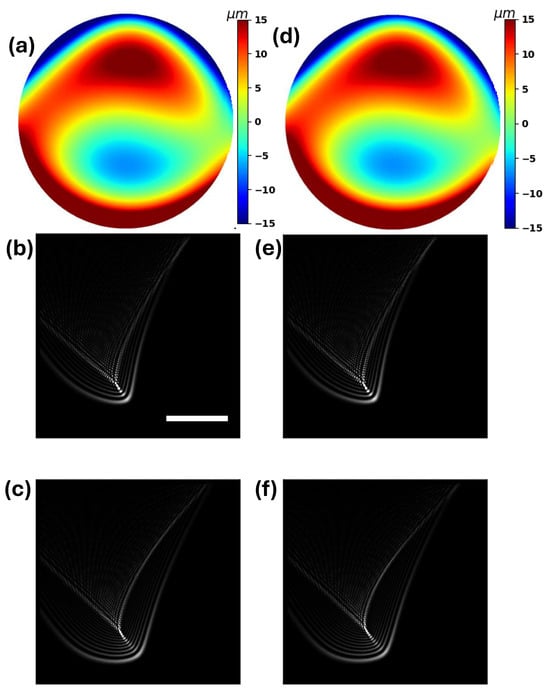
Figure 1.
(a–c) display the reference wavefront, the corresponding PSF and the PSF of the HOAs. (d–f) follow the ration of (a–c) for the translated wavefront under a lateral shift of 40 m. (a,d) are defined within a diameter of 8 mm with a resolution of 7.8 m. The resolution in (b–f) is 110 nm, e.g., the white scale bar indicates 0.4 m.
Therefore, through this work, without any loss of generality, the vertex refers to the wavefront’s centre. Additionally, the vertex provides a consistent reference point regardless of pupil size or shape and is regarded as a relatively stable anatomical landmark, less influenced by changes in pupil size or accommodation.
3.2. Preservation of Wavefront Representation
In the following, we demonstrate the conversion from the Zernike basis to Gatinel–Malet basis using the SLE and the method introduced in [23] (referred to as Feed–Refit). The reference (corneal) wavefront (WRF) was positioned at the vertex and generated by weighting coefficients up to the 21st term (fifth order).
We chose a reference wavefront that resembles the characteristics of keratoconus [35]; however, any wavefront could be used as the reference. Here, we emphasised the resemblance to an ophthalmological case for illustrative purposes. In keratoconus, large amounts of tilt and coma, along with severe levels of negative spherical aberrations, help illustrate and emphasise the differences between the conventional Zernike and the new Gatinel–Malet spaces, potentially providing clearer insights for diagnosis and interpretation.
Figure 2b,c show the reconstructions of the reference wavefront (Figure 2a) in the Gatinel–Malet space by the SLE and Feed–Refit approaches. The red bars in Figure 2d are the Zernike coefficients; the green and black bars represent the coefficients in the Gatinel–Malet space utilising the SLE and Feed–Refit approaches. The SLE approach results in a significantly smaller compared to the Feed–Refit by surpassing the numerical uncertainty of the fitting process. Therefore, the heuristic of is admissibly met via the SLE approach rather than the Feed–Refit equivalence.
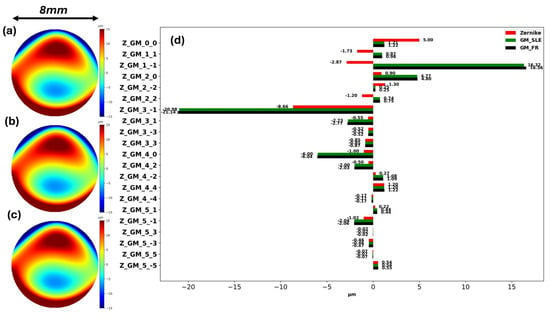
Figure 2.
(a−c) represent the reference wavefront, the reconstructed wavefront by the SLE, and Feed−Refit approaches at the Gatinel−Malet space. (d) illustrates the coefficients corresponding to each representation. The red bars present the Zernike coefficients; the green and black bars are the coefficients in the Gatinel−Malet space utilising the SLE and Feed−Refit approaches.
The root mean square (RMS) of higher-order (high-degree) aberrations is among the critical metrics for understanding vision quality and the performance of corrective treatments such as lens and refractive surgery. We define the RMS for the HOA (HD, respectively) as follows:
The coefficients given in Figure 2d determine a significant discrepancy, m against m and m versus m. This major disparity originated from the exclusion of the linear and parabolic terms () from the HD and accumulating their contribution to the LD leading to significant amplification of and compared to their Zernike correspondence. A similar effect can be concluded through and , considering the difference of the normalisation factors as well.
Intriguingly, in the GM representation, the tilt mode exhibits a sign reversal with respect to the coma (). Considering the overall shape of the given keratoconic corneal wavefront, one would expect a positive tilt (a phase advance in the superior part), which is observed in the GM decomposition. The negative value of the tilt in the Zernike representation compensates for its counterpart within the Zernike coma () term.
Figure 3 demonstrates the identical total PSFs in both spaces ((a–c) in the sequence of Figure 2); however, the minimised loss levels in the SLE approach lead to a more apt analogy between Figure 3a,b. Both Figure 3e,f reflect the pronounced coma terms in HD of the Gatinel–Malet space compared to the broader Zernike representation, ascribed to the presence of low-degree astigmatism and parabolic terms, as shown in Figure 3d.

Figure 3.
The upper panel showcases the total PSFs corresponding to Figure 2. The lower panel illustrates PSFs of HOA/HD in each basis. As expected, (e,f) would share common properties. The white scale bar is m (i.e., a resolution of 110 nm), and applies to (a–f).
Additionally, Figure 3a,d illustrate a vertical shift attributed to the tilt term (). This vertical shift would be absent in the PSF of HOA if the linear terms were exclusively allocated to the LOAs, as clearly achieved in Figure 3b,e due to the LD/HD polynomial definitions, rectifying that the GM representation can better align with the separation of spectacle and non-spectacle correctable aberrations.
The brighter central spot in Figure 3e relates to the higher weighting of the coma terms by the SLE approach comapred to Feed–Refit, as shown in Figure 2d.
The stability and reliability of the direct conversion approach were evaluated by transforming the coefficients of 100 wavefronts from the Zernike space to the Gatinel–Malet space, each repeated 10 times. In every instance, the SLE solver produced unique solutions without any significant deviations.
Notably, the SLE approach significantly reduces the numerical and computational effort required for the explicit simulation of Gatinel–Malet polynomials, potentially speeding up computations and minimising numerical residuals.
3.3. Change of Gatinel–Malet Aberration with Pupil Sizes
The impact of pupil size on lower- and higher-order (degree) aberrations has been a topic of significant interest in ophthalmology, particularly within refractive surgery. Over the past decade, wavefront-guided customised ablations have gained momentum, delivering promising results. However, it is crucial to consider the effect of pupil size on induced variations in both lower- and higher-order Zernike aberrations. Numerous studies have demonstrated that pupil size significantly affects Zernike aberrations, especially higher-order aberrations [36,37,38,39,40].
The work of [41] developed an algorithmic transformation relationships for pupil resizing. Utilising the given algorithm, the Zernike coefficients for the wavefront defined in Figure 2 were calculated at 3 mm, 5 mm, 6 mm, and 7 mm pupil diameter. By using the SLE approach, all resized coefficients were converted in the Gatinel–Malet space, enabling the investigation of the evolution of coefficients versus the pupil diameter.
Table 2 summarises the Zernike and Gatinel–Malet coefficients for the different pupil diameters. LD aberrations, which include defocus and astigmatism, are influenced by pupil size. Similar to HD aberrations, LD aberrations tend to increase as pupil size increases. However, the impact of pupil size on LD aberrations seems to be less pronounced compared to HD aberrations, i.e., by varying from 5 mm to 7 mm, a threefold upscale can be observed in the HD terms, while the LD terms do not exceed a more than approximately twofold increase.

Table 2.
Gatinel–Malet representation of rescaled Zernike coefficients using the SLE approach.
Moreover, the coefficients corresponding to m > 2 for each degree of n are similar in both spaces, matching the definition in Equation (4) considering that, through the SLE approach, the polynomials are not explicitly simulated.
Given the wavelength as and the pupil diameter as , the optical power follows as [42]
Analogously, considering the GM polynomials, the same conversion can be made to determine the optical power, since the low-order/low-degree polynomials are identical in equation. Furthermore, in the absence of HOA, the first- and second-order coefficients are identical.
The optical power (OP) might be better preserved (invariant with respect to the pupil diameter) in the Gatinel–Malet space compared to the Zernike space. This consistency allows for more predictable optical corrections, as the effect of optical power does not vary with changes in pupil size. It can be also seen that, e.g., in bright light conditions, where the pupil naturally constricts, the OP derived by GM approaches Seidel’s refraction [43,44,45] which is, advantageously, less dependent on the analysis diameter. Additionally, the invariance of OP facilitates the customisation of advanced optical corrections, such as those used in LASIK surgery or customised contact lenses, by providing a stable baseline. To add to that, the GM-derived refraction would tend to be systematically biased towards paraxial curvature. Moreover, it can be seen that a natural scaling of might hold comparably better via the GM basis.
We note that, for all pupil sizes, the was calculated for the rescaled wavefronts in the Zernike space versus the Gatinel–Malet, assuring the analysis of the same wavefront in both spaces. All were less than 2 × , illustrating the same wavefront representation in both spaces.
Utilising the values from Table 2, yet another interesting feature of the Gatinel–Malet representation can be revealed by the SLE approach. Figure 4 presents the calculated PSF, over the 5 mm and 7 mm pupil sizes, obtained using the total wavefront aberrations (a–d) and solely HOA/HD (e–h) in both the Zernike and Gatinel–Malet spaces. The PSF of HD on a relatively smaller pupil size can resemble properties of the corresponding HD’s PSF over a larger pupil size. This feature may not apply in the Zernike space due to the particular influence of pupil size change on different terms.
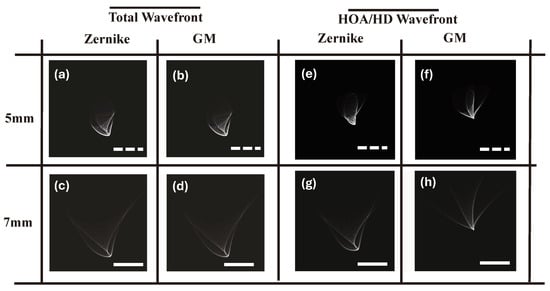
Figure 4.
(a–d) are the total PSF of 5 mm and 7 mm pupil sizes accordingly in both Zernike (a,c) and the Gatinel–Malet spaces (b,d). (e–h) represent the PSF of HOA/HD for the sequence of (a–d). The information loss in the Gatinel–Malet space is significantly less than in the Zernike space. The dashed white and solid line scale bars are m and m (i.e., resolutions of 150 nm and 115 nm, respectively).
The SLE approach leverages computational and analytical power to transfer current understanding of wavefronts into the Gatinel–Malet space without a need for simulating polynomials, directly realising the potential of this new basis.
4. Conclusions
We proposed an analytical approach to transform aberration coefficients from the conventional Zernike basis to a clinically justified basis referred to as the Gatinel–Malet basis. This approach significantly outperformed the former proposed method of conversion [23] by lifting the inevitable numerical uncertainties through fitting processes.
The SLE approach, for the first time, to our knowledge, enabled a conversion without the explicit need for polynomial inclusion. The combination of computation deployment and analytical derivation resulted in a fast, less than 1 s in the Python programming language, and reproducible bijection. Even increasing the orders did not require a computation time longer than 5 s to solve a 12 × 12 linear equation system. Solving a similar system in Feed–Refit significantly increased the processing time and effort needed.
It was demonstrated that the coefficients of the Gatinel–Malet space resulted in approximately the same wavefront, with a . This measure ensured minimal information loss in interconversion, particularly considering that the SLE approach can be regarded as lossless. Nevertheless, we have formulated an analytical heuristic to delineate the proximity of both the pupil centre and vertex within the wavefront presentation and the associated qualitative measures remain largely unchanged.
We demonstrated that, with the advantages of the SLE approach, the impact of pupil size on aberrations can be thoroughly studied. It was observed that PSFs of HD share more common features over various aperture sizes compared with their equivalent on the Zernike basis.
We believe that the SLE approach would open an avenue to utilise and exploit the potential of the novel wavefront basis in ophthalmology, ranging from diagnostics to refractive surgery planning. We envision that, to exploit the potential of the Gatinel–Malet representation, the mathematical properties of the proposed polynomials under rotation, translation, resizing, and pupil shape variations are to be extensively studied, which form the scope of future work.
Author Contributions
Conceptualisation, S.A.M. and M.M.; methodology, M.M. and J.M.; computation, M.M.; validation, all authors contributed equally; writing—original draft preparation, M.M.; writing—review and editing, S.A.M. and D.G.; visualisation, M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HOA | High-order aberration |
| LOA | Low-order aberration |
| HD | High degree |
| LD | Low degree |
| SLE | System of linear equations |
| PSF | Point spread function |
| RMS | Root mean square |
| WRF | Reference wavefront |
| WRE | Reconstructed wavefront |
| OP | Optical power |
References
- Lawless, M.A.; Hodge, C. Wavefront’s role in corneal refractive surgery. Clin. Exp. Ophthalmol. 2005, 33, 199–209. [Google Scholar] [CrossRef]
- MacRae, S.M.M.; Yoon, G.P. The wavefront revolution. J. Cataract. Refract. Surg. 2021, 47, 1387–1388. [Google Scholar] [CrossRef]
- Ang, M.; Gatinel, D.; Reinstein, D.E.A. Refractive surgery beyond 2020. Eye 2021, 35, 362–382. [Google Scholar] [CrossRef]
- Mello, G.R.; Rocha, K.M.; Santhiago, M.R.; Smadja, D.; Krueger, R.R. Applications of wavefront technology. J. Cataract. Refract. Surg. 2012, 38, 1671–1683. [Google Scholar] [CrossRef]
- Langman, M.; Dighiero, P.; Gicquel, J. The basics of wavefront aberrometry. Acta Ophthalmol. Scand. 2007, 85. [Google Scholar] [CrossRef]
- David, A.A. Wavefront aberrations and their clinical application. Clin. Exp. Optom. 2009, 92, 171–172. [Google Scholar] [CrossRef]
- Vacalebre, M.; Frison, R.; Corsaro, C.; Neri, F.; Conoci, S.; Anastasi, E.; Curatolo, M.C.; Fazio, E. Advanced Optical Wavefront Technologies to Improve Patient Quality of Vision and Meet Clinical Requests. Polymers 2022, 14, 5321. [Google Scholar] [CrossRef]
- Doane, J.F.; Slade, S.G. An Introduction to Wavefront-Guided Refractive Surgery. Int. Ophthalmol. Clin. 2003, 43, 101–117. [Google Scholar] [CrossRef]
- Li, S.-M.; Kang, M.-T.; Wang, N.-L.; Abariga, S. Wavefront excimer laser refractive surgery for adults with refractive errors. Cochrane Database Syst. Rev. 2020, 12, CD012687. [Google Scholar] [CrossRef]
- Hofmeister, E.M.M.; Cason, J.B.M.; Murdoch, D.M.P.; Yau, I.W.P.; Wang, Y.M.; Parizadeh, D.D.P.; Janakiraman, D.P.; Kasthurirangan, S.P. Wavefront-guided PRK treatment of myopia using a refractive aberrometer. J. Cataract. Refract. Surg. 2023, 49, 292–298. [Google Scholar] [CrossRef]
- Oliveira, C.M.; Ferreira, A.; Franco, S.P. Wavefront analysis and Zernike polynomial decomposition for evaluation of corneal optical quality. J. Cataract. Refract. Surg. 2012, 38, 343–356. [Google Scholar] [CrossRef] [PubMed]
- Omidi, P.; Cayless, A.; Langenbucher, A. Evaluation of optimal Zernike radial degree for representing corneal surfaces. PLoS ONE 2022, 17, e0269119. [Google Scholar] [CrossRef] [PubMed]
- Niu, K.; Tian, C. Zernike polynomials and their applications. J. Opt. 2022, 24, 123001. [Google Scholar] [CrossRef]
- Kligman, B.E.; Baartman, B.J.; Dupps, W.J.J. Errors in Treatment of Lower-order Aberrations and Induction of Higher-order Aberrations in Laser Refractive Surgery. Int. Ophthalmol. Clin. 2016, 56, 19–45. [Google Scholar] [CrossRef]
- Klyce, S.D.; Karon, M.D.; Smolek, M.K. Advantages and Disadvantages of the Zernike Expansion for Representing Wave Aberration of the Normal and Aberrated Eye. J. Refract. Surg. 2004, 20. [Google Scholar] [CrossRef]
- Iskander, D.R.; Morelande, M.R.; Collins, M.J.; Davis, B.A. An alternative polynomial representation of the wavefront error function. Investig. Ophthalmol. Vis. Sci. 2002, 43, 1898. [Google Scholar]
- Atchison, D.A. Recent advances in representation of monochromatic aberrations of human eyes. Clin. Exp. Optom. 2004, 87, 138–148. [Google Scholar] [CrossRef]
- Johnson, T.P.; Sasian, J. Zernike monomials in wide field of view optical designs. Appl. Opt. 2020, 59, G146–G153. [Google Scholar] [CrossRef]
- Treviño, C.I.; Pérez-Álvarez, M.; Artal, P. Comparison of Zernike polynomials and Bessel circular functions in wavefront reconstruction in optical systems. J. Opt. Soc. Am. 2013, 30, 480–490. [Google Scholar]
- Khorin, P.A.; Khonina, S.N. Simulation of the Human Myopic Eye Cornea Compensation Based on the Analysis of Aberrometric Data. Vision 2023, 7, 21. [Google Scholar] [CrossRef]
- Iskander, D.R.; Morelande, M.R.; Collins, M.J.; Davis, B. Modeling of corneal surfaces with radial polynomials. IEEE Trans. Biomed. Eng. 2002, 49, 320–328. [Google Scholar] [CrossRef]
- Robert Iskander, D.; Davis, B.A.; Collins, M.J.; Franklin, R. Objective refraction from monochromatic wavefront aberrations via Zernike power polynomials. Ophthalmic Physiol. Opt. 2007, 27, 245–255. [Google Scholar] [CrossRef] [PubMed]
- Gatinel, D.; Malet, J.; Dumas, L. Polynomial decomposition method for ocular wavefront analysis. J. Opt. Soc. Am. A 2018, 35, 2035–2045. [Google Scholar] [CrossRef] [PubMed]
- Gatinel, D.; Rampat, R.; Dumas, L.; Malet, J. An Alternative Wavefront Reconstruction Method for Human Eyes. J. Refract. Surg. 2020, 36, 74–81. [Google Scholar] [CrossRef] [PubMed]
- Rampat, R.; Malet, J.; Dumas, L.; Gatinel, D. Wavefront sensing, novel lower degree/higher degree polynomial decomposition and its recent clinical applications: A review. Indian J. Ophthalmol. 2020, 68, 2670–2678. [Google Scholar] [CrossRef] [PubMed]
- Born, M.; Wolf, E. Principles of Optics: Electromagnetic Theory of Propagation, Interference and Diffraction of Light, 7th ed.; Cambridge University Press: Cambridge, UK, 1999. [Google Scholar]
- Van de Velde, E.F. LU-Decomposition. In Concurrent Scientific Computing; Springer: New York, NY, USA, 1994; pp. 97–123. [Google Scholar] [CrossRef]
- Jiang, W.; Li, H. Hartmann-Shack wavefront sensing and wavefront control algorithm. In Proceedings of the Adaptive Optics and Optical Structures, Hague, The Netherlands, 14–15 March 1990; In-den Baeumen, J.J.S., Tyson, R.K., Eds.; International Society for Optics and Photonics, SPIE: San Francisco, CA, USA, 1990; Volume 1271, pp. 82–93. [Google Scholar] [CrossRef]
- Shatokhina, I.; Hutterer, V.; Ramlau, R. Review on methods for wavefront reconstruction from pyramid wavefront sensor data. J. Astron. Telesc. Instruments, Syst. 2020, 6, 010901. [Google Scholar] [CrossRef]
- Mosquera, S.A.; Ewering, T. New Asymmetric Centration Strategy Combining Pupil and Corneal Vertex Information for Ablation Procedures in Refractive Surgery: Theoretical Background. J. Refract. Surg. 2012, 28, 567–575. [Google Scholar] [CrossRef]
- Mosquera, S.A.; Verma, S. The Centration Dilemma in Refractive Corrections: Why Is It Still a Dilemma and How to Cope? Photonics 2024, 11, 822. [Google Scholar] [CrossRef]
- Chapra, S.C.; Canale, R.P. Numerical Methods for Engineers; chapter Taylor Series and Error Analysis; McGraw-Hill: New York, NY, USA, 2006; pp. 75–102. [Google Scholar]
- Bueeler, M.; Mrochen, M.; Seiler, T. Maximum permissible lateral decentration in aberration-sensing and wavefront-guided corneal ablation. J. Cataract. Refract. Surg. 2003, 29, 257–263. [Google Scholar] [CrossRef]
- Chuang, K.S.; Huang, H.K. Comparison of chi-square and join-count methods for evaluating digital image data. IEEE Trans. Med. Imaging 1992, 11, 28–33. [Google Scholar] [CrossRef]
- Castillo, J.; Hanna, R.; Berkowitz, E.; Tiosano, B. Wavefront Analysis for Keratoconus. Int. J. Keratoconus Ectatic Corneal Dis. 2014, 3, 76–83. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, K.; Jin, Y.; Niu, Y.; Zuo, T. Changes of Higher Order Aberration With Various Pupil Sizes in the Myopic Eye. J. Refract. Surg. 2003, 19, S270–S274. [Google Scholar] [CrossRef] [PubMed]
- Iseli, H.; Bueeler, M.; Hafezi, F.; Seiler, T.; Mrochen, M. Dependence of Wave Front Refraction on Pupil Size Due to the Presence of Higher Order Aberrations. Eur. J. Ophthalmol. 2005, 15, 680–687. [Google Scholar] [CrossRef] [PubMed]
- Karimian, F.; Feizi, S.; Doozande, A. Higher-order aberrations in myopic eyes. J. Ophthalmic Vis. Res. 2010, 5, 3–9, Erratum in: J. Ophthalmic Vis. Res. 2010, 5, 214. [Google Scholar] [PubMed]
- Comastri, S.A.; Perez, L.I.; Pérez, G.D.; Martin, G.; Bianchetti, A. Corneal aberrations in keratoconic eyes: Influence of pupil size and centering. J. Physics: Conf. Ser. 2011, 274, 012109. [Google Scholar] [CrossRef]
- Kong, W.; Huang, J.; He, Y.; Shi, G. Adaptive Optics Methods to Rat Eye Properties: Impact of Pupil Diameter on Wavefront Detection. Photonics 2024, 11, 359. [Google Scholar] [CrossRef]
- Dai, G.M. Validity of Scaling Zernike Coefficients to a Larger Diameter for Refractive Surgery. J. Refract. Surg. 2011, 27, 837–841. [Google Scholar] [CrossRef]
- Grosvenor, T.; Fannin, T. Clinical Optics; Butterworth-Heinemann: Oxford, UK, 1987. [Google Scholar]
- Welford, W.T. Aberrations of Optical Systems; Taylor and Francis Group: Abingdon, UK, 1986. [Google Scholar]
- Kidger, M.J. Fundamental Optical Design; SPIE: San Francisco, CA, USA, 2001; Volume PM 92. [Google Scholar]
- Mouroulis, P.; Macdonald, J. Geometrical Optics and Optical Design; Oxford University Press: Oxford, UK, 1997. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).