Robust Sensing Based on Exceptional Points in Detuned Non-Hermitian Scattering System
Abstract
1. Introduction
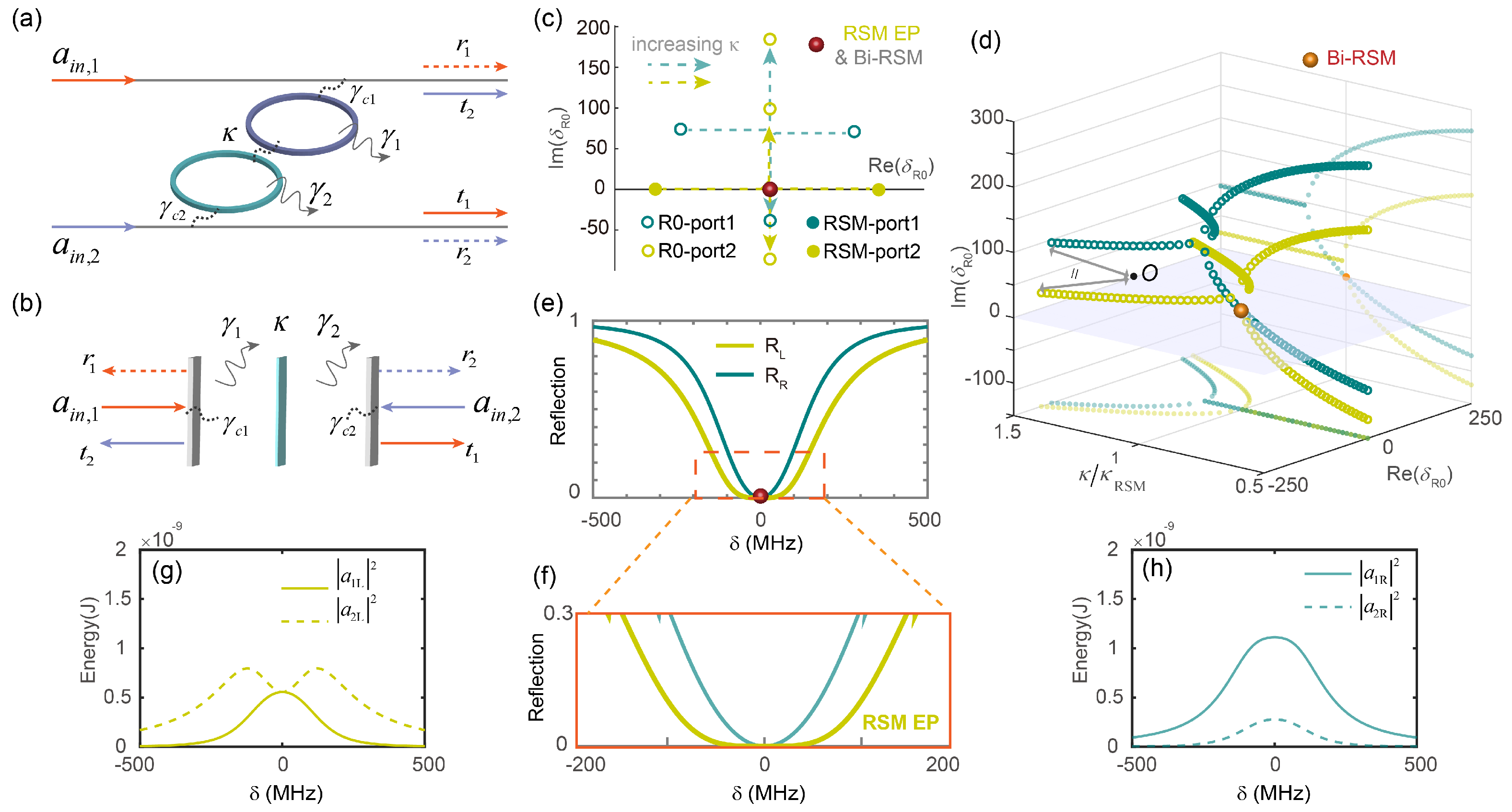
2. Non-Hermitian Scattering Matrix
3. Non-Detuned Case
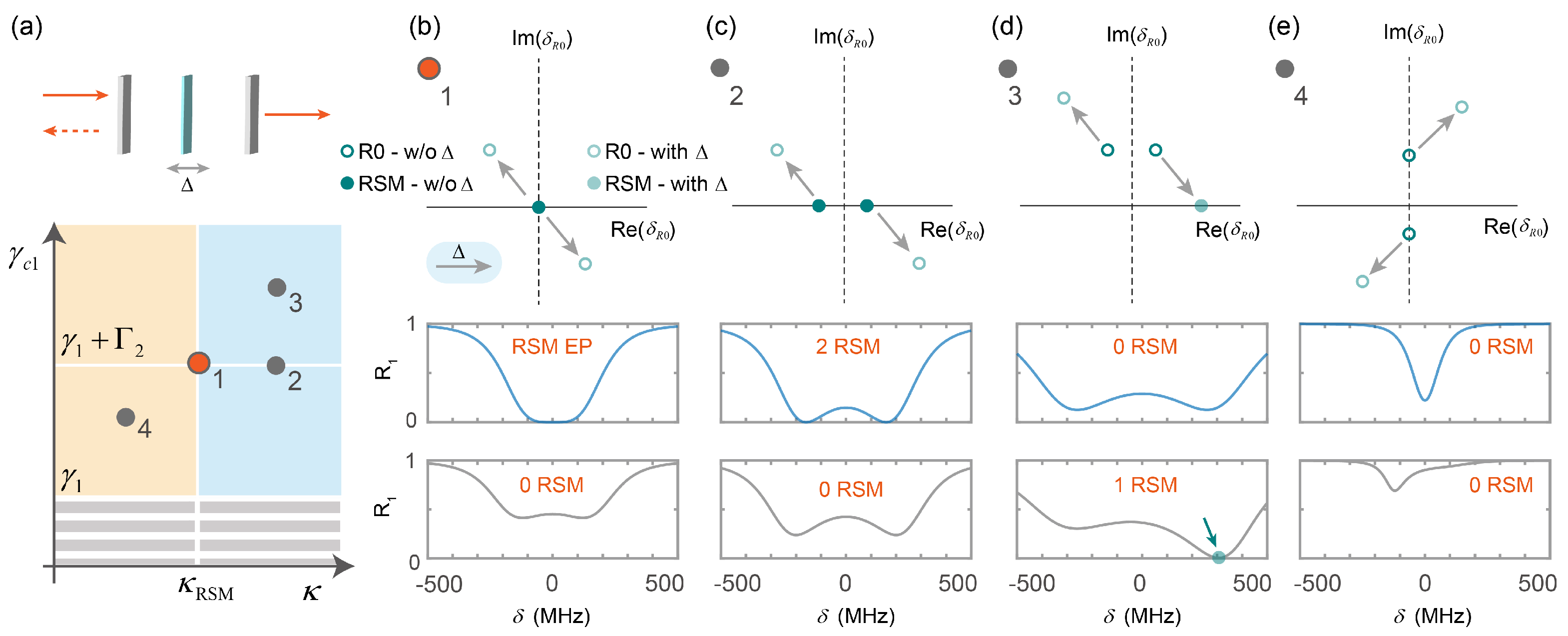
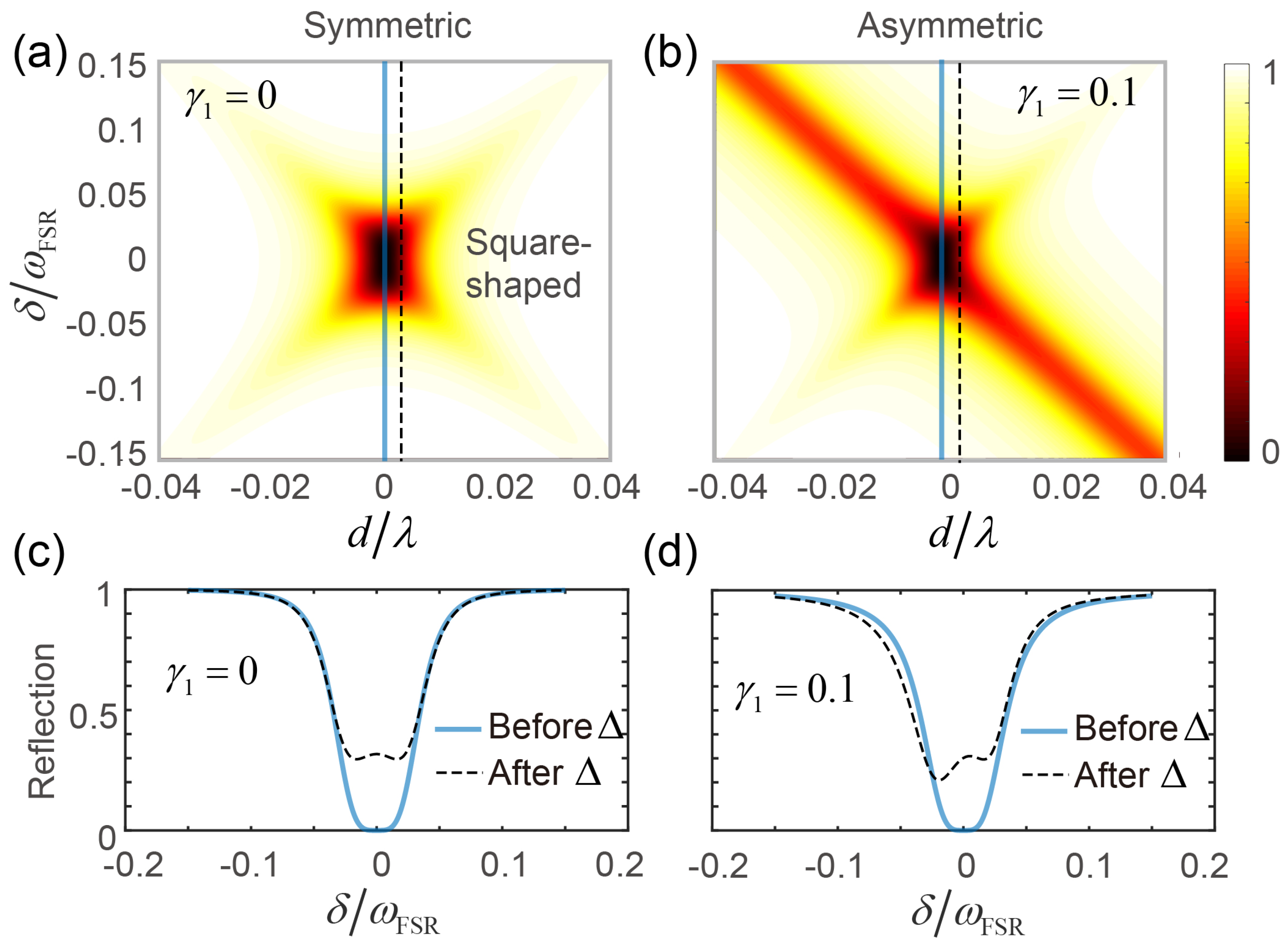
4. Detuned Case
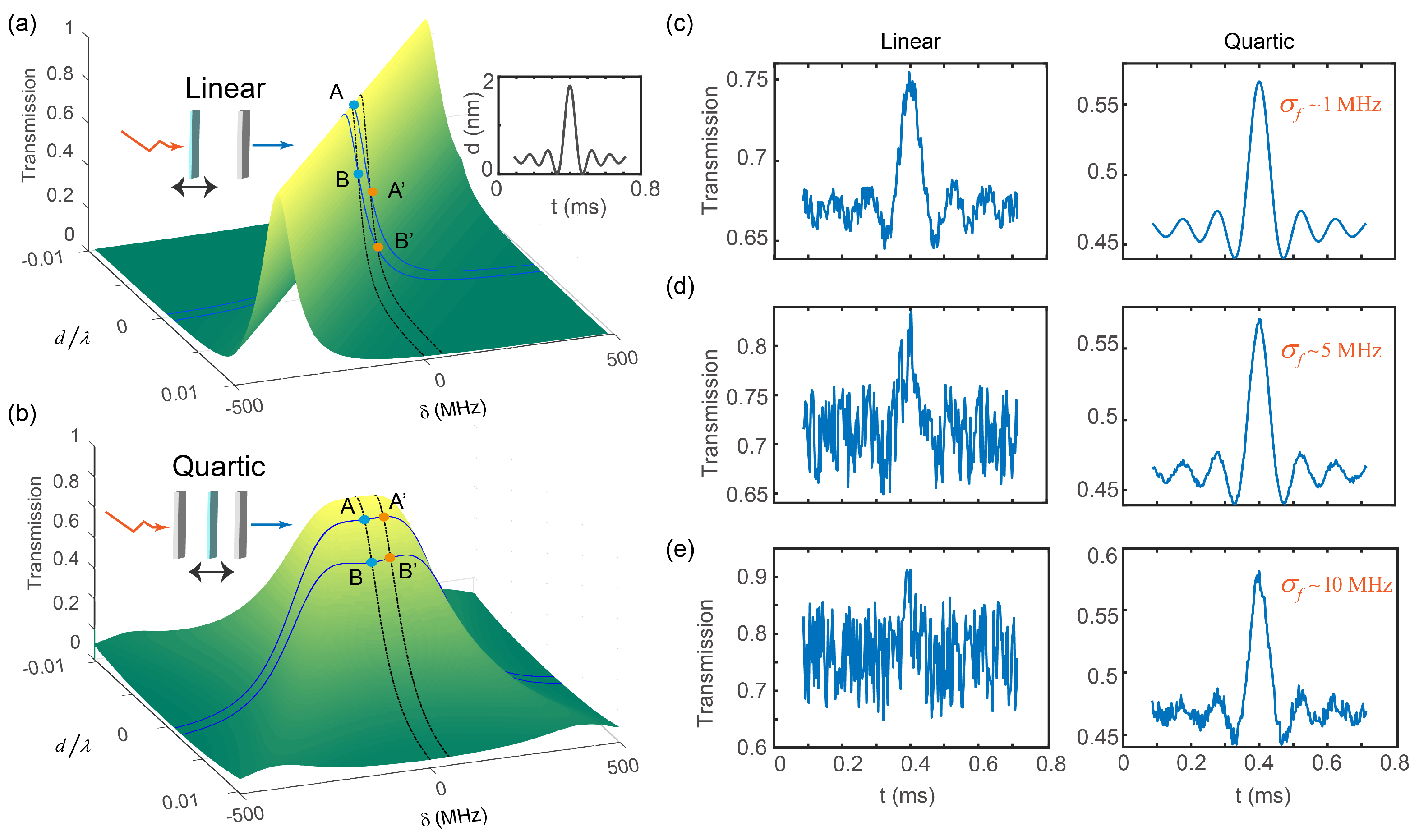
5. Robust RSM EP Sensing
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Numerical Model of the One-Dimensional Cavity
Appendix B. RSM Existence Conditions with Cavity Detuning
Appendix C. Derivation of the Detuning Response Symmetry Condition
References
- Konotop, V.V.; Yang, J.; Zezyulin, D.A. Nonlinear waves in PT-symmetric systems. Rev. Mod. Phys. 2016, 88, 035002. [Google Scholar] [CrossRef]
- Feng, L.; El-Ganainy, R.; Ge, L. Non-Hermitian photonics based on parity-time symmetry. Nat. Photonics 2017, 11, 752–762. [Google Scholar] [CrossRef]
- El-Ganainy, R.; Makris, K.G.; Khajavikhan, M.; Musslimani, Z.H.; Rotter, S.; Christodoulides, D.N. Non-Hermitian physics and PT symmetry. Nat. Phys. 2018, 14, 11–19. [Google Scholar] [CrossRef]
- Özdemir, Ş.K.; Rotter, S.; Nori, F.; Yang, L. Parity–time symmetry and exceptional points in photonics. Nat. Mater. 2019, 18, 783–798. [Google Scholar] [CrossRef]
- Miri, M.A.; Alù, A. Exceptional points in optics and photonics. Science 2019, 363, eaar7709. [Google Scholar] [CrossRef]
- Guo, A.; Salamo, G.J.; Duchesne, D.; Morandotti, R.; Volatier-Ravat, M.; Aimez, V.; Siviloglou, G.A.; Christodoulides, D.N. Observation of PT-Symmetry Breaking in Complex Optical Potentials. Phys. Rev. Lett. 2009, 103, 093902. [Google Scholar] [CrossRef] [PubMed]
- Peng, B.; Özdemir, Ş.K.; Rotter, S.; Yilmaz, H.; Liertzer, M.; Monifi, F.; Bender, C.M.; Nori, F.; Yang, L. Loss-induced suppression and revival of lasing. Science 2014, 346, 328–332. [Google Scholar] [CrossRef]
- Wong, Z.J.; Xu, Y.l.; Kim, J.; O’Brien, K.; Wang, Y.; Feng, L.; Zhang, X. Lasing and anti-lasing in a single cavity. Nat. Photonics 2016, 10, 796–801. [Google Scholar] [CrossRef]
- Bergholtz, E.J.; Budich, J.C.; Kunst, F.K. Exceptional topology of non-Hermitian systems. Rev. Mod. Phys. 2021, 93, 015005. [Google Scholar] [CrossRef]
- Sweeney, W.R.; Hsu, C.W.; Stone, A.D. Theory of reflectionless scattering modes. Phys. Rev. 2020, 102, 063511. [Google Scholar] [CrossRef]
- Kononchuk, R.; Cai, J.; Ellis, F.; Thevamaran, R.; Kottos, T. Exceptional-point-based accelerometers with enhanced signal-to-noise ratio. Nature 2022, 607, 697–702. [Google Scholar] [CrossRef] [PubMed]
- Sweeney, W.R.; Hsu, C.W.; Rotter, S.; Stone, A.D. Perfectly Absorbing Exceptional Points and Chiral Absorbers. Phys. Rev. Lett. 2019, 122, 093901. [Google Scholar] [CrossRef] [PubMed]
- Farhi, A.; Mekawy, A.; Alù, A.; Stone, D. Excitation of absorbing exceptional points in the time domain. Phys. Rev. A 2022, 106, L031503. [Google Scholar] [CrossRef]
- Wang, C.; Sweeney, W.R.; Stone, A.D.; Yang, L. Coherent perfect absorption at an exceptional point. Science 2021, 373, 1261–1265. [Google Scholar] [CrossRef]
- Lee, H.; Kecebas, A.; Wang, F.; Chang, L.; Özdemir, Ş.; Gu, T. Chiral exceptional point and coherent suppression of backscattering in silicon microring with low loss Mie scatterer. eLight 2023, 3, 20. [Google Scholar] [CrossRef]
- Jiang, X.; Yin, S.; Li, H.; Quan, J.; Goh, H.; Cotrufo, M.; Kullig, J.; Wiersig, J.; Alù, A. Coherent control of chaotic optical microcavity with reflectionless scattering modes. Nat. Phys. 2023, 20, 109–115. [Google Scholar] [CrossRef]
- Xu, J.; Mao, Y.; Li, Z.; Zuo, Y.; Zhang, J.; Yang, B.; Xu, W.; Liu, N.; Deng, Z.J.; Chen, W.; et al. Single-cavity loss-enabled nanometrology. Nat. Nanotechnol. 2024. [Google Scholar] [CrossRef]
- Hodaei, H.; Hassan, A.U.; Wittek, S.; Garcia-Gracia, H.; El-Ganainy, R.; Christodoulides, D.N.; Khajavikhan, M. Enhanced sensitivity at higher-order exceptional points. Nature 2017, 548, 187–191. [Google Scholar] [CrossRef]
- Hokmabadi, M.P.; Schumer, A.; Christodoulides, D.N.; Khajavikhan, M. Non-Hermitian ring laser gyroscopes with enhanced Sagnac sensitivity. Nature 2019, 576, 70–74. [Google Scholar] [CrossRef] [PubMed]
- Wiersig, J. Review of exceptional point-based sensors. Photonics Res. 2020, 8, 1457. [Google Scholar] [CrossRef]
- Zhong, Q.; Ren, J.; Khajavikhan, M.; Christodoulides, D.N.; Özdemir, Ş.K.; El-Ganainy, R. Sensing with Exceptional Surfaces in Order to Combine Sensitivity with Robustness. Phys. Rev. Lett. 2019, 122, 153902. [Google Scholar] [CrossRef] [PubMed]
- Soleymani, S.; Zhong, Q.; Mokim, M.; Rotter, S.; El-Ganainy, R.; Özdemir, Ş.K. Chiral and degenerate perfect absorption on exceptional surfaces. Nat. Commun. 2022, 13, 599. [Google Scholar] [CrossRef] [PubMed]
- Cannata, F.; Dedonder, J.P.; Ventura, A. Scattering in PT-symmetric quantum mechanics. Ann. Phys. 2007, 322, 397–433. [Google Scholar] [CrossRef]
- Sol, J.; Alhulaymi, A.; Stone, A.D.; del Hougne, P. Reflectionless programmable signal routers. Sci. Adv. 2023, 9, eadf0323. [Google Scholar] [CrossRef]
- Qian, J.; Meng, C.H.; Rao, J.W.; Rao, Z.J.; An, Z.; Gui, Y.; Hu, C.M. Non-Hermitian control between absorption and transparency in perfect zero-reflection magnonics. Nat. Commun. 2023, 14, 3437. [Google Scholar] [CrossRef]
- Feng, L.; Xu, Y.L.; Fegadolli, W.S.; Lu, M.H.; Oliveira, J.E.; Almeida, V.R.; Chen, Y.F.; Scherer, A. Experimental demonstration of a unidirectional reflectionless parity-time metamaterial at optical frequencies. Nat. Mater. 2013, 12, 108–113. [Google Scholar] [CrossRef]
- Ge, L.; Chong, Y.D.; Stone, A.D. Conservation relations and anisotropic transmission resonances in one-dimensional PT-symmetric photonic heterostructures. Phys. Rev. A 2012, 85, 023802. [Google Scholar] [CrossRef]
- Zhao, H.; Chen, Z.; Zhao, R.; Feng, L. Exceptional point engineered glass slide for microscopic thermal mapping. Nat. Commun. 2018, 9, 1764. [Google Scholar] [CrossRef]
- Yoo, G.; Sim, H.S.; Schomerus, H. Quantum noise and mode nonorthogonality in non-Hermitian PT-symmetric optical resonators. Phys. Rev. A 2011, 84, 063833. [Google Scholar] [CrossRef]
- Hashemi, A.; Busch, K.; Christodoulides, D.N.; Ozdemir, S.K.; El-Ganainy, R. Linear response theory of open systems with exceptional points. Nat. Commun. 2022, 13, 3281. [Google Scholar] [CrossRef]
- Aspelmeyer, M.; Kippenberg, T.J.; Marquardt, F. Cavity optomechanics. Rev. Mod. Phys. 2014, 86, 1391–1452. [Google Scholar] [CrossRef]
- Petermann, K. Laser Diode Modulation and Noise; Springer: Dordrecht, The Netherlands, 1988. [Google Scholar]
- Thompson, J.D.; Zwickl, B.M.; Jayich, A.M.; Marquardt, F.; Girvin, S.M.; Harris, J.G.E. Strong dispersive coupling of a high-finesse cavity to a micromechanical membrane. Nature 2008, 452, 72–75. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Mao, Y.; Liu, K.; Zhu, Z. Robust Sensing Based on Exceptional Points in Detuned Non-Hermitian Scattering System. Photonics 2024, 11, 882. https://doi.org/10.3390/photonics11090882
Xu J, Mao Y, Liu K, Zhu Z. Robust Sensing Based on Exceptional Points in Detuned Non-Hermitian Scattering System. Photonics. 2024; 11(9):882. https://doi.org/10.3390/photonics11090882
Chicago/Turabian StyleXu, Jipeng, Yuanhao Mao, Ken Liu, and Zhihong Zhu. 2024. "Robust Sensing Based on Exceptional Points in Detuned Non-Hermitian Scattering System" Photonics 11, no. 9: 882. https://doi.org/10.3390/photonics11090882
APA StyleXu, J., Mao, Y., Liu, K., & Zhu, Z. (2024). Robust Sensing Based on Exceptional Points in Detuned Non-Hermitian Scattering System. Photonics, 11(9), 882. https://doi.org/10.3390/photonics11090882





