A Fast Solution of the Dynamic Rate Equation for a High-Power Fiber Laser

Abstract

In the study of dynamic behaviors, such as nonlinear effects, power evolution, and pulse evolution of light in fiber gain media, solving dynamic rate equations in fiber laser systems is involved, which is computationally intensive and directly affects overall computational efficiency. A modified difference scheme is proposed to solve fiber dynamic rate equations efficiently. The advantages of the improved scheme and its convergence rate are analyzed. By incorporating a correction coefficient into the finite difference, the approximations of spatial and temporal derivatives are improved, greatly enhancing the performance of the numerical method. The computational results of the proposed method are compared with those of the conventional upwind difference scheme, demonstrating that the improved method is more stable and requires fewer sampling points to maintain a certain level of precision, thereby saving significant computation time and computational resources. The power and spectral evolutions of the fiber laser oscillator under different pump conditions are simulated and compared with experimental data, validating the applicability and reliability of the rapid solving method.

1. Introduction

In recent years, ytterbium-doped fiber lasers have been widely used in various fields, including scientific research [1,2,3], industrial manufacturing [4,5,6], medical treatment [7], and national defense [8]. The gain medium is an essential component of fiber laser systems. The study of dynamic behaviors, such as nonlinear effects, power evolution, and pulse evolution of light in fiber gain media, involves solving fiber laser rate equations. These equations, known as dynamic rate equations (DREs), describe the dynamics of the gain medium with reasonable accuracy [9,10,11,12]. However, solving these equations can be computationally intensive, directly affecting overall computational efficiency. Therefore, finding fast, accurate, and stable solutions for DREs is crucial. DREs are partial differential equations containing derivatives of optical power with respect to position and time, which are often analytically intractable. Currently, numerical methods for solving DREs primarily involve finite difference methods, including upwind schemes [13,14,15,16], Lax–Wendroff methods [17], Runge–Kutta methods [18], and Parallelizable Bidirectional methods [19]. In some cases, with high computational requirements, the conventional first-order upwind scheme (FOUWS, first-order upwind scheme) is simple in form, but it converges slowly. Dense sampling in both space and time may be necessary to ensure the relative accuracy and stability of the solution, which can lead to longer computation times. On the other hand, other high-order schemes are more complex to implement and computationally intensive, with certain dependencies on initial and boundary values.

This paper proposes an improved upwind scheme for solving DREs. By incorporating correction factors derived from approximate analytical solutions into the finite difference (i.e., numerical approximation of spatial and temporal derivatives in DREs), the proposed method significantly enhances computational the accuracy and stability without altering the simplicity of the numerical implementation or increasing the computational cost. The fast solution methods discussed here can also be adapted for more complex forms of DREs.

2. Theory

In fiber laser simulations, DREs are generally similar in form. However, modifications to these equations may be required based on the spatial scale and beam quality requirements of the specific problem, as well as the various physical effects pertinent to different types of lasers. Initial and boundary conditions must be defined according to the laser’s structure. For instance, in fibers with large mode field areas or stringent beam quality requirements, a more complex transverse spatial gain model may be necessary. This complexity arises due to the significant spatial variation in doping ion density in such fibers, which necessitates accounting for spatial dependence, mode intensity distributions, and the effects of beam intensity variations on gain saturation. Consequently, the complete forms of the DREs can be quite intricate.

The amplified spontaneous emission (ASE) effect, which influences laser output power and spectral characteristics, is a ubiquitous phenomenon in fiber lasers. For near single-mode fibers, using a simplified model that averages the doping ion density over the entire fiber cross-section can be reasonable. In practice, regardless of the specific model used, the fundamental approach to solving the rate equations remains consistent and is determined primarily by the domain of the differential equations rather than their specific forms.

Here, we consider a relatively simple form of DREs to describe ytterbium-doped fibers, where the three-level Yb energy system is simplified to a two-level energy system, and the equations can be written as follows [13]:

$${\displaystyle \frac{\mathsf{\partial }{n}_2\left(z,t\right)}{\mathsf{\partial }t}}=\sum _l{\displaystyle \frac{{\Gamma }_p\left(P_{p,l}^{+}+P_{p,l}^{-}\right)}{h{\nu }_{p,l}{A}_{dope}}}\left(n_1{\sigma }_{a,p,l}-n_2{\sigma }_{e,p,l}\right)+\sum _k{\displaystyle \frac{{\Gamma }_s\left(P_{s,k}^{+}+P_{s,k}^{-}\right)}{h{\nu }_{s,k}{A}_{dope}}}\left(n_1{\sigma }_{a,s,k}-n_2{\sigma }_{e,s,k}\right)-{\displaystyle \frac{n_2}{\tau }},$$

(1)

$$\pm {\displaystyle \frac{\mathsf{\partial }{P}_{p,l}^{\pm }\left(z,t\right)}{\mathsf{\partial }z}}+{\displaystyle \frac{1}{v_g^{p,l}}}{\displaystyle \frac{\mathsf{\partial }{P}_{p,l}^{\pm }\left(z,t\right)}{\mathsf{\partial }t}}={\Gamma }_p{P}_{p,l}^{\pm }\left(n_2{\sigma }_{e,p,l}-n_1{\sigma }_{a,p,l}-{\alpha }_p\right),$$

(2)

$$\pm {\displaystyle \frac{\mathsf{\partial }{P}_{s,k}^{\pm }\left(z,t\right)}{\mathsf{\partial }z}}+{\displaystyle \frac{1}{v_g^{\mathrm{s},k}}}{\displaystyle \frac{\mathsf{\partial }{P}_{s,k}^{\pm }\left(z,t\right)}{\mathsf{\partial }t}}={\Gamma }_s{P}_{s,k}^{\pm }\left(n_2{\sigma }_{e,s,k}-n_1{\sigma }_{a,s,k}-{\alpha }_s\right)+2{\Gamma }_s{P}_{s,k}^{SE}{n}_2{\sigma }_{e,s,k}$$

(3)

Here, $z$ and $t$ represent the spatial coordinate and time coordinate, respectively; $n$ denotes the doping particle number density, and $n_1$ and $n_2$ are the particle number densities of the upper and lower energy levels, respectively, with $n_1+n_2=n$. In considering the broadband case, $l$ and $k$ represent the spectral channels for the pump and signal light, respectively. ${\Gamma }_p$ and ${\Gamma }_s$ are the power filling factors for the pump and signal light, with subscripts $P$ and s indicating the pump and signal light, respectively. $A_{dope}$ represents the area of the doped region, which is equal to the area of the fiber core unless a partial doping method is used. Depending on the subscript used, $\sigma$ can be either the absorption or emission cross-section, a denotes absorption, and e denotes emission. $h$, $\nu$, ${\nu }_g$, and $\tau$ represent Planck’s constant, the light frequency, the group velocity, and the upper-level lifetime of Yb³⁺ ions, respectively. $P_{s,k}^{SE}=h{v}_{s,k}\Delta v_s$ is related to the spontaneous emission, where $\Delta v_s$ is the channel width. The superscripts + and − denote the different propagation directions of the light waves.

Here, infinitesimal terms are neglected. To calculate the numerical solution at any time $t=m\Delta t(m=0,1,2,3\dots )$, initial conditions must be given. For example, they can be set as follows: $P_{(p,l)}^{\pm }(z_j,t_0)=0$, $P_{s,k}^{\pm }\left(z_j,t_0\right)=0$, and $n_2\left(z_j,t_0\right)=0$.

Additionally, boundary conditions must be considered. Depending on the input pump and signal powers in different directions, as well as the transmittance and reflectance at the ends of the doped fiber, the first and last elements of $P_{p,l}^{\pm }\left(z_j,t_m\right)$ and $P_{s,k}^{\pm }\left(z_j,t_m\right)$ at the boundaries are rewritten as follows:

$$\begin{gathered} P_{p,l}^{+}\left(z_0,t_m\right)=T_{p,l}^{+}{P}_{p,l}^{+,in}+R_{p,l}{P}_{p,l}^{-}\left(z_0,t_m\right), \\ {P}_{p,l}^{-}\left(z_{\mathrm{N}},t_m\right)=T_{p,l}^{-}{P}_{p,l}^{-,in}+R_{p,l}{P}_{p,l}^{+}\left(z_{\mathrm{N}},t_m\right), \\ {P}_{s,k}^{+}\left(z_0,t_m\right)=T_{s,k}^{+}{P}_{s,k}^{+,in}+R_{s,k}{P}_{s,k}^{-}\left(z_0,t_m\right), \\ {P}_{s,k}^{+}\left(z_0,t_m\right)=T_{s,k}^{+}{P}_{s,k}^{+,in}+R_{s,k}{P}_{s,k}^{-}\left(z_0,t_m\right). \end{gathered}$$

(4)

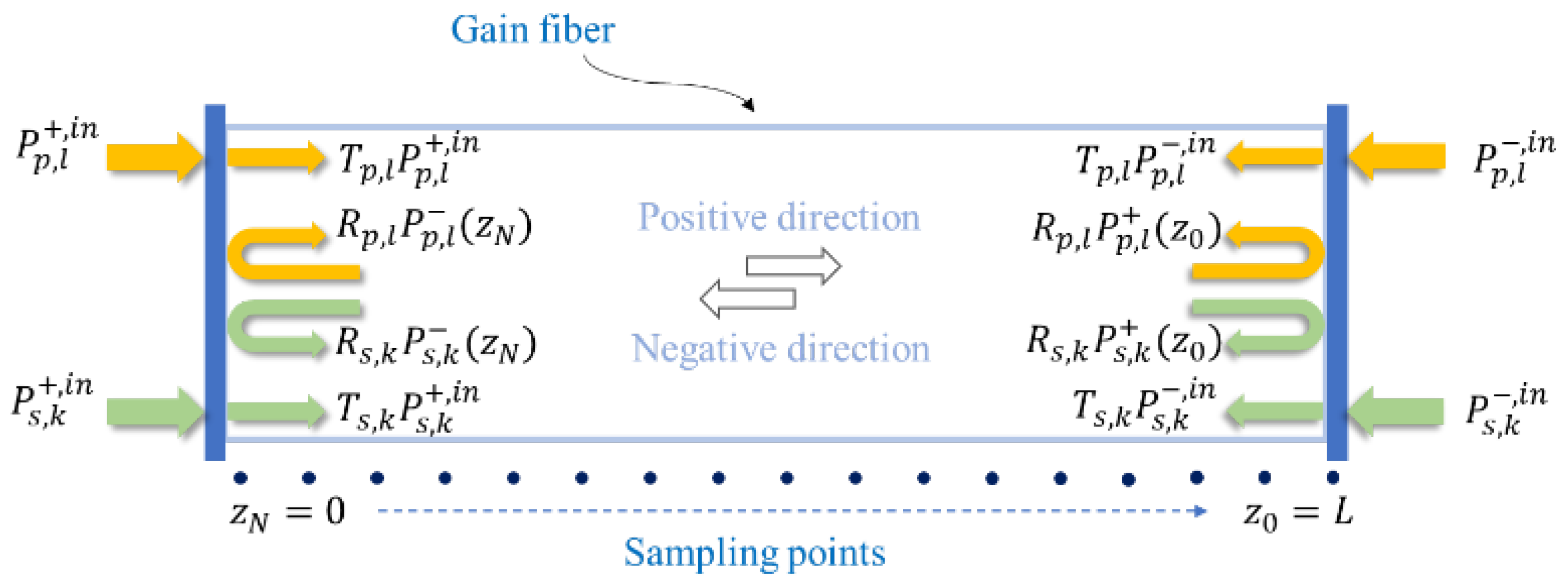
As shown in Figure 1, the superscript “in” denotes the input, representing the injected pump power and signal power; $T$ and $R$ are the transmissivity and reflectivity of the pump or signal light at the fiber end, which may vary with the wavelength of the light. In general, $T$ and $R$ can be considered independent parameters. Finally, it is important to note that in order to ensure the stability of the computation, the following Courant–Friedrichs–Lewy (CFL) condition must be satisfied:

$$\left|{\displaystyle \frac{v_g^{p,l}\Delta t}{\Delta z}}\right|\le 1,\left|{\displaystyle \frac{v_g^{s,k}\Delta t}{\Delta z}}\right|\le 1,$$

(5)

In the subsequent simulations, we set $\left|v_g^{p,l}\Delta t/\Delta z\right|=0.9$, such that $\Delta t=0.9\Delta z/v_g^{p,l}$.

3. Numerical Approach

By removing the time-dependent terms from Equation (2), at a certain moment $t_m$, one can obtain a similar expression to the steady-state Equation (6), as shown below. This simplification is applicable for very short time intervals, such as within $\Delta t$, because the parameters change very little over time; hence, the time terms can be neglected.

$$\begin{gathered} {\displaystyle \frac{\mathsf{\partial }{P}_{p,l}^{\pm }\left(z,t_m\right)}{\mathsf{\partial }z}}=\pm g\left(z,t_m\right)P_{p,l}^{\pm }\left(z,t_m\right), \\ g\left(z,t_m\right)={\Gamma }_p\left(n_2{\sigma }_{e,p,l}-n_1{\sigma }_{a,p,l}-{\alpha }_p\right). \end{gathered}$$

(6)

The approximate analytical solution of this equation can be expressed as follows:

$$P_{p,l}^{\pm }\left(z,t_m\right)=P_{p,l}^{\pm }\left(0,t_m\right)e^{\pm \underset{0}{\overset{z}{{\displaystyle \int }}}g\left(z,t_m\right)dz}.$$

(7)

Building on this, the analytical form of the spatial derivative at any point $z_j$ can be derived as follows:

$${\displaystyle \frac{\mathsf{\partial }{P}_{p,l}^{\pm }\left(z_j,t_m\right)}{\mathsf{\partial }z}}=\pm P_{p,l}^{\pm }\left(0,t_m\right)g\left(z_j,t_m\right)e^{\pm \underset{0}{\overset{z_j}{{\displaystyle \int }}}g\left(z,t_m\right)dz}.$$

(8)

On the other hand, the first-order finite difference used in the FOUWS can be rewritten as follows:

$${\displaystyle \frac{P_{p,l}^{+}\left(z_j,t_m\right)-P_{p,l}^{+}\left(z_{j-1},t_m\right)}{\Delta z}}={\displaystyle \frac{P_{p,l}^{+}\left(0,t_m\right)\left(e^{{{\displaystyle \int }}_0^{z_j}g\left(z,t_m\right)dz}-e^{{{\displaystyle \int }}_0^{z_j-\Delta z}g\left(z,t_m\right)dz}\right)}{\Delta z}}\approx {\displaystyle \frac{P_{p,l}^{+}\left(0,t_{\mathrm{m}}\right)e^{{{\displaystyle \int }}_0^{{\mathrm{z}}_j}g\left(z,{\mathrm{t}}_{\mathrm{m}}\right)dz}\left(1-e^{-g\left(z_j,t_m\right)\Delta z}\right)}{\Delta z}},$$

(9)

$${\displaystyle \frac{P_{p,l}^{-}\left(z_{j+1},t_m\right)-P_{p,l}^{-}\left(z_j,t_m\right)}{\Delta z}}={\displaystyle \frac{P_{p,l}^{-}\left(0,t_m\right)\left(e^{-{{\displaystyle \int }}_0^{z+\Delta z}g\left(z,t_m\right)dz}-e^{-{{\displaystyle \int }}_0^{z_j}g\left(z,t_m\right)dz}\right)}{\Delta z}}\approx {\displaystyle \frac{P_{p,l}^{-}\left(0,t_m\right)e^{-{{\displaystyle \int }}_0^{z_j}g\left(z,t_{\mathrm{m}}\right)dz}\left(e^{-g\left(z_j,t_m\right)\Delta z}-1\right)}{\Delta z}}.$$

(10)

The newly obtained finite difference form is compared with the analytical form of the spatial derivative, yielding the following results:

$${\displaystyle \frac{\mathsf{\partial }{P}_{p,l}^{+}\left(z_j,t_m\right)}{\mathsf{\partial }z}}\approx {\displaystyle \frac{P_{p,l}^{+}\left(z_j,t_m\right)-P_{p,l}^{+}\left(z_{j-1},t_m\right)}{\Delta z}}\times {\displaystyle \frac{g\left(z_j,t_m\right)\Delta z}{1-e^{-g\left(z_j,t_m\right)\Delta z}}},$$

(11)

$${\displaystyle \frac{\mathsf{\partial }{P}_{p,l}^{-}\left(z_j,t_m\right)}{\mathsf{\partial }z}}\approx {\displaystyle \frac{P_{p,l}^{-}\left(z_j,t_m\right)-P_{p,l}^{-}\left(z_{j+1},t_m\right)}{\Delta z}}\times {\displaystyle \frac{g\left(z_j,t_m\right)\Delta z}{1-e^{-g\left(z_j,t_m\right)\Delta z}}}.$$

(12)

Here, ${\displaystyle \frac{g\left(z_j,t_m\right)\Delta z}{1-e^{-g\left(z_j,t_m\right)\Delta z}}}$ is the so-called correction factor. By using the correction factor, we can modify the finite difference form to make it closer to the exact derivative. For the signal light, neglecting the impact of ASE is reasonable, considering its relatively small contribution. Similarly, by neglecting the spatially dependent terms, a correction factor for the time derivative can also be obtained as follows:

$${\displaystyle \frac{g\left(z_j,t_m\right)\Delta t{v}_g^{p,l}}{e^{g\left(z_j,t_m\right)\Delta t{v}_g^{p,l}}-1}} or {\displaystyle \frac{g\left(z_j,t_m\right)\Delta t{v}_g^{s,k}}{e^{g\left(z_j,t_m\right)\Delta t{v}_g^{s,k}}-1}} .$$

(13)

By incorporating these correction factors into Equations (2) and (3), the finite difference numerical forms of these equations can be written as follows:

$$P_{p,l}^{+}(z_j,t_{m+1})=P_{p,l}^{+}(z_j,t_m)+\Delta t{v}_g^{p,l}[g(z_j,t_m)P_{p,l}^{+}(z_j,t_m)-{\displaystyle \frac{(P^{+}(z_j,t_m)-P^{+}(z_{j-1},t_m))}{\Delta z}}\times {\displaystyle \frac{g(z_j,t_m)\Delta z}{(1-e^{(-g(}{z_j,t_m)}^{\Delta z)})}}]{\displaystyle \frac{e^{g\left(z_j,t_m\right)\Delta t{v}_g^{p,l}}-1}{g\left(z_j,t_m\right)\Delta t{v}_g^{p,l}}},$$

(14)

$$P_{p,l}^{-}(z_j,t_{m+1})=P_{p,l}^{-}(z_j,t_m)+\Delta t{v}_g^{p,l}[g(z_j,t_m)P_{p,l}^{-}(z_j,t_m)-{\displaystyle \frac{(P_{p,l}^{+}(z_j,t_m)-P_{p,l}^{+}(z_{j+1},t_m))}{\Delta z}}{\displaystyle \frac{g(z_j,t_m)\Delta z}{(1-e^{(-g(}{z}_j,t_m)\Delta z))}}]{\displaystyle \frac{{\mathrm{e}}^{g\left(z_j,t_m\right)\Delta t{v}_g^{p,l}}-1}{g\left(z_j,t_m\right)\Delta t{v}_g^{p,l}}},$$

(15)

$$P_{s,k}^{+}\left(z_j,t_{m+1}\right)=P_{s,k}^{+}\left(z_j,t_m\right)+\Delta t{v}_g^{s,k}[g\left(z_j,t_m\right)P_{s,k}^{+}\left(z_j,t_m\right)-{\displaystyle \frac{P_{s,k}^{+}\left(z_j,t_m\right)-P_{s,k}^{+}\left(z_{j-1},t_m\right)}{\Delta z}}{\displaystyle \frac{g\left(z_j,t_m\right)\Delta z}{1-e^{-g\left(z_j,t_m\right)\Delta z}}}+2{\Gamma }_s{P}_{s,k}^{SE}{n}_2{\sigma }_{e,s,k}]{\displaystyle \frac{e^{g\left(z_j,t_m\right)\Delta t{v}_g^{s,k}}-1}{g\left(z_j,t_m\right)\Delta t{v}_g^{s,k}}},$$

(16)

$$P_{s,k}^{-}\left(z_j,t_{m+1}\right)=P_{s,k}^{-}\left(z_j,t_m\right)+\Delta t{v}_g^{s,k}[g\left(z_j,t_m\right)P_{s,k}^{-}\left(z_j,t_m\right)-{\displaystyle \frac{P_{s,k}^{+}\left(z_j,t_m\right)-P_{s,k}^{+}\left(z_{j+1},t_m\right)}{\Delta z}}{\displaystyle \frac{g\left(z_j,t_m\right)\Delta z}{1-e^{-g\left(z_j,t_m\right)\Delta z}}}+2{\Gamma }_s{P}_{s,k}^{SE}{n}_2{\sigma }_{e,s,k}]{\displaystyle \frac{e^{g\left(z_j,t_m\right)\Delta t{v}_g^{s,k}}-1}{g\left(z_j,t_m\right)\Delta t{v}_g^{s,k}}}.$$

(17)

It can be seen that the improved scheme, compared to the conventional upwind method’s numerical format, only multiplies the spatial and temporal difference components by a correction factor term (13), maintaining an overall simple form, which makes it easier to understand and numerically implement.

4. Results and Discussion

Based on the solutions to specific problems, the computational results of the improved FOUWS were compared with those of the original FOUWS, and the performance of the improved FOUWS was evaluated, mainly focusing on computational accuracy and speed. Since there is no perfectly accurate solution available as a benchmark for comparison, the solution obtained from the original FOUWS with a larger number of sampling points was used for the comparison. The numerical simulations were conducted on a laptop with an i7-8750H processor and 16 GB of memory. Considering that the output signal power is typically the most interesting component of simulations, the calculation error was measured using the power of the forward-propagating light wave at a specific position $z=z_N$, denoted as $P_{s,k}^{+}\left(z_N,t\right)$. The reference power $P_{s,k,0}^{+}\left(z_N,t\right)$ was obtained using 8000 sampling points (N = 8000) through the unimproved FOUWS. Here, we define the absolute error ${\mathsf{\epsilon }}_1$ and the relative error ${\mathsf{\epsilon }}_2$ between the computed value and the reference as follows:

$${\mathsf{\epsilon }}_1=\sqrt{{\displaystyle \frac{1}{k}}\sum _{i=0}^k{\left[P_{s,k}^{+}\left(z_N,t\right)-P_{s,k,0}^{+}\left(z_N,t\right)\right]}^2},$$

(18)

$${\mathsf{\epsilon }}_2=\sqrt{{\displaystyle \frac{1}{k}}\sum _{i=0}^k\left|{\displaystyle \frac{P_{s,k}^{+}\left(z_N,t\right)-P_{s,k,0}^{+}\left(z_N,t\right)}{P_{s,k,0}^{+}\left(z_N,t\right)}}\right|}.$$

(19)

The simulation was conducted using the parameter values listed in

Table 1. The values of the changed parameters for the first test.

Parameter	Symbol	Value [Units]
Fiber length	$L$	20 m
High-reflectivity FBG	$R_{s,k}^{+}$	90%
Output coupling FBG	$R_{s,k}^{-}$	50%
Time span	$T_{span}$	$0~1\times {10}^{-6}$ s
Forward pump power	$P_p^{+,in}$	500 W
Backward pump power	$P_p^{-,in}$	500 W
Pump channel	${\mathit{\lambda }}_p$	976 nm
Signal channel	${\mathit{\lambda }}_s$	[1000:1:1100] nm
Doping area	$A_{dope}$	$9.5033\times {10}^{-11}$ m2
Number density of doped particles	$N$	$5.1633\times {10}^{25}/$ m3
Upper-level lifetime	$\tau$	0.84 ms
Pump filling factors	${\Gamma }_p$	0.00716
Signal filling factors	${\Gamma }_s$	0.85

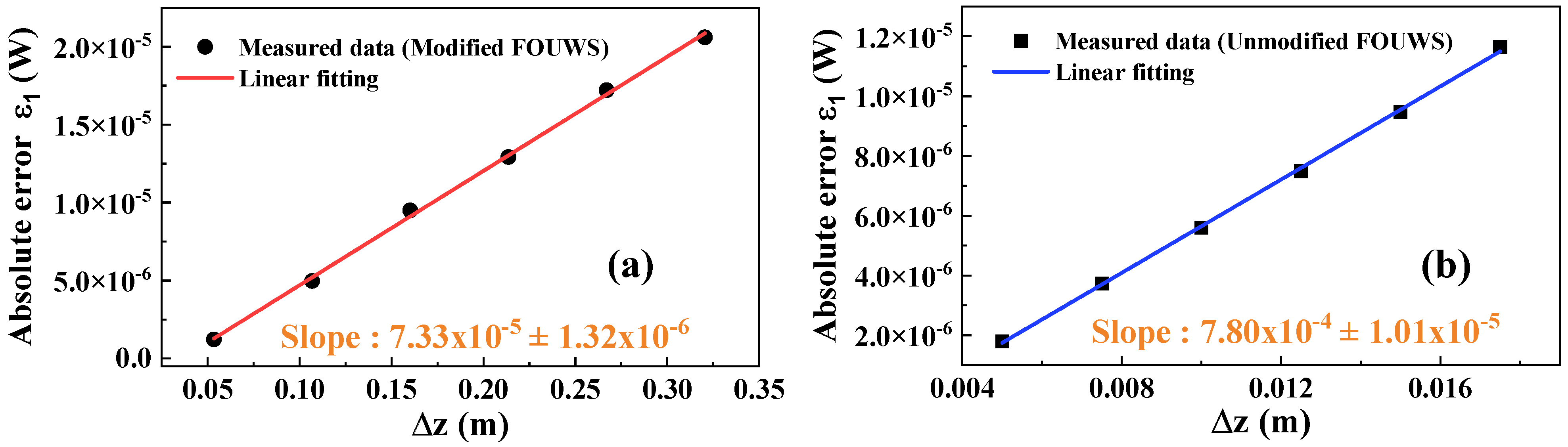
. Figure 2 describes the variation in the error with the size of $\Delta z$ at time $T=5\times {10}^{-7}$ s. This figure clearly shows that the absolute error of the improved FOUWS increases linearly with $\Delta z$. This trend indicates that our improved FOUWS, like the unimproved FOUWS (see Figure 2b), remains a first-order method. However, we can also observe that the slope of the improved FOUWS is much smaller than that of the unimproved FOUWS, suggesting that the improved FOUWS is less affected by the number of sampling points, thus providing more accurate results. Moreover, due to its specific precision requirements, the improved FOUWS requires a fewer number of sampling points, which allows for faster computation of the results.

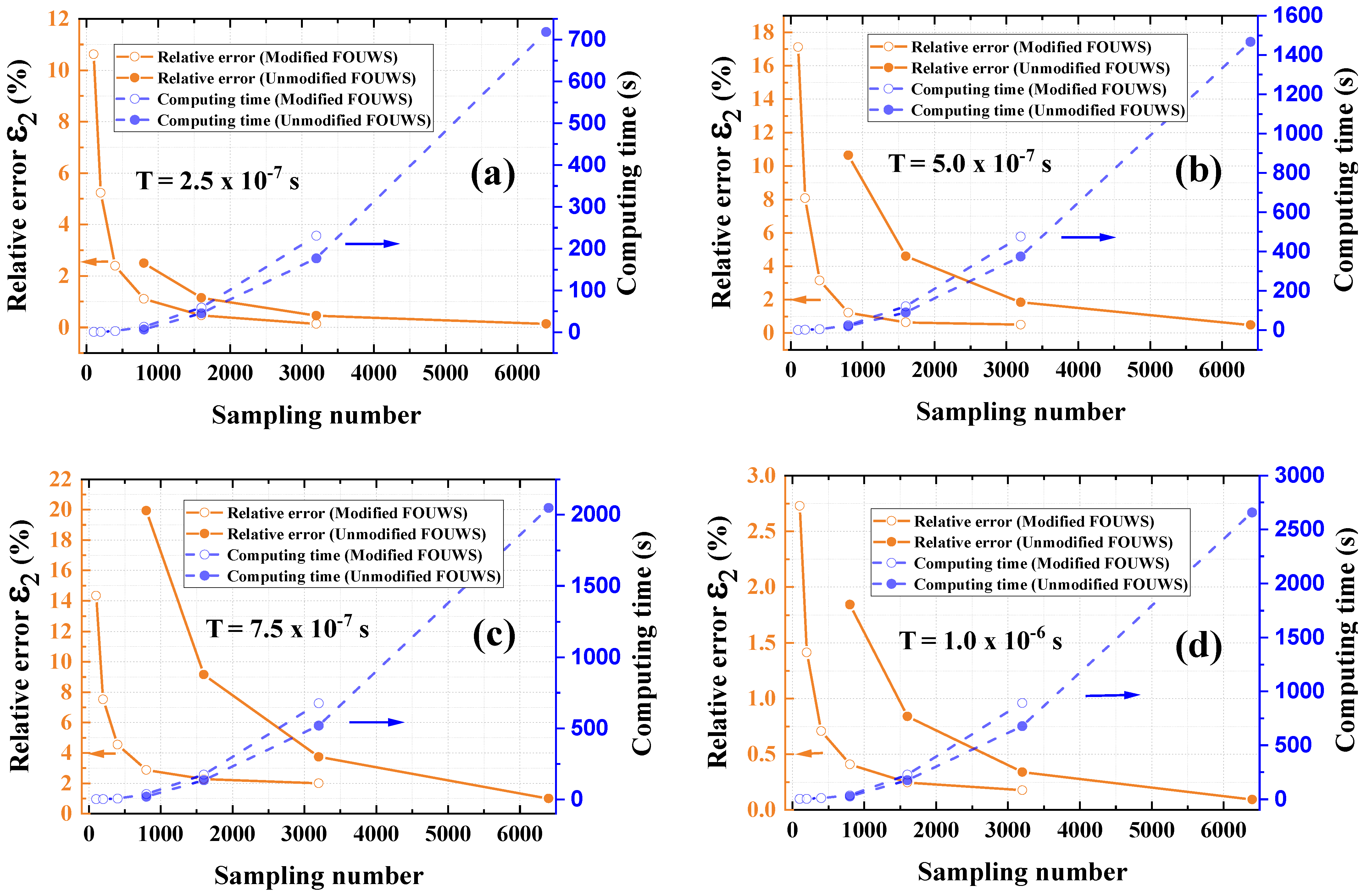
To demonstrate the computational efficiency advantage of the improved algorithm, the relative error and computation time with varying numbers of sampling points were calculated for different time spans ($2.5\times {10}^{-7}$ s, $5\times {10}^{-7}$ s, $7.5\times {10}^{-7}$ s, and $1\times {10}^{-6}$ s). The results in Figure 3 show that the improved method converges much faster than the conventional method. To achieve a certain level of accuracy, the improved method requires fewer sampling points, especially in cases where the conventional method has a relatively large error. The advantage of the improved method in terms of speed and accuracy is more pronounced. The most direct benefit of using fewer sampling points is the reduction in computation time. Taking Figure 3c as an example, when the number of sampling points is 400, the relative error of the improved method is approximately 4.5%, and the computation time is only 5.8 s. For the unimproved method, when the number of sampling points is 1600, the relative error is 9.2% and the computation time is 134.3 s, both of which are much higher than those of the improved method. The unimproved method requires 3200 sampling points and a computation time of 517 s to reduce the relative error to 3.7%, while the improved method can achieve a relative error of no more than 2.9% with only 800 sampling points and a computation time of about 37 s.

It is worth noting that if the sampling is too sparse, the unmodified method often encounters uncontrollable noise amplification, which is the phenomenon where small errors in the initial conditions or rounding errors are gradually magnified, ultimately leading to a significant deviation between the numerical solution and the true solution. However, the improved method seems to be less affected by this problem. This is also the reason why the minimum number of sampling points for the two methods is 800 and 50 in Figure 3, respectively. In fact, in the tests, the modified method only required five sampling points to perform calculations. Due to the large error, the results are not displayed here. However, this phenomenon indicates that the improved method effectively suppresses noise amplification and improves the stability of numerical calculations.

Furthermore, we simulated the establishment of an ASE laser by changing the number of optical channels. Here, the parameters with changes are listed in

Table 2. The values of the changed parameters for the second test.

Parameter	Symbol	Value [Units]
Fiber length	$L$	5 m
High-reflectivity FBG	$R_{\mathrm{s},k}^{+}$	90%
Output coupling FBG	$R_{\mathrm{s},k}^{-}$	50%
Time span	$T_{span}$	$5\times {10}^{-5}$ s
Forward pump power	$P_p^{+,in}$	10 W
Backward pump power	$P_p^{-,in}$	0 W
Signal channel	${\mathit{\lambda }}_s$	[1000:0.1:1100] nm

. Under the conditions of a shorter fiber length, lower pump power, and greater number of optical channels, the advantages of this improved FOUWS are more pronounced. Due to the aforementioned CFL condition, the spatial step size $\Delta z$ for short fibers is usually smaller, which also leads to a smaller time step size $\Delta t$. The low pump power means that the particle number densities $n_1$ and $n_2$ and the optical powers $P_{p,l}^{\pm }$ and $P_{s,k}^{\pm }$ change slowly over time, thus requiring a longer computation time span. A large number of optical channels directly lead to a heavy computational burden.

Using the results of the unimproved FOUWS with 400 sampling points as a benchmark for comparison, the total computation time is approximately 21,626 s. In this simulation, the minimum number of sampling points for the unimproved FOUWS is approximately 130, and using fewer sampling points would lead to an unreasonable result. The total computation time for the unimproved method with 130 sampling points is about 1263 s. The improved FOUWS uses 40 sampling points, with a total computation time of 140 s. 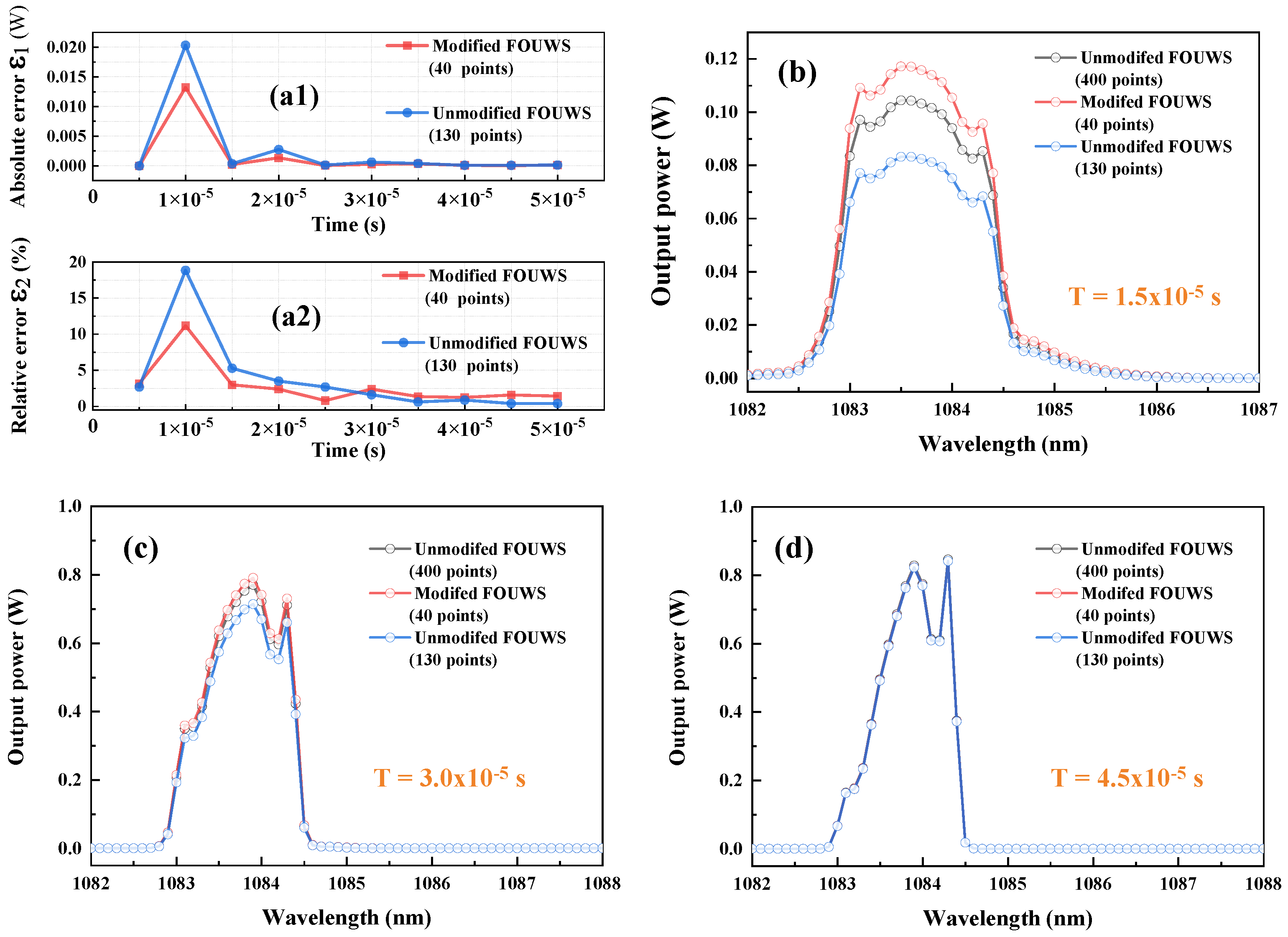Figure 4 depicts the errors and forward output spectra for these three sampling computations. Figure 4(a1,a2) show the absolute error and relative error, respectively, between the improved FOUWS (40 sampling points) and the unimproved FOUWS (130 sampling points) against the benchmark (i.e., the unimproved FOUWS with 400 sampling points). This indicates that the improved method (40 sampling points) has a precision that is comparable to or slightly higher than that of the unimproved method (130 sampling points). When the computation time span exceeds 3.0 × 10⁻⁵ s, the relative error of the improved method (40 sampling points) is greater than that of the unimproved method (130 sampling points), which is primarily due to the increase in ε2 in the low-power part of the spectrum, where the optical power is close to zero. The improved method still demonstrates good performance in the relatively high-power part of the spectrum, as shown in Figure 4b (1082.5–1084.5 nm) and Figure 4c (1083.0–1084.5 nm), and as the time span increases, the deviation in spectral power tends to become negligible, as shown in Figure 4d.

It can be seen that the improved FOUWS achieves a precision similar to that of the unimproved FOUWS with only one-quarter of the sampling points, and the computation time is only one-ninth of the latter, saving 1123 s of computation time. It should be noted that, as mentioned above, 130 points are the minimum number of sampling points for the unimproved FOUWS. This means that the unimproved FOUWS cannot further shorten the computation time by sacrificing computational accuracy through reducing the number of sampling points. However, for the improved FOUWS, under the condition of meeting the accuracy requirements, the computation time can be further reduced by reducing the number of sampling points.

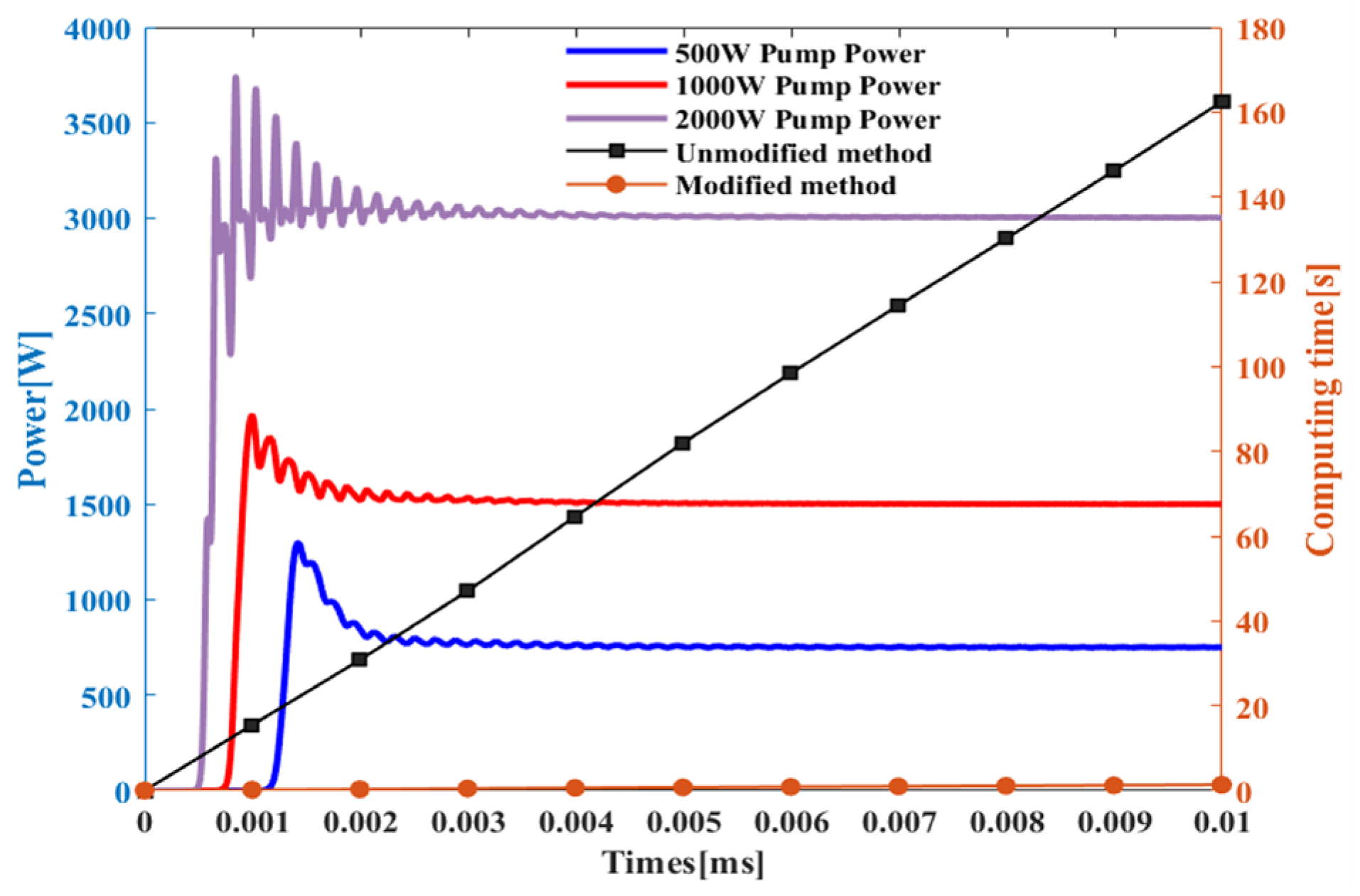
Furthermore, when simulating the pump power increasing step by step from 500 W to 1000 W and then to 2000 W to allow the signal light temporal establishment process to take place, the improved algorithm can complete the evaluation of laser performance more quickly and accurately. The simulation results are shown in Figure 5, where it can be seen that the establishment of the signal light has a distinct threshold time, from which point onwards, the signal light begins to be established very quickly. Moreover, the higher the pump power, the shorter the threshold time, and the faster the signal light reaches saturation during a rapid oscillation process. Different pump powers cause differences in the relaxation oscillation phenomenon of the signal, indicating that due to the presence of the resonant cavity, the changes in the photons and particle reversal process within the fiber laser resonant cavity are more intense, making it easier to cause relaxation oscillation phenomena. The variation in pump power affects the internal dynamics of the laser, thus influencing the occurrence time of relaxation oscillation phenomena. Additionally, with the increase in time, the output of the fiber oscillator tends to stabilize, but there is a slight fluctuation. From the results, the higher the pump power, the longer the process of establishing a stable state. Moreover, through testing, it was found that the unimproved algorithm requires at least 700 sampling points to achieve the approximation precision of the improved algorithm with only 40 sampling points, with both exhibiting a relative error of about 3%. A further comparison of the computational speed between the two methods is shown in Figure 5. The computation time of the unimproved algorithm increases approximately linearly with the increase in the simulation time span, whereas the computation time of the improved algorithm does not show significant changes at the scale of seconds. Therefore, it is necessary to choose the more stable and rapid improved method.

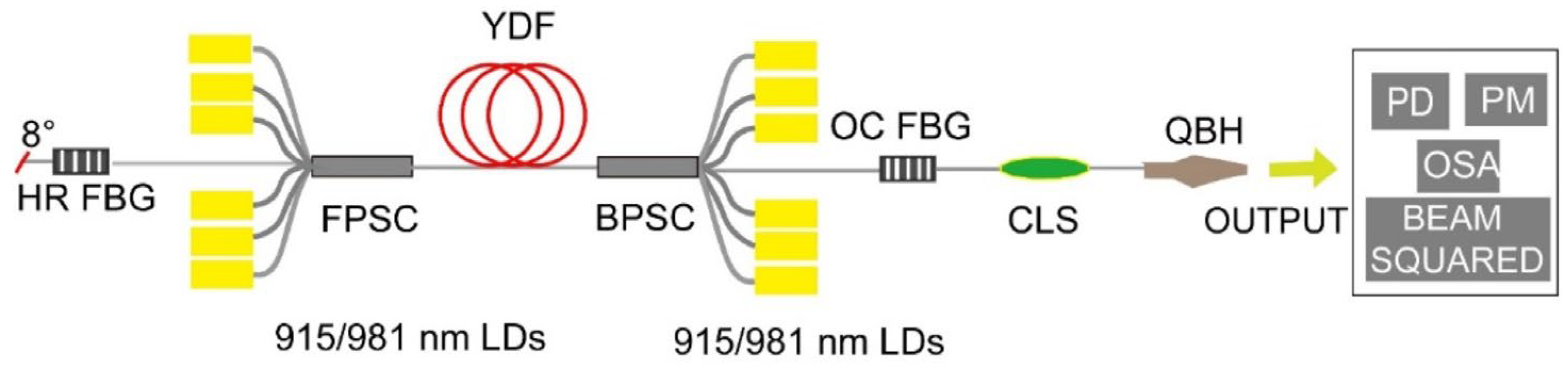
In 2022, Wen.Y from the National University of Defense Technology conducted the first demonstration and comparison of a 5 kW monolithic fiber laser oscillator pumped by 915 nm and 981 nm LDs [20]. We have simulated the experimental results to validate our numerical method. The schematic diagram of the high-power fiber laser oscillator is shown in Figure 6.

The bidirectional fiber-pumped oscillator was constructed to investigate the output characteristics of the fiber laser oscillator using LD pumps with different wavelengths. The experimental section utilized 915 nm and 981 nm LD pumping schemes. The former used a total pump power of 6558 W, comprising 1766 W of forward pumping power and 4792 W of backward pumping power, while the latter used a total pump power of 5883 W, consisting of 1523 W of forward pumping power and 4360 W of backward pumping power. The HR FBG had a reflectivity of 99.8% with a 3 dB bandwidth of 3.92 nm, and the OC FBG had a reflectivity of 8.2% with a 3 dB bandwidth of 0.97 nm. The core diameter and cladding diameter of the YDF were 25 µm and 400 µm, respectively, with a numerical aperture (NA) of 0.065. The paper mentions that under the two schemes, the maximum output power of the fiber laser oscillator was 5070 W for the 915 nm pump and 5120 W for the 981 nm pump, with optical-to-optical (O-O) efficiencies of 77.6% and 87%, respectively. This indicates that the 981 nm pumping scheme provides higher O-O efficiency and better SRS suppression.

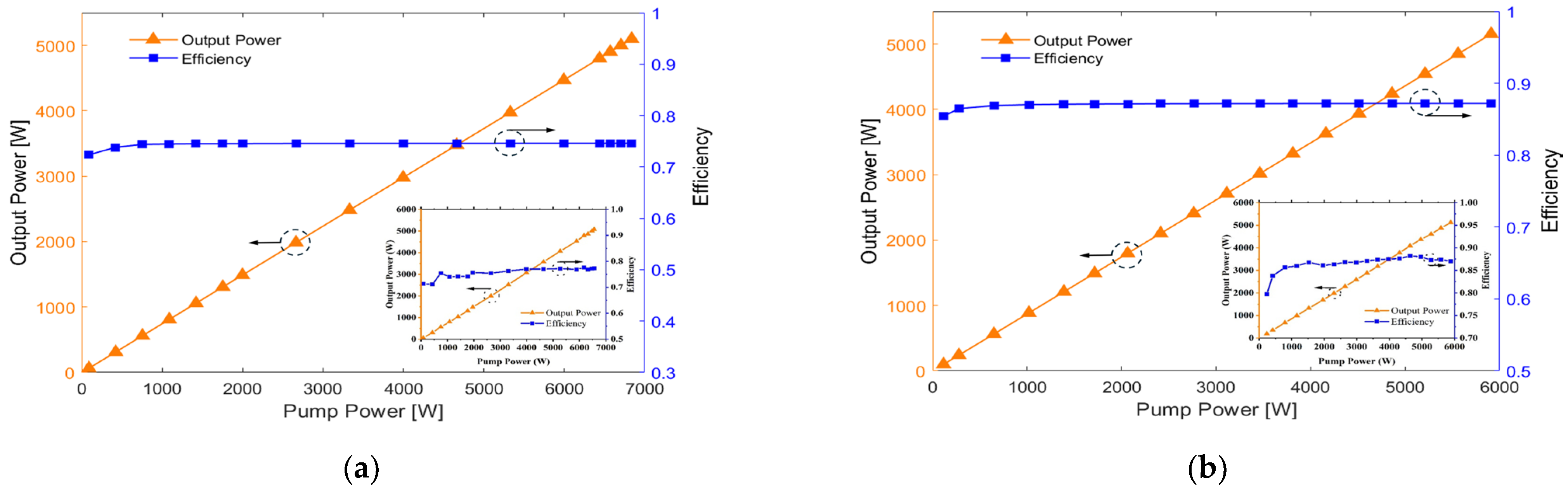
We performed simulations using the parameters above, and the results are shown in Figure 7. It can be observed that the 981 nm pumping scheme exhibits higher overall output power and O-O efficiency compared to the 915 nm pumping scheme. This improvement is attributed to the higher quantum efficiency and absorption coefficient of the 981 nm pump source, which allows for more effective absorption by the YDF fiber. The simulation results for the relationship between the laser output power and pump power closely match the experimental results (see Figure 7). In the experimental data, the O-O efficiency is lower at low pump powers. However, in the simulation, the variation in the optical-to-optical efficiency at lower pump levels is less pronounced, stabilizing as the pump power increases, which aligns with the trend observed under stable pump conditions. This discrepancy is likely due to the fact that at low power levels, the pump source’s current is low, which may cause wavelength drift and prevent wavelength locking, thereby reducing the absorption efficiency of the gain fiber and causing fluctuations in the laser output power. As the pump power increases, the characteristics of the LD source stabilize, whereas such effects are not present in the simulation. Additionally, under the 915 nm pumping scheme, the simulated maximum output power is 5099 W, with an O-O efficiency of 76%, while in the experiment, these values are 5070 W and 77.6%, respectively, as shown in Figure 7a. Under the 981 nm pumping scheme, the simulated maximum output power is 5135 W, with an O-O efficiency of 87.2%, while in the experiment, these values are 5120 W and 87%, respectively, as shown in Figure 7b. These minor differences are due to uncertainties in the spectral properties, combiner, grating, and gain fiber in the all-fiber laser system, which are affected by process defects, insertion losses, and unknown fiber absorption and emission cross-sections. Nonetheless, these small variations do not undermine the validity of the numerical simulation in predicting the results, and the numerical results fit well with the experimental data, thereby confirming the reliability of the simulation algorithm.

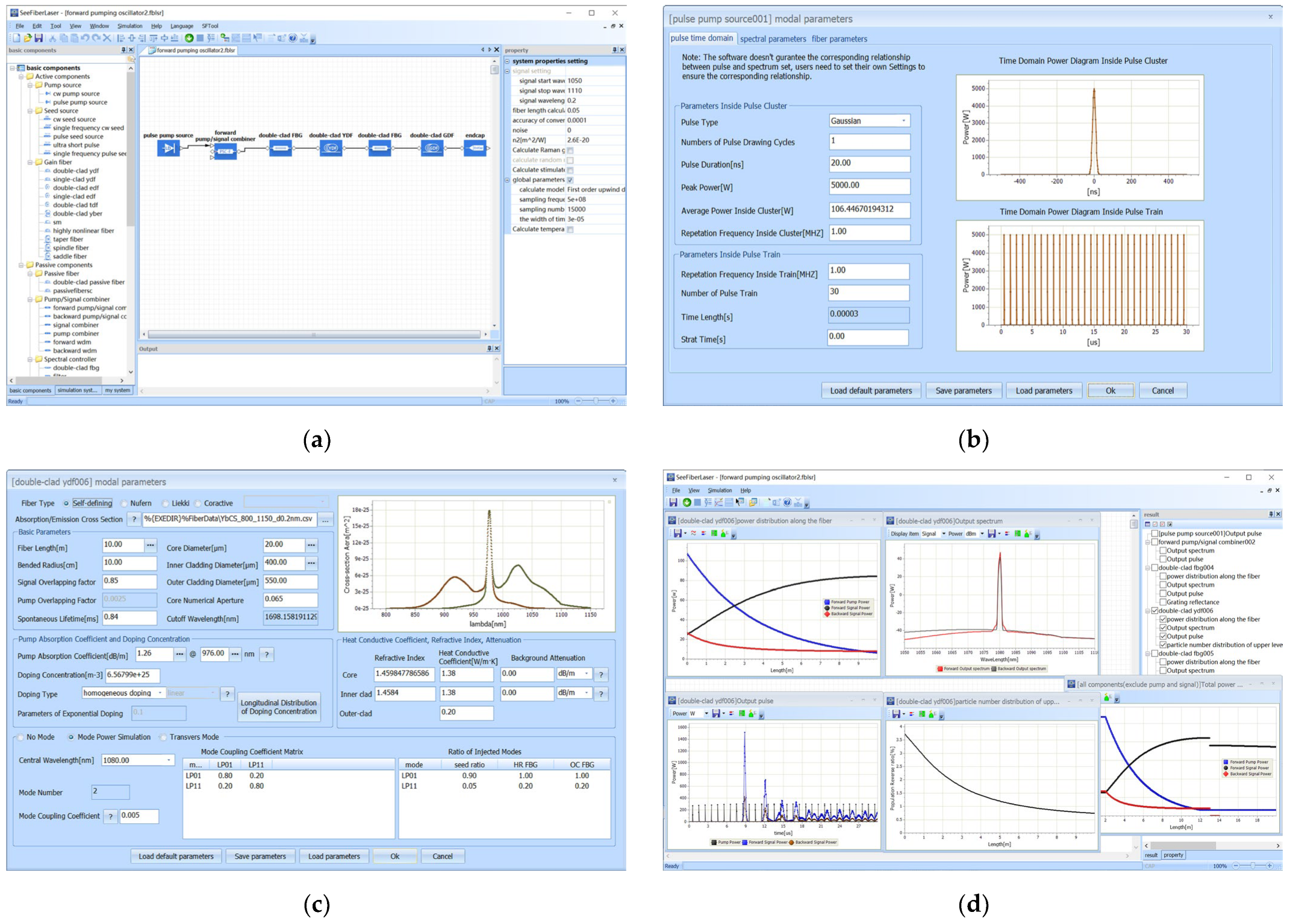
The above simulation processes all involve continuous pump injection. If pulse injection is taken into account, with the influences of different pulse widths, peak powers, and duty cycles, it is inevitable that more finely sampled time and spatial channels will be required. From this perspective, we believe that the advantages of the improved FOUWS over the conventional method are more evident. It is worth noting that the research team has developed a fiber laser simulation software called ‘SeeFiberLaser’ [21], which is currently at version 3.0.3 and incorporates the improved FOUWS algorithm and significantly improves the calculation time. The software can simulate continuous or pulsed fiber oscillators and amplifiers under different time-domain conditions. The software interface is shown in Figure 8a, which can simulate the output pulse characteristics under pulse pump conditions. The pulse parameter settings are shown in Figure 8b, the ytterbium-doped fiber parameters are shown in Figure 8c, and some simulation results are shown in Figure 8d.

5. Conclusions

In this article, a modified numerical method of the first-order upwind scheme is presented. By analyzing the differences between the derivatives and their first-order finite difference approximations, some correction factors were derived, which could be applied to improve the accuracy of the finite difference approximations. Consequently, the calculation accuracy and stability of the upwind scheme were improved as well. The modified method still had an accuracy of first order, but its error increased more slowly when the sampling number went down. For a certain accuracy requirement, a much smaller number of sampling points were needed in the modified method; hence, a large amount of computing time could be saved.

We compared a set of simulations with a bidirectional injection of 1000 W and a fiber length of 20 m. The unmodified method required 3200 sampling points and 517 s of computation time to reduce the relative error to 3.7%. In contrast, the improved method achieved a relative error of no more than 2.9% with only 800 sampling points and approximately 37 s of computation time. This advantage became more obvious if the simulation involved a short fiber length, low pump power, and large number of light-wave channels. For a short fiber of 5 m with a low pump power of 10 W under forward-pump multi-channel simulations, the modified FOUWS achieved similar accuracy to the unmodified FOUWS with only one-quarter of the sampling points (40 points), and the computation time was only one-ninth of the latter. When increasing the pump power to 2000 W, as the simulation time window span increased, the unmodified algorithm required 700 sampling points, with the computation time increasing approximately linearly with the time span. In contrast, the improved algorithm needed only 40 sampling points to achieve similar accuracy, and the computation time showed no significant variation in the seconds range. In particular, in some situations when one cannot further shorten the computing time by sacrificing the accuracy through sparse sampling, the modified method with a very small sampling number is a good choice to obtain an acceptable rough result for a quick check. Finally, by comparing the simulation results with experimental data from the literature, the trends were consistent, validating the effectiveness of the algorithm.

Although the methods are proposed based on the theoretical mode of ytterbium-doped fiber lasers, the underlying mathematical methods and algorithms can also be adapted for other rare-earth-doped high-power lasers.