Abstract
Light contains both spin and orbital angular momentum. Despite contributing equally to the total photonic angular momentum, these components derive from quite different parts of the electromagnetic field profile, namely its polarization and spatial variation, respectively, and therefore do not always share equal influence in light–matter interactions. With the growing interest in utilizing light’s orbital angular momentum to practice added control in the study of atomic systems, it becomes increasingly important for students and researchers to understand the subtlety involved in these interactions. In this article, we present a review of the fundamental concepts and recent experiments related to the interaction of beams containing orbital angular momentum with atoms. An emphasis is placed on understanding light’s angular momentum from the perspective of both classical waves and individual photons. We then review the application of these beams in recent experiments, namely single- and few-photon transitions, strong-field ionization, and high-harmonic generation, highlighting the role of light’s orbital angular momentum and the atom’s location within the beam profile within each case.
1. Introduction
The study and control of electron dynamics has dominated scientific inquiry and technological advancement for the past century. Among the most effective tools in this endeavor is the laser, whose ability to generate monochromatic, coherent light pulses with tunable frequency and intensity has been indispensable to the atomic, molecular, and optical physics community. An essential and extensively studied property of laser light in its interaction with electronic systems is its spin angular momentum (SAM) which manifests classically in its polarization. Since the creation of laser beams exhibiting phase singularities [1,2,3] and the demonstration that such fields can carry nontrivial orbital angular momentum (OAM) in addition to SAM [4,5], there has been growing interest in the application of these pulses to study light–matter interactions [6]. For example, optical OAM has already been exploited in the fields of communication [7], optical tweezing [8], and Bose–Einstein condensates [9]. Whereas light’s SAM is bounded in magnitude to unity, its OAM can in theory take on arbitrary integer values, lending way to additional freedom and control in the study of electronic processes. However, this added control comes with added nuance and complexity, as the light’s two angular momentum contributions are not always on an equal footing in the system’s induced dynamics. In an effort to elucidate the role of light’s orbital angular momentum in the realms of strong-field and ultrafast physics, and to promote advances in these fields, we discuss a set of fundamental concepts and recent experimental findings pertaining to the interaction between vortex light and atomic systems.
A major motivation for this article’s creation is the subtlety and apparent contradictions one encounters when learning about the application of photonic vortices to the study of atoms. Vortex beams are equipped with orbital angular momentum due to their spatial profile [4] and, therefore, one expects the total angular momentum of the light–matter system to be conserved in the interaction. Though it is typically ignored for sufficiently short pulses and despite initial experimental findings to the contrary [10,11,12,13], after accounting for the light’s spatial variation, modified selection rules can be achieved in atomic transitions [14,15,16,17,18], implying that OAM is actually transferred to the electronic state. However, in making the jump from single-photon transitions to above-threshold ionization with many photons, there is no apparent transfer of orbital angular momentum to the atomic system [19]. Adding then to the confusion is the well-established fact of orbital angular momentum conservation in high-harmonic generation [20,21], whereby strong-field ionized electrons generate radiation which multiplies the OAM value of the driving vortex field with harmonic order. Given these seemingly incongruous results, an overarching goal of this work is to elucidate what exactly is meant by the spin and orbital angular momentum of an electromagnetic field, address the specific influence of light’s OAM in the cases of single-photon transitions, strong-field ionization, and HHG, and to delineate the microscopic physical mechanisms at play which make the light’s OAM relevant or not in each of these cases.
The remainder of the article is structured as follows: Section 2 provides a detailed review of plane electromagnetic waves, establishing them as a familiar base case before delving into spatially structured fields in Section 3. In the latter section, the article focuses in particular on two forms of photonic vortices: Bessel and Laguerre–Gaussian beams. Connections between vortex and non-vortex light are made in both sections by invoking the partial wave expansion to demonstrate that plane waves can be decomposed into a sum of vortex fields. Likewise, vortex light can be interpreted as a combination of plane waves. The spin and orbital angular momentum content of each beam profile is also discussed, making a connection with classical and quantum mechanical descriptions of angular momenta for particles. Section 4 then applies these waves to the study of single-photon atomic ionization, where novel dynamics are initiated by vortex fields for atoms placed near the vortex center. Contrastingly, emission is determined to be indistinguishable from plane-wave behavior for atoms placed far from the vortex center. Section 5 extends this same analysis to the case of strong-field ionization, wherein ionization is virtually impossible at the vortex center and continuum electrons interspersed throughout the beam profile interact locally with plane electromagnetic waves. It is then demonstrated in Section 6 how, despite not absorbing orbital angular momentum, individual electrons store phase information from the ionizing radiation in their continuum trajectories which allows for the conservation of orbital angular momentum in the far-field harmonic spectrum. Recent experiments are contextualized throughout Section 4, Section 5 and Section 6. Finally, potential future directions for the study of intense vortex light–matter interactions are discussed in Section 7.
2. Review of Plane-Wave Fields
The primary objective of our review is to delineate the characteristics of vortex radiation and explore scenarios where these fields trigger unique dynamics. By “unique”, we refer to behaviors and phenomena that are not commonly observed or expected based on traditional theories or models. To clarify this, we need a reference point for comparison.
This section delves into the fundamental characteristics of a field characterized by a homogeneous photon density. In such a field, all photons coherently propagate in the same direction, sharing identical momentum. These fields, known as plane-wave fields, surprisingly include photons with non-zero OAM. However, they are not classified as vortex beams due to the absence of an OAM component around the propagation axis. Although it is uncommon for fields in nature to be infinitely extensive, they can be locally approximated as plane waves during spatially limited interactions. These fields serve as a benchmark, enabling us to highlight the unique dynamics initiated by vortex radiation.
We provide a succinct review of monochromatic solutions to Maxwell’s equation in a vacuum. The discussion includes how the polarization vector of a radiation field manifests as the SAM of light. OAM is introduced in a classical context, through the trajectory motion of photons in space. The concept of particle–wave duality is briefly touched upon, explaining how OAM is encapsulated within the scalar coordinate components of the electromagnetic wave. This is compared to the Schrödinger equation of scalar electrons in free space, highlighting the similarities between the two.
Building on this correspondence, the OAM of scalar waves is reviewed. Following this, both the scalar OAM and vector SAM components of the radiation field are combined to discuss the quantum numbers of photons within the field. For OAM, the quantum numbers are and, for SAM, the quantum numbers are .
The section culminates with an exploration of the selection rules governing photoionization. The so-called dipole limit of ionization at long wavelengths is elucidated, where only photons lacking OAM interact with atomic electrons to facilitate emission. The short-wavelength non-dipole limit is also examined, where photons possessing OAM contribute to emission. A significant deviation from these findings is demonstrated later in Section 4, where the ionization process is instigated by photons originating from a vortex field. This deviation underscores the unique dynamics introduced by vortex radiation in the ionization process.
Polychromatic radiation fields are not discussed in this work, as they can be represented as a linear combination of monochromatic components, which will be discussed in detail. Each frequency component corresponds to a unique mode of the field, with distinct polarization and spatial profiles [22]. Ionization is determined by the absorption of photons from any combination of the field’s modes, adding complexity to the process [23]. The selection rules discussed for plane waves, and later for vortex beams, are applied to transitions resulting from each constituent photon in a process, similar to that discussed in ref. [23]. Examples of such fields include ultra-short pulses, which consist of a distribution of photons with energies centered around a specific value, and cross-polarized or bi-circular radiation fields, which involve linearly polarized or circularly polarized fields with different polarizations and wavelengths striking a target [24,25,26,27,28,29,30,31]. Additional photonic degrees of freedom in these applications lead to novel dynamics and enhanced control.
In this work, we adopt Hartree atomic units. These units are derived by setting the electronic mass (), the elementary charge (), and the reduced Planck constant (ℏ) to unity within the Gaussian cgs system unless otherwise stated.
2.1. The Helmholtz Equation
Photonic vortices and plane-wave radiation fields, both being solutions to Maxwell’s equations in a vacuum, exhibit distinct characteristics. Plane-wave radiation, as outlined in [22,32,33], pertains to fields that contain monochromatic photons of energy propagating at the speed of light c with identical momentum () and are uniformly distributed throughout space. Conversely, photonic vortices consist of monochromatic radiation fields which are unevenly distributed throughout space, lending way to the fields’ nontrivial orbital angular momentum. The starting point to understanding either form of light is the vector Helmholtz equation:
which depends on the linear momentum operator and describes the propagation of monochromatic radiation in a vacuum where the vector potential of the field is determined from the real part of the complex quantity as discussed in refs. [32,33]. Working in the transverse (Coulomb) gauge enforces the transversality condition
In words, this gauge choice requires that the vector potential is always perpendicular to the direction of wave propagation given by . The most straightforward solution to the Helmholtz equation satisfying this constraint is given by the plane-wave field
where represents a constant polarization throughout all of space and represents the momentum of photons contained within the field. The magnitude is proportional to the number density of photons contained within the field and is uniform throughout all of space.
2.2. Spin Angular Momentum
The transversality condition in electromagnetism stipulates that the field cannot have a component in its direction of propagation. For plane waves, this condition is expressed as , indicating that the wave vector is orthogonal to the polarization vector . If we choose a coordinate system such that the fields propagate along the positive axis, the polarization vector must be a complex vector confined to the x–y plane. This means that polarization along the z-axis is not permitted, ensuring that the polarization is strictly transverse to the direction of propagation.
The spin angular momentum content of a plane electromagnetic wave is attributed to its polarization vector , which can be written in the following form [32,33]:
where represents the ellipticity of the polarization. Note that this choice of polarization vector satisfies the transversality condition (2) for a field propagating along the direction. When , the field is linearly polarized along the x-axis. describes right-handed () and left-handed () circularly polarized fields within the x–y plane. The two extreme values of correspond to the two possible spin states of a photon.
Spin, a form of intrinsic angular momentum, is represented by the Cartesian vector [22,34,35]. While this can be interpreted as the angular momentum of a particle rotating around its own center, this interpretation is less applicable to photons, which are point-like objects. Wolfgang Pauli [36] described spin as a “classically non-describable two-valuedness”. For photons, spin must be considered an internal degree of freedom with no classical analog, exhibiting angular momentum around an axis defined by the direction of . Unlike classical objects in everyday life, which can have any amount of angular momentum, photons can only have two possible values of spin: +1 or −1 around the direction of their propagation. These spin states are defined as the components with polarization vectors for each spin state. The polarization vector in vacuum must satisfy the transversality condition , meaning they cannot have a component in the direction of propagation . Therefore, the spin projection corresponding to oriented along the propagation axis is not allowed. This restriction ensures that the polarization is strictly transverse to the direction of propagation. Explicitly, these photonic spin states may be written as [37,38,39,40]
where the spin projection matrix is given by
While individual photons may contain spin components of magnitude unity, a superposition of these spin states allows for a general elliptical polarization in a classical field with .
Since the polarization does not depend on position , spin can be thought of as an internal degree of freedom in the field. For a plane wave, this corresponds to the real part of a quantity proportional to the product of the polarization vector and the monochromatic time dependence up to a phase . In the case of elliptical polarization, we have [32,33]
where the polarization vector traces out an ellipse as spans from 0 to . A single unit of SAM manifests itself as the circular motion of the polarization vector with as a function of time. This is a key aspect of the vector nature of light.
Interestingly, if we not only investigate the component resulting from the operator but instead consider the total SAM squared resulting from the operator sum as defined in [38], we observe the following:
when acting on any element of the complete spin basis. Note that photons have spin vectors of magnitude rather than . A photon must have a non-zero spin component both parallel and perpendicular to its direction of propagation. Utilizing the conventions defined in Ref. [41], the notation indicates the absolute bounds of a single spin component, such as , and does not represent the SAM magnitude .
Spin projections simultaneously diagonalize both and due to their commutative property [42]. Explicitly, we have the following:
In contrast, it is well known that does not commute with either or , implying that they cannot be simultaneously diagonalized. A direct consequence of this fact is the Heisenberg uncertainty relation [42]:
where represents the standard deviation (uncertainty) of either or , and represents the average (expectation value) over all of space, determined from a general polarization vector . The uncertainty in both and must be non-zero whenever the expectation value of is non-zero. All three components of may not be known simultaneously.
2.3. Orbital Angular Momentum
In addition to spin angular momentum, electromagnetic waves can also contain orbital angular momentum on account of their spatial profile. However, the orbital angular momentum of a classical field is something not often discussed in electromagnetism courses. In an effort to bridge this gap, this subsection reviews the concept of orbital angular momentum in classical (particle) and quantum mechanics and extends this analysis to classical electromagnetic fields. We then demonstrate how individual photons within plane-wave fields can possess non-zero OAM. However, when all microscopic contributions are added, the field exhibits no net OAM. It is noteworthy that plane-wave fields exhibit an OAM density that is contingent on the specific coordinate within a field. Yet, they possess no OAM when all coordinates are integrated over the entirety of space. In Section 2.4, we discuss the combined description of an electrodynamic field in terms of its combined SAM and OAM content which will be subsequently applied in Section 2.5 to demonstrate that the OAM of individual photons absorbed during an interaction may or may not be significant, depending on the scales associated with the problem. This nuanced understanding of photon absorption and its potential implications for OAM will be explored in detail.
2.3.1. Analogies with Classical Mechanics
Consider a plane wave propagating in an arbitrary direction, denoted by the vector . Each photon within this field moves in the same direction and at the same speed. Now, let us select a specific photon within the field, located at position . In classical mechanics, a form of angular momentum, denoted as the vector , is associated with the rotational motion of particles. This orbital angular momentum, relative to the origin of a coordinate system, serves as a rotational analog to linear momentum. It is computed using the cross product , where and are the photon’s position and linear momentum, respectively. The -component of OAM is given by . In the specific case where a photon propagates in the -direction with and is located at a position and , this OAM simplifies to . Here, b denotes the proximity of the photon’s path to the origin of the coordinate system. At a later time, when the photon is located at position , , and , having moved from the origin, the OAM remains . Here, is the speed of light in atomic units. This demonstrates that the orbital angular momentum of particles is a conserved quantity, remaining constant over time. This conservation principle is a key aspect of classical mechanics and plays a crucial role in understanding particle propagation.
A single photon within the plane wave carries OAM. However, when considering the field as a whole, does it contain OAM when integrated over all photons across all of space? Given that plane-wave photons have a constant number density n, one can write the total angular momentum of the field as
where the angular momentum density has been integrated over all of space. Each component (, and ) of the OAM vector is zero, as the integral of an odd function over an even domain is always zero. This is true for a plane-wave field containing a constituent photon traveling along the -axis at position and with OAM . A mirror image of this photon exists at and negating the initial contribution with OAM . This principle holds for fields traveling along any momentum . A photon at position will negate the OAM of a photon at position , resulting in no net orbital angular momentum.
2.3.2. Wave Interpretation of Electromagnetic Radiation
The discussion so far has focused on the orbital angular momentum of classical particles. However, it is often simpler to view electromagnetic fields as waves rather than a collection of individual particles. This perspective becomes clear when we consider the linear momentum operator, denoted as , which extracts the momentum of the wave at each infinitesimal position in space.
Classically, the total linear momentum is given by the equation
where we have N photons within a volume V.
When we look at this from the perspective of waves, we obtain the same result from the equation
which closely mirrors the “expectation value” of momentum from quantum mechanics. The momentum operator extracts the constant momentum from the field where the classical result is recovered. This equation shows that the particle and wave interpretations of radiation are equivalent.
2.3.3. The Magnetic Quantum Number
What is the nature of OAM, and how does it manifest for waves? We will focus on the component and permit field propagation in any direction denoted by .
The classical result for the -component of OAM, as previously established, is given by
Our objective is to identify an OAM operator that isolates the factor , akin to how extracts the linear momentum of individual photons. This is achieved in spherical polar coordinates with
by constructing the angular momentum operator , where denotes a partial derivative with respect to .
In this context,
This result aligns with the classical outcome, paralleling the case of linear momentum. The operator characterizes the motion of waves revolving around the -axis of the coordinate system, analogous to how describes the linear motion of waves.
The eigenvalue problem for establishes the conserved linear momentum of plane waves, represented by in space. Similarly, the eigenvalue problem for the operator yields the conserved angular momentum of particles in space, often referred to as the “magnetic” quantum number. The angular phase factor is interpreted as the motion of a photon around a ring of unit radius centered at the origin (discussed in ref. [43]). In this context, the linear variables and are replaced with their angular counterparts and . As the eigenvalue of increases, the “spiraling phase” oscillates more rapidly, reflecting the accelerated motion of classical particles around the ring.
Furthermore, wave functions must be single-valued and continuous, necessitating the phase factor to return to its initial value after completing an orbit. Specifically, the spiraling phase factor must yield the same result for both and , which is only possible for integer values of OAM [43]. This single-valuedness of the wave function implies that only those values of angular momentum are permissible which allow the photon to propagate around the ring for an integer number of “wavelengths” [44].
In the case of a plane wave, the situation is somewhat uninteresting. When the field propagates along the positive z-axis, there is no component of OAM around this propagation axis. Not only is the net OAM zero around this axis but so is the OAM density . All photons within the field propagate with . Photons possess non-zero OAM , but the component around the propagation axis is identically zero. This observation underscores the unique properties and behaviors of photons within the context of plane-wave fields.
2.3.4. Azimuthal Quantum Number L
While we have a solid understanding of the component of the OAM , the overall magnitude warrants further investigation. To address this, we consider a related problem frequently encountered in undergraduate courses: the quantum-mechanical propagation of a free (scalar) electron with a definite energy. In this context, we consider a free quantum-mechanical particle characterized by the wave function . The behavior of this particle is dictated by the non-relativistic, time-independent Schrödinger equation, as discussed in refs. [40,41,42,45,46,47]:
This equation exhibits spherical symmetry and remains invariant under rotations. Such symmetry allows us to decompose the kinetic energy into two components: the radial contribution and the OAM contribution:
which closely mirrors the classical result. Here,
represents the radial non-relativistic kinetic energy, and
provides the squared OAM. This approach provides a comprehensive understanding of the particle’s behavior in terms of its radial and angular momentum contributions.
Problems of this type can be solved using separation of variables, yielding the general solution:
where the spherical harmonics describe states of definite OAM magnitude and magnetic contribution and form a complete basis of functions over a unit-radius sphere. The radial functions represent states of definite energy for a given OAM and . The radial functions are determined from
after the separation of variables with boundary conditions and bounded for and [48] yielding the well-behaved solutions
where spherical Bessel functions describe spherical waves traveling with kinetic energy and l discussed in the next paragraph is related to the total OAM of the state .
Spherical harmonics are states of definite OAM and satisfy
yielding the spectra of permissible OAM values with . The azimuthal quantum numbers are integers resulting from the single-valuedness of the wave function over the surface of a unit sphere (discussed in ref. [49]), analogous to the quantization of the magnetic quantum number over a unit-radius ring. In colloquial terms, l is often referred to as the OAM, with the understanding that it represents the value of corresponding to the quantum number l. These functions simultaneously satisfy Equation (24) as well as
and are therefore states of definite OAM and . More explicitly, states of this type are given by
up to a normalization constant. is an associated Legendre Polynomial which encapsulates the dependence of the harmonics on the polar angle and azimuthal quantum number l. The spiraling phase describes the dependence on the azimuthal angle and magnetic quantum number . Somewhat confusingly, the azimuthal quantum number l is unrelated to the azimuthal angle . These terms are purely historical.
These functions can simultaneously diagonalize both and due to their commutative property. Explicitly, we have the following:
In contrast, it is well known that does not commute with either or , implying that they cannot be simultaneously diagonalized. A direct consequence of this fact is the Heisenberg uncertainty relation:
where represents the standard deviation (uncertainty) of either or , and represents the average (expectation value) over all of space, determined from the wave function . The uncertainty in both and must be non-zero whenever the expectation value is non-zero. All three components of may not be known simultaneously.
The fusion of the radial and angular components provides a complete portrayal of a scalar wave in free space, as demonstrated by the following equation:
In this scenario, states with a distinct energy of are expanded in terms of their OAM content, denoted by l and , and characterized by their complex-valued expansion coefficients, . The Bessel functions for OAM, spanning from to , are illustrated in Figure 1. It is worth noting that, at , achieves its maximum value, while all other partial waves (corresponding to different OAM values) are zero at this point.
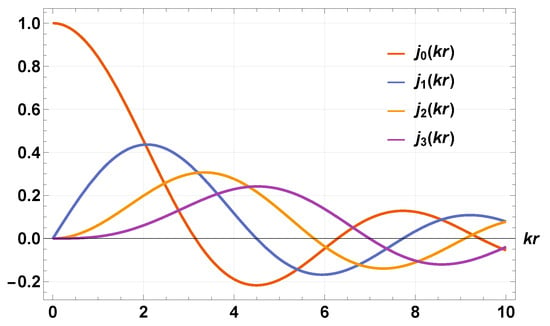
Figure 1.
Plot of spherical Bessel functions against for up to .
Scalar plane-wave fields, which also depict the propagation of particles in free space, can be expressed in this manner. In the next subsection, we will utilize this decomposition to determine the OAM content of particles represented by these fields. The discussion here followed along the lines of refs. [41,42].
2.3.5. Plane-Wave OAM
Both plane waves and spherical waves, as discussed in the previous subsection, provide a description of scalar particles in free space. However, since plane waves are not spherically symmetric, they must be described in terms of a combination of OAM quantum numbers . In this context, we obtain the partial wave expansion [40,41,42]
This equation signifies that plane waves carry a density of orbital angular momentum. They include contributions when the magnitude of the orbital angular momentum, , is greater than zero. From a quantum mechanical standpoint, there exists a certain probability for the electron to occupy any of these states of orbital angular momentum. In a similar vein, for classical radiation, there is a specific number density of photons in a given orbital state. However, when averaged over all of space, their orbital angular momentum is zero. Moreover, if the wave propagation is oriented such that it is directed along the -direction, we observe that is proportional to . This observation underscores the fact that plane waves do not contain a spiraling phase around their propagation axis.
In Figure 2, we break down the real part of the plane-wave field into its OAM components. We choose a wavelength of , where nm is the Bohr radius of a hydrogen atom [41,46,47]. The z-axis represents a location along the propagation direction, and the x-axis represents a perpendicular location.
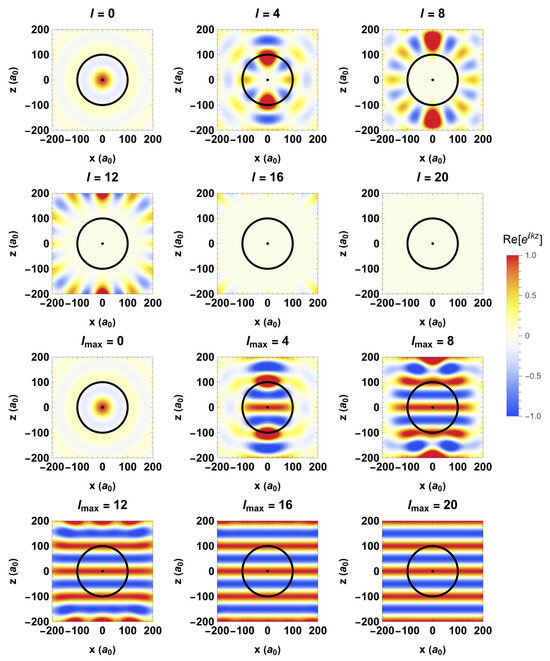
Figure 2.
OAM decomposition of the plane-wave radiation field with wavelength given by Equation (30). Subplots labeled as “” describe a single OAM contribution l (). Plots labeled “” indicate a superposition of OAM contributions from up to . Circles within each plot have Bohr radii and .
Subplots labeled as “” display plane-wave contributions from a single OAM value l. Contributions from “” are localized closest to the origin, which is the point from which OAM is determined. As l increases, these contributions are displaced from the origin and pushed outwards until they become negligible within the plot domain at the largest considered value of . The angular beating within each subplot l corresponds to the orbital angular momentum of each OAM state.
Plots labeled “” depict scenarios where all plane-wave components from up to are included. The first significant subplot at demonstrates that the plane wave is accurately represented near the origin but not at greater distances. As increases, the plane wave progressively recovers larger length scales. By the time reaches 20, we achieve a quantitative match with the plane wave across the entire plot domain. To reconstruct the plane-wave behavior at large distances, higher OAM values l are required. However, at the origin, the wave can be accurately described using only .
2.4. Complete Orbital and Spin Representation of Radiation Fields
The energy of a photon, as dictated by classical mechanics, is represented by . This energy depends on the magnitude of the momentum k, not its direction. The square of this magnitude emerges as the eigenvalue of the vector Helmholtz equation. By multiplying both sides of Equation (1) by , we obtain a vectorized form of the Klein–Gordon–Fock equation [22,35]:
which stipulates the permissible energy squared values of photons within the field. Interestingly, this equation bears a resemblance to the time-independent equation for an electron in free space, as discussed earlier. We will therefore use the linearity of the problem to solve for each component independently.
This equation is resolved within the spin basis as follows:
In this context, each spin component satisfies the following spherically symmetric (scalar) equation:
where components are restricted to those which satisfy the transversality condition (2).
The solutions [41,42] lead to the orbital angular momentum expansion:
for each scalar component. Here,
expresses the radial dependence of a specific angular momentum channel in terms of expansion coefficients and a spherical Bessel function.
We can expand plane-wave radiation in a similar manner. Assuming circular polarization and propagation along the -axis with momentum , we obtain the following field:
This proportionality is true up to a set of constant pre-factors. The field contains photons in orbital angular momentum states with in either the spin angular momentum state or .
In the relativistic theory of photons, the orbital angular momentum and the spin of a moving particle are not conserved separately under Lorentz transformations [22]. Instead, only the total angular momentum is conserved. As a result, the spin component in any fixed direction (like the z-axis) is not conserved in general and cannot be used to determine the polarization states of the particle. However, the spin component in the direction of photonic propagation is conserved. Since , the product equals the conserved product . This quantity, known as helicity , is useful for decomposing a general radiation field into plane-wave constituents. For the plane-wave field of Equation (36), we have since the field propagates along the direction. For massive particles, helicity is not conserved under Lorentz transformations [22]. This occurs because the perceived velocity, and consequently the helicity, of a massive particle like an electron can change sign depending on the relative velocity of the reference frame to the particle. For our purposes, helicity should be understood as circular polarization quantized along the axis of propagation of the plane-wave photon.
In the following subsection, we discuss the photoionization of atoms by plane-wave radiation fields of this form. We will delve into the conservation of total angular momentum and the significance of both spin and orbital angular momentum during ionization. Electronic transitions are driven by the helical spin component alone.
2.5. Plane-Wave Selection Rules
Consider an atomic ionization process where an atom, located at the origin of the coordinate system (), interacts with a circularly polarized field propagating along the z-axis. In this scenario, emission is contributed by a select subset of multipole orders around this center. The weak-field (perturbative) emission of scalar electrons by the absorption of a single photon () is represented by the velocity gauge matrix element of the interaction [41,45,46], proportional to
between an initial electronic state with energy and definite OAM and a final state of definite OAM with energy where the radiation field is expanded in the OAM and SAM components as in Equation (36). The matrix element defines how the final OAM of ejected electrons is obtained from the addition of both the spin and orbital angular momentum of photons with the initial electronic OAM where we have assumed circular polarization for each photon in the field.
Bound-continuum transitions occur within an interaction volume described by regions of non-zero bound state density. This volume is characterized by the effective Bohr radius a of a specific target, determined from the ionization potential . Bound-state wave functions scale as in the limit [41]. Regions where therefore contribute most towards emission.
In Figure 2, we include circles within each subplot to visualize the overlap between the initial electronic state and multipole orders of the radiation field present in Equation (36). Transitions are allowed when both coincide and are forbidden otherwise. A smaller circle of radius is intended to depict the ground state of hydrogen and the larger circle of radius is intended to depict a Rydberg state. The hydrogenic case is 100 times smaller than the wavelength of applied radiation, while the radius of the Rydberg state is equal to the wavelength of applied radiation.
In scenarios where a is significantly smaller than the wavelength of the incident radiation, the wave vector satisfies the condition . This leads to the lowest-order polynomial approximation for the spherical Bessel function , given by the following [40,41,50]:
In such scenarios, the radiation field varies slowly across the electron density, and the contributions predominantly come from the smallest values of l. For instance, in the case of hydrogen (), we have , leading to . This suggests that only the contribution from the lowest-order partial wave () is significant to emission, leading to
in the limit where . This behavior is incorporated in the limit of Figure 1. This principle is referred to as the dipole approximation, which assumes that the field carries no orbital angular momentum and is frequently employed in atomic physics. In the case of atomic hydrogen, the Bohr radius is approximately 0.053 nm, which corresponds to a photon in the X-ray spectrum.
As depicted in Figure 2, the hydrogenic state is localized at the origin of the coordinate system. It exhibits significant overlap with the spherically symmetric OAM state and negligible overlap with higher-order OAM states. Although the field contains photons with , they do not interact with the ground-state density. In contrast, the Rydberg state overlaps not only with the OAM state but also with finite OAM states up to approximately . Consequently, electrons within this cloud interact with multiple multipole orders.
For and beyond, neither the hydrogenic nor the Rydberg states considered here overlap with the multipole orders of the radiation field. This is consistent with classical expectations, where the trajectory of a particle (photon) passing the origin of the coordinate system would have an OAM , with b being the closest distance to the origin.
While we are dealing with an electromagnetic field rather than a classical particle, the underlying principles remain similar. As shown in Figure 1 and Figure 2, the first local maximum of the oscillatory Bessel functions shifts outward with increasing OAM. Transitions are permitted when , indicating substantial overlap between the ground-state density and radiation of OAM l and forbidden when indicating a region of little overlap. The first local maximum of each OAM order is located at a distance (refer to Appendix A), closely mirroring the classical result. Hence, photons carrying a higher OAM pass further away from the atoms, prohibiting transitions.
Within the framework of the dipole approximation, the interaction between light and matter, particularly the photon absorption process, is encapsulated by the operator . This interaction facilitates the conversion of a single unit of photonic SAM to OAM of the electron. Notably, the interaction term introduces a spin-1 factor of into the interaction, as detailed in the appendix of Ref. [45].
The product contained within the transition matrix element represents an addition of angular momentum and yields the set of allowed OAM states after photon absorption. When circularly polarized radiation is absorbed () by an electron, it transitions into continuum states given by the following:
These conditions, discussed in refs. [41,46,47], are known as the dipole selection rules. We use boxes throughout the text to indicate different types of angular momentum selection rules.
The dipole approximation offers a precise representation of single-photon ionization by fields within the ultraviolet spectrum and other less energetic spectra. However, this approximation is not universal and may vary depending on the target and application. For instance, in the emission from Rydberg atoms or molecules, where the electron cloud spans a larger volume, the electrons may interact with a broader profile of the field. As illustrated in Figure 2, additional partial-wave contributions from Equation (30) may become significant.
The selection rules for these additional channels are determined not solely by the photonic SAM but by the total angular momentum (TAM) of photons obtained from the addition of photonic angular momentum as discussed in ref. [49] with the following:
In this situation, photon absorption involves the addition of angular momentum resulting in the set of electronic OAM states given by the following [49]:
A subset of photons within the field carry , leading to a breakdown of the dipole approximation and an extended set of electronic transitions. While plane waves macroscopically contain , they microscopically contain photons with . A detailed discussion of non-dipole emission is provided in refs. [51,52,53,54,55,56,57,58,59].
In this discussion, we have demonstrated that transitions are driven not only by the SAM of photons within a plane wave but also by their OAM content obtained earlier in Section 2.4. By combining OAM with l and , and SAM with and , we obtained a photon distribution characterized by their total angular momentum j with projection . We then showed that this total angular momentum induces electronic transitions from an initial electronic OAM state to a final electronic OAM state . It is common practice in the literature to instead utilize an alternative basis set of so-called vector spherical harmonics [22,32,40] which define radiation fields directly in terms of their total angular momentum (TAM) content instead of the separated SAM and OAM quantum numbers discussed in this section. Both representations are appropriate, but one may be more convenient than the other depending on the problem at hand. The findings presented up to this point serve as a benchmark for electromagnetic fields and their interactions with matter.
At this point, it is sensible to define the term “chiral light,” a broad concept applied in various contexts within the study of light–matter interactions and radiation. An electromagnetic field with chirality possesses a distinct “handedness” or asymmetry. A straightforward case of synthetic chiral light [60] involves a superposition of polychromatic plane-wave fields, each propagating in different directions. These fields are often spatially uniform over the profile of an atomic target. Within the dipole approximation, the electric field vector traces a chiral, 3D Lissajous curve in time at a given position. This can be interpreted as a chiral signal due to the local spin of constituent photons within the field, as the vector nature and not the position dependence of the field is of interest. An alternative example of chiral light [61], similar to what we will soon discuss, may simply correspond to interactions involving fields that inherently contain orbital angular momentum around their axis of propagation.
Now that the structure and properties of plane waves are established, one may compare them to the case of spatially structured light.
3. Vortex Fields
This section identifies the properties unique to vortex radiation fields compared to plane waves, in particular their spiraling phase along the propagation axis (). In these fields, all photons move coherently in the same azimuthal direction, each carrying an identical projection of orbital angular momentum, represented as , where . These fields are unique due to their non-zero total orbital angular momentum, .
Our exploration begins with Bessel beams, a distinct class of vortex fields, informed by the findings of refs. [62,63,64]. These beams, distinguished by their specific linear momentum and TAM projection , incorporate spin components from and are composed of three vortex beams, each with a unique OAM projection . Unlike individual plane waves that propagate along , Bessel beams consist of circularly polarized plane-wave constituents. Each constituent revolves around its own propagation axis, which is slightly divergent from . We will demonstrate how the individual plane-wave photons follow a trajectory that deviates by an angle from the collective axis, as illustrated in Figure 3.
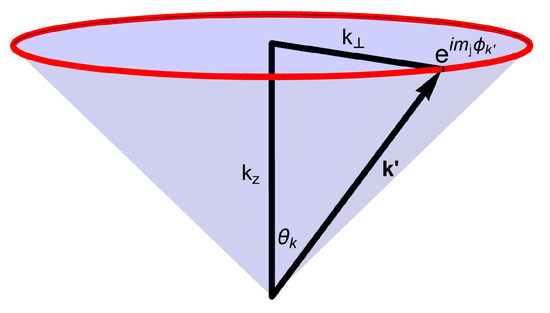
Figure 3.
The decomposition of a Bessel beam, defined by its linear momentum , transverse momentum , TAM component , and helicity . The beam is segmented into plane-wave components, each exhibiting circular polarization around their own propagation axis, as dictated by . These components are represented as all possible momentum vectors sharing a common origin and terminating at the (red) circular base of the cone. A particular component, labeled as , is emphasized. The angle measures the deviation of each plane-wave photon from the main propagation axis. denotes the azimuthal angle at which is located on the circular base. The phase specifies the TAM component of the overall beam.
Next, we consider a limit where , causing the propagation of individual photons to closely align with the collective propagation axis . This alignment results in the field exhibiting near-circular polarization. This feature enables us to approximate the field using a single spin component and an orbital state . However, this approximation can lead to fields that do not satisfy the transversality condition, resulting in errors. These errors are minimal in situations that fall under the realm of paraxial optics. As a natural extension of this discussion, we introduce Laguerre–Gaussian vortex beams, which serve as accurate representations of experimental conditions in numerous paraxial studies.
In a final subsection, we discuss the spin angular momentum, orbital angular momentum, and total angular momentum of radiation fields using the framework of classical electrodynamics. We construct these quantities starting with the momentum density of the field, demonstrating consistency with the framework discussed in Section 2. These concepts are applied in the context of paraxial fields to demonstrate that and are indeed angular momentum quanta associated with a photon of definite energy .
In Section 4, we engage atomic targets with these fields to elucidate photoionization selection rules, similar to the context of plane-wave radiation. Following this, in Section 5, we employ vortex radiation to ascertain the necessary conditions for observing vortex effects in strong field ionization. Lastly, in Section 6, we explore how phase matching effects enable vortex radiation fields to drive high-order harmonic processes, leading to the emergence of higher-frequency vortices. The outcomes instigated by vortex radiation will be compared with plane-wave results in each context, with the relevance of OAM effects varying depending on the specific physical situation.
3.1. Bessel Beams
Beams propagating collectively along a preferred axis lack spherical symmetry, requiring a mix of OAM contributions in Equation (34) to define their properties. This is clear when considering plane-wave radiation via constituent photons in the field, which have and (assuming propagation along ). Here, the displacement of photon trajectories from the coordinate system’s center determines the OAM of individual photons, while the problem’s cylindrical symmetry and uniform phase in a plane transverse to propagation allow for a field description in terms of a single magnetic quantum number . A subset of photons in the field possess OAM (indicating OAM density), but the total vanishes upon integration over all space. Plane waves, providing a complete solution set, enable the creation of all monochromatic radiation fields in a vacuum. This leads to the question how can we build vortex fields from plane-wave contributions? The answer involves waves propagating in directions diverging from the collective propagation axis and careful design of the phase and polarization components to achieve the spiraling phase .
With this foundation, we move forward to construct a specific type of vortex beam from a linear combination of plane waves. These so-called Bessel beams were introduced in refs. [65,66,67] and are constructed from contributions where each constituent wave displays identical circular polarization with helicity around its individual propagation axis. The conventions established in the studies on Bessel beams, as referenced in [62,63,64], are crucial to our understanding and applied in this discussion.
In this setup, plane-wave photons with momentum result in a rotated polarization vector
Here, denotes the offset angle from the -axis. The terms and represent the momentum components in the collective propagation direction and in a direction transverse to it, respectively. These momentum components are related to by with .
These beams are characterized by the equal weighting of contributions from all plane-wave photons that share common momentum components and . These contributions collectively form a ring in momentum space, akin to the one depicted in Figure 3. In this configuration, plane waves aligned along each angle are incorporated with equal intensity but varying phases. Each plane-wave photon exhibits circular polarization relative to its own axis. This characteristic is significant as plane-wave fields of this nature maintain the transversality condition .
Interestingly, the expansion of these polarization vectors into spin components yields
where and . This indicates a non-zero polarization component along the collective propagation direction of the field. This is somewhat surprising and adds a layer of complexity to our understanding of these vortex beams.
In order to construct these fields, we perform an integration of momentum vectors over a ring, akin to the one depicted in Figure 3. During this process, we maintain the constancy of , , and the amplitude of each contribution, with the exception of a phase. Our focus is primarily on phase factors , which are single-valued and consequently limit the quantum number to integer values. We employ the symbol to denote this phase as an indeterminate integer. Upon completion of the field construction, we establish that this is indeed the projection of the TAM. This demonstration adds a significant dimension to our understanding of these complex fields.
Mathematically, the aforementioned procedure manifests as
and results in
after substitution of Equation (44) into Equation (45) and integration. This form represents a cylindrical decomposition of the Bessel field in terms of all three SAM projections and a set of three OAM projections for a single fixed . The new coordinate represents a cylindrical distance from the -axis and is an arbitrary (complex) constant. The outcome bears a striking resemblance to the field expansion of Equation (34), which is applicable to any radiation field in vacuum. However, it lacks the expansion of the azimuthal quantum number l and exhibits a dependence on the cylindrical distance , which is a function of . Phase factors associated with each spin component are resolved within a complete basis of OAM states , where l ranges from to infinity in increments of 1, and .
The comprehension of this OAM content becomes crucial in Section 4, where we delve into the photoionization of atomic systems by these “twisted” photons. While it is essential to understand the non-zero OAM components, we will refrain from determining the expansion coefficients of Equation (34) for these fields. This approach allows us to focus on the broader implications of these complex interactions.
In Figure 4, we plot against and for the OAM index . The top two rows illustrate the absolute value of these fields, while the bottom two rows represent the phase alone. For , we observe radial oscillations that correspond solely to the constituent Bessel function, exhibiting cylindrical symmetry around the propagation axis, akin to a plane-wave field. When , an asymmetry across the -axis becomes apparent, indicating a change of parity and the accumulation of phase around the propagation axis. As we consider larger values of , we notice a faster phase accumulation with respect to the cylindrical angle. These characteristics significantly deviate from the behavior of plane waves.
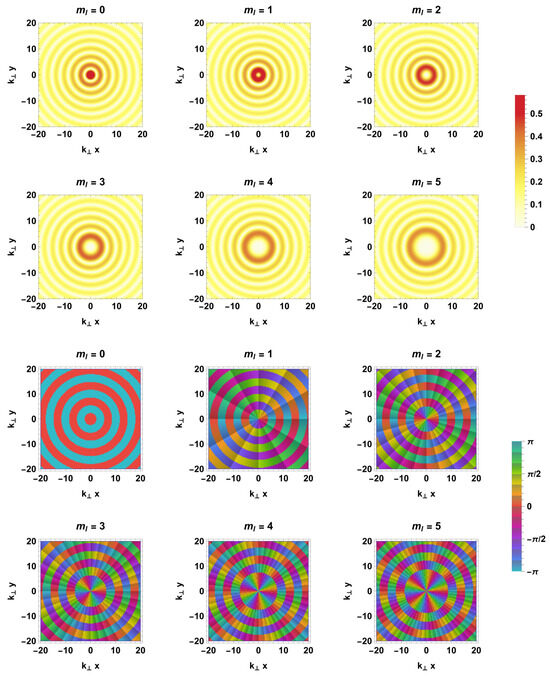
Figure 4.
The top two rows of the figure illustrate plots of the absolute value of the function , with values ranging from 0 to 5. The bottom two rows display phase plots of the same function. For enhanced readability, the phase map is divided into intervals of size . Both the absolute value of the function and the phase are plotted against the transverse variables and with .
Let us now affirm that indeed represents the TAM projection around the propagation axis. In this context, it is beneficial to define the TAM operator projection as [42,62]
which is discussed further in Section 3.3. It becomes evident that each spin component is dependent on a single OAM component . When acted upon a single spin component, we obtain
for each component . Here, is identically equal to which is therefore the TAM projection of the field along the propagation axis. The vortex fields discussed here are constructed from a linear combination of plane-wave fields, as illustrated in Figure 3. The precise selection of phases for each plane wave, aligned along the cylindrical angle in momentum space, results in the OAM of light.
Transverse and Longitudinal Angular Momentum
We briefly define the terminology of transverse and longitudinal angular momentum, which are frequently discussed in the literature. These concepts apply to the SAM, OAM, and TAM of radiation fields. Longitudinal angular momentum refers to angular momentum with a component in the direction of beam propagation. Conversely, transverse angular momentum refers to angular momentum with a component perpendicular to the beam’s propagation. Ref. [68] provides a detailed discussion of these components. Longitudinal angular momentum can be visualized as the rotation of an airplane propeller around its axis of propagation. Similarly, transverse angular momentum can be visualized as the rotation of a bicycle wheel, which points along an axis perpendicular to the direction of the bicycle’s motion.
Consider a plane-wave field propagating upwards with photons of common helicity, denoted as . In this scenario, the quantum-mechanical spin of an individual photon is represented by the vector , with the longitudinal spin component given by . As discussed earlier in Section 2.2, the spin vector has a length of , indicating the presence of a unit of transverse spin in a direction perpendicular to the photonic propagation. This transverse component, as described in the vector model of angular momentum (discussed in ref. [44]), lies on the circular perimeter at the base of a cone in space. The height of this cone is determined by the helical spin component. Due to the uncertainty principle, the exact location of the spin vector on its circular base remains unknown. Since we are dealing with classical fields, it is best to interpret the local expectation value [69,70] as the spin observable, where only the helical direction of unit norm survives—a purely longitudinal quantity. Interactions of fields with electrons are determined by the polarization and, therefore, the helicity alone. The vector does not appear in the Hamiltonian.
An example of non-vanishing transverse SAM can be obtained from the superposition of two plane-wave fields with identical intensity and opposite helicity, offset by an angle from their collective axis. One plane wave propagates at an angle and the other at , both confined to the x–z plane. In this configuration, the field contains no longitudinal SAM (along the z-axis) as each plane-wave field contributes with opposite signs and equal magnitudes. In contrast, the transverse SAM (along the x-axis) of each plane-wave field is of the same magnitude and sign. Therefore, the collective field contains transverse SAM oriented along the x-axis, but not longitudinal SAM. A detailed discussion of this can be found in ref. [71].
These components manifest similarly for OAM and TAM. Suppose we have a Bessel beam centered at the origin of the coordinate system and propagating upwards (). In this scenario, photons revolve around the propagation axis with a definite value of , indicating non-zero longitudinal TAM. Furthermore, when decomposed into the combined SAM and OAM basis, we observe the longitudinal components and . This field expresses no transverse angular momentum as photons propagate uniformly with common momenta and the intensity profile exhibits cylindrical symmetry around the propagation axis.
As discussed in Section 2.3.1, a classical particle moving with constant velocity will exhibit transverse orbital angular momentum if its motion is displaced from the origin of a coordinate system. Similarly, a Bessel beam displaced from the center of the coordinate system will exhibit the same form of transverse OAM. For a comprehensive discussion of longitudinal and transverse angular momentum, refer to ref. [70]. Their review provides a detailed analysis and includes numerous graphical representations of these quantities, surpassing our surface-level discussion.
3.2. The Paraxial Approximation
3.2.1. Bessel Beam Limits
In this subsection, we explore a scenario where the offset angle is small, causing only slight deviations of each plane-wave component from the vortex beam’s collective propagation axis. This situation, known as the paraxial limit, arises when the transverse momentum is significantly smaller than the field’s longitudinal momentum . In this context, results in a single non-zero spin component due to and the field (44) reduced to
as is demonstrated in Ref. [62]. In this circularly polarized field, only a single orbital projection persists. The spin and orbital angular momentum decouple in this paraxial limit. These paraxial photons coherently propagate upwards in space with a common linear momentum and shared angular momentum projection , twisting around their common propagation axis, akin to the rotation of classical particles around a shared axis. This analogy aligns with our earlier interpretation of plane waves as an ensemble of photons moving upwards in space with a common linear momentum. In the non-paraxial regime, photons still propagate with momentum , but instead exhibit a superposition of different OAM projections , revolving around the propagation axis for each polarization state .
3.2.2. Violation of the Transversality Condition
Fields of this type simplify the analysis process as they consist of a single spin component associated with circular polarization and a single OAM state , leading to a single spiraling phase term . Regrettably, fields of this type are neither compatible with the transversality condition nor are they solutions to Maxwell’s equations [72,73]. These so-called paraxial fields are a simplified approximation of beams which propagate with negligible transverse momentum.
Assume for the sake of argument that these fields do indeed satisfy the transversality condition:
This would suggest that the field component becomes null when acted upon by the directional derivative:
Here, we have expressed and in cylindrical coordinates and utilized the momentum operator corresponding to the cylindrical radius (Ref. [74]).
When acting on the - and -dependent factors within the Bessel beam component , we obtain the following:
after applying derivative identities from ref. [75] and
with
from recurrence relations contained in ref. [75].
The transversality condition is not satisfied by these results unless . This arises from the fact that the difference in Bessel functions derived from is linearly independent of the sum of the same Bessel functions derived from . Furthermore, as , we find that , leading to the plane-wave limit [62]:
This limit does not possess OAM and lacks a spiraling phase around the propagation axis. Nevertheless, paraxial beams with finite OAM are beneficial, despite the violation of the transversality condition. They significantly simplify the analysis, as long as is sufficiently small for the application at hand.
3.2.3. The General Case
Our study of Bessel beams has predominantly centered on non-paraxial beams, from which we derived a limiting case to yield a simplified paraxial field. However, an alternative approach exists. Instead of initially formulating non-paraxial fields and subsequently taking the paraxial limit, we can directly modify the wave equation. This direct modification not only streamlines the analysis but also facilitates the direct construction of paraxial fields.
Building on our earlier discussion about light rays forming small angles with their collective propagation axis, we can further explore the methodology grounded in the approximation . This approximation is typically invoked when the divergence angle is minimal, which simplifies the representation of radiation fields in terms of a single constant polarization vector. In such instances, the field is expressed as follows:
This expression recovers the plane-wave limit when . Here, we assume collective beam propagation along the direction and elliptical polarization confined to the x–y plane. The field has the majority of its momentum aligned along the z-axis. In this context, denotes an electric field amplitude, while k and represent the wave number and frequency, respectively. The quantity is assumed to vary slowly with respect to z, specifically under the condition . The “fast” oscillations of the wave along the propagation direction are captured by , leaving only “slow” oscillations in with respect to z.
Upon substituting this representation into the Helmholtz equation (Equation (1)), we obtain the paraxial differential equation [72,73,76]:
In this equation, the approximation corresponds to setting the right-hand side identically equal to 0, resulting in a departure from transversality. Here, represents the Laplacian operator in a plane restricted to the transverse coordinates. The equation is identical to the non-relativistic time-dependent Schrödinger equation in the spatial dimensions x and y due to their inclusion within the Laplacian operator. The first derivative associated with the z-dependence of the problem acts as the “time” variable. This approach provides a direct and simplified way to construct paraxial fields [77].
3.2.4. Laguerre–Gaussian Beams
Bessel beams are often employed in theoretical calculations since they are not paraxially approximated. Their factorizable nature makes them a convenient basis for discussing interactions with electrons bound to an atom, similar to those discussed in Section 4. These beams can be dissected into several components: a plane-wave component along the propagation axis, Bessel functions in the transverse direction, and OAM states encircling the propagation axis. Despite their utility, their application in practical experiments is curtailed due to their infinite spatial extent resulting from uniform intensity along the propagation axis, a trait they share with plane waves. As discussed in ref. [78], these beams are only an idealization which is approximated in experiment with a beam of finite extent. This subsection will briefly summarize a different type of paraxial beam that is prevalently used in experimental settings, which proves instrumental in describing realistic scenarios involving an ensemble of atoms dispersed over a beam profile of finite extent.
We now turn our attention to Laguerre–Gaussian (LG) beams, whose OAM content was initially investigated theoretically in ref. [4] and observed experimentally in ref. [79]. These beams are cylindrical solutions to the paraxial differential Equation (57) and are written as follows (refs. [19,80]):
In this equation, is the beam waist radius, is the beam waist, and is the Gouy phase. The Rayleigh length is , is the wave number, and the constant
defines a normalization convention.
The study of Laguerre–Gaussian beams offers profound insights into their structure and behavior, which is crucial when modeling scenarios involving an ensemble of atoms distributed over a finite spatial extent of the beam profile. In Section 5, exactly these situations will be discussed in the context of strong-field ionization. Similar to Gaussian beams, the intensity profile of Laguerre–Gaussian beams diminishes with the transverse distance . Additionally, the intensity decreases for large along the propagation axis due to the pre-factor , relative to the beam waist radius at position z. This characteristic sharply contrasts with Bessel beams, which maintain a constant intensity along their propagation axis. This distinction underscores the unique propagation characteristics of Laguerre–Gaussian and Bessel beams, highlighting their experimental utility.
The radial solutions of Laguerre–Gaussian beams are represented by Gaussian beam profiles modified by polynomial functions. The LG mode, which corresponds to the typical Gaussian beam profile, is considered trivial. Altering results in a spiraling transverse phase profile and zero intensity along the propagation axis. Nontrivial p corresponds to the number of peaks or troughs in the radial intensity profile. The OAM indices are integer values and are unbounded.
In Figure 5, we have plotted both the absolute value and phase of the LG OAM modes with and . This is similar to what we did earlier in Figure 4 for the Bessel beams. For , we observe cylindrical symmetry around the vortex center, akin to a paraxially approximated Bessel case. However, we do not observe oscillations in either the absolute value or phase due to the cylindrical radius. While Bessel functions oscillate an infinite number of times, LG modes do not oscillate at all. This trend is observed for all higher-order , where spiraling phase accumulation progresses exactly as in the Bessel case, but with differing oscillations in the radial direction. Depending on the specifics of the investigation, these differences may or may not be significant.
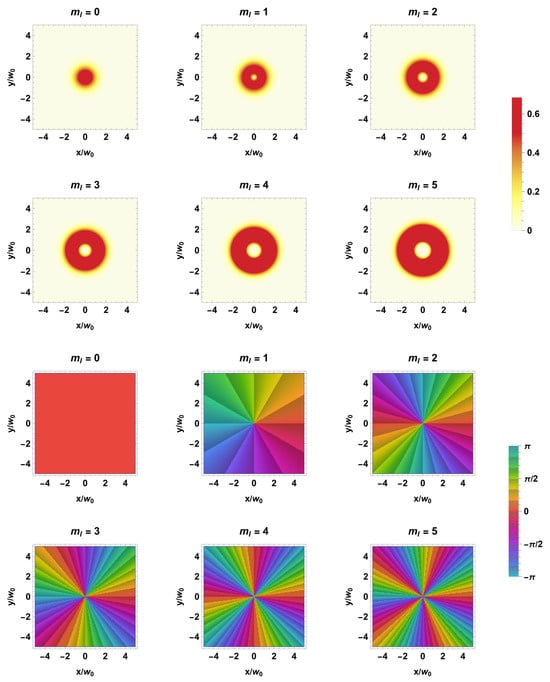
Figure 5.
The top two rows of the figure illustrate plots of the absolute value of the LG beam profile given in Equation (58), with and values ranging from 0 to 5. The bottom two rows display phase plots of the same function. For enhanced readability, the phase map is divided into intervals of size . Both the absolute value of the function and the phase are plotted against the transverse variables and with .
3.2.5. Scale Considerations and Refinements to the Paraxial Theory
We have established that the paraxial approximation is a valuable simplification, enabling the separation of spin and orbital angular momentum in wave dynamics when the radiation exhibits minimal transverse momentum relative to the overall propagation of the wave. While the criteria is qualitatively clear, we have yet to provide examples of when this breakdown occurs. An insightful discussion of this limit is presented in ref. [81], where paraxially approximated Laguerre–Gaussian beams are derived directly from a limiting case of the full Helmholtz equation, which describes exact waves. This method is based on the angular spectrum method of ref. [82] and is conceptually similar to the work of ref. [72], who demonstrated how the Helmholtz equation can be solved exactly using a series expansion involving a parameter .
We have expressed this quantity in terms of the wave vector with wavelength , representing the total linear momenta of constituent photons, and an effective transverse momentum scale , characterizing the transverse momentum of a Laguerre–Gaussian beam. Here, represents the beam’s waist, indicating the narrowest point of the beam and a measure of its width at the focus. As the beam becomes narrower in real space, its spread in transverse momentum space increases.
The paraxial approximation corresponds to the limit of minimal transverse momenta () or the lowest order of the series expansion discussed in refs. [72,81]. In this limit, spin and orbital angular momentum are separable. Conversely, higher-order corrections to the paraxial limit are required in the regime of larger f, where the transverse and longitudinal scales are no longer well separated. In this situation, spin and orbital angular momentum are no longer separable, as discussed in our earlier examination of Bessel beams.
In the trivial limit , ref. [81] reported that the paraxial approximation is applicable for parameters satisfying . For applications involving nontrivial indices , the paraxial limit now requires . Titanium:sapphire lasers, with their broad emission wavelength range and high damage threshold, are ideal light sources for studying ultrafast physics [83,84]. These lasers operate with a characteristic wavelength of 800 nm. The non-paraxial criteria corresponds to a breakdown for a beam waist of or smaller for the lowest-order mode at and or smaller for the higher-order modes at .
To put this into perspective, experiments commonly use lowest-order Gaussian modes with beam waists of or larger [85,86,87], indicating applications well within the paraxial regime. However, paraxial breakdown may be possible for these parameters in nontrivial situations where photons contain a large amount of OAM , yielding and a further reduced threshold for f. Higher-order modes deviate more strongly from the paraxial limit. An insightful discussion of how these bounds are determined can be found in the original work of ref. [81].
The discussion thus far has considered paraxial fields as a systematic approximation to the exact solution of the Helmholtz equation. While this is conceptually important, the primary interest often lies in the lowest-order corrections to existing paraxial models. The paraxial beams under discussion have non-zero field components only in directions transverse to the collective propagation of the wave. As discussed earlier, this implies that the transverse constraint is not satisfied because the constituent plane waves within the field propagate in directions other than the collective axis. An improved (but still inexact) approximation to these waves may be found as in ref. [88] by decomposing the field as follows:
where we have introduced an unknown longitudinal field component which is determined from the anti-derivative
of the zero-th-order paraxial solution , which explicitly enforces the transverse constraint. This approach is most commonly applied in the region of a tight focus (sizable f) where the beam is expected to have a large degree of transverse momentum.
3.3. The Angular Momentum of a Vortex Field
In the previous subsections, it was demonstrated how vortex radiation can be decomposed into a combination of plane electromagnetic waves. In the case of Bessel beams, each photon in this assembly exhibits a unique helicity along its propagation axis. The collective beam advances along the z-axis, while the momentum of each photon deviates from this axis by an angle , forming a ring in momentum space. By meticulously phasing and integrating these photons, we can sculpt a beam with a distinct TAM projection, . Upon applying the paraxial approximation, we find that the photons within these fields simultaneously exhibit a definite OAM projection and SAM projection . The same is true for Laguerre–Gaussian beams, which serve as exact solutions to the approximated Helmholtz Equation (57).
Our assertion that each photon carries spin and embodies angular momentum has been a consistent theme since our review of SAM and OAM in Section 2. However, we have not yet provided a comprehensive justification for this claim. In this subsection, we begin our discussion by constructing the TAM of a general monochromatic field from the cross product of position with momentum density, as discussed in classical electrodynamics. We then separate out the OAM and SAM components and illustrate the emergence of quantum-like wave operators that we have utilized thus far without justification. This progression enables us to bridge the gap between wave and electrodynamics representations of angular momentum. As an application, we will demonstrate that every photon of energy contained within a paraxial field carries SAM and OAM .
3.3.1. Classical Electrodynamics
In classical electrodynamics, one obtains the TAM [32,89,90]
from the integrated cross-product of position with linear momentum density
of the electromagnetic field. Expressing the magnetic field in terms of the vector potential and following the steps given in Appendix B allows us to separate the TAM into OAM
and SAM
contributions. Here, we have used the Cartesian components .
3.3.2. Wave Operators
The time average of the macroscopic quantities and resulting from the combined contributions of all field photons are related to the microscopic operators and whose spectrum defines the discrete set of angular momentum states permissible for an individual photon. We achieve this goal by representing the electrodynamic field in terms of the complex vector potential alone. Inserting these representations for both the vector potential and electric field results in the time-averaged orbital contribution
with the familiar operator . Similarly, the spin is given by the following:
with
where the conjugate transpose is given by † and corresponds to a unit vector in the j’th Cartesian direction. Furthermore, we have used the photonic spin operators defined in Section 2 and as in refs. [37,38,39] for the other projections.
Both contributions have an operator representation similar to the quantum-mechanical expectation value of the operators and . The eigenvalues correspond to the discrete set of angular momentum states allowed for an individual photon. The macroscopic properties of the field are determined from a sum over all photons. The vector potential , whose magnitude scales proportionally to the square root of the photon number density , is used as a classical state from which macroscopic results are determined from a combination of microscopic contributions. This approach allows us to bridge the gap between the macroscopic and microscopic descriptions of the classical field.
3.3.3. How Much OAM and SAM Do Individual Photons Have?
Individual “photons” within the field contain the same (monochromatic) energy . The total energy contained within the electromagnetic wave is therefore equal to the following [32]:
where the time average
yields an expression for the integrated energy density proportional to the total number of photons contained within the field:
which is expressed in terms of the photon number density:
at the coordinate . N here is a real number and assumed to be much larger than the number of quanta that participate in an interaction with an atom or molecule. In a fully quantum theory, we have [22] where the number of field photons N is restricted to integer values .
A subset of monochromatic paraxial beams propagating in the direction with vector potential containing photons of definite spin projection (circular polarization) and definite orbital projection (same spiraling phase around propagation axis) are proportional to .
Inserting states of this form into Equations (66) and (67) results in the orbital and spin angular momentum content:
which yields the total angular momentum projection:
Allen et al. [4,5] demonstrated these result in the ratio of the angular momentum component to the field energy U:
This equation indicates that each energy “quantum” possesses orbital and spin angular momentum quanta and . The particle number N falls out of the problem. This result holds both locally as the ratio of angular momentum and energy flux densities as discussed in refs. [4,5] and globally over the entire field as we have written. We now will discuss how photons possessing these angular momentum quanta and interact with electrons bound to an atom.
4. Single- and Few-Photon Ionization with Vortex Fields
In Section 2, we delved into the ionization of an arbitrary single-electron target by plane-wave radiation, thereby introducing the concept of the dipole approximation. Plane waves represent a system of uniform density where all monochromatic constituent particles propagate coherently in the same direction. While individual photons in these fields do carry orbital angular momentum , the integrated OAM is zero. Moreover, only the lowest-order constituent photons couple to the electronic ground state in the long-wavelength limit where the effective Bohr radius a is significantly smaller than the wavelength . Thus, photons impart orbital angular momentum onto electrons solely due to their spin content. Additionally, plane-wave fields contain photons with only , leading to the absence of a spiraling phase factor transverse to the propagation axis (). This raises the question how do emission processes resulting from an incident vortex field discussed in Section 3 differ from those resulting from plane-wave radiation? If differences are found, are they confined to higher-order multipole channels, or do they also manifest in the long-wavelength limit? This section aims to review perturbative photon processes and address these intriguing questions.
4.1. Perturbative Single Photon Ionization
In our earlier discussion of plane-wave ionization in Section 2.5, we utilized a transition matrix element proportional to without justification. This subsection briefly underscores its origin and addresses the nuances associated with the use of “exact” versus paraxial fields.
The interaction between an atomic electron and an applied radiation field is described by the time-dependent Schrödinger equation:
where
describes the propagation of an electron bound to an atomic potential.
In the velocity gauge, the interaction between electrons and the radiation field is obtained from and given by the following [41,42,45,46,47]:
where brackets { and } around indicate that acts on and not on quantities outside. In the transverse gauge, and this contribution may be neglected. Within the paraxial limit, this condition is only approximately met, as discussed earlier in Section 3.2. The paraxial approximation is unjustified in situations where this term becomes comparable to other contributions.
Perturbative photon absorption processes between the initial and final states of definite OAM, denoted by and , respectively, are governed by transition matrix elements. These elements are proportional to
This holds for a monochromatic field with states of energy difference . Analogously, photon emission matrix elements with are obtained by replacing with its complex conjugate . Transitions due to the weaker interaction are ignored in our discussion.
In Section 2.5, we delved into the interaction between circularly polarized plane-wave photons and atomic-bound electrons. This interaction, depicted in an atomic coordinate system, had partial contributions proportional to . This corresponds to photons with a total angular momentum of and a projection of . The prominence of each orbital order, l, was heavily influenced by the wavelength of the applied radiation. In scenarios where the wavelength significantly exceeded the effective Bohr radius a, the dipole approximation came into play. This meant that photons with did not interact with the electron cloud. Consequently, a single quantum of photonic spin angular momentum from photons of OAM was transferred into the orbital angular momentum of electrons.
Moreover, the selection rules for electronic orbital angular momentum transitions are atom-centric [41,42], while the angular momentum content of vortex beams is most commonly defined relative to their own center. Given that these centers are typically displaced and the angular momentum depends on the origin from which is measured, it is advantageous to operate within an atom-centered frame. This can be achieved by using a displaced version of the fields, . Emission exhibits distinct characteristics when a single atom is placed at the vortex center versus when it is placed far from the vortex center. These phenomena have been thoroughly explored in both theoretical [14,15,62,91,92] and experimental [16,17,18] studies.
4.2. What If an Atom Is Placed Exactly at the Vortex Center?
Consider an atom, strategically positioned at the epicenter of a vortex field that is paraxially approximated and exhibits circular polarization. When this atom absorbs a photon, it ejects an electron that was initially in an orbital state characterized by quantum numbers . Within this field, each photon carries identical quantum numbers, and , and spans a distribution where . They are in a superposition of l states. When discussing interactions involving radiation fields with matter, it was advantageous to discuss electronic transitions in terms of the TAM content of photons as in our earlier discussion of plane waves in Section 2.5.
Adding the OAM and SAM components together for these vortex fields results in the TAM states [49]:
This mirrors our discussion of plane waves, but with instead of alone.
Once these photons are absorbed by atomic electrons, a set of permissible electronic OAM states are obtained satisfying the following [49]:
Here, the electronic OAMs are determined from the absorption of photonic TAMs and each carry an identical component . The result again mirrors our discussion of plane waves in Section 2.5 when is set to zero.
4.3. The Long Wavelength Limit
Indeed, these results deviate significantly from plane-wave outcomes. But does this deviation persist when the wavelength of the applied radiation is considerably larger than the size of an atom? To explore this, we consider a scenario where a point-like atom is precisely positioned at the center of a vortex field.
In this setup, we would expect intensity at the vortex center for , but no intensity for . This might initially suggest that ionization is impossible for . However, even atoms that are considered “point-like” occupy a certain volume in space, meaning there is always a portion of the electron cloud that is displaced from the vortex center.
Assuming this displacement is infinitesimally small, the transverse field profile for a Bessel beam simplifies to
as derived from ref. [93]. While the transverse field profile is indeed zero exactly at the origin, it is finite at all neighboring points in space. Thus, even at the vortex center, the electron cloud bound to an atom experiences a non-zero field intensity, allowing for ionization.
This can be visualized in Figure 6, where we have zoomed into the vortex centers of Figure 4 for OAM components and 2. For , there is intensity at the origin and no spiraling phase around the propagation axis as expected. Conversely, for , there is no intensity at the origin but a spiraling phase is present. An atom placed at the origin would have a portion of its electron cloud at every cylindrical angle in space. This means that all possible phases are sampled in space. This spiraling phase implies a large deviation from plane-wave behavior, even at very long wavelengths.
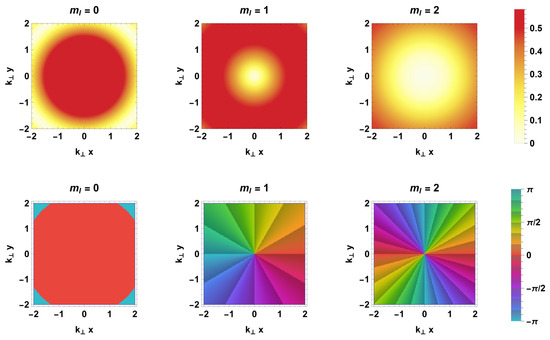
Figure 6.
Zoomed- in version of Figure 4. The top row illustrates plots of the absolute value of the function , with values ranging from 0 to 2. The bottom row displays the phase plots of the same function. For enhanced readability, the phase map is divided into intervals of size . Both the absolute value of the function and the phase are plotted against the transverse variables and with .
This approach can be extended to deduce selection rules in more complex scenarios, such as those involving non-paraxial beams or elliptical polarization. These situations correspond to a beam in a superposition of OAM and SAM states.
Our discussion thus far has focused on photons containing a single and a single which, when combined, form a complete basis of radiation fields. Non-paraxial or elliptically polarized fields may be expanded in terms of OAM and SAM components using Equation (34), where the selection rules of this section may be applied to each element.
These selection rules were first explored by Picon et al. in refs. [14,15], where they considered hydrogen atoms situated at the center of Laguerre–Gaussian vortex beams. The authors provide a comprehensive discussion of the selection rules, which correspond to the term that we also consider, in addition to the more subtle two-photon contribution. They derive precise probability amplitudes for individual partial-wave channels, and provide a detailed analysis of the dominant pathways. Experimental verification of the modified selection rules at the vortex center are given in refs. [16,17,18].
4.4. What If Atoms Are Displaced Far from the Vortex Center?
In our previous discussions, we delved into the fascinating regime of ionization scenarios, specifically focusing on atoms located at the vortex center. We discovered that circularly polarized beams with a fixed OAM projection, , led to a superposition of final electronic states. These states, characterized by an orbital angular momentum and , navigated through ionization channels that were strikingly different from those observed in the plane-wave scenario. This observation prompts an intriguing question: do the selection rules remain consistent when atoms are displaced from the vortex center, or do these translated fields exhibit fundamentally different behavior?
To explore this, let us consider a point-like atom, displaced from the vortex center by a distance . By “point-like”, we imply that the effective Bohr radius a is significantly smaller than both the displacement and the transverse length scale of the field, denoted by . An atom that meets these conditions houses an electron cloud that spans a range of angles with respect to the vortex center and tends towards zero as increases.
Interestingly, the vortex phase remains uniform across the electron cloud. Electronic transitions are dependent on a representation of the vortex field with respect to the atomic center, not the vortex center. The atom locally perceives radiation containing OAM alone with respect to its own center, similar to the ionization by plane-wave radiation discussed earlier in Section 2.5. This implies that novel selection rules are not observed. These features of ionization and a discussion connecting processes far from and positioned at the vortex center have been discussed theoretically in refs. [62,91,92] and both theoretically and experimentally in ref. [17].
In Figure 7, we present a zoomed-out version of Figure 6. Beams with , and 2 are now displayed for . Interestingly, the absolute values of and are nearly indistinguishable upon initial observation, except for locations very close to . However, in practice, these fields possess a different radial profile due to their dependence on the OAM through the Bessel functions . Therefore, differences in ionization are less about the spiraling phase and more about differences in the radial profile.
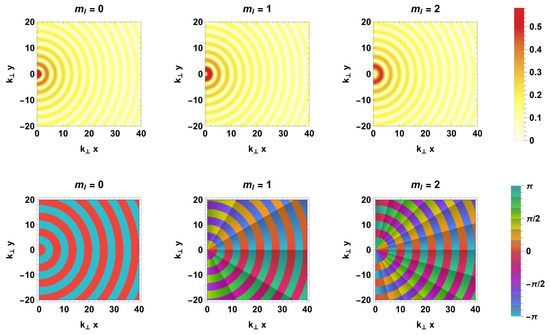
Figure 7.
Shifted version of Figure 4. The top row illustrates plots of the absolute value of the function , with values ranging from 0 to 2. The bottom row displays the phase plots of the same function. For enhanced readability, the phase map is divided into intervals of size . Both the absolute value of the function and the phase are plotted against the transverse variables and with .
A generalized version of the dipole approximation [94,95,96] can be applied in cases similar to these where an atom is displaced far from the vortex center and electrons bound to it experience the same field. In this situation the field is taken to be
in the vortex-centered frame. The electronic coordinate is assumed to be in close enough proximity to the parent atom located at position such that they both experience essentially the same field.
5. Strong-Field Ionization by Vortex Fields
Given the significant influence of both spin and orbital angular momentum on the photoionization selection rules elucidated in Section 4, one might intuitively expect that, in the strong-field regime, light’s OAM plays an equally important role. However, experimental results indicate that there is no substantial variation in the photoelectron momentum distributions generated by linearly polarized Gaussian and Laguerre–Gaussian beams [19]. To understand this apparent discrepancy and interpret other experimental results, it is useful to introduce a semi-classical model for strong-field ionization which accounts for the vortex beam’s spatial profile.
Compared to the single-photon transitions discussed in the previous section, strong-field ionization involves the absorption of many low-frequency photons to reach the continuum. Therefore, it is insufficient to treat the laser field perturbatively. Rather, it is more accurate to apply the strong-field approximation [97,98], which treats the atomic potential as a correction to the continuum electronic Hamiltonian . Using this approach, strong-field ionization in the gas phase can be understood as a two-step process [97] illustrated in Figure 8a,b: bound-state electrons are first ionized into the continuum by an intense laser pulse, then propagate as classical charged particles interacting primarily with the laser electric field. A useful framework for understanding and simulating this physical process is the classical trajectory Monte Carlo method [99], which also accounts for the atomic potential in the continuum.
For our discussion, we assume a sub-picosecond laser pulse, allowing liberated electrons to explore only a localized region of the field profile. The ponderomotive force of the light field is negligible [100], and electronic trajectories are determined by the lowest-order constant term of Equation (83). For longer pulses, electrons experience a larger portion of the field’s spatial profile, making the higher-order polynomial terms in Equation (83) more relevant. A thorough discussion of these simplifications for strong-field emission by sub-picosecond vortex beams can be found in the insightful work of ref. [96].
In the limit of adiabatic tunneling, where the Keldysh parameter (with the electron’s ionization potential and and describing the laser’s frequency and peak electric field strength, respectively), the probability of ionization is well described by the model of Ammasov, Delone, and Krainov (ADK) [101]. For an intuitive derivation of this result, see Section 2.3.2 of ref. [99]:
This equation indicates the relative probability of an electron to be ionized at the atomic location (impact parameter) with velocity transverse to the field direction at time t. The ionization rate’s spatiotemporal dependence is captured in the instantaneous field amplitude . As is shown graphically in Figure 9, ionization is exponentially suppressed away from the field peak. In the trivial case of ionization by a Gaussian beam (Equations (56) and (58) with ), the field peak is a single point along the propagation axis. For beams equipped with orbital angular momentum , in particular Laguerre–Gaussian beams with trivial radial index (), the field is maximized along the ring of maximum intensity given by
Because the atom is most likely to be ionized far from the vortex center, the overwhelming majority of electrons experience a spatially uniform electric field with local intensity and phase shifts given by in Equation (58).
After electrons are tunnel ionized, they may be treated as classically charged particles interacting with the laser electric field and the atomic potential. Their resulting dynamics are therefore determined by Newton’s equation
In the strong-field limit when the laser field dominates in the interaction and the dipole approximation of Equation (83) applies, the force exerted on the electron becomes space-independent, the atomic potential may be neglected, and the conservation of canonical momentum can be employed to determine the final velocity after ionization:
From Equation (87), one sees why the photoelectron momentum distributions in ref. [19] do not differ much between Gaussian and LG beams. The final electron velocity depends only on the initial velocity and the vector potential at the time of ionization and impact parameter . To leading order, the final electron momenta are independent of the field’s spatial variation and, therefore, photoelectrons are unaware of the ionization radiation’s OAM content.
Figure 8.
The 3-step model for high-harmonic generation. (a) Electrons, represented as red circles, are first tunnel ionized out of the electric potential (blue shaded region) into the continuum. (b) They then propagate and eventually recombine with the atom’s nucleus and emit a high-energy photon (magenta arrow), as is shown in (c). Steps (a,b) without recombination represent the semi-classical two-step model for strong-field ionization. Electrons that do recombine with the parent ion accumulate phase in the continuum that eventually is transferred to the resulting high harmonics, lending way to the conservation of orbital angular momentum in the far field. (d) Schematic of macroscopic HHG over the entire vortex beam profile. Electrons located throughout the gas jet can be thought of as independent radiators that generate far-field harmonics which conserve orbital angular momentum. Sub-figure (d) borrowed from ref. [102].
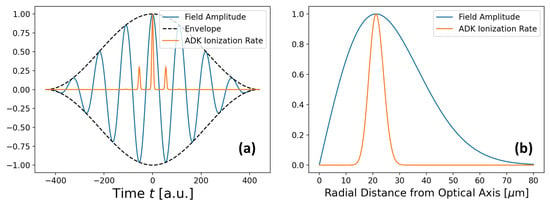
Figure 9.
Ionization probabilities within the vortex beam. (a) Instantaneous ADK ionization rate (Equation (84)) compared to the electric field amplitude of an 8-cycle, 800 nm, laser pulse. (b) The same ionization rate as a function of radial distance from the vortex center in an , Laguerre–Gaussian vortex beam.
Significantly modifying trajectories with the beam’s spatial profile would require electrons to break the dipole approximation (Equation (83)) during the propagation step. More specifically, the excursion distance of the electron in the presence of the alternating laser electric field, also known as the quiver radius
would need be comparable to the beam waist radius . For 800 nm light in the intensity range of – , the quiver radius is roughly 5–16 a.u., much smaller than the beam waist which is typically tens of microns. Alternatively, achieving a 1 micron quiver radius with 800 nm light would require a peak intensity of , far beyond what is produced experimentally. In short, in both the ionization and propagation steps of strong-field ionization with a low-frequency laser pulse, there is no discernible angular momentum transfer between the light and photoelectrons, as is confirmed experimentally in ref. [19].
Though experiments have focused on employing Laguerre–Gaussian beams to study strong-field ionization, modified momentum distributions can be achieved for ionization by Bessel beams (46) which include a nontrivial electric field longitudinal to the beam’s propagation direction [96,103] and therefore impart additional momentum to electrons in this direction. Furthermore, strong-field ionization can be performed by not just a single beam but a combination of pulses. For example, a noncollinear set of vortex beams can be used to control the location of the phase and polarization singularities in the beam profile, leading to modified momentum distributions [104]. Employing a circularly polarized vortex field plus a second-color, co-rotating Gaussian pulse creates fields with a sharp intensity peak which depends strongly on the phase between the two pulses, allowing one to distinguish between ionization by trivial and nontrivial vortex fields from the PMD [105]. Spatially sculpting the Gaussian probe leads to added control over the ionization location in the beam profile and allows one to determine the pump vortex pulse’s magnitude and sign [105]. Additionally, performing above-threshold ionization by a linearly polarized vortex beam and a transverse terahertz probe allows one to sample the vortex beam intensity profile and diagnose the orbital angular momentum index from resulting electron momenta [106]. Despite all the modified electron dynamics achieved by these multicolor and noncollinear fields, in none of these instances is it apparent that light’s orbital angular momentum is transferred to electrons.
6. High-Harmonic Generation and OAM Conservation
Given the challenge of observing OAM effects in strong-field ionization, it may seem surprising that light’s orbital angular momentum is conserved in high-harmonic generation (HHG) [102,107]. OAM conservation was first demonstrated in second-harmonic generation with the conversion of an fundamental beam to an second harmonic [108]. While the first HHG experiment with vortex beams seemed to contradict the expected conservation law [109], subsequent theoretical [20] and experimental [21,110] results have demonstrated OAM conservation, including the creation of an extreme ultraviolet (XUV) pulse with OAM index from a fundamental vortex beam [111]. The success of this field, however, seems contradictory to the results presented in Section 5 indicating that there is no transfer of orbital angular momentum to strong-field ionized electrons. Given that these electrons are the mediators of high-harmonic generation, it is perplexing then that they are able to transfer information about the driving light’s OAM state to resulting harmonics.
To understand OAM conservation, it is helpful to introduce the HHG model presented by Lewenstein and colleagues. For a detailed discussion and derivation of the model, consult the original article [112] or any recent tutorial on the subject such as ref. [113], which this article follows closely. Within the Lewenstein model, the electron is treated quantum mechanically according to the Schrödinger Equation (76). It is assumed in the model that the electron tunnel ionizes into the continuum and, once there, interacts only with the laser electric field. Therefore, while accounts for the field’s full spatial profile, as in the case of strong-field ionization with vortex light, interactions with the field are significantly suppressed near the vortex center (see Figure 9). Furthermore, since the electron’s characteristic length scales, namely the Bohr radius a and the quiver radius , are both too small to experience any spatial variation in the electric field, it is safe to presume that during the entirety of the laser’s duration.
In order to generate radiation in the interaction, the electron must be accelerated. Therefore, the observable of interest in high-harmonic generation is the induced dipole moment:
from which the relative power spectrum of emitted radiation can be calculated using Larmor’s formula:
Here, is given by a Fourier transform (89). Though calculating (89) can in general be performed numerically, Lewenstein and colleagues [112] achieved an analytical and physically insightful result by assuming that (I) the ground (initial) state |g⟩ is the only bound state populated during the interaction, (II) the ground state is never depleted during interaction with the laser field, and (III) the ionized electron propagates as a free particle interacting only with the laser electric field and not the atomic potential. The resulting dipole is given by
where represents a transition from the ground state |g⟩ into the continuum state and the action S is given by
The velocity of the ejected electrons, denoted as , is defined as the sum of the canonical momentum and the vector potential divided by the speed of light c. Equation (91) implies the following intuitive physical picture for electrons which contribute to the harmonic spectrum: An electron begins in the ground state |g⟩ with bound-state energy until time , at which point it is ionized into the continuum state by the strong electric field . The electron then propagates in the continuum and accumulates phase given by its semi-classical action (92) until time t, at which point it recombines into the ground state and emits a photon.
By Fourier transforming (91) into frequency space, employing the saddle-point approximation to variables t, , and , and solving for their respective stationary points , , and , one recovers the semi-classical three-step model for HHG [112,114] presented in [115]. According to the three-step model, electrons are first ionized from a bound state into the continuum at time . When the electron reaches the continuum, it propagates as a classical charged particle driven primarily by the laser electric field. Finally, these driven electrons recombine with the parent ion at time and emit a photon with energy equivalent to the ionization potential plus the electron’s kinetic energy . A schematic of this process is presented in Figure 8.
Within this semi-classical picture, the total phase associated with the qth-order harmonic is given by [116]
The phases associated with ionization and recombination are assumed to be constant and therefore ignored. Though the electron is treated classically in the continuum, it still accumulates phase equal to its action S which is transferred to the resulting harmonics. There is also a phase shift in the harmonic associated with the absorption of q photons given by the phase of the fundamental beam at the time of recombination, .
The discussion so far has focused on a single electron ionized by plane-wave radiation. To account for the beam’s spatial profile in the harmonic spectrum, one must focally average over the entire beam profile. However, to intuitively understand the conservation of orbital angular momentum in HHG with vortex fields, one can simply consider the harmonics generated by independent radiators separated by an angle relative to the field propagation axis. At the same distance from the propagation axis , these electrons are driven by identical beam profiles up to the space-dependent phase shift . When considering the qth-order harmonic, the semi-classical action (92) accumulated by both electrons is identical because the vector potential , ionization and recombination times all move in lock-step when the phase shift is applied. Therefore, plugging the phase shift into the expression for harmonic phase (93) leads to
Thus, the phase of the qth-order harmonic generated at the azimuthal angle receives a phase shift given by . Assuming that the phase of the harmonic spectrum corresponds to the atomic location in the near-field beam profile (see Figure 8d), this result lends way to the conservation of orbital angular momentum in the high-harmonic generation process, which can be summarized by the simple expression .
Along with energy and spin conservation, the conservation of OAM represents a unique, added control in the high-harmonic generation process [20,107]. For ionization by a single vortex beam, the orbital angular momentum and energy both scale with the harmonic order. When multiple beams are employed, the same conservation rules apply for photons absorbed by each constituent pulse. Employing two beams equipped with OAM to perform strong-field ionization has led to the creation of attosecond pulses with time-dependent OAM [117]. When harmonics are generated from a two-color, counter-rotating beam, one achieves additional influence over the polarization and vortex charge of individual harmonics [118,119]. Performing HHG with two linearly polarized vortex fields whose OAM indices are of opposite sign has led to the creation of harmonics with tunable divergence and line spacing [120]. The work carried out so far demonstrates great strides towards the goal of fully customizable structured attosecond pulses.
7. Discussion
Despite apparent contradictions outlined in the introduction, one can understand photonic OAM’s varying role in single-photon transitions, tunnel ionization, and high-harmonic generation after taking into account the electron’s location and spatial extent within the vortex field. For atomic transitions involving atoms located exactly at the vortex center, the photonic and atomic axes are perfectly aligned and the nontrivial spiraling phase terms lend way to experimentally observed modified selection rules (81) which indicate the conservation of total (atomic and photonic) angular momentum in the interaction. However, atoms located far away from the vortex center experience spatially homogeneous fields within the volume of the electronic wave function, approximated by the Bohr radius cubed. For these atoms displaced from the photonic axis, vortex light’s spatial structure manifests only as local phase and intensity variations in the field and new selection rules are not expected. Likewise, in the strong-field regime wherein the characteristic length scale is the quiver radius , the electron’s excursion distance is still much too small to experience spatial variation in the radiation field when ionization takes place near the peak of the pulse (85). Therefore, individual electrons located throughout the beam profile and ionized by an intense, low-frequency field according to the ADK tunneling rate (84) have no knowledge of the field’s variation, and there is no apparent transfer of orbital angular momentum [19] to individual electrons. However, local phase information from the driving field is stored in these electrons’ trajectories. For those electrons that eventually recombine with the atomic core, local phase shifts are passed on to resulting harmonics and multiplied with harmonic order (93), allowing for the conservation or orbital angular momentum in the far field.
An interesting extension of the experiments presented in this paper is the measurement of photoionization delays [121] with vortex fields [122,123,124,125]. Broadly speaking, these time delay experiments involve the use of an XUV pump to perform single-photon ionization followed by continuum transitions induced by an infrared probe delayed in time with respect to the XUV pulse. This setup allows one to extract the time taken by the electron to enter the continuum or its photoionization delay. Implementing a vortex XUV or IR pulse in these experiments would therefore provide access to arbitrary angular momentum states in the continuum. A significant application of this control has already been seen with circularly polarized pulses in the separation of photoionization and measurement-induced delays [126]. Furthermore, relative time delays between dipole and non-dipole transitions have been measured for Gaussian beams [127]. Performing the ionization step instead from the center of a vortex beam could allow for a more in-depth study on the nature of these non-dipole time delays.
In addition to atoms, there is also great promise in using OAM-equipped light to investigate larger, more complex systems. For example, chiral molecules, or molecules with definite handedness, are a great candidate for future investigation in the strong-field and ultrafast regime. OAM dichroism has already been displayed in chiral molecules interacting with hard X-rays [128], and there exists growing interest in the use of intense, synthetic chiral light composed of a noncollinear combination of plane wave pulses to study these systems [60,129,130]. Therefore, it seems natural to suspect that dichroic effects could also be observed in chiral molecules from intense or ultrafast vortex fields. Additionally, an exciting yet largely unexplored area of study is the application of vortex beams to condensed matter systems [131] in the ultrafast and strong-field regime. Since Bloch electronic states are in principle extended throughout the material sample, crystalline systems offer an opportunity to study the ensuing dynamics when the electron wave function is spread across the beam profile. Already, light’s orbital angular momentum has been proposed as a means to exert added control in the inverse Faraday effect [132,133,134] and to induce skyrmionic states in two-dimensional materials [135] and ultrathin films [136].
8. Conclusions
The aim of this work was to equip the reader with an in-depth understanding of what it means for light to contain spin and orbital angular momentum and the resulting electron dynamics that ensue. We demonstrated that, while light’s spin can be attributed to its polarization state, its angular momentum must come from spatial variation in the field. Although plane waves (3), Bessel beams (46), and Laguerre–Gaussian beams (58) in principle each contain local spin and orbital angular momentum density, only the latter two may possess net orbital angular momentum, which can be attributed to their spiraling transverse phases . These nontrivial space-dependent phases go on to play a crucial role in describing light–matter interactions with these fields, and there is great promise in the added control gained by light’s orbital angular momentum in the study of atomic, molecular, and condensed matter systems.
Author Contributions
A.S.L., S.W., and A.S. conceptualized the study. S.W. and A.S. performed the calculations and prepared the original draft. A.S.L. reviewed the draft and acquired funding. All authors have read and agreed to the published version of the manuscript.
Funding
Work performed by A.S. and A.S.L. was supported by NSF Investigator-Initiated Research grant, Award ID 2208040. Work performed by S.W. was supported by DOE Investigator-Initiated Research grant, Award ID DE-SC0022093.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No new data were created or analyzed in this study. Data sharing is not applicable to this article.
Acknowledgments
We extend our gratitude to Harrison Pasquinilli for his invaluable discussions and perceptive feedback, which significantly helped in the preparation of this work.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HHG | High-harmonic generation |
| LG | Laguerre–Gaussian |
| OAM | Orbital angular momentum |
| SAM | Spin angular momentum |
| TAM | Total angular momentum |
Appendix A. Plane-Wave OAM
In Section 2.5, we explored the photoionization of atoms with an effective Bohr radius a. We discussed how the photoionization of bound electrons is possible for photons containing finite OAM l, in situations where the electronic ground-state density approximated as a sphere of radius a overlaps strongly with the th multipole order of the field which is proportional to a spherical Bessel function and correspond to photons containing total OAM . We discussed how these Bessel-function contributions are maximized for when and grow in for until a local maximum is reached at a finite value of which is bounded below by . In finite l cases where , overlap of the electron cloud with the radiation field is minimal, leading to forbidden transitions. Conversely, for finite l situations with , significant overlap results in allowed transitions. To support our discussion, we’ll review the lower bound and provide a brief justification for this commonly used estimate. Spherical Bessel functions are solutions to the ordinary differential equation [137]
which when integrated gives the integro-differential equation
where primes indicate derivatives. If x is the first maximum of , then indicating that the right-hand side of the above equation is zero. As for finite l and when from Equation (38), we must integrate over an interval large enough such that the factor contains both positive and negative values. This is only possible for , leading to our desired result when .
Appendix B. Classical Electrodynamics
In Section 3.3.1, we established that the OAM [Equation (64)] and the SAM [Equation (65)] contributions of the electromagnetic field can be derived from the TAM [Equation (62)] by incorporating the magnetic field representation . The goal of this appendix is to determine these contributions.
Our desired result is the topic of exercise 7.27 in Jackson’s book on Classical Electrodynamics [32] and is obtained by inserting the linear momentum density into the TAM and expressing the vector product
in an alternative way. This is achieved by introducing the Levi-Civita symbol [138]
which represents the cross product between vectors through using so-called Einstein notation where it is implied that repeated indices are summed over integers 1, 2, and 3 without explicitly writing the sums out.
Using this notation, we obtain
where we have dropped from quantities for simplicity and use subscripts to represent the Cartesian components of each quantity. This situation is simplified using the identity [138]
which yields
where the first term on the right-hand side corresponds to
and immediately yields the field OAM (64)
once substituted into Equation (62).
The SAM component of the field is obtained from the second term on the right-hand side of Equation (A7) which we then apply the product rule to express as
where
with in vacuum and Kronecker delta which evaluates to 1 if both indices are the same and 0 otherwise.
In this situation, we have which gives
and yields the SAM
of the classical radiation field and gives our desired result.
Surprisingly, we are left with a final contribution which must be integrated over all of space as
We have applied the divergence theorem in moving from the left-most expression to the central after the equals sign [32] with surface normal defined as . Subscripts V or S are intended to imply integration over a three-dimensional volume and the two-dimensional surface bounding it, respectively. Physical fields are assumed to be localized in space. Our volume of integration V is over all of space. This means that the integral over the surface S is zero and that this final contribution vanishes.
References
- Heckenberg, N.; McDuff, R.; Smith, C.; White, A. Generation of optical phase singularities by computer-generated holograms. Opt. Lett. 1992, 17, 221–223. [Google Scholar] [CrossRef] [PubMed]
- Tamm, C.; Weiss, C.O. Bistability and optical switching of spatial patterns in a laser. JOSA B 1990, 7, 1034–1038. [Google Scholar] [CrossRef]
- Bazhenov, V.Y.; Vasnetsov, M.; Soskin, M. Laser beams with screw dislocations in their wavefronts. Jetp Lett. 1990, 52, 429–431. [Google Scholar]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Padgett, M.J.; Babiker, M. IV The Orbital Angular Momentum of Light. In Progress in Optics; Wolf, E., Ed.; Elsevier: Amsterdam, The Netherlands, 1999; Volume 39, pp. 291–372. [Google Scholar] [CrossRef]
- Shen, Y.; Wang, X.; Xie, Z.; Min, C.; Fu, X.; Liu, Q.; Gong, M.; Yuan, X. Optical vortices 30 years on: OAM manipulation from topological charge to multiple singularities. Light. Sci. Appl. 2019, 8, 90. [Google Scholar] [CrossRef]
- Gibson, G.; Courtial, J.; Padgett, M.J.; Vasnetsov, M.; Pas’ko, V.; Barnett, S.M.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef]
- He, H.; Friese, M.E.J.; Heckenberg, N.R.; Rubinsztein-Dunlop, H. Direct Observation of Transfer of Angular Momentum to Absorptive Particles from a Laser Beam with a Phase Singularity. Phys. Rev. Lett. 1995, 75, 826–829. [Google Scholar] [CrossRef]
- Andersen, M.; Ryu, C.; Cladé, P.; Natarajan, V.; Vaziri, A.; Helmerson, K.; Phillips, W.D. Quantized rotation of atoms from photons with orbital angular momentum. Phys. Rev. Lett. 2006, 97, 170406. [Google Scholar] [CrossRef] [PubMed]
- Araoka, F.; Verbiest, T.; Clays, K.; Persoons, A. Interactions of twisted light with chiral molecules: An experimental investigation. Phys. Rev. A—Atomic Mol. Opt. Phys. 2005, 71, 055401. [Google Scholar] [CrossRef]
- Löffler, W.; Broer, D.; Woerdman, J. Circular dichroism of cholesteric polymers and the orbital angular momentum of light. Phys. Rev. A—Atomic. Mol. Opt. Phys. 2011, 83, 065801. [Google Scholar] [CrossRef]
- Mathevet, R.; de Lesegno, B.V.; Pruvost, L.; Rikken, G.L. Negative experimental evidence for magneto-orbital dichroism. Opt. Express 2013, 21, 3941–3945. [Google Scholar] [CrossRef] [PubMed]
- Kaneyasu, T.; Hikosaka, Y.; Fujimoto, M.; Konomi, T.; Katoh, M.; Iwayama, H.; Shigemasa, E. Limitations in photoionization of helium by an extreme ultraviolet optical vortex. Phys. Rev. A 2017, 95, 023413. [Google Scholar] [CrossRef]
- Picón, A.; Mompart, J.; Aldana, J.R.V.d.; Plaja, L.; Calvo, G.F.; Roso, L. Photoionization with orbital angular momentum beams. Opt. Express 2010, 18, 3660–3671. [Google Scholar] [CrossRef] [PubMed]
- Picón, A.; Benseny, A.; Mompart, J.; Aldana, J.R.V.d.; Plaja, L.; Calvo, G.F.; Roso, L. Transferring orbital and spin angular momenta of light to atoms. New J. Phys. 2010, 12, 083053. [Google Scholar] [CrossRef]
- Schmiegelow, C.T.; Schulz, J.; Kaufmann, H.; Ruster, T.; Poschinger, U.G.; Schmidt-Kaler, F. Transfer of optical orbital angular momentum to a bound electron. Nat. Commun. 2016, 7, 12998. [Google Scholar] [CrossRef] [PubMed]
- Afanasev, A.; Carlson, C.E.; Schmiegelow, C.T.; Schulz, J.; Schmidt-Kaler, F.; Solyanik, M. Experimental verification of position-dependent angular-momentum selection rules for absorption of twisted light by a bound electron. New J. Phys. 2018, 20, 023032. [Google Scholar] [CrossRef]
- De Ninno, G.; Wätzel, J.; Ribič, P.R.; Allaria, E.; Coreno, M.; Danailov, M.B.; David, C.; Demidovich, A.; Di Fraia, M.; Giannessi, L.; et al. Photoelectric effect with a twist. Nat. Photonics 2020, 14, 554–558. [Google Scholar] [CrossRef]
- Sen, A.; Sinha, A.; Sen, S.; Sharma, V.; Gopal, R. Above-threshold ionization of argon with ultrashort orbital-angular-momentum beams. Phys. Rev. A 2022, 106, 023103. [Google Scholar] [CrossRef]
- Hernández-García, C.; Picón, A.; San Román, J.; Plaja, L. Attosecond Extreme Ultraviolet Vortices from High-Order Harmonic Generation. Phys. Rev. Lett. 2013, 111, 083602. [Google Scholar] [CrossRef] [PubMed]
- Gariepy, G.; Leach, J.; Kim, K.T.; Hammond, T.; Frumker, E.; Boyd, R.W.; Corkum, P. Creating High-Harmonic Beams with Controlled Orbital Angular Momentum. Phys. Rev. Lett. 2014, 113, 153901. [Google Scholar] [CrossRef] [PubMed]
- Berestetskii, V.B.; Lifshitz, E.M.; Pitaevskii, L.P. Quantum Electrodynamics: Volume 4; Butterworth-Heinemann: Oxford, UK, 1982; Volume 4. [Google Scholar]
- Faisal, F.H. Theory of Multiphoton Processes; Springer: New York, NY, USA, 1987. [Google Scholar] [CrossRef]
- Eichmann, H.; Egbert, A.; Nolte, S.; Momma, C.; Wellegehausen, B.; Becker, W.; Long, S.; McIver, J. Polarization-dependent high-order two-color mixing. Phys. Rev. A 1995, 51, R3414. [Google Scholar] [CrossRef] [PubMed]
- Lambert, G.; Vodungbo, B.; Gautier, J.; Mahieu, B.; Malka, V.; Sebban, S.; Zeitoun, P.; Luning, J.; Perron, J.; Andreev, A.; et al. Towards enabling femtosecond helicity-dependent spectroscopy with high-harmonic sources. Nat. Commun. 2015, 6, 6167. [Google Scholar] [CrossRef] [PubMed]
- Gaumnitz, T.; Jain, A.; Pertot, Y.; Huppert, M.; Jordan, I.; Ardana-Lamas, F.; Wörner, H.J. Streaking of 43-attosecond soft-X-ray pulses generated by a passively CEP-stable mid-infrared driver. Opt. Express 2017, 25, 27506–27518. [Google Scholar] [CrossRef] [PubMed]
- Barreau, L.; Veyrinas, K.; Gruson, V.; Weber, S.J.; Auguste, T.; Hergott, J.F.; Lepetit, F.; Carré, B.; Houver, J.C.; Dowek, D.; et al. Evidence of depolarization and ellipticity of high harmonics driven by ultrashort bichromatic circularly polarized fields. Nat. Commun. 2018, 9, 4727. [Google Scholar] [CrossRef]
- Galli, M.; Wanie, V.; Lopes, D.P.; Månsson, E.P.; Trabattoni, A.; Colaizzi, L.; Saraswathula, K.; Cartella, A.; Frassetto, F.; Poletto, L.; et al. Generation of deep ultraviolet sub-2-fs pulses. Opt. Lett. 2019, 44, 1308–1311. [Google Scholar] [CrossRef] [PubMed]
- Walker, S.; Reiff, R.; Jaron-Becker, A.; Becker, A. Characterization of vacuum and deep ultraviolet pulses via two-photon autocorrelation signals. Opt. Lett. 2021, 46, 3083–3086. [Google Scholar] [CrossRef] [PubMed]
- Ghomashi, B.; Walker, S.; Becker, A. Enabling elliptically polarized high harmonic generation with short cross polarized laser pulses. Sci. Rep. 2023, 13, 12843. [Google Scholar] [CrossRef]
- Finger, K.; Walker, S.; Becker, A. Pulse characterization via two-photon auto- and cross-correlation. Opt. Express 2024, 32, 34732–34748. [Google Scholar] [CrossRef]
- Jackson, J.D. Classical Electrodynamics; John Wiley & Sons: Hoboken, NJ, USA, 2021. [Google Scholar]
- Landau, L.D. The Classical Theory of Fields; Elsevier: Amsterdam, The Netherlands, 2013; Volume 2. [Google Scholar]
- Zee, A. Quantum Field Theory in a Nutshell, 2nd ed.; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Schwartz, M.D. Quantum Field Theory and the Standard Model; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Fierz, M.; Weisskopf, V.F. Theoretical Physics in the Twentieth Century: A Memorial Volume to Wolfgang Pauli; Interscience Publishers: Genève, Switzerland, 1960. [Google Scholar]
- Wei, E.; Lan, Z.; Chen, M.L.; Chen, Y.P.; Sun, S. Spin and Orbital Angular Momenta of Electromagnetic Waves: From Classical to Quantum Forms. IEEE J. Multiscale Multiphysics Comput. Tech. 2024, 9, 113–117. [Google Scholar] [CrossRef]
- Rose, M.E. Multipole Fields; Wiley: New York, NY, USA, 1955. [Google Scholar]
- Yang, L.P.; Khosravi, F.; Jacob, Z. Quantum field theory for spin operator of the photon. Phys. Rev. Res. 2022, 4, 023165. [Google Scholar] [CrossRef]
- Blatt, J.M.; Weisskopf, V.F. Theoretical Nuclear Physics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics: Non-Relativistic Theory; Elsevier: Amsterdam, The Netherlands, 2013; Volume 3. [Google Scholar]
- Merzbacher, E. Quantum Mechanics; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Merzbacher, E. Single valuedness of wave functions. Am. J. Phys. 1962, 30, 237–247. [Google Scholar] [CrossRef]
- Herzberg, G.; Spinks, J.W.T. Atomic Spectra and Atomic Structure; Courier Corporation: North Chelmsford, MA, USA, 1944. [Google Scholar]
- Bethe, H.A.; Salpeter, E.E. Quantum Mechanics of One- and Two-Electron Atoms; Springer: Boston, MA, USA, 1977. [Google Scholar] [CrossRef]
- Shankar, R. Principles of Quantum Mechanics; Springer: New York, NY, USA, 1994. [Google Scholar] [CrossRef]
- Sakurai, J.J.; Napolitano, J. Modern Quantum Mechanics, 3rd ed.; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Baz, A.I.; Zeldovich, Y.B.; Perelomov, A.M. Scattering, Reactions and Decay in Nonrelativistic Quantum Mechanics; Israel Program for Scientific Translations: Springfield, VA, USA, 1969. [Google Scholar]
- Rose, M.E. Elementary Theory of Angular Momentum; Courier Corporation: North Chelmsford, MA, USA, 1995. [Google Scholar]
- National Institute of Standards and Technology. 10.53 Power Series. NIST Digital Library of Mathematical Functions. 2024. Available online: https://dlmf.nist.gov/10.53 (accessed on 4 July 2024).
- Wang, B.; Li, L.; Zhang, Y.; Zhai, C.; Zhu, X.; Lan, P.; Lu, P. Non-dipole effect in vortex high-order harmonic generation. J. Phys. B At. Mol. Opt. Phys. 2020, 53, 215601. [Google Scholar] [CrossRef]
- Starace, A.F. Photoionization of atoms. In Springer Handbook of Atomic, Molecular, and Optical Physics; Springer: Berlin/Heidelberg, Germany, 2006; pp. 383–394. [Google Scholar] [CrossRef]
- Krässig, B.; Jung, M.; Gemmell, D.; Kanter, E.; LeBrun, T.; Southworth, S.; Young, L. Nondipolar asymmetries of photoelectron angular distributions. Phys. Rev. Lett. 1995, 75, 4736. [Google Scholar] [CrossRef] [PubMed]
- Hemmers, O.; Guillemin, R.; Kanter, E.; Krässig, B.; Lindle, D.W.; Southworth, S.; Wehlitz, R.; Baker, J.; Hudson, A.; Lotrakul, M.; et al. Dramatic Nondipole Effects in Low-Energy Photoionization: Experimental and Theoretical Study of Xe 5s. Phys. Rev. Lett. 2003, 91, 053002. [Google Scholar] [CrossRef]
- Kanter, E.; Krässig, B.; Southworth, S.; Guillemin, R.; Hemmers, O.; Lindle, D.W.; Wehlitz, R.; Amusia, M.Y.; Chernysheva, L.; Martin, N. E1 − E2 interference in the vuv photoionization of He. Phys. Rev. A 2003, 68, 012714. [Google Scholar] [CrossRef]
- Lindle, D.W.; Hemmers, O. Breakdown of the dipole approximation in soft-X-ray photoemission. J. Electron Spectrosc. Relat. Phenom. 1999, 100, 297–311. [Google Scholar] [CrossRef]
- Brumboiu, I.E.; Eriksson, O.; Norman, P. Atomic photoionization cross sections beyond the electric dipole approximation. J. Chem. Phys. 2019, 150. [Google Scholar] [CrossRef]
- Rezvan, D.; Klyssek, K.; Grundmann, S.; Pier, A.; Novikovskiy, N.; Strenger, N.; Tsitsonis, D.; Kircher, M.; Vela-Peréz, I.; Fehre, K.; et al. Observation of Nondipole-Induced Asymmetry in the Angular Emission Distribution of Photoelectrons from Fixed-in-Space CO Molecules. Phys. Rev. Lett. 2022, 129, 253201. [Google Scholar] [CrossRef]
- Hosaka, K.; Adachi, J.; Golovin, A.; Takahashi, M.; Teramoto, T.; Watanabe, N.; Yagishita, A.; Semenov, S.; Cherepkov, N. Non-dipole effects in the angular distribution of photoelectrons from the K-shell of N2 molecule. J. Phys. B At. Mol. Opt. Phys. 2005, 39, L25. [Google Scholar] [CrossRef]
- Ayuso, D.; Neufeld, O.; Ordonez, A.F.; Decleva, P.; Lerner, G.; Cohen, O.; Ivanov, M.; Smirnova, O. Synthetic chiral light for efficient control of chiral light–matter interaction. Nat. Photonics 2019, 13, 866–871. [Google Scholar] [CrossRef]
- Rosales-Guzmán, C.; Volke-Sepulveda, K.; Torres, J.P. Light with enhanced optical chirality. Opt. Lett. 2012, 37, 3486–3488. [Google Scholar] [CrossRef] [PubMed]
- Matula, O.; Hayrapetyan, A.G.; Serbo, V.G.; Surzhykov, A.; Fritzsche, S. Atomic ionization of hydrogen-like ions by twisted photons: Angular distribution of emitted electrons. J. Phys. B At. Mol. Opt. Phys. 2013, 46, 205002. [Google Scholar] [CrossRef]
- Ivanov, I.P. Colliding particles carrying nonzero orbital angular momentum. Phys. Rev. D 2011, 83, 093001. [Google Scholar] [CrossRef]
- Ivanov, I.; Serbo, V. Scattering of twisted particles: Extension to wave packets and orbital helicity. Phys. Rev. A 2011, 84, 033804. [Google Scholar] [CrossRef]
- Durnin, J.; Miceli Jr, J.; Eberly, J.H. Diffraction-free beams. Phys. Rev. Lett. 1987, 58, 1499. [Google Scholar] [CrossRef] [PubMed]
- Durnin, J.; Miceli, J.; Eberly, J.H. Comparison of Bessel and Gaussian beams. Opt. Lett. 1988, 13, 79–80. [Google Scholar] [CrossRef] [PubMed]
- Vasara, A.; Turunen, J.; Friberg, A.T. Realization of general nondiffracting beams with computer-generated holograms. JOSA A 1989, 6, 1748–1754. [Google Scholar] [CrossRef]
- Aiello, A.; Banzer, P.; Neugebauer, M.; Leuchs, G. From transverse angular momentum to photonic wheels. Nat. Photonics 2015, 9, 789–795. [Google Scholar] [CrossRef]
- Saito, S. Quantum field theory for coherent photons: Isomorphism between Stokes parameters and spin expectation values. Front. Phys. 2024, 11. [Google Scholar] [CrossRef]
- Bliokh, K.Y.; Nori, F. Transverse and longitudinal angular momenta of light. Phys. Rep. 2015, 592, 1–38. [Google Scholar] [CrossRef]
- Bekshaev, A.Y.; Bliokh, K.Y.; Nori, F. Transverse spin and momentum in two-wave interference. Phys. Rev. X 2015, 5, 011039. [Google Scholar] [CrossRef]
- Lax, M.; Louisell, W.H.; McKnight, W.B. From Maxwell to paraxial wave optics. Phys. Rev. A 1975, 11, 1365–1370. [Google Scholar] [CrossRef]
- Agrawal, G.P.; Pattanayak, D.N. Gaussian beam propagation beyond the paraxial approximation. JOSA 1979, 69, 575–578. [Google Scholar] [CrossRef]
- Weisstein, E.W. Cylindrical Coordinates. 2024. From MathWorld—A Wolfram Web Resource. Available online: https://mathworld.wolfram.com/CylindricalCoordinates.html (accessed on 4 July 2024).
- Olver, F.W.J.; Maximon, L.C. NIST Digital Library of Mathematical Functions, Chapter 10: Bessel Functions. 2024. Available online: https://dlmf.nist.gov/10 (accessed on 28 July 2024).
- Vaveliuk, P.; Ruiz, B.; Lencina, A. Limits of the paraxial approximation in laser beams. Opt. Lett. 2007, 32, 927–929. [Google Scholar] [CrossRef] [PubMed]
- de Boer, M.; Beetle, C. On the paraxial approximation in quantum optics II: Henochromatic modes of a Maxwell field. arXiv 2023, arXiv:2302.05478. [Google Scholar] [CrossRef]
- Arlt, J.; Hitomi, T.; Dholakia, K. Atom guiding along Laguerre-Gaussian and Bessel light beams. Appl. Phys. B 2000, 71, 549–554. [Google Scholar] [CrossRef]
- Beijersbergen, M.W.; Allen, L.; Van der Veen, H.; Woerdman, J. Astigmatic laser mode converters and transfer of orbital angular momentum. Opt. Commun. 1993, 96, 123–132. [Google Scholar] [CrossRef]
- Wang, A.; Yu, L.; Li, J.; Liang, X. Evolution of orbital angular momentum spectrum of broadband Laguerre–Gaussian beam in OPCPA process. Sci. Rep. 2023, 13, 55. [Google Scholar] [CrossRef]
- Cerjan, A.; Cerjan, C. Orbital angular momentum of Laguerre–Gaussian beams beyond the paraxial approximation. JOSA A 2011, 28, 2253–2260. [Google Scholar] [CrossRef][Green Version]
- Bouwkamp, C.J. Diffraction Theory. Rep. Prog. Phys. 1954, 17, 35. [Google Scholar] [CrossRef]
- Moulton, P.F. Spectroscopic and laser characteristics of Ti:Al2O3. J. Opt. Soc. Am. B 1986, 3, 125–133. [Google Scholar] [CrossRef]
- Rapoport, W.R.; Khattak, C.P. Efficient, Tunable Ti:Sapphire Laser. In Proceedings of the Tunable Solid-State Lasers II, Zigzag, OR, USA, 4–6 June 1986; Budgor, A.B., Esterowitz, L., DeShazer, L.G., Eds.; Springer: Berlin/Heidelberg, Germany, 1986; pp. 212–217. [Google Scholar]
- Barty, C.; Gordon Iii, C.; Lemoff, B. Multiterawatt 30-fs Ti: Sapphire laser system. Opt. Lett. 1994, 19, 1442–1444. [Google Scholar] [CrossRef] [PubMed]
- Loh, Z.H.; Khalil, M.; Correa, R.E.; Santra, R.; Buth, C.; Leone, S.R. Quantum state-resolved probing of strong-field-ionized xenon atoms using femtosecond high-order harmonic transient absorption spectroscopy. Phys. Rev. Lett. 2007, 98, 143601. [Google Scholar] [CrossRef]
- Pathak, V.B.; Lee, S.K.; Pae, K.H.; Hojbota, C.I.; Kim, C.M.; Nam, C.H. Strong field physics pursued with petawatt lasers. AAPPS Bull. 2021, 31, 1–20. [Google Scholar] [CrossRef]
- Novotny, L.; Hecht, B. Principles of Nano-Optics; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Andrews, D.L.; Babiker, M. (Eds.) The Angular Momentum of Light; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar] [CrossRef]
- Götte, J.B. Integral and Fractional Orbital Angular Momentum of Light. Ph.D. Thesis, University of Strathclyde, Glasgow, Scotland, 2006. [Google Scholar]
- Pavlov, I.; Chaikovskaia, A.; Karlovets, D. Generation of vortex electrons by atomic photoionization. arXiv 2024, arXiv:2405.15030. [Google Scholar] [CrossRef]
- Kiselev, M.D.; Gryzlova, E.V.; Grum-Grzhimailo, A.N. Angular distribution of photoelectrons generated in atomic ionization by twisted radiation. Phys. Rev. A 2023, 108, 023117. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Ludwig, A.; Maurer, J.; Mayer, B.; Phillips, C.; Gallmann, L.; Keller, U. Breakdown of the Dipole Approximation in Strong-Field Ionization. Phys. Rev. Lett. 2014, 113, 243001. [Google Scholar] [CrossRef] [PubMed]
- Maurer, J.; Keller, U. Ionization in intense laser fields beyond the electric dipole approximation: Concepts, methods, achievements and future directions. J. Phys. B At. Mol. Opt. Phys. 2021, 54, 094001. [Google Scholar] [CrossRef]
- Böning, B.; Paufler, W.; Fritzsche, S. Above-threshold ionization by few-cycle Bessel pulses carrying orbital angular momentum. Phys. Rev. A 2018, 98, 023407. [Google Scholar] [CrossRef]
- Ivanov, M.Y.; Spanner, M.; Smirnova, O. Anatomy of strong field ionization. J. Mod. Opt. 2005, 52, 165–184. [Google Scholar] [CrossRef]
- Amini, K.; Biegert, J.; Calegari, F.; Chacón, A.; Ciappina, M.F.; Dauphin, A.; Efimov, D.K.; Faria, C.F.d.M.; Giergiel, K.; Gniewek, P.; et al. Symphony on strong field approximation. Rep. Prog. Phys. 2019, 82, 116001. [Google Scholar] [CrossRef] [PubMed]
- Ortmann, L. Trajectory-Based Analyses of Ultrafast Strong Field Phenomena. Ph.D. Thesis, Max-Planck-Institüt für Physik komplexer Systeme, Dresden, Germany, 2019. [Google Scholar]
- Freeman, R.R.; Bucksbaum, P.H.; Milchberg, H.; Darack, S.; Schumacher, D.; Geusic, M.E. Above-threshold ionization with subpicosecond laser pulses. Phys. Rev. Lett. 1987, 59, 1092–1095. [Google Scholar] [CrossRef] [PubMed]
- Ammosov, M.V.; Delone, N.B.; Krainov, V.P. Tunnel ionization of complex atoms and atomic ions in electromagnetic field. High Intensity Laser Process 1986, 664, 138–141. [Google Scholar]
- Hernández-García, C.; Vieira, J.; Mendonça, J.T.; Rego, L.; San Román, J.; Plaja, L.; Ribic, P.R.; Gauthier, D.; Picón, A. Generation and Applications of Extreme-Ultraviolet Vortices. Photonics 2017, 4, 28. [Google Scholar] [CrossRef]
- Paufler, W. Strong-field ionization with twisted laser pulses. Phys. Rev. A 2018, 97. [Google Scholar] [CrossRef]
- Fang, Y.; Guo, Z.; Ge, P.; Ma, X.; Han, M.; Yu, X.; Deng, Y.; Gong, Q.; Liu, Y. Strong-field photoionization of intense laser fields by controlling optical singularities. Sci. China Phys. Mech. Astron. 2021, 64, 274211. [Google Scholar] [CrossRef]
- Fang, Y.; Guo, Z.; Ge, P.; Dou, Y.; Deng, Y.; Gong, Q.; Liu, Y. Probing the orbital angular momentum of intense vortex pulses with strong-field ionization. Light. Sci. Appl. 2022, 11, 34. [Google Scholar] [CrossRef] [PubMed]
- Pasquinilli, H.; Schimmoller, A.; Walker, S.; Landsman, A.S. Determining the Orbital Angular Momentum of a Vortex Beam Using Strong Field Ionization. Photonics 2023, 10, 1322. [Google Scholar] [CrossRef]
- Paufler, W.; Böning, B.; Fritzsche, S. High harmonic generation with Laguerre–Gaussian beams. J. Opt. 2019, 21, 094001. [Google Scholar] [CrossRef]
- Toda, Y.; Honda, S.; Morita, R. Dynamics of a paired optical vortex generated by second-harmonic generation. Opt. Express 2010, 18, 17796–17804. [Google Scholar] [CrossRef] [PubMed]
- Zürch, M.; Kern, C.; Hansinger, P.; Dreischuh, A.; Spielmann, C. Strong-field physics with singular light beams. Nat. Phys. 2012, 8, 743–746. [Google Scholar] [CrossRef]
- Gauthier, D.; Ribič, P.R.; Adhikary, G.; Camper, A.; Chappuis, C.; Cucini, R.; DiMauro, L.F.; Dovillaire, G.; Frassetto, F.; Géneaux, R.; et al. Tunable orbital angular momentum in high-harmonic generation. Nat. Commun. 2017, 8, 14971. [Google Scholar] [CrossRef] [PubMed]
- Pandey, A.K.; de las Heras, A.; Larrieu, T.; San Román, J.; Serrano, J.; Plaja, L.; Baynard, E.; Pittman, M.; Dovillaire, G.; Kazamias, S.; et al. Characterization of Extreme Ultraviolet Vortex Beams with a Very High Topological Charge. ACS Photonics 2022, 9, 944–951. [Google Scholar] [CrossRef]
- Lewenstein, M.; Balcou, P.; Ivanov, M.Y.; L’Huillier, A.; Corkum, P.B. Theory of high-harmonic generation by low-frequency laser fields. Phys. Rev. A 1994, 49, 2117–2132. [Google Scholar] [CrossRef] [PubMed]
- Le, A.T.; Wei, H.; Jin, C.; Lin, C.D. Strong-field approximation and its extension for high-order harmonic generation with mid-infrared lasers. J. Phys. B At. Mol. Opt. Phys. 2016, 49, 053001. [Google Scholar] [CrossRef]
- Lewenstein, M.; Salières, P.; L’Huillier, A. Phase of the atomic polarization in high-order harmonic generation. Phys. Rev. A 1995, 52, 4747–4754. [Google Scholar] [CrossRef] [PubMed]
- Corkum, P.B. Plasma perspective on strong field multiphoton ionization. Phys. Rev. Lett. 1993, 71, 1994–1997. [Google Scholar] [CrossRef] [PubMed]
- Balcou, P.; Salières, P.; L’Huillier, A.; Lewenstein, M. Generalized phase-matching conditions for high harmonics: The role of field-gradient forces. Phys. Rev. A 1997, 55, 3204–3210. [Google Scholar] [CrossRef]
- Rego, L.; Dorney, K.M.; Brooks, N.J.; Nguyen, Q.L.; Liao, C.T.; San Román, J.; Couch, D.E.; Liu, A.; Pisanty, E.; Lewenstein, M.; et al. Generation of extreme-ultraviolet beams with time-varying orbital angular momentum. Science 2019, 364, eaaw9486. [Google Scholar] [CrossRef]
- Paufler, W.; Böning, B.; Fritzsche, S. Tailored orbital angular momentum in high-order harmonic generation with bicircular Laguerre-Gaussian beams. Phys. Rev. A 2018, 98, 011401. [Google Scholar] [CrossRef]
- Dorney, K.M.; Rego, L.; Brooks, N.J.; San Román, J.; Liao, C.T.; Ellis, J.L.; Zusin, D.; Gentry, C.; Nguyen, Q.L.; Shaw, J.M.; et al. Controlling the polarization and vortex charge of attosecond high-harmonic beams via simultaneous spin–orbit momentum conservation. Nat. Photonics 2019, 13, 123–130. [Google Scholar] [CrossRef]
- Rego, L.; Brooks, N.J.; Nguyen, Q.L.D.; Román, J.S.; Binnie, I.; Plaja, L.; Kapteyn, H.C.; Murnane, M.M.; Hernández-García, C. Necklace-structured high-harmonic generation for low-divergence, soft x-ray harmonic combs with tunable line spacing. Sci. Adv. 2022, 8, eabj7380. [Google Scholar] [CrossRef] [PubMed]
- Pazourek, R.; Nagele, S.; Burgdörfer, J. Attosecond chronoscopy of photoemission. Rev. Mod. Phys. 2015, 87, 765–802. [Google Scholar] [CrossRef]
- Wätzel, J.; Berakdar, J. Discerning on a sub-optical-wavelength the attosecond time delays in electron emission from magnetic sublevels by optical vortices. Phys. Rev. A 2016, 94, 033414. [Google Scholar] [CrossRef]
- Giri, S.; Ivanov, M.; Dixit, G. Signatures of the orbital angular momentum of an infrared light beam in the two-photon transition matrix element: A step toward attosecond chronoscopy of photoionization. Phys. Rev. A 2020, 101, 033412. [Google Scholar] [CrossRef]
- Ansari, I.N.; Jadoun, D.S.; Dixit, G. Angle-Resolved Attosecond Streaking of Twisted Attosecond Pulses. arXiv 2020, arXiv:2006.01582. [Google Scholar] [CrossRef]
- Wätzel, J.; Berakdar, J. Spatiotemporal delay in photoionization by polarization-structured laser fields. Phys. Rev. A 2021, 103, 063107. [Google Scholar] [CrossRef]
- Han, M.; Ji, J.B.; Leung, C.S.; Ueda, K.; Wörner, H.J. Separation of photoionization and measurement-induced delays. Sci. Adv. 2024, 10, eadj2629. [Google Scholar] [CrossRef]
- Liang, J.; Han, M.; Liao, Y.; Ji, J.b.; Leung, C.S.; Jiang, W.C.; Ueda, K.; Zhou, Y.; Lu, P.; Wörner, H.J. Attosecond-resolved non-dipole photoionization dynamics. Nat. Photonics 2024, 18, 311–317. [Google Scholar] [CrossRef]
- Rouxel, J.R.; Rösner, B.; Karpov, D.; Bacellar, C.; Mancini, G.F.; Zinna, F.; Kinschel, D.; Cannelli, O.; Oppermann, M.; Svetina, C.; et al. Hard X-ray helical dichroism of disordered molecular media. Nat. Photonics 2022, 16, 570–574. [Google Scholar] [CrossRef]
- Mayer, N.; Ayuso, D.; Decleva, P.; Khokhlova, M.; Pisanty, E.; Ivanov, M.; Smirnova, O. Chiral topological light for detecting robust enantio-sensitive observables. arXiv 2023, arXiv:2303.10932. [Google Scholar] [CrossRef]
- Wanie, V.; Bloch, E.; Månsson, E.P.; Colaizzi, L.; Ryabchuk, S.; Saraswathula, K.; Ordonez, A.F.; Ayuso, D.; Smirnova, O.; Trabattoni, A.; et al. Capturing electron-driven chiral dynamics in UV-excited molecules. Nature 2024, 630, 109–115. [Google Scholar] [CrossRef] [PubMed]
- Quinteiro Rosen, G.F.; Tamborenea, P.I.; Kuhn, T. Interplay between optical vortices and condensed matter. Rev. Mod. Phys. 2022, 94, 035003. [Google Scholar] [CrossRef]
- Hertel, R. Theory of the inverse Faraday effect in metals. J. Magn. Magn. Mater. 2006, 303, L1–L4. [Google Scholar] [CrossRef]
- Ali, S.; Davies, J.R.; Mendonca, J.T. Inverse Faraday Effect with Linearly Polarized Laser Pulses. Phys. Rev. Lett. 2010, 105, 035001. [Google Scholar] [CrossRef] [PubMed]
- Longman, A.; Fedosejevs, R. Kilo-Tesla axial magnetic field generation with high intensity spin and orbital angular momentum beams. Phys. Rev. Res. 2021, 3, 043180. [Google Scholar] [CrossRef]
- Fujita, H.; Sato, M. Ultrafast generation of skyrmionic defects with vortex beams: Printing laser profiles on magnets. Phys. Rev. B 2017, 95, 054421. [Google Scholar] [CrossRef]
- Gao, L.; Prokhorenko, S.; Nahas, Y.; Bellaiche, L. Dynamical Control of Topology in Polar Skyrmions via Twisted Light. Phys. Rev. Lett. 2024, 132, 026902. [Google Scholar] [CrossRef] [PubMed]
- Weisstein, E.W. Spherical Bessel Differential Equation. 2024. Available online: https://mathworld.wolfram.com/SphericalBesselDifferentialEquation.html (accessed on 21 July 2024).
- Griffiths, D.J. Introduction to Electrodynamics; Cambridge University Press: Cambridge, UK, 2023. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).