A Hybrid Design for Frequency-Independent Extreme Birefringence Combining Metamaterials with the Form Birefringence Concept
Abstract
1. Introduction
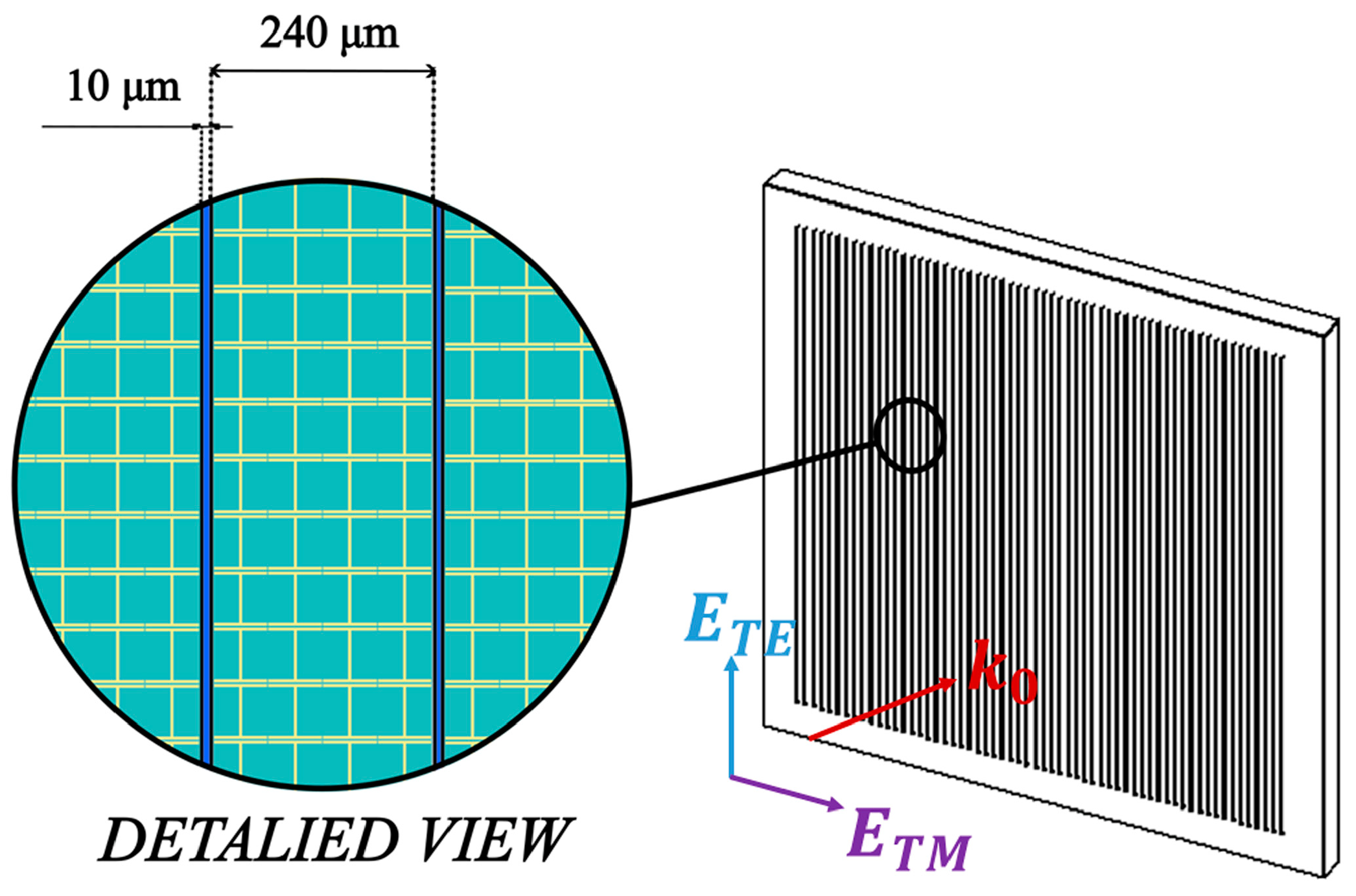
2. Materials and Methods
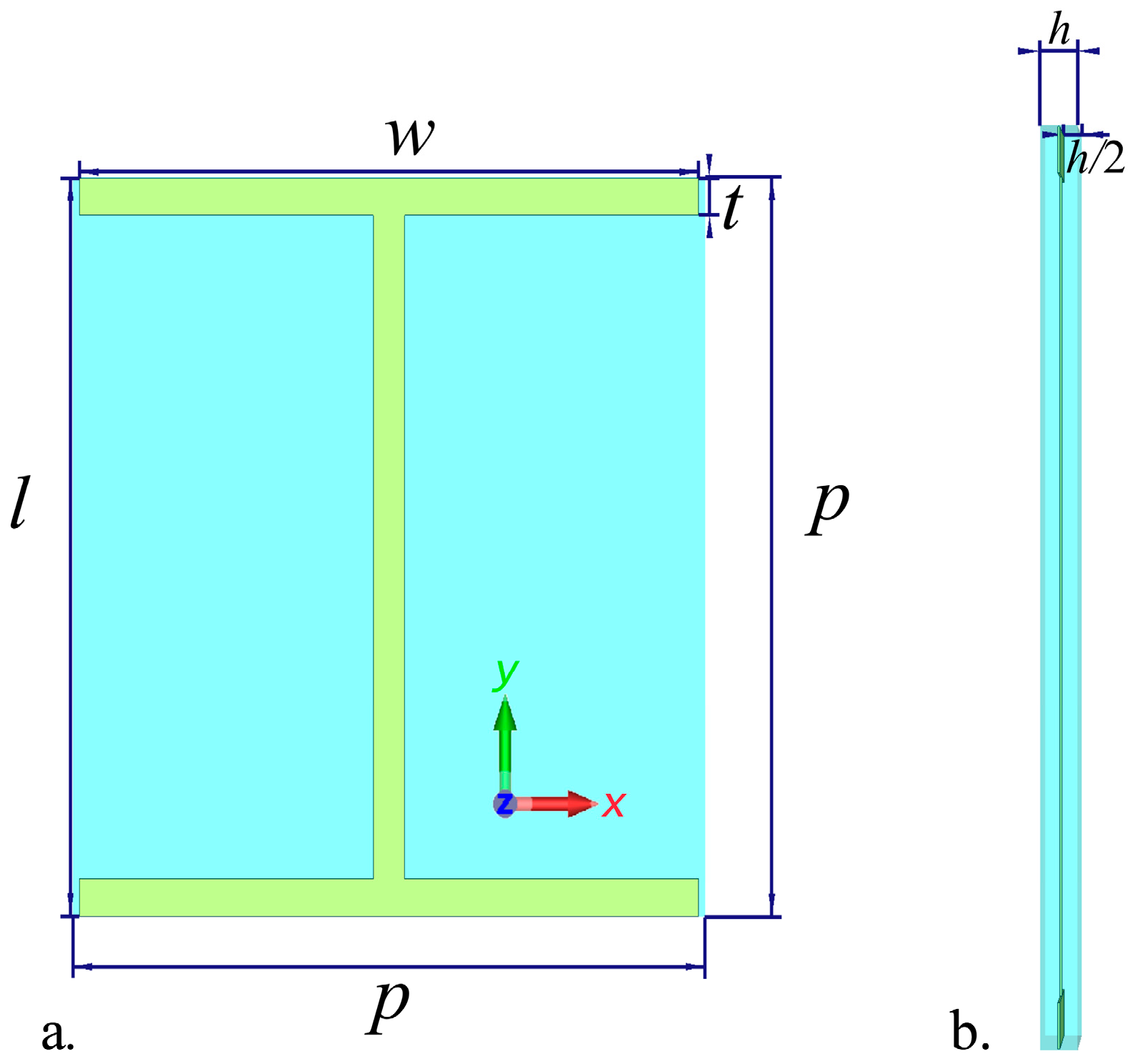
2.1. Metamaterial Design and S-Parameter Results
2.2. Refractive Index Retrieving Method from S-Parameters
2.3. Calculation of Form Birefringence
3. Results and Discussion
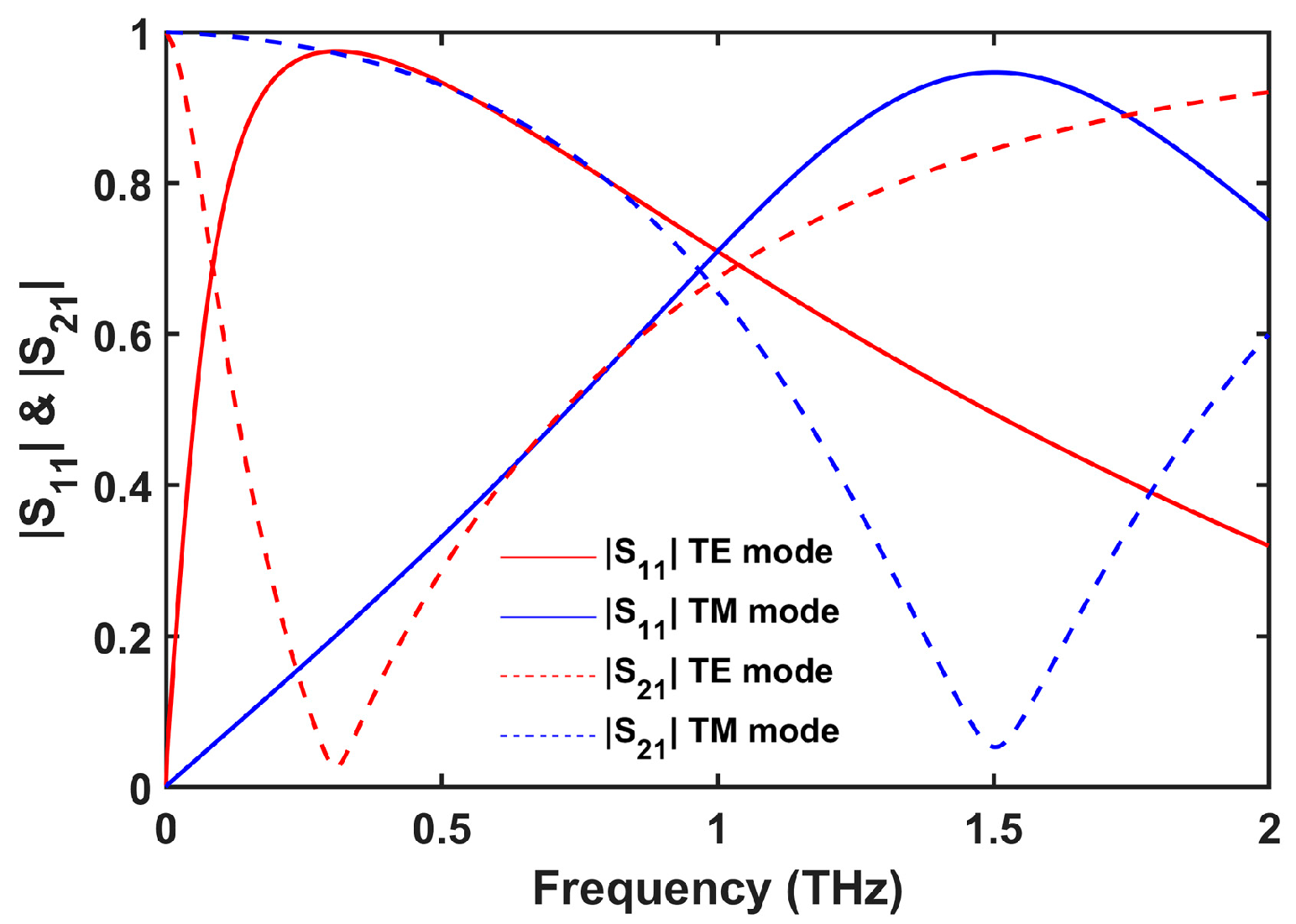
3.1. S-Parameter Results
3.2. Effective Refractive Index Properties of the Metamaterial
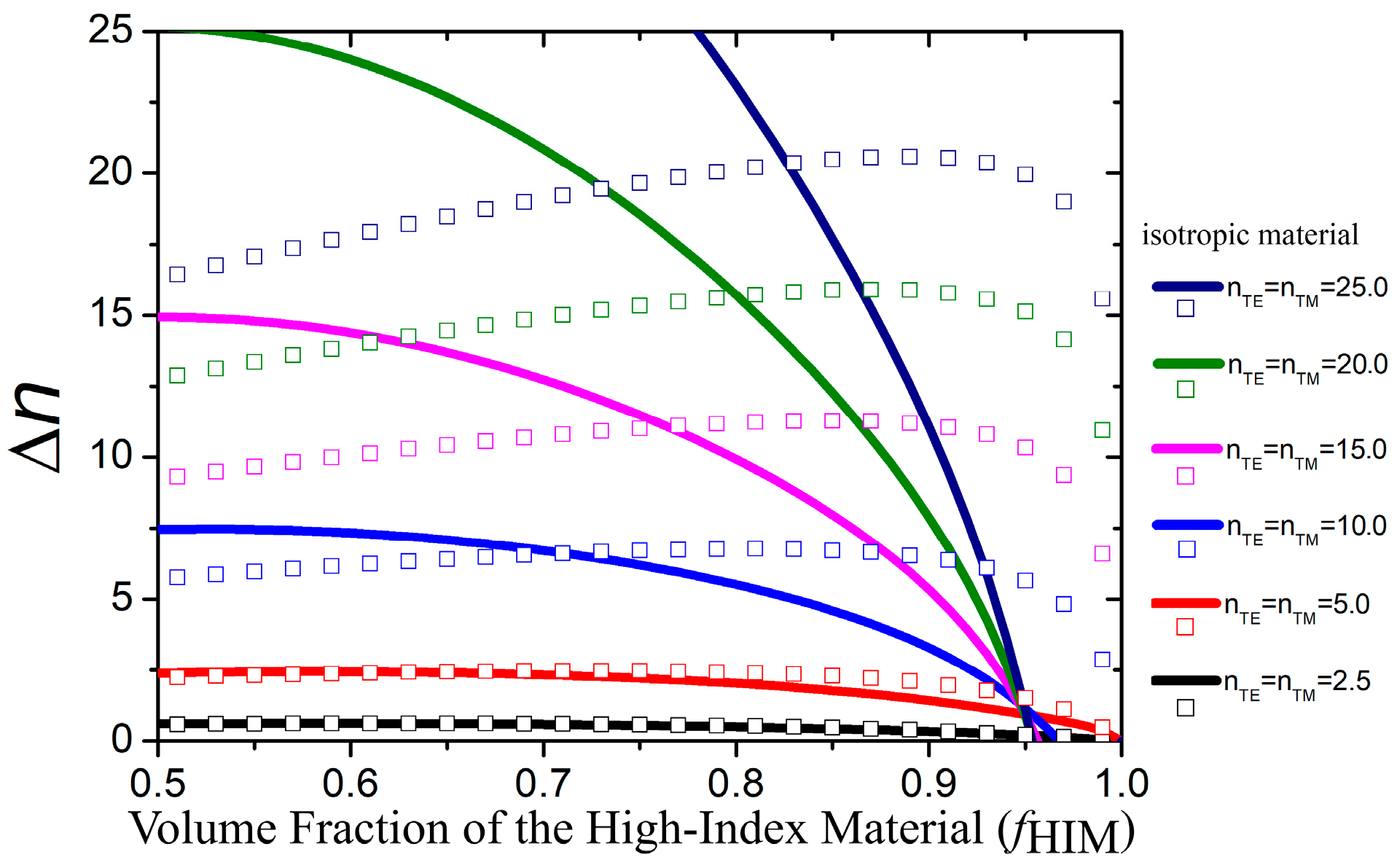
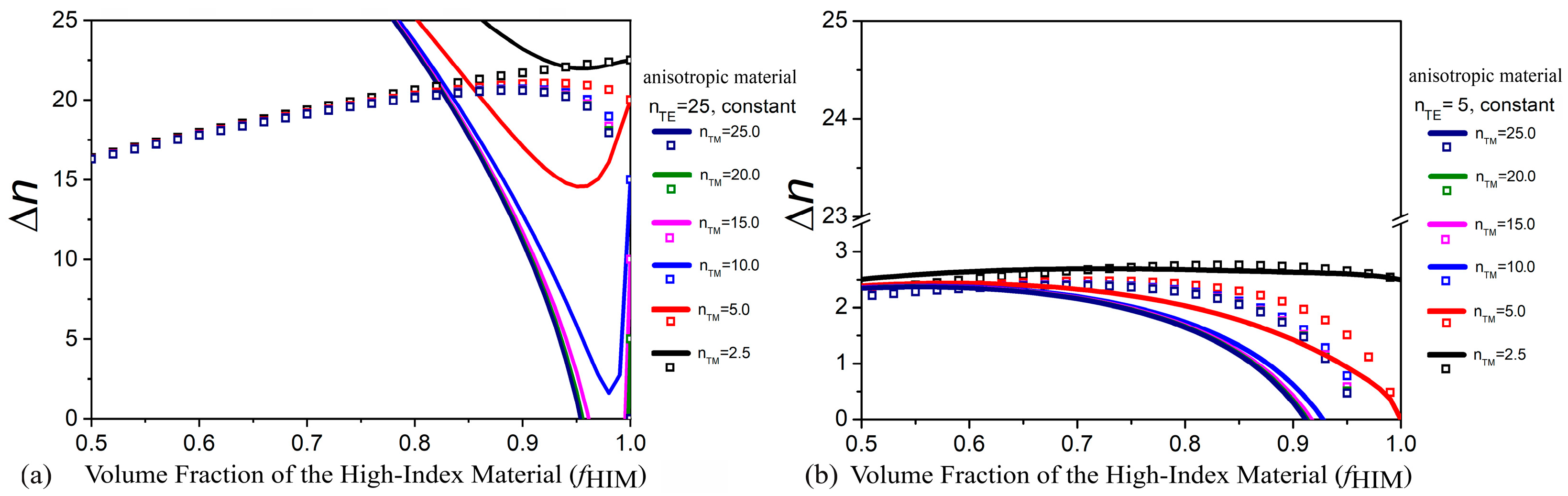
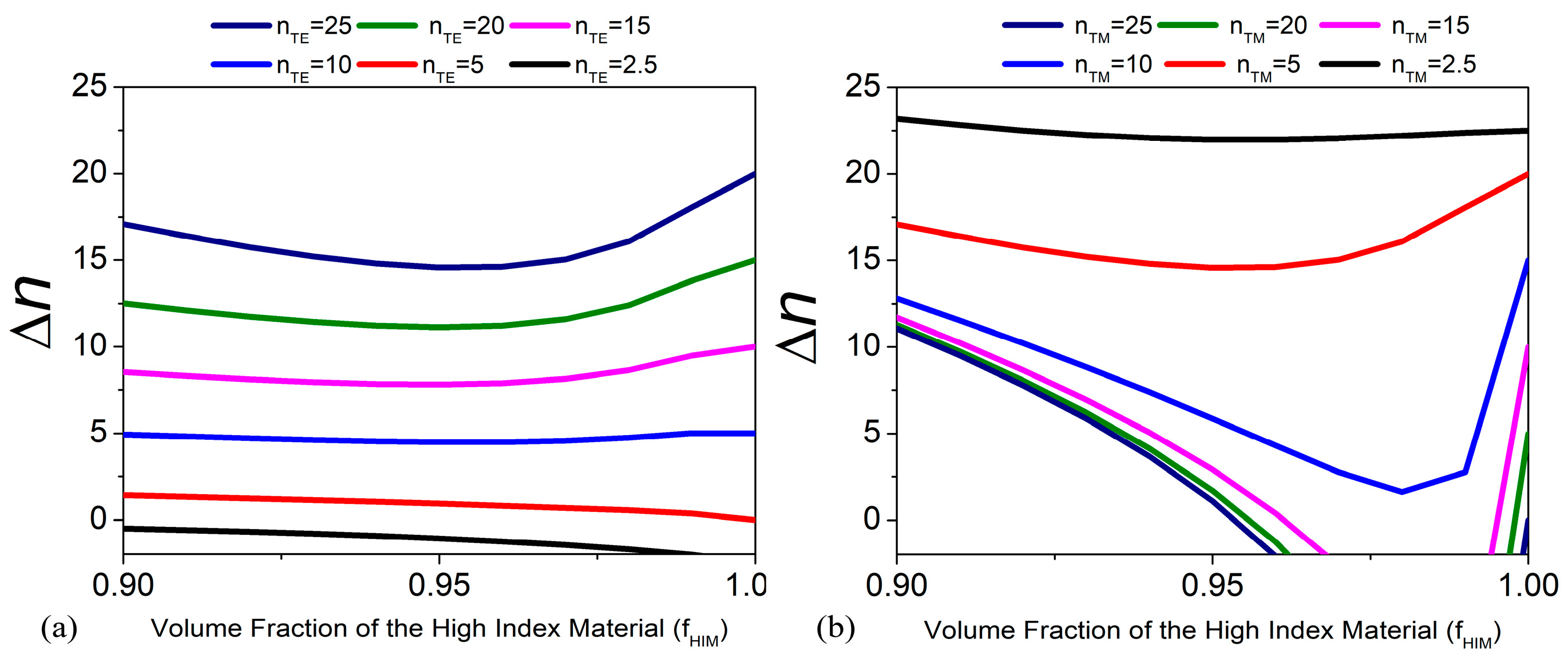
3.3. Form Birefringence in Highly Anisotropic Media
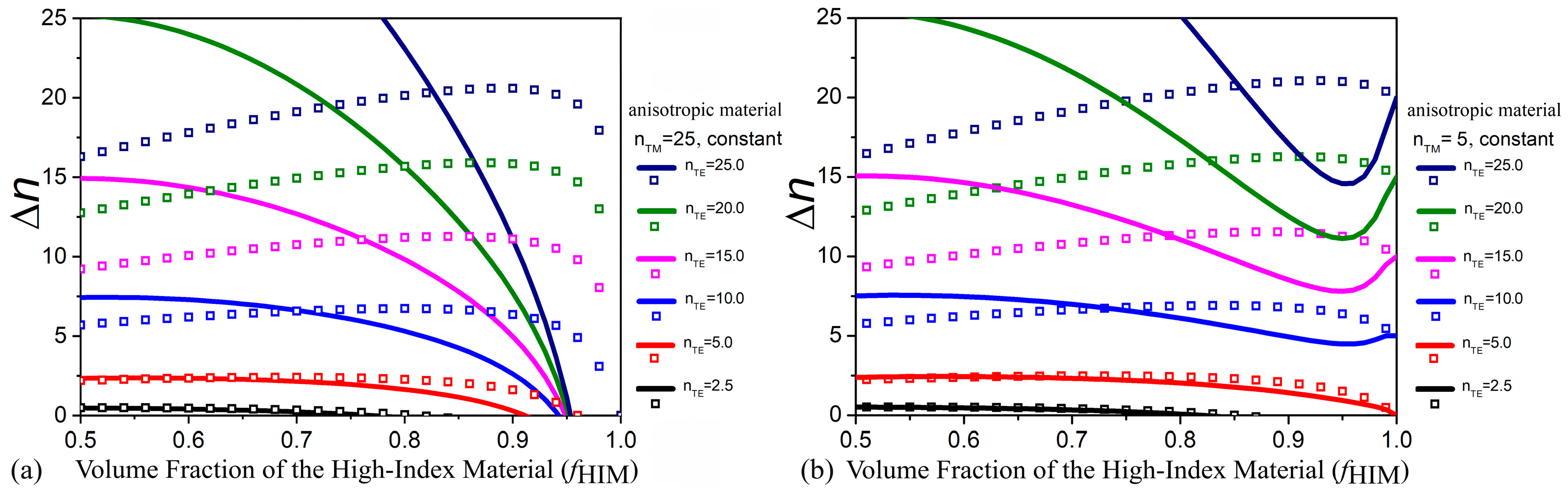
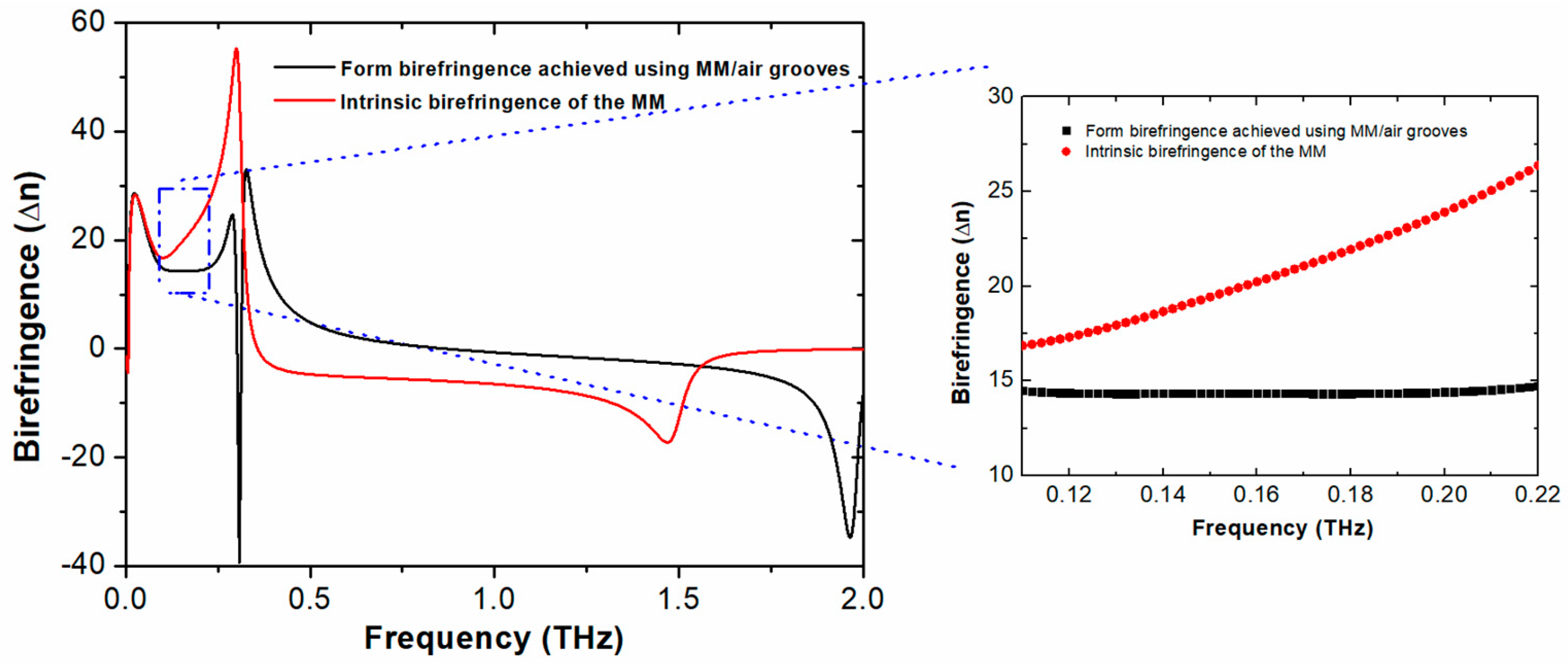
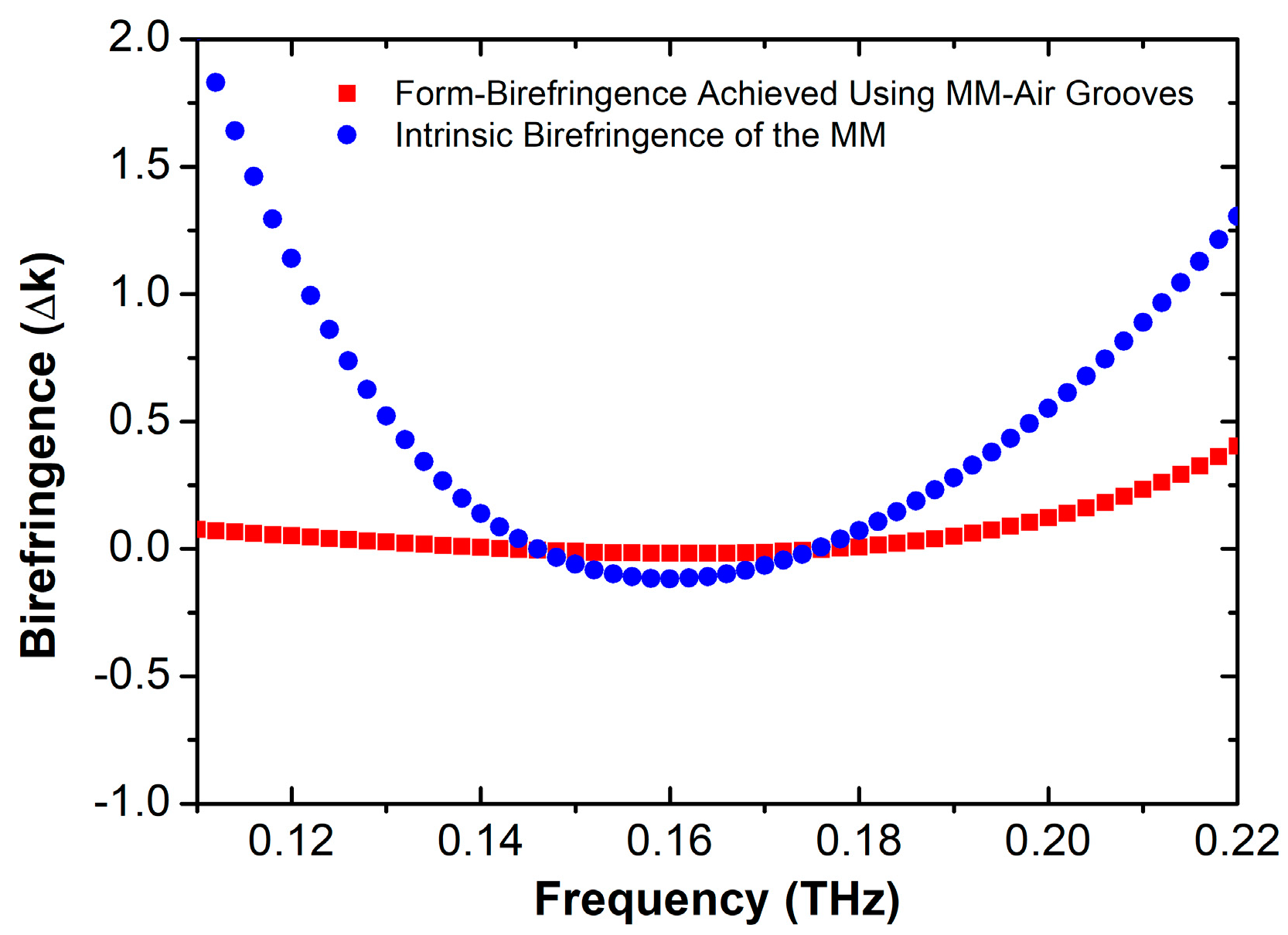
3.4. Birefringence Properties of the Proposed Hybrid Material
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Mantsch, H.H.; Naumann, D. Terahertz spectroscopy: The renaissance of far infrared spectroscopy. J. Mol. Struct. 2010, 964, 1–4. [Google Scholar] [CrossRef]
- Leitenstorfer, A.; Moskalenko, A.S.; Kampfrath, T.; Kono, J.; Castro-Camus, E.; Peng, K.; Qureshi, N.; Turchinovich, D.; Tanaka, K.; Markelz, A.G.; et al. The 2023 terahertz science and technology roadmap. J. Phys. D Appl. Phys. 2023, 56, 223001. [Google Scholar] [CrossRef]
- Yang, X.; Zhao, X.; Yang, K.; Liu, Y.; Liu, Y.; Fu, W.; Luo, Y. Biomedical Applications of Terahertz Spectroscopy and Imaging. Trends Biotechnol. 2016, 34, 810–824. [Google Scholar] [CrossRef]
- Jepsen, P.; Cooke, D.; Koch, M. Terahertz spectroscopy and imaging—Modern techniques and applications. Laser Photonics Rev. 2011, 5, 124–166. [Google Scholar] [CrossRef]
- Patil, M.R.; Ganorkar, S.B.; Patil, A.S.; Shirkhedkar, A.A. Terahertz Spectroscopy: Encoding the Discovery, Instrumentation, and Applications toward Pharmaceutical Prospectives. Crit. Rev. Anal. Chem. 2020, 52, 343–355. [Google Scholar] [CrossRef]
- Piccirillo, B.; Paparo, D.; Rubano, A.; Andreone, A.; Conti, M.R.; Giove, D.; Vicuña-Hernández, V.; Koral, C.; Masullo, M.R.; Mettivier, G.; et al. Liquid Crystal-Based Geometric Phase-Enhanced Platform for Polarization and Wavefront Analysis Techniques with the Short-TeraHertz FEL Oscillator TerRa@BriXSinO. Symmetry 2022, 15, 103. [Google Scholar] [CrossRef]
- Koral, C.; Mazaheri, Z.; Papari, G.P.; Andreone, A.; Drebot, I.; Giove, D.; Masullo, M.R.; Mettivier, G.; Opromolla, M.; Paparo, D.; et al. Multi-Pass Free Electron Laser Assisted Spectral and Imaging Applications in the Terahertz/Far-IR Range Using the Future Superconducting Electron Source BriXSinO. Front. Phys. 2022, 10, 725901. [Google Scholar] [CrossRef]
- Först, M.; Hoffmann, M.C.; Dienst, A.; Kaiser, S.; Rini, M.; Tobey, R.I.; Gensch, M.; Manzoni, C.; Cavalleri, A. THz Control in Correlated Electron Solids: Sources and Applications. In Terahertz Spectroscopy and Imaging; Springer: Berlin/Heidelberg, Germany, 2013; pp. 611–631. [Google Scholar] [CrossRef]
- Yang, H.; Zheng, S.; He, W.; Yu, X.; Zhang, X. Terahertz orbital angular momentum: Generation, detection and communication. China Commun. 2021, 18, 131–152. [Google Scholar] [CrossRef]
- Wang, H.; Song, Q.; Cai, Y.; Lin, Q.; Lu, X.; Shangguan, H.; Ai, Y.; Xu, S. Recent advances in generation of terahertz vortex beams and their applications. Chin. Phys. B 2020, 29, 097404. [Google Scholar] [CrossRef]
- Fickler, R.; Lapkiewicz, R.; Plick, W.N.; Krenn, M.; Schaeff, C.; Ramelow, S.; Zeilinger, A. Quantum entanglement of high angular momenta. Science 2012, 338, 640–643. [Google Scholar] [CrossRef] [PubMed]
- Gibson, G.; Courtial, J.; Padgett, M.J.; Vasnetsov, M.; Pas’ko, V.; Barnett, S.M.; Franke-Arnold, S. Free-space information transfer using light beams carrying orbital angular momentum. Opt. Express 2004, 12, 5448–5456. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Li, X.; Gao, Y.; Wang, H.; Cheng, Y. Microwave imaging of spinning object using orbital angular momentum. J. Appl. Phys. 2017, 122, 124903. [Google Scholar] [CrossRef]
- Park, G.S.; Kim, Y.H.; Han, H.; Han, J.K.; Ahn, J.; Son, J.H.; Park, W.Y.; Jeong, Y.U. Convergence of Terahertz Sciences in Biomedical Systems; Springer: Dordrecht, The Netherlands, 2012; pp. 1–435. [Google Scholar] [CrossRef]
- Watanabe, S. Terahertz polarization imaging and its applications. Photonics 2018, 5, 58. [Google Scholar] [CrossRef]
- Nowack, T.S.; Shah, Y.D.; Escorcia, I.; Grant, J.P.; Kenney, M.; Pusino, V.; Faccio, D.; Wasige, E.; Cumming, D.R.S. Terahertz polarimetry with a monolithic metasurface. Opt. Lett. 2022, 47, 4199–4202. [Google Scholar] [CrossRef]
- Mazaheri, Z.; Koral, C.; Andreone, A. Accurate THz ellipsometry using calibration in time domain. Sci. Rep. 2022, 12, 7342. [Google Scholar] [CrossRef]
- Liu, M.; Li, M.; Jiang, C.; Yan, X.; Wan, Y. Research progress on high birefringence terahertz photonic crystal fibers. Laser Optoelectron. Prog. 2017, 54, 090006. [Google Scholar] [CrossRef]
- Wang, L.; Xiao, R.-W.; Ge, S.-J.; Shen, Z.-X.; Lü, P.; Hu, W.; Lu, Y.-Q. Research progress of terahertz liquid crystal materials and devices. Wuli Xuebao/Acta Phys. Sin. 2019, 68, 084205. [Google Scholar] [CrossRef]
- Wiesauer, K.; Jördens, C. Recent advances in birefringence studies at THz frequencies. J. Infrared Millim. Terahertz Waves 2013, 34, 663–681. [Google Scholar] [CrossRef]
- Ma, Y.; Shan, Y.; Cheng, Y.; Yang, R.; Kwok, H.-S.; Zhao, J. The Birefringence and Extinction Coefficient of Ferroelectric Liquid Crystals in the Terahertz Range. Photonics 2023, 10, 1368. [Google Scholar] [CrossRef]
- Hsieh, C.-F.; Lai, Y.-C.; Pan, R.-P.; Pan, C.-L. Polarizing terahertz waves with nematic liquid crystals. Opt. Lett. 2008, 33, 1174–1176. [Google Scholar] [CrossRef]
- Vieweg, N.; Shakfa, M.; Koch, M. BL037: A nematic mixture with high terahertz birefringence. Opt. Commun. 2011, 284, 1887–1889. [Google Scholar] [CrossRef]
- Sun, L.; Huang, L.; Wang, Y.; Lian, Y.; Huang, G.; Zhao, H.; Zheng, K. Ultra-Low Loss Graphene Plasmonic Waveguide for Chip-Scale Terahertz Communication. IEEE Photonics J. 2021, 13, 4800706. [Google Scholar] [CrossRef]
- Chen, M.; Sheng, P.; Sun, W.; Cai, J. A symmetric terahertz graphene-based hybrid plasmonic waveguide. Opt. Commun. 2016, 376, 41–46. [Google Scholar] [CrossRef]
- Massaro, A.; Cingolani, R.; De Vittorio, M.; Passaseo, A. Bragg reflector by means of the form birefringence effect in dielectric rings. Superlattices Microstruct. 2010, 47, 219–224. [Google Scholar] [CrossRef]
- Koral, C.; Mazaheri, Z.; Andreone, A. THz Multi-Mode Q-Plate with a Fixed Rate of Change of the Optical Axis Using Form Birefringence. Micromachines 2022, 13, 796. [Google Scholar] [CrossRef]
- Scherger, B.; Scheller, M.; Vieweg, N.; Cundiff, S.T.; Koch, M. Paper terahertz wave plates. Opt. Express 2011, 19, 24884–24889. [Google Scholar] [CrossRef]
- Wu, C.-J.; Chen, M.-S.; Yang, T.-J. Photonic band structure for a superconductor-dielectric superlattice. Phys. C Supercond. Its Appl. 2005, 432, 133–139. [Google Scholar] [CrossRef]
- Aly, A.H.; Ryu, S.-W.; Hsu, H.-T.; Wu, C.-J. THz transmittance in one-dimensional superconducting nanomaterial-dielectric superlattice. Mater. Chem. Phys. 2009, 113, 382–384. [Google Scholar] [CrossRef]
- Zhang, B.; Gong, Y. Achromatic terahertz quarter waveplate based on silicon grating. Opt. Express 2015, 23, 14897–14902. [Google Scholar] [CrossRef]
- Koral, C.; Mazaheri, Z.; Andreone, A. A Large Area Wide Bandwidth THz Phase Shifter Plate for High Intensity Field Applications. Photonics 2023, 10, 825. [Google Scholar] [CrossRef]
- Xiao, S.; Wang, T.; Liu, T.; Zhou, C.; Jiang, X.; Zhang, J. Active metamaterials and metadevices: A review. J. Phys. D Appl. Phys. 2020, 53, 503002. [Google Scholar] [CrossRef]
- Ali, A.; Mitra, A.; Aïssa, B. Metamaterials and Metasurfaces: A Review from the Perspectives of Materials, Mechanisms and Advanced Metadevices. Nanomaterials 2022, 12, 1027. [Google Scholar] [CrossRef] [PubMed]
- Kumar, N.S.; Naidu, K.C.B.; Banerjee, P.; Babu, T.A.; Reddy, B.V.S. A review on metamaterials for device applications. Crystals 2021, 11, 518. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect metamaterial absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Bağci, F. A Terahertz Metamaterial Absorber-Based Temperature Sensor Having Nine Resonance Peaks. Gazi Univ. J. Sci. 2021, 34, 1163–1177. [Google Scholar] [CrossRef]
- Bagci, F.; Medina, F. Design of a wide-angle, polarization-insensitive, dual-band metamaterial-inspired absorber with the aid of equivalent circuit model. J. Comput. Electron. 2017, 16, 913–921. [Google Scholar] [CrossRef]
- Burokur, S.N.; Sellier, A.; Kanté, B.; de Lustrac, A. Symmetry breaking in metallic cut wire pairs metamaterials for negative refractive index. Appl. Phys. Lett. 2009, 94, 201111. [Google Scholar] [CrossRef]
- Valentine, J.; Zhang, S.; Zentgraf, T.; Ulin-Avila, E.; Genov, D.A.; Bartal, G.; Zhang, X. Three-dimensional optical metamaterial with a negative refractive index. Nature 2008, 455, 376–379. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, C.; Sun, S.; Yi, N.; Gao, Y.; Song, Q.; Xiao, S. Polarization-independent metamaterial with broad ultrahigh refractive index in terahertz region. Opt. Mater. Express 2015, 5, 1949–1953. [Google Scholar] [CrossRef]
- Choi, M.; Lee, S.H.; Kim, Y.; Kang, S.B.; Shin, J.; Kwak, M.H.; Kang, K.-Y.; Lee, Y.-H.; Park, N.; Min, B. A terahertz metamaterial with unnaturally high refractive index. Nature 2011, 470, 369–373. [Google Scholar] [CrossRef]
- Jing, X.; Gui, X.; Xia, R.; Hong, Z. Ultrabroadband Unnaturally High Effective Refractive Index Metamaterials in the Terahertz Region. IEEE Photonics J. 2017, 9, 59001077. [Google Scholar] [CrossRef]
- Konstantinidis, K.; Feresidis, A.P. Broadband near-zero index metamaterials. J. Opt. 2015, 17, 105104. [Google Scholar] [CrossRef]
- Jiang, L.; Fang, B.; Yan, Z.; Fan, J.; Qi, C.; Liu, J.; He, Y.; Li, C.; Jing, X.; Gan, H.; et al. Terahertz high and near-zero refractive index metamaterials by double layer metal ring microstructure. Opt. Laser Technol. 2020, 123, 105949. [Google Scholar] [CrossRef]
- Min, L.; Huang, L.-R.; Sun, R.; Xi, M.-M.; Li, Z.-W. Dual Metamaterial with Large Birefringence. IEEE Photonics J. 2015, 7, 4600608. [Google Scholar] [CrossRef]
- Jing, X.; Xia, R.; Gui, X.; Wang, W.; Tian, Y.; Zhu, D.; Shi, G. Design of ultrahigh refractive index metamaterials in the terahertz regime. Superlattices Microstruct. 2017, 109, 716–724. [Google Scholar] [CrossRef]
- Smith, D.R.; Schultz, S.; Markoš, P.; Soukoulis, C.M. Determination of effective permittivity and permeability of metamaterials from reflection and transmission coefficients. Phys. Rev. B—Condens. Matter Mater. Phys. 2002, 65, 195104. [Google Scholar] [CrossRef]
- Markos, P.; Soukoulis, C. Transmission properties and effective electromagnetic parameters of double negative metamaterials. Opt. Express 2003, 11, 649–661. [Google Scholar] [CrossRef]
- Chen, X.; Grzegorczyk, T.M.; Wu, B.-I.; Pacheco, J.J.; Kong, J.A. Robust method to retrieve the constitutive effective parameters of metamaterials. Phys. Rev. E—Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 2004, 70, 016608. [Google Scholar] [CrossRef]
- Scheller, M.; Jördens, C.; Koch, M. Terahertz form birefringence. Opt. Express 2010, 18, 10137–10142. [Google Scholar] [CrossRef]
- Neff, C.W.; Summers, C.J. A photonic crystal superlattice based on triangular lattice. Opt. Express 2005, 13, 3166–3173. [Google Scholar] [CrossRef]
- Hernandez-Serrano, A.I.; Castro-Camus, E.; Lopez-Mago, D. q-plate for the Generation of Terahertz Cylindrical Vector Beams Fabricated by 3D Printing. J. Infrared Millim. Terahertz Waves 2017, 38, 938–944. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koral, C.; Bagci, F. A Hybrid Design for Frequency-Independent Extreme Birefringence Combining Metamaterials with the Form Birefringence Concept. Photonics 2024, 11, 860. https://doi.org/10.3390/photonics11090860
Koral C, Bagci F. A Hybrid Design for Frequency-Independent Extreme Birefringence Combining Metamaterials with the Form Birefringence Concept. Photonics. 2024; 11(9):860. https://doi.org/10.3390/photonics11090860
Chicago/Turabian StyleKoral, Can, and Fulya Bagci. 2024. "A Hybrid Design for Frequency-Independent Extreme Birefringence Combining Metamaterials with the Form Birefringence Concept" Photonics 11, no. 9: 860. https://doi.org/10.3390/photonics11090860
APA StyleKoral, C., & Bagci, F. (2024). A Hybrid Design for Frequency-Independent Extreme Birefringence Combining Metamaterials with the Form Birefringence Concept. Photonics, 11(9), 860. https://doi.org/10.3390/photonics11090860





