Abstract
Free-space optical (FSO) communication has received widespread attention as a high-bandwidth, low-latency communication technique. However, the scintillation effect caused by atmospheric turbulence leads to intensity fluctuations of the transmission signal, which, in turn, affects the performance of the FSO communication system. This paper proposes a channel correlation-based adaptive power transmission for FSO communications. Based on the correlation between uplink and downlink turbulence channels, the power of the reverse transmission signal is adjusted by the fluctuation strength of the received uplink or downlink transmission signal and the channel correlation coefficient to improve the system’s performance. The proposed technique is investigated through a simulation using established uplink and downlink channels with different link distances and turbulence intensities. The simulation results show that the bit error rate (BER) performance of the proposed technique is significantly improved compared to the fixed threshold decision (FTD) technique, and it is close to the adaptive threshold decision (ATD) technique. The proposed technique provides an effective optimization scheme for FSO communications.
1. Introduction
Free-space optical (FSO) communication, as a cutting-edge technique for high-speed data transmission, is gradually becoming an important choice for solving modern communication needs [1]. It uses light waves to transmit information in free space, which can achieve high data rate transmission and also has a large bandwidth, and it is widely used in the fields of satellite communication, unmanned aerial vehicle (UAV) communication, and military security communication. Although the advantages of FSO communication are significant, many challenges are also faced, among which the effect of atmospheric turbulence is particularly noticeable [2]. The atmospheric turbulence is the irregular movement of airflow in the atmosphere, which is mainly caused by the inhomogeneity of temperature and humidity distribution [3]. The transmission optical signal attenuation, distortion, and even positional drift are caused by atmospheric turbulence [4]. Therefore, the suppression of the turbulence scintillation effect is becoming one of the critical research directions to improve the stability and reliability of FSO communication systems.
Many techniques have been investigated to dampen the effects of atmospheric turbulence. The aperture averaging technique is applied to mitigate the atmospheric scintillation due to its relative simplicity and straightforwardness. Ref. [5] deployed aperture averaging receivers at the relay and destination sides to reduce the variance of intensity fluctuations. However, a larger aperture receiver is more susceptible to scattering and absorption in the atmosphere, which leads to increased signal attenuation. Also, a higher level of alignment accuracy is required. Refs. [6,7] studied the multiple-input multiple-output (MIMO) diversity technique, and the efficiency of the system was improved with the increase in the number of transmitters and receivers. However, it is difficult to deploy multiple transmitters and receivers due to the rise in physical size and complexity of the system. Ref. [8] installed an optical spatial filter (OSF) at the focus of the receiver lens to improve the strength of the received signal and remove unwanted higher-order modes and noises. However, some of the light energy is blocked or scattered during processing, which results in an optical loss. In addition, an unstable or ineffective filtering effect may be caused if the stability of the light source is poor. Ref. [9] investigated an adaptive optics (AO) architecture that detects and corrects optical wavefront aberrations caused by atmospheric turbulence. However, AO systems usually contain multiple high-precision components, which are more complex to integrate and debug. Ref. [10] proposed a scheme for the use of an electrical equalizer on the receiver. The electrical equalizer is mainly used to compensate for distortions introduced during signal transmission. However, complex algorithms and a large amount of computational resources are required to obtain highly accurate equalization results. The fixed threshold decision (FTD) technique is utilized for its simple algorithms and faster processing of the received optical signals. The received signal is decided by setting a fixed threshold value. However, the FTD technique is unable to automatically adapt to signal fluctuations due to changing channel environments [11]. The signal is decided bit by bit with a dynamically adjusted threshold based on channel state information (CSI) in the adaptive threshold decision (ATD) technique [12]. However, it is highly dependent on the accuracy of the CSI.
In recent years, the adaptive power transmission technique has been widely studied to mitigate the scintillation effect for its greater flexibility and adaptability. Moreover, a certain degree of correlation is presented between the uplink and downlink turbulence channels. The channel correlation coefficient is an important measure of the correlation between signal propagation paths in FSO communication [13,14]. The degree of similarity in the phase and amplitude of the signal between different transmission paths is reflected by the value of the channel correlation coefficient. A high channel correlation coefficient means that the channel characteristics are similar between the different links, and the opposite indicates a large difference in channel characteristics. Therefore, the channel correlation coefficient is used as a reference metric to adjust the power of the reverse transmission signal to simplify the system design and increase the transmission efficiency in the proposed technique.
In this study, we propose a channel correlation-based adaptive power transmission for FSO communications, which aims to achieve the compensation of the turbulence scintillation effect. The signal power at the transmitting end of the reverse transmission is dynamically adjusted based on the fluctuation strength of the received uplink or downlink transmission signal and the channel correlation coefficient between the uplink and downlink. The uplink and downlink channels with different link distances and turbulence intensities are established. To validate the effectiveness of the proposed technique, the proposed adaptive power transmission technique was compared to the conventional FTD and ATD techniques. The simulation results illustrated that the bit error rate (BER) performance of the proposed technique was significantly enhanced compared to the FTD technique, and it was close to the ATD technique in different transmission conditions. The turbulence scintillation effect was effectively compensated for.
2. Theoretical Analysis
The theoretical analysis is divided into two sections. The mathematical model of the turbulence channel is described in detail in Section 2.1, and the operation principle of the proposed adaptive power transmission technique is elaborated in Section 2.2.
2.1. Channel Model
The quality of signal transmission is often challenged in the turbulence channel. At the receiver side, the signal power instability is faced. In particular, the transmission performance of the FSO communication system is directly affected, which is more significant in high-speed data transmission and long-distance communication. The effect of atmospheric turbulence on signal strength can be described by the Rytov variance , and is given by
where is the Hufnagel–Valley model-based atmospheric refractive index structure constant, is the wave number, and is the link distance. The atmospheric refractive index structure constant is given by
where is the wind speed, is the altitude, and is the atmospheric refractive index structure constant at the surface. Moreover, the scintillation effect caused by atmospheric turbulence gradually increases as grows. The scintillation index is used to measure the magnitude of the scintillation effect and the degree of signal fluctuation [15,16]. The large scintillation index is accompanied by great signal fluctuations, and is represented by
where is the fluctuation intensity of the transmission signal and is the ensemble mean value. The lognormal distribution model is employed in this study. Figure 1 illustrates the probability density function (PDF) of the modeled turbulence channel with of 0.37 and 0.5, which coincides with the lognormal distribution, and the PDF is expressed by
where and are the mean and standard deviation of the lognormal distribution. A greater turbulence intensity usually implies a larger standard deviation in the PDF, which leads to a wider fluctuation range and more violent light intensity fluctuation.
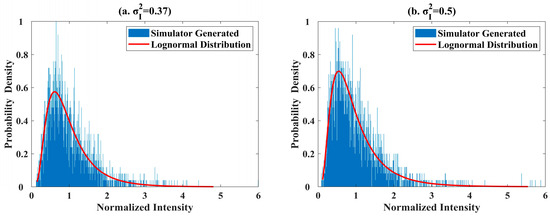
Figure 1.
Probability density function of the modeled turbulence channel. (a) = 0.37, (b) = 0.5.
2.2. Operation Principle
Figure 2 presents the block diagram of the proposed adaptive power transmission technique. In order to visually and efficiently adjust the signal power, non-return-to-zero on-off-keying (NRZ-OOK) modulation is used, which expresses bit ‘1’ or bit ‘0’ by the level of light intensity. The channel correlation coefficient is extracted based on the signal’s fluctuation intensities after passing through the uplink and downlink turbulence channels, and is given by
where and are the fluctuation intensities of the uplink and downlink transmission signal through the turbulence channels, respectively; is the covariance between and ; and are standard deviations of and , respectively [17]. In a real system, a feedback path needs to be added between the transmitter and the receiver to feedback the signal’s fluctuation intensities for extracting the channel correlation coefficient. Then, the power of the reverse transmission signal is adjusted, and the adjusted power is expressed by
where is the maximum allowable transmitting power, is an adaptation factor obtained from the fluctuation strength of the received uplink or downlink transmission signal, is the initial transmitting power, and is the minimum value taken from and . The modulated optical NRZ-OOK signal after a power adjustment is emitted into the turbulence channel by a 1550 nm wavelength laser diode (LD) for reverse transmission. At the receiving end of the reverse transmission, the photodiode (PD) detects the transmitted optical signal and performs photoelectric conversion. The received electrical signal after PD is represented by
where is the transmitted NRZ-OOK signal after a power adjustment, and is the average noise power comprising PD and background noise. The different signal-to-noise ratio (SNR) values are used to indicate the magnitude of noise, and it is given by
where and are the effective power of the signal and noise, respectively [18]. The FTD technique is used to identify the signal. A fixed threshold is set at the receiver side in the FTD technique compared to the ATD technique, which dynamically adjusts the decision threshold bit-by-bit based on the CSI. The bit ‘1’ is determined when the signal level is above the set threshold, and the bit ‘0’ is determined when it is below the set threshold. Ultimately, the BER is computed to evaluate the performance of the proposed adaptive power technique, and it is expressed by
where is the PDF of , and is the Q-function [19].
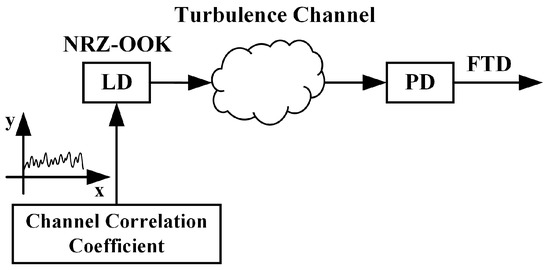
Figure 2.
Block diagram of the proposed adaptive power transmission technique. LD: laser diode; PD: photodiode; FTD: fixed threshold decision.
3. Simulations and Results
The proposed technique was evaluated through a simulation. The different link distances and turbulence intensities were used to reduce the chance of the experimental results. The parameters of the LD used for simulation are shown in Table 1. The additive white gaussian noise (AWGN) was considered when detecting the optical signal using PD, and other parameters will be discussed in future research.

Table 1.
Parameters of the LD.
Figure 3 illustrates the time domain fluctuations of the signal when passing through the uplink and downlink turbulence channel with different turbulence intensities for a 30 km FSO link. Figure 3a shows the time domain fluctuations of the uplink and downlink transmissions with of 0.37 and 0.15, respectively. Figure 3b shows the time domain fluctuations of the uplink and downlink transmissions with of 0.5 and 0.2, respectively. Figure 3c shows the time domain fluctuations of the uplink and downlink transmissions with of 0.65 and 0.28, respectively. When establishing the uplink and downlink turbulence channels, the single random normal distribution function is employed to generate the normal-distribution random sequence to ensure the reliability of the simulation results. This is due to the relatively high correlation that occurs between uplink and downlink turbulence channels at short-distance transmissions [20]. And as a result, there is a difference in the fluctuation strength propagated through the same region of the atmosphere for the established uplink and downlink turbulence channels in the case of alignment. The signal fluctuation during uplink transmission is noticeably higher than those during downlink transmission, which is due to the difference in link geometry [21]. The optical signal suffers from atmospheric turbulence at the initial stage during uplink transmission, which results in the distortion, scattering, and attenuation of the beam. During a downlink transmission, the optical signal is transmitted from a high altitude downwards. Although the optical signal is also affected by atmospheric turbulence at the end of the transmission route, since it is transported in a relatively stable atmosphere for most of the time, it is probably relatively slightly affected by turbulence. Therefore, it is known that , , and of the uplink are larger than those of the downlink according to Equations (1) and (4). Thus, the uplink exponential parameter and downlink exponential parameter are generated using a normal-distribution random sequence with and . Then, the exponential transformation is conducted on the uplink and downlink exponential parameters, and the exponentially transformed data are resampled to generate the intensity fluctuated signal and for uplink and downlink turbulence channels, respectively. The sampling frequency was set to 20 MHz because the data rate was configured as 10 Mbps. The BER was reduced due to the turbulence scintillation effect for both uplink and downlink transmissions. But there was a correlation between different uplink and downlink turbulence channels. Therefore, a channel correlation-based adaptive power transmission technique is proposed to mitigate the turbulence scintillation effect.
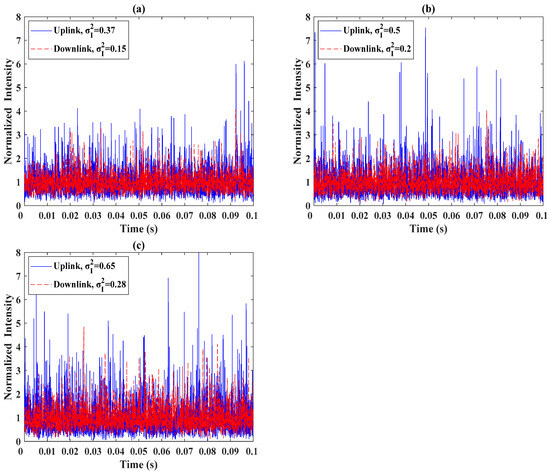
Figure 3.
Time domain fluctuations of the signal when passing through the uplink and downlink turbulence channels with different turbulence intensities for a 30 km FSO link. (a) Uplink and downlink with of 0.37 and 0.15, respectively; (b) uplink and downlink with of 0.5 and 0.2, respectively; (c) uplink and downlink with of 0.65 and 0.28, respectively.
Table 2 demonstrates the channel correlation coefficients between the uplink and downlink for different link distances and turbulence intensities. The channel correlation coefficient is variable due to the change in the channel environment, and even if the signal is transmitted in the same channel, the channel correlation coefficient is different. This is due to the random characteristics of the background and PD noise during signal transmission, which leads to the difference in the received signal fluctuation intensity. It is easily observed that the correlation coefficient between the uplink and downlink decreases with the increase in .

Table 2.
Channel correlation coefficients between the uplink and downlink for different link distances and turbulence intensities.
Figure 4 and Figure 5 demonstrate the comparison of the BER performance of the proposed technique with FTD and ATD techniques under different turbulence intensities for 30 km and 40 km FSO links, respectively. This paper focuses on the BER performance of the proposed technique for distance transmissions of 30 km and 40 km. The BER performance of the proposed technique at shorter transmission distances will be discussed in a subsequent study. Figure 4a and Figure 5a illustrate the comparison of the BER performance of the three techniques for uplink transmission. Figure 4b and Figure 5b present the comparison of the BER performance of the three techniques for downlink transmission. It is obviously seen that the BER performance of the proposed technique is significantly better than the FTD technique, and it is close to the ATD technique under different link distances and turbulence intensities. The FTD technique uses the same threshold to determine the received signal, and it is unable to more accurately determine the received signal with unstable power due to changes in channel conditions. The BER floor remains flat even if the SNR is high. Therefore, the proposed adaptive power transmission technique is investigated, and it is easier to decide the signal at the receiving end by the FTD technique. The reason is that the detected optical power at the receiving end is improved by adapting the power of the transmitted signal. As shown in Figure 3, although a correlation is observed between the corresponding uplink and downlink turbulence channels, there is a difference in the time domain fluctuations during uplink and downlink signal transmissions. And the proposed technique is not able to cope well with the severe signal strength degradation within the channel at certain moments due to the limitation of the transmitted power. However, the ATD technique is able to adapt better to different channel conditions by dynamically adjusting the threshold at the receiver side via CSI. Therefore, the BER of the proposed technique is lower than the BER of the ATD technique. But the CSI used in the ATD technique is the comprehensive description of the whole channel state, including the information of signal scattering, environmental fading, distance decay, etc., which makes it difficult to obtain the accurate CSI in a real system. In contrast, the signal fluctuation strength is a relatively simple measurement that directly reflects the power level of the received signal. The proposed technique combines signal fluctuation strength and channel correlation coefficient to improve the transmitted power, which reduces the system complexity and improves the system energy efficiency. In addition, the BER performance of the uplink transmission is more similar to the BER of the ATD technique compared to the downlink transmission. This is because the uplink transmission is usually subject to greater signal fluctuations caused by atmospheric turbulence. The BER performance of the uplink transmission is more easily improved by adjusting the power of the transmission signal. Therefore, the proposed adaptive power transmission technique effectively compensates for the turbulence scintillation effect, and it needs to be further studied in the future.
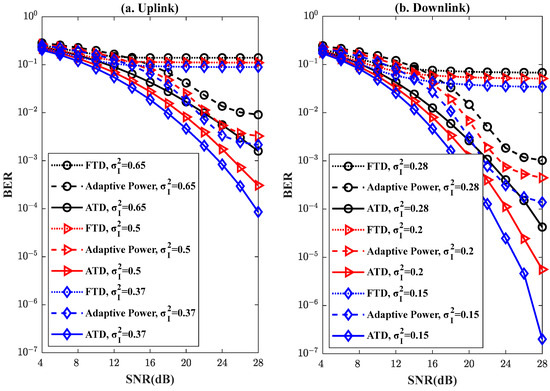
Figure 4.
Comparison of the BER performance of the proposed technique with FTD and ATD techniques under different turbulence intensities for a 30 km FSO link. (a) Uplink transmission, (b) downlink transmission.
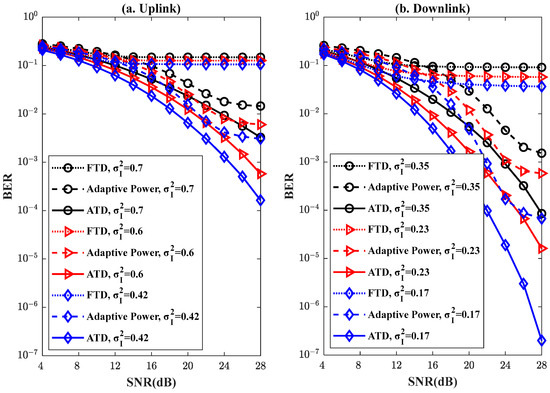
Figure 5.
Comparison of the BER performance of the proposed technique with FTD and ATD techniques under different turbulence intensities for a 40 km FSO link. (a) Uplink transmission, (b) downlink transmission.
4. Conclusions
In conclusion, a channel correlation-based adaptive power transmission is proposed by deeply analyzing the correlation between uplink and downlink turbulence channels for FSO communications. The power of the reverse transmission signal is dynamically adjusted according to the fluctuation strength of the received uplink or downlink transmission signal and the channel correlation coefficient between the uplink and downlink. The uplink and downlink channels with different link distances and turbulence intensities were modeled. The BER performance of the proposed technique was compared to the FTD and ATD techniques to verify the reliability of the proposed technique. Simulation results showed that the proposed technique had a significant improvement compared to the FTD technique, and it was close to the ATD technique. Therefore, it is a promising technique for FSO communication systems.
Author Contributions
Conceptualization, B.-S.Z.; Formal analysis, P.-F.L. and B.-S.Z.; Data curation, P.-F.L. and Y.-Q.H.; Project administration, B.-S.Z.; Writing—original draft preparation, P.-F.L. and B.-S.Z.; Writing—review and editing, B.-S.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the Educational Department of Liaoning Province General. Program (JYTMS20231214).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Dataset available on request from the authors.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Al-Gailani, S.A.; Salleh, M.F.M.; Salem, A.A.; Shaddad, R.Q.; Sheikh, U.U.; Algeelani, N.A.; Almohamad, T.A. A Survey of Free Space Optics (FSO) Communication Systems, Links, and Networks. IEEE Access 2021, 9, 7353–7373. [Google Scholar] [CrossRef]
- Samy, R.; Yang, H.-C.; Rakia, T.; Alouini, M.-S. Space-Air-Ground FSO Networks for High-Throughput Satellite Communications. IEEE Commun. Mag. 2022, 60, 82–87. [Google Scholar] [CrossRef]
- Esmail, M.A. Experimental performance evaluation of weak turbulence channel models for FSO links. Opt. Commun. 2021, 486, 126776. [Google Scholar] [CrossRef]
- Kaushal, H.; Kaddoum, G. Optical communication in space: Challenges and mitigation techniques. IEEE Commun. Surv. Tutor. 2017, 19, 57–96. [Google Scholar] [CrossRef]
- Sharma, P.K.; Bansal, A.; Garg, P.; Tsiftsis, T.; Barrios, R. Relayed FSO communication with aperture averaging receivers and misalignment errors. IET Commun. 2017, 11, 45–52. [Google Scholar] [CrossRef]
- Israr, A.; Israr, A.; Khan, F.; Khan, F. Optimal modulation technique for MIMO FSO link. Wirel. Pers. Commun. 2019, 109, 695–714. [Google Scholar] [CrossRef]
- Hasan, S.M.A.; Ahmed, S.; Islam, A.K.M.N. Simulation of A Massive MIMO FSO System Under Atmospheric Turbulence. In Proceedings of the 2021 5th International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Dhaka, Bangladesh, 18–20 November 2021. [Google Scholar]
- Darusalam, U.; Priambodo, P.S.; Rahardjo, E.T. SNR and BER performance enhancement on FSO induced by atmospheric turbulence using optical spatial filter. Int. J. Opt. Appl. 2015, 5, 51–57. [Google Scholar]
- Mao, H.; Zhong, J.; Yu, S.; Xiao, P.; Yang, X.; Lu, G. An Atmospheric Turbulence Compensation Algorithm Based on FSM-DM Cascaded AO Architecture for FSO Communications. Network 2022, 2, 270–287. [Google Scholar] [CrossRef]
- Nguyen, D.-N.; Zvanovec, S.; Ghassemlooy, Z. Mitigation of dispersion and turbulence in a hybrid optical fibre and free-space optics link using electronic equalisation. Optik 2019, 196, 163154. [Google Scholar] [CrossRef]
- Choi, J.-Y.; Lee, J.-W.; Han, S.-K. Stochastic Approximation Aided Adaptive Thresholding for Optical Detection in PAM4 Based FSO Transmission. IEEE Access 2021, 9, 106451–106458. [Google Scholar] [CrossRef]
- Jing, Q.-W.; Hong, Y.-Q.; Liu, M.-F. RZ-PPM impulse tone-based CSI estimation for adaptive threshold decision in FSO communications. Microw. Opt. Technol. Lett. 2024, 66, e34239. [Google Scholar] [CrossRef]
- Chen, Z.; Yu, S.; Wang, T.; Wu, G.; Wang, S.; Gu, W. Channel correlation in aperture receiver diversity systems for free-space optical communication. J. Opt. 2012, 14, 125710. [Google Scholar] [CrossRef]
- Priyadarshani, R.; Jaiswal, A.; Bhatnagar, M.R.; Bohata, J.; Zvanovec, S.; Ghassemlooy, Z. Impact of Channel Correlation on Different Performance Metrics of OSSK-Based FSO Systems. IEEE Trans. Wirel. Commun. 2020, 19, 1593–1609. [Google Scholar] [CrossRef]
- Choi, I.-Y.; Shin, W.-H.; Han, S.-K. CSI estimation with pilot tone for scintillation effects mitigation on satellite optical communication. Opt. Commun. 2019, 435, 88–92. [Google Scholar] [CrossRef]
- Lv, P.; Hong, Y.; Jing, Q.; Liu, W. Average SNR Based Adaptive Power Transmission Technique in FSO Links. J. Nav. Aviat. Univ. 2024, 39, 235–240. [Google Scholar]
- Hong, Y.-Q.; Li, G.; Liu, Z.-Y. Optical adaptive power transmission using APC-EDFA for turbulence-tolerant FSO communications. Opt. Express 2021, 29, 23777–23785. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.; Chen, X.; Liu, M.; Hong, Y. Bidirectional Atmospheric Channel Reciprocity-Based Adaptive Power Transmission. Photonics 2023, 10, 1067. [Google Scholar] [CrossRef]
- Navidpour, S.M.; Uysal, M.; Kavehrad, M. BER Performance of Free-Space Optical Transmission with Spatial Diversity. IEEE Trans. Wirel. Commun. 2007, 6, 2813–2819. [Google Scholar] [CrossRef]
- Kwon, D.-H.; Han, S.-K. Optical wireless channel reciprocity-based temporal power allocation technique for FSO communications. Opt. Commun. 2023, 529, 129089. [Google Scholar] [CrossRef]
- Maharjan, N.; Devkota, N.; Kim, B.W. Atmospheric Effects on Satellite–Ground Free Space Uplink and Downlink Optical Transmissions. Appl. Sci. 2022, 12, 10944. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).